View PDF VersionPrevious ArticleNext Article

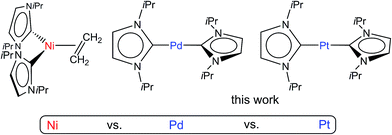
Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C4SC02998D (Edge Article) Chem. Sci., 2015, 6, 1426-1432

Bite-angle bending as a key for understanding group-10 metal reactivity of d10-[M(NHC)2] complexes with sterically modest NHC ligands†‡

Florian Hering a, Jörn Nitsch a, Ursula Paul a, Andreas Steffen a, F. Matthias Bickelhaupt *bc and Udo Radius *a
aInstitut für Anorganische Chemie, Julius-Maximilians-Universität Würzburg, Am Hubland, D-97074 Würzburg, Germany. E-mail: u.radius@uni-wuerzburg.de
bDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling, VU University Amsterdam, De Boelelaan 1083, NL-1081 HV Amsterdam, The Netherlands
cInstitute of Molecules and Materials, Radboud University Nijmegen, Heyendaalseweg 135, NL-6525 AJ Nijmegen, The Netherlands. E-mail: F.M.Bickelhaupt@vu.nl

Received 29th September 2014 , Accepted 3rd December 2014

First published on 3rd December 2014

Abstract

Synthesis, characterization and investigations on the reactivity of the novel metal basic, yet isolable 14 VE NHC-complexes [M0(iPr2Im)2] (M = Pd 3, Pt 4; iPr2Im = 1,3-di-isopropyl-imidazolin-2-ylidene; VE = valence electron; NHC = N-heterocyclic carbene) is reported and compared to the chemistry of the corresponding nickel complex. Quantum chemical analyses reveal that differences in the reactivity of group 10 NHC complexes are caused by differences in the rigidity and thus activation strain associated with bending the corresponding d10-[M(NHC)2] fragments during reaction. These results should have implications for the understanding of the fundamental steps in catalytic cycles, in which such complex fragments are employed.

Introduction

Transition metal-mediated activation and functionalization of element–element bonds is a vital area of homogeneous catalysis research. For low-valent, electron-rich transition metal complexes, bond activation is by and large achieved by either σ-bond metathesis or oxidative addition to a metal center, and especially complexes of d8 transition metals play a crucial role in this chemistry aiming at catalysis.1,2 In the last two decades, N-heterocyclic carbenes (NHCs) have emerged as one of the most important classes of spectator ligands in organometallic chemistry.3 Due to their better σ-donor capabilities compared to tertiary phosphines, the employment of NHCs in transition metal complexes can create more electron-rich metal centers. Complexes stabilized with NHCs are expected to exceed the activity of related phosphine compounds for many applications, and NHC complexes of noble metals have already large impact in the field of catalysis.3 The isolation of unsaturated, metal basic complexes, such as 14 VE (valence electron) species d10-[ML2] or synthons thereof, is highly desirable for investigations concerning the reactivity of NHC complexes and of elementary steps in catalytic cycles as well as for their use in catalysis.

Over the last years we have explored the manifold chemistry of the {Ni(iPr2Im)2} complex fragment (iPr2Im = 1,3-di-isopropyl-imidazolin-2-ylidene), as provided by dinuclear [Ni2(iPr2Im)4(COD)] (COD = 1,5-cyclooctadiene) or mononuclear [Ni(iPr2Im)2(η2-C2H4)] (see Scheme 1), in stoichiometric and catalytic reactions.4 In course of these studies we became more and more interested in synthesizing precursors for [M0(iPr2Im)2] (M = Pd, Pt; see Scheme 1), either complexes [M0(iPr2Im)2] themselves or suitable synthons of them. For M = Ni, a two coordinate complex [M(NHC)2] of iPr2Im is currently unknown.5 Investigations on isolated palladium(0) and especially on platinum(0) complexes bearing two NHC ligands are scarce and mainly involve NHCs with sterically demanding nitrogen substituents.6,7 For palladium, two major pathways for the synthesis of complexes [M(NHC)2] have been established: (i) ligand substitution at [Pd(P{oTol}3)2] (oTol = 2-CH3–C6H4) developed by Herrmann et al.6a and (ii) ligand substitution at dimeric [(Pd(η3-C4H7)Cl)2] in the presence of sodium dimethylmalonate, developed by Caddick and Cloke et al.6b The latter procedure does not require the unappealing synthesis of the [Pd(P{oTol}3)2] precursor,8 but the stoichiometry has to be controlled carefully due to equilibration in solution, since NHC dissociation from palladium seems to be more facile than generally envisioned.6c However, using these methods, complexes such as [Pd(Dipp2Im)2] (Dipp = 2,6-diisopropyl-phenyl), [Pd(Mes2Im)2] (Mes = 2,4,6-trimethyl-phenyl), [Pd(tBu2Im)2], [Pd(Ad2Im)2] (Ad = adamantyl) and of other NHCs with sterically demanding substituents at nitrogen have been prepared.6 Furthermore, synthesis of [Pd(Me2Im)2] via potassium reduction of [Pd(Me2Im)2Cl2] and the characterization of this complex including X-ray analysis has been described lately.6j In course of these studies, it turned out that complexes of the type [Pd(NHC)2] are extremely air sensitive and form isolable peroxo or peroxocarbonate complexes. Isolation of [Pd(iPr2Im)2] has been claimed twice in the literature,6a,j but the NMR data provided are in neither case in accordance with a D2d or D2h type structure of this complex.


image file: c4sc02998d-s1.tif
Scheme 1 {M(iPr2Im)2}-precursors: [Ni(iPr2Im)2(η2-C2H4)] A, [Pd(iPr2Im)2] and [Pt(iPr2Im)2].

The chemistry of isolated complexes [Pt(NHC)2] is virtually unexplored.7 Arduengo et al.7a and Nolan et al.7c described the synthesis of [Pt(Mes2Im)2] and [Pt(Dipp2Im)2] starting from the NHC and [Pt(COD)2] or [Pt(COD)(Me)2], respectively. Intramolecular C–H activation of the ligand was observed for [Pt(Mes2Im)2] in the latter case.7c This procedure seems to be further limited since the use of tBu2Im leads to formation of [Pt(tBu2Im)(tBu2Im)′(H)(Me)2] (′ denotes coordination at the backbone as an “abnormal” NHC). Additionally, Braunschweig et al. reported the synthesis of [Pt(SIMes)2] (SIMes = bis-(mesityl)imidazolidin-2-ylidene) via ligand exchange at [Pt(PCy3)2], whereas the same reaction with tBu2Im led to mixed substituted [Pt(tBu2Im)(PCy3)].7d

Herein, we report the synthesis, spectroscopic and chemical characterization, and quantum chemical analysis of the complexes [Pd(iPr2Im)2] (3) and [Pt(iPr2Im)2] (4).

Results and discussion

Synthesis and characterization of [M0(iPr2Im)2] (M = Pd, Pt)

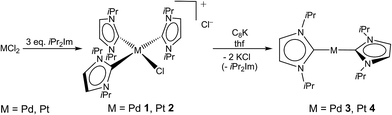
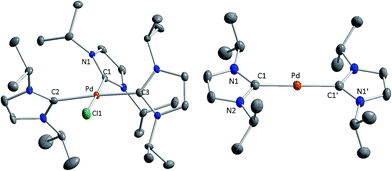
All attempts to isolate the complexes [M0(iPr2Im)2] (M = Pd, Pt) bearing NHC ligands with modest steric demand by the methods introduced above failed in our hands. However, we have found that complexes [M(iPr2Im)3Cl]+Cl− (M = Pd 1, Pt 2; see Scheme 2) are suitable precursors for the synthesis of 3 and 4. Complexes 1 and 2 have been prepared by the reaction of the metal halides MCl2 and three equivalents (or an excess) of the NHC (see Scheme 2).9 The use of K2[PtCl4] instead of PtCl2 as platinum source also leads selectively to [Pt(iPr2Im)3Cl]+Cl− (2). In some instances the formation of the imidazolium salt iPr2Im·HCl as a side product was detected for this reaction. The imidazolium salt and complexes 1 and 2, respectively, are difficult to separate, since these compounds reveal similar solubility in common organic solvents. The NMR spectra of 1 and 2 are those typically observed for a T-shaped alignment of three iPr2Im ligands and a X-ray analysis of 1 confirms the square planar structure with a T-shaped, propeller-like alignment of the three NHCs ligands of the 16 VE cation (see Fig. 1).
image file: c4sc02998d-s2.tif
Scheme 2 Synthesis of [M(iPr2Im)3Cl]+Cl− (M = Pd 1, Pt 2) and [M(iPr2Im)2] (M = Pd 3, Pt 4).

image file: c4sc02998d-f1.tif
Fig. 1 X-ray crystal structure of the cation of [Pd(iPr2Im)3Cl]+Cl− (1; left) and of [Pd(iPr2Im)2] (3; right) in the solid state (ellipsoids set at 50% probability level). Hydrogen atoms have been omitted for clarity. Selected bond lengths (Å) and angles (deg.) for [Pd(iPr2Im)3Cl]+: Pd–Cl1 2.3553(9), Pd–C1 2.0181(34), Pd–C2 2.0590(35), Pd–C3 2.0474(30); Cl1–Pd–C1 178.169(95), C2–Pd–C3 175.967(140). Selected bond lengths (Å) for 1: Pd–C1 2.0231 (18).

The reduction of 1 and 2 with potassium graphite leads in good yields to the two-coordinated complexes [Pd(iPr2Im)2] (3) and [Pt(iPr2Im)2] (4) (see Scheme 2), which were isolated as orange (3) or yellow (4) solids. The release of one equivalent iPr2Im as well as the presence of minor amounts of iPr2Im·HCl does not affect the reaction, since 3 and 4 do not react with additional iPr2Im to afford [M(iPr2Im)3]. For nickel, we have shown earlier that threefold coordination is feasible, as exemplified by the synthesis of [Ni(Me2Im)3] from the reaction of [Ni(COD)2],4c and we have also proof for the existence of [Ni(iPr2Im)3]. For both, 3 and 4, the analytical data are in agreement with a coordination of the metal with two NHC ligands as proposed in Scheme 2. The 1H NMR and 13C{1H} NMR spectra reveal one set of signals for the ligands of each complex comprising a doublet for the isopropyl methyl protons (3: 1.34 ppm, 4: 1.33 ppm), a septet for the isopropyl methine protons (3: 6.03 ppm, 4: 6.26 ppm), and a singlet for the olefinic protons of the backbone (3: 6.46 ppm, 4: 6.40 ppm) in the 1H NMR spectrum. The 195Pt NMR spectrum of 4 shows a resonance at δ = −5943 ppm, which is close to 195Pt NMR shifts reported for other [PtL2] complexes ([Pt(PCy3)2]: −6501 ppm, [Pt(SIMes)(PCy3)]: −6151 ppm, [Pt(tBu2Im)(PCy3)] −6156 ppm, [Pt(SIMes)2]: −5462 ppm vs. [Pt(PPh3)3]: −4583 ppm).7a,d,10

Single crystals of [Pd(iPr2Im)2] (3) suitable for X-ray diffraction have been obtained via slow diffusion of the solvent from a saturated solution of 3 in diethyl ether. The compound crystallizes in the space group P21/c with the palladium atom located on a crystallographically imposed inversion center.

Both imidazole rings of 3 are coplanar arranged, which leads to a D2h symmetric compound with Pd–C bond lengths of 2.0231(18) Å (Fig. 1). However, for steric reasons, a D2d symmetric structure with staggered NHC ligands should be expected. A search on all currently known X-ray crystal structures of d10-[M(NHC)2] complexes reveal that the dihedral angles between the NHC nitrogen and NHC carbene carbon atoms increases for bulky substituents.5a,6,7,11 Calculations on [M(H2Im)2] presented earlier12 predict a D2d type structure also for sterically less demanding NHCs. However, calculations on [M(iPr2Im)2] (M = Ni, Pd, Pt) performed at BP86/def2-TZVPP level (see ESI†) reveal a shallow potential for the rotation of the NHC ligands and differences in energy between a D2d and D2h type structure below 5 kJ mol−1 in favor of a staggered alignment. Thus, we attribute the reason for experimentally observed D2h type symmetry of 3 to packing forces.

Reactivity of [Pt(iPr2Im)2] (4)

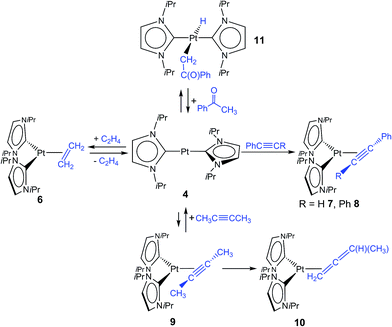
We reported earlier stable NHC nickel η2-olefin, η2-alkyne, and η2-ketone complexes [Ni(iPr2Im)2(η2-C2R4)], [Ni(iPr2Im)2(η2-C2R2)], and [Ni(iPr2Im)(η2-[C with combining low line][O with combining low line]–{O[double bond, length as m-dash]CR1R2})].4 Due to the fact that complexes 3 and 4 did not react with additional NHC in solution, we became interested to investigate reactions of these two-coordinated complexes with π-acceptor ligands such as olefins, alkynes and ketones. In stark contrast to [Ni(iPr2Im)2], its Pd congener 3 merely shows weak interactions with ethylene giving [Pd(iPr2Im)2(η2-C2H4)] (5), which is very unstable even under an atmosphere of the olefin (see ESI†). However, if a solution of [Pt(iPr2Im)2] (4) is pressurized with 3 bars ethylene, [Pt(iPr2Im)2(η2-C2H4)] (6) is formed in quantitative yield and remains stable under an ethylene atmosphere (Scheme 3). This compound reveals one set of resonances for the NHC ligand (in C6D6 at 1.04, 5.48, 6.47 ppm), substantially shifted from the signals of 4 (1.33, 6.26, 6.40 ppm; see Fig. 2). More significantly, resonances of the η2-coordinated ethylene ligand were detected at 1.99 ppm with a 195Pt-coupling constant 2JPtH of 54.7 Hz in the 1H NMR spectrum and at 13.3 ppm (1JPtC = 253.8 Hz) in the 13C NMR spectrum of 6. If the ethylene pressure is reduced, complex 4 reforms in quantitative yield. This cycle can be repeated for several times without any loss of complex 4. To our surprise, no reaction has been observed between 4 and more electron rich alkenes such as 1,5-cyclooctadiene or cyclooctene.
image file: c4sc02998d-s3.tif
Scheme 3 Reactions of [Pt(iPr2Im)2] (4) with π-acceptor ligands.

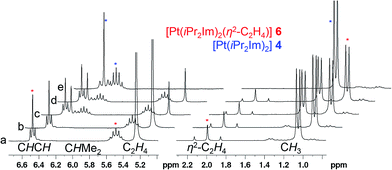
image file: c4sc02998d-f2.tif
Fig. 2 1H NMR of [Pt(iPr2Im)2(η2-C2H4)] 6 in C6D6: (a) sample of [Pt(iPr2Im)2] 4 after pressurizing with ethylene to give 6, (b) same sample after 14 d (revealing the stability of the complex in solution), (c) same sample after replacing the ethylene atmosphere with argon (revealing that 4 was formed from 6 after ethylene has been partially removed), (d) same sample after 5 h at room temperature; (e) sample after removal of all volatile material and addition of fresh C6D6 (= complex 4).

Accordingly, we were interested in the reactivity of complex 4 with respect to different alkynes such as phenyl and diphenyl acetylene, and 2-butyne (see Scheme 3). For nickel, we reported earlier the formation of stable nickel alkyne complexes [Ni(iPr2Im)2(η2-RC[triple bond, length as m-dash]CR′)].4a,c The reaction of phenyl acetylene and diphenyl acetylene with 4 afforded the alkyne complexes [Pt(iPr2Im)2(η2-HC[triple bond, length as m-dash]CPh)] (7) and [Pt(iPr2Im)2(η2-PhC[triple bond, length as m-dash]CPh)] (8) as the main products.

If 2-butyne is used for the reaction with 4, quantitative conversion cannot be observed (Scheme 3). For the reaction of 4 and 2-butyne in an equimolar stoichiometry an equilibrium was reached that contains approximately 33% of the reaction product [Pt(iPr2Im)2(η2-MeC[triple bond, length as m-dash]CMe)] (9) and 66% of the starting material [Pt(iPr2Im)2] (4). After prolonged standing in solution the isomerization of the 2-butyne ligand to an 1,2-butadiene (allene) ligand in the coordination sphere of platinum can be observed. Complex [Pt(iPr2Im)2(η2-H2[C with combining low line][double bond, length as m-dash][C with combining low line][double bond, length as m-dash]C(H)Me)] (10) has been identified in solution in a mixture containing 4, 9, and 10 using 1H and 13C NMR spectroscopy. The resonances of the allene ligand for complex 10 were detected at 2.06 ppm (CH2), 6.02 ppm (CH) and 2.57 ppm (CH3) in the proton NMR spectrum with 195Pt coupling to the CH2 (2JPtH = 54.2 Hz) and CH (3JPtH = 47.0 Hz) signals, which is in agreement with an 1,2-coordination of the allene ligand as proposed in Scheme 3. The assignment of the resonances was confirmed by a 1H–1H COSY experiment (see ESI†). The allene carbon atoms attached to platinum reveal resonances at −4.3 ppm and 158.4 ppm in the 13C{1H} NMR spectrum. Complex 10 represents to our knowledge one of the few examples of an allene complex formed from the isomerization of an alkyne ligand in the coordination sphere of platinum.13

The reaction of 4 with acetophenone leads to an equilibrium between 4 and the α-C–H bond activation product trans-[Pt(iPr2Im)2(H)(–[C with combining low line]H2–C{O}Ph)] (11) (Scheme 3). Other likely reaction products such as a η2-ketone complex or a complex resulting from ortho-metallation of the phenyl ring of the ketone have not been observed. The formation of 11 is quantitative if an excess of acetophenone is used at elevated temperatures (80 °C). The hydride ligand of 11 gives rise to a resonance at −10.11 ppm (1JPtH = 1133.3 Hz) and the metal bound methylene unit to a resonance at 3.22 ppm (2JPtH = 70.6 Hz) in the proton NMR spectrum. Notably, benzene solutions of compound 11 are not stable and slowly decompose to starting material. We have demonstrated earlier that [Ni2(iPr2Im)4(COD)] reacts with ketones to give stable and thermally robust nickel ketone complexes [Ni(iPr2Im)2(η2-{[O with combining low line][double bond, length as m-dash][C with combining low line]R1R2})] (see Fig. 3). DFT calculations (BP86/def2-TZVPP) on the relative stabilities of complexes [M(iPr2Im)(η2-{[O with combining low line][double bond, length as m-dash][C with combining low line]PhMe})] and trans-[M(iPr2Im)2(H)(–[C with combining low line]H2–C{O}Ph)] for nickel and platinum (see Fig. 3 and ESI†) reveal a significant stabilization (−41.7 kJ mol−1) of the platinum complex 11 with respect to an η2-ketone complex. A platinum η2-ketone complex would be unstable with respect to cleavage into 4 and acetophenone, according to these calculations. For nickel, the DFT calculations reveal the opposite trend, i.e. the η2-ketone complex is the global minimum, stabilized by −57.1 kJ mol−1 with respect to [Ni(iPr2Im)2] and acetophenone and −60.9 kJ mol−1 with respect to [Ni(iPr2Im)2(H)(–[C with combining low line]H2–C{O}Ph)] (see Fig. 3).


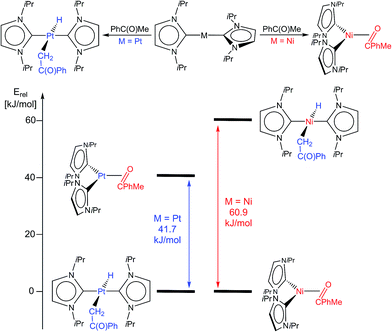image file: c4sc02998d-f3.tif
Fig. 3 Top: contrary reactivity of [Ni(iPr2Im)2] (as provided by [Ni2(iPr2Im)4(COD)] and [Pt(iPr2Im)2] towards acetophenone: Formation of the η2-ketone complexes [Ni(iPr2Im)2(η2-{[O with combining low line][double bond, length as m-dash][C with combining low line]PhMe})] for nickel and the α-C–H bond activation product trans-[Pt(iPr2Im)2(H)(–[C with combining low line]H2–C{O}Ph)] (11) for platinum. Bottom: results of DFT calculations (BP86/def2-TZVPP; see ESI†) on the relative stabilities of the α-C–H bond activation products trans-[M(iPr2Im)2(H)(–[C with combining low line]H2–C{O}Ph)] and η2-ketone complexes [M(iPr2Im)2(η2-{[O with combining low line][double bond, length as m-dash][C with combining low line]PhR2})] for M = Pt (left side) and M = Ni (right side).

Catalytic C–H bond activation reactions at positions α to the carbonyl group are currently of interest because they provide atom economic entries into the α-functionalization of organic carbonyl compounds.14 Compound 11 represents to our knowledge the first well characterized example of an α-CH bond activation product of a ketone at platinum (0) to give the corresponding hydrido α-keto–alkyl complex.15,16 Further investigations on the reactivity of 11 are underway.

Calculations on model systems

In order to understand the reasons for these differences in nickel, palladium and platinum chemistry, we have performed calculations on model systems [M(H2Im)2(η2-C2H4)] using the ADF program at the ZORA-BLYP/TZ2P level.17 The calculated bond energies for the ethylene ligand dissociation in complexes [M(H2Im)2(η2-C2H4)] into [M(H2Im)2] and ethylene clearly reveal the trend observed experimentally, i.e. that ethylene binds significantly more strongly to the nickel than to the palladium and platinum complexes: −104.2 kJ mol−1 (Ni), −25.0 kJ mol−1 (Pd) and −20.5 kJ mol−1 (Pt; see Table 1, Fig. 4 and ESI†).
Table 1 Energy decomposition analysis [kJ mol−1] of the metal–ethylene bond in [M(H2Im)2(η2-C2H4)] complexesa
M ΔVelstat ΔEpauli ΔEsteric ΔEoi ΔEint ΔEstrain ΔE
a Computed at ZORA-BLYP/TZ2P; for full data, see Table S1; ΔE = ΔEstrain + ΔEint; ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp (see text and ref. 17).
Ni −543.5 +741.8 +198.4 −417.1 −245.0 +140.8 −104.2
Pd −521.3 +695.7 +174.4 −334.5 −184.2 +159.2 −25.0
Pt −773.2 +1038.2 +265.0 −523.4 −284.1 +263.6 −20.5


image file: c4sc02998d-f4.tif
Fig. 4 Analysis of metal–ethylene bonding in [M(H2Im)2(η2-C2H4)] complexes using the activation strain model and ADF's energy decomposition analysis (EDA) (see text).

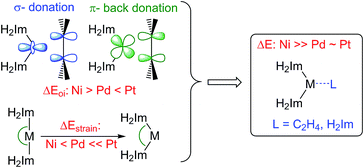
We have analyzed the metal–ethylene bonding in [M(H2Im)2(η2-C2H4)] complexes using the activation strain model and ADF's energy decomposition analysis (EDA).17b,c Thus, the bond energy ΔE is decomposed into the strain energy ΔEstrain associated with the deformation of the fragments [M(H2Im)2] and C2H4 during the bond formation reaction plus the mutual interaction ΔEint between the deformed fragments. The latter is further decomposed into classical electrostatic attraction ΔVelstat, steric (Pauli) repulsion ΔEPauli, and bonding orbital interactions ΔEoi.17b The results are given in Table 1. Note that the orbital interaction ΔEoi is least stabilizing for the 4d metal palladium: −415.1 kJ mol−1 (Ni); −334.5 kJ mol−1 (Pd); −523.4 kJ mol−1 (Pt).18 Our analyses show that, in line with the work of Dewar, Chatt and Duncanson,19 the bonding can be described as ligand to metal σ-donation and a π-back donation from the metal to the unoccupied π*-orbital of ethylene. In agreement with studies presented earlier,20,21 the orbital interaction of π-symmetry has for each metal a larger impact compared to the orbital interaction of σ-symmetry and increases for [M(H2Im)2(η2-C2H4)] from Pd (−249.6 kJ mol−1, 75% of ΔEoi) to Ni (−317.4 kJ mol−1, 76%) to Pt (−369.0 kJ mol−1, 71%). The interaction energy ΔEint follows this trend in ΔEoi: −245.0 kJ mol−1 (Ni); −184.2 kJ mol−1 (Pd); −284.1 kJ mol−1 (Pt).

We find that the overall bond energies ΔE is significantly weakened for palladium (−25.0 kJ mol−1) and platinum (−20.5 kJ mol−1) compared to nickel (−104.2 kJ mol−1). The main reason lies in an increase in strain energy ΔEstrain going from Ni to Pd and especially Pt. This strain ΔEstrain appears to stem mainly from the bending of the [M(H2Im)2] fragment from its preferred linear geometry towards smaller L–M–L bite angles. While the deformation energies of the ethylene ligand (for Pd: +42.2; Ni: +48.6 and Pt: +74.3 kJ mol−1) depend on the strength of π-back donation, the origin of the deformation energies for the [M(H2Im)2] fragment are more subtle and increase from Ni (+92.2 kJ mol−1) to Pd (+117.0 kJ mol−1) to Pt (+189.3 kJ mol−1). Bending of linear [M(H2Im)2] is costly in energy, and it has to be emphasized that this energy loss upon bending is by and large an electronic effect. In addition to steric factors, it has been shown earlier that fourteen-electron dicoordinate group-10 metal complexes d10-[ML2] adopt linear geometries mainly due to a significant destabilization of one of the occupied, in the linear case nonbonding d orbitals (dxz; for a schematic Walsh diagram see ESI†).22 An alternative but, ultimately equivalent way of understanding the resistance of d10-[ML2] complexes to L–M–L bending is that such bending destabilizes the interaction ΔEint between ML and L through increasing Pauli repulsion between the ligands' lone-pair orbital lobes and a destabilization of the ML dz2s hybrid orbital.22e For the good σ-donating NHC ligands, the d10-[ML2] bending strain is relatively high in the case of the noble metals Pd and Pt and – in combination with the weak orbital interaction ΔEoi term for Pd – is mainly responsible for the weak metal olefin bond. Note that NHC-coordinated palladium and platinum olefin complexes are known to be stable if one utilizes chelating bidentate NHC ligands, for which the linearization of the [M(NHC)2] moiety is not possible.23 The importance of [M(NHC)2]-bending to this chemistry can also be illustrated with the aid of an analysis on the stability of the model complexes [M(H2Im)3] with respect to a cleavage into [M(H2Im)2] and H2Im (Table 2). The deformation energies of the H2Im ligand are small and lie between 1 and 3 kJ mol−1 (for Pd: +1.0; Pt: +1.9 and Ni: +2.8 kJ mol−1), while the strain energies ΔEstrain for the [M(H2Im)2] fragments are much higher and increase substantially going from Ni (+70.7 kJ mol−1) to Pd (+90.5 kJ mol−1) to Pt (+130.4 kJ mol−1). Thus, the energy gain ΔEint obtained from the interaction of [M(H2Im)2] with H2Im is almost used up for palladium and platinum due to the L–M–L bending strain of [M(H2Im)2]. As a result, we calculate a significant overall binding energy for Ni (−107.9 kJ mol−1) and a much more reduced binding energy for the metals with larger radii Pd (−25.6) and Pt (−26.5 kJ mol−1).

Table 2 Energy decomposition analysis [kJ mol−1] of the metal–carbene bond in [M(H2Im)3] complexes between [M(H2Im)2] and H2Ima
M ΔEsteric ΔEoi ΔEint ΔEstrain ΔE
a Computed at ZORA-BLYP/TZ2P; for full data, see Table S2; ΔE = ΔEstrain + ΔEint; ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp (see text and ref. 17).
Ni +123.4 −278.5 −181.3 +73.4 −107.9
Pd +132.4 −224.7 −117.1 +91.5 −25.6
Pt +225.8 −357.3 −158.8 +132.3 −26.5

Our DFT calculations show the same trend in bond energy ΔE for the full complexes [M(iPr2Im)2(L)] as discussed above for the truncated models [M(H2Im)2(L)] (see ESI†). In agreement with the experiment, these calculations reveal that addition of another iPr2Im ligand to [M(iPr2Im)2] should be repulsive for palladium (+4.4 kJ mol−1) and platinum (+13.1 kJ mol−1). In addition, we calculated even smaller BDEs for 2-butyne complexes [M(iPr2Im)2(η2-C2Me2)] than for the ethylene complexes [M(iPr2Im)2(η2-C2H4)] of palladium and platinum.

Conclusions

We have reported the synthesis, characterization and first investigations concerning the reactivity of the novel complexes [M0(iPr2Im)2] (M = Pd 3, Pt 4), stabilized with an NHC ligand of low steric demand. These complexes represent rare examples of metal basic, yet isolable 14 VE complexes of the type d10-[ML2]. Complexes 3 and 4 do not react with additional NHC and the reaction with selected π-acidic ligands leads in some cases, if at all, to π-complexes, which are much less stable compared to the corresponding nickel complexes. The reactions presented here are illustrative examples of the differences one can observe by changing the central atom in a complex going from a 3d metal to a 4d or 5d metal atom within the same ligand framework and clearly show that L–M–L bending strain of d10-[ML2] is a key to understand group 10 metal reactivity. This is a new appearance of the concept of bite-angle flexibility that was recently introduced in the context of metal-mediated C–H bond activation.22f

Acknowledgements

This work was supported by the Julius-Maximilians-University Würzburg and the Deutsche Forschungsgemeinschaft (DFG). F.M.B. also thanks the Netherlands Organization for Scientific research (NWO-CW and NWO-EW) and the National Research School Combination-Catalysis (NRSC-C) for financial support.

Notes and references

  1. (a) J. Hartwig, Organotransition Metal Chemistry – from Bonding to Catalysis, University Science Books, Sausalito, 2010 Search PubMed; (b) C. Elschenbroich, Organometallics, Weinheim, 3rd edn, 2006 Search PubMed; (c) R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, Wiley, Hoboken, 4th edn, 2005 Search PubMed.
  2. (a) Applied Homogeneous Catalysis with Organometallic Compounds, ed. B. Cornils and W. A. Herrmann, Weinheim, 2nd edn, 2002 Search PubMed; (b) D. Steinborn, Grundlagen der metallorganischen Komplexkatalyse, 2, Auflage, Vieweg + Teubner, Wiesbaden, 2010 Search PubMed.
  3. (a) W. A. Herrmann, Angew. Chem., Int. Ed., 2002, 41, 1290 CrossRef CAS; (b) N-Heterocyclic Carbenes in Synthesis, ed. S. P. Nolan, Wiley-VCH, Weinheim, 2006 Search PubMed; (c) N-Heterocyclic Carbenes in Transition Metal Catalysis, Topics in Organometallic Chemistry, ed. F. Glorius, Springer, Berlin, 2007, vol. 21 Search PubMed; (d) M. C. Jahnke and F. E. Hahn, Angew. Chem., Int. Ed., 2008, 47, 3122 CrossRef PubMed; (e) S. Diez-Gonzalez, N. Marion and S. P. Nolan, Chem. Rev., 2009, 109, 3612 CrossRef CAS PubMed; (f) T. Dröge and F. Glorius, Angew. Chem., Int. Ed., 2010, 49, 6940 CrossRef PubMed; (g) N-Heterocyclic Carbenes – From Laboratory Curiosities to Efficient Synthetic Tools, RSC Catalysis Series, ed. S. Díez-González, RSC, Cambridge, 2011 Search PubMed; (h) H. D. Velazquez and F. Verpoort, Chem. Soc. Rev., 2012, 41, 7032 RSC; (i) R. H. Crabtree, Coord. Chem. Rev., 2013, 257, 755 CrossRef CAS PubMed; (j) L.-A. Schaper, S. J. Hock, W. A. Herrmann and F. E. Kühn, Angew. Chem., Int. Ed., 2013, 52, 270 CrossRef CAS PubMed; (k) K. Riener, S. Haslinger, A. Raba, M. P. Högerl, M. Cokoja, W. A. Herrmann and F. E. Kühn, Chem. Rev., 2014, 114, 5215 CrossRef CAS PubMed; (l) J. A. Mata, F. E. Hahn and E. Peris, Chem. Sci., 2014, 5, 1723 RSC.
  4. (a) T. Schaub and U. Radius, Chem.–Eur. J., 2005, 11, 5024 CrossRef CAS PubMed; (b) T. Schaub, M. Backes and U. Radius, J. Am. Chem. Soc., 2006, 128, 15964 CrossRef CAS PubMed; (c) T. Schaub, M. Backes and U. Radius, Organometallics, 2006, 25, 4196 CrossRef CAS; (d) T. Schaub, M. Backes and U. Radius, Chem. Commun., 2007, 2037 RSC; (e) T. Schaub, C. Döring and U. Radius, Dalton Trans., 2007, 1993 RSC; (f) T. Schaub, P. Fischer, A. Steffen, T. Braun, U. Radius and A. Mix, J. Am. Chem. Soc., 2008, 130, 9304 CrossRef CAS PubMed; (g) T. Schaub, M. Backes and U. Radius, Eur. J. Inorg. Chem., 2008, 2680 CrossRef CAS; (h) T. Schaub, M. Backes, O. Plietzsch and U. Radius, Dalton Trans., 2009, 7071 RSC; (i) T. Zell, M. Feierabend, B. Halfter and U. Radius, J. Organomet. Chem., 2011, 696, 1380 CrossRef CAS PubMed; (j) T. Zell and U. Radius, Z. Anorg. Allg. Chem., 2011, 637, 1858 CrossRef CAS; (k) T. Zell, T. Schaub, K. Radacki and U. Radius, Dalton Trans., 2011, 1852 RSC; (l) T. Schaub, P. Fischer, T. Meins and U. Radius, Eur. J. Inorg. Chem., 2011, 3122 CrossRef CAS; (m) P. Fischer, K. Götz, A. Eichhorn and U. Radius, Organometallics, 2012, 31, 1374 CrossRef CAS; (n) T. Zell, P. Fischer, D. Schmidt and U. Radius, Organometallics, 2012, 31, 5065 CrossRef CAS; (o) B. Zarzycki, T. Zell, D. Schmidt and U. Radius, Eur. J. Inorg. Chem., 2013, 2051 CrossRef CAS; (p) T. Zell and U. Radius, Z. Anorg. Allg. Chem., 2013, 639, 334 CrossRef CAS; (q) D. Schmidt, T. Zell, T. Schaub and U. Radius, Dalton Trans., 2014, 10816 RSC.
  5. Danopoulos et al. reported the formation of a new signal set in the proton NMR for the thermal decomposition reaction of cis-[Ni(iPr2ImMe2)2Me2] at 50 °C, which was attributed to the formation of the related complex [Ni(iPr2ImMe2)2] (iPr2ImMe2 = 1,3-diisopropyl-4,5-dimethylimidazolin-2-ylidene). This complex was never characterized or mentioned thereafter: (a) A. A. Danopoulos and D. Pugh, Dalton Trans., 2008, 30 RSC . Own investigations on the related complex trans-[Ni(iPr2Im)2Me2] revealed stability with respect to a thermal decomposition to [Ni(iPr2Im)2]; (b) P. Fischer, T. Linder and U. Radius, Z. Anorg. Allg. Chem., 2012, 638, 1491 CrossRef CAS.
  6. (a) V. P. W. Böhm, C. W. K. Gstöttmayr, T. Weskamp and W. A. Herrmann, J. Organomet. Chem., 2000, 595, 186 CrossRef; (b) S. Caddick, F. G. N. Cloke, G. K. B. Clentsmith, P. B. Hitchcock, D. McKerrecher, L. R. Titcomb and M. R. V. Williams, J. Organomet. Chem., 2001, 617–618, 635 CrossRef CAS; (c) L. R. Titcomb, S. Caddick, F. G. N. Cloke, D. J. Wilson and D. McKerrecher, Chem. Commun., 2001, 1388 RSC; (d) K. Arentsen, S. Caddick, F. G. N. Cloke, A. P. Herring and P. B. Hitchcock, Tetrahedron Lett., 2004, 45, 3511 CrossRef CAS PubMed; (e) C. W. K. Gstöttmayr, V. P. W. Böhm, E. Herdtweck, M. Grosche and W. A. Herrmann, Angew. Chem., Int. Ed., 2002, 41, 1363 CrossRef; (f) G. Altenhoff, R. Goddard, C. W. Lehmann and F. Glorius, Angew. Chem., Int. Ed., 2003, 42, 3690 CrossRef CAS PubMed; (g) M. M. Konnick, I. A. Guzei and S. S. Stahl, J. Am. Chem. Soc., 2004, 126, 10212 CrossRef CAS PubMed; (h) M. Yamashita, K. Goto and T. Kawashima, J. Am. Chem. Soc., 2005, 127, 7294 CrossRef CAS PubMed; (i) S. Fantasia and S. P. Nolan, Chem.–Eur. J., 2008, 14, 6987 CAS; (j) E. Lee and D. V. Yandulov, J. Organomet. Chem., 2011, 696, 4095 CrossRef CAS PubMed.
  7. (a) A. J. Arduengo III, S. F. Gamper, J. C. Calabrese and F. Davidson, J. Am. Chem. Soc., 1994, 116, 4391 CrossRef; (b) P. L. Arnold, F. G. N. Cloke, T. Geldbach and P. B. Hitchcock, Organometallics, 1999, 18, 3228 CrossRef CAS; (c) G. C. Fortman, N. M. Scott, A. Linden, E. D. Stevens, R. Dorta and S. P. Nolan, Chem. Commun., 2010, 46, 1050 RSC; (d) J. Bauer, H. Braunschweig, P. Brenner, K. Kraft, K. Radacki and K. Schwab, Chem.–Eur. J., 2010, 16, 11985 CrossRef CAS PubMed.
  8. M. Matsumoto, H. Yoshioko, K. Nakatsu, T. Yoshida and S. Otsuka, J. Am. Chem. Soc., 1974, 96, 3322 CrossRef CAS.
  9. Details on the reaction of iPr2Im with the metal halides MCl2 (M = Pd, Pt) will be given elsewhere.
  10. (a) P. S. Pregosin, Group 10: Nickel to Platinum, in Transition Metal Nuclear Magnetic Resonance, ed. P. S. Pregosin, Elsevier, Amsterdam, 1991, pp. 216–263 Search PubMed; (b) R. Benn, H. M. Büch and R.-D. Reinhardt, Magn. Reson. Chem., 1985, 23, 559 CrossRef CAS.
  11. (a) S. Caddick, F. G. N. Cloke, P. B. Hitchcock and A. K. d. K. Lewis, Angew. Chem., Int. Ed., 2004, 43, 5824 CrossRef CAS PubMed.
  12. (a) U. Radius and F. M. Bickelhaupt, Organometallics, 2008, 27, 3410 CrossRef CAS; (b) U. Radius and F. M. Bickelhaupt, Coord. Chem. Rev., 2009, 253, 678 CrossRef CAS PubMed.
  13. The other example we are aware of involves methylation of an alkynylphosphine ligand: M. A. Bennett, L. Kwan, A. D. Rae, E. Wenger and A. C. Willis, Dalton Trans., 2002, 226 RSC.
  14. (a) F. Bellina and R. Rossi, Chem. Rev., 2010, 110, 1082 CrossRef CAS PubMed; (b) C. C. C. Johansson and T. J. Colacot, Angew. Chem., Int. Ed., 2010, 49, 676 CrossRef CAS PubMed.
  15. In many cases the formation of stable η2-ketone complexes or orthometallation of the aryl ring is the dominant path for the reaction of benzophenone with a suitable transition metal precursor; for the latter see for example: (a) F. Kakiuchi and S. Murai, Acc. Chem. Res., 2002, 35, 826 CrossRef CAS PubMed.
  16. Some platinum hydrido α-keto-alkyl complexes are known but have been prepared using other routes: (a) A. Albinati, G. Bracher, D. Carmona, J. H. P. Jans, W. T. Klooster, T. F. Koetzle, A. Macchioni, J. S. Ricci, R. Thouvenot and L. M. Venanzi, Inorg. Chim. Acta, 1997, 265, 255 CrossRef CAS; (b) C. E. Shuchart, R. R. Willis, A. Wojcicki, A. L. Rheingold and B. S. Haggerty, Inorg. Chim. Acta, 2000, 307, 1 CrossRef CAS; (c) T. F. Vaughan, D. J. Koedyk and J. L. Spencer, Organometallics, 2011, 30, 5170 CrossRef CAS.
  17. (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS; (b) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed; (c) I. Fernandez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC.
  18. See, for example: (a) T. Ziegler and J. Autschbach, Chem. Rev., 2005, 105, 2695 CrossRef CAS PubMed; (b) J. Li and T. Ziegler, Organometallics, 1996, 15, 3844 CrossRef CAS; (c) S. Dapprich and G. Frenking, Angew. Chem., Int. Ed., 1995, 34, 354 CrossRef CAS.
  19. (a) M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 71 Search PubMed; (b) J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939 RSC.
  20. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717 CrossRef CAS PubMed.
  21. (a) K. Kitaura, S. Sakaki and K. Morokuma, Inorg. Chem., 1981, 20, 2292 CrossRef CAS; (b) T. Ziegler, Inorg. Chem., 1985, 24, 1547 CrossRef CAS; (c) J. Li, G. Schreckenbach and T. Ziegler, Inorg. Chem., 1995, 34, 3245 CrossRef CAS.
  22. (a) T. A. Albright, J. K. Burdett and M. H. Whangbo, Orbital Interactions in Chemistry, Wiley & Sons, New York, 1985 Search PubMed; (b) K. Tatsumi, R. Hoffmann, A. Yamamoto and J. K. Stille, Bull. Chem. Soc. Jpn., 1981, 54, 1857 CrossRef CAS; (c) M.-D. Su and S.-Y. Chu, Inorg. Chem., 1998, 37, 3400 CrossRef CAS; (d) M. A. Carvajal, J. J. Novoa and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1465 CrossRef CAS PubMed ; For consequences for the reactivity, see: ; (e) L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2013, 2, 106 CrossRef CAS PubMed; (f) L. P. Wolters, W. J. van Zeist and F. M. Bickelhaupt, Chem.–Eur. J., 2014, 20, 11370 CrossRef CAS PubMed.
  23. See for example: (a) M. Brendel, C. Braun, F. Rominger and P. Hofmann, Angew. Chem., Int. Ed., 2014, 53, 8741 CrossRef CAS PubMed; (b) S. N. Sluijter, S. Warsink, M. Lutz and C. J. Elsevier, Dalton Trans., 2013, 7365 RSC.

Footnotes

† Electronic supplementary information (ESI) available: Additional figures and tables; experimental, crystallographic and computational details. CCDC 1025170 and 1025171. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc02998d
‡ Dedicated to Prof. Dr. Reinhold Tacke on the occasion of his 65th birthday.
This journal is © The Royal Society of Chemistry 2015
Click here to see how this site uses Cookies. View our privacy policy here.