Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
What can NMR spectroscopy of selenoureas and phosphinidenes teach us about the π-accepting abilities of N-heterocyclic carbenes?†
Sai V. C.
Vummaleti
a,
David J.
Nelson
bc,
Albert
Poater
d,
Adrián
Gómez-Suárez
b,
David B.
Cordes
b,
Alexandra M. Z.
Slawin
b,
Steven P.
Nolan
*b and
Luigi
Cavallo
*a
aKAUST Catalyst Center, Physical Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Saudi Arabia. E-mail: luigi.cavallo@kaust.edu.sa
bEaStCHEM School of Chemistry, University of St Andrews, Purdie Building, North Haugh, St Andrews, Fife KY16 9ST, UK. E-mail: snolan@st-andrews.ac.uk
cWestCHEM Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, 295 Cathedral Street, Glasgow, G1 1XL, UK
dInstitut de Química Computacional i Catàlisi and Department de Química, Universitat de Girona, Campus de Motilivi, E-17071, Girona, Spain
First published on 2nd January 2015
Abstract
The electronic nature of the interaction of NHCs with metal centres is of interest when exploring their properties, how these properties influence those of metal complexes, and how these properties might depend on ligand structure. Selenourea and phosphinidene complexes have been proposed to allow the measurement of the π-accepting ability of NHCs, independent of their σ-donating ability, via the collection of 77Se or 31P NMR spectra, respectively. Herein, the synthesis and characterisation of selenoureas derived from a range of imidazol-2-ylidenes, 4,5-dihydroimidazol-2-ylidenes and triazol-2-ylidenes are documented. Computational studies are used to explore the link between the shielding of the selenium centre and the electronic properties of the NHCs. Results show that δSe is correlated to the energy gap between a filled lone pair orbital on Se and the empty π* orbital corresponding to the Se–NHC bond. Bond energy decomposition analysis indicated no correlation between the orbital σ-contribution to bonding and the chemical shielding, while a good correlation was found between the π-contribution to bonding and the chemical shielding, confirming that this technique is indeed able to quantify the ability of NHCs to accept π-electron density. Calculations conducted on phosphinidene adducts yielded similar results. With the link between δSe and δP and π-back bonding ability clearly established, these compounds represent useful ways in which to fully understand and quantify this aspect of the electronic properties of NHCs.
Introduction
The use of N-heterocyclic carbenes is now commonplace in a variety of fields of chemistry, including organometallic and main group synthesis, and catalysis.1–5 The exploration and quantification of their properties, via methods such as the Tolman Electronic Parameter (TEP)6,7 and Percent Buried Volume (%Vbur)8,9 have allowed the electronic and steric properties of these exciting species to be elucidated and compared.10,11 The TEP is the most commonly used probe of the electronic properties of NHCs, and is based on the fact that the C–O bond in a metal carbonyl complex is weakened by d → π*CO back-bonding; the frequency at which the C–O bond vibrates in the infra-red spectrum is therefore correlated to how electron-rich the metal centre is. Classically, [Ni(CO)3L] complexes have been used, although [MCl(CO)2L] (M = Rh or Ir)12,13 complexes provide less toxic alternatives.NHCs‡ were originally believed to be purely σ-donors, with negligible contributions from π-bonding. Subsequent studies have established that NHCs can accept electron density via π-back donation to an extent that cannot be neglected when considering their electronic properties.14–16 In some cases, NHCs can even function as π-donors.17 As the TEP requires that all ligands (L) being compared have a similar degree of π-accepting ability (it reflects the net electron density at the metal centre) it is not merely an indicator of σ-donating ability. For example, 4,5-dihydroimidazol-2-ylidenes appear to be less electron-donating than the equivalent imidazol-2-ylidenes (from the TEP),7 yet in reality they are more σ-donating, but also more π-accepting.18
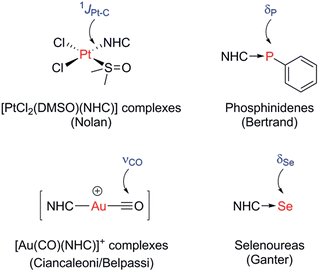
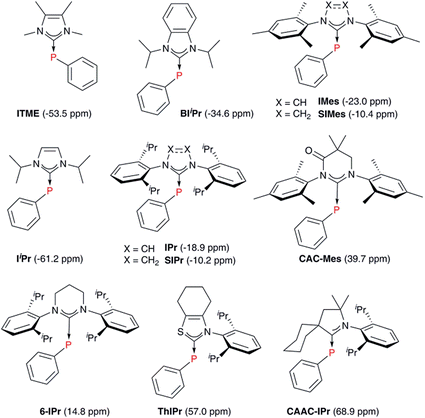
A number of methods to assess the π-accepting ability of NHCs have been proposed (Fig. 1). Nolan demonstrated the use of 1JPt–C coupling constants in [PtCl2(DMSO)(NHC)] complexes, prepared in one step from the free NHC and [PtCl2(DMSO)2].18 Bertrand used 31P NMR spectroscopy of phosphinidene adducts, which were prepared from the reaction of the free NHC with PPhCl2, followed by reduction with KC8 or Mg.19 Ganter utilised 77Se NMR spectroscopy of selenourea compounds, which were synthesised from the reaction of the imidazolium salt with KHMDS at −78 °C in the presence of elemental selenium;20 later work by us has shown that these can be prepared conveniently at room temperature using potassium tert-butoxide as the base.21,22 A linear correlation between δSe (for the selenoureas) and δP (for the phosphinidenes) has been demonstrated for seven examples.20 More recently, Ciancaleoni and Belpassi conducted a detailed and thorough theoretical study of [Ni(CO)3L] and [Au(CO)L] complexes, showing that while the νCO of the former are excellent indicators of the overall electron density at the nickel centre, the latter indicate solely the π-accepting ability of L.23 Only a limited number of such gold complexes have been disclosed, but a synthetic route is known.24,25 Belpassi and Zuccaccia have also examined the effect of ligand L on σ-donation and π-back bonding in [AuL(NHC)] complexes.26
The phosphinidene and selenourea systems are the only systems where a considerable number of experimental data points are available; relatively few (structurally quite similar) examples of platinum and gold complexes of the necessary forms have been disclosed. For the phosphinidenes and selenoureas, the chemical shift trends are consistent with by chemical intuition what one might expect the scale of π-accepting ability to look like. 4,5-Dihydroimidazol-2-ylidenes are known to be more π-accepting than their imidazol-2-ylidene congeners, while one would expect the presence of carbonyl groups on the backbone to increase the π-accepting ability. However, a thorough and detailed analysis of the bonding in such compounds has yet to be carried out, in order to assess how well these chemical shift scales reflect bonding characteristics. We report the synthesis and characterisation of a range of selenoureas derived from imidazol-2-ylidenes, 4,5-dihydroimidazol-2-ylidenes and triazol-2-ylidenes. The selenourea adducts were prepared in preference to the phosphinidenes due to the more convenient synthetic protocol, requiring only a single synthetic step directly from the moisture- and air-stable imidazolium, 4,5-dihydroimidazolium or triazolium salts, and a simple work-up on the laboratory bench. We have used computational methods to explore the nature of the bonding in these compounds; in particular, we wished to explore whether these species do indeed allow quantification of π-backbonding alone.
Results and discussion
Synthesis and characterisation of new selenoureas
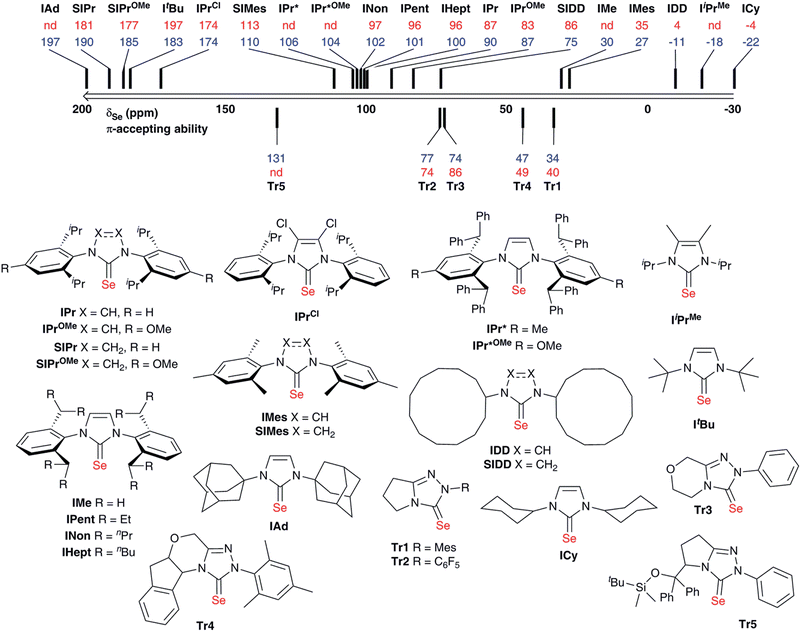
A range of selenourea compounds were prepared from the corresponding free NHCs or imidazolium salts in a straightforward manner; full details of the synthesis and characterisation of these species can be found in the ESI.† Compounds were prepared either by addition of the free carbene to excess elemental selenium, or by deprotonation of the NHC salt in the presence of excess selenium. For the latter approach, KOtBu was used to deprotonate imidazolium and 4,5-dihydroimidazolium salts. Attempts to use the same base with triazolium salts led to decomposition; instead, it was found that an excess of K2CO3 could deprotonate the triazolium salt in situ, in a manner somewhat analogous to that used to prepare a wide range of NHC–metal complexes (M = Cu, Au, Pd, Rh, Ir).27–30 While triazolium salts are more acidic than (4,5-dihydro)imidazolium species, the pKa is still relatively high (ca. 17 in aqueous solution versus ca. 20–25 for (4,5-dihydro)imidazolium salts).31,32 All products were air- and moisture-stable and could be worked up using bench-grade solvents. Some species, such as [Se(ItBu)], were unstable when stored in solution for extended periods, however. All new compounds were fully characterised by 1H, 13C{1H} and 77Se{1H} NMR spectroscopy in chloroform-d; the latter analysis was also performed in acetone-d6 (where solubility permitted) to allow comparison with the results of Ganter.20 All materials were determined to be analytically pure by elemental analysis.Data are presented in Fig. 2 for our complete set of selenoureas (24), which includes those synthesised as part of this study as well as those we have reported previously.21,22 The 77Se chemical shifts cover a range from 197 to −22 ppm, versus the range of 800–80 ppm reported by Ganter for a set of seven structurally very diverse selenoureas.20 This narrower range is somewhat expected, given that the majority of the compounds here feature a N,N′-diarylimidazol-2-ylidene motif, plus some selected triazol-2-ylidenes, while Ganter's original study covered a much wider range of carbene compounds. It should be noted at this point that the δSe values considered henceforth are those recorded in chloroform-d.
Some interesting trends are apparent from our data. Unsaturated imidazol-2-ylidenes bearing secondary alkyl N-substituents exhibit the lowest δSe (<0 ppm) and ought then to be the least π-accepting, followed by unsaturated N,N′-diarylimidazol-2-ylidenes and one example of a saturated N,N′-dialkyl-4,5-dihydroimidazol-2-ylidene (ca. 30–100 ppm). Saturated N,N′-diaryl species exhibit higher δSe (110–190 ppm), while IPrCl, which bears chloride substituents on the backbone, also appears in this region (δSe = 174 ppm). Most interesting, ItBu and IAd, which bear quaternary N-alkyl substituents, exhibit very high chemical shifts (δSe = 183 and 197 ppm, respectively). While saturated NHCs are known to be more π-accepting than unsaturated NHCs, this difference amongst N,N′-dialkylimidazol-2-ylidenes was very intriguing.
Notably, structurally similar unsaturated bis(aryl) NHCs led to quite different values of δSe (cf. [Se(IMes)] and [Se(IPr)]), although the selenoureas derived from IPr, IPent, IHept and INon (which differ only in the aryl 2,6-substitution pattern) all exhibit similar δSe. For the triazol-2-ylidenes, Tr2 exhibited higher δSe than Tr1, while Tr5 exhibited the highest δSe of these compounds.
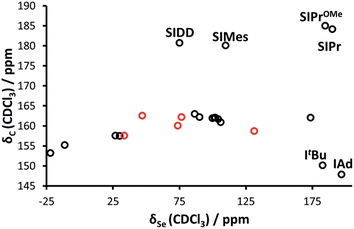
Interestingly, while Bertrand demonstrated a linear correlation between δP and δC (for the carbene C2) in the phosphinidene adducts, the correlation is much poorer for selenourea compounds based on imidazol-2-ylidene compounds (Fig. 3), with selenoureas derived from saturated NHCs and bulky bis(alkyl) NHCs clearly lying away from the others. Bertrand's study does cover a greater variety of structures, and it should be noted that in the aforementioned study, IMes/IPr and SIMes/SIPr lie on opposite sides of the δP/δC trendline.
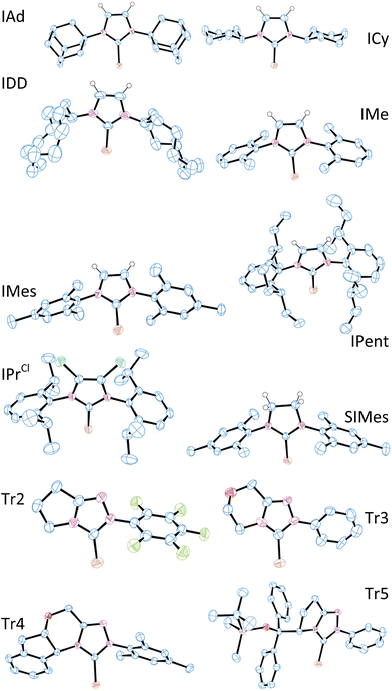
X-ray crystal structure data were obtained for most of these selenoureas (Fig. 4). The crystal structures of [Se(IiPrMe)], [Se(IPr)], [Se(SIPr)], [Se(IPr*)], [Se(IPrOMe)], [Se(SIPrOMe)], and [Se(IPr*OMe)] are already known.21,33 Crystals suitable for these studies were typically prepared from slow diffusion of pentane or hexane into an acetone or dichloromethane solution of the compound. Unfortunately, suitable data for [Se(IHept)] and [Se(INon)] could not be obtained due to the highly disordered nature of the alkyl chains, while [Se(ItBu)] and [Se(SIDD)] decomposed in solution. Full crystal structure data can be found in the ESI.† C–Se bond lengths varied between 1.82 and 1.86 Å, but there was no correlation between C–Se distance and δSe. In one example ([Se(Tr3)]) where there were two independent structures in the unit cell, the C–Se bond lengths were 1.831(12) Å and 1.857(14) Å, suggesting that ca. 0.03 Å bond length differences are not meaningful. Some compounds exhibit rather short Se–H distances which are close to or within the sum of Van der Waals radii (ca. 3.1 Å) (e.g. [Se(IPr*)], 3.207 Å; [Se(IPr*OMe)], 3.002 Å; [Se(IPr)], 3.162 Å; [Se(ICy)] and [Se(IDD)], ca. 2.8 Å).
Computational studies of selenoureas
With these data in hand, DFT calculations were approached. X-ray crystal structure data were used (where available) as a starting point for geometry optimisations. A total of 24 selenoureas (covering derivatives of imidazol-2-ylidenes, 4,5-dihydroimidazol-2-ylidenes and triazol-2-ylidenes) were considered using DFT methods. Calculations were carried out using the Amsterdam density functional suite34–36 at the BP86/TZ2P level of theory37,38 (see the ESI† for full computational details). As for a comparison between DFT and X-ray structures, focusing on the most relevant NHC–Se bond length, plotting the DFT optimised distances versus the X-ray distances of the selenoureas of Fig. 4 results in a clear correlation, with R2 = 0.84.Initial efforts were made to reproduce the experimental trend of the Se chemical shift in the selenoureas, which was seen as an important prerequisite before conducting more detailed analyses of the bonding and energies involved. Going into details, an excellent correlation (R2 = 0.89) was obtained between the DFT isotropic shielding of the Se atom and the experimental chemical shift (Fig. 5). The only outlier was the triazole complex [Se(Tr5)] and by excluding this complex the correlation was improved significantly (R2 = 0.94). Thus, complex [Se(Tr5)] was omitted from the analysis. The otherwise excellent correlation between the experimental Se chemical shift and the DFT calculated isotropic shielding validates the following analysis.
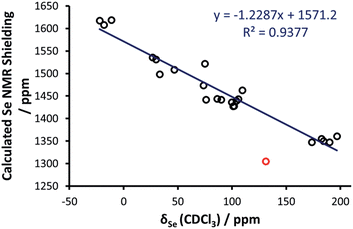 | ||
| Fig. 5 Calculated chemical shielding versus experimental NMR chemical shift for the selenium centres in the selenoureas in Fig. 2, where the red point corresponds to [Se(Tr5)] and is not included in the trendline. | ||
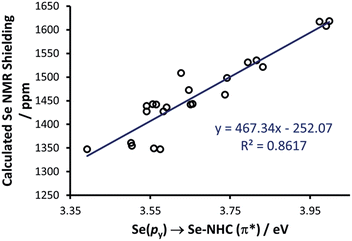
To rationalise the calculated NMR shielding of the Se atom in the 23 selenoureas considered (i.e. excluding [Se(Tr5)]), we examined the diamagnetic and paramagnetic shielding terms (σd and σp). This analysis indicated that the main variable is the σp term, which oscillates in a range of 271 ppm, while the σd term remains almost the same, covering a range of only 3 ppm (see Table S2 in the ESI†). The paramagnetic shielding results from transitions of electrons between occupied and virtual orbitals, properly connected by symmetry, induced by the external magnetic field, and the amount of the shielding is related to the energy gap between these two orbitals.39–41 Analysis of the paramagnetic shielding tensor indicates that the largest changes are in the σp component oriented along the Se–NHC bond, σp(xx), which corresponds to the x axis in Fig. 6(a). More detailed analysis of the paramagnetic shielding in terms of orbitals,40,42 indicated that σp(xx) mainly depends on Se(py) → Se–NHC(π*) transitions between the occupied py orbital on the Se atom and the virtual π* orbital of the selenourea; Fig. 6(b) and (c) show the Se(py) and Se–NHC(π*) orbitals for [Se(IiPrMe)].
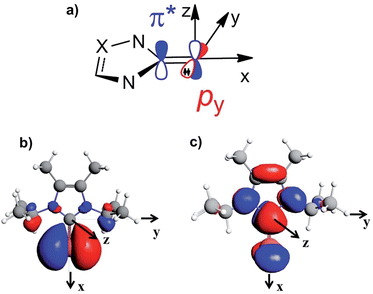 | ||
| Fig. 6 (a) Schematic representation of the filled Se(py) and empty Se–NHC(π*) orbitals; (b) and (c) isodensity plots for the Se(py) and Se–NHC(π*) orbitals of [Se(IiPrMe)]. | ||
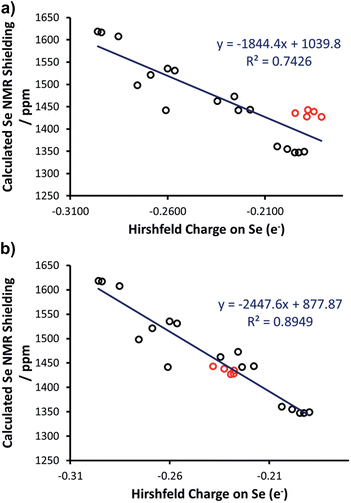
Thus, we plotted the calculated Se chemical shielding versus the Se(py) → Se–NHC(π*) energy gap and we observed a reasonably good correlation (R2 = 0.86) (Fig. 7); full results including the orbital energies of Se(py), Se–NHC(π*), and their energy gap can be found in Table S3 of the ESI.† While the above analysis offers an explanation for the origin of the chemical shift of Se, the Se(py) → Se–NHC(π*) energy gap depends on the overall electron density on the Se atom. For this reason, we searched for a correlation between the calculated isotropic shielding of Se and the Hirshfeld atomic charge on the Se atom (Fig. 8(a)); while the correlation is rather good (R2 = 0.74), a group of outliers was evident on the plot (selenoureas of IPr*, IPr*OMe, IPent, IHept, and INon, highlighted in red). Inspection of the optimised geometries revealed short (3.0–3.2 Å) Se–H distances (Fig. 9). These distances are much shorter than those found in closely-related compounds (e.g. [Se(IPr)]).
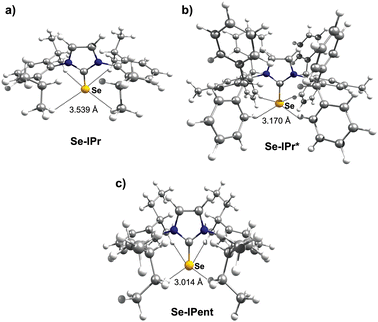 | ||
| Fig. 9 Optimized geometries for (a) [Se(IPr)], (b) [Se(IPr*)] and (c) [Se(IPent)], showing Se–H distances. | ||
Considering that Hirshfeld charges are built by partitioning electron density in each point of space to atoms according to a distance based criterion, we tested if imposing a minimum Se–H distance of 3.5 Å would improve the correlation between the isotropic Se shielding and the Hirshfeld charges. Therefore, restrained optimisations for all the outlier complexes of Fig. 8(a) were carried out with short Se–H distance frozen to 3.5 Å. This constraint resulted in geometries slightly higher in energy with the maximum energy penalty amounting to 3.0 kcal mol−1 (for [Se(IPent)]) and changed the DFT chemical shieldings by a maximum of 1.0 ppm (for [Se(IPr*OMe)]), indicating that these constrained geometries also capture the structure and the NMR properties of the system well. However, the Hirshfeld charges of the constrained geometries are clearly different, providing a fairly good correlation with the DFT chemical shielding (R2 = 0.89) (Fig. 8(b)).
As a further test, the Hirshfeld charges were calculated for the [Se(IPr)] and [Se(IPent)] adducts using the hybrid B3LYP functional, but again the Se charge in the two systems is clearly different (0.214e versus 0.170e). Besides a possible weakness of the Hirshfeld charges in this case, a possible explanation is that the optimised geometries poorly represent the real behaviour in solution. Indeed, it has been clearly demonstrated that NHC ligands are flexible,43 and this could be particularly relevant for large ‘bulky but flexible’ NHCs such as IPr*, IPr*OMe, IHept, IPent and INon. However, answering this question is beyond the scope of the present work. Nevertheless, in the remainder of this work these restrained geometries were used for these selenoureas.
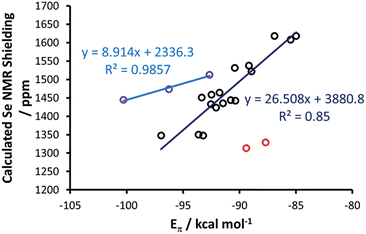
At this point, a bond energy decomposition analysis (BDA) on the Se–NHC complexes, rigidly fragmented into the Se and NHC moieties, was performed to shed light on the nature of the Se–NHC bond, with a focus on the extent of σ-donation from the NHC lone pair to the empty sp orbital of Se and, particularly, of π-back donation from a filled Se pz orbital to the empty NHC π-orbital (see Fig. 10). To this end, the geometries of all the complexes were re-optimised under the constraint of CS symmetry, with the NHC ring lying in the σxy plane, i.e. with the systems oriented as in Fig. 6(a), since this allows the orbital interaction energy contribution of the A′ and A′′ irreducible representations to be associated with the σ and π Se–NHC bonds (Eσ and Eπ), respectively (see the computational details in the ESI†). These constrained geometry optimisations were performed for all the compounds, including those derived from saturated NHCs and Tr1-3, since forcing them to be CS-symmetric requires only minor deformation. [Se(Tr4)] was excluded from this analysis, since forcing it into a plane would correspond to an unrealistic deformation. Both the Eσ and Eπ plotted versus the calculated Se shielding result in poor correlations (R2 = 0.25 and 0.28, respectively; see Fig. S3 in the ESI†). However, analysis of the residual errors (see Table S4 in the ESI†) indicated that the calculated Se shielding is consistently poorly correlated to Eσ for all systems, whereas in the case of Eπ the correlation is normally good, and only a few systems have clearly larger residual errors, indicative of poor correlation. Specifically, the outliers are the IAd and the ItBu selenoureas, with an Eπ clearly too small, and the three selenoureas containing a triazole ring. Focusing on the latter, it was evident that the additional heteroatom in the triazol-2-ylidene ring completely altered the σ and π Se–NHC bonding scheme relative to classic imidazol-2-ylidene and 4,5-dihydroimidazol-2-ylidene complexes, justifying their separate treatment. Indeed, correlating Eπ to the Se shielding in the triazol-2-ylidene adducts results in excellent correlation (R2 = 0.99) (Fig. 11), but this only comprises three data points.
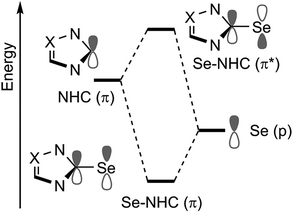 | ||
| Fig. 10 Schematic representation of the frontier molecular orbitals involving the Se(p) and NHC(π) orbitals. Se to NHC back-bonding occurs through in phase combination between a filled p orbital on Se with an empty π orbital of the NHC (Se–NHC (π)). Out of phase combination of the same orbitals (Se–NHC (π*)) is instead responsible for the paramagnetic shielding (Fig. 6(a)). | ||
Regarding the imidazol-2-ylidene and 4,5-dihydro-imidazol-2-ylidene complexes, it should be noted that the IAd and ItBu Se adducts already proved to be outliers in the correlation between the experimental δC (carbene C2) and the δSe (see Fig. 3) thus we decided to exclude them also from this analysis. Indeed, focusing on the remaining 17 imidazol-2-ylidene and 4,5-dihydroimidazol-2-ylidene complexes, a strong correlation (R2 = 0.85) is gratifyingly achieved (Fig. 11), supporting the hypothesis that the δSe is indeed a measure of the π accepting capability of NHCs.
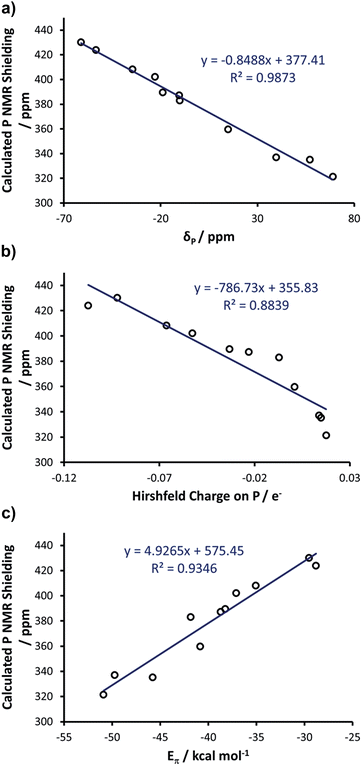
Computational studies of phosphinidene adducts
With these insights into the selenourea compounds in hand, the properties of the phosphinidene compounds were also explored, due to the similar way in which they are proposed to indicate the π-accepting properties (or lack thereof) of carbene compounds.19 The set of compounds in Fig. 12 was studied in silico. All of these species have been prepared and characterised by Bertrand and co-workers, although it should be noted that the solvent used for 31P NMR experiments varied (typically benzene-d6, but occasionally THF-d8 or CDCl3). These compounds were treated in a similar manner, yielding an excellent correlation (R2 = 0.99) between the experimental δP chemical shift and the calculated chemical shielding (Fig. 13(a)); full results including the values of σd and σp components and Hirshfeld charges can be found in Table S5 of the ESI.† Subsequently, the calculated isotropic shielding of P was plotted versus the Hirshfeld atomic charge on the P atom, and a reasonably good correlation (R2 = 0.88) was observed (Fig. 13(b)). For BDA, the geometry of all the phosphinidene complexes was re-optimised under the constraint of CS symmetry. Similar to the selenium adducts, the calculated P shielding is poorly correlated to Eσ for all systems (R2 = 0.10), whereas an excellent correlation (R2 = 0.93) was found in the case of Eπ (Fig. 13(c); see Table S6 in the ESI†). In short, consistent with the BDA in selenoureas, in the case of the NHC phosphinidene adducts we also found a good correlation between the chemical shielding and the amount of P to NHC back donation.Correlating Se and P
As final remarks, examination of data for the Se and PPh adducts with IMes, SIMes, IPr and SIPr allows for a comparison of the different NHCs, and of the relative strengths of the NHC–Se and NHC–PPh bonds. According to the Eσ and Eπ for these systems (see Tables S4 and S6 in the ESI†), the Se–NHC bond is clearly stronger than the P–NHC bond, with Eσ and Eπ for Se–NHC around 270 and 90 kcal mol−1 respectively, almost double the values for P–NHC (ca. 170 and 40 kcal mol−1, respectively). Nevertheless, for both systems the Eπ is between 17 and 38% of Eσ, highlighting the remarkable π-accepting capability of NHCs. As for a comparison between imidazol-2-ylidenes and 4,5-dihydroimidazol-2-ylidenes, the Eσ for SIMes and SIPr is 1–2 kcal mol−1 larger than that calculated for IMes and IPr, both for Se–NHC and P–NHC compounds. This slightly higher σ-donicity calculated for 4,5-dihydroimidazol-2-ylidenes than imidazol-2-ylidenes is consistent with previous analyses.18Focusing on π-acidity, Eπ for SIMes and SIPr is about 2–3 kcal mol−1 larger than that calculated for IMes and IPr, both for Se–NHC and P–NHC compounds. Although the difference is not particularly large, it is consistent with the higher π-accepting capability expected from 4,5-dihydroimidazol-2-ylidenes. Despite the difference in Eπ being relatively small, it is responsible for the observed difference in the chemical shielding of 77Se, of about 80–100 ppm both experimentally and theoretically, between IMes and SIMes, as well as between IPr and SIPr. However, the window of about 250 ppm covered by experimental and DFT NMR data corresponds to a window in Eπ of 12 kcal mol−1, and therefore this metric can identify and quantify considerable differences in π-accepting ability.
Since the above calculations indicated the capability of the chosen methodology to rationalise both selenourea and phosphinidene compounds independently, and in line with the evidence that there is a linear correlation between the experimental δp and δSe,20 we explored further the possibility of correlating the two classes within a single framework. To this end, we enlarged the comparison to 11 systems, by calculating the selenoureas corresponding to all the phosphinidenes shown in Fig. 12 (see Table S7 in the ESI† for DFT 77Se shielding and Eπ values). Plotting the DFT chemical shielding of 77Se versus that of 31P for the above 11 compounds results in a excellent linear correlation (R2 = 0.92, similar to that reported by Ganter from experimental δSe and δP data) (Fig. 14(a)).20 At this point, we plotted Eπ for the above 11 phosphinidenes versus Eπ for the corresponding selenoureas, which results in quite a good correlation considering the enormous variation in structure amongst these examples (R2 = 0.84) (Fig. 14(b)).
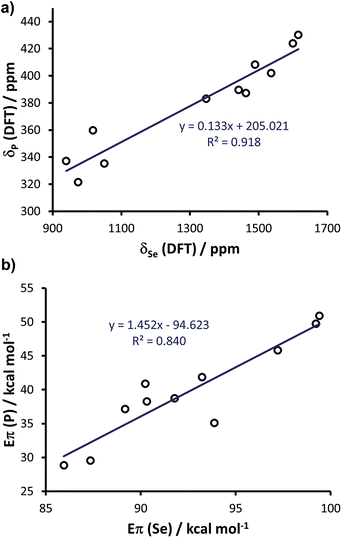 | ||
| Fig. 14 (a) Calculated chemical shielding of phosphinidenes versus selenoureas and (b) calculated Eπ for 11 phosphinidenes (see Fig. 12) versus calculated Eπ in the corresponding 11 selenoureas. | ||
Analysis of Fig. 14(b) indicates that Eπ for the phosphinidenes spans a 22 kcal mol−1 range in the 28.8–50.9 kcal mol−1 window, while selenoureas span a 13 kcal mol−1 range in the 86.0–99.4 kcal mol−1 window. The quantitative link between these two systems, established by this study, plus the known quantitative link between experimental δSe and δP, allows for NHCs to be evaluated using either system and mapped onto the same quantitative scale.
While there is a clear quantitative trend that links these two systems, the different absolute values of Eπ must result from the interactions of different orbitals on atoms with quite different properties (i.e. Se 4pz and P 3pz). The good quantitative link between Se and P systems suggests very strongly that similar links between Se and/or P models and transition metal systems (which will interact via d → π* back-bonding) ought to be quantifiable. Such links require further, detailed calculations of model transition metal systems, and are beyond the scope of the current study.
Conclusions
In conclusion, the link between the δSe chemical shifts of 24 selenoureas and δP chemical shifts of 11 phosphinidene compounds and the electronic properties of the NHCs from which they are derived have been probed. Experimentally, a range of (4,5-dihydro)imidazol-2-ylidene- and triazol-2-ylidene-based selenoureas have been prepared and fully characterised. For 24 selenoureas, NMR shieldings derived from calculations correlated well with those obtained experimentally (R2 = 0.89, or 0.94 by excluding the triazol-2-ylidene-based complex [Se(Tr5)]). The calculated NMR shielding was found to be strongly correlated to the Se(py) → Se–NHC(π*) energy gap (R2 = 0.86) and the charge at the selenium centre (R2 = 0.90). Finally, bond decomposition analysis indicated that the NMR shielding is correlated to the π-orbital interaction energy (R2 = 0.85 for the imidazol-2-ylidenes, with two exceptions in the form of ItBu and IAd; R2 = 0.99 for 3 triazol-2-ylidenes). For 11 carbene–phosphinidene complexes, we observed an excellent correlation (R2 = 0.99) between the experimental P chemical shift and the calculated chemical shielding. The latter was found to be strongly correlated to the charge at the phosphorous centre (R2 = 0.89), as well as to the π orbital interaction energy (R2 = 0.93). In summary, the chemical shifts of these NHC adducts do indeed reflect the importance of π-back bonding in the overall interaction with the selenium or phosphorus centre.The key outcomes of this study are therefore fourfold: (i) a detailed analysis of the origin of the chemical shift measurements obtained experimentally has been carried out using DFT techniques; (ii) the link between δSe or δP and the ability of the corresponding NHC ligand to accept π-electron density has been established unambiguously, meaning that these techniques can be deployed with confidence to characterise and quantify the π-accepting capability of new and existing NHC ligands; (iii) the groundwork has been laid for the use of these calculations to predict the properties of NHCs; and finally (iv) data have been furnished for a series of key NHCs of interest to chemists utilising them as ligands in transition metal promoted catalysis, on their own as organocatalysts, or in conjunction with Lewis acids in frustrated Lewis pair promoted reactivity.
Acknowledgements
S.P.N. thanks the ERC (Advanced Investigator Award ‘FUNCAT’), the EPSRC and Syngenta for funding. S.P.N. is a Royal Society Wolfson Merit Award Holder. D.J.N. thanks the University of Strathclyde for a Chancellor's Fellowship. We thank Dr James E. Taylor and Professor Andrew D. Smith (University of St Andrews) for samples of the triazolium salts of Tr1-5. S.P.N. and L.C. thank King Abdullah University of Science and Technology (CCF project) for support. A.P. thanks the Spanish MINECO for a Ramón y Cajal contract (RYC-2009-05226) and the European Commission for a Career Integration Grant (CIG09-GA-2011-293900).Notes and references
- M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496 CrossRef CAS PubMed.
- S. Díez-González, N. Marion and S. P. Nolan, Chem. Rev., 2009, 109, 3612–3676 CrossRef PubMed.
- W. A. Herrmann, Angew. Chem., Int. Ed., 2002, 41, 1290–1309 CrossRef CAS.
- S. Bellemin-Laponnaz and S. Dagorne, Chem. Rev., 2014, 114, 8747–8774 CrossRef CAS PubMed.
- M. Melaimi, M. Soleilhavoup and G. Bertrand, Angew. Chem., Int. Ed., 2010, 49, 8810–8849 CrossRef CAS PubMed.
- C. A. Tolman, Chem. Rev., 1977, 77, 313–348 CrossRef CAS.
- R. Dorta, E. D. Stevens, N. M. Scott, C. Costabile, L. Cavallo, C. D. Hoff and S. P. Nolan, J. Am. Chem. Soc., 2005, 127, 2485–2495 CrossRef CAS PubMed.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
- A. Poater, B. Cosenza, A. Correa, S. Giudice, F. Ragone, V. Scarano and L. Cavallo, Eur. J. Inorg. Chem., 2009, 2009, 1759–1766 CrossRef.
- T. Dröge and F. Glorius, Angew. Chem., Int. Ed., 2010, 49, 6940–6952 CrossRef PubMed.
- D. J. Nelson and S. P. Nolan, Chem. Soc. Rev., 2013, 42, 6723–6753 RSC.
- R. A. Kelly III, H. Clavier, S. Giudice, N. M. Scott, E. D. Stevens, J. Bordner, I. Samardjiev, C. D. Hoff, L. Cavallo and S. P. Nolan, Organometallics, 2007, 27, 202–210 CrossRef.
- S. Wolf and H. Plenio, J. Organomet. Chem., 2009, 694, 1487–1492 CrossRef CAS PubMed.
- H. Jacobsen, A. Correa, C. Costabile and L. Cavallo, J. Organomet. Chem., 2006, 691, 4350–4358 CrossRef CAS PubMed.
- H. Jacobsen, A. Correa, A. Poater, C. Costabile and L. Cavallo, Coord. Chem. Rev., 2009, 253, 687–703 CrossRef CAS PubMed.
- A. A. D. Tulloch, A. A. Danopoulos, S. Kleinhenz, M. E. Light, M. B. Hursthouse and G. Eastham, Organometallics, 2001, 20, 2027–2031 CrossRef CAS.
- N. M. Scott, R. Dorta, E. D. Stevens, A. Correa, L. Cavallo and S. P. Nolan, J. Am. Chem. Soc., 2005, 127, 3516–3526 CrossRef CAS PubMed.
- S. Fantasia, J. L. Petersen, H. Jacobsen, L. Cavallo and S. P. Nolan, Organometallics, 2007, 26, 5880–5889 CrossRef CAS.
- O. Back, M. Henry-Ellinger, C. D. Martin, D. Martin and G. Bertrand, Angew. Chem., Int. Ed., 2013, 52, 2939–2943 CrossRef CAS PubMed.
- A. Liske, K. Verlinden, H. Buhl, K. Schaper and C. Ganter, Organometallics, 2013, 32, 5269–5272 CrossRef CAS.
- D. J. Nelson, A. Collado, S. Manzini, S. Meiries, A. M. Z. Slawin, D. B. Cordes and S. P. Nolan, Organometallics, 2014, 33, 2048–2058 CrossRef CAS.
- D. J. Nelson, F. Nahra, S. R. Patrick, D. B. Cordes, A. M. Z. Slawin and S. P. Nolan, Organometallics, 2014, 33, 3640–3645 CAS.
- G. Ciancaleoni, N. Scafuri, G. Bistoni, A. Macchioni, F. Tarantelli, D. Zuccaccia and L. Belpassi, Inorg. Chem., 2014, 53, 9907 CrossRef CAS PubMed.
- M. A. Celik, C. Dash, V. A. K. Adiraju, A. Das, M. Yousufuddin, G. Frenking and H. V. R. Dias, Inorg. Chem., 2012, 52, 729–742 CrossRef PubMed.
- C. Dash, P. Kroll, M. Yousufuddin and H. V. R. Dias, Chem. Commun., 2011, 47, 4478–4480 RSC.
- D. Marchione, L. Belpassi, G. Bistoni, A. Macchioni, F. Tarantelli and D. Zuccaccia, Organometallics, 2014, 33, 4200 CrossRef CAS.
- A. Collado, A. Gomez-Suarez, A. R. Martin, A. M. Z. Slawin and S. P. Nolan, Chem. Commun., 2013, 49, 5541–5543 RSC.
- O. Santoro, A. Collado, A. M. Z. Slawin, S. P. Nolan and C. S. J. Cazin, Chem. Commun., 2013, 49, 10483–10485 RSC.
- R. Savka and H. Plenio, Dalton Trans., 2015, 44, 891–893 RSC.
- C. J. O'Brien, E. A. B. Kantchev, C. Valente, N. Hadei, G. A. Chass, A. Lough, A. C. Hopkinson and M. G. Organ, Chem.–Eur. J., 2006, 12, 4743–4748 CrossRef PubMed.
- E. M. Higgins, J. A. Sherwood, A. G. Lindsay, J. Armstrong, R. S. Massey, R. W. Alder and A. C. O'Donoghue, Chem. Commun., 2011, 47, 1559–1561 RSC.
- R. S. Massey, C. J. Collett, A. G. Lindsay, A. D. Smith and A. C. O'Donoghue, J. Am. Chem. Soc., 2012, 134, 20421–20432 CrossRef CAS PubMed.
- N. Kuhn, G. Henkel and T. Kratz, Z. Naturforsch., Teil B, 1993, 48, 973–977 CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, P. R. T. Schipper, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakolev, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2013 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. J. Arduengo, D. A. Dixon, K. K. Kumashiro, C. Lee, W. P. Power and K. W. Zilm, J. Am. Chem. Soc., 1994, 116, 6361–6367 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, Int. J. Quantum Chem., 1997, 61, 899–918 CrossRef CAS.
- J. Autschbach, J. Chem. Phys., 2008, 128, 164112 CrossRef PubMed.
- F. Ragone, A. Poater and L. Cavallo, J. Am. Chem. Soc., 2010, 132, 4249–4258 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Full characterisation data including NMR spectra for new compounds; full DFT data and co-ordinates from computational studies. CCDC 1024807–1024818. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc03264k |
| ‡ Trivial names and chemical names for the NHCs discussed herein: IPr, 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene; IPrOMe, 1,3-bis(2,6-diisopropyl-4-methoxyphenyl)imidazol-2-ylidene; SIPr, 1,3,-bis(2,6-diisopropylphenyl)-4,5-dihydroimidazol-2-ylidene; SIPrOMe, 1,3-bis(2,6-diisopropyl-4-methoxyphenyl)-4,5-dihydroimidazol-2-ylidene; IPrCl, 1,3-bis(2,6-diisopropylphenyl)-4,5-dichloroimidazol-2-ylidene; IPr*, 1,3-bis(2,6-diphenylmethyl-4-methylphenyl)imidazol-2-ylidene; IPr*, 1,3-bis(2,6-diphenylmethyl-4-methoxyphenyl)imidazol-2-ylidene; IiPrMe, 1,3-diisopropyl-4,5-dimethylimidazol-2-ylidene; IMes, 1,3-bis(2,4,6-trimethylphenyl)imidazol-2-ylidene; SIMes, 1,3-bis(2,4,6-trimethylphenyl)-4,5-dihydroimidazol-2-ylidene; IDD, 1,3-dicyclododecylimidazol-2-ylidene; SIDD, 1,3-dicyclododecyl-4,5-dihydroimidazol-2-ylidene; ItBu, 1,3-di-tert-butylimidazol-2-ylidene; IMe, 1,3-bis(2,6-dimethylphenyl)imidazol-2-ylidene; IPent, 1,3-bis(2,6-diisopentylphenyl)imidazol-2-ylidene; IHept, 1,3-bis(2,6-diisoheptylphenyl)imidazol-2-ylidene; INon, 1,3-bis(2,6-diisononylphenyl)imidazol-2-ylidene; IAd, 1,3-diadamantylimidazol-2-ylidene; ICy, 1,3-dicyclohexylimidazol-2-ylidene; ITME, 1,3,4,5-tetramethylimidazol-2-ylidene; BIiPr, 1,3-diisopropylbenzimidazol-2-ylidene; IiPr, 1,3-diisopropylimidazol-2-ylidene; CAC-Mes, 1,3-dimesityl-5,5-dimethyl-4-oxo-3,4,5,6-tetrahydropyrimid-2-ylidene; 6-IPr, 1,3-bis(2,6-diisopropylphenyl)-3,4,5,6-tetrahydropyrimid-2-ylidene; ThIPr, 3-(2,6-diisopropylphenyl)-4,5,6,7-tetrahydrobenzothiazol-2-ylidene; CAAC-IPr, 1′-(2,6-diisopropylphenyl)-1′,2′,4′,5′,6′,7′-hexahydrospiro[cyclohexane-1,3′-indol-2-ylidene]. |
| This journal is © The Royal Society of Chemistry 2015 |