Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Critical analysis of the limitations of Bleaney's theory of magnetic anisotropy in paramagnetic lanthanide coordination complexes†
Alexander M.
Funk
,
Katie-Louise N. A.
Finney
,
Peter
Harvey
,
Alan M.
Kenwright
,
Emily R.
Neil
,
Nicola J.
Rogers
,
P.
Kanthi Senanayake
and
David
Parker
*
Department of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: david.parker@dur.ac.uk
First published on 17th December 2014
Abstract
The origins of the breakdown of Bleaney's theory of magnetic anisotropy are described, based on an analysis of eleven different complexes of the second half of the 4f elements that form isostructural series. An examination of the chemical shift and relaxation rate behaviour of resonances located at least four bonds away from the paramagnetic centre was undertaken, and correlated to theoretical predictions. The key limitations relate to comparability of ligand field splitting with spin–orbit coupling, variation in the position of the principal magnetic axis between Ln complexes and the importance of multipolar terms in describing lanthanide ligand field interactions.
Introduction
We describe experimental evidence showing that Bleaney's theory of magnetic anisotropy has severe limitations. The origins of the breakdown are traced and the implications assessed for the design of paramagnetic probes in magnetic resonance.Bleaney's theory of magnetic anisotropy1 has been a key reference point for over 40 years, when considering the chemical shift of NMR resonances that are at least four bonds from a paramagnetic lanthanide centre. Under these conditions, any contact contribution to the shift is usually very small and the measured paramagnetic shift is predominantly a pseudocontact shift (δp)1,2 that can be defined in terms of the geometric coordinates, the ligand field, temperature and the nature of the lanthanide ion, eqn (1) to (2),
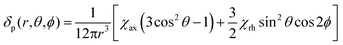 | (1) |
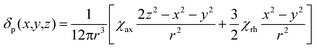 | (2) |
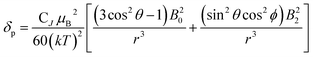 | (3) |
| CJ = g2J(J + 1)(2J − 1)(2J + 3)〈J|α|J〉 | (4) |
Limitations of Bleaney theory
There are several assumptions in this theory that need scrutinising. First, Bleaney assumed that the ligand field splitting is much less than kT (205 cm−1 at 298 K). Generally, this is not the case. Values for B20 of between 80 and 1500 cm−1 have been established,3 with the majority of coordination complexes having B20 values of more than two times kT. The theory ignores the contribution of higher order crystal field terms that may play an important role in determining the overall ligand field, especially in low symmetry systems. This aspect has been addressed in part by Golding in detailed mathematical analyses that lack physicochemical relevance.4 Second, it is assumed that the electron is a point charge at the coordinate origin, and that its relaxation is instantaneous. This is evidently also not true, and consideration of f electron density probability functions suggest that a distributed model may be more apt. Such an approach has been put forward recently by Kuprov, in an important step.5 Furthermore, models of f electron distributions, highlighted by Long,6 show how certain ions (e.g. Eu, Yb, Tm and Er) possess a prolate f electron density distribution, whilst others (e.g. Ce, Pr, Tb, Dy) are oblate. Such behaviour correlates with the differing sense of shift, incorporated in the Bleaney constant, CJ. Third, it is assumed that the position of the principal magnetic axis does not vary as the lanthanide ion changes in an isostructural series of complexes. However, Sessoli has recently demonstrated that in the solid-state at very low temperature, the principal (easy) axis of magnetisation in the C4 symmetric complexes of [Ln.DOTA(H2O)] (DOTA = 1,4,7,10-cyclododecane-tetracetate), changes position as the Ln series is traversed.7,8 It rotates by up to 90° from Tb to Yb, for example, and aligns approximately with the molecular C4 axis only for those ions that have a prolate f electron distribution, i.e. Yb, Tm and Eu.Finally, in devising the Bleaney constants (CJ), it is implicitly assumed that J is a good quantum number that defines the spin–orbit coupling. However, the Russell–Saunders coupling scheme may not be appropriate for these relatively heavy elements and the values of the spin–orbit coupling energies (typically of the order of 650 to 1800 cm−1), are not much bigger than the overall ligand field splitting terms in some cases, in complexes where the ligand field is large. In this situation, the concept of ‘J mixing’ is often invoked,9,10 as a means of correcting for, or simply recognising imprecision in J. The measurements of Sessoli were carried out in the solid state at cryogenic temperatures. Under these conditions, the orientation of the principal axis of the magnetic anisotropy relative to the molecular symmetry axis should not be regarded as breaking the primacy of the molecular symmetry axis in solution at room temperature. Sessoli argues that the orientation of the principal axis, in the plane perpendicular to the molecular symmetry axis, changes by up to 90° according to whether a water molecule occupies the axial coordination site, (and exchange of water at this site is known to be rapid in aqueous solution at room temperature, which tends to average any anisotropy in the plane perpendicular to the molecular symmetry axis). Furthermore, rapid isotropic molecular tumbling in solution at room temperature also tends to average anisotropy perpendicular to the molecular symmetry axis. Since the principal magnetic axis corresponds to the largest Cartesian component of the anisotropy tensor, in the presence of averaging in the plane perpendicular to the molecular symmetry axis, a principal axis perpendicular to the molecular symmetry axis corresponds to an oblate tensor while a principal axis collinear with the molecular symmetry axis corresponds to a prolate tensor. Indeed, it seems likely that Sessoli and Long report mutually consistent conclusions, expressed in rather different terms. It is clear from the number of 1H NMR signals observed for the symmetric complexes that they have effectively zero anisotropy, on the relevant timescale, in the plane perpendicular to the molecular symmetry axis in solution at room temperature. The same averaging does not apply to non-symmetric complexes.
The limitations of Bleaney theory have been expressed previously,1,2 notably by Binnemans.10,11 He examined the theoretical impact of distortion from rotational symmetry on the local magnetic anisotropy in selected model systems, and suggested that the effect could be significant.
Results and discussion
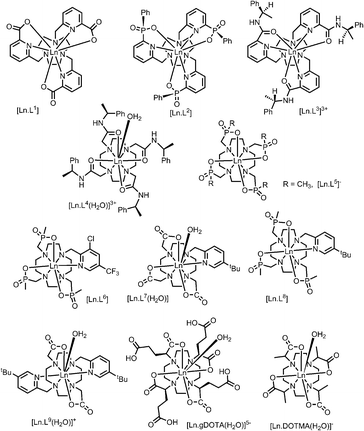
A systematic analysis was undertaken of shift and relaxation rate data for lanthanide(III) complexes that have been shown to form an isostructural series from Tb to Yb. The resonances analysed were separated by at least four bonds from the lanthanide ion, in order to minimise any contribution arising from a contact shift.1d In all, eleven different systems were studied, ranging from three complexes possessing a time-averaged C3 axis of symmetry [Ln.L1–3]12–14 certain systems with average C4 symmetry e.g., [Ln.L4(H2O)]3+,15 [Ln.L5]−,16 (plus selected complexes of [Ln.gDOTA(H2O)]5− and [Ln.DOTMA(H2O)]− that themselves do not form an isostructural series, yet whose hydration state and degree of twist is established),17,18 to a set of lower symmetry cyclen complexes, which divide into 9-coordinate carboxylate and 8-coordinate phosphinate examples,19,20 (Scheme 1). For each of these examples, the value of the second order crystal field term B20 was estimated by analysis of the splitting of the ΔJ = 1 band in the emission spectrum of the corresponding Eu(III) complex, following established methods.21The values of crystal field coefficients are generally considered to decrease only slightly across the lanthanide series, for complexes in a common coordination environment. The values of B22 are generally smaller than those for B20 and are not so readily obtained by spectral analysis.22
Shift behaviour of the C3 symmetric series, [Ln.L1–3]
The three complexes, [Ln.L1–3], differ in the nature of the oxygen donor. The ligand field in these systems is comparatively small and is less than [Ln.L1–2] or of the same order as kT [Ln.L3]3+. Due to their C3 symmetry, the second order crystal field splitting parameter, B20 should characterise the overall crystal field splitting dependence of each complex, according to Bleaney theory. Assignments of each ligand proton NMR resonance have been reported earlier and were verified by measuring the rate of relaxation of each resonance at five different magnetic fields (4.7 to 16.5 T).12–14 This data set also allowed the distance of each resonance from the paramagnetic centre in the solution state to be estimated and compared to that established by the X-ray structural analyses, reported in each case. Intramolecular nuclear relaxation rate data is most commonly analysed using Bloch–Redfield–Wangsness theory. The paramagnetic relaxation arises from rotational and conformational modulation of the electron–nuclear dipolar interaction, eqn (5) and (6).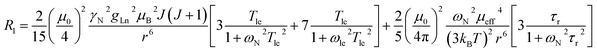 | (5) |
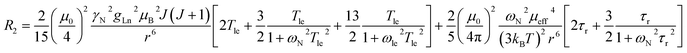 | (6) |
These equations are also based on certain assumptions. First, the point-dipole approximation is assumed and the dipolar and Curie contributions are treated as additive and ignore any cross-relaxation. The zero-field splitting (ZFS) of the energy levels is neglected, although Luchinat has proposed a modification to the dipolar term that gives weight to the size of the ZFS term, leading to an increase in T1e.23 Finally, the rotational correlation time, τr, is treated as isotropic and is assumed to be the same for each resonance examined. This is evidently not true, as perfect motional coupling does not occur. The occurrence of localised rotational correlation times has been quantified by Szabo, for cases where the local motion of the atom or groups of atoms under consideration is not strongly coupled to the overall molecular tumbling rate.24
The variation of experimental relaxation rate data12 with field was used to estimate the Ln–proton average distance, r, and the complex rotational correlation time, τr, using global minimisation methods25 for the six complexes (Tb–Yb) individually. Using literature values of μeff, fits to eqn (5) were allowed to minimise, and converged to well-defined minima. The computed distances correlate well with those found by X-ray analysis, consistent with correct NMR assignments, (Table 2).
| Ln3+ | δ H/ppm | |||||
|---|---|---|---|---|---|---|
| pyH3 | pyH4 | |||||
| [Ln.L1] | [Ln.L2] | [Ln.L3]3+ | [Ln.L1] | [Ln.L2] | [Ln.L3]3+ | |
| a Averaged overall of the six lanthanide(III) ions examined; the ionic radius of Ln3+ ions in 8 and 9 coordination contracts by 0.06 Å from Tb to Yb; b for [Ln.L1–3], values rise from +75 to +110 and +235 cm−1 respectively. c Magnetic susceptibilities used in the fitting analysis here: Tb (9.8); Dy (10.3); Ho (10.4); Er (9.4); Tm (7.6); Yb (4.3) BMA. | ||||||
| Tb | 0.1 | −7.1 | −11.0 | 4.9 | −2.3 | −3.2 |
| Dy | 9.4 | −1.4 | 1.9 | 10.6 | 1.4 | 5.0 |
| Ho | 3.9 | 2.3 | −5.5 | 6.2 | 4.1 | −0.4 |
| Er | 8.3 | 13.6 | 8.2 | 7.9 | 11.9 | 7.9 |
| Tm | 14.2 | 18.6 | 23.0 | 13.5 | 16.4 | 19.6 |
| Yb | 9.5 | 10.7 | 11.6 | 9.1 | 10.3 | 11.2 |
| Average ra/Å | 5.56 | 5.71 | 5.50 | 6.28 | 6.58 | 6.46 |
| X-ray rc/Å | 5.40 | 5.53 | 5.48 | 6.22 | 6.36 | 6.26 |
A general increase of the pseudocontact shift with increasing ligand field is evident from [Ln.L1] to [Ln.L3]3+. However, the order and strengths of the magnetic anisotropies show irregularities. In particular, Er(III) stands out, due to the absence of a paramagnetic shift in both [Er.L1] and [Er.L3]3+. The complex [Dy.L1] also shows unexpected behaviour with a variable sign for the shift, not shown by the Tb analogue. This is the only case observed where the sign of a pseudocontact shift value does not follow the trend of the sign of the Bleaney constant. The chemical shifts of the pyH3 resonance do not follow the predicted values of magnetic anisotropy. The expected order of Dy(III) > Tb(III) ≫ Ho(III) is not conserved in each series. Here, the Tb(III) complexes give rise to the biggest pseudocontact shift and each Dy(III) complex behaves differently. Even in these systems with a small ligand field, the order of magnetic anisotropy predicted by Bleaney's theory is not followed. The shift behaviour of pyH4 and pyH5 in these complexes was similar to pyH3 (ESI†).
The unusual shift behaviour here suggested the need to consider that there might be a significant contact shift for the pyH3–5 resonances, notwithstanding their 4 and 5-bond separations from the paramagnetic centre. Using the ‘two nuclei’ method devised by Reuben,1e plots of the paramagnetic shift of pyH4 divided by 〈Sz〉 versus pyH3/〈Sz〉 gave linear correlations (ESI†) for each complex (R2 > 0.99) with intercepts of <0.1. These plots are independent of CJ and any crystal field term. The linear relationship confirms isostructurality, and the intercept gives a measure of the hyperfine coupling constant. The near-zero intercepts found (ESI,† pp. 24–27) are consistent with a very small contact shift contribution, as hypothesised above.
Binnemans10,11 suggested that the local magnetic anisotropy is modulated by the shape and degree of distortion of the coordination polyhedron in series of lanthanide(III) complexes. An analysis of the twist angle of the mean plane of the 9N3 ring with reference to the three oxygen donor atoms in the X-ray structures of the C3 symmetric complexes ([Ln.L1–3]) was undertaken.12 No correlation between the twist angles (22 ± 2° in each system) and the measured magnetic anisotropy was found, indicating that polyhedral distortion does not seem to explain the observed shift variation in this case.
Shift behaviour in C4-symmetric systems
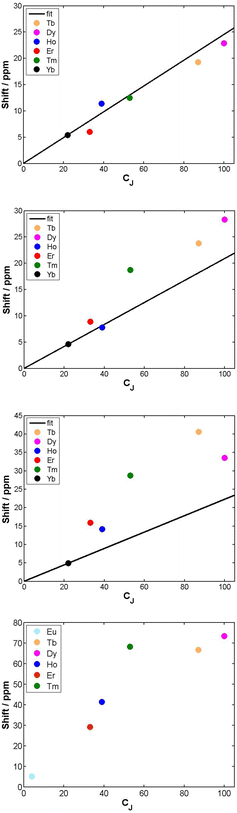
The cationic lanthanide(III) complexes of the tetra-amide ligand, L4, form an isostructural series across the f block, with each complex adopting a mono-capped square-antiprismatic structure with an axial water molecule.15 The paramagnetic shift, for Yb and Eu complexes, has been shown to be particularly sensitive to the polarisability of the capping donor ligand, giving rise to 1H NMR shift variations of up to 60 ppm for an axial ring proton in the Yb complex.26 Such magnetic anisotropy behaviour may be consistent with the hypothesis of the importance of the matching of a prolate f electron density distribution (e.g. Yb, Eu) with the ligand geometry, in defining the orientation of the principal magnetic axis.7 The other complexes in C4 symmetry that were analysed were the mono-aqua isomers of [Ln.DOTMA(H2O)]− and the [Ln.gDOTA(H2O)]5− analogues (Scheme 1) that exist in a capped square-antiprismatic coordination environment,17,18 and the eight-coordinate series of tetra-phosphinates, [Ln.L5]−, in which there is no bound water molecule and the twist angle about the C4 axis of the N4 and O4 planes reduces from 40° to 29°.16The tetra-amide shifted resonances analysed were the methyl and the phenyl ring protons. In each case, and as observed for every complex examined here in which the proton was >4.5 Å distant, the observed paramagnetic shift varied linearly with T−2 (ESI†). The degree of deviation from ideal Bleaney behaviour was assessed by plotting the shift versus the Bleaney coefficient, (Fig. 2 and ESI†). In each case, it was assumed that the plot went through the origin (yttrium case) and that Yb systems were the best behaved,1c and so these two points were used to define the line drawn, i.e. not a ‘best-fit’ plot. The plots for [Ln.L4(H2O)]3+ show a reasonable correlation, indeed better than for any other system examined here, although the Ho, Er and Tm cases showed significant deviations.
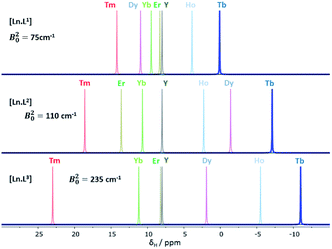 | ||
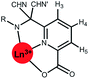
| Fig. 1 Schematic illustration of the chemical shift behaviour of the pyridyl H3 resonance in [Ln.L1–3]; (295 K, 9.4 T, [Ln.L1] in D2O, [Ln.L2,3] in CD3OD); Bleaney CJ values: Tb(−89), Dy(−100), Ho(−39), Er(+33), Tm(+55), Yb(+22) do not correlate well with this shift behaviour (ESI† for plots). Similar plots arise for the other two pyridyl proton resonances (ESI†); the Y complex serves as the diamagnetic reference. | ||
The second order crystal field splitting of [Ln.DOTMA(H2O)]− is one of the largest considered here (−700 cm−1, major isomer vs. −470 cm−1 for the tetra-amide complex). The 1H NMR pseudocontact shifts of the methyl group for [Ln.DOTMA(H2O)]− do not correlate very well with CJ; the Tm(III) complex in particular shows a large deviation.1c Similar behaviour is evident in the 8-coordinate phosphinate series, [Ln.L5]−, where even greater scatter was found for the methyl group shifts (Fig. 2; the Me proton is separated by 4 bonds from the Ln(III) ion).
Eight and nine-coordinate complexes in lower symmetry
The series of complexes, [Ln.L6–9] have lower time-averaged symmetry and allow a comparison of 9-coordinate (q = 1) carboxylate systems with 8-coordinate (q = 0) phosphinate analogues. In the complexes of L6, a CF3 group is located 6.1 Å from the metal centre,19 whereas in the other three cases a tBu group is 6.6 (±0.2) Å distant, each separated by 5 bonds. Paramagnetic shift data for the tBu resonance revealed dramatic differences between the 9 and the 8-coordinate complexes, (Table 3), that lack an axial donor.| Ln3+ | δ H/ppm [Ln.L7] | [Ln.L8] | [Ln.L9]+ | C J |
|---|---|---|---|---|
| Tb | −11.6 | −76.9 | −7.2 | −89 |
| Dy | −20.5 | −75.0 | −17.8 | −100 |
| Ho | −7.4 | −31.8 | −7.0 | −39 |
| Er | 7.0 | 38.2 | 3.4 | +33 |
| Tm | 10.8 | 67.0 | 6.2 | +55 |
| Yb | 6.3 | 16.3 | 9.1 | +22 |
| B 20/cm−1 | −550 | −570 | −350 |
The shift increased by over 50 ppm for the Tb, Dy and Tm complexes, which is independent of any change simply related to the variation of B20. The Tb, Ho and Er complexes of L7 and L9 show rather small shifts, about the same as for Yb in the latter case. The proton NMR dipolar shifts do not follow the Bleaney constant variation, within either series. Furthermore, when comparing the 19F shift of the CF3 resonances in [Dy.L6] (δF −162; dipolar shift −99 ppm) and the mono-aqua 9-coordinate analogue, [Dy.L10(H2O)],27 the difference was 47 ppm (δF −115; dipolar shift −52 ppm). The trend in the fluorine shift correlates fairly well with the CJ value, except for the Tm complex (Fig. 3).
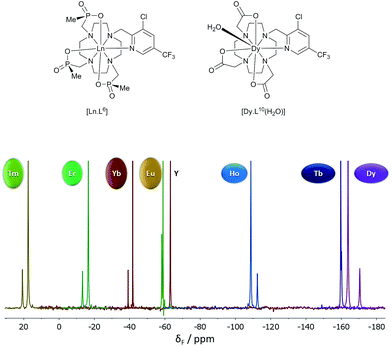 | ||
| Fig. 3 19F NMR spectra for [Ln.L6] (295 K, D2O), showing the two major chiral stereoisomers (RRR-Δ and RRR-Λ); the Y example serves as the diamagnetic reference. | ||
It has been shown that the dipolar shift in the 9-coordinate cationic complexes of L4 with Eu and Yb, is primarily determined by the nature of the neutral axial donor group and its relative polarisability.26 Therefore, it was considered appropriate to compare complexes of ions with an oblate electron density distribution (e.g. Ce, Tb), examining their shift sensitivity to axial donor permutation. Accordingly, the variation of the ligand proton resonances in these complexes as a function of axial donor polarisability was examined in solution, under similar conditions to those studied originally (dry CD3CN, 295 K, 10 fold excess of added donor: (H2O, MeOH, DMAP, DMF, DMSO)). It was found that changing the donor in the Ce, Tb and Tm complexes gave rise to proportionate pseudocontact shift variations in each case, similar in relative size to those observed for Eu and Yb complexes, (ESI†). This finding lends support to the notion that the nature of the axial donor in Cn symmetric complexes is the major factor determining the dipolar ligand field interaction, in a manner that is proportional to the second order term, B20,26 and that this effect is largely independent of the spatial distribution of the f electron cloud (prolate or oblate).
Summary and conclusions
Bleaney theory suggests that there are four key terms that determine the pseudocontact shift: the absolute temperature; the ligand field, defining the interaction between the f electron cloud and the ligand donors; the geometric coordinates of the nucleus with respect to the main axis of magnetisation; the degree of spin–orbit coupling and its relative size with respect to the ligand field. The latter term is related to the Bleaney constant (sign/magnitude), yet is confounded with any ligand field parameter.The temperature dependence of the pseudocontact shift strictly followed a T−2 relationship for each case examined here. For resonances where a dominant pseudocontact shift occurs (at least 4 bonds separated; most resonances examined here are >6 Å), a strict T−2 variation of the paramagnetic shift was followed in every example measured (ESI†); resonances subject to a major contact shift contribution are predicted to show a T−1 variation.1,2
The second main feature to consider is the proportionality of the pseudocontact shift with the ligand field parameter, B20, for axially symmetric isostructural series. The total 1H NMR spectral width for Cn symmetric complexes of Yb and Tm was plotted against B20 (Fig. 4). These two ions possess a similar f electron density distribution, and Yb complexes have been regarded, in the past, as adhering most faithfully to Bleaney theory, as they possess the largest pseudocontact/contact shift ratio.1d The linear correlations (R2 = 0.70 and 0.83 for Yb and Tm respectively) reveal the extent of this dependence. This behaviour is supported by the ligand-field/shift dependence in complexes of L4 (Ce, Eu, Tb, Dy, Tm, Yb), when the axial donor is permuted.
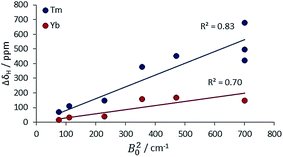 | ||
| Fig. 4 Variation of the total 1H NMR spectral width with B20 for Tm and Yb complexes with axial symmetry (ESI† for tabulated data). | ||
In the complexes of lower symmetry examined herein, higher order ligand field terms must be invoked, relating to multipolar contributions to the overall electrostatic interaction. Such terms are considered, for example, in assessing the non-linear optical behaviour of lanthanide coordination complexes.13 The higher order ligand field parameters, Bkq, where k = 4 and 6, can be over 1000 cm−1 in size, according to data reported from detailed analyses of emission spectra.28,29
The very large changes observed in the chemical shift of both the CF3 groups in the Dy, Er and Tm complexes of L6 and L10 and the tBu resonances in L7–L9, cannot be attributed simply to ligand field variation, as defined by B20 (Table 3), nor to any significant conformational shift of the position of these groups in these relative rigid structures. One explanation is to consider the extent to which the principal axis of magnetisation might have changed position from the complexes of the prolate (e.g. Yb, Tm, Eu) to the oblate ions (e.g. Tb, Ce, Dy, Ho). Thus, the angular terms defining the multipolar interaction can vary from one lanthanide to another, especially the rhombic terms (that are related to the higher order crystal field coefficients), as these complexes are not axially symmetric.
This hypothesis is supported by consideration of the shift behaviour of the 9-coordinate, C3 symmetric systems, [Ln.L1–3], in which the ligand field splitting is the smallest of the cases examined here. No obvious explanation can be put forward for the anomalous shift behaviour of the complexes of Dy, Er and Ho, examining the pyridyl resonances that reside four or five bonds (5.5 to 6.5 Å) away from the paramagnetic centre (Table 1 and ESI†). Moreover, there is no compelling evidence to suggest that there is a significant contact contribution in these cases. Indeed, the modified Reilley plots (ESI† pp. 24–28) suggest that any contact contribution is very small. Furthermore, Tb and Dy have similar intrinsic contact shift sensitivities1,2 yet behave completely differently (Fig. 1). One can hypothesise that either the position of the principal axis is varying in these systems or that the CJ values are not robust constants and may not be independent parameters, i.e. they are confounded.7 Of course, such a situation more obviously arises in cases where the ligand field is large, when J may not be a ‘good’ quantum number, so that CJ values are less likely to be robust, as in the low symmetry phosphinate complexes.
A related issue that emerges from this analysis, is that the generally accepted model for lanthanide paramagnetism (Landé, van Vleck) is based on the assumption that the ligand field splitting is small compared to the spin–orbit coupling, and that J is a good quantum number. This approximation led to the premise that the magnetic susceptibility of lanthanide complexes is independent of coordination environment. Evidently, it appears that this may not necessarily be the case for coordination complexes with a relatively large ligand field splitting. Further evidence in support of such a hypothesis, addressed by examining the field-dependent relaxation behaviour of these systems, will be reported in the near future.
Finally, this study provides some guidance in the design of chemical shift (‘PARASHIFT’) probes for use in magnetic resonance imaging and spectroscopy.20 A pre-requisite in the design of such probes for use in vivo, is to observe a fast-relaxing, reporter resonance that is shifted by over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz from the water (and fat) signals, as this allows fast pulse sequences to be used with large sweep widths. The tBu resonances of the low-symmetry, 8-coordinate pyridyl-triphosphinate series, e.g. [Ln.L8], examined here are much better suited for this application than analogous 9-coordinate carboxylate complexes. They possess relaxation rates of the order of 100 s−1 at 3 to 7 Tesla, and a very large proton chemical shift of +67 (Tm) or −75 (Dy) ppm, Moreover, their linewidths are not too great (ESI†), and R1/R2 ratios are in the range 0.5 to 0.85 at 4.7 T, allowing the use of fast imaging pulse sequences.
000 Hz from the water (and fat) signals, as this allows fast pulse sequences to be used with large sweep widths. The tBu resonances of the low-symmetry, 8-coordinate pyridyl-triphosphinate series, e.g. [Ln.L8], examined here are much better suited for this application than analogous 9-coordinate carboxylate complexes. They possess relaxation rates of the order of 100 s−1 at 3 to 7 Tesla, and a very large proton chemical shift of +67 (Tm) or −75 (Dy) ppm, Moreover, their linewidths are not too great (ESI†), and R1/R2 ratios are in the range 0.5 to 0.85 at 4.7 T, allowing the use of fast imaging pulse sequences.
Further details of ‘PARASHIFT’ imaging in vivo, with systems related to [Ln.L8] will be reported shortly, using this approach.
Acknowledgements
We thank the ERC (FCC 266804) and EPSRC for support, and Professor Mauro Botta (Alessandria) for a sample of [Tm.DOTMA]−, Dmitry Yufit for the X-ray analysis of [Tm.gDOTA(H2O)]−, Mark Woods for access to X-ray data for mono-hydrated [Ln.DOTMA]− complexes and Ilya Kuprov for various helpful comments.Notes and references
- (a) B. Bleaney, J. Magn. Reson., 1972, 8, 91–100 CAS; (b) J. A. Peters, J. Huskens and D. J. Raber, Prog. Nucl. Magn. Reson. Spectrosc., 1996, 28, 283–350 CrossRef CAS; (c) S. Di Pietro, S. Lo Piano and L. Di Bari, Coord. Chem. Rev., 2011, 255, 2810–2820 CrossRef CAS: the shift data reported by Di Bari is consistent with that found here; (d) Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and V. K. Pecharsky, Elsevier, 2003, vol. 33, pp. 353–463 Search PubMed; (e) Consideration of the relative size of contact and dipolar contributions that sum to give the observed paramagnetic shift has often been studied, although it has not yet proved possible to assess the contact shift contribution accurately. The expectation value, 〈Sz〉 gives an indication of the strength of the contact shift for a given Ln(iii) ion. By calculating the ratio of CJ/〈Sz〉, a figure of merit can be obtained that estimates the theoretical pseudocontact/contact shift ratio for a given ion. These values are as follows: Tb (2.7); Dy (3.5); Ho (1.7); Er (2.1); Tm (6.4); Yb (8.5). A fuller discussion and further examples are given in the ESI† (pages 24–27). See also: J. Reuben and G. A. Elgavish, J. Magn. Reson., 1980, 39, 421–430 CAS; (f) J. Ren, S. Zhang, A. D. Sherry and C. F. G. C. Geraldes, Inorg. Chim. Acta, 2002, 339, 273–282 CrossRef CAS.
- I. Bertini, C. Luchinat and G. Parigi, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249 CrossRef CAS.
- C. Görller-Walrand and K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier, 1996, vol. 23, pp. 121–283 Search PubMed.
- R. M. Golding and P. Pyykkö, Mol. Phys., 1973, 26, 1389–1396 CrossRef CAS.
- G. T. P. Charnock and I. Kuprov, Phys. Chem. Chem. Phys., 2014, 16, 20184–20189 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem. Int. Ed., 2013, 52, 350–354 CrossRef CAS PubMed . A small change in the position of the principal magnetic axis can have a large effect on the pseudocontact shift, because of the steep angular dependence (eqn (3)). Intuitively, chemists consider the molecular symmetry axis as representing this magnetic axis, for rapidly tumbling molecules in solution. Sessoli's work (in the solid state and at low temperature) suggests that this analysis needs careful thought. Er, Yb, Tm (and Eu) shift in one sense whereas the oblate ion complexes (Ce, Tb, Dy, Ho) shift in the other sense, and are distinguished by their differing f electron spatial distributions. In this situation, the idea that the product of the Bleaney constant (of varying size and magnitude for each ion, Table 3) and the angular geometric term may be a corollary of a principal axis whose position varies with the nature of the Ln3+ ion and the ligand geometry, needs to be considered further.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- A. S. Souza and M. A. Couto dos Santos, Chem. Phys. Lett., 2012, 521, 138–141 CrossRef CAS.
- V. S. Mironov, Y. G. Galyametdinov, A. Ceulemans, C. Görller-Walrand and K. Binnemans, J. Chem. Phys., 2002, 116, 4673–4685 CrossRef CAS.
- V. S. Mironov, Y. G. Galyametdinov, A. Ceulemans, C. Görller-Walrand and K. Binnemans, Chem. Phys. Lett., 2001, 345, 132–140 CrossRef CAS.
- E. R. Neil, A. M. Funk, D. S. Yufit and D. Parker, Dalton Trans., 2014, 43, 5490–5504 RSC.
- J. W. Walton, R. Carr, N. H. Evans, A. M. Funk, A. M. Kenwright, D. Parker, D. S. Yufit, M. Botta, S. De Pinto and K.-L. Wong, Inorg. Chem., 2012, 51, 8042–8056 CrossRef CAS PubMed.
- G. Nocton, A. Nonat, C. Gateau and M. Mazzanti, Helv. Chim. Acta, 2009, 92, 2257–2273 CrossRef CAS.
- D. Parker, H. Puschmann, A. S. Batsanov and P. K. Senanayake, Inorg. Chem., 2003, 42, 8646–8651 CrossRef CAS PubMed.
- S. Aime, A. S. Batsanov, M. Botta, R. S. Dickins, S. Faulkner, C. E. Foster, A. Harrison, J. A. K. Howard, J. M. Moloney, T. J. Norman, D. Parker, L. Royle and J. A. G. Williams, J. Chem. Soc., Dalton Trans., 1997, 3623–3636 RSC.
- M. Woods, S. Aime, M. Botta, J. A. K. Howard, J. M. Moloney, M. Navet, D. Parker, M. Port and O. Rousseaux, J. Am. Chem. Soc., 2000, 122, 9781–9792 CrossRef CAS.
- S. Aime, M. Botta, Z. Garda, B. E. Kucera, G. Tircso, V. G. Young and M. Woods, Inorg. Chem., 2011, 50, 7955–7965 CrossRef CAS PubMed.
- A. M. Funk, P. Fries, A. M. Kenwright, P. Harvey and D. Parker, J. Phys. Chem. A, 2013, 117, 905–917 CrossRef CAS PubMed.
- P. Harvey, A. M. Blamire, J. I. Wilson, K.-L. N. A. Finney, A. M. Funk, P. K. Senanayake and D. Parker, Chem. Sci., 2013, 4, 4251–4258 RSC.
- K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 245, 75–78 CrossRef CAS.
- W. T. Carnall, G. L. Goodman, K. Rajnakand and R. S. Rana, J. Chem. Phys., 1989, 90, 3443–3457 CrossRef CAS.
- I. Bertini, F. Capozzi, C. Luchinat, G. Nicastro and Z. Xia, J. Phys. Chem., 1993, 97, 6351–6354 CrossRef CAS.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 102, 4546–4559 CrossRef.
- K. H. Chalmers, E. De Luca, N. H. M. Hogg, A. M. Kenwright, I. Kuprov, D. Parker, M. Botta, J. I. Wilson and A. M. Blamire, Chem.–Eur. J., 2010, 16, 134–148 CrossRef CAS PubMed.
- R. S. Dickins, D. Parker, J. I. Bruce and D. J. Tozer, J. Chem. Soc., Dalton Trans., 2003, 1264–1271 RSC.
- P. Harvey, PhD thesis, Durham University, 2012. For the Tm analogues the 19F shifts of [Tm.L6] and [Tm.L10(H2O)] (ESI†) were +17.1 and −42.1 ppm (295 K, D2O), i.e. dipolar shifts of +80.1 and +21.0 ppm respectively, with respect to the diamagnetic resonance (−63.0/−63.1 ppm).
- T. A. Hopkins, J. P. Bolender, D. H. Metcalf and F. S. Richardson, Inorg. Chem., 1996, 35, 5347–5355 CrossRef CAS.
- J.-G. Kang and T.-J. Kim, Bull. Korean Chem. Soc., 2005, 26, 1057–1064 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterisation of selected complexes, NMR spectral figures, tables of shift (including T dependence) and relaxation rate data at 5 magnetic field strengths. The X-ray structure of [Tm.gDOTA(H2O)]is available. CCDC 1032378. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc03429e |
| This journal is © The Royal Society of Chemistry 2015 |