Theoretical studies on a carbonaceous molecular bearing: association thermodynamics and dual-mode rolling dynamics

Abstract

The thermodynamics and dynamics of a carbonaceous molecular bearing comprising a belt-persistent tubular molecule and a fullerene molecule have been investigated using density functional theory (DFT). Among ten representative methods, two DFT methods afforded an association energy that reasonably reproduced the experimental enthalpy of −12.5 kcal mol⁻¹ at the unique curved π-interface. The dynamics of the molecular bearing, which was assembled solely with van der Waals interactions, exhibited small energy barriers with maximum values of 2–3 kcal mol⁻¹ for the rolling motions. The dynamic motions responded sensitively to the steric environment and resulted in two distinct motions, precession and spin, which explained the unique NMR observations that were not clarified in previous experimental studies.

---

Introduction

Assembled solely by van der Waals force, supramolecular complexes between single-wall carbon nanotubes (SWNT) and fullerenes, the so-called peapod structure, represents a unique class of host–guest complexes and has attracted attention from both chemists and physicists.¹ The tube-sphere combination behaves as a carbonaceous bearing, and the inner fullerene journal moves dynamically.² In addition to the direct observation of sliding and rolling motions in an infinite SWNT by transmission electron microscopy,^3,4 detailed experimental analyses of the thermodynamics and dynamic motions are currently being exploited with finite SWNT molecules as the outer bearing to reveal fundamental structural features of peapod bearings.^5–8 Notably, the introduction of a substituent on the fullerene molecule allowed for a single-axis rolling motion of the journal,^5,6a which should permit the modular design of carbonaceous molecular bearings. Although the non-directional nature of the association force is also unique among molecular machines,⁹ an understanding of the dynamic behaviors has not been achieved thus far due to anomalous molecular structures. We herein report quantum chemical studies of the peapod bearing. Along with evaluations of appropriate methods for theoretical studies on curved π-systems, we report on the energetics and dynamics of the single-axis rolling motions of the peapod bearing. The theoretical study revealed the presence of a minute energy barrier for dynamic motions as well as dual-mode rolling dynamics of the fullerene journal. The present theoretical picture should be informative for the future molecular design of carbonaceous bearings with elaborate functions.

Results and discussion

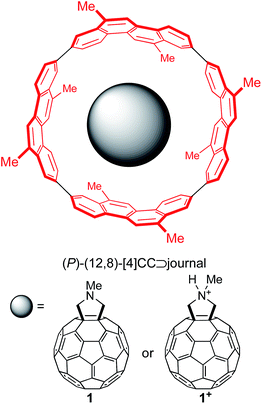
Single-axis rolling motions of the fullerene journal have been experimentally demonstrated with a series of fullerene molecules encapsulated in a finite SWNT molecule, (P)-(12,8)-[4]cyclo-2,8-crysenylene ([4]CC),^5,6a and, as a representative journal for this theoretical investigation, we adopted fulleropyrrolidine (1) and its protonated pyrrolidinium (1⁺) (Fig. 1). The substituents on the outer bearing were modeled with methyl groups, which mimic alkyl groups with minimum conformational variations.¹⁰

Fig. 1 Chemical structures of peapod bearings for theoretical studies.

Evaluation of methods of density functional theory (DFT) for association energetics

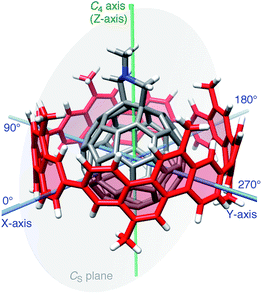
Considering the lack of established methods for theoretical studies of curved π-systems, we first screened the level of theory among representative DFT methods for the reproducibility of experimental thermodynamics of association.¹¹ We used 6-311G(d) as a common basis set throughout the DFT investigations.¹²In vacuo, basis set superposition errors (BSSE) were corrected by the counterpoise method (Table S3†),^13,14 and, in a theoretical solvated state, dichloromethane was incorporated via the polarizable continuum model (PCM).¹⁵ For DFT methods, we selected six methods from long range-corrected (LC)-DFT (CAM-B3LYP,¹⁶ LC-BOP,¹⁷ LC-ωPBE,¹⁸ LC-BLYP,¹⁹ ωB97X²⁰ and ωB97 (ref. 20)), two methods with implementation of dispersion forces (B97-D²¹ and ωB97X-D²²) and two other popular methods (BMK²³ and M06-2X²⁴).

A molecular structure for this screening study is described. As a representative geometry, we started with the molecular structure shown in Fig. 2. In this geometry, a central axis of 1 through the gravity center of two sp³-carbon atoms at the hexagon–hexagon junction of the fullerene and the gravity center of two sp²-carbon atoms at the opposite hexagon–hexagon junction were aligned on the C₄ symmetry axis of the [4]CC bearing. As a result, the C₄ axis of the [4]CC bearing (green axis in Fig. 2) is placed on the C_S mirror plane of the journal molecule 1 (gray plane in Fig. 2). Note that this structure represents one of the time-averaged structures that have been experimentally deduced by NMR analysis.^5,25 As we discuss the details in the following section, this orientation also corresponds to one of the global minima of idealized single-axis rolling motions (0° in Fig. 3).

Fig. 2 Molecular structure of (P)-(12,8)-[4]CC⊃1 from the calculation (LC-BLYP/6-311G(d), geometry optimized). Hydrogen atoms are colored in white, carbon atoms of [4]CC are colored in red, carbon atoms of 1 are colored in gray, and a nitrogen atom of 1 is colored in blue. Representative symmetry elements are also shown: for [4]CC, the C₄ axis is shown as a green tube, and, for 1, the C_S mirror plane is shown as a gray transparent plane. For the discussion of rotation motions, X- and Y-axes are defined and shown as light-blue tubes. Note that the green C₄ axis in this figure also serves as Z-axis in the fixed system. Representative rolling angles θ for single-axis motions are shown as X- and Y-axes.

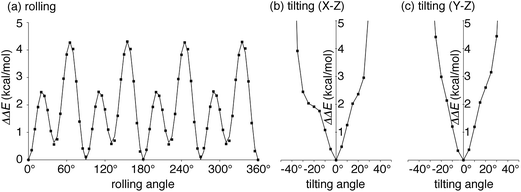Fig. 3 Energetics of the idealized motions of 1⁺ in (P)-(12,8)-[4]CC from single-point calculations with LC-BYLP/6-311G(d)/PCM. (a) Energetics of single-axis rolling motions. Data from DFT calculations are plotted as filled squares, and the fitting curve is derived from eqn (1). (b) Energetics of tilting motions along the X–Z plane. (c) Energetics of tilting motions along the Y–Z plane.

After geometry optimizations, the structures of (P)-(12,8)-[4]CC⊃1 converged, independent of the DFT methods, into an essentially identical structure with a small root-mean-square deviation (RMSD) of 0.195 Å (Fig. S1†).²⁶ We estimated the theoretical association energy (ΔE) for the formation of (P)-(12,8)-[4]CC⊃1 both in vacuo and in PCM dichloromethane solution by comparing the potential energy of (P)-(12,8)-[4]CC⊃1 with those of each component. As a reference, we also carried out isothermal calorimetry (ITC) analysis to derive the experimental enthalpy for the association of (P)-(12,8)-[4]CC⊃1 in dichloromethane and obtained a value of −12.5 ± 0.2 kcal mol⁻¹ (Fig. S2†).^5,27–29 The energetics of the association is summarized in Table 1. The PCM implementation commonly contributed to the energy in a positive manner by ca. +3 kcal mol⁻¹, and these data with PCM solvation were compared with the experimental value. The dependence of the association energy on the DFT method was considerably large, and the energy values varied between +7.6 kcal mol⁻¹ and −66.6 kcal mol⁻¹. Among the ten DFT methods examined in this study, the LC-BLYP/PCM method afforded a value of −9.2 kcal mol⁻¹ and the smallest deviation of +3.3 kcal mol⁻¹ from the experimental value. Albeit counterintuitively, the implementation of dispersion force in DFT methods did not necessarily improve the theoretical prediction, which might indicate that the dispersion effects at the curved π-interfaces are overestimated by the present DFT methods with pairwise dispersion forces.³⁰ The BMK/PCM method gave the second nearest value of −7.6 kcal mol⁻¹ with a deviation of +4.9 kcal mol⁻¹.³¹ The superiority of the BMK method has been previously reported for van der Waals π–π interactions,³² but the reproducibility tendencies of other methods are different in curved π-systems.³³ The present result of the screening study could thus serve as a benchmark for the theoretical studies on curved π-structures including infinite SWNTs. Examination of other curved systems, for instance with LC-BLYP and BMK, is of interest for examining the versatility of the methods.³⁴ The van der Waals interactions including effects of resultant charge transfer in the peapod systems^6c may be modeled well by LC-BLYP.^19,35

Table 1 Experimental and theoretical energetics of association of (P)-(12,8)-[4]CC⊃1^ab

Methods	ΔE in vacuo^c	ΔE with PCM	Deviation^d
a The basis set of 6-311G(d) was commonly used. b Data are shown in kcal mol^−1. c See Table S3 for BSSE corrections. d Deviation from the experimental value. The value from DFT calculations with PCM solvation was subtracted by the experimental value of −12.5 kcal mol^−1. e The experimental value (ΔH) was obtained from ITC analysis in dichloromethane. See Fig. S2 for the data.
Experiment^e	—	−12.5	—
CAM-B3LYP	+5.3	+7.6	+20.1
LC-BOP	+1.7	+4.3	+16.8
LC-ωPBE	−4.1	−1.3	+11.2
BMK	−10.5	−7.6	+4.9
LC-BLYP	−12.0	−9.2	+3.3
ωB97X	−27.8	−25.0	−12.5
ωB97	−35.9	−32.9	−20.4
M06-2X	−47.9	−44.5	−32.0
B97-D	−62.2	−59.2	−46.7
ωB97X-D	−69.8	−66.6	−54.1

---

Energetics of idealized single-axis rolling dynamics

We next explored the energetics hitherto unavailable by experiments. The effects of protonation with the fullerene journal were first examined by DFT methods with PCM solvation. Note that the dynamics of the journal were experimentally investigated with the protonated form of (P)-(12,8)-[4]CC⊃1⁺, but the association energetics were not readily accessible by experiments.⁵ As shown in Table S2,† the protonation of the pyrrolidine ring was common in the stabilization of the complex by ca. −1 kcal mol⁻¹ without any structural deviations in both the bearing and the journal. The small difference indicated a minor contribution of electrostatic interactions for the association of fullerene, which was consistent with the experimental analysis for the association of Li⁺-encapsulated C₆₀.^6a

With this protonated structure of (P)-(12,8)-[4]CC⊃1⁺ in hand, we then investigated the energetics of idealized single-axis rolling motions. As we observed in the crystallographic analysis of (12,8)-[4]CC⊃C₆₀,^6b the structural rigidity of the bearing and the journal allows, experimentally, for rolling motions without affecting the curved sp²-structures of each component: hence, the energetics from single-point calculations of different molecular orientations should provide coarse yet valuable information on the energy profiles. We therefore rolled journal 1⁺ from the geometry obtained for the association energetics (Fig. S3†) by 5° around the Z-axis of the fixed system of coordinates, i.e., the C₄ symmetry axis of the [4]CC bearing, and obtained the energetics. The relative potential energies (ΔΔE) obtained with LC-BLYP/PCM method are plotted with squares in Fig. 3a.³⁶ The highest energy barrier for the idealized single-axis motions was estimated to be +4.3 kcal mol⁻¹, which is as small as the experimental barrier for methyl rotations.³⁷ The small barriers found in this study also explains the dynamic motions of the molecular bearing of (12,8)-[4]CC⊃C₆₀ in the solid state where four different orientations of C₆₀ molecules were observed in the absence of structural fluctuations in the [4]CC bearing.^6b

Four sets of nearly identical potential barriers appeared periodically at the intervals of 1/4 rotations through one circle of the rolling motion. Each of the curves for 1/4 rotations accompanied two energy minima and two saddle points. As a result of a Fourier series expansion of the energetics, we found that the potential curve can be fitted by the following equation

ΔΔE = −0.86 sin θ + 0.37 sin 8θ − 0.42 cos 4θ − 1.46 cos 8θ + 1.89 (1)

where θ is the rolling angle of 1⁺ (cf.Fig. 2). The potential curve fitted with this equation is shown as a line in Fig. 3a, which shows that the DFT energetics for the rolling motion can be well described by this equation. Although we could not deduce any apparent electronic origin of this equation from the orbital analysis, a phenomenological interpretation can be made from the sterics analysis. The periodicity of the potential energy curve corresponds well to the periodicity of the passing of two carbon atoms on the C₆₀ equator over the C₂ symmetry axes of [4]CC (Fig. S3†), and the energy minima appear when the equator carbon atoms are located over the C₂ symmetry axes.³⁸ Note that a pair of carbon atoms on opposite sites defines the longest C–C distance, i.e., diameter of C₆₀. This simplification of the energetics with an equation largely owes its origin to the van der Waals nature of the contacts without any directional and biasing interactions from substituents. This energy profile estimated by single-point calculations does not deviate much from the transition-state (TS) analysis of realistic motions (vide infra), which is most likely ascribed to the unique tube-sphere molecular recognition with persistent molecular shapes.⁶

For the idealized rolling motions, we also examined self-consistent-charge density-functional-based tight-binding (SCC-DFTB) method as a computationally cheaper substitute to be explored further in molecular dynamics (MD) simulations.^39–41 As shown in Fig. S4,† the SCC-DFTB method afforded a potential energy curve with two saddle points and two local minima for 1/4 rotations, which is qualitatively similar to that of the DFT result.⁴² Attention must be paid, however, to the quantitative discussion of the SCC-DFTB method because a deviation of ca. −3 kcal mol⁻¹ from the LC-BLYP/PCM method was observed for the energy barrier. Nonetheless, the similar shapes of energy profiles between DFTB and DFT methods might preferably lead to similar trajectories, for instance, in MD simulations (vide infra).

Energetics of tilting fluctuation toward realistic rolling motions

The idealized single-axis rolling motions describe the simplified, time-averaged dynamics of the experiments, and we further investigated another possible fluctuation in the structure to step into realistic motions. Another possible fluctuation is the tilting motions of 1⁺. We thus calculated the tilting energetics for two directions in a range of ±45°. The central axis of 1⁺ was thus tilted along either the X–Z plane or Y–Z plane by 5° (cf.Fig. 2), and the energies are shown in Fig. 3b and c. The titling fluctuation of 1⁺ for both directions were below 4 kcal mol⁻¹ until ±30° with minute kinks of steric origins in the profile. The height of the tilting energetics within ±30° is therefore lower than that of the rolling energetics, which indicates that the rolling motions might also accompany the tilting fluctuations.

Theoretical studies of the dynamic motions: dual-mode dynamics

Finally, theoretical investigations on realistic dynamic motions of 1⁺ revealed the structural origins of anomalous spectroscopic observations from experiments. Previous spectroscopic studies are briefly summarized.^5,43 Proton NMR studies on (P)-(12,8)-[4]CC⊃1⁺ in dichloromethane confirmed the rolling motions of 1⁺ by demonstrating symmetric relationships among four chrysenylene units through motions of encapsulated 1⁺. Methylene resonances on the pyrrolidinium unit, however, behaved unexpectedly: at low temperature (<25 °C), four protons, i.e., two equatorial protons (eq-1, eq-2) and two axial protons (ax-1, ax-2) (Fig. 4a), appeared separately as expected, but at elevated temperature (25 °C), they were unexpectedly merged into two broad resonances (see Fig. 2e in ref. 5).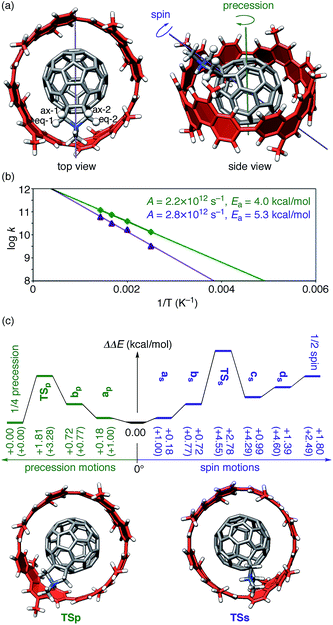

Fig. 4 Realistic dynamics of (P)-(12,8)-[4]CC⊃1⁺. (a) The tilted geometry of (P)-(12,8)-[4]CC⊃1⁺ showing axes for precession motions (green) and spin motions (purple). Four methylene protons of pyrrolidiniums are shown in ball-and-stick models and are labeled. This geometry was located as an energy minimum for the X–Z tilting motion with SCC-DFTB calculations and was used as the starting geometry for MD simulations. (b) Kinetics of precession motions (green) and spin motions (purple) from MD simulations at 400–700 K. (c) Energetics from TS calculations with LC-BLYP/6-311G(d)/PCM//SCC-DFTB. Values in parenthesis show the energies obtained by SCC-DFTB. See Fig. S5† for energetics with SCC-DFTB and LC-BLYP/6-311G(d)//SCC-DFTB and Fig. S6† for the structures.

The MD simulations of (P)-(12,8)-[4]CC⊃1⁺ thus revealed the presence of two different types of motions in real time.⁴⁴ One is a “precession” motion, and the other is a “spin” motion (Fig. 4a). Note that these two motions emerge from a combination of the idealized single-axis motion (Fig. 3a) and the tilting motion (Fig. 3b and c). We performed MD simulations at a time increment of 1 fs for 200 ps by using the SCC-DFTB method. The simulations were performed for 20 trajectories at each temperature varying from 400 K to 700 K, and the frequencies of each motion were counted to afford rate constants for the motions (Tables S3 and S4†). The rate constants were plotted against 1/T to generate the Arrhenius plots shown in Fig. 4b, which gave pre-exponential factors (A) and activation energies (E_a) of 2.2 × 10¹² s⁻¹ and 4.0 kcal mol⁻¹, respectively, for the precession and 2.8 × 10¹² s⁻¹ and 5.3 kcal mol⁻¹, respectively, for the spin. The MD simulations thus show that among these two motions found in dynamics analysis, the precession motions proceed faster than spin motions.

The energy barriers for the two motions were further examined by TS analysis. We first allocated TS by searching the energy surface with a global reaction route mapping (GRRM) method⁴⁵ combined with SCC-DFTB. We then performed single-point calculations with LC-BLYP both in the absence and in the presence of PCM solvation. The energy diagrams are shown in Fig. S5† and 4c. The TS allocated with the SCC-DFTB method were located +3.28 kcal mol⁻¹ (TS_p in Fig. S5†) and +4.60 kcal mol⁻¹ (TS_s in Fig. S5†) above the global minimum for the precession motion and for the spin motion, respectively.⁴⁶ The single-point analysis with LC-BLYP in vacuo negligibly affected the energetics (Fig. S5†). Because the energy barriers matched qualitatively with the values estimated from MD simulations (Fig. 4b), we concluded that the TS analysis yielded reasonable structures for rolling motions. Further implementation of PCM solvation resulted in the energy profile (Fig. 4c) where the PCM solvation lowered the energies of some species most likely through suppression of an overestimation of interactions with charges. With the LC-BLYP/6-311G(d)/PCM//SCC-DFTB method, the energy barrier for precession was thus estimated as +1.81 kcal mol⁻¹, and the one for spin was estimated as +2.78 kcal mol⁻¹. All the analysis of the realistic dynamic motions indicate that the precession motion is preferred over the spin motion by ca. 1 kcal mol⁻¹.

The two motions, i.e., precession and spin, should exert distinct effects over the proton atoms on the pyrrolidinium unit. The precession motions move the methylene protons along the arylene rims and do not change the relative locations from the [4]CC bearing and, as a result, the magnetic effects from the arylene units. However, the spin motions flip the pyrrolidinium unit and its methylene protons, which results in a change in the relative locations from the [4]CC bearing and thus in the magnetic effects from the arylene units. We can therefore interpret the unique spectroscopic behaviors of methylene protons as the result of two different motions with different rate constants.⁴⁷ At low temperature, the precession motions predominate to give four independent resonances of methylene protons, and at high temperature, the spin motions begin to merge the two resonances.

Conclusion

Theoretical studies on a carbonaceous molecular bearing have been conducted. The first extensive evaluation of various DFT methods for application to curved π-systems revealed a considerable method dependence of the theoretical estimation of the association energies. Among ten DFT methods examined in this study, two methods, i.e., LC-BLYP and BMK, reproduced the experimental enthalpy for the association. These methods should be of interest for the theoretical studies of ever-increasing curved π-systems, and their versatilities should be examined in the future studies. The theoretical energetics demonstrates the presence of small energy barriers for the rolling motions, which gives the theoretical/chemistry background of the unique friction-free carbonaceous bearings.^3,5,6 The molecular dynamics studies on the dynamic behavior also revealed dual-mode motions in the dynamics, which led to a clear-cut understanding of the spectroscopic observations that remained unanswered in previous experimental studies. The theoretical background reported in this study is informative for further molecular designs of molecular complexes assembled solely by the van der Waals force. We hope that, together with recent advancements of relevant theoretical methods,^34,48,49 this study will lead to the development of carbonaceous molecular machines with elaborate functions in the future.⁵⁰

Experimental section

Materials

The molecular bearing, (P)-(12,8)-[4]CC⊃1, was prepared by the method reported in the literature.⁵

ITC analysis

The experiments were performed following the methods reported in the literature with a GE Healthcare MicroCal VP-ITC microcalorimeter.⁵

Theoretical calculations

Outline. The geometry optimization with DFT calculations was carried out with Gaussian 09, Revision D.01 except for the LC-BOP method¹⁷ with a development version of Revision A.02.⁵¹ The dichloromethane solvent was modeled for single-point calculations with the integral equation formalism PCM (IEFPCM).¹⁵ For the computationally expensive calculations such as MD simulations, the SCC-DFTB method was adopted and was performed with DFTB+ program version 1.2 in combination with the mio-1-1 parameter set.⁵² Note that preceding theoretical studies on nanocarbons have demonstrated the applicability of the DFTB method for carbonaceous systems.^44,53 Transition state analyses were performed with the DFTB+ program in combination with the GRRM method (version 1.21) for exploring the reaction pathways.⁴⁵

Association energetics. To minimize the BSSE from basis-set truncations, we adopted a procedure of the counterpoise corrections for the association energy estimations in vacuo.¹⁴ In short, the energy of one component before the association is estimated in the presence of another component's basis functions and is compared with the associated complex. The amount of energy corrections (ΔE_c) found for each method is summarized in Table S3.† The energy corrections for BSSE were found in a range of 7–10 kcal mol⁻¹, and certain care should be paid to any theoretical investigations of association energetics of curved π-systems. Assuming that the same amount of BSSE is present in the energies with IEFPCM, we also added ΔE_c to the association energies obtained from DFT/PCM calculations.

Idealized motions. Single-point calculations were performed to elucidate the coarse energy profiles for the structural fluctuations of the molecular bearing. The relative orientations of the 1⁺ journal was thus changed by 5° in the directions described in the main text.

Molecular dynamics. No thermostats were set for MD simulations with electronic structure calculations of SCC-DFTB to conserve the total energy of the system. We started the MD simulations from the molecular structure of the global minimum in SCC-DFTB calculations (Fig. 4a). After inputting initial velocities of the nuclei at random, we observed a ca. 50% decrease in the total kinetic energy of nuclei within 50 fs. After an equilibrium time of 1 ps, the total kinetic energy converged to the mean kinetic energy (K) with a minute fluctuation. The K value was used to obtain the effective temperature (T) by T = 2K/3Nk_B where k_B is the Boltzmann constant and N is the number of atoms. For each of the four temperature variations of 400, 500, 600 and 700 K, we ran 20 trajectories of 200 ps temporal length. We began to count the precession and spin motions after the equilibrium stage of 1 ps and, by using the total frequencies accumulated for 4000 ps (Table S3†), obtained the rate constant k shown in Table S4.† Note that we observed sufficient linear correlations in the Arrhenius plots that were derived from this procedure.

Transition-state calculations. The GRRM method allows for ascending the potential energy surface toward the direction of a large anharmonic downward distortion and, thus, for allocating the transition state of complicated systems.⁴⁵ For the present study dealing with over 200 atoms, the GRRM program was slightly modified to enable the calculations of such large systems. The transition state analysis was initially performed by SCC-DFTB, and the single-point energies were then obtained by LC-BLYP/6-311G(d) in the absence and in the presence of PCM solvation. Note that the energy barriers estimated by TS calculations with SCC-DFTB matched well with those of MD calculations (see Fig. 4b and S5†), which indicated that the rate-determining steps were preserved in these two different approaches.

Acknowledgements

This study was partly supported by KAKENHI (24241036, 25107708, 25102007, 24245001, 25810018). The computational studies were in part supported by the Strategic Programs for Innovative Research (SPIRE, MEXT) and the Computational Materials Science Initiative (CMSI), Japan. Calculations were partly performed on the supercomputers of the Research Center for Computational Science, Okazaki, Japan. We thank Prof. S. Nishizawa (Tohoku Univ.) for the ITC instrument.

Notes and references

1. (a) B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323–324; (b) I. V. Krive, R. I. Shekhter and M. Jonson, Low Temp. Phys., 2006, 32, 1171–1194; (c) M. Monthioux, Carbon, 2002, 40, 1809–1823; (d) S. Iijima, Phys. B, 2002, 323, 1–5.
2. Adopting a technological term used by bearing engineers (cf.ref. 50), we describe the dynamic motions of fullerene journals as “rolling”. This description also helps to avoid the confusion with the other dynamics of arylene units or alkyl substituents that have freedom of “rotations”.
3. J. Cumings and A. Zettl, Science, 2000, 289, 602–604.
4. (a) N. Solin, M. Koshino, T. Tanaka, S. Takenaga, H. Kataura, H. Isobe and E. Nakamura, Chem. Lett., 2007, 36, 1208–1209; (b) M. Koshino, N. Solin, T. Tanaka, H. Isobe and E. Nakamura, Nat. Nanotechnol., 2008, 3, 595–597.
5. H. Isobe, S. Hitosugi, T. Yamasaki and R. Iizuka, Chem. Sci., 2013, 4, 1293–1297.
6. (a) S. Hitosugi, R. Iizuka, T. Yamasaki, R. Zhang, Y. Murata and H. Isobe, Org. Lett., 2013, 15, 3199–3201; (b) S. Sato, T. Yamasaki and H. Isobe, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8374–8379; (c) S. Hitosugi, K. Ohkubo, R. Iizuka, Y. Kawashima, K. Nakamura, S. Sato, H. Kono, S. Fukuzumi and H. Isobe, Org. Lett., 2014, 16, 3352–3355; (d) T. Matsuno, S. Sato, R. Iizuka and H. Isobe, Chem. Sci., 2015, 6, 909–916.
7. For synthesis, discussion and evaluations of the structures of finite SWNT molecules, see: (a) T. Matsuno, H. Naito, S. Hitosugi, S. Sato, M. Kotani and H. Isobe, Pure Appl. Chem., 2014, 86, 489–495; (b) http://www.orgchem2.chem.tohoku.ac.jp/finite/ ; (c) T. Matsuno, S. Kamata, S. Hitosugi and H. Isobe, Chem. Sci., 2013, 4, 3179–3183; (d) S. Hitosugi, T. Yamasaki and H. Isobe, J. Am. Chem. Soc., 2012, 134, 12442–12445; (e) S. Hitosugi, W. Nakanishi and H. Isobe, Chem.–Asian J., 2012, 7, 1550–1552.
8. For supramolecular complexes of fullerenes with flexible nanorings, see: (a) T. Kawase and H. Kurata, Chem. Rev., 2006, 106, 5250–5273; (b) T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344; (c) T. Iwamoto, Y. Watanabe, H. Takaya, T. Haino, N. Yasuda and S. Yamago, Chem.–Eur. J., 2013, 46, 6777–6785; (d) T. Iwamoto, Z. Slanina, N. Mizorogi, J. Guo, T. Akasaka, S. Nagase, H. Takaya, N. Yasuda, T. Kato and S. Yamago, Chem.–Eur. J., 2014, 47, 14403–14409; (e) J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021; (f) Y. Nakanishi, H. Omachi, S. Matsuura, Y. Miyata, R. Kitaura, Y. Segawa, K. Itami and H. Shinohara, Angew. Chem., Int. Ed., 2014, 53, 3102–3106.
9. (a) E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2006, 46, 72–191; (b) D. Canevet, E. M. Pérez and N. Martín, Angew. Chem., Int. Ed., 2011, 50, 9248–9259.
10. Structure-thermodynamics studies indicated that the contribution of alkyl chains on the thermodynamics is not large for [4]CC. See ref. 6b.
11. Representative examples of relevant studies with theoretical investigations: S. Kigure and S. Okada, J. Phys. Soc. Jpn., 2013, 82, 094717; L. A. Girifalco, M. Hodak and R. S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13104 and ref. 8.
12. (a) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648; (b) K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
13. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
14. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
15. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
16. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
17. J.-W. Song, T. Hirosawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2007, 126, 154105.
18. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109.
19. (a) H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544; (b) A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946; (c) Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433.
20. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
21. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
22. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
23. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
24. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
25. In solution, the pyrrolidine ring on the fullerene molecule acts as a shaft for the single-axis rolling motion of the journal, and, in the time-averaged structure, this five-membered ring stands aligned along the C₄ symmetry axis of the outer [4]CC bearing.
26. RMSD was obtained after matching the coordinates of all the atoms with Chimera. For chimera, see: E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
27. F. P. Schmidtchen, in Supramolecular Chemistry: From Molecules to Nanomaterials, ed. J. W. Steed and P. A. Gale, Wiley, Chichester, 2012, vol. 2, pp. 275–296.
28. Note that ITC analysis directly provides an experimental enthalpy for the association, which enables straightforward comparisons with theoretical energetics without nuisance considerations of entropic terms (see also ref. 48 and 49).
29. The association enthalpy of unsubstituted C₆₀ in dichloromethane is −11.6 ± 0.4 kcal mol⁻¹ (ref. 5 and 6d), which shows that introduction of substituents does not hinder but rather enforces the association of the journal by ca. −1 kcal mol⁻¹.
30. The dispersion force is undoubtedly playing a key role for the peapod formation with close van der Waals contacts (ref. 6b), and the present results indicate its premature treatment in the present DFT methods (see also ref. 34). Effects on the lengthening of the tubular structure is thus of great interest for in the near future. (See also ref. 6d).
31. The geometries from LC-BLYP/PCM and BMK/PCM methods matched with RMSD of 0.090 Å. See Fig. S1†.
32. (a) R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2008, 4, 2030–2048; (b) R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2010, 6, 1924.
33. Yamago and coworkers also reported a tendency of overestimate of association energies with M06-2X. See ref. 8.
34. One reviewer expressed his/her interest in further extensions of polarization functions over hydrogen atoms as well as in other DFT methods with more recent dispersion treatments. Albeit preliminary within a framework of the Gaussian program, these comparisons were made by single-point calculations, and the results were summarized in Table S1.† In short, the extension of polarization functions to (d,p) setting did not affect the results considerably. The inclusion of dispersion effects with modern D3 methods did not improve the results by showing overestimations of the association energy over 35 kcal mol⁻¹. The results may indicate that further improvements in the theoretical models of dispersion forces are necessary especially for the curved π-systems. The present results also show that our carbonaceous molecular bearing provides an interesting and challenging test case for theoretical evaluations (ref. 48d), and the evaluation of other recent dispersion models, such as many-body dispersion models implemented in the Amsterdam Density Functional program, may be of interest for the further theoretical studies in the future. See ref. 48 for representative examples.
35. Z.-Q. You, Y.-C. Hung and C.-P. Hsu, J. Phys. Chem. B DOI:10.1021/jp511216c , published online.
36. The rolling energetics also shows that the starting geometry is the global minimum for the single-axis rolling motions by showing the minimum at 0° in Fig. 3.
37. D. Casarini, L. Lunazzi and A. Mazzanti, Eur. J. Org. Chem., 2010, 2035–2056.
38. The two carbon atoms on the equator are located in the middle of biaryl linkages. A similar anomalous location of carbon atoms on the biaryl linkages is also experimentally observed in the solid state. See ref. 6b.
39. (a) D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957; (b) G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185–192; (c) M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
40. The association energy of (P)-(12,8)-[4]CC⊃1⁺ was estimated as −78.9 kcal mol⁻¹ by the DFTB method. This value was larger than that of ωB97X-D method (−69.8 kcal mol⁻¹, cf.Table 1).
41. PCM implementation in the DFTB method is not accessible with our resource using DFTB+ program (cf.ref. 52).
42. Although the relative stabilities of two minima were switched from the LC-BLYP calculations, the energy differences of minima were as small as <0.2 kcal mol⁻¹ for SCC-DFTB calculations and <0.6 kcal mol⁻¹ for LC-BLYP calculations. The switching of two minima may be the origin of minimum-switching of realistic motions (Fig. S5†): stabilities of 1/4 precession and b_p structures were switched between SCC-DFTB and LC-BLYP calculations.
43. Because of minute differences in the chemical shifts of resonances, we could not study the experimental dynamics of this system.
44. (a) N. Niitsu, M. Kikuchi, H. Ikeda, K. Yamazaki, M. Kanno, H. Kono, K. Mitsuke, M. Toda and K. Nakai, J. Chem. Phys., 2012, 136, 164304; (b) A. B. Marahatta, M. Kanno, K. Hoki, W. Setaka, S. Irle and H. Kono, J. Phys. Chem. C, 2012, 116, 24845–24854.
45. (a) K. Ohno and S. Maeda, Chem. Phys. Lett., 2004, 384, 277–282; (b) S. Maeda and K. Ohno, J. Phys. Chem. A, 2005, 109, 5742–5753; (c) K. Ohno and S. Maeda, J. Phys. Chem. A, 2006, 110, 8933–8941.
46. The energy barriers from MD and TS analysis are comparable to the one estimated with LC-BLYP/PCM for the idealized rolling motions (Fig. S4,† +4.3 kcal mol⁻¹).
47. M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley, Chichester, United Kingdom, 2001, ch 15.5.
48. (a) A. Tkatchenko, D. Alfé and K. S. Kim, J. Chem. Theory Comput., 2012, 8, 4317–4322; (b) A. Ambrosetti, D. Alfé, R. A. DiStasio Jr and A. Tkatchenko, J. Phys. Chem. Lett., 2014, 5, 849–855; (c) L. Kronik and A. Tkatchenko, Acc. Chem. Res., 2014, 47, 3208–3216; (d) S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964; (e) T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591; (f) J. Antony, R. Sure and S. Grimme, Chem. Commun., 2015, 51, 1764–1774.
49. Delicate care must be taken in the comparison of experimental and theoretical data especially for large supramolecular systems. As we experimentally demonstrated in our systems (ref. 6), entropy terms in the association should be very complicated by the involvement of conformations and solvent molecules. Such entropy effects cannot be readily reproduced by any simple theoretical models (ref. 48).
50. A. Harnoy, Bearing Design in Machinery: Engineering Tribology and Lubrication, Dekker, New York, USA, 2003, ch. 1.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
52. Bremen Center for Computational Materials Science, University of Bremen. See also http://www.dftb-plus.info.
53. G. Zheng, S. Irle and K. Morokuma, Chem. Phys. Lett., 2005, 412, 210–216.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary figures, tables and atomic coordinates of representative geometries. See DOI: 10.1039/c5sc00335k

---