Open Access Article
Open Access ArticleThe origin of surfactant amphiphilicity and self-assembly in protic ionic liquids
Andrew
Dolan
a,
Rob
Atkin
b and
Gregory G.
Warr
*a
aSchool of Chemistry, The University of Sydney, Sydney, NSW 2006, Australia. E-mail: gregory.warr@sydney.edu.au
bCentre for Advanced Particle Processing and Transport, Chemistry Building, The University of Newcastle, Callaghan, NSW 2308, Australia
First published on 4th August 2015
Abstract
The nature of amphiphilic self-assembly in alkylammonium protic ionic liquids (PILs) is examined by systematically varying the ionic structure and composition, H-bonding capacity, and nanostructure of both the PIL and micelle-forming cationic surfactant, and contrasted with self-assembly in water. Using small-angle neutron scattering, micelle structure and concentrations are determined for primary – quaternary dodecylammonium salts in nitrate and thiocyanate PILs. While the solvophobic driving force depends only on the average polarity of the PIL, surprisingly strong, specific interactions of the head group and counterion with the PIL H-bond network are found. This suggests the importance of developing designer amphiphiles for assembling soft matter structures in PILs.
Introduction
Ionic liquids (ILs) are salts that are molten at room temperature. They are broadly divided into protic ionic liquids (PILs)1 and aprotic ionic liquids,2 both of which can exhibit amphiphilic nanostructure in the bulk3–5 and near surfaces.6,7 Both classes can be further subdivided based on chemical moieties or properties, such as water miscibility.8–10 Many PILs have been shown to promote self-assembly of a variety of conventional surfactants,11–17 as well as block copolymers18,19 and, uniquely, the homologous series of primary alcohols.20In molecular solvents, it has been known since the work of Ray21,22 that a dense, three-dimensional H-bond network is critical in driving amphiphilic self-assembly.23 Comparisons of the self-assembly behavior of surfactants in the PIL ethylammonium nitrate (EAN) and water, initially made by Evans in the early 1980s,24,25 have been reviewed recently.14 EAN was also recognized has having a dense H-bond network in those early studies, as well as more recently.26
The most obvious characteristic of ILs is their extremely high ionic strength (∼12 M in EAN). In water, high electrolyte concentrations can profoundly alter surfactant self-assembly through charge screening and specific ion effects, lowering the critical micelle concentration and favouring less-curved micelles.27–29 The high ionic strength of PILs does not produce the same effects on aggregation as high salt concentrations in aqueous systems. The surfactant aggregates formed in EAN are similar to those in water but critical aggregation concentrations are higher. This is generally attributed to a lower solvophobic driving force.
Studies of amphiphile self-assembly in PILs have so far largely focused on understanding solvophobicity, with little attention given to the other essential ingredient, a solvophilic moiety. EAN and water both have negative entropies of transfer of nonpolar gases into the liquid,30 which indicates both solvents require significant rearrangement around non-polar solutes. However, when mixed with alcohols, EAN behaves unlike water and like other polar aprotic solvents such as DMF and DMSO:31 water and alcohols have decreasing negative enthalpies of mixing and large increasing specific heat capacities as alcohol chain length increases, while EAN and polar aprotic solvents have small, increasing enthalpies of mixing and small decreasing specific heat capacities.
Studies of nonionic amphiphile self-assembly in PILs, whether surfactants or block copolymers, have all contained poly(oxyethylene) groups, which are virtually ubiquitous in aqueous systems as polar moieties. We have shown previously that EAN and similar PILs are almost as good solvents as water for these polymers.32,33
This similarity is highlighted by the partitioning behaviour of a range of monoalkyl poly(ethylene oxide) surfactants between oil and water, EAN or propylammonium nitrate (PAN).34 The Gibbs free energy of transfer of polar ethoxy groups from oil to an EAN or PAN polar phase (∼−2.6 kJ mol−1) was almost identical to transfer into water (−2.61 ± 0.08 kJ mol−1),35–37 while that for methylene groups was significantly lower in EAN (2.2 kJ mol−1) and PAN (1.3 kJ mol−1) than water (3.45 kJ mol−1).38 The effects on the solvophilic and solvophobic components of replacing water with a PIL are very different.
Similarly, studies of ionic surfactants have largely simply taken quaternary ammonium or pyridinium salts from their aqueous context, considering neither their solvophilicity in a PIL, nor the role of the accompanying counterion. The behavior of alkyltrimethylammonium cationic surfactants in water depends strongly on the counter ion,39,40 but its role in PILs is unknown.
The effect of varying the number of methyl groups around the ammonium head-group of cationic surfactants is expected to be different in water and PILs. Quaternary (4°) ammonium salts are widely used in water to avoid deprotonation by hydrolysis in neutral or basic solution, leading to mixed micelles or precipitation.41 In strong PILs, exemplified by EAN, such deprotonation will not occur and we anticipate that H-bonding by the head group may be more significant than electrostatic dissociation in determining solvophilic character.
In water, the effect of head-group structure in primary though quaternary (1°–4°) dodecylammonium chloride surfactants has been investigated using the isoplethal phase tube method.42 Changing the head group in this way varies the number of hydrogen bonding sites on the head group, which affects the size of the hydrated head group, the strength of the H-bonding/hydration interactions and ultimately the counter ion binding.43 Full phase diagrams were determined and two trends were noted. The first is that the concentration range of the normal hexagonal phase increased as the number of methyl groups on the head group increased, while that of the lamellar phase decreased; this suggests that as the head group is methylated, curved structures become more stable. Also dodecyltrimethylammonium chloride (DTAC) has a discrete micellar cubic phase (I1) between the isotropic (L1) and the hexagonal (H1) phases, consistent with high-curvature aggregates remaining stable up to high concentrations.44 The second trend is that the Krafft temperatures decrease as the number of methyl groups on the head group increases, from 33 °C for dodecylammonium chloride (DAC) to −16 °C for DTAC.42 (It should be noted that the phase boundaries for DTAC and dodecyldimethylammonium chloride (DDMAC) are both metastable and the reported temperature limits occur at the intersection of the L1/solid + liquid line and the L1/cubic (for DTAC) and L1/H1 (for DDMAC) lines where the Krafft temperature is at its minimum.)
In this paper we compare the self-assembly of primary (1°), secondary (2°), tertiary (3°) and quaternary (4°) ammonium amphiphiles into micelles in several PILs with that in water using small angle neutron scattering (SANS). In particular we seek to understand amphiphilicity in PILs by examining (i) the role of the hydrogen bonding capacity of both the surfactant and IL, and (ii) whether counterion effects also influence the structure and stability of micelles in PIL solutions. Neutron scattering offers unique insights into polymeric and soft condensed matter systems45 and was used in this study because it allows us to examine the size and shape of dilute micellar solutions; this enables close scrutiny of amphiphile–solvent interactions.
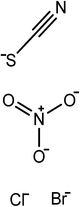
The ionic liquids used in this study (see Table 1) are EAN, PAN, ethanolammonium nitrate (EtAN), ethylammonium thiocyanate (EASCN) and ethanolammonium thiocyanate (EtASCN). These ionic liquids were chosen because of the differences in their nanostructure. Alkylammonium PILs have a unique sponge-like nanostructure where the polar ammonium head groups and counter ions (in this case nitrate and thiocyanate) partition into a polar domain and the alkyl chains partition into a non-polar domain. PIL nanostructure depends strongly on the cation and weakly on the anion.46 Increasing the cation alkyl chain length naturally increases the size of the non-polar domains, but it also leads to small reductions in the effective packing parameter of the cation and consequently the curvature of the nanostructure.46 Changing from an alkyl group to an alkanol group completely disrupts the bicontinuous nanostructure of the liquid and significantly changes the spatial distributions of ions around one another.47
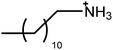
The surfactants studied are: dodecylammonium chloride (DAC), nitrate (DAN) and thiocyanate (DASCN); dodecylmethylammonium chloride (DMAC), dodecylmethylammonium nitrate (DMAN) and thiocyanate (DMASCN); DDMAC, dodecyldimethylammonium nitrate (DDMAN) and thiocyanate (DDMASCN); dodecyltrimethylammonium bromide (DTAB), DTAC, dodecyltrimethylammonium nitrate (DTAN) and thiocyanate (DTASCN). These were chosen because there is a systematic variation in the number of hydrogen bond donor sites from dodecylammonium, which has the same polar group as the primary ammonium IL cations, through to the DTA+ salts, which cannot H-bond at all.
In all cases the ammonium nitrate surfactants were used in the nitrate ILs and the ammonium thiocyanate surfactants were used in the thiocyanate ILs in order to avoid unnecessarily mixing anions. Counter ion variation was then examined separately in nitrate PILs.
Materials and methods
The ionic liquids were prepared following published procedures,13,48 with the exception of EASCN. EASCN was prepared by mixing aqueous solutions of ethylammonium sulfate and barium thiocyanate. The solution was allowed to stand overnight and the barium sulfate was precipitated via centrifugation, where the top two-thirds of the liquor were collected and the water removed under vacuum. The 1°–3° ammonium nitrate surfactants, DAN, DMAN and DDMAN, were prepared by neutralizing the parent amine with an equimolar amount of nitric acid. These reactions are initially biphasic but proceed vigorously. DTAN was prepared by silver nitrate metathesis of DTAC. DASCN and DDMASCN were prepared by adding equimolar amounts of the parent amine to solutions of ammonium thiocyanate. The ammonia was removed under vacuum until a neutral pH was obtained, then the surfactants were freeze dried. This method was unsuccessful for the preparation of DMASCN. DMASCN was prepared by mixing DMAC and sodium thiocyanate in boiling acetone. The solution was hot filtered, the solvent evaporated and the crude product recrystallized from acetone/ethanol. DTASCN was made by precipitating it from DTAN and ammonium thiocyanate, exploiting the higher Krafft temperature of the thiocyanate salt.Partial deuteration of the ILs was performed by switching all exchangeable protons in an excess of deuteriumoxide. For EAN and EASCN 3 mL of deuterium oxide was added per mL of IL to be exchanged. The solution was stirred for 5 min and dried on a rotary evaporator. This process was repeated once more, then the ILs were dried on a freeze-dryer. For EtAN and EtASCN 3 mL of deuteriumoxide was added per mL of IL to be exchanged. The solution was stirred overnight and dried on a rotary evaporator. This process was repeated once more, then the ILs were dried on a freeze-dryer. The extent of deuteration was checked after freeze-drying in all cases and was found to be in excess of 98% exchange.
None of the surfactants were deuterated prior to mixing with the ILs, however it is assumed that all exchangeable (head-group) protons (cf.Table 1) are completely exchanged for deuterons upon mixing because of the very large molar excess of IL in the solution.
All surfactant/IL samples were made at 5 wt% surfactant and all surfactant/D2O samples were made at 1 wt% of surfactant. Scattering patterns of IL samples were collected at 60 °C, as the melting point of EASCN and EtAN are 50 °C and 52 °C respectively. Scattering patterns of D2O samples were collected at both 25 °C and 60 °C. Small angle neutron scattering experiments were carried out on the QUOKKA49 beam line at the Australian Nuclear Science and Technology Organisation (ANSTO). Experiments were performed with λ = 4.95 Å (Δλ/λ = 0.0655). Scattering was collected from 2.0 mm thick samples onto a 1.0 m × 1.0 m 2D detector with 192 × 192 elements. We used two sample-to-detector distances of 1.3 m (30 cm offset) and 8.8 m to give a q range of 0.0091–0.72 Å−1. Raw SANS data were reduced to 1D data in Igor Pro 6.12A, using the reduction package provided by NIST50 and analyzed using SASView 3.3.0. Instrumental smearing was not accounted for as it is not significant in the q-range of interest compared to the effect of polydispersity. Scattering length densities were calculated using the NCNR SLD calculator,51,52 although the contrast was allowed to vary as part of the fit. Several batches of each IL were used over the course of the study, so the SLD of each sample varies somewhat depending on the extent of deuteration. Structure factors were used for analysis of all samples: aqueous samples used the Hayter–Penfold MSA for screened Coulomb potentials53 and IL samples used a hard sphere model for excluded volumes.54,55 Schulz polydispersity56 was accounted for using an average structure factor approximation.
Results
Nitrate surfactants in nitrate PILs
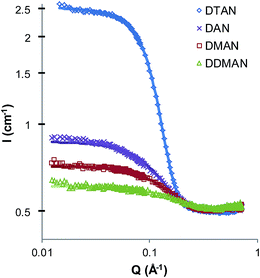
Fig. 1 shows the SANS patterns of 5 wt% DAN, DMAN, DDMAN and DTAN solutions in d3-EAN, together with best-fits to a model of polydisperse homogeneous hard spheres with excluded volume interactions.54,55 As expected from the high ionic strength, there is no evidence of a correlation or structure factor peak arising from long-range electrostatic interactions between micelles. Corresponding best fit parameters are listed in Table 2, and in all cases the fitted micelle volume fraction is sufficiently low that the SANS pattern is well-described by form factor scattering. Note that the small peak at large scattering angles, around 0.7 Å−1, is caused by the underlying nanostructure of EAN, and is visible due to the neutron contrast between ammonium deuterons and ethyl hydrogens.4 The low angle scattering, caused by the formation of large aggregates in solution, reaches the flat baseline before the solvent peak, so we have fitted this data only in the range 0.12–0.4 Å−1.| IL | Surfactant | φ mic | CMC (wt%) | r (Å) | SLDIL × 10−6 (Å−2) | Schultz PD |
|---|---|---|---|---|---|---|
| a Ref. 17. | ||||||
| EAN | DAN | 0.022 | 3.2 | 14 | 2.60 | 0.24 |
| DMAN | 0.013 | 3.9 | 13 | 3.33 | 0.19 | |
| DDMAN | 0.009 | 4.3 | 12 | 3.32 | 0.20 | |
| DTAN | 0.004 | 4.7 | 11 | 3.33 | 0.21 | |
| DTAC | 0.006 | 4.5 | 11 | 3.33 | 0.17 | |
| DTAB | 0.025 | 3.0 | 15 | 3.24 | 0.10 | |
| 2.3 ± 0.2a | ||||||
| EtAN | DAN | 0.015 | 3.9 | 12 | 4.00 | 0.29 |
| DMAN | 0.011 | 4.2 | 13 | 3.99 | 0.19 | |
| DDMAN | 0.007 | 4.5 | 14 | 4.00 | 0.00 | |
| DTAN | 0.081 | — | 20 | 2.96 | 0.19 | |
| DTAC | 0.087 | — | 19 | 3.46 | 0.24 | |
| DTAB | 0.087 | — | 20 | 3.67 | 0.19 | |
The fitted volume fractions of micelles in these is lower than would be expected for 5.0 wt% solution (φmic = 0.062) assuming negligible volumes of mixing, and surfactant and EAN densities of approximately 1.0 and 1.17 g cm−3 (calculated by extrapolation from data collected by Zarrougui et al.57 and Allen et al.58), respectively. This indicates that there is a high concentration of dissolved monomer in solution, from which we can estimate critical micelle concentrations (CMC) in EAN.
Table 2 shows that the CMC in EAN increases monotonically as methyl substitution around the head group increases from DAN to DTAN, consistent with the observed decrease in scattering intensity (Fig. 1). This indicates that for these surfactants in EAN the ability of the head group to hydrogen bond to the PIL strongly influences their CMCs.
The SANS patterns of 5 wt% solutions of all surfactants in PAN showed only background scattering consistent with dissolved, monomeric surfactants indicating that no micelles were present. This is consistent with a reported CMC for DTAB in PAN of 0.26 molal (∼10 wt%).59 As PAN has larger non-polar domains than EAN, the CMCs are expected to be much higher because of its greater capacity to solvate the surfactant alkyl tails. This is also consistent with previous work on nonionic microemulsions, where much higher surfactant concentrations were required in PAN than in EAN to produce comparable effects.60,61 These results support the idea that the capacity of the non-polar domain to solubilize the alkyl chains without significant reorganization of the solvent plays an important role in determining CMCs in PILs.
The best-fit mean micelle radii in EAN decrease monotonically as the number of head group methyls increases, from 14 Å for DAN to 11 Å for DTAN. Although this is near the resolution limit for SANS, the trend across the group is clear, and can also be seen in the shape of the scattering patterns around Q = 0.35 Å−1. Further, this trend is the opposite of that expected if the micelles were all identical in structure, and the SANS patterns differed only due to the different H/D exchange between the head-groups and the IL. Instead, greater hydrogen bonding between the head group and the IL in DAN leads to larger micelles. The trend in sizes is the same as is generally seen in aqueous micellar solutions: larger micelles are correlated to lower CMCs.62
Micelle shape and size is generally understood in terms of the surfactant packing parameter, v/a0lc, where v and lc are the alkyl chain volume and fully-extended (all-trans) length, respectively.63 The effective head group area at the micelle–solvent interface, a0, is determined by a balance of interfacial forces: hydrocarbon/solvent interfacial tension drive reduction in a0, while head group repulsions drive its increase. Whereas for ionic surfactants in water the repulsion is primarily electrostatic (modulated by counterion binding), at the typical ionic strength of ILs it will be steric. The bare head-group area should thus very slightly increase as the number of methyl groups on the head group increases, leading to the decrease in micelle size noted here.
Fig. 2 shows the SANS patterns of DAN, DMAN, DDMAN and DTAN in EtAN, with corresponding best-fit parameters for a polydisperse, homogeneous hard spheres model are shown in Table 1. (Note that the high-Q solvent peak is much diminished in EtAN compared to EAN, or PAN,4 due to its weaker bulk nanostructure.) The behavior in EtAN is strikingly different from that in EAN; here the scattered intensity from the 4° surfactant DTAN is much greater than for the other three surfactants. The scattered intensity from DAN, DMAN and DDMAN is similar to and in the same scattered intensity order as in EAN. The derived CMCs of DAN, DMAN and DDMAN in EtAN are approximately the same as in EAN, and also lie in the same order, but DTAN has a CMC in EtAN that is too small to determine from fitted volume fractions. (The density used for EtAN is 1.265 g cm−3 and is the only available value: a super-cooled sample at 27 °C (ref. 64).)
In EtAN, the micelle radii increase slightly as methyl substitution increases the head group size, however the micelle radius of DTAN is substantially larger than the others, and close to its value in water65 (see also below).
Thiocyanate surfactants in thiocyanate PILs
Fig. 3a and b show SANS patterns of 5 wt% thiocyanate surfactant solutions in d3-EASCN and d4-EtASCN, respectively, and Table 3 shows their best-fit parameters. There is only very weak scattering above baseline by any of these surfactants in EASCN, consistent with their CMCs at 60 °C being even higher than in EAN (and all just below 5 wt%). By visual inspection, the scattered intensities and hence micelle volume fractions decreases from DASCN to DTASCN, consistent with CMCs increasing in the same order. This agrees with the trends in the very small fitted volume fractions, but lie within experimental uncertainty. The fitted micelle radii are broadly similar those found for nitrate surfactants in EAN (Table 2), although the micelles are about 1 Å smaller in EASCN than in EAN.| IL | Surfactant | φ mic | r (Å) | SLDIL × 10−6 (Å−2) | PD |
|---|---|---|---|---|---|
| EASCN | DASCN | 0.005 | 13 | 2.90 | — |
| DMASCN | 0.005 | 9 | 2.90 | — | |
| DDMASCN | 0.005 | 12 | 2.90 | — | |
| DTASCN | 0.007 | 9 | 2.90 | — | |
| EtASCN | DASCN | — | — | — | — |
| DMASCN | 0.002 | 12 | 3.10 | — | |
| DDMASCN | — | — | — | — | |
| DTASCN | 0.067 | 19 | 3.10 | 0.19 |
In EtASCN the quaternary ammonium surfactant DTASCN forms notably larger micelles with a mean radius of 19 Å, comparable with the radius of DTAN in EtAN, or in water. Its high scattering intensity also implies a much a lower CMC than DMASCN in EtASCN or any of the EASCN systems. The high Krafft temperatures of DASCN and DDMASCN in EtASCN make this data set incomplete.
Counterion effects
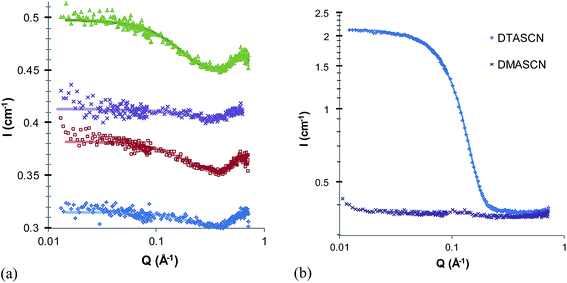
The unusual behavior of quaternary ammonium surfactants in EtAN and EtASCN, but not in corresponding ethylammonium salts, suggests that micelle formation in these ILs is particularly sensitive to interactions in the head-group region. In aqueous solutions, counterions are known to strongly affect both CMC and micelle morphology. In ILs it has been assumed that counterion binding effects are negligible due to the high ionic strength of the solvent,24,25 but ion-specific effects may still arise. Fig. 4 shows SANS patterns of 5 wt% solutions of the quaternary dodecyltrimethylammonium salt with nitrate, chloride and bromide counterions (DTAN, DTAB and DTAC) in EtAN and EAN. The best-fit parameters for fits to a polydisperse, homogeneous, hard spheres model are listed in Table 2. | ||
| Fig. 4 SANS pattern of 5 wt% dodecyltrimethylammonium chloride, bromide and nitrate in (a) EtAN and (b) EAN at 60 °C. | ||
In EtAN, the observed scattering patterns and fitting parameters are similar for all three surfactants. The volume fraction of micelles in DTAN is somewhat lower than that of DTAC and DTAB, hence DTAN has a slightly higher CMC than either DTAC and DTAB in EtAN. The best-fit radii of all three micelles are the same within the resolution of the technique (Table 2). This indicates that, as expected, the ionic liquid behaves similarly to a swamping amount of electrolyte and all counterions are exchanged. Therefore the only ion specific effects in self-assembly of ILs are those associated with the mixing behavior and CMC, there is no effect of counterion on the micelle size and shape, since all counterions will be exchanged with the solvent.
Fig. 4b shows the scattering patterns of the same quaternary ammonium surfactant salts in EAN. As observed for the nitrate salts, the scattered intensity and fitted micelle volume fractions of DTAC and DTAB (Table 2) are much lower in EAN than EtAN; DTAC and DTAN, thus also both have high CMCs in EAN. The estimated CMC of DTAB (3.0 wt%) compares well with the value of 2.3 ± 0.2 wt% determined previously by surface tension.24 Here also a counterion-specific effect is seen, with the CMC of DTAB in EAN measurably smaller than that of DTAC, which in turn is only slightly lower than DTAN.
Comparison with aqueous solutions
Fig. 5 shows the scattering patterns of DTAN, DTAC and DTAB in water at 25 °C, with corresponding best-fit parameters to a polydisperse spheres with screened Coulomb potential interactions given in Table 4. These data are included as the aqueous CMCs of these surfactants are known at room temperature28,65,66 which facilitates comparison; at elevated temperatures the CMCs are less reliably known and were allowed to vary as part of the fitting.| Surfactant | φ mic | r (Å) | Salt conc. (M) | Charge | PD | ΔSLD × 10−6 (Å−2) |
|---|---|---|---|---|---|---|
| At 60 °C | ||||||
| DAN | 0.003 | 16 | 0.008 | 20.5 | 0.26 | 6.49 |
| DMAN | 0.003 | 17 | 0.007 | 14.3 | 0.20 | 6.84 |
| DDMAN | 0.005 | 18 | 0.007 | 13.9 | 0.18 | 6.56 |
| DTAN | 0.006 | 15 | 0.008 | 8.8 | 0.24 | 6.03 |
| DAC | 0.004 | 16 | 0.011 | 15.1 | 0.19 | 8.78 |
| DMAC | 0.005 | 16 | 0.010 | 13.5 | 0.18 | 8.18 |
| DDMAC | 0.004 | 15 | 0.010 | 10.3 | 0.21 | 8.39 |
| DTAC | 0.004 | 12 | 0.015 | 5.7 | 0.28 | 6.85 |
| DTAB | 0.007 | 15 | 0.009 | 6.8 | 0.23 | 6.72 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| At 25 °C | ||||||
| DTAN | 0.007 | 18 | 0.012* | 6.4 | 0.19 | 7.20 |
| DTAC | 0.005 | 16 | 0.022* | 12.5 | 0.17 | 8.86 |
| DTAB | 0.008 | 19 | 0.014* | 13.9 | 0.12 | 4.68 |
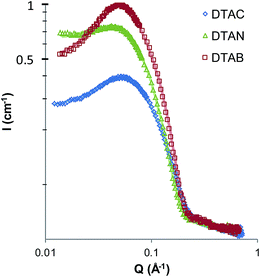
The scattering intensity from DTAC is lower than DTAN and DTAB, because there are fewer micelles present at 1 wt%. This is because the solution is only slightly above the CMC of the chloride surfactant (22 mM) relative to that of the bromide (14 mM) and nitrate (12 mM). Additionally, the interaction peak for DTAN is somewhat smaller than the other salts. This is likely due to stronger binding of nitrate to the micelle surface,67 but may also be influenced by small amounts of residual salt from the synthesis affecting the apparent surface charge. At 25 °C the radii of the micelles of DTAB and DTAN are very similar, 18 Å and 19 Å, respectively, and the radii of the DTAC micelles are somewhat smaller at 15 Å. This is consistent with expectations; weaker counterion binding raises CMCs, but also increases electrostatic repulsion between head groups and therefore favours smaller micelles.40
The scattering patterns for the series of nitrate and chloride surfactants in water at 60 °C are shown in Fig. 6. The fitted radii of the quaternary ammonium salts, listed in Table 4, are all smaller than at 25 °C, but the distinction between the radii of DTAB (not shown) and DTAN (both 15 Å) and that of DTAC (12 Å) remains evident.
 | ||
| Fig. 6 Scattering of 1 wt% dodecylammonium (a) nitrate and (b) chloride surfactants in water at 60 °C. | ||
Qualitatively, the effect of changing head-group from 1° to 4° ammonium in aqueous solutions in the same for both chloride and nitrate salts; the 4° surfactants DTAC and DTAN have the smallest radii, while the other surfactants are all similar and 2–3 Å larger. This is consistent with inferences drawn from the phase diagrams determined by Hoerr et al.42 and Balmbra et al.44 where the preference of DAC for low curvature surfaces is evidenced by its large Lα region and very small H1 region and the preference of DTAC to form high curvature surfaces is evidenced by the occurrence of a discrete cubic phase and a relatively small Lα region.
The surface charge of the nitrate and chloride surfactants in water follows the trend of the micelle radius for both chloride and nitrate surfactants: the largest micelles, formed by the primary surfactants, have the highest charge, while the smallest micelles, formed by the quaternary surfactants, have the lowest charge. In all cases the nitrates have slightly higher charges than the chlorides.
Discussion
In order to understand these results we consider the solvophobic and solvophilic contributions to micellization in the PILs examined and in water. In all surfactants the solvophobic component is expected to be approximately the same in each IL, as this is primarily a function of alkyl chain length. However as the head group methylation increases from 1° to 4° or as counterion is changed, the solvophilic component is expected to change significantly as e.g. the H-bond capacity of the head group to the PIL decreases.In water, electrostatic repulsions between surfactant head groups oppose micellization. As the high ionic strength of the PIL will reduce the intensity of these repulsions, it may be expected that CMCs are lower in PILs than water. However, the opposite trend is observed. For all surfactants in all PILs examined the CMCs derived from SANS are much higher than they are in water. These results are consistent with previously reported studies of CMCs of both ionic24,25 and nonionic24,68,69 surfactants in PILS, (which predominantly means EAN), where CMCs are typically an order of magnitude larger than in water. This indicates that the amphiphile is more soluble in the PIL and in water, and that reduced headgroup repulsions are not a dominant effect. This leads us to consider the role of the PIL nanostructure.
Despite EAN and EtAN having very different bulk liquid nanostructures, the CMCs of 1°–3° nitrate surfactants in EAN and EtAN are the same. While CMCs in thiocyanate PILs are slightly higher than in the nitrates, CMCs of (the accessible) thiocyanate surfactants in EASCN and EtASCN are also similar to each other.
At first sight this is at odds with the known differences in the underlying nanostructure of amphiphilic (EAN, EASCN, PAN) and non-amphiphilic (EtAN, EtASCN) solvents, which would lead us to expect different solvation environments for aliphatic chains. Whereas the alkylammonium cation is amphiphilic, allowing its bulk liquid phase to form a sponge-like nanostructure with polar and non-polar domains, the terminal hydroxyl functionality prevents such nano-segregation in EtA+ salts.47 The present results suggest instead that the alkyl chain solubility – the main solvophobic contributor to micelle formation – is only sensitive to the average polarity of the solvent, and not to nanostructure.
As noted by Karve and Dutt,70 different polarity measurements of nanostructured liquids may be contradictory: Kamlet–Taft analysis of PAN indicates that it is a stronger H-bond donor than acceptor, whereas the Abraham approach suggests the opposite. Poole has compared available ET(30) and Kamlet–Taft results for numerous ILs, which show little difference between nitrate and thiocyanate PILs,71 although Ab Rani et al.,72 noted more generally for ILs that a strongly coordinating anion reduces the H-bond acidity of the cation. This highlights that molecular-probe approaches measure a weighted average solvent polarity that depends on the strongest interactions between a probe and its microenvironment as well as its location,73,74 and hence may be skewed in nanoheterogeneous media. In ILs this de-emphasises non-polar (alkyl) moieties, so that PAN and EAN, for example, are almost indistinguishable.
The CMC results also correspond well with thermodynamic measurements of the partitioning of nonionic surfactants between water and some PILs and octane, in which we showed that the Gibbs free energy of transfer of methylene groups was sensitive to the average polarity of the IL, but that the polar groups were sensitive only to the ionic, H-bonding moieties in the solvent.34
Other evidence suggests that the effect depends on the size of the non-polar solute. Alkanol–PIL mixtures self-assemble into micelle- and microemulsion-like structures when the alkyl chain length exceeds about twice the hydrophobic domain size in amphiphilic PILs, but shorter chains, comparable in length to the PIL cation, are incorporated into and modify the underlying nanostructure.20 As conventional surfactants all consist of much longer chains than PIL cations, the solvent nanostructure cannot accommodate them and an average medium is instead experienced.
In EAN and EASCN, the CMCs and micelle sizes of quaternary ammonium surfactants differ little from those of the other surfactant head groups. In the corresponding ethanolammonium ILs their CMCs are markedly lower and micelles larger. Whereas the head groups (and matching counterions) of 1°–3° ammonium surfactants can be incorporated to some extent into the H-bonded networks of their respective ILs, the quaternary ammonium head group cannot. Nevertheless it must remain in the vicinity of a counterion for simple reasons of electroneutrality. We interpret the difference between micellization behavior of quaternary ammoniums in EA+ and EtA+ salts to therefore arise from the amphiphilic PILs' greater ability to accommodate the non-H-bonding head group, either within its existing bicontinuous nanostructure or by solvophobically solvating the quaternary ammonium group. In the non-amphiphilic EtA+ salts, it is thus a solvophobic interaction with the head-group that lowers the CMC and favors larger micelles.
We attribute the observed differences between CMCs in nitrate and thiocyanate ILs to differences between the types of H-bonds formed in EAN and PAN versus EASCN,75 although this would be clarified by an analysis of H-bonding in ethanolammonium ILs and a broader range of anions.
This picture also accounts for the somewhat unexpected counterion specificity seen in the quaternary ammonium systems. Both chloride and bromide are expected to be poorly solvated by the H-bond network of these PILs, so they have good reason to be associated with the micelles, or form ion-pairs with the quaternary nitrogen center. In EAN, the CMCs based on micelle volume fractions decrease in the order DTAN > DTAC > DTAB and, although CMCs in EtAN were too low to determine by this method, the same trend is expected based on scattering intensities. This implies that bromide is a more strongly binding counterion than chloride, just as it is in aqueous micellar systems, and as expected from solvation and H-bonding propensity. Nitrate, however, behaves as the least strongly binding counterion in EAN and EtAN, whereas in water it binds even more strongly than bromide (Table 4).67
Conclusions
Micelle formation by ammonium cationic surfactants in ethylammonium and ethanolammonium nitrate and thiocyanate protic ionic liquids exhibit several unexpected features. They are largely insensitive to IL nanostructure, with the solvophobic driving force for self-assembly dominated by the average solvent character. While the H-bond network structure in the solvent is an important factor in driving self-assembly, the presence or absence of amphiphilic nanostructure in the solvent itself has little effect on either the CMC or micelle size for surfactants with 1°–3° ammonium head groups. As with molecular solvents that support surfactant self-assembly, CMCs are higher and micelles are smaller in these ILs than in water.Significant differences do emerge in quaternary ammonium systems, which have been the focus of previous investigations of ionic surfactant self-assembly in PILs, where H-bonding to the surfactant head group is absent. Here, the amphiphilic bulk liquid nanostructure in ethyl- and propyl-ammonium ILs seems to play a critical role in enhancing surfactant solubility by solvating the head-group, and thus raising CMC and reducing micelle size. In less or un-structured ILs, the CMC is dramatically lowered and micelle radii are comparable to those in water.
Surprisingly, significant counterion specific effects were found in the CMCs and micelle sizes of quaternary ammonium surfactants in EAN and EtAN. This is attributed to poor solvation of chloride and bromide by the ILs.
Amphiphilicity in these PILs differs markedly from that in water. In designing surfactants for optimal performance in ionic liquid solvents, whether for adsorption or colloidal stabilization, or for building new forms of soft, self-assembled matter, both solvophobic and solvophilic character in the PIL must be considered. Whereas solvophobicity is adequately described by a mean–field interaction between the alkyl chain and the solvent, surfactant performance in PILs depends more subtly on the solvophilic moiety. Without the dominance of electrostatics seen in molecular solvents, self-assembly of ionic amphiphiles is controlled by specific, short-range solvation and H-bonding interactions between the surfactant and the particular PIL. The same principle is expected to apply to anionic surfactants and soaps, to other nonionic surfactants, and to the vast range of possible amphiphilic copolymers: hydrophilicity ≠ solvophilicity.
Acknowledgements
This work was supported by a Discovery Project Grant from the Australian Research Council, and a Future Fellowship to RA. We acknowledge the support of the Bragg Institute, Australian Nuclear Science and Technology Organisation, in providing the neutron research facilities used in this work. We would like to thank Dr K. Wood (ANSTO) and Dr P. A. FitzGerald (The University of Sydney) for assistance in performing SANS experiments and analyzing the data.References
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed
.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed
.
- K. Binnemans, Chem. Rev., 2005, 105, 4148–4204 CrossRef CAS PubMed
.
- R. Atkin and G. G. Warr, J. Phys. Chem. B, 2008, 112, 4164–4166 CrossRef CAS PubMed
.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed
.
- H. Li, F. Endres and R. Atkin, PCCP Phys. Chem. Chem. Phys., 2013, 15, 14624–14633 RSC
.
- A. J. Page, A. Elbourne, R. Stefanovic, M. a. Addicoat, G. G. Warr, K. Voïtchovsky and R. Atkin, Nanoscale, 2014, 6, 8100–8106 RSC
.
- S. C. Sharma, R. Atkin and G. G. Warr, J. Phys. Chem. B, 2013, 117, 14568–14575 CrossRef CAS PubMed
.
- J. L. Anderson, V. Pino, E. C. Hagberg, V. V. Sheares and D. W. Armstrong, Chem. Commun., 2003, 2444–2445 RSC
.
- L. Y. Wang, X. Chen, Y. C. Chai, J. C. Hao, Z. M. Sui, W. C. Zhuang and Z. W. Sun, Chem. Commun., 2004, 2840–2841 RSC
.
- Z. Chen, T. L. Greaves, R. A. Caruso and C. J. Drummond, J. Phys. Chem. B, 2015, 119, 179–191 CrossRef CAS PubMed
.
- C. R. López-Barrón, D. Li, L. DeRita, M. G. Basavaraj and N. J. Wagner, J. Am. Chem. Soc., 2012, 134, 20728–20732 CrossRef PubMed
.
- M. U. Araos and G. G. Warr, J. Phys. Chem. B, 2005, 109, 14275–14277 CrossRef CAS PubMed
.
- T. L. Greaves and C. J. Drummond, Chem. Soc. Rev., 2008, 37, 1709–1726 RSC
.
- E. C. Wijaya, T. L. Greaves and C. J. Drummond, Faraday Discuss., 2013, 167, 191–215 RSC
.
- J. C. Thater, V. Gérard and C. Stubenrauch, Langmuir, 2014, 30, 8283–8289 CrossRef CAS PubMed
.
- W. Kunz, T. Zemb and A. Harrar, Curr. Opin. Colloid Interface Sci., 2012, 17, 205–211 CrossRef CAS PubMed
.
- R. Atkin, L. M. de Fina, U. Kiederling and G. G. Warr, J. Phys. Chem. B, 2009, 113, 12201–12213 CrossRef CAS PubMed
.
- Z. Chen, P. A. FitzGerald, Y. Kobayashi, K. Ueno, M. Watanabe, G. G. Warr and R. Atkin, Macromolecules, 2015, 48, 1843–1851 CrossRef CAS
.
- H. J. Jiang, P. A. FitzGerald, A. Dolan, R. Atkin and G. G. Warr, J. Phys. Chem. B, 2014, 118, 9983–9990 CrossRef CAS PubMed
.
- A. Ray, J. Am. Chem. Soc., 1969, 91, 6511 CrossRef CAS
.
- A. Ray, Nature, 1971, 231, 313–315 CrossRef CAS PubMed
.
- A. H. Beesley, D. F. Evans and R. G. Laughlin, J. Phys. Chem., 1988, 92, 791–793 CrossRef CAS
.
- D. F. Evans, A. Yamauchi, R. Roman and E. Z. Casassa, J. Colloid Interface Sci., 1982, 88, 89 CrossRef CAS
.
- D. F. Evans, A. Yamauchi, G. J. Wei and V. A. Bloomfield, J. Phys. Chem., 1983, 87, 3537–3541 CrossRef CAS
.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2009, 48, 3184 CrossRef CAS PubMed
.
- L. J. Magid, Z. Han, G. G. Warr, M. A. Cassidy, P. D. Butler and W. A. Hamilton, J. Phys. Chem. B, 1997, 101, 7919–7927 CrossRef CAS
.
- P. Mukerjee and K. J. Mysels, Critical Micelle Concentrations of Aqueous Surfactant Systems, National Standard Reference Data System, US Government Printing Office, Washington, DC, 1971 Search PubMed.
- S. Ikeda, S. Ozeki and M.-A. Tsunoda, J. Colloid Interface Sci., 1980, 73, 27–37 CrossRef CAS
.
- D. F. Evans, S.-H. Chen, G. W. Schriver and E. M. Arnett, J. Am. Chem. Soc., 1981, 103, 481–482 CrossRef CAS
.
- D. Mirejovsky and E. M. Arnett, J. Am. Chem. Soc., 1983, 105, 1112–1117 CrossRef CAS
.
- O. Werzer, G. G. Warr and R. Atkin, J. Phys. Chem. B, 2011, 115, 648–652 CrossRef CAS PubMed
.
- J. A. Smith, G. Webber, G. G. Warr, A. Zimmer, R. Atkin and O. Werzer, J. Colloid Interface Sci., 2014, 430, 56–60 CrossRef CAS PubMed
.
- I. L. Topolnicki, P. A. FitzGerald, R. Atkin and G. G. Warr, ChemPhysChem, 2014, 15, 2485–2489 CrossRef CAS PubMed
.
- E. H. Crook, D. B. Fordyce and G. F. Trebbi, J. Colloid Sci., 1965, 20, 191–204 CrossRef CAS
.
- M. Ben Ghoulam, N. Moatadid, A. Graciaa and J. Lachaise, Langmuir, 2002, 18, 4367–4371 CrossRef
.
- A. D. James, J. M. Wates and E. Wyn-Jones, J. Colloid Interface Sci., 1993, 160, 158 CrossRef CAS
.
-
C. A. Tanford, The Hydrophobic Effect: Formation of Micelles and Biological Membranes, Wiley, New York, 1980 Search PubMed
.
- B. W. Ninham, D. F. Evans and G. J. Wei, J. Phys. Chem., 1983, 87, 5020–5025 CrossRef CAS
.
- J. E. Brady, D. F. Evans, G. G. Warr, F. Grieser and B. W. Ninham, J. Phys. Chem., 1986, 90, 1853–1859 CrossRef CAS
.
-
Cationic Surfactants, ed. E. Jungermann, Marcel Dekker, New York, 1970 Search PubMed
.
- C. W. Hoerr and H. J. Harwood, J. Am. Chem. Soc., 1951, 73, 3350–3352 CrossRef
.
- L. Kellaway and G. G. Warr, J. Colloid Interface Sci., 1997, 193, 312–314 CrossRef CAS
.
- R. R. Balmbra, J. S. Clunie and J. F. Goodman, Nature, 1969, 222, 1159 CrossRef CAS PubMed
.
-
P. Lindner and T. Zemb, Neutron, X-Ray and Light Scattering, Elsevier, Boston, 2002 Search PubMed
.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, J. Phys. Chem. C, 2014, 118, 13998 CAS
.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237–3247 RSC
.
- C. F. Poole, B. R. Kersten, S. S. J. Ho, M. E. Coddens and K. G. Furton, J. Chromatogr. A, 1986, 352, 407 CrossRef CAS
.
- E. P. Gilbert, J. C. Schulz and T. J. Noakes, Phys. B, 2006, 385–386, 1180–1182 CrossRef CAS PubMed
.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS
.
- A. Munter, Neutron Scattering Lengths & Cross Sections, http://www.ncnr.nist.gov/resources/n-lengths/list.html.
- D. Brown and P. Kienzle, Neutron Activation and Scattering Calculator, http://www.ncnr.nist.gov/resources/activation/.
- J. B. Hayter and J. Penfold, Mol. Phys., 1981, 42, 109–118 CrossRef CAS PubMed
.
- L. C. Roess and C. G. Shull, J. Appl. Phys., 1947, 18, 308–313 CrossRef CAS PubMed
.
- S. R. Aragón and R. Pecora, J. Chem. Phys., 1976, 64, 2395 CrossRef PubMed
.
- G. V. Schulz, Z. Phys. Chem., Abt. B, 1939, 43, 25–46 Search PubMed
.
- R. Zarrougui, M. Dhahbi and D. Lemordant, J. Solution Chem., 2010, 39, 1531–1548 CrossRef CAS
.
- M. Allen, D. F. Evans and R. Lumry, J. Solution Chem., 1985, 14, 549–560 CrossRef CAS
.
- B. Fernández-Castro, T. Mendez-Morales, J. Carrete, E. Fazer, O. Cabeza, J. R. Rodriguez, M. Turmine and L. M. Varela, J. Phys. Chem. B, 2011, 115, 8145–8154 CrossRef PubMed
.
- R. Atkin and G. G. Warr, J. Phys. Chem. B, 2007, 111, 9309–9316 CrossRef CAS PubMed
.
- R. Atkin, S. M. C. Bobillier and G. G. Warr, J. Phys. Chem. B, 2010, 114, 1350–1360 CrossRef CAS PubMed
.
- S. S. Berr, E. Caponetti, J. S. Johnson, R. R. M. Jones and L. J. Magid, J. Phys. Chem., 1986, 90, 5766–5770 CrossRef CAS
.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1526–1568 RSC
.
- T. L. Greaves, A. Weerawardena, C. Fong, I. Krodkiewska and C. J. Drummond, J. Phys. Chem. B, 2006, 110, 22479–22487 CrossRef CAS PubMed
.
- M. F. Emerson and A. Holtzer, J. Phys. Chem., 1967, 71, 1898–1907 CrossRef CAS
.
- A. W. Ralston, F. K. Broome and H. J. Harwood, J. Am. Chem. Soc., 1949, 71, 671 CrossRef CAS
.
- J. Morgan, D. Napper, G. Warr and S. Nicol, Langmuir, 1994, 1, 797–801 CrossRef
.
- M. U. Araos and G. G. Warr, Langmuir, 2008, 24, 9354–9360 CrossRef CAS PubMed
.
- T. L. Greaves, S. T. Mudie and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 20441–20452 RSC
.
- L. Karve and G. B. Dutt, J. Phys. Chem. B, 2012, 116, 9107–9113 CrossRef CAS PubMed
.
- C. F. Poole, J. Chromatogr. A, 2004, 1037, 49–82 CrossRef CAS PubMed
.
- M. a. Ab Rani, A. Brant, L. Crowhurst, A. Dolan, M. Lui, N. H. Hassan, J. P. Hallett, P. a. Hunt, H. Niedermeyer, J. M. Perez-Arlandis, M. Schrems, T. Welton and R. Wilding, PCCP Phys. Chem. Chem. Phys., 2011, 13, 16831–16840 RSC
.
- G. G. Warr and D. F. Evans, Langmuir, 1988, 4, 217–224 CrossRef CAS
.
- C. J. Drummond, F. Grieser and T. W. Healy, Faraday Discuss. Chem. Soc., 1986, 81, 95–106 RSC
.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 52, 4623–4627 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |