Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis and investigation of donor–porphyrin–acceptor triads with long-lived photo-induced charge-separate states†
Julien B.
Kelber
 ab,
Naitik A.
Panjwani
b,
Di
Wu
a,
Rafael
Gómez-Bombarelli
c,
Brendon W.
Lovett
*d,
John J. L.
Morton
*b and
Harry L.
Anderson
ab,
Naitik A.
Panjwani
b,
Di
Wu
a,
Rafael
Gómez-Bombarelli
c,
Brendon W.
Lovett
*d,
John J. L.
Morton
*b and
Harry L.
Anderson
 *a
*a
aOxford University, Chemistry Research Laboratory, 12 Mansfield Road, OX1 3TA, Oxford, UK. E-mail: harry.anderson@chem.ox.ac.uk
bUniversity College London, London Centre for Nanotechnology, Gower Place, WC1E 6BT, London, UK. E-mail: jjl.morton@ucl.ac.uk
cHarvard University, Department of Chemistry and Chemical Biology, 12 Oxford St. 02138, Cambridge, MA, USA
dUniversity of St Andrews, SUPA, School of Physics and Astronomy, KY16 9SS, St Andrews, UK. E-mail: bwl4@st-andrews.ac.uk
First published on 31st July 2015
Abstract
Two donor–porphyrin–acceptor triads have been synthesized using a versatile Suzuki-coupling route. This synthetic strategy allows the powerful donor tetraalkylphenylenediamine (TAPD) to be introduced into tetraarylporphyrin-based triads without protection. The thermodynamics and kinetics of electron transfer in the new triads are compared with a previously reported octaalkyldiphenyl-porphyrin triad exhibiting a long-lived spin-polarized charge separate state (CSS), from theoretical and experimental perspectives, in both fluid solution and in a frozen solvent glass. We show that the less favorable oxidation potential of the tetraaryl-porphyrin core can be offset by using C60, as a better electron-acceptor than triptycenenaphthoquinone (TNQ). The C60–porphyrin–TAPD triad gives a spin-polarized charge-separated state that can be observed by EPR-spectroscopy, with a mean lifetime of 16 ms at 10 K, which is longer than in the previously reported TNQ–porphyrin–TAPD triad, following the predicted trend from calculated charge-recombination rates.
Introduction
Photo-induced intramolecular electron transfer can generate a charge-separated state (CSS) consisting of a hole and an electron with a spatial separation of 1–3 nm.1a In most cases, the hole and electron recombine rapidly (from ps to ns) to regenerate the ground-state. However, in some cases, the CSS can have a longer lifetime1 (from μs up to possibly hours1h,i), allowing chemical, physical or biological processes to exploit its high energy and unusual electronic structure.Long-lived photo-excited CSSs are important for a variety of applications. They are studied to understand and mimic electron transfer in natural photosynthesis, in which energy from sunlight is converted into chemical potential.2 In the area of quantum information processing, control of the spin dynamics of a CSS may allow the manipulation of a nuclear or electronic spin, to encode or transfer information.3 It is also thought that some birds, such as the European robin, use the magnetic field-dependence of the recombination rate of a CCS to orient themselves in the earth's magnetic field. Mimicking this avian compass may enable small magnetic fields to be detected.4
In the high-temperature limit, where solvent dynamics and nuclear motions can be treated as classical harmonic oscillators, recombination rates of CSSs are given by the Marcus equation5 (eqn (1)),
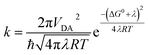 | (1) |
Wasielewski et al.7 designed a donor–porphyrin–acceptor triad TNQ–ZnP–TAPD (Fig. 1) with three desirable features. First, the strong electron-donating and -accepting behavior of the tetraalkylphenylenediamine (TAPD) and triptycenenaphthoquinone (TNQ) moieties make charge separation favorable, even in a frozen solvent where the solvent cannot reorganize to stabilize the photo-generated zwitterion. Secondly, the produced electron/hole pair has no through π-bond electronic coupling (because the donor and the acceptor moieties are separated by isolating methylene bridges), and weak through-σ-bond coupling, due to the near-orthogonal porphyrin core. Finally, the charges are rigidly separated by a distance of 2.3 nm, limiting through-space coupling. These last two features yield a very small VDA and consequently extend the lifetime of the CSS. TNQ–ZnP–TAPD showed a CSS with a lifetime of 4 ms, together with a spin-polarized radical-pair that closely mimics the bacteriochlorophyll cation–quinone anion pair found in photosynthetic reaction centers.8
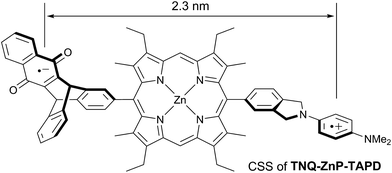 | ||
| Fig. 1 Wasielewski's design of a long-lived photo-generated radical pair.7 | ||
The initial objective of the work presented here was to synthesize porphyrin-based triads exhibiting long-lived CSSs, such as TNQ–ZnP–TAPD, so that they could be used for quantum information storage experiments. Since we also wanted to modulate the properties of our triads, we sought a versatile synthetic route with few steps from accessible precursors, which would tolerate a wide range of functional groups.
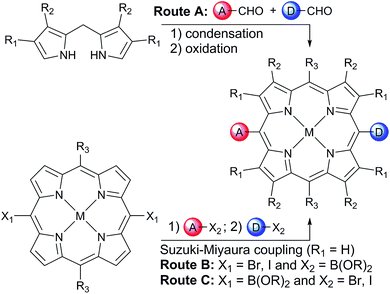
In order to avoid aggregation and enhance the solubility of 5,15-diarylporphyrins, two positions are available to introduce solubilizing groups (Scheme 1). Porphyrins can be substituted on the β-pyrrole positions (R1 and R2 on Scheme 1), generally with aliphatic chains, providing a locked 80–90° dihedral angle between the porphyrin and the aryls groups. However, β-substituted pyrroles are less readily available than pyrrole, and the steric hindrance at the 5 and 15 meso-positions prevents cross-coupling strategies from being used to introduce the donor and acceptor moieties.
Another well-established strategy to avoid aggregation and enhance solubility in 5,15-diarylporphyrins is to introduce bulky aryl groups in the two remaining 10 and 20 meso-positions (R3 = Ar; R1 = R2 = H on Scheme 1). This substitution pattern avoids steric hindrance around the 5 and 15 positions.
TAPD derivatives, also known as Würster blue,9 are highly electron-rich (oxidation potential: −0.24 V vs. Fc/Fc+, see later) and are therefore promising electron donors. On the other hand, their low oxidation potentials makes them reactive towards oxygen and other oxidants, such as those used in porphyrin synthesis.
One retro-synthetic route to 5-acceptor–15-donor disubstituted porphyrin triads is the statistical condensation of a dipyrromethane with two aldehydes substituted with the donor and acceptor moieties (Scheme 1, top, Route A), and subsequent oxidation of the porphyrinogen, typically with DDQ or chloranil. This route is incompatible with the use of oxidation-sensitive donors such as TAPD. Indeed, isoindolines are known to be oxidized to isoindoles, which then react further via dimerization or Diels–Alder reactions.10 Therefore the synthesis of TNQ–ZnP–TAPD required masking of the terminal dimethylamine as a nitro-group, resulting in a less convergent route (Scheme 2a).7a
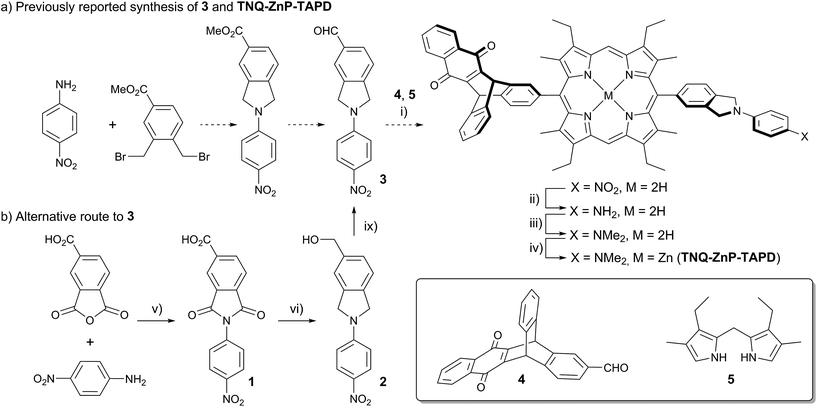 | ||
| Scheme 2 (a) Reported synthetic route of TNQ–ZnP–TAPD using the protected TAPD precursor 3.7a,b (i) BF3·OEt2, DCM then DDQ; (ii) SnCl2, HCl; (iii) NaBH3CN, CH2O; (iv) Zn(OAc)2, CHCl3/MeOH; (b) new synthesis of 3. (v) AcOH, 12 h, 118 °C, 95%; (vi) BH3·THF, THF, 12 h, 66 °C, 75%; (vii) activated MnO2, CHCl3, 15 min, 25 °C, 70%. | ||
Alternatively, a symmetrical 5,15-diaryl-10,20-dibromoporphyrin11 can be synthesized, and functionalized with two different moieties via successive cross-coupling reactions (Scheme 1, bottom). Suzuki–Miyaura coupling is widely used as a mild, non-toxic, and efficient approach for the convergent synthesis of aromatic molecular materials,12 including porphyrin derivatives.13 In this case, Suzuki–Miyaura coupling allows not only an efficient synthesis of asymmetrical donor–porphyrin–acceptor triads, but also the introduction of the sensitive donor moiety in the very last step, as the mild conditions do not require the donor to be protected from oxidation.
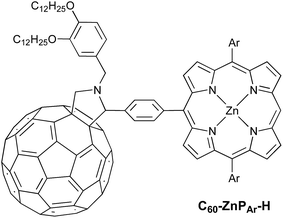
Here we present a short and efficient synthesis of useful 2-(4-dialkylaminophenyl)isoindoline electron-donating moieties (Scheme 2b), and their use in the Suzuki pathway as a convenient route to oxidation-sensitive acceptor–porphyrin–TAPD triads (Scheme 3). We also used this versatile approach to synthesize a triad with a C60 acceptor moiety, which was predicted, and found, to have a longer-lived CSS than TNQ–ZnP–TAPD.
Results and discussion
Synthesis
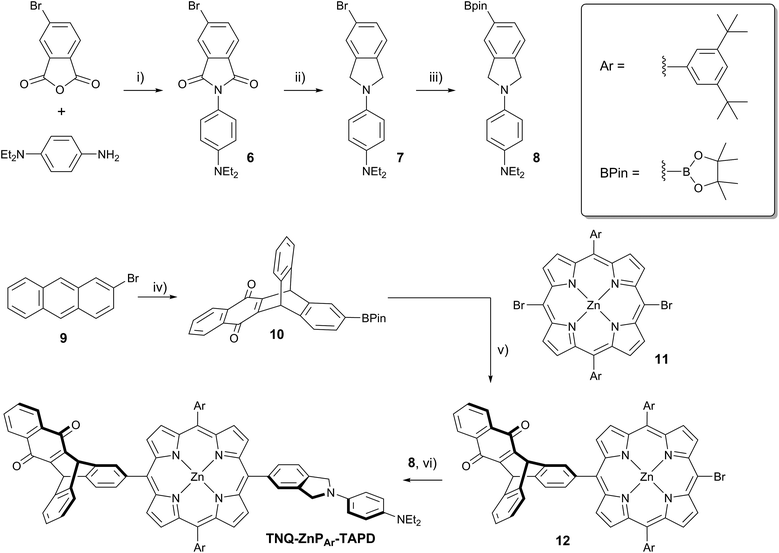
At the start of this project, we attempted to synthesize TNQ–ZnP–TAPD as reported by Wasielewski et al. (Scheme 1, Route A and Scheme 2a).7 We developed an efficient three-step synthesis of aldehyde 3 (Scheme 2b): first, 4-nitroaniline was condensed with 1,2,4-benzenetricarboxylic anhydride to yield 1. The imide and carboxylic acid functions were then simultaneously reduced with borane to give 2 and this benzyl alcohol was re-oxidized using activated manganese dioxide to yield aldehyde 3, in 50% over 3 steps. However, in our hands, the condensation of aldehydes 3 and 4 with tetraalkyl-dipyrromethane 5 did not give the desired porphyrin. Therefore, we decided to explore Suzuki coupling routes to the closely related triad TNQ–ZnPAr–TAPD (Scheme 1, Route B, and Schemes 3 and 4).The boronic ester substituted donor moiety was synthesized in good yield using the phthalimide route developed for the synthesis of aldehyde 3: 4-(N,N-diethylamino)aniline was condensed with 4-bromophthalic anhydride in refluxing acetic acid to yield 6, which was then reduced to the isoindoline using borane in refluxing tetrahydrofuran to obtain 7. Its borylated equivalent 8 was subsequently obtained via palladium-catalyzed borylation in an overall 45% yield. The acceptor boronic ester 10 was synthesized (Scheme 3) from 2-bromoanthracene 9 (ref. 14) through Diels–Alder reaction with 1,4-naphthoquinone,15 and subsequent palladium-catalyzed borylation16 of the bromo-triptycenequinone.
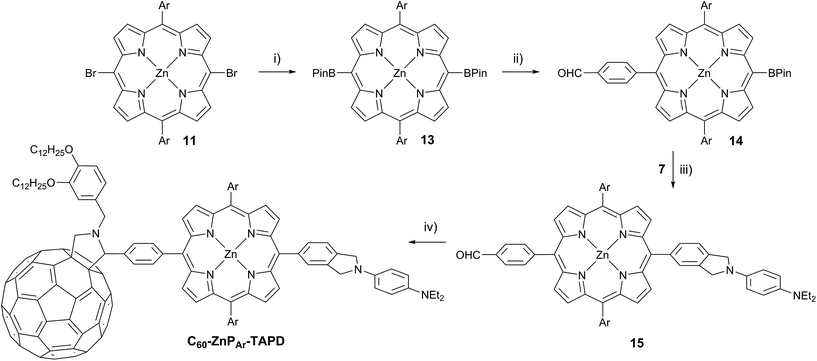
The donor and acceptor moieties were linked to the central porphyrin core via a two-step Suzuki cross-coupling. First, the reaction of 3 equivalents of dibromo-porphyrin1111 with 1 equivalent of the acceptor boronic ester 10 gave 12 in 69% yield, which was reacted in a second step with 1.1 equivalents of the donor boronic ester 8 to yield TNQ–ZnPAr–TAPD in 72% yield. Performing the Suzuki couplings in two successive steps gave better yields and made purification easier than the simultaneous statistical one-pot coupling of both the donor and the acceptor to the porphyrin. To test the versatility of the Suzuki-based route to porphyrin triads, we synthesized another triad, C60–ZnPAr–TAPD (Scheme 4), using the second Suzuki route (Scheme 1, Route C). When we performed the Suzuki coupling of 13 (ref. 17) with 4-iodobenzaldehyde, substantial deborylation of the porphyrin was observed. Therefore, the reaction was carried out with an excess of 4-iodobenzaldehyde and stopped as soon as formation of the bis(p-benzaldehyde)porphyrin adduct was detected by thin layer chromatography (TLC), to obtain 14 in 35% yield. Using an excess of 8, in the second Suzuki coupling yielded 15 in 88%, which was then transformed into C60–ZnPAr–TAPD using 2-((3,4-bis(dodecyloxy)benzyl)amino)acetic acid and C60 in a fast Prato reaction.18
Thermodynamics of electron transfer
Upon photo-excitation, the triads can undergo three consecutive electron transfer (ET) processes: (1) ET from the excited porphyrin to the acceptor, (2) ET from the donor to the oxidized porphyrin and finally, (3) back-ET from the reduced acceptor to the oxidized donor (Fig. 2). Triad TNQ–ZnPAr–TAPD is, by design, similar to TNQ–ZnP–TAPD, since it possesses the same donor and acceptor moieties, and only differs by the substitution on the porphyrin core. In order to evaluate the consequences of this different substitution pattern, and the effect of switching from a quinone to a fullerene acceptor in C60–ZnPAr–TAPD, we estimated the energies of the first and second charge-separated states, both experimentally and computationally.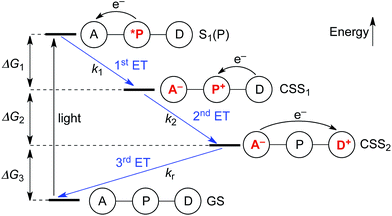 | ||
| Fig. 2 Electron transfer processes occurring upon photo-excitation of a triad. A = acceptor, P = zinc porphyrin, D = donor. | ||
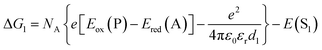 | (2) |
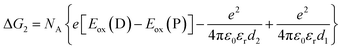 | (3) |
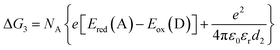 | (4) |
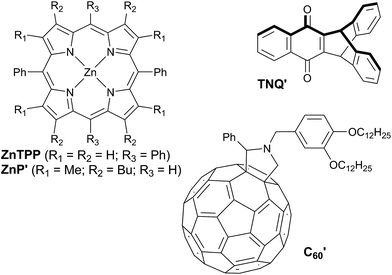
The redox potentials Eox(D) and Ered(A) were measured using squarewave voltammetry, and E(S1) values were estimated from absorption spectra (Table 1), using reference compounds 7 and those in Fig. 3 as models for the isolated donor, porphyrins and acceptor units. Electrochemical measurements on the complete triads gave very similar redox potentials to their isolated components, for example C60–ZnPAr–TAPD shows oxidation waves at −0.29 V (TAPD) and 0.32 V (ZnPAr) and reduction waves at −0.95 V (C60) and −1.84 V (ZnPAr). The values of ΔG for electron transfer for steps 1–3 (Fig. 2) derived from the electrochemical potentials in Table 1 according to eqn (2)–(4) are listed in Table 2.
| ZnP′ | ZnP′Ar (=ZnTPP) | TAPD (=7) | TNQ′ | C′60 | |
|---|---|---|---|---|---|
| a Measured by squarewave voltammetry vs. Fc/Fc+ in dichloromethane with 0.1 M NBu4PF6 as electrolyte. b λ max of the longest absorption band in dichloromethane. c E(S1) = hc/λmax. Structures of reference compounds ZnTPP, ZnP′, C′60 and TNQ′ are displayed in Fig. 3. | |||||
| E ox (V) | 0.17 | 0.32 | −0.24 | — | — |
| E red (V) | −2.13 | −1.85 | — | −1.15 | −0.99 |
| λ max (nm) | 572 | 585 | — | — | — |
| E(S1)c (eV) | 2.17 | 2.12 | — | — | — |
| TNQ–ZnP–TAPD | TNQ–ZnPAr–TAPD | C60–ZnPAr–TAPD | |
|---|---|---|---|
| a Experimental values where calculated using eqn (2)–(4), from optical and electrochemical data determined in dichloromethane reported in Table 1. b Values measured for the formerly reported triad in butyronitrile.7b c Theoretical values are shown in the order CAM-B3LYP/M062X/B3LYP; these values were calculated using the 6-31G(d) basis set. d PCM solvation model in butyronitrile, for the complete triads. e Data not available due to problems with calculating the energy of CSS1. | |||
| Experimental, fluid solution | |||
| ΔG1 | −1.01 (−0.86b) | −0.81a | −0.97a |
| ΔG2 | −0.32a (−0.45b) | −0.47a | −0.47a |
| ΔG1 + ΔG2 | −1.33a (−1.31b) | −1.28a | −1.44a |
| ΔG3 | −0.84a (−0.84b) | −0.84a | −0.68a |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Calculated, fluid solution , | |||
| ΔG1 | −1.08/−0.94/−1.07 | −0.85/−0.78/−0.97 | —e |
| ΔG2 | −0.51/−0.63/−0.63 | −0.68/−0.73/−0.68 | —e |
| ΔG1 + ΔG2 | −1.59/−1.57/−1.70 | −1.53/−1.51/−1.65 | −1.31/−1.44/−1.69 |
| ΔG3 | −0.79/−0.85/−0.72 | −0.79/−0.85/−0.72 | −1.01/−0.92/−0.75 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Calculated, frozen glass | |||
| ΔG1 | −0.32/−0.18/−0.42 | −0.04/+0.03/−0.32 | —e |
| ΔG2 | +0.11/−0.07/−0.01 | −0.06/−0.17/−0.06 | —e |
| ΔG1 + ΔG2 | −0.21/−0.25/−0.43 | −0.10/−0.15/−0.38 | −0.06/−0.23/−0.46 |
| ΔG3 | −2.17/−2.17/−1.99 | −2.17/−2.17/−1.99 | −2.26/−2.13/−1.98 |
For the first electron transfer in solution, ΔG1 is negative for all triads (−1.01 eV for TNQ–ZnP–TAPD, −0.81 eV for TNQ–ZnPAr–TAPD and −0.97 eV for C60–ZnPAr–TAPD). The second electron transfer step is also exergonic for all the triads because Eox(TAPD) ≪ Eox(ZnPAr) < Eox(ZnP). The strong favorability of electron transfer is clear from the total free energies of electron transfer (ΔG1 + ΔG2). The aim of this project was to create triads that would give long-lived CSSs at low temperatures, in a frozen solvent glass, for EPR quantum information experiments. This makes the huge driving force for charge separation important, because it enables electron transfer to be favorable even at low temperatures, under the conditions of a frozen solvent glass, when solvent dipoles cannot reorient in response to the new charge distribution in CSS1 and CSS2, as discussed below. The third electron transfer, corresponding to the charge recombination, is also exergonic for all three triads because TAPD is not a strong enough electron donor to reduce the ground-state acceptors TNQ and C60.
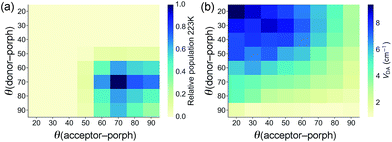
The geometries of all three triads were calculated at the B3LYP/6-31G(d) level. Calculated dihedral angles between the porphyrin and the donor unit, as well as between the porphyrin and the acceptor moiety (Table 3) agree well with the distributions from our CSD analysis. The less orthogonal geometries in ZnPAr, compared to ZnP, lead to stronger electronic coupling, as discussed below. The Boltzmann distribution of dihedral angles in TNQ–ZnPAr–TAPD at the temperature relevant to our EPR studies (223 K, the freezing point of xylene) is presented in Fig. 4a.
| θ (donor–porph) | θ (acceptor–porph) | |
|---|---|---|
| a B3LYP/6-31G(d) equilibrium geometry. | ||
| TNQ–ZnP–TAPD | 82° | 86° |
| TNQ–ZnPAr–TAPD | 70° | 68° |
| C60–ZnPAr–TAPD | 68° | 71° |
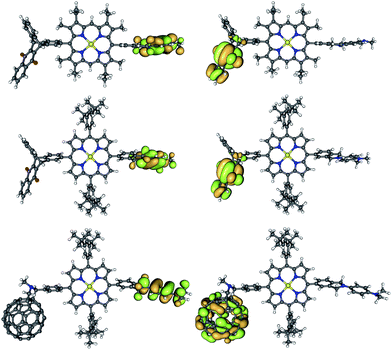 | ||
| Fig. 5 Frontier orbitals shapes (HOMO on the left, LUMO on the right) of TNQ–ZnP–TAPD (top), TNQ–ZnPAr–TAPD (middle) and C60–ZnPAr–TAPD (bottom) (B3LYP/6-31G(d)). | ||
The calculated donor (TAPD) and acceptor (TNQ and C60) orbital energies (HOMO and LUMO) show little variation between the three compounds (Table 4, see ESI† for other levels of theory). However, the tetraaryl porphyrin core ZnPAr has a smaller gap (2.84 vs. 2.97 eV; HOMO−1 to LUMO+1) and is a somewhat weaker electron donor (lower HOMO−1) than alkyl ZnP (−4.92 vs. −4.79 eV), due to the lack of electron-donating alkyl groups. TD-DFT calculations confirm a 0.05/0.06 eV lower optical gap, with S1 at 2.37/2.32 eV in ZnPAr compared to 2.42/2.38 eV for alkyl ZnP at B3LYP/6-31G(d) and CAM-B3LYP/6-31G(d), respectively. Ionization potential calculations (IP, see below and ESI†) suggest a 0.05–0.20 eV difference in oxidation potential. This is in good agreement with the 0.15 eV difference in oxidation potential between the two ZnP and ZnPAr porphyrins as measured by squarewave voltammetry, and the 0.05 eV difference in absorption energy from UV-visible spectroscopy (Table 1).
| TNQ–ZnP–TAPD | TNQ–ZnPAr–TAPD | C60–ZnPAr–TAPD | |
|---|---|---|---|
| a P, A and D indicate the location of the orbital on the porphyrin, acceptor or donor. b The LUMO of C60 is triply degenerate, but the saturation at the pyrrolidine linking breaks the symmetry. | |||
| LUMO+2 (P) | −1.80 | −2.05 | −2.09 |
| LUMO+1 (P) | −1.82 | −2.08 | −2.10 |
| LUMO (A) | −3.02 | −3.07 | −3.10; −2.99; −2.75b |
| HOMO (D) | −4.35 | −4.25 | −4.27 |
| HOMO−1 (P) | −4.79 | −4.92 | −4.95 |
| HOMO−2 (P) | −4.90 | −5.08 | −5.12 |
The reaction free energies ΔG1, ΔG2 and ΔG3 were estimated for solution-phase ET using DFT. Since the singlet–triplet gap for long-range charge-transfer systems such as these is negligible, we modeled the CSSs as the lowest unrestricted DFT triplet. The effect of the solvent was included using the Integral Equation Formalism Polarizable Continuum Model (IEFPCM) as implemented in Gaussian 09 with Universal Force Field (UFF) radii and default parameters. Energies calculated using the SMD model21 were within 0.05 eV of these values. Calculations in liquid solution were carried out using εr, the static (or zero-frequency) dielectric constant of the solvent, which includes the effect of electronic and dipolar polarization. Given their small effect in the donor–acceptor charge transfer energies, the bis-3,5-tert-butylphenyl side groups in ZnPAr were substituted by hydrogen atoms to reduce the number of nuclear and electronic degrees of freedom when the calculations did not involve states located on the porphyrin.
The results of these calculations, using three different computational methods (CAM-B3LYP/M062X/B3LYP), are compared with ΔG values from electrochemical measurements in Table 2. The calculated free energies confirm that the intermediate CSS1 is systematically shifted up in energy by the structural modification in ZnP → ZnPAr, making ΔG1 less exergonic and ΔG2 more exergonic.
Our UDFT calculations for the CSS1C60−–ZnPAr+–TAPD did not converge to the diradical state, but rather to a localized triplet, preventing calculation of ΔG1 and ΔG2. However for C60–ZnPAr–TAPD, we can still calculate the total free energy change for electron transfer (ΔG1 + ΔG2), as shown in Table 2. All DFT functions tested incorrectly predicted TNQ to be a more powerful acceptor in solution than C60 (between 0.15 to 0.05 eV, with both the 6-31G(d) and 6-311G(d,p)). In vacuum, however, this trend was reversed and the correct behavior was recovered, with a difference of 0.2–0.4 eV, as is the case when the effect of the frozen solvent is taken into account (see below). This discrepancy may be attributed to the failure of continuum solvent models to treat cavitation–dispersion interactions.
These calculations were carried out for butyronitrile as the solvent, for consistency with earlier studies by Wasielewski and co-workers,7 however other solvents have quite similar optical dielectric constants (ε∞ ≈ n2, where n is the refractive index) so that the free energies changes are expected to be similar in other frozen solvents.
Calculated rates of charge recombination
Rates of electron transfer are governed by a combination of the reaction thermodynamics (ΔG), the stiffness of the potential energy surface (λ) and the coupling of the initial and final states (VDA), as discussed above (eqn (1)).The electronic coupling between the ground state and the CSS2 (HOMO → LUMO excitation) was estimated using two-state approximation schemes: the Generalized Mulliken–Hush (GMH)22 and the Fragment-Charge Difference23 (FCD) methods. Both approaches produced very similar VDA values for the three compounds, with TNQ–ZnPAr–TAPD showing the largest coupling in the series (Table 5).
| TNQ–ZnP–TAPD | TNQ–ZnPAr–TAPD | C60–ZnPAr–TAPD | |
|---|---|---|---|
| V DA(FCD) (cm−1) | 0.23 | 2.6 | 0.27 |
| V DA(GMH) (cm−1) | 0.30 | 3.0 | 0.31 |
| λ (eV) | 0.44 | 0.44 | 0.30 |
The electronic couplings listed in Table 5 were calculated by considering only the lowest energy conformation of each molecule. In the case of TNQ–ZnPAr–TAPD, we also calculated the coupling VDA(GMH) as a function of the dihedral angles to the donor and acceptor (Fig. 4b). This plot, together with the Boltzmann distribution of dihedral angles (Fig. 4a), shows that the range of conformations populated in frozen xylene (θ ≈ 90 ± 30°) show modest variation in coupling (VDA ≈ 3 ± 2 cm−1). The energy ΔG3 of the CSS2 of TNQ–ZnPAr–TAPD is also insensitive to the dihedral angle (ca. 1% variation for θ = 90 ± 30°, see ESI Fig. S2†) which indicates that it is reasonable to consider only the lowest energy conformation of this molecule.
The treatment of low-frequency, thermally accessible vibrational modes in Marcus theory is fairly straightforward via a harmonic potential with a recombination energy. However, in the low-temperature regime where reactions progress almost exclusively through tunneling, electron-vibration coupling must be treated more explicitly. We modeled vibronic coupling under the Franck–Condon approximation by determining the Huang–Rhys factors (S) for the electron transfer.24 We used several approaches to estimate S (see ESI† for details), using both the ground state and CSS2 vibrational modes. The results from these two methods were consistent with each other. At each level of theory, there is one Sq for each vibrational mode q, of frequency ωq. For ease of comparison, these can be rolled into classical reorganization energies 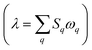 . Table 5 reports vibrational (inner-sphere) reorganization energy for the two donor–acceptor combinations. The system with a C60 acceptor has a lower reorganization energy by around 0.15 eV, in keeping with the known low λ of fullerenes in general.25
. Table 5 reports vibrational (inner-sphere) reorganization energy for the two donor–acceptor combinations. The system with a C60 acceptor has a lower reorganization energy by around 0.15 eV, in keeping with the known low λ of fullerenes in general.25
Electron transfer rates (kr, Fig. 2), in the low-temperature-limit, were estimated using eqn (5)
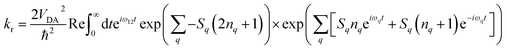 | (5) |
Combining the different levels of theory (CAM-B3LYP/6-31G(d), M062X/6-31G(d) and B3LYP/6-31G(d)) and the various estimates of S we obtained a range of values for these rates in frozen butyronitrile at 4 K. Very little temperature dependence of the results was observed in the 0–10 K regime. The predicted recombination lifetimes of TNQ–ZnP–TAPD range between 0.2 and 6.2 ms, with a geometric mean of 1.6 ms, in remarkable agreement with the experimentally reported 4 ms. Since the only difference between TNQ–ZnP–TAPD and TNQ–ZnPAr–TAPD in our models is VDA (increased by a factor of 10, averaging between GMH and FCD) we predicted a lifetime 0.02 ms for TNQ–ZnPAr–TAPD. Since C60–ZnPAr–TAPD has VDA close to TNQ–ZnP–TAPD, but a much lower reorganization energy, the vibronic coupling between initial and final state is lower. Thus, using eqn (5) we estimated a much longer lifetime (geometric mean prediction 260 ms, range between 6 and 2700 ms).
Experimental characterization of CSS2 by EPR
We measured the time-resolved EPR spectrum of the photo-excited triad TNQ–ZnPAr–TAPD under similar conditions to those reported by Wasielewski and co-workers in three different solvents (butyronitrile, 2-methyltetrahydrofuran and xylenes). Disappointingly, we were not able to detect any trace of a long-lived photo-excited charge-separate state. Instead we only detected the signal of the porphyrin triplet excited state. This was confirmed by comparing with zinc tetraphenylporphyrin in the same solvent and concentration, which gave an identical transient EPR spectrum of the zinc-porphyrin triplet state (Fig. 6). The failure to detect a long-lived CSS for TNQ–ZnPAr–TAPD, whereas one was observed for TNQ–ZnP–TAPD, can be explained by the greater electronic coupling, VDA, which arises from the orthogonal dihedral angle between the porphyrin unit and the benzene rings linking the donor and the acceptor (Fig. 4b). The slight differences in the thermodynamics of electron transfer between these molecules, also makes charge separation less favorable in TNQ–ZnPAr–TAPD (Table 2). The singlet excited state of the tetraaryl porphyrin (ZnPAr) is lower than that of the diaryl porphyrin (ZnP) by about 0.05 eV which slightly reduces the total driving force (ΔG1 + ΔG2) for formation of CSS2 in TNQ–ZnPAr–TAPD. However the main difference between these two systems is probably the lower oxidation potential of ZnPAr which makes ΔG1 less favorable for charge separation. This subtle change in thermodynamics appears to be enough to prevent charge separation in a frozen solvent matrix.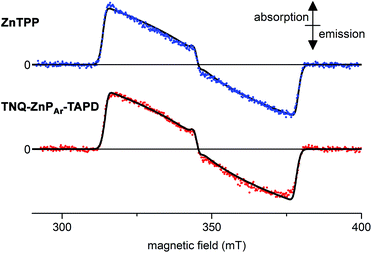 | ||
| Fig. 6 Experimental (dots) and simulated (lines, see ESI† for parameters) X-band time-resolved continuous wave EPR spectra of photo-excited ZnTPP (top) and TNQ–ZnPAr–TAPD (bottom). Concentration: 100 μM in xylenes; temperature: 10 K; excitation: 10 mJ monochromatic 20 Hz laser (590 nm); spectra recorded 1.0 μs after the laser flash. | ||
Field-sweep photo-EPR experiments on C60–ZnPAr–TAPD showed the expected signal of the spin-polarized long-lived CSS2 (Fig. 7a, bottom, central emission/absorption feature (A)) on the top of a polarized 3C60 triplet spectrum. The spectrum of the reference compound C60–ZnPAr–H, recorded under identical conditions (Fig. 7a, top), shows only the 3C60 triplet signal (B). The CSS2 signal was observed for solutions of C60–ZnPAr–TAPD in xylene and in 2-methyltetrahydrofuran (but could not be investigated in butyronitrile due to limited solubility).
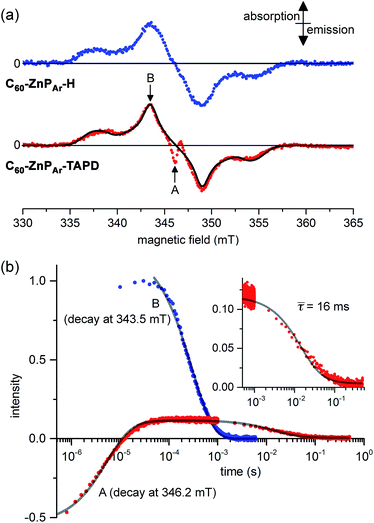 | ||
| Fig. 7 (a) X-band transient continuous-wave EPR spectra of photo-excited C60–ZnPAr–H (top) and C60–ZnPAr–TAPD (bottom); experimental (dots) and simulated 3C60 triplet spectrum (line). (b) X-band pulsed-EPR flash delay experiment performed on C60–ZnPAr–TAPD. (A) Field: 346.2 mT (radical pair signal). (B): Field: 343.5 mT (3C60 signal); both decays were fitted using a kinetic model described in the ESI.† The insert is the later part of the decay for (A), with the mean decay time, τ = (64)−1 s. 100 μM in xylenes at 10 K. Excitation: 10 mJ, 1 Hz, 590 nm; spectra recorded 1.2 μs after the laser flash. (A and B) are the fields indicated in part (a). | ||
We performed pulsed EPR experiments in which the integrated Hahn-echo intensity at a particular magnetic field position in the spectrum was recorded as a function of the time after laser excitation, to explore the time-evolution of the transient species probed at the chosen field position. These echo-integrated flash delay experiments were carried out at two different field positions corresponding to the fullerene triplet state (Fig. 7b, curve B) and the radical pair state (Fig. 7b, curve A) of C60–ZnPAr–TAPD. We were able to simulate both decay curves using a kinetic model, considering the 3C60 triplet, the singlet CSS2 and the three sub-levels, T0, T+ and T− of the triplet CSS2 (see ESI†). The 3C60 signal (curve B) follows a mono-exponential decay, with a lifetime of 300 ± 3 μs, which is consistent with previous reports.27 On the other hand, the radical pair signal (curve A) displays two different decay processes. In the μs regime, the emission/absorption signal becomes inverted to an absorption/emission pattern. This is attributed to the spin-allowed decay of the S–T0 sublevels of the radical pair. We fitted this decay to a Gaussian distribution of rate constants (mean: 1.8 × 105 s−1; standard deviation: 0.7 × 105 s−1) corresponding to a mean lifetime of 5.6 μs.
In the ms regime, we observe the decay of a positive signal (Fig. 7b, curve A and insert), corresponding to decay of the remaining T+–T− sublevel population of the CSS2 radical pair. This decay process was modeled with a Gaussian distribution of rate constants (mean: 64 ± 6 s−1; standard deviation: 32 s−1). This distribution of rate constants for both decay processes, from S–T0 and T+–T− sublevels, probably reflects the spread of molecular conformation in the frozen solution. The mean lifetime of the charge-separate state of 16 ms is among the longest reported in the literature, and is about four times longer than for TNQ–ZnP–TAPD,1,7 in keeping with the trend predicted by our computational studies.
Comparison of the integrated intensity of the EPR signal from CSS2 with that of the C60 triplet, at early times after excitation, indicates that the quantum yield of formation of CSS2 in C60–ZnPAr–TAPD is about 0.1. This is a rough estimate, based on the assumptions that formation of CSS2 and the C60 triplet are the dominant decay channels, and that these species have similar polarizations. It is difficult to accurately integrate the CSS2 signal as it has overlapping emissive and absorptive bands (see ESI† for details).
Conclusions
In this study, we have reported a versatile and convergent route to donor–zinc tetraphenylporphyrin–acceptor triads via Suzuki cross coupling reactions, which is compatible with oxidation-sensitive moieties. This approach was applied to synthesize two tetralkylphenylenediamine/zinc porphyrin/acceptor triads. We explored the kinetics and thermodynamics of charge separation in both systems. Triads exhibiting long-lived CSSs at low temperatures in frozen solvents are needed for experiments in the area of quantum information processing, yet it is difficult to achieve charge-separation under these conditions, because the frozen solvent molecules cannot reorient to stabilize the new charge distribution. For the first triad, TNQ–ZnPAr–TAPD, our calculations indicated that there would be almost no thermodynamic driving force for charge-separation in a frozen solvent. In keeping with this prediction, we were unable to detect a CSS in this system by EPR. For the second triad, C60–ZnPAr–TAPD, the greater electron-affinity of C60 was expected to make electron transfer favorable, while the weak coupling between the donor and the acceptor, VDA, and the small reorganization energy, λ, were predicted to result in an exceptionally long-lived CSS. These predictions were confirmed by the observation of a long-lived CSS in the solid state by EPR spectroscopy. The characteristic lifetime of the triplet CSS of this system is 16 ms, in xylenes at 10 K, which is among the longest reported.1 Changing the acceptor from TNQ to C60 has three important consequences: (1) it increases the driving force for electron transfer, making charge-separation favorable, even in a frozen solvent, (2) it reduces the coupling term VDA, resulting in a slow rate of charge recombination, and (3) it reduces the reorganization energy, λi, also contributing towards a slow recombination rate. Further spectroscopic studies on triad C60–ZnPAr–TAPD are in progress, and will be described in a future report.This work illustrates the value of quantum mechanical modeling for guiding the synthesis of electron-transfer systems. It also demonstrates the power of Suzuki coupling methodology, using a porphyrin core with either bromine or boronic acid substituents, for building triads with sensitive donor groups. The strategy developed here should provide a route to preparing advanced molecular materials with long photoexcited CSS lifetimes, for applications such as photo-voltaic devices, and optically gated molecular wires.28
Experimental section
General information
All chemical reagents were used as received. 2-Bromoanthracene14 and [5,15-bis-(3,5-bis-tert-butylphenyl)-10,20-bisbromoporphinato]zinc(II)13 were synthesized following a literature procedures. Dichloromethane (DCM) and tetrahydrofuran (THF) were dried over activated alumina prior to use. Anhydrous N,N-dimethylformamide (DMF), acetic acid, nitrobenzene, pyridine, toluene, xylenes and anhydrous 2-methyltetrahydrofuran (MTHF) were supplied by Aldrich and used without further purification. Purge gas was high purity argon. Chromatography was performed on silica (200–400 mesh). 1H NMR spectra were acquired on a 400 MHz (Bruker AVII 400), 500 MHz (Bruker AVII 500) or 700 MHz (Bruker AVIII 700) spectrometer. Chemical shifts (in the ppm scale) were determined versus TMS using the residual solvent peak as the internal reference (CHCl3, δ = 7.26 ppm). The 1H NMR spectra of the final triads, TNQ–ZnPAr–TAPD and C60–ZnPAr–TAPD were fully assigned by comparison with the spectra of reference compounds, in combination with 2D techniques (COSY and HSQC); see ESI.† Deuterated chloroform was stored over potassium carbonate to avoid any acid trace. UV/Vis absorption spectra were recorded using a Perkin Elmer Lambda 20 UV-Vis Spectrometer. The absorption wavelengths are reported in nm with the extinction coefficient in M−1 cm−1. Infra-red spectra were recorded in the solid state (neat) using a Bruker Tensor27 FT-IR spectrometer. Mass spectroscopy was performed either on ESI-TOF (Waters LCT Premier) or MALDI-TOF (Waters MALDI Micro MX) spectrometer or using the Bruker Ultraflextreme MALDI-TOF/TOF spectrometer from the EPSRC National Mass Spectrometry Service (Swansea). Preparative scale size exclusion chromatography (SEC) was carried out using BioRad Bio-Beads S-X1 with toluene as eluent. ESR samples were prepared in 3.8 mm quartz tubes, sealed under vacuum and kept at 77 K in the dark.Computational details
DFT calculations were performed with Gaussian 09.29 The B3LYP, CAM-B3LYP and M062X functionals were used, in conjunction with the 6-31G(d) and 6-311+G(d,p) basis sets. Minima were confirmed by harmonic analysis. Atomic displacements were projected onto vibrational modes using the FCHT keyword. Solvent effects were included via the IEFPCM formalism, using default radii (butyronitrile, εr = 24.3, ε∞ = 1.9). Electronic coupling calculations were carried out using QChem 4.2.30Synthetic procedures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with DCM (47 mg; 57 μmol; 0.15 eq.), bis(pinacolato)diboron (146 mg; 573 μmol; 1.5 eq.), potassium acetate (75 mg; 764 μmol; 2 eq.) and 7 (150 mg; 382 μmol; 1 eq.) were charged in a 2-neck flask under argon. A degassed solution of dry DMF (20 mL) was then added and the solution was stirred at 90 °C for 6 h. The mixture was poured into water (30 mL), extracted with DCM (3 × 100 mL), dried over MgSO4 and filtered. The solution was purified by filtration over SiO2 (eluent: DCM/MeOH/NEt3: 98/2/2) to obtain 8 with 10% mol mol−1 of bis(pinacolato)diboron as a white mixture of powders (118 mg; 302 μmol; 79%). Further chromatography (SiO2; dichloromethane 95/5 MeOH) purification for analytical purposes was achieved but resulted in significant material loss. Analytical data: 1H NMR (400 MHz, CDCl3): δH = 7.78 (s, 1H), 7.74 (d, 8.0 Hz, 1H), 7.34 (d, 8.0 Hz, 1H), 6.88 (br d, 9.2 Hz, 2H), 6.65 (d, 9.2 Hz, 2H), 4.61 (br, 4H), 3.22 (q, 6.8 Hz, 4H), 1.36 (s, 12H), 1.09 (t, 6.8 Hz, 6H) ppm (bispinacolatodiboron impurity: δH = 1.26 (s, 24H) ppm); 13C NMR (100 MHz, CDCl3): δC = 141.8, 140.8, 139.9, 137.9, 133.6, 128.8, 128.2, 121.9, 118.5, 112.5, 83.8 (2 carbons), 54.3, 53.9, 46.3 (2 carbons), 24.9 (4 carbons), 12.5 (2 carbons) ppm; mass spectroscopy (MALDI-TOF): calculated for [M]+ C24H33BN2O2+m/z = 392.3; found: m/z = 392.3; IR: 665 (m), 722 (m), 798 (m), 826 (w), 857 (w), 966 (w), 1074 (w), 1109 (w), 1142 (s), 1200–1250 (w), 1351 (s), 1523 (m), 1739 (m), 2000–2200 (w), 2700–2970 (w) cm−1.
1 complex with DCM (47 mg; 57 μmol; 0.15 eq.), bis(pinacolato)diboron (146 mg; 573 μmol; 1.5 eq.), potassium acetate (75 mg; 764 μmol; 2 eq.) and 7 (150 mg; 382 μmol; 1 eq.) were charged in a 2-neck flask under argon. A degassed solution of dry DMF (20 mL) was then added and the solution was stirred at 90 °C for 6 h. The mixture was poured into water (30 mL), extracted with DCM (3 × 100 mL), dried over MgSO4 and filtered. The solution was purified by filtration over SiO2 (eluent: DCM/MeOH/NEt3: 98/2/2) to obtain 8 with 10% mol mol−1 of bis(pinacolato)diboron as a white mixture of powders (118 mg; 302 μmol; 79%). Further chromatography (SiO2; dichloromethane 95/5 MeOH) purification for analytical purposes was achieved but resulted in significant material loss. Analytical data: 1H NMR (400 MHz, CDCl3): δH = 7.78 (s, 1H), 7.74 (d, 8.0 Hz, 1H), 7.34 (d, 8.0 Hz, 1H), 6.88 (br d, 9.2 Hz, 2H), 6.65 (d, 9.2 Hz, 2H), 4.61 (br, 4H), 3.22 (q, 6.8 Hz, 4H), 1.36 (s, 12H), 1.09 (t, 6.8 Hz, 6H) ppm (bispinacolatodiboron impurity: δH = 1.26 (s, 24H) ppm); 13C NMR (100 MHz, CDCl3): δC = 141.8, 140.8, 139.9, 137.9, 133.6, 128.8, 128.2, 121.9, 118.5, 112.5, 83.8 (2 carbons), 54.3, 53.9, 46.3 (2 carbons), 24.9 (4 carbons), 12.5 (2 carbons) ppm; mass spectroscopy (MALDI-TOF): calculated for [M]+ C24H33BN2O2+m/z = 392.3; found: m/z = 392.3; IR: 665 (m), 722 (m), 798 (m), 826 (w), 857 (w), 966 (w), 1074 (w), 1109 (w), 1142 (s), 1200–1250 (w), 1351 (s), 1523 (m), 1739 (m), 2000–2200 (w), 2700–2970 (w) cm−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with DCM (30 mg; 37 μmol; 0.12 eq.), bis(pinacolato)diboron (142 mg; 560 μmol; 1.9 eq.) and potassium acetate (85 mg; 861 μmol; 3 eq.) were then charged in a 2-neck flask under argon and dry degassed DMF (40 mL) was added. The solution was stirred at 90 °C for 6 h, poured into water (30 mL), extracted with DCM (3 × 100 mL), dried over MgSO4 and filtered. The obtained solution was further purified by chromatography (SiO2; eluent: DCM) to remove the triptycenequinone impurity and obtain 90 mg of 9 as a yellow powder (196 μmol; 68%; overall yield over 2 steps 55%). Analytical data: 1H NMR (400 MHz, CDCl3): δH = 8.04 (m, 2H), 7.92 (s, 1H), 7.65 (m, 2H), 7.49 (dd, 1.2 Hz, 7.2 Hz, 1H), 7.47 (d, 7.2 Hz, 1H), 7.44 (m, 2H), 7.03 (m, 2H), 6.03 (s, 1H), 6.02 (s, 1H), 1.30 (s, 12H) ppm; 13C NMR (100 MHz, CDCl3): δC = 181.0, 180.9, 153.8, 153.3, 146.8, 143.5, 143.1, 143.0, 133.45, 133.41, 132.5, 131.68, 131.64, 130.1, 126.1, 125.5, 125.4, 124.4, 124.3, 123.9, 83.7, 47.7, 47.5, 24.7, 24.6 ppm; HRMS (ESI): calculated for [M + Na]+ C30H25BNaO4+: m/z = 483.1743; found m/z = 483.1738. Calculated for [M + H]+ C30H26BO4: m/z = 483.1743; found m/z = 483.1738; IR: 685 (w), 717 (m), 802 (w), 1000–1142 (w), 1216 (s), 1260 (w), 1354 (s), 1458 (m), 1656 (m), 1739 (s), 2853–2970 (m) cm−1.
1 complex with DCM (30 mg; 37 μmol; 0.12 eq.), bis(pinacolato)diboron (142 mg; 560 μmol; 1.9 eq.) and potassium acetate (85 mg; 861 μmol; 3 eq.) were then charged in a 2-neck flask under argon and dry degassed DMF (40 mL) was added. The solution was stirred at 90 °C for 6 h, poured into water (30 mL), extracted with DCM (3 × 100 mL), dried over MgSO4 and filtered. The obtained solution was further purified by chromatography (SiO2; eluent: DCM) to remove the triptycenequinone impurity and obtain 90 mg of 9 as a yellow powder (196 μmol; 68%; overall yield over 2 steps 55%). Analytical data: 1H NMR (400 MHz, CDCl3): δH = 8.04 (m, 2H), 7.92 (s, 1H), 7.65 (m, 2H), 7.49 (dd, 1.2 Hz, 7.2 Hz, 1H), 7.47 (d, 7.2 Hz, 1H), 7.44 (m, 2H), 7.03 (m, 2H), 6.03 (s, 1H), 6.02 (s, 1H), 1.30 (s, 12H) ppm; 13C NMR (100 MHz, CDCl3): δC = 181.0, 180.9, 153.8, 153.3, 146.8, 143.5, 143.1, 143.0, 133.45, 133.41, 132.5, 131.68, 131.64, 130.1, 126.1, 125.5, 125.4, 124.4, 124.3, 123.9, 83.7, 47.7, 47.5, 24.7, 24.6 ppm; HRMS (ESI): calculated for [M + Na]+ C30H25BNaO4+: m/z = 483.1743; found m/z = 483.1738. Calculated for [M + H]+ C30H26BO4: m/z = 483.1743; found m/z = 483.1738; IR: 685 (w), 717 (m), 802 (w), 1000–1142 (w), 1216 (s), 1260 (w), 1354 (s), 1458 (m), 1656 (m), 1739 (s), 2853–2970 (m) cm−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CS2
CS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyridine-d5 = 48
pyridine-d5 = 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (v/v/v)): δH = 8.89 (m, 8H), 8.32 (br, 4H), 8.15 (s, 1H), 8.12 (d, 7.6 Hz, 1H), 8.05 (m, 4H), 7.77 (s, 2H), 7.67 (d, 7.6 Hz, 1H), 7.39 (d, 1.9 Hz, 1H), 7.35 (dd, 8.4, 1.9 Hz, 1H), 7.04 (d, 8.4 Hz, 1H), 6.84 (d, 8.8 Hz, 2H), 6.74 (d, 8.8 Hz, 2H), 5.52 (s, 1H), 5.02 (d, 8.3 Hz, 1H), 4.95 (d, 13.5 Hz, 1H), 4.94 (s, 2H), 4.88 (s, 2H), 4.34 (d, 8.3 Hz, 1H), 4.16 (t, 6.6 Hz, 2H), 4.05 (t, 6.6 Hz, 2H), 3.96 (d, 13.4 Hz, 1H), 3.26 (q, 6.9 Hz, 4H), 1.86 (m, 4H), 1.51 (m, 36H), 1.27–1.19 (br, 36H), 1.13 (t, 6.9 Hz, 6H), 0.90–0.83 (m, 6H) ppm; mass spectroscopy (MALDI-TOF positive ionization): calculated for [M + H]+ C166H134N7O2Zn+: m/z = 2310.99; found: m/z = 2311.02.
2 (v/v/v)): δH = 8.89 (m, 8H), 8.32 (br, 4H), 8.15 (s, 1H), 8.12 (d, 7.6 Hz, 1H), 8.05 (m, 4H), 7.77 (s, 2H), 7.67 (d, 7.6 Hz, 1H), 7.39 (d, 1.9 Hz, 1H), 7.35 (dd, 8.4, 1.9 Hz, 1H), 7.04 (d, 8.4 Hz, 1H), 6.84 (d, 8.8 Hz, 2H), 6.74 (d, 8.8 Hz, 2H), 5.52 (s, 1H), 5.02 (d, 8.3 Hz, 1H), 4.95 (d, 13.5 Hz, 1H), 4.94 (s, 2H), 4.88 (s, 2H), 4.34 (d, 8.3 Hz, 1H), 4.16 (t, 6.6 Hz, 2H), 4.05 (t, 6.6 Hz, 2H), 3.96 (d, 13.4 Hz, 1H), 3.26 (q, 6.9 Hz, 4H), 1.86 (m, 4H), 1.51 (m, 36H), 1.27–1.19 (br, 36H), 1.13 (t, 6.9 Hz, 6H), 0.90–0.83 (m, 6H) ppm; mass spectroscopy (MALDI-TOF positive ionization): calculated for [M + H]+ C166H134N7O2Zn+: m/z = 2310.99; found: m/z = 2311.02.
Acknowledgements
We thank the EPSRC for funding (grants EP/I035536/1 and EP/J015067/1) and the EPSRC UK National Mass Spectrometry Facility at Swansea University for mass spectra. B. W. L. and R. G. B. acknowledge the DARPA QuBE program for financial support.Notes and references
- (a) P. Piotrowiak, Chem. Soc. Rev., 1999, 28, 143 RSC; (b) L. Flamigni, E. Baranoff, J. P. Collin and J. P. Sauvage, Chem.–Eur. J., 2006, 12, 6592 CrossRef CAS PubMed; (c) H. Imahori, D. M. Guldi, K. Tamaki, Y. Yoshida, C. Luo, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 6671 Search PubMed; (d) D. Curiel, K. Ohkubo, J. R. Reimers, S. Fukuzumi and M. J. Crossley, Phys. Chem. Chem. Phys., 2007, 9, 5260 RSC; (e) S. H. Lee, A. G. Larsen, K. Ohkubo, Z. L. Cai, J. R. Reimers, S. Fukuzumi and M. J. Crossley, Chem. Sci., 2012, 3, 257 RSC; (f) K. Ohkubo, H. Kotani, J. Shao, Z. Ou, K. M. Kadish, G. Li, R. K. Pandey, M. Fujitsuka, O. Ito, H. Imahori and S. Fukuzumi, Angew. Chem., Int. Ed., 2004, 116, 853 CrossRef PubMed; (g) Y. Kashiwagi, K. Ohkubo, J. A. McDonald, I. M. Blake, M. J. Crossley, Y. Araki, O. Ito, H. Imahori and S. Fukuzumi, Org. Lett., 2003, 5, 2719 CrossRef CAS PubMed; (h) S. Fukuzumi, H. Kotani, K. Ohkubo, S. Ogo, N. V. Tkachenko and H. Lemmetyinen, J. Am. Chem. Soc., 2004, 126, 1600 CrossRef CAS PubMed; (i) J. W. Verhoeven, H. J. van Ramesdonk, H. Zhang, M. M. Groeneveld, A. C. Benniston and A. Harriman, Int. J. Photoenergy, 2005, 7, 103 CrossRef CAS.
- (a) P. K. A. Mazzioa and C. K. Luscombe, Chem. Soc. Rev., 2015, 44, 78 RSC; (b) L.-L. Li and E. W.-G. Diau, Chem. Soc. Rev., 2013, 42, 291 RSC; (c) P. D. Frischmann, K. Mahataa and F. Würthner, Chem. Soc. Rev., 2013, 42, 1847 RSC; (d) A. J. Cowan and J. R. Durrant, Chem. Soc. Rev., 2013, 42, 2281 RSC; (e) D. Gust and T. A. Moore, Science, 1989, 244, 35 CAS; (f) D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 1993, 26, 198 CrossRef CAS; (g) M. R. Wasielewski, Chem. Rev., 1992, 92, 435 CrossRef CAS; (h) K. Möbius, Chem. Soc. Rev., 2000, 29, 129 RSC; (i) A. J. Bard and A. M. Fox, Acc. Chem. Res., 1995, 28, 141 CrossRef CAS; (j) M. Di Valentin, A. Bisol, G. Agostini, M. Fuhs, P. A. Liddell, A. L. Moore, T. A. Moore, D. Gust and D. Carbonera, J. Am. Chem. Soc., 2004, 126, 17074 CrossRef CAS PubMed; (k) M. R. Wasielewski, J. Org. Chem., 2006, 71, 5051 CrossRef CAS PubMed.
- (a) L. Kobr, D. M. Gardner, A. L. Smeigh, S. M. Dyar, S. D. Karlen, R. Carmieli and M. R. Wasielewski, J. Am. Chem. Soc., 2012, 134, 12430 CrossRef CAS PubMed; (b) T. Miura and M. R. Wasielewski, J. Am. Chem. Soc., 2011, 133, 2844 CrossRef CAS PubMed; (c) A. S. Lukas, P. J. Bushard and M. R. Wasielewski, J. Am. Chem. Soc., 2001, 123, 2440 CrossRef CAS. For an overview of organic material-based spintronics, see: (d) S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336 RSC; (e) A. J. Epstein, MRS Bull., 2003, 28, 492 CrossRef CAS; (f) S. A. Wolf, D. D. Awschalom, R. A. Burhman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488 CrossRef CAS PubMed.
- (a) T. Ritz, R. Wiltschko, P. J. Hore, C. T. Rodgers, K. Stapput, P. Thalau, C. R. Timmel and W. Wiltschko, Biophys. J., 2009, 96, 3451 CrossRef CAS PubMed; (b) T. Ritz, M. Ahmad, H. Mouritsen, R. Wiltschko and W. Wiltschko, J. R. Soc., Interface, 2010, 7, 135 CrossRef PubMed; (c) I. K. Kominis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 056115 CrossRef CAS; (d) J. M. Cai, G. G. Guerreschi and H. J. Briegel, Phys. Rev. Lett., 2010, 104, 220502 CrossRef; (e) E. M. Gauger, E. Rieper, J. J. L. Morton, S. C. Benjamin and V. Vedral, Phys. Rev. Lett., 2011, 106, 040503 CrossRef; (f) H. J. Hogben, T. Biskup and P. J. Hore, Phys. Rev. Lett., 2012, 109, 220501 CrossRef; (g) K. Maeda, K. B. Henbest, F. Cintolesi, I. Kuprov, C. T. Rodgers, P. A. Liddell, D. Gust, C. R. Timmel and P. J. Hore, Nature, 2008, 453, 387 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS.
- (a) M. N. Paddon-Row, Acc. Chem. Res., 1994, 27, 18 CrossRef CAS; (b) A. Osuka, S. Marumo, N. Mataga, S. Taniguchi, T. Okada, I. Yamazaki, Y. Nishimura, T. Ohno and K. Nozaki, J. Am. Chem. Soc., 1996, 118, 155 CrossRef CAS; (c) D. Gust, T. A. Moore, A. L. Moore, A. N. Macpherson, A. Lopez, J. M. DeGraziano, I. Gouni, E. Bittersmann, G. R. Seely, F. Gao, R. A. Nieman, X. C. Ma, L. J. Demanche, S.-C. Hung, D. K. Luttrull, S.-J. Lee and P. K. Kerrigan, J. Am. Chem. Soc., 1993, 115, 11141 CrossRef CAS.
- (a) M. R. Wasielewski, G. L. Gaines, M. P. O'Neil, W. A. Svec and M. P. Niemczyk, J. Am. Chem. Soc., 1990, 112, 4559 CrossRef CAS; (b) M. R. Wasielewski, G. L. Gaines, M. P. O'Neil, W. A. Svec and M. P. Niemczyk, Mol. Cryst. Liq. Cryst., 1991, 194, 201 CrossRef CAS PubMed; (c) K. Laukenmann, S. Weber, G. Kothe, C. Oesterle, A. Angerhofert, M. R. Wasielewski, W. A. Svec and J. R. Norris, J. Phys. Chem., 1995, 99, 4324 CrossRef CAS; (d) A. M. Kiefer, S. M. Kast, R. M. Wasielewski, K. Laukenmann and G. Kothe, J. Am. Chem. Soc., 1999, 121, 188 CrossRef CAS; (e) A. J. an der Est, G. Fuechsle, D. Stehlik and M. R. Wasielewski, Appl. Magn. Reson., 1997, 13, 317 CrossRef; (f) A. J. van der Est, G. Fuechsle, D. Stehlik and M. R. Wasielewski, Ber. Bunsenges. Phys. Chem., 1996, 100, 2081 CrossRef CAS PubMed; (g) M. R. Wasielewski, D. G. Johnson, W. A. Svec, K. M. Kersey and D. W. Minsek, J. Am. Chem. Soc., 1988, 110, 7219 CrossRef CAS.
- C. Kirmaier and D. Holten, Photosynth. Res., 1987, 13, 225 CrossRef CAS PubMed.
- C. Wurster and E. Schobig, Ber. Dtsch. Chem. Ges., 1879, 12, 1807 CrossRef PubMed.
- (a) R. P. Kreher and N. Kohl, Angew. Chem., Int. Ed., 1984, 96, 507 CrossRef CAS PubMed; (b) L. A. Carpino, R. E. Padykula, D. E. Barr, F. H. Hall, J. G. Krause, R. F. Dufresne and C. J. Thoman, J. Org. Chem., 1988, 53, 2565 CrossRef CAS; (c) R. Bonnett, S. A. North, R. F. Newton and D. I. C. Scopes, Tetrahedron, 1983, 39, 1401 CrossRef CAS.
- (a) S. G. DiMagno, V. S.-Y. Lin and M. J. Therien, J. Am. Chem. Soc., 1993, 115, 2513 CrossRef CAS; (b) J. Plater, S. Aikena and G. Bourhill, Tetrahedron, 2002, 58, 2405 CrossRef.
- For an overview, see: (a) I. J. S. Fairlamb and A. F. Lee, C–H and C–X Bond Functionalization, Chapter 3 Fundamental Pd0/PdII Redox Steps in Cross-coupling Reactions: Homogeneous, Hybrid Homogeneous–Heterogeneous to Heterogeneous Mechanistic Pathways for C–C Couplings, RSC books, 2013 Search PubMed; (b) N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457 CrossRef CAS.
- (a) M. A. Filatov, R. Guilard and P. D. Harvey, Org. Lett., 2010, 12, 196 CrossRef CAS PubMed; (b) L. Yu, K. Muthukumaran, I. V. Sazanovich, C. Kirmaier, E. Hindin, J. R. Diers, P. D. Boyle, D. F. Bocian, D. Holten and J. S. Lindsey, Inorg. Chem., 2003, 42, 6629 CrossRef CAS PubMed; (c) N. Aratani and A. Osuka, Chem. Commun., 2008, 4067 RSC; (d) M. Pawlicki, M. Morisue, N. K. S. Davis, D. G. McLean, J. E. Haley, E. Beuerman, M. Drobizhev, A. Rebane, A. L. Thompson, S. I. Pascu, G. Accorsi, N. Armarolie and H. L. Anderson, Chem. Sci., 2012, 3, 1541 RSC.
- R. S. Coleman and M. A. Mortensen, Tetrahedron Lett., 2003, 44, 1215 CrossRef CAS.
- M. R. Wasielewski, M. P. Niemczyk, D. G. Johnson, W. A. Svec and D. W. Minsek, Tetrahedron, 1989, 45, 4785 CrossRef CAS.
- (a) M. T. Stone and H. L. Anderson, Chem. Commun., 2007, 2387 RSC; (b) T. Ishiyama, M. Murata and N. Miyaura, J. Org. Chem., 1995, 60, 7508 CrossRef CAS.
- N. K. S. Davis, A. L. Thompson and H. L. Anderson, Org. Lett., 2010, 12, 2124 CrossRef CAS PubMed.
- (a) M. Maggini, G. Scorrano and M. Prato, J. Am. Chem. Soc., 1993, 115, 9798 CrossRef CAS; (b) B. J. Farrington, M. Jevric, G. A. Rance, A. Ardavan, A. N. Khlobystov, G. A. D. Briggs and K. Porfyrakis, Angew. Chem., Int. Ed., 2012, 51, 3587 CrossRef CAS PubMed.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259 CrossRef CAS PubMed.
- (a) H. N. Fonda, J. V. Gilbert, R. A. Cormier, J. R. Sprague, K. Kamioka and J. S. Connolly, J. Phys. Chem., 1993, 97, 7024 CrossRef CAS; (b) H. L. Anderson, Chem. Commun., 1999, 2323 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15 CrossRef CAS.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607 CrossRef CAS PubMed.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- D. M. Guldi and S. Fukuzumi, The Small Reorganisation Energy of Fullerenes, in Fullerenes: From Synthesis to Optoelectronic Properties, ed. D. M. Guldi and N. Martin, Developments in Fullerene Science 4, Springer, Netherlands, 2002, p. 237 Search PubMed.
- (a) G. C. Schatz and M. A. Ratner, Quantum Mechanics in Chemistry, Courier Dover Publications, 2002 Search PubMed; (b) P. Siders and R. A. Marcus, J. Am. Chem. Soc., 1981, 103, 741 CrossRef CAS; (c) T. Holstein, Ann. Phys., 1959, 325(8), 343 CrossRef.
- (a) V. Filidou, S. Mamone, S. Simmons, S. D. Karlen, H. L. Anderson, C. W. M. Kay, A. Bagno, F. Rastrelli, Y. Murata, K. Komatsu, X. Lei, Y. Li, N. J. Turro, M. H. Levitt and J. J. L. Morton, Philos. Trans. R. Soc., A, 2013, 371, 20120475 CrossRef PubMed; (b) M. R. Fraelich and R. B. Weisman, J. Phys. Chem., 1993, 97, 11145 CrossRef CAS.
- S. Battacharyya, A. Kibel, G. Kodis, P. A. Liddell, M. Gervaldo, D. S. Gust and S. Lindsay, Nano Lett., 2011, 11, 2709 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Shao, et al. , Mol. Phys., 2015, 2, 184 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc01830g |
| This journal is © The Royal Society of Chemistry 2015 |