Open Access Article
Open Access ArticleUnravelling the effect of temperature on viscosity-sensitive fluorescent molecular rotors†
Aurimas
Vyšniauskas
 a,
Maryam
Qurashi
a,
Nathaniel
Gallop
a,
Milan
Balaz‡
b,
Harry L.
Anderson
b and
Marina K.
Kuimova
*a
a,
Maryam
Qurashi
a,
Nathaniel
Gallop
a,
Milan
Balaz‡
b,
Harry L.
Anderson
b and
Marina K.
Kuimova
*a
aChemistry Department, Imperial College London, Exhibition Road, SW7 2AZ, UK. E-mail: m.kuimova@imperial.ac.uk
bChemistry Department, University of Oxford, Chemistry Research Laboratory, Oxford, OX1 3TA, UK
First published on 6th July 2015
Abstract
Viscosity and temperature variations in the microscopic world are of paramount importance for diffusion and reactions. Consequently, a plethora of fluorescent probes have evolved over the years to enable fluorescent imaging of both parameters in biological cells. However, the simultaneous effect of both temperature and viscosity on the photophysical behavior of fluorophores is rarely considered, yet unavoidable variations in temperature can lead to significant errors in the readout of viscosity and vice versa. Here we examine the effect of temperature on the photophysical behavior of three classes of viscosity-sensitive fluorophores termed ‘molecular rotors’. For each of the fluorophores we decouple the effect of temperature from the effect of viscosity. In the case of the conjugated porphyrin dimer, we demonstrate that, uniquely, simultaneous dual-mode lifetime and intensity measurements of this fluorophore can be used for measuring both viscosity and temperature concurrently.
Introduction
Molecular rotors have demonstrated their usefulness as fluorescent molecules sensitive to the viscosity of their environment.1–5 The sensitivity of such fluorophores is typically brought about by the interplay between ‘bright’ and ‘dark’ excited states, which is controlled by the rate of intramolecular rotation.6 In a viscous environment, the intramolecular rotation is slowed down, and the non-radiative decay of a molecular rotor is consequently suppressed. Thus both the fluorescence quantum yield and the lifetime of molecular rotors can be correlated to the viscosity of the surrounding environment, and can therefore be exploited for viscosity measurements in micro-heterogeneous systems such as biological cells,3,4,7,8 atmospheric aerosols,9 and on the microscale of inhomogeneous materials.10,11Likewise, temperature can also affect the balance in the relative population of the bright and dark excited states of fluorophores by enabling or precluding the bright-to-dark state transitions. However, to the best of our knowledge, the effect of temperature on the photophysical behaviour of molecular rotors has not been systematically examined. Here we consider the effect of temperature on the photophysical behaviour of three molecular rotors: Bodipy-C10 (1), sulforhodamine B (2) and a conjugated porphyrin dimer (3) (Scheme 1). Despite the fact that changing temperature also causes changes in viscosity, we demonstrate how, for each of these fluorophores, the effect of temperature can be decoupled in order to provide independent measurements of either (or even both) of these parameters.
Fluorescent molecules 1 and 3 have been used previously as viscosity sensors in cells and membranes.3,4,12,13 For molecular rotors similar to 1 it was established that temperature does not change the population of dark vs. bright excited states of this molecular rotor, and the effect of changing the temperature is that of changing viscosity alone,7,12 similar to the conclusions of Haidekker and co-workers for DCVJ, CCVJ and other anilino-based molecular rotors.14 In contrast, it is well known that 2 can be employed as a temperature sensor,15,16 although it has been used as a viscosity probe on several occasions.9,17 Temperature dependence of the photophysics of 3 has not been previously examined or utilized.
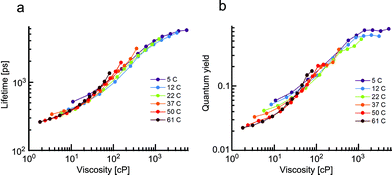
Initially, we measured fluorescence quantum yields and lifetimes of 1 in methanol/glycerol mixtures of different viscosities at different temperatures in order to untangle the viscosity and temperature sensitivity. Thus, it allowed us to (i) study the widest range of possible viscosities, and (ii) examine the effect of temperature on the fluorescence lifetime and the quantum yield of 1, Fig. 1.
The fluorescence of 1 decayed monoexponentially in all solvents. The fitted lifetimes ranged from 260 ps to 5700 ps for viscosities between 1.8 and 5400 cP. The corresponding fluorescence quantum yield increased from 0.02 to 0.77 in the same viscosity range. Importantly, for both the lifetime and the quantum yield graphs, a good overlap of values measured at the same viscosity was observed, even though both the temperature and the solvent composition was varied. A slight spread of values obtained from solutions of 1 with viscosity of less than 30 cP (particularly for the quantum yields in Fig. 1b) is likely due to small variations in dielectric constants of these mixtures at different temperatures (see the ESI for more details†).
Overall, the close overlap indicates that the photophysical parameters of 1 depend on viscosity alone. Thus, changes in temperature do not affect the population of the bright and dark states of 1 directly, but only affect the viscosity of the mixtures. We have previously demonstrated that molecular rotors with analogous structures (e.g.: Bodipy-phenyl with a C12 (ref. 12) or doubly charged7 chain) are similarly unaffected by the temperature.
Thus, molecular rotors of the Bodipy family can measure viscosity in a temperature-independent manner. The photophysical behaviour of these dyes (at least at high viscosities) is also unaffected by the polarity of their environment.18 Both of these factors are extremely useful properties for a molecular rotor.
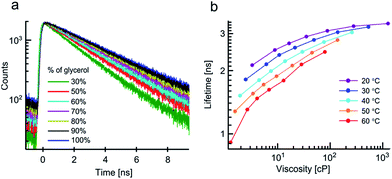
Next we examined the effect of viscosity and temperature on 2 in water/glycerol mixtures between 20 and 60 °C. The lifetime of 2, which was previously used as both a temperature and a viscosity marker,9,15–17 shows pronounced viscosity dependence (Fig. 2).
In contrast to the data for 1, the lifetimes recorded for 2 measured at the same viscosity or temperature do not overlap. Thus, the lifetimes of 2 are strongly dependent on both viscosity and temperature. A similar behaviour was also observed for 2 in methanol/glycerol mixtures. However, in these mixtures the viscosity-driven response is somewhat weaker (Fig. S2a and c†), This effect can be attributed to the lower polarity of methanol/glycerol mixtures, which likely alters the position of the dark state and/or the barrier height between the bright and the dark states for 2.
In summary, the viscosity can only be rigorously measured using 2 if the temperature is known and vice versa. While viscosity measurements at fixed temperatures are easy to perform, the reverse measurement (temperature at a fixed viscosity) is rarely possible. This is due to the fact that the change in temperature often leads to changes of viscosity and in this case these two parameters cannot be decoupled. This problem applies to viscous environments found in lipid membranes, cellular organelles, and, generally, in viscous materials. It is conceivable that this problem is not limited to molecular rotors and that, for some of the reported temperature-sensitive fluorophores,19–22 viscosity of the environment may play a role.
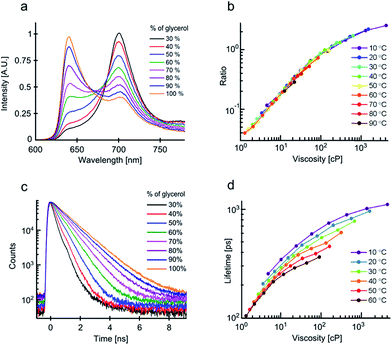
Finally, we have examined the temperature- and viscosity-dependent photophysical behaviour of molecular rotor 3, constructed as a conjugated porphyrin dimer. We have previously demonstrated that viscosity responses of this molecular rotor can be calibrated using both ratiometric and lifetime approaches.13 Viscosity-dependent spectra of 3 recorded in glycerol–methanol mixtures are shown in Fig. 3a. Two fluorescence peaks can be seen at 640 nm and 700 nm, assigned to the interconverting ‘twisted’ and ‘planar’ conformers of the dimer, respectively.23 The ratio of these peaks responds to viscosity changes. It is clear from Fig. 3b that all 640/700 nm ratios recorded in various mixtures at different temperatures overlap perfectly. Thus, the ratiometric viscosity measurements of 3, in a manner similar to 1, can provide viscosity values that are unbiased by temperature. We also note that the spread of values, even at small viscosities, is extremely small compared to Fig. 1a, indicating that polarity affects the photophysics of 3 to an even lesser extent than that of 1.
We next measured the fluorescence decay traces of 3 in the same mixtures (Fig. 3c). The fitted lifetimes are shown in Fig. 3d. The fluorescence lifetimes increase following an increase in viscosity, consistent with a slower rate of interconversion between the twisted and the planar conformers, arising from a restriction of rotation at higher viscosities.
It is also clear to see that in the case of the fluorescence lifetime of 3, temperature plays a significant role, as the lifetimes recorded at identical viscosities – but at different temperatures – do not overlap.
This result was unexpected, since the fluorescence lifetime was expected to follow a similar trend to that of the intensity ratio of a fluorophore. Thus, the lack of correlation between the temperature dependence of fluorescence lifetimes and ratios indicates that an additional de-excitation pathway exists for both the twisted and planar conformers of 3, which becomes more efficient at higher temperatures.
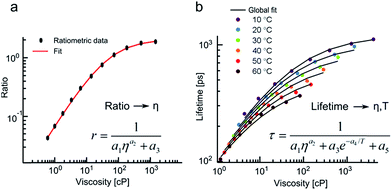
We have fitted the viscosity dependence of fluorescence ratios using a variant of a Hill function (see equation in the inset of Fig. 4a), where r is ratio, η is viscosity and ai are fitting parameters. The equation has been derived theoretically.13
We have then confirmed that an addition of the Arrhenius term (see equation in the inset of Fig. 4b) allows to globally fit both viscosity and temperature dependent lifetimes of 3 (Fig. 4b).
Thus, fluorescence ratios of 3 can be correlated to viscosity in a temperature independent manner, while the lifetimes of 3 change as a function of both temperature and viscosity according to the well-defined framework of the above equations.
We believe that the above phenomenon presents a unique opportunity for simultaneous imaging of both viscosity and temperature using a single fluorophore 3 in dual ratiometric and lifetime modes. Specifically, fluorescence peak ratios report on viscosity alone, while the viscosity and temperature dependence of fluorescence lifetime of 3 can be decoupled if the viscosity is known from the ratiometric measurements.
To test this method we placed a room temperature methanol/glycerol mixture (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) containing 3 in an imaging chamber under a microscope, capable of both ratiometric and fluorescence lifetime imaging (FLIM). A hot copper wire (heated via a contact with a soldering iron) was inserted in the imaging chamber. Consequently, the temperature and viscosity of the mixture around the wire changed as a function of time and was imaged by dual mode acquisition of ratios and lifetimes of 3.
7) containing 3 in an imaging chamber under a microscope, capable of both ratiometric and fluorescence lifetime imaging (FLIM). A hot copper wire (heated via a contact with a soldering iron) was inserted in the imaging chamber. Consequently, the temperature and viscosity of the mixture around the wire changed as a function of time and was imaged by dual mode acquisition of ratios and lifetimes of 3.
Ratiometric images were recorded by obtaining the ratio of the fluorescence intensities in each pixel of two sequentially measured images: acquired in the 635–645 nm and 690–700 nm ranges respectively (Fig. 5a). A series of FLIM images of the same chamber were recorded by monitoring fluorescence emission of 3 at 640 ± 5 nm (Fig. 5b).
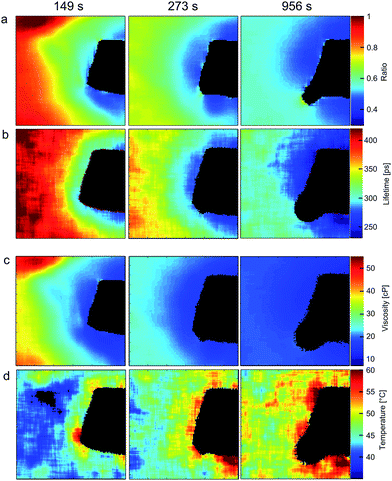 | ||
Fig. 5 Ratiometric (a) and FLIM images (b) of 3 together with calculated viscosity (c) and temperature (d) maps of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 methanol/glycerol mixture during the course of heating with hot copper wire (black object in each image). A black round structure appearing at later heating times (column three) is a gas bubble. Estimated error for imaging viscosity (ratiometric) is 1%; errors associated with imaging temperature are discussed in the ESI.† 7 methanol/glycerol mixture during the course of heating with hot copper wire (black object in each image). A black round structure appearing at later heating times (column three) is a gas bubble. Estimated error for imaging viscosity (ratiometric) is 1%; errors associated with imaging temperature are discussed in the ESI.† | ||
The viscosity maps (Fig. 5c) were calculated from the ratiometric images using the calibration curve (Fig. 4a). Finally, the temperature maps (Fig. 5d) were calculated from FLIM images using the calibration surface shown in Fig. 4b, given the viscosity maps displayed in Fig. 5c. The black rectangular object visible in the image is the end of the copper wire, which does not transmit/emit light. It is evident that the temperature is higher and the viscosity decreases closer to the wire at all times after the start of heating. Furthermore, at each point, the viscosity decreases and temperature increases with increasing heating time.
We have compared the temperature maps obtained using the dual imaging of 3 with known viscosity–temperature correlation data for a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 methanol/glycerol mixture (ESI, Fig. S6 and S7†) and subsequently find excellent agreement. We note, however, that the temperature maps (Fig. 5d) are less smooth compared to the viscosity maps (Fig. 5c) obtained by ratiometric imaging of 3, likely due to fact that the small measurement errors from the ratiometric method add to the fitting error of the biexponential decays of 3. In summary, data in Fig. 5 shows that, in principle, it is possible to use a single fluorophore 3 as both a viscosity and a temperature probe for a wide range of temperatures and viscosities, giving a unique chance to decouple both intertwined parameters.
7 methanol/glycerol mixture (ESI, Fig. S6 and S7†) and subsequently find excellent agreement. We note, however, that the temperature maps (Fig. 5d) are less smooth compared to the viscosity maps (Fig. 5c) obtained by ratiometric imaging of 3, likely due to fact that the small measurement errors from the ratiometric method add to the fitting error of the biexponential decays of 3. In summary, data in Fig. 5 shows that, in principle, it is possible to use a single fluorophore 3 as both a viscosity and a temperature probe for a wide range of temperatures and viscosities, giving a unique chance to decouple both intertwined parameters.
A number of spectroscopic viscosity probes2,5,24 and temperature probes24–27 were reported in the literature over the past decade. To the best of our knowledge, 3 is the first example of a fluorophore that allows simultaneous measurement and imaging of viscosity and temperature in heterogeneous environments. However, we believe that the significance of our finding is more far-reaching and can allow, for the first time, reliable measurement of temperature in heterogeneously viscous environments.
While viscosity measurements at fixed temperatures are feasible (e.g. using molecular rotors such as 1), the temperature measurements in an unknown system are considerably more challenging.28 A change in the temperature, e.g. of a methanol/glycerol mixture (Fig. 5), or of a lipid bilayer,12 will lead to significant changes in viscosity. As such these two parameters cannot normally be decoupled. A conjugated porphyrin dimer 3 offers a solution to this problem, as it allows, uniquely, a simultaneous measurement of both parameters.
Conclusions
In this work we have examined the effect of viscosity and temperature on the photophysical properties of a series of molecular rotors. The photophysical behaviour of 1 is dependent on viscosity alone and these measurements are not biased by potential changes in temperature. Conversely, 2 shows strong temperature dependence, which is either comparable to or stronger than its dependence on viscosity. As a result, the viscosity measurements at variable temperature using 2 are not possible. Importantly, 2 is also not suitable for temperature measurements in viscous media, since temperature and viscosity effects on its photophysics cannot be separated. In contrast, molecular rotor 3 is capable of simultaneous measurements of both the viscosity and the temperature using dual mode ratiometric and lifetime imaging. To the best of our knowledge, this is the only example of a fluorophore with such dual functionality. Importantly, this means that 3 is unique in being capable of accurate temperature measurements in viscous environments, since the dual-mode measurement using 3 accounts for both the temperature and the viscosity effect on its photophysical behaviour.Experimental section
Dyes and solvents
Syntheses of 1 (ref. 29) and 3 (ref. 30) have been reported previously, 2 was obtained from Sigma-Aldrich in an acid form (95% purity). All solvents used were spectroscopic grade. Methanol and DMSO were obtained from Sigma-Aldrich. Glycerol was obtained from Alfa-Aesar. Deionised water was used in all experiments. The viscosities of solvent mixtures were measured using an SVM 3000 viscometer (Anton Paar) with 1% accuracy.Absorption and fluorescence spectra, quantum yield measurements
Quartz cuvettes with a 10 mm path length were used in all measurements. Absorption spectra were measured using an Agilent 8453 UV-Vis spectrophotometer. Fluorescence spectra and quantum yields were recorded using a Fluoromax-4 spectrofluorometer (Jobin-Yvon; Horiba). Temperature inside the cuvettes was controlled by Peltier thermostated cuvette holder (F3004, Jobin-Yvon; Horiba), to 0.5 °C accuracy, and additionally verified by inserting a thermocouple (2006T, Digitron) into the cuvette. The quantum yields of 1 were determined by comparative method relative to fluorescein as a standard (ϕf = 0.95 in 0.1 M NaOHaq)31 and adjusted for variations in the refractive index of methanol/glycerol solutions.Fluorescence decay measurements
Fluorescence decays of 1 were measured using an IBH 5000F time-correlated single photon counting (TCSPC) device (Jobin Yvon, Horiba) equipped with a 467 nm NanoLED as an excitation source (200 ps pulse duration, HORIBA). A DeltaFlex TCSPC device (Horiba) was used for measuring the fluorescence decays of 2 in glycerol–methanol mixtures with a 560 nm NanoLED as an excitation source (1.3 ns pulse duration, Horiba). The time window was 100 ns with 4096 time bins. The decays were accumulated until 2000 counts were reached at the peak. Temperature was controlled by a circulating thermostat (RE104, Lauda Technology Ltd.) to 1 °C and additionally verified by inserting a thermocouple (2006T, Digitron) into the cuvette.Fluorescence decays of 2 in glycerol–water mixtures and 3 in glycerol–methanol mixtures were measured on a home-built TCSPC setup, based on a DCC-100 detector control module (Becker & Hickl) with a PMC-100-1 PMT (Hamamatsu), grating monochromator (Omni-λ 150, LOT-Quantum Design), cuvette holder (qpod, Quantum Northwest) and Peltier temperature controller (TC 125, Quantum Northwest). Samples were excited at 453 nm (dye 3) and at 540 nm (dye 2) using a frequency doubled output of a Coherent Chameleon Vision II mode-locked femtosecond Ti:sapphire laser (140 fs pulse duration, 1 mW power) at different temperatures. Detection wavelength was 640 nm with 10 nm detection window. Time window was 12.5 ns with 1024 time bins. Decays of 2 and 3 had 2000 and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 counts at the peak respectively.
500 counts at the peak respectively.
Fluorescence lifetime microscopy (FLIM)
The FLIM setup consisted of a Coherent Chameleon Vision II mode-locked femtosecond Ti:sapphire laser, tuneable over the 680–1080 nm range producing 140 fs pulses at 80 MHz, coupled to a Leica SP5-II confocal microscope equipped with a Becker & Hickl SPC-830 photon counting card. Excitation light was frequency doubled using a second harmonic generation (SHG) crystal (Harmonic, Coherent) to produce 453 nm pulses. Fluorescence was detected using an internal microscope detector (PMC-100-1 photomultiplier tube, Hamamatsu) over the 635–645 nm range. All images were 128 × 128 pixels and 256 time bins were used in each decay. Scattering from the glass surface was used for measuring an instrument response function (IRF). Biexponential fitting (Fig. S5†) was performed for each decay in the FLIM image. Image pixels were binned over 15 × 15 pixel area (bin = 7 in B&H software) before fitting to achieve an optimal signal/noise ratio. The estimated error of lifetime fitting (using approximately 1000 counts in peak maxima in each bin) was 5%.Ratiometric calibration and ratiometric imaging of 3
Fluorescence spectra of 3 were measured following 453 nm excitation at temperatures between 10 and 90 °C using the spectrofluorometer (Fluoromax-4, Jobin-Yvon Horiba). Ratios were calculated by dividing the fluorescence intensity in the peak maxima of the twisted vs. the planar conformers (639 vs. 706 nm). An additional calibration suitable for interpreting microscopy measurements was performed at 20 °C using a confocal microscope (Leica SP5-II). For these measurements methanol–glycerol solutions of 3 were placed in Lab-Tek (Nunc, Thermo Scientific) chamber slides and excited with 453 nm light using the laser setup described above. Fluorescent light was collected by two internal detectors; the light of the desired wavelength was selected by dispersing all emitted light through the prism and changing the width and the position of the slits in front of the PMTs. Fluorescence intensities collected over (635–645 nm) and (690–700 nm) ranges were used for calculating the ratios.The identical setup was used for measuring ratiometric images, for which the signal from 15 × 15 pixel area was averaged to achieve a better signal/noise ratio. The estimated error of ratiometric detection of viscosity (using at least 5000 counts in each channel in each bin) was 1%.
Glycerol–methanol mixture heating experiment
The heating chamber was assembled by securing two microscope slides (76 × 26 mm, Menzel-Gläser) containing a PDMS spacer in-between with two metal clips. The methanol/glycerol mixture was injected inside the chamber. Heating was achieved by inserting a copper wire wrapped around an Antex Electronics 25 W soldering iron, into the chamber.Data analysis
Decays of 1 and 2 in glycerol–methanol mixtures were fitted using DAS6 v6.5 software (HORIBA Scientific). Decays of 3 were analysed using home-written code in MATLAB R2012a (MathWorks). FLIM images were fitted using FLIMfit software tool developed at Imperial College London (v4.6.1).32 All other data processing and analysis was done on MATLAB R2012a and Origin Pro 8.6. The estimated errors for temperature imaging using 3 are discussed in the ESI, Fig. S7.†Acknowledgements
AV thanks the EPSRC for the Prize Studentship. MKK is thankful to the EPSRC for the Career Acceleration Fellowship (EP/I003983/1). This work was partially supported by the European Commission in the form of a Marie Curie individual Fellowship to M. B. under the contract MEIT-CT-2006–041522.Notes and references
- M. A. Haidekker and E. A. Theodorakis, Org. Biomol. Chem., 2007, 5, 1669–1678 CAS.
- M. K. Kuimova, Phys. Chem. Chem. Phys., 2012, 14, 12671 RSC.
- M. K. Kuimova, G. Yahioglu, J. A. Levitt and K. Suhling, J. Am. Chem. Soc., 2008, 130, 6672–6673 CrossRef CAS PubMed.
- M. K. Kuimova, S. W. Botchway, A. W. Parker, M. Balaz, H. A. Collins, H. L. Anderson, K. Suhling and P. R. Ogilby, Nat. Chem., 2009, 1, 69–73 CrossRef CAS PubMed.
- M. A. Haidekker, M. Nipper, A. Mustafic, D. Lichlyter, M. Dakanali and E. A. Theodorakis, Dyes with Segmental Mobility: Molecular Rotors, Springer, Berlin, Heidelberg, 2010, vol. 8 Search PubMed.
- M. S. A. Abdel-Mottaleb, R. O. Loutfy and R. Lapouyade, J. Photochem. Photobiol., A, 1989, 48, 87–93 CrossRef CAS.
- I. López-Duarte, T. T. Vu, M. A. Izquierdo, J. A. Bull and M. K. Kuimova, Chem. Commun., 2014, 50, 5282–5284 RSC.
- N. Jiang, J. Fan, S. Zhang, T. Wu, J. Wang, P. Gao, J. Qu, F. Zhou and X. Peng, Sens. Actuators, B, 2014, 190, 685–693 CrossRef CAS PubMed.
- N. A. Hosny, C. Fitzgerald, C. Tong, M. Kalberer, M. K. Kuimova and F. D. Pope, Faraday Discuss., 2013, 165, 343–356 RSC.
- G. Hungerford, A. Allison, D. McLoskey, M. K. Kuimova, G. Yahioglu and K. Suhling, J. Phys. Chem. B, 2009, 113, 12067–12074 CrossRef CAS PubMed.
- J. M. Nölle, C. Jüngst, A. Zumbusch and D. Wöll, Polym. Chem., 2014, 5, 2700–2703 RSC.
- Y. Wu, M. Štefl, A. Olzyńska, M. Hof, G. Yahioglu, P. Yip, D. R. Casey, O. Ces, J. Humpolíčková and M. K. Kuimova, Phys. Chem. Chem. Phys., 2013, 15, 14986–14993 RSC.
- A. Vyšniauskas, M. Balaz, H. L. Anderson and M. K. Kuimova, Phys. Chem. Chem. Phys., 2015, 7548–7554 RSC.
- S. Howell, M. Dakanali, E. A. Theodorakis and M. A. Haidekker, J. Fluoresc., 2012, 22, 457–465 CrossRef CAS PubMed.
- D.-A. Mendels, E. M. Graham, S. W. Magennis, A. C. Jones and F. Mendels, Microfluid. Nanofluid., 2008, 5, 603–617 CrossRef CAS.
- M. A. Bennet, P. R. Richardson, J. Arlt, A. McCarthy, G. S. Buller and A. C. Jones, Lab Chip, 2011, 11, 3821–3828 RSC.
- T.-Y. Dora Tang, C. Rohaida Che Hak, A. J. Thompson, M. K. Kuimova, D. S. Williams, A. W. Perriman and S. Mann, Nat. Chem., 2014, 6, 527–533 CrossRef CAS PubMed.
- M. R. Dent, I. López Duarte, C. J. Dickson, N. D. Geoghegan, J. M. Cooper, I. R. Gould, R. Krams, J. A. Bull, N. J. Brooks and M. K. Kuimova, Phys. Chem. Chem. Phys., 2015, 17, 18393–18402 RSC.
- D. Ross, M. Gaitan and L. E. Locascio, Anal. Chem., 2001, 73, 4117–4123 CrossRef CAS.
- G. Kwak, S. Fukao, M. Fujiki, T. Sakaguchi and T. Masuda, Chem. Mater., 2006, 18, 2081–2085 CrossRef CAS.
- C. Cao, X. Liu, Q. Qiao, M. Zhao, W. Yin, D. Mao, H. Zhang and Z. Xu, Chem. Commun., 2014, 50, 15811–15814 RSC.
- J. Feng, K. Tian, D. Hu, S. Wang, S. Li, Y. Zeng, Y. Li and G. Yang, Angew. Chem., Int. Ed., 2011, 50, 8072–8076 CrossRef CAS PubMed.
- M. U. Winters, J. Karnbratt, M. Eng, C. J. Wilson, H. L. Anderson and B. Albinsson, J. Phys. Chem. C, 2007, 111, 7192–7199 CAS.
- Z. Yang, J. Cao, Y. He, J. H. Yang, T. Kim, X. Peng and J. S. Kim, Chem. Soc. Rev., 2014, 43, 4563–4601 RSC.
- R. K. P. Benninger, Y. Koç, O. Hofmann, J. Requejo-Isidro, M. A. A. Neil, P. M. W. French and A. J. DeMello, Anal. Chem., 2006, 78, 2272–2278 CrossRef CAS PubMed.
- E. M. Graham, K. Iwai, S. Uchiyama, A. P. de Silva, S. W. Magennis and A. C. Jones, Lab Chip, 2010, 10, 1267–1273 RSC.
- K. Okabe, N. Inada, C. Gota, Y. Harada, T. Funatsu and S. Uchiyama, Nat. Commun., 2012, 3, 705 CrossRef PubMed.
- G. Baffou, H. Rigneault, D. Marguet and L. Jullien, Nat. Methods, 2014, 11, 899–901 CrossRef CAS PubMed.
- J. A. Levitt, M. K. Kuimova, G. Yahioglu, P. H. Chung, K. Suhling and D. Phillips, J. Phys. Chem. C, 2009, 113, 11634–11642 CAS.
- M. Balaz, H. A. Collins, E. Dahlstedt and H. L. Anderson, Org. Biomol. Chem., 2009, 7, 874–888 CAS.
- J. H. Brannon and D. Magde, J. Phys. Chem., 1978, 82, 705–709 CrossRef CAS.
- S. C. Warren, A. Margineanu, D. Alibhai, D. J. Kelly, C. Talbot, Y. Alexandrov, I. Munro, M. Katan, C. Dunsby and P. M. W. French, PLoS One, 2013, 8, e70687 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional spectroscopic and imaging data. See DOI: 10.1039/c5sc02248g |
| ‡ Present Address: Department of Chemistry, University of Wyoming, Laramie, WY, USA. |
| This journal is © The Royal Society of Chemistry 2015 |