Open Access Article
Open Access ArticleXe affinities of water-soluble cryptophanes and the role of confined water†
Lu
Gao‡
a,
Wenhao
Liu‡
a,
One-Sun
Lee
b,
Ivan J.
Dmochowski
a and
Jeffery G.
Saven
*a
aDepartment of Chemistry, University of Pennsylvania, 231 S. 34th Street, Philadelphia, PA 19104, USA. E-mail: saven@upenn.edu
bQatar Environment and Energy Research Institute, Hamad Bin Khalifa University, Qatar Foundation, Doha, Qatar
First published on 22nd September 2015
Abstract
Given their relevance to drug design and chemical sensing, host–guest interactions are of broad interest in molecular science. Natural and synthetic host molecules provide vehicles for understanding selective molecular recognition in aqueous solution. Here, cryptophane–Xe host–guest systems are considered in aqueous media as a model molecular system that also has important applications. 129Xe–cryptophane systems can be used in the creation of biosensors and powerful contrast agents for magnetic resonance imaging applications. Detailed molecular information on the determinants of Xe affinity is difficult to obtain experimentally. Thus, molecular simulation and free energy perturbation methods were applied to estimate the affinities of Xe for six water-soluble cryptophanes. The calculated affinities correlated well with the previously measured experimental values. The simulations provided molecular insight on the differences in affinities and the roles of conformational fluctuations, solvent, and counter ions on Xe binding to these host molecules. Displacement of confined water from the host interior cavity is a key component of the binding equilibrium, and the average number of water molecules within the host cavity is correlated with the free energy of Xe binding to the different cryptophanes. The findings highlight roles for molecular simulation and design in modulating the relative strengths of host–guest and host–solvent interactions.
Introduction
Host–guest interactions are of broad interest in chemistry and offer many potential applications, including the development of drugs, sensors and agents for molecular delivery. Synthetic host–guest systems also provide vehicles for probing the roles of host structure and solvent on the affinities for particular guest species. A variety of noncovalent features can play important roles in the binding of guest molecules, including complementarity of shapes and volumes, van der Waals interactions, hydrogen bonding, hydrophobic contacts, electrostatic interactions, and solvation of both the guest and host. Synthetic host molecules provide a means to dissect some of these interactions, but a detailed molecular picture is often difficult to achieve experimentally. Herein, molecular simulations are used to explore the binding of a rare gas guest, Xe, to cryptophane host molecules in aqueous environments. The findings provide a molecular perspective on the relative affinities of these versatile cryptophane host molecules and highlight the roles of solvent in the formation of the Xe-bound complex.Cryptophanes are cage-like molecules with two cyclotriguaiacylene caps linked by three variable-length alkyl chains to form nearly spherical cavities of tunable internal volume (Fig. 1). The binding of small molecules to cryptophanes has been explored extensively in organic solvents. These host molecules bind a variety of neutral and charged guest molecules, including methane,1 halogenated alkane derivatives,2–4 alkyl-ammonium ions,5 and rare gases.6 Water-soluble cryptophane variants have been created,7–9 which exhibit useful affinities for Xe and can be used in biosensors. The binding of Xe in aqueous media is particularly relevant for applications in magnetic resonance based detection and imaging (MRI), where the cryptophane can bind to this essentially inert element. Functionalization of the cage exterior improves cryptophane solubility while also enabling biosensing and Xe targeting to biomolecules of interest.10
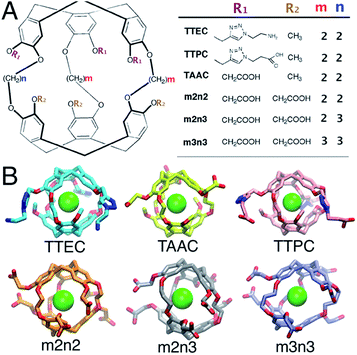 | ||
| Fig. 1 (A) The structures of six water-soluble cryptophanes. (B) Renderings of cryptophane molecules with Xe bound. | ||
The 129Xe nuclear spin can be hyperpolarized, the basis of its applications in biosensing11 and MRI.12–15 The resonance of the 129Xe spin-1/2 nucleus is sensitive to the local chemical environment and presents a nearly 300 ppm range of chemical shifts when bound to cryptophane in water.16 Changes in the chemical shift of Xe have been used to monitor binding to cryptophanes and to determine molecular affinities.10 Delivering xenon to a specific biological target, however, can be difficult due to the fact that the atom is nonreactive and has weak, non-specific affinity for proteins and other analytes.17 Thus, cryptophanes provide a means to bind, localize, and “chemically functionalize” Xe in a variety of solvent environments.11,18,19 Appropriately derivatized cryptophanes can be used to target Xe in aqueous environments.20–22
In aqueous media, the Xe affinities for cryptophane derivatives at neutral pH have been measured. These cage variants can be distinguished by the lengths of the bridging linkers between the two cyclotriveratrylene capping moieties and the side chain groups that confer solubility (Fig. 1); m and n denote the number of carbon atoms in the three alkyl linkers. While cryptophanes m2n2 and m3n3 maintain three-fold symmetry with uniform ethyl and propyl linkers, m2n3 has one longer (propyl) linker that breaks the symmetry. Three hexa-acid cryptophane derivatives have been reported with Xe association constants in the range of Ka = 1000–6800 M−1 at rt.7 Among the hexa-acid cages, the m2n2 variant (a derivative of cryptophane-A)23 has the greatest affinity, Ka = 0.68 × 104 M−1 (Fig. 1). More recently, cryptophanes with only three ionizable side chains have been studied. At pH = 7.5, tris-(triazole ethylamine)cryptophane (TTEC) is singly protonated with an experimentally determined Xe association constant, Ka = 4.2 × 104 M−1. At pH = 2.5, TTEC is triply protonated with Ka = 3.4 × 104 M−1 (293 K).6 These are the highest reported cryptophane–Xe affinities in aqueous media. Other soluble derivatives include a triacetic acid cryptophane-A derivative (TAAC, Ka = 3.3 × 104 M−1)21 and tris-(triazole propionic acid) cryptophane-A derivative (TTPC, Ka = 1.7 × 104 M−1).24 In addition, a Ru-coordinated cryptophane-111 derivative has a Xe affinity comparable to that of TAAC, Ka = 2.9 × 104 M−1.25 A variety of distinct experimental methods have been used to determine these Xe affinities. Shifts in NMR spectral peaks have been used to estimate the affinities of the hexa-acid cryptophanes (m2n2, m2n3, m3n3) and the cryptophane-111 derivative.20,25 Fluorescence quenching and isothermal titration calorimetry have been used to determine the affinities of TTEC, TAAC, and TTPC.6,21,24 Interestingly, the central cavities of m2n2, TTEC, TTPC, and TAAC are identical in chemical structure, but these molecules have appreciably different Xe affinities. A molecularly detailed, quantitative framework for understanding the relative affinities of this series of cryptophanes is desirable.
Herein, molecular simulations are used to estimate the association free energies involving Xe and six water-soluble cryptophanes (Fig. 1). The molecular properties of these systems in an aqueous environment are also explored. Molecular simulations have been widely used to estimate affinities of host–guest molecular systems,26,27 and such simulations have provided insight to the structural fluctuations and binding properties of cryptophanes.28–30 Herein, a free energy perturbation methodology was applied to calculate the binding free energy of Xe to six different water-soluble cryptophane derivatives. The experimentally determined binding constants correspond to a range of binding free energies spanning only about 2 kcal mol−1. Such subtle differences can be difficult to discern with free energy calculations. Nonetheless, the calculated results correlate well with measured experimental values. The simulations also provide molecular insight into the relative binding affinities of different cryptophanes. The distributions of water molecules and counter ions (Na+, Cl−) within and near the cryptophane molecules are characterized. The average number of solvent molecules within the interior cavity is correlated with the free energy of Xe binding.
Methods
Alchemical free energy perturbation
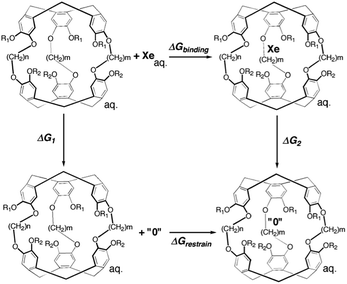
An alchemical double decoupling method31,32 based upon free energy perturbation theory was used to estimate the binding free energy between Xe and cryptophane, ΔGbinding, in the presence of explicit solvent (water) and counter ions. The binding free energy was estimated by performing two simulations, one with the Xe atom in only water solvent (no cryptophane) and the other with the Xe atom within the interior of the solvated cryptophane. For each simulation, the potential energy interactions that couple the Xe atom to the remainder of the system gradually vanish; Xe is “decoupled” during the course of the calculation. The thermodynamic cycle for estimating ΔGbinding from the simulations is illustrated in Fig. 2. From the thermodynamic cycle, we have:| ΔGbinding = ΔG1 − ΔG2 + ΔGrestrain | (1) |
An alchemical free energy perturbation method33–37 implemented in NAMD2 (ref. 38) is used to calculate ΔG1 and ΔG2. The hybrid potential energy that comprises interactions between the Xe atom with the other atoms in its environment is determined by a decoupling parameter λ and is expressed as,
| UXe–X(λ) = (1 − λ)UXe–X | (2) |
ΔA(λi → λi+1) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−(U(λi+1)−U(λi))/kBT〉i ln〈e−(U(λi+1)−U(λi))/kBT〉i | (3) |
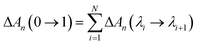 | (4) |
| ΔGn(0 → 1) = ΔAn(0 → 1) + P(Vλ=1 − Vλ=0) | (5) |
The free energy change associated with restraining the noninteracting Xe within the host molecule31 is calculated using
ΔGrestrain = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c0Vrestrain) ln(c0Vrestrain) | (6) |
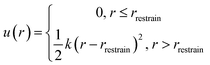 | (7) |
MD simulations
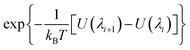 was 1 ns or less for each window. A block average statistical analysis50 was used to determine the length of the sampling time of each window. A block's length was chosen to be the above correlation time (1 ns). The number of blocks was increased until the standard deviation of block averages was no longer dependent on the number of blocks and the calculated free energy change obtained using n blocks was within 0.01 kcal mol−1 of that obtained using the previous n − 1 blocks. As λ increases, water molecules may enter the cryptophane interior. The residence time of water molecules at the end point λ = 1 was on average 0.1 ns and is shown in ESI Table S2.† Thus, the sampling time was selected to be much larger than this residence time of water molecules. As λ increased, longer sampling times were used to obtain converged results. The total sampling time ranged from about 3 ns for the first [0, 0.1] λ window to about 10 ns for the last [0.9, 1] λ window. To avoid the “end-point catastrophes” near λ = 1 where overlapping particles lead to singularities in the Lennard-Jones potential, a modified soft-core potential51,52 was used with a radius-shifting coefficient set at 5. For the ΔG2 pathway, to confine the Xe atom inside the host molecule, an isotropic harmonic potential u(r) (eqn (7)) was exerted using the COLVAR module,53 and the radial coordinate r of the Xe atom was measured with respect to the center of mass of the aromatic carbon atoms of the host cryptophane molecule.
was 1 ns or less for each window. A block average statistical analysis50 was used to determine the length of the sampling time of each window. A block's length was chosen to be the above correlation time (1 ns). The number of blocks was increased until the standard deviation of block averages was no longer dependent on the number of blocks and the calculated free energy change obtained using n blocks was within 0.01 kcal mol−1 of that obtained using the previous n − 1 blocks. As λ increases, water molecules may enter the cryptophane interior. The residence time of water molecules at the end point λ = 1 was on average 0.1 ns and is shown in ESI Table S2.† Thus, the sampling time was selected to be much larger than this residence time of water molecules. As λ increased, longer sampling times were used to obtain converged results. The total sampling time ranged from about 3 ns for the first [0, 0.1] λ window to about 10 ns for the last [0.9, 1] λ window. To avoid the “end-point catastrophes” near λ = 1 where overlapping particles lead to singularities in the Lennard-Jones potential, a modified soft-core potential51,52 was used with a radius-shifting coefficient set at 5. For the ΔG2 pathway, to confine the Xe atom inside the host molecule, an isotropic harmonic potential u(r) (eqn (7)) was exerted using the COLVAR module,53 and the radial coordinate r of the Xe atom was measured with respect to the center of mass of the aromatic carbon atoms of the host cryptophane molecule.
The statistical uncertainties in the free energies of association (Table 1) were determined using the standard deviation of the block averages for each increment in λ; the trajectory of each such increment was divided into blocks of 1 ns of sampled configurations, and the variance of the free energy σ2 was estimated using the values of the free energies estimated for each λ window: σ2[ΔG0→1] = σ2[ΔG0→0.1] + σ2[ΔG0.1→0.2] + … + σ2[ΔG0.9→1].
| Experimental | Calculated | ||
|---|---|---|---|
| K a (M × 104) | ΔG*bindingb (kcal mol−1) | ΔGbindingc (kcal mol−1) | |
a Previously reported values.6,20,21,24
b ΔG*binding = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KaM).
c ΔGbinding = ΔG1 + ΔGrestrain − ΔG2.
d Experimentally, TTEC is found to be roughly singly protonated at pH 7.5 and triply protonated at pH 2.5. The experimental Xe binding equilibrium constant of triply protonated TTEC is presented. Ka = 42 ln(KaM).
c ΔGbinding = ΔG1 + ΔGrestrain − ΔG2.
d Experimentally, TTEC is found to be roughly singly protonated at pH 7.5 and triply protonated at pH 2.5. The experimental Xe binding equilibrium constant of triply protonated TTEC is presented. Ka = 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000 M−1 for mono-protonated TTEC.6
e Experimentally measured binding affinity for mono-protonated TTEC is −6.20 ± 0.03 kcal mol−1.
f Xe binding affinity of mono-protonated TTEC is calculated to be −6.07 kcal ± 0.13 kcal mol−1. 000 ± 2000 M−1 for mono-protonated TTEC.6
e Experimentally measured binding affinity for mono-protonated TTEC is −6.20 ± 0.03 kcal mol−1.
f Xe binding affinity of mono-protonated TTEC is calculated to be −6.07 kcal ± 0.13 kcal mol−1.
|
|||
| TTEC | 3.40 ± 0.10d | −6.07 ± 0.02e | −5.97 ± 0.09f |
| TAAC | 3.33 ± 0.28 | −6.06 ± 0.05 | −5.89 ± 0.10 |
| TTPC | 1.70 ± 0.17 | −5.67 ± 0.06 | −5.78 ± 0.15 |
| m2n2 | 0.68 ± 0.23 | −5.13 ± 0.24 | −4.89 ± 0.06 |
| m2n3 | 0.22 ± 0.04 | −4.48 ± 0.12 | −4.55 ± 0.10 |
| m3n3 | 0.10 ± 0.04 | −4.02 ± 0.30 | −4.10 ± 0.18 |
Results
Binding free energy calculation results
Molecular dynamics simulations were used to estimate the free energies of binding (Fig. 2 and eqn (1)) for the six cryptophanes presented in Table 1. To estimate ΔG1, a single decoupling calculation was performed for a Xe atom solvated in water. To obtain the Gibbs free energy change for the NPT ensemble, the work contributed by the volume change between the initial and end states should be estimated. At constant pressure, the volume change of the periodic box for each decoupling pathway is less than 100 Å3, resulting in a negligible contribution due to pressure–volume work (PΔV < 1.5 × 10−3 kcal mol−1). As a result, we take that ΔA1 = ΔG1 and ΔA2 = ΔG2. The calculated free energy of solvation of Xe is ΔG1 = −0.40 ± 0.06 kcal mol−1. This value is within 1 kcal mol−1 of the experimentally inferred value for transfer of Xe from a dilute gas to water,54,55 ΔG1 = −1.34 kcal mol−1, and the discrepancy may arise from the simple models used here for solvent and for the Xe atom. As ΔG1 is the same for each cryptophane system considered and the major emphasis of this study is the relative Xe affinities of the different cryptophanes, the experimentally inferred value of ΔG1 was used in estimating ΔGbinding. ΔGrestrain is associated with the confinement of the ideal (noninteracting or decoupled) Xe atom to the interior of the cryptophane, and for all the systems considered here ΔGrestrain = 1.72 kcal mol−1 (eqn (6)). To estimate ΔG2, free energy perturbation (decoupling) calculations were performed for Xe associated with each of the six systems listed in Fig. 1: TTEC, TAAC, TTPC, m2n2, m2n3 and m3n3. Values of ΔGbinding were found to be invariant upon slight variation of rrestrain, e.g., for TAAC, ΔGbinding(rrestrain = 2.8 Å) = 6.27 kcal mol−1 and ΔGbinding(rrestrain = 2.0 Å) = 6.26 kcal mol−1. The resulting calculated binding free energies ΔGbinding were in excellent agreement with the experimentally inferred affinities, having a correlation coefficient r = 0.98 (Table 1, Fig. 3). Thus the simulations and free energy perturbation approach applied here is useful for quantitatively reproducing the relative ordering of the free energies of Xe binding to the cryptophane systems considered.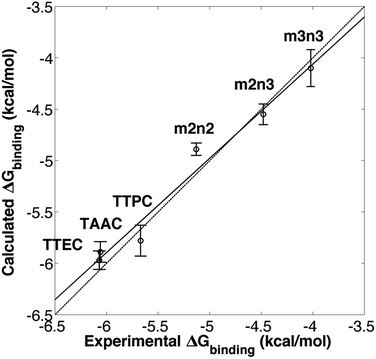 | ||
| Fig. 3 Experimental6,20,21,24 and calculated free energies of Xe binding. The solid line is a linear least squares fit. The dotted line corresponds to equality of the experimental and calculated values of ΔG. | ||
Host structural variation upon Xe binding
As shown in Table 2, the distance between the centers of mass of the two cyclotriguaiacylenes increased with the length of the linkers. Due to the flexibility of dihedral angles of the propyl linkers in m2n3 and m3n3, these interior distances as well as the sizes of the cages fluctuated more than in cryptophanes with only ethyl linkers. Thus, for cryptophanes with propyl linkers, the distances were such that the cage was substantially larger and less suited for Xe binding. While m3n3 and m2n3 had the largest interior cavities by these distance measures, the remaining cryptophanes had similar, well-defined interior cavity dimensions. Thus, differences in xenon affinities could not be resolved in terms of the cavity size and structural fluctuations alone.| d (Å) | ||
|---|---|---|
| Xe bound | Xe absent | |
| a d is the distance between the centers of mass of the aromatic carbon atoms of the two cyclotriguaiacylene units of the cryptophane. | ||
| TTEC | 6.47 ± 0.13 | 6.53 ± 0.13 |
| TAAC | 6.48 ± 0.12 | 6.55 ± 0.13 |
| TTPC | 6.46 ± 0.13 | 6.53 ± 0.13 |
| m2n2 | 6.49 ± 0.13 | 6.55 ± 0.13 |
| m2n3 | 6.60 ± 0.17 | 6.70 ± 0.17 |
| m3n3 | 6.93 ± 0.25 | 7.16 ± 0.31 |
Host–solvent interactions
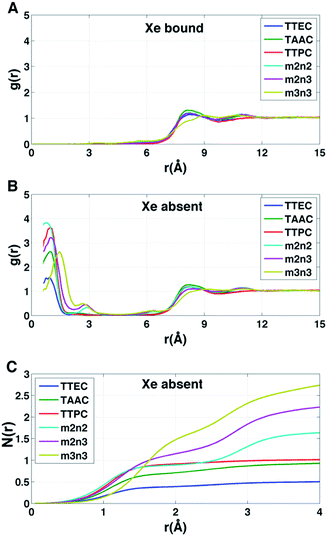
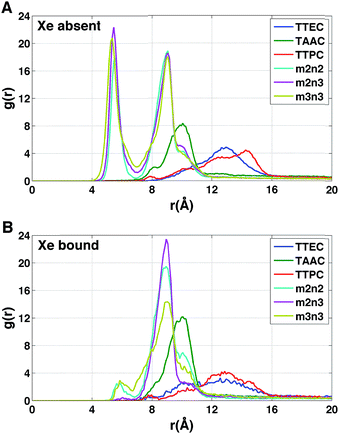
Each cryptophane was observed to accommodate water molecules within the interior cavity. When multiple waters were present within the cavity, these were often observed to hydrogen bond to each other (Fig. 4). The radial distribution functions of water molecules as functions of the distance r from an oxygen atom to the center of mass of the aromatic carbons of the cryptophane are shown in Fig. 5. The radial distribution function indicated low probability of water molecules over the range r = 3.0–6.5 Å. This was expected since the average distance of carbon atoms in the cyclotriguaiacylene units from the center of mass were in the range r = 4.5–5.5 Å; the steric interactions with the cryptophane prevents water from being observed at these values of r. Thus, oxygen atoms having r < 4 Å corresponded to interior water molecules within the cavity. Each of the cryptophanes was free of interior water with Xe present in the cage. Fig. 5A indicates no water within 6 Å to the center of the cage. However, when Xe is absent, water molecules occupy the cavity as shown in Fig. 5B. The peaks near r = 1 Å arise due to the water molecules near the center of the cryptophane cavity. Representative interior water configurations are shown in Fig. 4. The position of the interior peak is slightly displaced for m3n3 to r = 1.5 Å, which is not unexpected due to the larger interior cavity. A second peak near r = 3 Å was also observed for the hexa-acid cryptophanes m2n2, m2n3, and m3n3. This peak corresponds to the water molecules at the 3 pores (Fig. 4), where the hydrophilic side-chains and counter ions localize these water molecules. This second peak was not observed for tri-functionalized cryptophanes TTEC, TAAC and TTPC, presumably due in part to the substitution of three carboxylate groups with hydrophobic methyl side chains. The hexa-acid cryptophanes possess greater water occupancies within the cavity than the tri-functionalized cryptophanes (Fig. 5C). In contrast, the higher Xe affinity cryptophanes are empty (lacking water) for a large fraction of the sampled configurations (ESI Fig. S2†). The average numbers of water molecules inside each cage are 0.50 for TTEC, 0.92 for TAAC, 1.01 for TTPC, 1.63 for m2n2, 2.23 for m2n3, and 2.73 for m3n3, respectively. This trend is also the order of decreasing Xe binding affinity for these cryptophanes.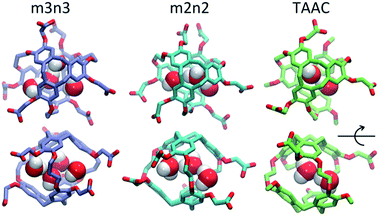 | ||
| Fig. 4 Configurations with water molecules inside cryptophanes m3n3, m2n2 and TAAC. In the lower row, each configuration is rotated 90°. | ||
The affinity of Xe for the cryptophanes is believed to result in part from release of the waters that form an ordered water structure that surrounds the Xe atom in aqueous solution.6 Xe in water was simulated to explore the water structure about the rare gas atom. The radial distribution function of water molecules about Xe in water is shown in Fig. 6A. Integration of this distribution function yields 15–20 water molecules within the first solvation shell (r < 5–6 Å from the Xe atom). Fig. 6B depicts 20 water molecules surrounding Xe as its first solvation shell within 6 Å. These estimates for the numbers of water molecules released upon sequestration of the Xe by a cryptophane are consistent with those inferred from isothermal titration data, which suggested that 20 water molecules were released upon binding.56
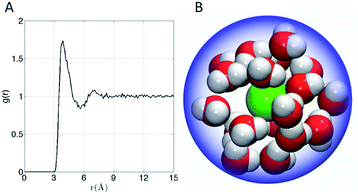 | ||
| Fig. 6 (A) Water radial distribution function g(r) about Xe in water, where r is Xe–O distance. (B) Sampled configuration depicting first solvation shell (waters within 6 Å) of Xe in water. | ||
Water map analysis
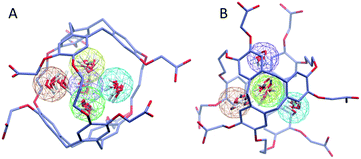
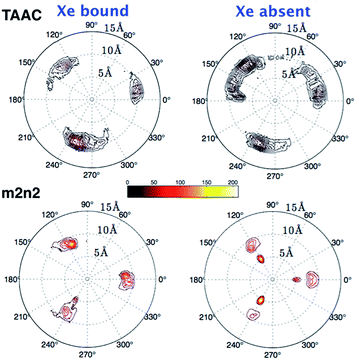
To investigate further the ordering and orientation of water molecules within the cryptophanes, a water map analysis was applied.57 In the absence of Xe, coordinates of all the water molecules within 4 Å of the center of the cage were collected from sampled configurations. All such coordinates were pooled, aligned and superimposed. The water molecule with the highest number of neighbors within 1 Å (O–O distance) was selected and taken as the center of a generated cluster. Such a cluster comprises water molecules from distinct sampled configurations in the molecular dynamics trajectory. The resulting water cluster was then excluded before a second cycle of cluster identification was performed. At most five water molecules were observed at the m3n3 interior (ESI, Fig. S2†), and the five most populated clusters of water molecules inside the cryptophane are shown in Fig. 7. Within each position-based cluster, clusters of orientations of the water molecules were obtained by using a similar algorithm, where the criterion for association with a particular cluster was |q1q2| > 0.9, where q is the quaternion that rotates a water molecule to a fiducial reference water orientation. In addition to the two water clusters near the center of the cryptophane, three other water clusters near the pores surrounded by side-chains were identified. These three water clusters were stabilized by hydrogen bonding to hydrophilic side-chains of hexa-acid cryptophanes and coordination of Na+ ions (Fig. 8). These cluster orientations showed that their oxygen atoms are directed outwardly from the interior of the cage to coordinate Na+ counter ions (Fig. 8).The other hexa-acid cryptophanes, m2n3 and m2n2, have smaller interiors but also exhibited water clusters near the pore regions. For the tri-functionalized cryptophanes, TAAC, TTPC and TTEC, water molecule clusters appeared at the cavity center, other water clusters at the three pore regions also existed but with lower populations (Fig. S4, ESI†); the hydrophobicity of the methyl side chains and the diminished presence of counter ions (Fig. 9b) likely reduced the likelihood of persistently structured water near the pores of these cryptophanes.
 | ||
| Fig. 9 The radial distribution g(r) of counter ions relative to the center of mass of the cryptophane molecule. (A) Xe atom is absent (λ = 1). (B) Xe atom is present within the cryptophane (λ = 0). | ||
Distribution of counter ions
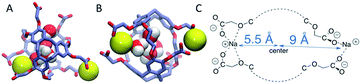
The radial distributions of counter ions are shown in Fig. 9. When no Xe atom was present in the hexa-acid cryptophanes (m2n2, m2n3 and m3n3), peaks in the counter ion (Na+) distribution appeared near r = 5.5 Å and r = 9 Å. For m2n2, m2n3 and m3n3, the peak near r = 9 Å corresponded to coordination of the Na+ counter ions with only the carboxylate oxygen atoms at the end of the side chains. The peak at r = 5.5 Å corresponded to configurations where Na+ was coordinated by both carboxylate and ether oxygen atoms of the side chains. The peak near r = 5.5 Å was not observed for the tri-functionalized cryptophanes TTEC, TAAC and TTPC.For the hexa-acid cryptophanes, the presence of the Xe atom within the host molecule precluded localization of the ions at r = 5.5 Å due to van der Waals overlap, as is evidenced by the corresponding reduction of the peak near r = 5.5 Å in the pair distribution (Fig. 9). On the other hand, for the tri-acid cryptophanes (TAAC, TTPC), the distribution of Na+ counter ions was less sensitive to the presence of Xe. This is presumably due to the reduced negative charge and three fewer coordinating carboxylate atoms in the tri-acid cryptophanes, which reduced the “tight binding” of Na+ counter ions.
The polar distributions of counter ions relative to the axis of three-fold symmetry of the TAAC and m2n2 cryptophanes are presented in Fig. 10. The counter ions have much less configurational freedom and have narrower distributions for the hexa-acid cryptophanes, such as m2n2. These hosts have six carboxylate side chains, which results in well-defined counter ion distributions about the cage. The peak located at r = 5.5 Å was lost upon binding of Xe. In TAAC, the counter ions were more broadly distributed and had much more configurational freedom about the cryptophane, as evidenced by the more diffuse distributions for the tri-acid TAAC compared to the hexa-acid m2n2 cryptophane (Fig. 10).
Distribution of solvent and counter ions
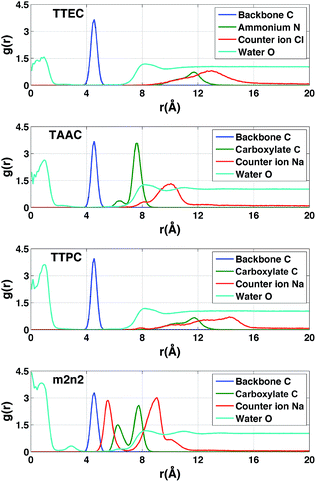
In the absence of Xe, the distributions of water molecules and counter ions were correlated (Fig. 11). The tri-functionalized cryptophanes for the most part had the charged side chain functional groups distal from the center of the cavity. For the hexa-acid cryptophane m2n2, the carboxylate side chains had an additional peak near 6.3 Å, which was associated with the presence of counter ions at 5.5 Å. This 5.5 Å peak in the counter ion distribution was accompanied by a peak at 3 Å for oxygen atoms of water molecules (Fig. 11). These water molecules were near the pores of cryptophane and in the first solvation shell for the sodium ion, having a Na+–O distance of 2.5 Å.58 For the tri-functionalized cryptophanes TTEC, TAAC and TTPC, the water peaks at r = 3 Å vanished, and counter ions did not appear closer than r = 7 Å to the center of the cage. Compared to m2n2, TAAC does not anchor Na+. For TAAC (Fig. 11), counter ions are much less probable at 5.5 Å compared with m2n2. Because the charged groups of TTEC (positive ammonium groups) and TTPC (negative carboxylate groups) are at the end of their long side-chains, the counter ions (Cl− for TTEC and Na+ for TTPC) are distributed further from the center of the cage (r = 8–16 Å).Solvation of side chains of cryptophanes
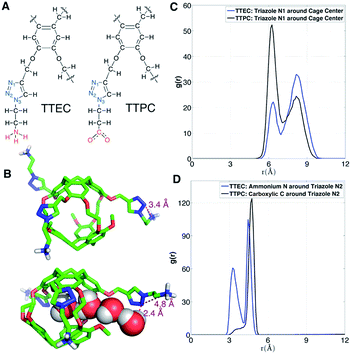
As shown in Fig. 12A, the long side chains of cryptophanes TTEC and TTPC both contain the triazole ring, but with oppositely charged terminal groups, ammonium and carboxylate respectively. Although the difference in their affinities is typically beyond the resolution of such free energy calculations, guided by the simulations we speculate on the origin of the different observed affinities. Due to the difference in side chains, the average number of interior water molecules when Xe is absent differs for the two cryptophanes: the water occupancy is nearly 1 water molecule for TTPC while an occupancy of only 0.5 water is observed for TTEC (Fig. 5C). The triazole ring helps to introduce and stabilize the water molecules near the cage pores. As shown in Fig. 12B, a chain of four hydrogen-bonded water molecules is rendered which extends from the interior of the cage through the pore to the triazole side chain. The N(2) atom on the triazole ring is directed inwardly and hydrogen bonds with the fourth water molecule with a H–N2 distance of 2.4 Å. However, this orientation of triazole side chain along with a water molecule chain was less often observed for TTEC than TTPC. The positively charged ammonium group of TTEC can coordinate with the triazole N(2) atom, yielding a N–N distance of 3.4 Å, consistent with hydrogen bonding (Fig. 12B). In this particular configuration, the nitrogen atoms of the triazole ring were oriented away from the entry channel. This configuration was not observed for TTPC. We plotted the radial distribution of ammonium N and carboxylic C about the triazole N(2) for TTEC and TTPC, respectively (Fig. 12D), and the additional peak at about 3.5 Å was observed for TTEC but not for TTPC. This additional peak of TTEC corresponds to the coordination state between its ammonium N and the triazole N(2). Furthermore, as shown in Fig. 12C, the N(2) atom (and also other triazole N atoms) are closer to the cage center for TTPC. These observations from the simulations and the distribution functions are consistent with the following picture: (1) the triazole ring aids in stabilizing the water molecule chain that traverses the pores of the cryptophane cage; (2) the particular coordination state between the ammonium N and the triazole N(2) atom in TTEC leads to configurations with outwardly directed N atoms, which are not available for stabilizing chains of water molecules that enter the cryptophane pores; (3) the triazole side chain is more extended in TTPC, and its triazole N atoms are available to hydrogen bond to water molecules that form chains or that are poised to enter the cage.Discussion
The simulation studies are insightful for understanding the xenon-binding properties of water-soluble cryptophanes. In addition to estimating free energies, the simulations provide a molecular perspective on cryptophane conformational fluctuations and local environment. The distribution of water and counter ions are addressed directly to aid understanding of their influence on Xe binding. The calculated affinities correlate well with the experimentally determined values (Fig. 3), despite the fact that the Ka values of various soluble cryptophanes for Xe only differ by factors of 2–3 (Table 1).Upon binding Xe to cryptophane, about 20 water molecules surrounding Xe (Fig. 7B) within its first solvation shell are restored to bulk-solvent local environments. In addition, water molecules in the cryptophane cavity (Fig. 4) are also displaced. The distributions for the numbers of interior water molecules varied for different cryptophanes (ESI, Fig. S2†). The average numbers of water molecules inside the cage calculated from ∼20 ns equilibrium trajectories were 0.50 for TTEC, 0.92 for TAAC, 1.01 for TTPC, 1.63 for m2n2, 2.23 for m2n3, and 2.73 for m3n3, respectively. This trend was also the order of decreasing Xe affinity for these cryptophanes (Fig. 13). Larger cryptophanes have more waters to displace upon Xe binding. The tri-functionalized cryptophanes are of the same size as m2n2, but they contain fewer water molecules on average due to their hydrophobic methyl side-chains and lack of ability to anchor the counter ions in well-defined regions close to the cavities. Previous molecular dynamics simulation studies suggested that the number of water molecules in the cavity of m3n3 (a derivative of cryptophane-E) ranges from 0 to 5, with an average number of 2.1,29 which is consistent with the simulation results presented here. Experimental studies of such interior water could be insightful. Bound water molecules have not yet been observed using solution 1H NMR spectroscopy at room temperature. Recently, the first X-ray structure of a cryptophane–water complex was obtained, and the cage contained essentially one interior water molecule but with partial electron density occupying seven distinct cryptophane locations.59
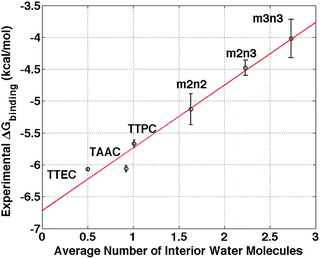 | ||
| Fig. 13 Correlation between the average number of interior water molecules and experimental free energies of Xe binding.6,20,21,24 The red solid line is a linear least squares fit. The radius cutoff for identifying interior waters was set at 4 Å relative to the center of mass of the 6 aromatic rings of cryptophane molecules. | ||
Water is commonly ignored or not treated explicitly when designing aqueous host–guest systems. Water molecules in many binding sites must necessarily be displaced to accommodate the binding of a guest species.27 The work required for such displacement is a component of the free energy of binding, and this component is expected to increase (lower binding affinity) with increasing numbers of water molecules to be displaced. For hydrophobic host cavities, this process is often accompanied by an entropy gain due to the release of the ordered water molecules sequestered inside a confined host environment into the bulk solvent. Accompanying this binding process is the formation of host–guest and water–water energetic (enthalpic) interactions. Similarly, for Xe to bind to a cryptophane, any water molecules in the cage must be displaced. For cryptophanes with ionic side-chains, anchored counter ions and some of their coordinating water molecules that are interior to the cryptophane must also be displaced upon binding. The results of this study highlight the importance of counter ions, and other studies have found that Xe–cryptophane binding is sensitive to the type of counter ion.60 In addition to water within the cryptophane interior, water that partially occludes the Xe binding site is also expected to decrease Xe affinity; such water can be part of the first solvation sphere of an anchored counter ion or hydrogen bonded to polar or ionizable moieties associated with the cryptophane. Modifications to the cryptophane that position polar functional groups and counter ion coordination sites further from the interior may reduce the number of ordered interior water molecules, increasing Xe affinity.
The simulation results indicate that the lowest occupancy of water molecules is associated with TTEC and that higher occupancies are observed for the hexa-acid cryptophanes. Among the molecules considered here, there is a linear correlation between free energy of Xe association and the average number of interior water molecules (Fig. 13). Although the calculations presented here use a simple model for water and do not include explicit polarizability of host and guest, the notion of increasing affinity with decreasing interior solvent occupation is in harmony with recent studies of cryptophane-E and its binding of tetrachloroethane in a variety of halogenated organic solvents.4
The findings herein suggest that molecular simulations and free energy calculations could be potentially useful in the design of cryptophane systems. For a set of cryptophane molecules under consideration, free energy calculations could be performed to identify those having targeted affinities for Xe (and other guest molecules) prior to synthesis. The data in Fig. 13 suggests that the average number of water molecules within the interior may be a strong indicator of Xe affinity, and the estimation of such water occupation of the cryptophane interior is a much less costly calculation than the explicit calculation of free energies of binding.
Conclusions
This study informs our understanding of the hierarchy of cryptophane binding affinities. The hexa-acid cryptophanes, m2n2, m2n3, m3n3 have the same side chains but different sizes due to different lengths of linkers, and affinity decreases with increasing cage size. However, the cryptophanes TTEC, TAAC, TTPC and m2n2 have identical cage cores, therefore their different affinities with Xe are a result of the differences in their side chains and the host–solvent, host–counter ion and solvent–counter ion interactions. Even though the cryptophane interior is hydrophobic, it accommodates water molecules and small water clusters. The binding with Xe thus requires interior water molecules to be displaced. The simulation results show that the occupancy numbers of water molecules inside the cryptophane are correlated with the binding free energies (Fig. 13). Furthermore, hexa-acid cryptophanes can chelate counter ions with two side chains. This “anchoring” is not observed in the cages with only three solubilizing moieties. The counter ions trapped by side chains of hexa-acid cryptophanes are displaced in order for a Xe atom to bind within the cryptophane molecule. Associated with these trapped counter ions are solvating water molecules inside the cryptophane cage, including near the pores. This results in the higher water occupancy observed for m2n2 (1.6), compared to those of TTEC (0.5), TAAC (0.9), and TTPC (1.0). The results presented here exemplify how simulations can potentially be used to understand and to guide the design of cryptophane molecules to possess both high aqueous solubility and high Xe affinity.Abbreviations
| TTEC | Tris-(triazole ethylamine) cryptophane |
| TAAC | Triacetic acid cryptophane |
| TTPC | Tris-(triazole propionic acid) cryptophane |
Acknowledgements
JGS and IJD acknowledge support from NIH R01-GM097478. IJD also acknowledges CDMRP-LCRP Concept Award #LC130824. Support was provided to JGS by the University of Pennsylvania's Nano/Bio Interface Center (NSF NSEC DMR 08-32802) and infrastructural support by the Laboratory for the Research on the Structure of Matter (NSF MRSEC DMR 11-20901). This research was supported in part by the National Science Foundation through XSEDE resources provided by NICS under grant number TG-CHE110041.Notes and references
- L. Garel, J. P. Dutasta and A. Collet, Angew. Chem., Int. Ed. Engl., 1993, 32, 1169–1171 CrossRef.
- J. Canceill, L. Lacombe and A. Collet, J. Am. Chem. Soc., 1985, 107, 6993–6996 CrossRef CAS.
- J. Canceill, L. Lacombe and A. Collet, J. Am. Chem. Soc., 1986, 108, 4230–4232 CrossRef CAS.
- G. Haberhauer, S. Woitschetzki and H. Bandmann, Nat. Commun., 2014, 5, 3542 Search PubMed.
- L. Garel, B. Lozach, J. P. Dutasta and A. Collet, J. Am. Chem. Soc., 1993, 115, 11652–11653 CrossRef CAS.
- D. R. Jacobson, N. S. Khan, R. Colle, R. Fitzgerald, L. Laureano-Perez, Y. B. Bai and I. J. Dmochowski, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10969–10973 CrossRef CAS PubMed.
- J. Canceill, L. Lacombe and A. Collet, J. Chem. Soc., Chem. Commun., 1987, 219–221 RSC.
- T. Traore, G. Clave, L. Delacour, N. Kotera, P. Y. Renard, A. Romieu, P. Berthault, C. Boutin, N. Tassali and B. Rousseau, Chem. Commun., 2011, 47, 9702–9704 RSC.
- A. Bouchet, T. Brotin, M. Linares, H. Ågren, D. Cavagnat and T. Buffeteau, J. Org. Chem., 2011, 76, 1372–1383 CrossRef CAS PubMed.
- O. Taratula and I. J. Dmochowski, Curr. Opin. Chem. Biol., 2010, 14, 97–104 CrossRef CAS PubMed.
- M. M. Spence, S. M. Rubin, I. E. Dimitrov, E. J. Ruiz, D. E. Wemmer, A. Pines, S. Q. Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed.
- K. Ruppert, J. R. Brookeman, K. D. Hagspiel, B. Driehuys and J. P. Mugler, NMR Biomed., 2000, 13, 220–228 CrossRef CAS PubMed.
- G. Duhamel, P. Choquet, E. Grillon, L. Lamalle, J. L. Leviel, A. Ziegler and A. Constantinesco, Magn. Reson. Med., 2001, 46, 208–212 CrossRef CAS PubMed.
- S. D. Swanson, M. S. Rosen, K. P. Coulter, R. C. Welsh and T. E. Chupp, Magn. Reson. Med., 1999, 42, 1137–1145 CrossRef CAS PubMed.
- S. Korchak, W. Kilian and L. Mitschang, Chem. Commun., 2015, 51, 1721–1724 RSC.
- D. Raftery, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Elsevier Academic Press Inc, San Diego, 2006, vol. 57, pp. 205–270 Search PubMed.
- S. M. Rubin, S. Y. Lee, E. J. Ruiz, A. Pines and D. E. Wemmer, J. Mol. Biol., 2002, 322, 425–440 CrossRef CAS PubMed.
- T. Brotin and J. P. Dutasta, Chem. Rev., 2009, 109, 88–130 CrossRef CAS PubMed.
- A. I. Joseph, S. H. Lapidus, C. M. Kane and K. T. Holman, Angew. Chem., Int. Ed., 2015, 54, 1471–1475 CrossRef CAS PubMed.
- G. Huber, T. Brotin, L. Dubois, H. Desvaux, J. P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed.
- P. A. Hill, Q. Wei, T. Troxler and I. J. Dmochowski, J. Am. Chem. Soc., 2009, 131, 3069–3077 CrossRef CAS PubMed.
- B. S. Kim, Y. H. Ko, Y. Kim, H. J. Lee, N. Selvapalam, H. C. Lee and K. Kim, Chem. Commun., 2008, 2756–2758 RSC.
- A. Collet, J. P. Dutasta, B. Lozach and J. Canceill, Top. Curr. Chem., 1993, 165, 103–129 CrossRef CAS.
- P. A. Hill, Q. Wei, R. G. Eckenhoff and I. J. Dmochowski, J. Am. Chem. Soc., 2007, 129, 11662 CrossRef CAS.
- R. M. Fairchild, A. I. Joseph, K. T. Holman, H. A. Fogarty, T. Brotin, J. P. Dutasta, C. Boutin, G. Huber and P. Berthault, J. Am. Chem. Soc., 2010, 132, 15505–15507 CrossRef CAS PubMed.
- K. N. Houk, A. G. Leach, S. P. Kim and X. Y. Zhang, Angew. Chem., Int. Ed., 2003, 42, 4872–4897 CrossRef CAS PubMed.
- P. P. Wanjari, B. C. Gibb and H. S. Ashbaugh, J. Chem. Phys., 2013, 139, 234502 CrossRef PubMed.
- J. CostanteCrassous, T. J. Marrone, J. M. Briggs, J. A. McCammon and A. Collet, J. Am. Chem. Soc., 1997, 119, 3818–3823 CrossRef CAS.
- P. D. Kirchhoff, M. B. Bass, B. A. Hanks, J. M. Briggs, A. Collet and J. A. McCammon, J. Am. Chem. Soc., 1996, 118, 3237–3246 CrossRef CAS.
- C. C. Roberts and C.-E. A. Chang, J. Chem. Theory Comput., 2013, 9, 2010–2019 CrossRef CAS PubMed.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- D. Hamelberg and J. A. McCammon, J. Am. Chem. Soc., 2004, 126, 7683–7689 CrossRef CAS PubMed.
- C. Chipot and D. A. Pearlman, Mol. Simul., 2002, 28, 1–12 CrossRef CAS.
- P. Kollman, Chem. Rev., 1993, 93, 2395–2417 CrossRef CAS.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- D. L. Beveridge and F. M. Dicapua, Annu. Rev. Biophys. Biophys. Chem., 1989, 18, 431–492 CrossRef CAS PubMed.
- T. P. Straatsma and J. A. McCammon, Annu. Rev. Phys. Chem., 1992, 43, 407–435 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- D. Cavagnat, T. Brotin, J. L. Bruneel, J. P. Dutasta, A. Thozet, M. Perrin and F. Guillaume, J. Phys. Chem. B, 2004, 108, 5572–5581 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. L. Jorgensen and J. Tiradorives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- A. A. Clifford, P. Gray and N. Platts, J. Am. Chem. Soc., 1977, 73, 381–382 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr., R. E. Stratman, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, P. Salvador, J. J. Dannenberg, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98 (Revision A.10), Gaussian Inc., Pittsburgh, PA, 2001 Search PubMed.
- F. Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski and P. Cieplak, Phys. Chem. Chem. Phys., 2010, 12, 7821–7839 RSC.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 2309 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- I. Balabin, M. Sotomayor and L. Trabuco, Autoionize Plugin, http://www.ks.uiuc.edu/Research/vmd/plugins/autoionize/, accessed August 2012.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, Waltham, MA (USA), 2nd edn, 2001 Search PubMed.
- T. C. Beutler, A. E. Mark, R. C. Vanschaik, P. R. Gerber and W. F. Vangunsteren, Chem. Phys. Lett., 1994, 222, 529–539 CrossRef CAS.
- M. Zacharias, T. P. Straatsma and J. A. McCammon, J. Chem. Phys., 1994, 100, 9025–9031 CrossRef CAS.
- J. Henin, G. Fiorin, C. Chipot and M. L. Klein, J. Chem. Theory Comput., 2010, 6, 35–47 CrossRef CAS PubMed.
- A. Bennaim and Y. Marcus, J. Chem. Phys., 1984, 81, 2016–2027 CrossRef CAS.
- E. Wilhelm, R. Battino and R. J. Wilcock, Chem. Rev., 1977, 77, 219–262 CrossRef CAS.
- P. Scharlin, R. Battino, E. Silla, I. Tunon and J. L. Pascual-Ahuir, Pure Appl. Chem., 1998, 70, 1895–1904 CrossRef CAS.
- T. Young, R. Abel, B. Kim, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 808–813 CrossRef CAS PubMed.
- N. T. Skipper and G. W. Neilson, J. Phys.: Condens. Matter, 1989, 1, 4141–4154 CrossRef CAS.
- O. Taratula, P. A. Hill, N. S. Khan, P. J. Carroll and I. J. Dmochowski, Nat. Commun., 2010, 1, 148 CrossRef PubMed.
- P. Berthault, H. Desvaux, T. Wendlinger, M. Gyejacquot, A. Stopin, T. Brotin, J. P. Dutasta and Y. Boulard, Chem.–Eur. J., 2010, 16, 12941–12946 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Molecular segments labeled by atom types and electrostatic charges (Fig. S1). The histograms of number of water molecules inside cryptophane molecules (Fig. S2). Helmholtz free energy changes ΔA1 and ΔA2 as functions of the decoupling parameter λ (Fig. S3). Water maps for water molecules inside m3n3, m2n3, m2n2, TTPC and TAAC (Fig. S4). Bond parameters (Table S1). Residence times of water molecules inside cryptophanes (Table S2). See DOI: 10.1039/c5sc02401c |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2015 |