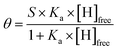Open Access Article
Open Access ArticleDetermination of association constants towards carbon nanotubes†
Alberto
de Juan
a,
Alejandro
López-Moreno
a,
Joaquín
Calbo
b,
Enrique
Ortí
 *b and
Emilio M.
Pérez
*b and
Emilio M.
Pérez
 *a
*a
aIMDEA Nanociencia, C/Faraday 9, Ciudad Universitaria de Cantoblanco, 28049, Madrid, Spain. E-mail: emilio.perez@imdea.org
bInstituto de Ciencia Molecular, Universidad de Valencia, 46980 Paterna, Spain. E-mail: enrique.orti@uv.es
First published on 7th September 2015
Abstract
Single-walled carbon nanotubes (SWNTs) are one of the most promising nanomaterials and their supramolecular chemistry has attracted a lot of attention. However, despite well over a decade of research, there is no standard method for the quantification of their noncovalent chemistry in solution/suspension. Here, we describe a simple procedure for the determination of association constants (Ka) between soluble molecules and insoluble and heterogeneous carbon nanotube samples. To test the scope of the method, we report binding constants between five different hosts and two types of SWNTs in four solvents. We have determined numeric values of Ka in the range of 1–104 M−1. Solvent effects as well as structural changes in both the host and guest result in noticeable changes of Ka. The results obtained experimentally were validated through state-of-the-art DFT calculations. The generalization of quantitative and comparable association constants data should significantly help advance the supramolecular chemistry of carbon nanotubes.
Introduction
Materials with at least one of their dimensions in the nanometer range, such as graphene,1–3 carbon nanotubes,4 quantum dots,5 metal nanoparticles,6 few layer transition metal chalcogenides7etc., are expected to revolutionize technology8 and have certainly transformed science already.9 In particular, the extreme aspect ratio and extraordinary physical properties of single-walled carbon nanotubes (SWNTs) have attracted a great deal of attention.10 Chemical modifications are usually necessary to take full advantage of their properties and/or to modulate them.11,12 A particularly attractive strategy is to utilize noncovalent forces to yield supramolecular constructs, since it guarantees the structural integrity of the nanotube, and changing the structure of the host, its concentration, the solvent, and/or temperature can modulate the stability of the associates.13,14 In this respect, the quantification of the supramolecular interactions is of paramount importance. From the experimental point of view, skillfully designed atomic force microscopy experiments have allowed for the measurement of interaction forces between single molecules and SWNTs.15 A kinetic model for the measurement of chirality-specific interactions of SWNTs with hydrogels has also been reported.16In silico investigations are far more abundant, and a wide variety of DFT methods have been tested.17 However, the overwhelming majority of publications on noncovalent chemistry of nanotubes do not report quantitative data.13,14,18 This is in sharp contrast with the literature on soluble host–guest systems, in which the determination of the association constant (Ka) is hardly ever overlooked, and comparison of the Ka data is the main tool to understand molecular recognition events. Needless to say, the lack of quantitative and comparable information represents a major obstacle in the progress of the supramolecular chemistry of SWNTs.Here, we describe a simple method for the determination of association constants between insoluble and heterogeneous nanotube samples and soluble molecules. To prove its validity, we have determined the association constants of five molecules towards two types of SWNTs in four different solvents.
Results and discussion
Due to the heterogeneous nature of most samples and the characteristic insolubility of SWNTs, it is virtually impossible to calculate their molar concentration in solution. This has hampered the determination of association constants in SWNT-based supramolecular systems, with a few notable exceptions based on approximations to apply standard spectroscopic titration methods.19–21 However, it is known that association constants can be calculated from the fraction of occupied binding sites and the concentration of the host–guest complex, the free host, or the free guest species only.22,23 This method is not usually applied to soluble host–guest systems because the total concentration of host and guest are known quantities and the calculation of the concentration of free species is problematic.23 We take advantage of the insolubility of the carbonaceous material to measure the concentration of bound and free species.The experimental procedure is described graphically in Scheme 1 and can be summarized as follows: SWNTs (1 mg mL−1, unless stated otherwise) are suspended in a solution of known concentration of the host molecule in a given solvent, and the mixture stirred for 2 hours to allow it to reach equilibrium. After this time, the suspension is filtered through a 0.2 μm-pore polytetrafluoroethylene membrane, retaining the host–SWNT complex. The solid is analysed through TGA (N2, 50 °C min−1) to quantify the amount of host in the complex, from which the concentration of free species is calculated by subtraction. Specifically, we measure the weight loss up to 600 °C, where all of the associated host has been desorbed and the nanotubes are still intact. From the degree of functionalization and the mass of the sample analysed, we calculate the total mass of host in the complex, from which its initial concentration in the equilibrium is immediate. Alternatively, the concentration of free species can be directly measured in the filtrate.‡ The same procedure is repeated for several initial concentrations of the host molecule, ranging from 0 to near saturation in the solvent under study. A blank experiment to determine the adsorbed/encapsulated solvent was run in all cases, and the data subtracted. All the experiments were performed at room temperature.
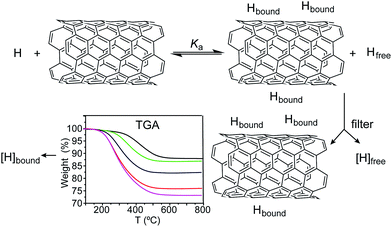 | ||
| Scheme 1 Procedure for the measurement of [H]bound and [H]free. A known concentration of host molecule H and SWNTs are allowed to reach equilibrium, and then complexed and free species are physically separated through filtration. The concentration of [H]bound is measured by TGA (typical results for a titration experiment are shown, see the ESI† for full data set). The concentration of [H]free can then be calculated by subtraction or directly measured in the filtrate. | ||
The binding isotherms are obtained by plotting the degree of functionalization against the concentration of free host, and were analyzed using a standard 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 isotherm:23
1 isotherm:23
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry does not refer to the host
1 stoichiometry does not refer to the host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SWNT molar ratio, but to the number of occupied binding sites on SWNT, so that it is necessarily 1
SWNT molar ratio, but to the number of occupied binding sites on SWNT, so that it is necessarily 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In this respect, the binding isotherm is both formally and conceptually equivalent to the Langmuir isotherm,24 widely used for the quantification of the adsorption of gases onto solid surfaces.
1. In this respect, the binding isotherm is both formally and conceptually equivalent to the Langmuir isotherm,24 widely used for the quantification of the adsorption of gases onto solid surfaces.
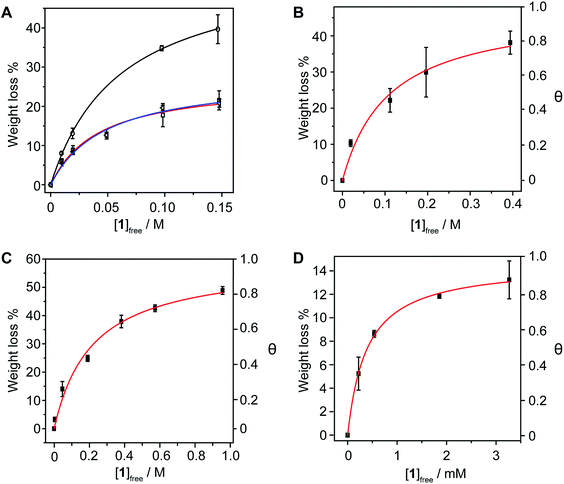
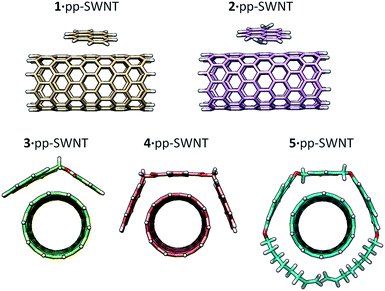
Pyrene is by far the most widely used supramolecular partner for SWNTs, so we based our investigations on pyrene and its derivatives. Fig. 1 shows the chemical structure of the hosts for SWNTs used in the present work. First, we titrated 1 against plasma-purified SWNTs (pp-SWNTs, 98% purity, 0.8–1.6 nm in diameter) in tetrahydrofuran (THF), dimethylformamide (DMF), tetrachloroethane (TCE), and methanol (MeOH) at room temperature. Fig. 2 shows results of these titrations, where each data point is the average of three separate experiments.
As a first test of the experimental validity of our approach, we decided to get data for titrations with significant variations in the concentration of SWNTs. In particular, we used 0.1, 1 and 10 mg mL−1 of nanotubes in THF (Fig. 2a), which afforded Ka = 16.4 ± 0.8 M−1,§ 24 ± 6 M−1, and 21 ± 4 M−1, respectively. We were pleased to find that all values for Ka are identical within experimental error. The main variability comes from the degree of functionalization at saturation, which is significantly larger for the more dilute sample. This reflects a more efficient disaggregation of the nanotubes, which in turn results in an increase in the availability of binding sites for 1. Therefore, the method works correctly for samples with significantly different degrees of aggregation of the SWNTs.
With regards to the effect of the solvent, the association constants increase with decreasing ability to solvate SWNTs, showing that solvophobic interactions play a relevant role in the binding event. In DMF and TCE, solvents commonly used to disperse SWNTs, the binding constants are very small: Ka = 9 ± 3 and 4.5 ± 0.9 M−1, respectively (Fig. 2b and c). In THF there is an increase of one order of magnitude, to Ka = 24 ± 6 M−1 (Fig. 2a), which is further amplified in MeOH, a notoriously bad solvent for SWNTs, to reach millimolar affinity with Ka = (2.6 ± 0.2) × 103 M−1 (Fig. 2d).
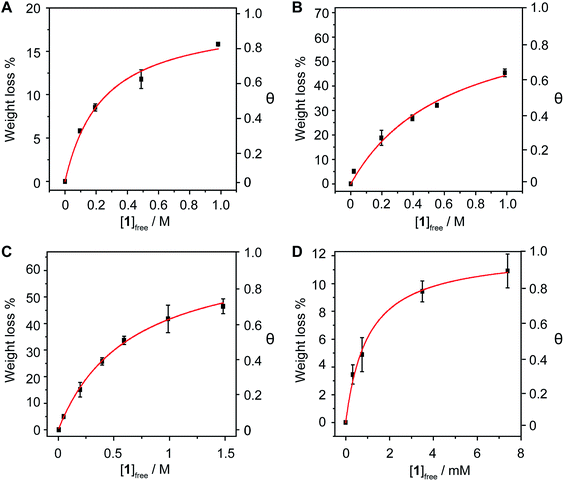
In order to investigate whether the method is sufficiently sensitive to detect small changes in the structure of the nanotubes, we carried out titrations of 1vs. (6,5)-enriched SWNTs (93% purity, 0.7–0.9 nm in diameter) in THF, DMF, TCE and MeOH at room temperature. The association constant towards (6,5)-SWNTs are: Ka = 41 ± 8 M−1 in THF, 1.6 ± 0.4 M−1 in DMF, 1.6 ± 0.1 M−1 in TCE, and (1.0 ± 0.1) × 103 M−1 in MeOH (Fig. 3). Therefore, with the only exception of THF, in which some unexpected solvent effect takes place, the association constants are smaller than those towards pp-SWNTs. Considering the planar geometry of pyrene, it is expected to establish stronger van der Waals interactions with nanotubes of larger diameter, a tendency that is corroborated by DFT calculations (see below). These results confirm that the method is sensitive enough to such subtle differences in the structure of the nanotube as a decrease in the average diameter of the sample.
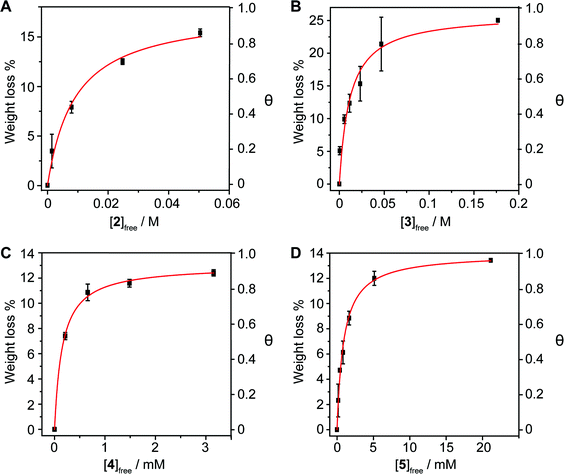
The method is also sensitive towards the structure of the host. To get experimental evidence, we designed a collection of hosts composed by 1,6-diaminopyrene (2), the benzoic and isophthalic esters of pyrene-1-methanol (3 and 4, respectively), and bis-pyrene U-shape molecule 5, which we have used in the synthesis of mechanically interlocked derivatives of SWNTs.25–28 Hosts 3–5 were titrated vs. pp-SWNTs in THF at room temperature, while we used DMF for the titration of 2 for solubility reasons.
Both electron-rich conjugated compounds and amines are known to interact strongly with SWNTs, so we expected 2 to show a significantly larger association constant compared to pyrene. This is indeed the case, as we calculated Ka = (2.2 ± 0.5) × 102 M−1 for the 2·pp-SWNTs associate (Fig. 4a), which is more than two orders of magnitude larger than the Ka of 1 in the same solvent. Addition of an extra aromatic ring in 3 also results in a significant increase in binding constant with respect to pyrene, reaching Ka = (9 ± 3) × 10 M−1 in THF (Fig. 4b). Bivalent tweezers-like hosts are a particularly popular design for the supramolecular association of SWNTs and fullerenes, as they typically show very good affinity at a relatively low synthetic cost.29 Indeed, 4 shows Ka = (6.5 ± 0.6) × 103 M−1 towards pp-SWNTs in THF (Fig. 4c). Finally, we decided to get an insight into the association of U-shaped molecule 5, which associates pp-SWNTs with Ka = (7 ± 2) × 103 M−1 (Fig. 4d), slightly larger than that of 4.
Note that 4 and 5 feature two pyrene binding motifs each, and might show multivalency and/or cooperativity phenomena.30 Since our method is based on measuring the concentration of the complex by desorbing it completely, it would not be valid to determine stepwise association constants. A possible approach to investigate such issues would be to utilize the Hill equation.31–33 Considering the clearly hyperbolic shape of the binding isotherms, we have determined average binding constants only.
To validate our experimental results, theoretical calculations were performed for the list of host–guest nanotube assemblies under the density functional theory (DFT) framework. The atom pair-wise Grimme's dispersion correction in its latest version (D3)34 was coupled to the hybrid density functional of Perdew–Burke–Hernzerhof (PBE0)35 through the Becke-Johnson damping function36 and including the three-body dispersion correction (EABC).37 The double-zeta Pople's 6-31G** basis set38 was employed throughout and the basis set superposition error (BSSE) was corrected according to the counterpoise (CP) scheme of Boys and Bernardi.39 The intensity of the interaction between host and guest was calculated by means of two different quantities. The interaction energy (Eint) is defined as the energy difference between the host–guest complex (HG) and the individual moieties separately (H and G), with all of them at the geometry of the complex:
| Eint = EHGHG − EHGH − EHGG |
Otherwise, the binding (or association) energy (Ebind) was calculated taking into account the relaxation of the separate monomers and, therefore, considering the deformation energy required to transform the host/guest moieties from their minimum-energy geometries to the geometry acquired in the assembly:
| Ebind = Edef + Eint |
| Edef = (EHGH − EHH) + (EHGG − EGG) |
As a general model for the pp-SWNTs we have utilized a fragment of a zig-zag (10,0)-SWNT. The effect of the length of the nanotube into the intermolecular interaction was assessed by increasing the SWNT size in a 1·SWNT complex, showing that the association energy is nearly converged with sizes slightly larger than the host length (see Table S2 and Fig. S21†).
Fig. 5 displays the minimum-energy geometries for the 1–5 hosts assembled with the pp-SWNT model of C160H20 computed at the PBE0-D3/6-31G** level of theory in gas phase. Among the different closely energetic conformations of 1 over pp-SWNT, the diagonal arrangement is found to be the most stable, with close π–π contacts in the range of 3.2–3.5 Å. The interaction energy of 1·pp-SWNT is computed at −15.24 kcal mol−1, which is slightly reduced to −14.84 kcal mol−1 for the binding energy as a consequence of the deformation energy penalty (0.59 kcal mol−1). Moving from the pyrene system to 1,6-diaminopyrene (2), additional n–π interactions arise from close nitrogen⋯nanotube contacts (approximately at 4.0 Å). The Eint of 2·pp-SWNT is calculated 1.3 kcal mol−1 larger than for 1·pp-SWNT, but this difference is not maintained in the binding energy (Table 1). The deformation energy, calculated to be 2.83 kcal mol−1 for 2·pp-SWNT, explains this trend. The inclusion of an extra aromatic ring in 3 results in a significant increase of the interaction energy up to −23.68 kcal mol−1, with close π–π benzene⋯SWNTs (3.5 Å) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯SWNTs (3.2 Å) contacts. Bivalent tweezers-like hosts further improve the supramolecular affinity vs. pp-SWNT with Eint as large as −38.78 and −63.23 kcal mol−1 in 4 and 5, respectively. The binding energy in host 4 (−36.42 kcal mol−1) is indeed approximately the sum of Eint for its constituting moieties 1 and 3 (−14.84 + (−21.52) = −36.36 kcal mol−1), which supports the theoretical approach undertaken. Whereas the Edef of 4 is computed similar to 2 and 3, it amounts 20.46 kcal mol−1 for 5 due to the accommodation of the alkoxy chains around the nanotube (Fig. 4). This disposition confers 5·pp-SWNT an increased Ebind of −42.78 kcal mol−1 due to close CH⋯π contacts calculated in the range of 2.7–3.2 Å, which contribution to the total binding energy amounts 6 kcal mol−1.
O⋯SWNTs (3.2 Å) contacts. Bivalent tweezers-like hosts further improve the supramolecular affinity vs. pp-SWNT with Eint as large as −38.78 and −63.23 kcal mol−1 in 4 and 5, respectively. The binding energy in host 4 (−36.42 kcal mol−1) is indeed approximately the sum of Eint for its constituting moieties 1 and 3 (−14.84 + (−21.52) = −36.36 kcal mol−1), which supports the theoretical approach undertaken. Whereas the Edef of 4 is computed similar to 2 and 3, it amounts 20.46 kcal mol−1 for 5 due to the accommodation of the alkoxy chains around the nanotube (Fig. 4). This disposition confers 5·pp-SWNT an increased Ebind of −42.78 kcal mol−1 due to close CH⋯π contacts calculated in the range of 2.7–3.2 Å, which contribution to the total binding energy amounts 6 kcal mol−1.
 | ||
| Fig. 5 Minimum-energy geometry for the supramolecular assemblies formed by hosts 1–5vs. the pp-SWNTs model calculated at the PBE0-D3/6-31G** level of theory. | ||
| System | E int | E def | E bind | CAa (Å2) |
|---|---|---|---|---|
| a The intermolecular contact area (CA) was calculated using the UCSF Chimera 1.7 software according to the formula: (area of the host + area of the guest − area of the complex)/2, where the areas used refer to solvent-excluded molecular surfaces, composed of probe contact, toroidal, and reentrant surface. | ||||
| 1·(6,5)-SWNT | −13.85 | 0.81 | −13.04 | 42.20 |
| 1·pp-SWNT | −15.24 | 0.59 | −14.84 | 42.70 |
| 2·pp-SWNT | −16.53 | 2.83 | −13.70 | 47.25 |
| 3·pp-SWNT | −23.68 | 2.16 | −21.52 | 75.30 |
| 4·pp-SWNT | −38.78 | 2.36 | −36.42 | 126.85 |
| 5·pp-SWNT | −63.23 | 20.46 | −42.78 | 188.55 |
Finally, the influence of the structure of the nanotube in the stability of the host–guest assembly was assessed by comparing the associates of pp-SWNT and (6,5)-SWNT with pyrene 1. The Eint of 1·(6,5)-SWNT was computed at −13.85 kcal mol−1, which is 1.4 kcal mol−1 smaller than the Eint of 1·pp-SWNT. The minimum energy structures calculated for the supramolecular complexes between pyrene and the two types of nanotubes (Fig. S22†) reveal subtle differences in terms of intermolecular contacts. The diameter of (6,5)-SWNT is computed at 7.5 Å, slightly smaller than for the pp-SWNT model (7.9 Å), which provokes a less efficient supramolecular assembly with pyrene. The deformation energy of 1·(6,5)-SWNT is computed somewhat larger than 1·pp-SWNT (Table 1), suggesting that the pyrene core is required to have a larger deformation to accommodate over the more-curved nanotube surface of (6,5)-SWNT. Moreover, the intermolecular contact area for 1·(6,5)-SWNT is calculated to be 0.5 Å2 smaller than in 1·pp-SWNT.
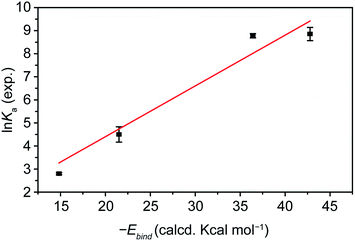
Most remarkably, the calculated Ebind energies and the experimentally determined Ka values show excellent quantitative agreement, despite the fact that desolvation and solvation energies are not included in our calculations. A plot of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kavs. −Ebind for molecules 1, 3, 4, and 5, towards pp-SWNTs in THF at room temperature, the largest set for which we have extracted comparable Ka data, is shown in Fig. 6. Fixing the intercept to 0, the data fit well (r2 = 0.984) to a straight line of slope 0.22 ± 0.01. Therefore, our analysis shows that the ΔGbind determined experimentally is proportional to the calculated Ebind.
Kavs. −Ebind for molecules 1, 3, 4, and 5, towards pp-SWNTs in THF at room temperature, the largest set for which we have extracted comparable Ka data, is shown in Fig. 6. Fixing the intercept to 0, the data fit well (r2 = 0.984) to a straight line of slope 0.22 ± 0.01. Therefore, our analysis shows that the ΔGbind determined experimentally is proportional to the calculated Ebind.
Conclusions
In summary, we have described a simple method for the determination of association constants between soluble molecules and insoluble and heterogeneous nanomaterials. The method is based on the measurement of the concentration of free host, and therefore does not require any approximation. The quantitative measurements were carried out using TGA data only, so in principle, any host molecule can be evaluated regardless of its spectroscopic properties.To illustrate the scope and limitations of this methodology, we have tested five different hosts and two types of SWNTs in four different solvents for a total of 17 binding constant determinations. The data fit well to the binding isotherm in all cases, with a minimum r2 of 0.937 (Table S1†). The method is sensitive to solvent effects, as well as to small structural changes in both the SWNT and the host. The numeric values of Ka span over approximately four orders of magnitude, showing that the method is valid both for very small and large binding constants. Our data were validated by DFT calculations, which correctly reproduce the trends observed experimentally.
Although the main objective of the present work was to develop a standard method for the determination of binding constants towards carbon nanotubes, several interesting observations can be made with the present data set of Ka. Perhaps the most relevant conclusion is that our results back the utilization of a single unit of pyrene as a noncovalent anchor to SWNTs in polar protic solvents,40 but caution against assuming that it will “adsorb irreversibly” to the nanotubes in any organic solvent,41 as the association constants can be as low as 1 M−1. This is particularly relevant in cases where the pyrene-SWNT supramolecular construct will be subjected to further modifications after association. In this respect, using two pyrene units connected to form a tweezers-like receptor seems a valid alternative.
Taking into account the simplicity of the methodology described, we sincerely hope that the determination of association constants will become routine for anyone interested in the supramolecular chemistry of carbon nanotubes. The generalization of such quantitative data will undoubtedly produce a significant leap in our understanding of their noncovalent chemistry.
The techniques and methods described here should also be applicable to other insoluble nanomaterials, such as few-layer graphene. We are currently working towards the extension of this method to such nanomaterials.
Acknowledgements
Financial support by the European Research Council (MINT, ERC-StG-2012-307609) the Ministerio de Economía y Competitividad (MINECO, CTQ2014-60541-P, and MINECO and FEDER funds CTQ2012-31914) and the Generalitat Valenciana (PROMETEO/2012/053) is gratefully acknowledged. JC thanks the MECD for a doctoral FPU grant.Notes and references
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- C. N. R. Rao, A. K. Sood, K. S. Subrahmanyam and A. Govindaraj, Angew. Chem., Int. Ed., 2009, 48, 7752–7777 CrossRef CAS PubMed.
- D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chem. Rev., 2006, 106, 1105–1136 CrossRef CAS PubMed.
- J. Y. Kim, O. Voznyy, D. Zhitomirsky and E. H. Sargent, Adv. Mater., 2013, 25, 4986–5010 CrossRef CAS PubMed.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, ACS Nano, 2015, 9, 1012–1057 CrossRef CAS PubMed.
- N. P. Dasgupta, X. Meng, J. W. Elam and A. B. F. Martinson, Acc. Chem. Res., 2015, 48, 341–348 CrossRef CAS PubMed.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- From a purely bibliometric point of view, there are 73 journals listed under Nanoscience & Nanotechnology in the Journal of Citation Reports, of which the first seven have impact factors larger than 10. Iijima's first report on carbon nanotubes (S. Iijima, Nature 1991, 354, 56) has been cited more than 22
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 times. Data from SciFinder, August 2015.
600 times. Data from SciFinder, August 2015. - Ph. Avouris, Z. Chen and V. Perebeinos, Nat. Nanotechnol., 2007, 2, 605–615 CrossRef CAS PubMed.
- P. Singh, S. Campidelli, S. Giordani, D. Bonifazi, A. Bianco and M. Prato, Chem. Soc. Rev., 2009, 38, 2214–2230 RSC.
- A. Hirsch, Angew. Chem., Int. Ed., 2002, 41, 1853–1859 CrossRef CAS.
- Supramolecular Chemistry of Fullerenes and Carbon Nanotubes, ed. N. Martín and J.-F. Nierengarten, Wiley-VCH Verlag GmbH & Co., KGaA, 2012 Search PubMed.
- Y.-L. Zhao and J. F. Stoddart, Acc. Chem. Res., 2009, 42, 1161–1171 CrossRef CAS PubMed.
- S. Iliafar, J. Mittal, D. Vezenov and A. Jagota, J. Am. Chem. Soc., 2014, 136, 12947–12957 CrossRef CAS PubMed.
- K. Tvrdy, R. M. Jain, R. Han, A. J. Hilmer, T. P. McNicholas and M. S. Strano, ACS Nano, 2013, 7, 1779–1789 CrossRef CAS PubMed.
- D. Umadevi, S. Panigrahi and G. N. Sastry, Acc. Chem. Res., 2014, 47, 2574–2581 CrossRef CAS PubMed.
- E. M. Pérez and N. Martín, Chem. Soc. Rev., 2015, 44, 6425–6433 RSC.
- P. Salice, A. Gambarin, N. Daldosso, F. Mancin and E. Menna, J. Phys. Chem. C, 2014, 118, 27028–27038 CAS.
- H. Oh, J. Sim and S.-Y. Ju, Langmuir, 2013, 29, 11154–11162 CrossRef CAS PubMed.
- J. K. Sprafke, S. D. Stranks, J. H. Warner, R. J. Nicholas and H. L. Anderson, Angew. Chem., Int. Ed., 2011, 50, 2313–2316 CrossRef CAS PubMed.
- K. A. Connors, Binding Constants. The Measurement of Molecular Complex Stability, John Wiley & sons, New York, 1987 Search PubMed.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1402 CrossRef CAS.
- A. de Juan, Y. Pouillon, L. Ruiz-González, A. Torres-Pardo, S. Casado, N. Martín, Á. Rubio and E. M. Pérez, Angew. Chem., Int. Ed., 2014, 53, 5394–5400 CrossRef CAS PubMed.
- A. de Juan and E. M. Pérez, Nanoscale, 2013, 5, 7141–7148 RSC.
- A. López-Moreno and E. M. Pérez, Chem. Commun., 2015, 51, 5421–5424 RSC.
- A. de Juan, M. Mar Bernal and E. M. Pérez, ChemPlusChem, 2015, 80, 1153–1157 CrossRef CAS PubMed.
- E. M. Pérez and N. Martín, Pure Appl. Chem., 2010, 82, 523–533 CrossRef.
- For a detailed discussion on the subject, see: C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS PubMed.
- For applications of the Hill equation to multifunctional synthetic pores, see: Y. Baudry, G. Bollot, V. Gorteau, S. Litvinchuk, J. Mareda, M. Nishihara, D. Pasini, F. Perret, D. Ronan, N. Sakai, M. R. Shah, A. Som, N. Sordé, P. Talukdar, D. H. Tran and S. Matile, Adv. Funct. Mater., 2006, 16, 169–179 CrossRef CAS PubMed.
- For an application of the Hill equation to the association of fullerenes, see: E. M. Pérez, L. Sánchez, G. Fernández and N. Martín, J. Am. Chem. Soc., 2006, 128, 7172–7173 CrossRef PubMed.
- Ercolani has argued against the use of the Hill equation for self-assembly processes: G. Ercolani, J. Am. Chem. Soc., 2003, 125, 16097–16103 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS PubMed.
- N. Nakashima, Y. Tomonari and H. Murakami, Chem. Lett., 2002, 31, 638–639 CrossRef.
- R. J. Chen, Y. Zhang, D. Wang and H. Dai, J. Am. Chem. Soc., 2001, 123, 3838–3839 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic details and characterization, thorough description of the method to determine the concentration of the relevant species, full set of TGA data, isotherms not shown in the main text, table with all the association constants, computational details and theoretical calibration of the nanotube length. See DOI: 10.1039/c5sc02916c |
| ‡ Somewhat counterintuitively, we find the direct measurement of [H]free in the filtrate more problematic experimentally. We believe the main reasons behind this are variations in the volume of solvent during the filtration process and spectral overlap of the hosts with the carbonaceous impurities present in the filtrate. |
| § Considering that each data point consists of three separate experiments, we have reported errors directly as obtained from the fitting software. Based on our previous experience determining association constants, an experimental error within 20% can be expected. |
| This journal is © The Royal Society of Chemistry 2015 |