Droplet coalescence on water repellant surfaces

Abstract

We report our hydrodynamic and energy analyses of droplet coalescence on water repellent surfaces including hydrophobic, superhydrophobic and oil-infused superhydrophobic surfaces. The receding contact angle has significant effects on the contact line dynamics since the contact line dissipation was more significant during the receding mode than advancing. The contact line dynamics is modeled by the damped harmonic oscillation equation, which shows that the damping ratio and angular frequency of merged droplets decrease as the receding contact angle increases. The fast contact line relaxation and the resulting decrease in base area during coalescence were crucial to enhance the mobility of coalescing sessile droplets by releasing more surface energy with reducing dissipation loss. The superhydrophobic surface converts ∼42% of the released surface energy to the kinetic energy via coalescence before the merged droplet jumps away from the surface, while oil-infused superhydrophobic and hydrophobic surfaces convert ∼30% and ∼22%, respectively, for the corresponding time. This work clarifies the mechanisms of the contact line relaxation and energy conversion during the droplet coalescence on water repellent surfaces, and helps develop water repellent condensers.

---

The condensation on water-repellent surfaces has been actively studied to improve heat and mass transfer performances in many applications including power generation, water harvesting, and thermal management.^1–5 Previous studies have shown that the heat transfer performance of dropwise condensation on hydrophobic surfaces is much higher than that of filmwise condensation due to the efficient gravity-driven droplet removal mechanism.^6–8 Superhydrophobic condenser surfaces also have attracted a lot of attention since condensates can be spontaneously removed via coalescence-induced jumping without any external forces such as gravity when they satisfied the energy criteria.^9–12 Recently, oil-infused superhydrophobic condenser surfaces were introduced to facilitate the condensate removal by minimizing contact line pinning and resulting hysteresis with the maintenance of a relatively large contact area compared with superhydrophobic surfaces.^13–16

Droplet coalescence is a key process in the growth and removal of condensates, and significantly affects the overall condensation behaviors on such surfaces. However, most of the previous studies have been focused on the coalescence of freely suspended drops whose kinetics are described well by the balance between the liquid viscosity and the surface tension.^17–19 The dynamic behaviors of sessile drop coalescence are governed by complex contact line motions and energy dissipations affected by the interactions among liquid, vapor and solid phases.

When droplets merge on solid substrates, initially the liquid bridge forms between the droplets and expands. Then the merged droplet rearranges its shape from elliptical to circular.^12,20,21 Previous studies have modeled the merged droplet relaxation dynamics during the latter stage of coalescence based on the experimental observation, and defined the droplet relaxation time as t_c = (1/U*)R, where U* represents the contact line relaxation rate and R is the final equilibrium radius.^20–22 These previous studies have found that the timescale required for the relaxation of coalescing droplets on a substrate is many orders of magnitude larger compared with that for the freely suspended droplet coalescence case,^20,21 which showed the significance of contact line dissipation for the sessile drop coalescence. Other previous studies applied the scaling analysis and showed that the width of the growing meniscus bridge between the two droplets on the highly wetting surface is proportional to t^1/2 at the early stage of coalescence.²³ These studies, however, were conducted on the substrates with moderate contact angles (40–90°)^20–22 or highly wetting surfaces²³ and the investigations were limited on the contact line dynamics without discussing associated hydrodynamic and energy behaviors. In our recent study, we investigated the droplet coalescence on a superhydrophobic surface with a 3D model but the discussion was limited on clarifying the droplet jumping mechanism.¹²

In this work, we investigated the hydrodynamic behaviors and energy conversion mechanisms of droplets coalescing on scalable hydrophobic (HPo), superhydrophobic (SHPo), oil-infused superhydrophobic (Oil-SHPo) condenser surfaces using a full 3D numerical model. We investigated the contact line dynamics during the entire coalescing event, showing that the receding contact angle has crucial effects on contact line dynamics by affecting contact line pining and viscous dissipation. Unlike previous studies, the contact line relaxation was modeled by the damped harmonic oscillation model, which shows that both the damped angular frequency and the damping ratio of merged droplets decrease with increasing receding angle. Fast contact line relaxation and the resulting decrease in base area were found to be crucial to facilitate the conversion from the surface energy to the kinetic energy, which explains why the droplets coalescing on SHPo and Oil-SHPo have higher mobility than those on HPo.

The investigated water repellent surfaces were fabricated as follows: the hydrophobic surfaces (HPo) were made by functionalizing oxygen plasma-treated commercially available copper foils with TFTS (trichloro(1H,1H,2H,2H-perfluorooctyl)silane, Sigma) through a vapor deposition process. The superhydrophobic surfaces (SHPo) were fabricated by nanostructuring the copper foils with the chemical oxidation scheme reported in our previous publications^24–26 followed by TFTS vapor deposition. To manufacture the oil-infused superhydrophobic surfaces (Oil-SHPo), we dispensed a low viscosity oil droplet (Krytox GPL 101) on the nanostructured superhydrophobic surfaces and blew a dry nitrogen gas to spread the oil uniformly on the surface.¹⁴ The dynamic and static contact angles measured on each investigated surface are summarized in Table 1 with the properties of the infused lubricant oil.

Table 1 Measured contact angles on the investigated samples

Sample	Advancing angle θa (°)	Receding angle θr (°)	Static angle θs (°)
a Infused oil: Krytox GPL 101 (ρ = 1870 kg m^−3, σ = 17.0 mN m^−1, ν = 16 × 10^−6 m^2 s^−1, at 20 °C).
SHPo (silanated CuO)	165.1 ± 1.6	159.8 ± 3.3	161.2 ± 1.6
Oil-SHPo^a (oil-infused silanated CuO)	119.2 ± 1.4	117.5 ± 1.1	118.2 ± 1.1
HPo (silanated cu)	122.7 ± 1.3	81.2 ± 1.8	116.6 ± 2.4

---

Detailed droplet evolution during the coalescence was investigated using a full 3D numerical model based on the level contour reconstruction method,²⁷ a hybrid scheme that combines the advantage of the front tracking²⁸ and level set method.²⁹ Two water droplets with a diameter of ∼30 μm are placed on the bottom of the domain and the initial shape of droplets was determined by the experimental observations on each surface. 30 μm was selected since the droplet jumping actively occurred on the SHPo when the droplets of d ≈ 10–50 μm merges together in our previous experiments.¹² The dynamic contact angles listed in Table 1 were incorporated into the numerical model. We use the simple Navier-slip model that allows the contact line movement proportional to the shear strain rate at the contact point. The contact line velocity U_cl is determined to be U_cl = λ∂u/∂n|_wall, where ∂u/∂n|_wall is the shear strain rate at the wall, and λ is the proportionality constant called an effective slip length.

The slip length of SHPo (λ_SHPo) was estimated from the previous correlation 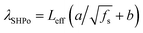,³⁰ where L_eff is the effective pitch between the CuO nanostructures contacting the liquid droplet and estimated to be 1–2 μm based on the SEM images provided in our previous studies.³¹ The coefficients a and b were determined from the previous experiments (a = 0.325 and b = −0.44).³⁰ The effective solid fraction f_s of CuO was estimated using the Cassie–Baxter equation cos θ_a = f_s(cos θ_s + 1) − 1. From the contact angles of the silanated CuO (∼161°) and the silanated smooth wafer (∼110°), f_s was estimated to be ∼0.08 and the resulting λ_SHPo was ∼1 μm. The slip length of Oil-SHPo (λ_Oil-SHPo) was calculated from 1/λ_Oil-SHPo = 1/{(1 − f_s)λ_ow} + 1/λ_SHPo.³⁰ The slip length between the water and the oil (Krytox GPL 101) layers was obtained from λ_ow = (μ_w/μ_oil)δ_oil, where δ_oil is the thickness of oil layer that was assumed to be equal to the average height of CuO nanostructures (∼1 μm). The λ_ow was estimated to be ∼33 nm and the resulting λ_Oil-SHPo was ∼30 nm. The slip length of HPo was assumed to be zero since it was reported to be <20 nm by previous studies.^32,33

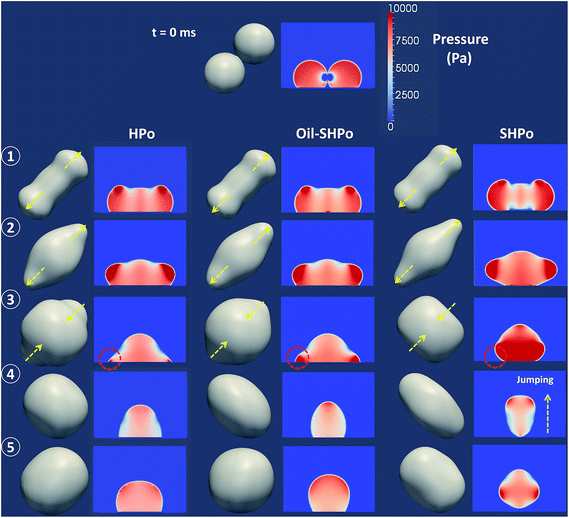
Fig. 1 shows the simulated contact line dynamics during the droplet coalescence. The evolution of the effective radius in x and y directions is defined as R_x and R_y, respectively, and extracted from the simulated results. The R_x and R_y were measured between the extremes of the liquid–vapor interface as shown in the inset of Fig. 1. The time-lapse top views and cross-sectional pressure distributions are shown in Fig. 2. The simulated pressure distributions show that when the tiny liquid bridge forms between the droplets at the beginning of evolution, a low pressure field forms near the bridge due to the negative curvature of the neck. The low pressure at the neck draws a flow from the side of the droplet and the bridge expands outward. The effective radii R_x and R_y remain near constant at the early stage of coalescence as shown in Fig. 1. Then R_x and R_y hit its minimum and maximum peak values at points 1 and 2, respectively, before experiencing the rapid change. At point 1 in Fig. 1 and 2, the high pressure zone locates near the upper center of each droplet, and then the high pressure zone circulates to the side of the merged droplet at point 2. The high pressure zone requires a small radius of curvature of the interface, which explains the minimum and maximum peaks at points 1 and 2, respectively.

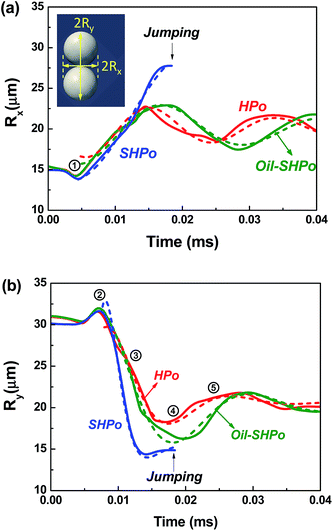Fig. 1 The evolution of a large effective radius R_x (a) and a small effective radius R_y (b); the solid lines show the results extracted from the simulation and the dotted lines show the best fits obtained from the damped harmonic oscillation equation with the parameters provided in Table 2. R_x and R_y were measured between the extremes of the liquid–vapor interface as shown in the inset. Points 1–5 represent t = 0.004, 0.007, 0.0108, 0.018, and 0.024 (ms), respectively.

Fig. 2 The time lapse images of the evolution of simulated droplets coalescing HPo, Oil-SHPo and SHPo. The top views of the liquid–vapor interfacial areas are shown with the cross-sectional pressure distributions at points 1–5 representing t = 0.004, 0.007, 0.0108, 0.018, and 0.024 (ms), respectively. The dotted circles in point 3 show the difference in the apparent receding angles and the resulting pressure field during the contact line receding on each surface.

Fig. 1 also shows that there was no significant difference in contact line dynamics up to point 2 among SHPo, Oil-SHPo and HPo. Note that the contact line dynamics involves only the advancing motion up to point 2 on each surface, and therefore this feature can be explained by considering the dissipation mechanism when the contact line advances.³⁴ The contact line dynamics during the contact line advancing is mainly impeded by two dissipation mechanisms: the contact line pinning (I) and viscous dissipation (II). During the contact line advancing, the dissipation rate by contact line pinning (per unit contact line) can be approximated to be I ∼ σ(cos θ_s − cos θ_a)U_cl, and one can expect that this contribution would be negligible for all three surfaces, as advancing θ_a and static θ_s contact angles are measured to be quite close to each other (Table 1).

Meanwhile, the viscous dissipation rate inside a drop (per unit contact line) is scaled as II ∼ μU_cl²R_b/h, as long as the contact angle is sufficiently large (i.e., >90°), with R_b and h being the base radius of the drop and the drop height, respectively. With O(h/R_b) ∼ 1, the viscous dissipation II is about μU_cl², which indicates that the viscous dissipation rate II would be similar among SHPo, Oil-SHPo and HPo due to no strong dependence on the contact angle. Based on these calculations, one can conclude that there would be no significant difference in contact line dynamics among SHPo, Oil-SHP and HPo up to point 2, due to a similar amount of the overall dissipation during the contact line advancing.

Similarly with the contact line advancing, the overall dissipation mechanism is divided into two dissipation mechanisms during the contact line receding: one due to the contact line pinning (I ∼ σ(cos θ_r − cos θ_s)U_cl) and the viscous dissipation (II). Only on HPo the dissipation by contact line pinning is non-negligible due to a large difference between receding θ_r and static θ_s contact angles on HPo, while its contribution remains negligible on SHPo and Oil-SHPo. Please note that when the contact angle is small and the contact line takes a wedge-like shape (as observed during the contact line receding on HPo and Oil-SHPo), the viscous dissipation would diverge near a contact line. In the small contact angle limit, the viscous dissipation rate (per unit contact line) can be approximated to be II ∼ μU_cl² log(R_b/a)/θ with a being the molecular cut-off length scale and log(R_b/a) reported to range between 15 and 20 in the previous study.³⁵

From the viscous dissipation in the small angle limit, it can be said that the viscous dissipation during the contact line receding is significantly larger than during the contact line advancing on HPo and Oil-SHPo due to much larger numerical coefficient involved (e.g., during receding II ∼ 20μU_cl²/θ ∼ 20μU_cl² with θ ∼ 60° versus during advancing II ∼ μU_cl²). Also, the viscous dissipation in the small angle limit has an explicit functional dependence on the contact angle, in a way that the smaller receding contact angle generally leads to the larger amount of dissipation although the change in U_cl according to the contact angle variation also needs to be considered to make an accurate comparison. The apparent contact angles during contact line receding become lower than the values reported in Table 1 to compensate the viscous force and extracted to be ∼155°, ∼75° and ∼50° on SHPo, Oil-SHPo and HPo, respectively, during the receding. The high apparent receding angles and the resulting small effective radius of curvature creates a high pressure field near the contact line, which increases the restoring force (see the dotted circles in Fig. 2). Therefore the contact line relaxation rate would be the highest on SHPo, followed by Oil-SHPo and then HPo as shown in Fig. 1.

During the sessile drop coalescence, the surface tension force is damped with the frictional forces. As the water repellency increases, the oscillation becomes more under-damped, and the Arrhenius relaxation model R_x,y(t) = R₀ exp[−(t − t₀)/t_c] applied in the previous studies^20,21 does not work well for highly water repellent surfaces. In order to capture the significant oscillation shown in Fig. 1, we model the droplet relaxation behavior with a damped oscillation equation R_x(y) = A e^−γt cos(w_dt + ϕ), where A is the initial amplitude, γ is the damping factor, ω_d is the damped angular frequency, and ϕ is the phase angle. The amplitude A and phase ϕ are constants determined under the initial conditions. The damped angular frequency, ω_d can be expressed as 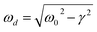, where ω₀ represents the natural angular frequency. The damping ratio ζ describing the level of damping can be calculated as ζ = γ/ω₀. Fig. 1 shows that the model describes well the contact line relaxation on water repellent surfaces, and the parameters for each best fit are provided in Table 2.

Table 2 Extracted parameters from the best fit for each case

		ω d (MHz)	γ (μs^−1)	ζ	A (μm)	ϕ (rad)
R x	SHPo	0.167	0.010	0.060	9.146	4.105
	Oil-SHPo	0.247	0.040	0.160	6.038	−2.632
	HPo	0.284	0.103	0.341	8.969	−2.798
R y	SHPo	0.258	0.035	0.135	19.564	0.569
	Oil-SHPo	0.277	0.091	0.312	23.549	−0.618
	HPo	0.343	0.137	0.371	30.584	−1.653

---

Due to the small viscous damping at the base area and the large restoring force associated with the high receding contact angle, the coalescence on SHPo becomes much more under-damped than other cases. On the investigated SHPo, however, the oscillation on the surface was observed only for a very short time since the coalesced droplet jumped away from the surfaces. Oil-SHPo has a smaller damping ratio than HPo mainly due to the high restoring force associated with the high receding angle as described previously. Both the damping ratio and the angular frequency decrease as the receding contact angle increases. The damping ratios of R_x and R_y on SHPo, Oil-SHPo and HPo are extracted to be 0.06, 0.160, and 0.341 and 0.135, 0.312, and 0.37. The damped angular frequencies of R_x and R_y on SHPo, Oil-SHPo and HPo were 0.167, 0.247, and 0.284 and 0.258, 0.277, and 0.343, respectively.

The resonant frequency for inviscid single spherical drops has been derived by previous studies^36,37 and is given by the following equation: 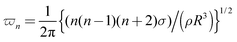, where n is the oscillation mode. For the second mode of oscillation (n = 2) and using R = 15 μm, ρ = 998 kg m⁻³ and σ = 72 mN m⁻¹ for a drop radius, the water density and surface tension, one obtains the resonant frequency of 0.165 MHz, which is close to the fitted frequency (0.167 MHz) in the R_x direction and comparable with the fitted frequency (0.258 MHz) in the R_y direction on SHPo. Note that the Rayleigh equation analysis is applied to predict the general behavior of droplets merging qualitatively since it cannot fully capture the complexities associated with droplet merging. The difference in the fitted frequency in R_x and R_y could result from the initial asymmetry of the droplet configuration, i.e., the larger R_y compared to R_x in the beginning of merging leads to the increase of the resonant frequency in the R_y direction over the R_x direction.

For other surfaces (Oil-SHPo, HPo), the larger difference between the calculation and the fitting parameter might be due to the stronger influence of the contact line as well as the complex dynamics of droplet merging. The influence of the contact angle of the substrate on the sessile drop has been investigated in the previous study, and it has been shown that the decrease of the contact angle leads to the increase of the resonant frequency when the contact angle ranges between 80° and 180°.³⁸ It agrees with the trend in the fitting frequency in the present study, which increases as the contact angle decreases.

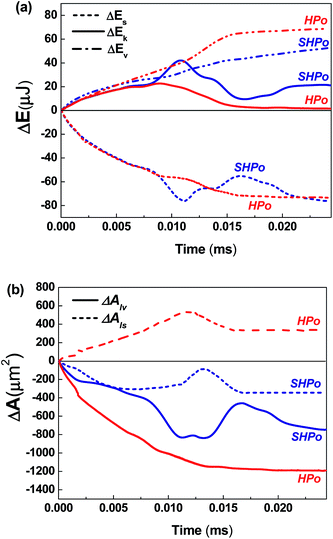
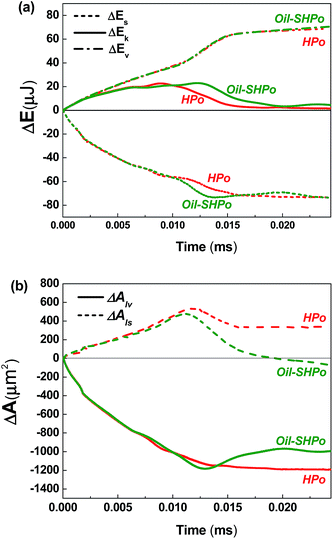
The changes in each energy term and interfacial areas during the entire coalescing processes were calculated from the simulated results. The detailed information on the calculation procedures for each energy term was described in our previous publication¹² and was not repeated here. The changes in the surface energy ΔE_s, kinetic energy ΔE_k, potential energy ΔE_p and viscous dissipations ΔE_v were plotted with the changes in the liquid–vapor ΔA_lv and liquid–solid ΔA_ls interfacial areas shown in Fig. 3 and 4, respectively. All the changes are calculated based on the initial state (ΔE = E − E₀ and ΔA = A − A₀).

Fig. 3 The changes in each energy term (a) and interfacial area (b) of the droplets merged on HPo and SHPo as a function of time during the coalescence period. All the changes are calculated based on the initial state (ΔE = E − E₀ and ΔA = A − A₀). When the coalescence starts, the base area A_ls decreases on SHPo (ΔA_ls < 0) while it increases on HPo (ΔA_ls > 0), which makes SHPo release a large amount of surface energy even with a relatively small decrease in the liquid–vapor interfacial area A_lv.

Fig. 4 The changes in each energy term (a) and the interfacial area (b) of droplets merged on HPo and Oil-SHPo as a function of time during the coalescence period. All the changes are calculated based on the initial state (ΔE = E − E₀ and ΔA = A − A₀). During the contact line receding, the base area decreases faster on Oil-SHPo due to the higher relaxation rate, which helps Oil-SHPo release a larger amount of surface energy compared to HPo.

Fig. 3a and b compare the changes in each energy term and the interfacial area of droplets merging on SHPo and HPo, respectively. Fig. 3a shows that the amount of the released surface energy ΔE_s during the initial stage of coalescence is similar for both SHPo and HPo, but the mechanism for the release is different. Even though the decrease in the liquid–vapor interfacial area A_lv of SHPo is smaller than that of HPo, the base area A_ls decreases on SHPo when the coalescence starts (ΔA_ls < 0) while it increases on HPo (ΔA_ls > 0) as shown in Fig. 3b, which makes ΔE_s similar on both surfaces. Note that the reduction of A_ls increases the amount of the released surface energy since ΔE_s = σ_lvΔA_lv + σ_lsΔA_ls + σ_svΔA_sv = σ_lv(ΔA_lv − ΔA_ls cos θ).

When the coalescence occurs on SHPo, the liquid bridge is formed between the droplets and the interfacial stress merges the droplets together with the formation of a dumbbell-shaped geometry (see Fig. 2). During the process, the base area (A_ls) of SHPo first decreases to fit the advancing contact angle. When the liquid bridges rapidly expand and hit the bottom surface, the base area increases for a short time (see the moderate peak of ΔA_ls of SHPo case shown in Fig. 3b) but the high pressure field formed at the bottom makes the merged droplet jump away from the surface, which decreases the base area again. Unlike SHPo, the liquid bridge forms in contact with the surface from the very beginning of the coalescence on HPo, which causes the initial increase in the base area.

The large ΔE_s with small A_ls allow SHPo to convert the surface energy to the kinetic energy more efficiently than HPo during the coalescence. The merged droplet on SHPo jumped away from the surface without any external force around 0.018 ms (point 4). Up to this point, SHPo converts ∼42% of the released surface energy to the kinetic energy on average, while HPo converts only ∼22% for the corresponding time period.

The changes in each energy term and the interfacial area of merging droplets on Oil-SHPo and HPo are compared in Fig. 4a and b, respectively. On both Oil-SHPo and HPo, the base area first increases as the liquid bridge forms in contact with the bottom surface at the beginning of coalescence, and then starts to decrease when the contact line relaxation starts. During the contact line receding, the base area decreases faster on Oil-SHPo than on HPo due to the higher relaxation rate of Oil-SHPo, which helps to release a larger amount of surface energy compared to HPo. Up to point 4, Oil-SHPo converts ∼30% of the released surface energy to kinetic energy on average, while HPo converts ∼22%. Fig. 3 and 4 show that the high contact line relaxation rate and the resulting rapid decrease in base area are crucial to facilitate the conversion from the surface energy to the kinetic energy, which explains how SHPo and Oil-SHPo can provide the enhanced mobility to the droplets via coalescence compared to HPo.

In summary, we investigated the hydrodynamic behaviors and energy conversion of droplets merging on HPo, SHPo, Oil-SHPo surfaces. The receding contact angle had significant effects on the contact line dynamics since the contact line pinning and viscous dissipation were more significant during the receding mode than advancing. The contact line relaxation was modeled with the damped harmonic oscillation equation instead of the previous Arrhenius model since the system became significantly under-damped as the receding contact angle increases. The damping ratio and angular frequency of merged droplets decreased with increasing receding contact angle, and the damping ratios of R_x and R_y on the invested SHPo, Oil-SHPo and HPo were found to be 0.06, 0.160, and 0.341 and 0.135, 0.312, and 0.37, respectively. The fast contact line relaxation and the resulting decrease in base area helped release a larger amount of surface energy with reducing dissipation loss, which provided the enhanced mobility to the coalescing sessile droplets. From the beginning of the coalescence to the jumping away from the surface, the coalescence on SHPo converts ∼42% of the released surface energy to the kinetic energy on average, while that on Oil-SHPo and HPo convert only ∼30% and 22% for the corresponding time period, respectively. This work clarifies the contact line relaxation and energy conversion mechanisms on water repellent surfaces with difficult wetting characteristics, and helps develop advanced water repellent condensers.

Acknowledgements

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (no. 2012R1A1A1014845) and the Ministry of Education (no. 2012R1A1A2004478).

References

1. H. G. Andrews, E. A. Eccles, W. C. E. Schofield and J. P. S. Badyal, Langmuir, 2011, 27(7), 3798.
2. J. M. Beér, Prog. Energy Combust. Sci., 2007, 33(2), 107.
3. A. D. Khawaji, I. K. Kutubkhanah and J.-M. Wie, Desalination, 2008, 221(1–3), 47.
4. N. A. Patankar, Soft Matter, 2010, 6(8), 1613.
5. L. Pérez-Lombard, J. Ortiz and C. Pout, Energ. Build., 2008, 40(3), 394.
6. J. W. Rose, Int. J. Heat Mass Transfer, 1967, 10(6), 755.
7. J. W. Rose, Proc. Inst. Mech. Eng., Part A, 2002, 216(2), 115.
8. D. W. Tanner, C. J. Potter, D. Pope and D. West, Int. J. Heat Mass Transfer, 1965, 8(3), 419.
9. J. B. Boreyko and C.-H. Chen, Phys. Rev. Lett., 2009, 103(18), 184501.
10. N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2012, 13(1), 179.
11. N. Miljkovic, R. Enright and E. N. Wang, ACS Nano, 2012, 6(2), 1776.
12. Y. Nam, H. Kim and S. Shin, Appl. Phys. Lett., 2013, 103(16), 161601.
13. R. Xiao, N. Miljkovic, R. Enright and E. N. Wang, Sci. Rep., 2013, 3, 1988.
14. C. Lee, H. Kim and Y. Nam, Langmuir, 2014, 30, 8400.
15. A. Lafuma and D. Quéré, EPL, 2011, 96(5), 56001.
16. T.-S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477(7365), 443.
17. J. Eggers, Phys. Rev. Lett., 1998, 80(12), 2634.
18. V. S. Nikolayev and D. A. Beysens, Phys. Fluids, 1997, 9(11), 3227.
19. S. G. Yiantsios and R. H. Davis, J. Colloid Interface Sci., 1991, 144(2), 412.
20. R. Narhe, D. Beysens and V. S. Nikolayev, Langmuir, 2004, 20(4), 1213.
21. D. A. B. C. Andrieu, V. S. Nikolayev and Y. Pomeau, J. Fluid Mech., 2002, 453, 427.
22. V. S. Nikolayev and D. A. Beysens, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65(4), 046135.
23. W. D. Ristenpart, P. M. McCalla, R. V. Roy and H. A. Stone, Phys. Rev. Lett., 2006, 97(6), 064501.
24. Y. Nam and Y. S. Ju, J. Adhes. Sci. Technol., 2013, 27, 2163.
25. Y. Nam, S. Sharratt, C. Byon, S.-J. Kim and Y. S. Ju, J. Microelectromech. Syst., 2010, 19(3), 581.
26. Y. Nam, S. Sharratt, G. Cha and Y. S. Ju, J. Heat Transfer, 2011, 133(10), 101502.
27. S. Shin and D. Juric, J. Comput. Phys., 2002, 180(2), 427.
28. S. O. Unverdi and G. Tryggvason, J. Comput. Phys., 1992, 100(1), 25.
29. S. Osher and R. P. Fedkiw, J. Comput. Phys., 2001, 169(2), 463.
30. C. Ybert, C. Barentin, C. Cottin-Bizonne, P. Joseph and L. Bocquet, Phys. Fluids, 2007, 19(12), 123601.
31. R. Enright, N. Miljkovic, N. Dou, Y. Nam and E. N. Wang, J. Heat Transfer, 2013, 135(9), 091304.
32. O. I. Vinogradova and G. E. Yakubov, Langmuir, 2003, 19(4), 1227.
33. C. Cottin-Bizonne, B. Cross, A. Steinberger and E. Charlaix, Phys. Rev. Lett., 2005, 94(5), 056102.
34. F. B.-W. P.-G. de Gennes and D. Quere, Capillarity and wetting phenomena, Springer, New York, 2004.
35. P. G. de Gennes, Rev. Mod. Phys., 1985, 57(3), 827.
36. P. Brunet and J. H. Snoeijer, Eur. Phys. J.: Spec. Top., 2011, 192(1), 207.
37. H. Lamb, Hydrodynamics, Cambridge University Press, Cambridge, 1975.
38. J. S. Sharp, D. J. Farmer and J. Kelly, Langmuir, 2011, 27(15), 9367.

---