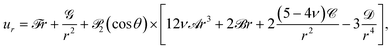Surface tension and the mechanics of liquid inclusions in compliant solids
Robert W.
Style
ab,
John S.
Wettlaufer
abc and
Eric R.
Dufresne
*a
aYale University, New Haven, CT 06520, USA. E-mail: eric.dufresne@yale.edu
bMathematical Institute, University of Oxford, Oxford, OX1 3LB, UK
cNordita, Royal Institute of Technology and Stockholm University, SE-10691 Stockholm, Sweden
First published on 1st December 2014
Abstract
Eshelby's theory of inclusions has wide-reaching implications across the mechanics of materials and structures including the theories of composites, fracture, and plasticity. However, it does not include the effects of surface stress, which has recently been shown to control many processes in soft materials such as gels, elastomers and biological tissue. To extend Eshelby's theory of inclusions to soft materials, we consider liquid inclusions within an isotropic, compressible, linear-elastic solid. We solve for the displacement and stress fields around individual stretched inclusions, accounting for the bulk elasticity of the solid and the surface tension (i.e. isotropic strain-independent surface stress) of the solid–liquid interface. Surface tension significantly alters the inclusion's shape and stiffness as well as its near- and far-field stress fields. These phenomena depend strongly on the ratio of the inclusion radius, R, to an elastocapillary length, L. Surface tension is significant whenever inclusions are smaller than 100L. While Eshelby theory predicts that liquid inclusions generically reduce the stiffness of an elastic solid, our results show that liquid inclusions can actually stiffen a solid when R < 3L/2. Intriguingly, surface tension cloaks the far-field signature of liquid inclusions when R = 3L/2. These results are have far-reaching applications from measuring local stresses in biological tissue, to determining the failure strength of soft composites.
I. Introduction
Eshelby's theory of inclusions1 provides a fundamental result underpinning a wide swath of phenomena in composite mechanics,2–5 fracture mechanics,6,7 dislocation theory,8 plasticity9,10 and even seismology.11 The theory describes how an inclusion of one elastic material deforms when it is embedded in an elastic host matrix. At an individual inclusion level, it predicts how the inclusion will deform in response to far-field stresses applied to the matrix. It also allows the prediction of the macroscopic material properties of a composite from a knowledge of its microstructure.Eshelby's theory does not include the effects of surface stresses at the inclusion/matrix boundary. However, recent work has suggested that surface stresses need to be accounted for in soft materials. This has been suggested both by theoretical models of nanoscale inclusions,12–14 and by recent experiments which have shown that surface tension (isotropic, strain-independent surface stress) can also significantly affect soft solids at micron and even millimetric scales. For example, solid capillarity limits the resolution of lithographic features,15–18 drives pearling and creasing instabilities,19–22 causes the Young–Dupré relation to break down for sessile droplets,23–28 and leads to a failure of the Johnson–Kendall–Roberts theory of adhesion.29–33 Of particular relevance are our recent experiments embedding droplets in soft solids, where we found that Eshelby's predictions could not describe the response of inclusions below a critical, micron-scale elastocapillary length.34 A similar break down was also seen in recent experiments that embedded bubbles in soft, elastic foams.35
To apply Eshelby's theory to a broad-class of mechanical phenomena in soft materials, we need to reformulate it to account for surface tension. Here, we derive analytic expressions for the deformation of individual inclusions, the deformation and stress fields around the inclusions, and the elastic moduli of soft composites. Our approach builds upon previous theoretical works that have: focused on strain-dependent surface stresses14,36–39 (which are relevant to nanoinclusions in stiffer materials, but not for softer materials such as gels40), only considered isotropic loadings,12 used incorrect boundary conditions13 (cf.41), or only considered incompressible solids and employed a dipole approximation to calculate composite properties.42
II. Stretching individual inclusions
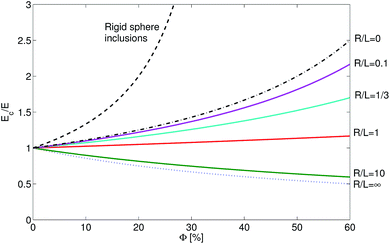
We begin by considering how surface tension affects Eshelby's solution for the deformation of individual inclusions embedded in elastic solids subjected to far-field stresses.1 We consider an isolated, incompressible, spherical droplet of radius R embedded in a linear-elastic solid that is deformed by a constant uniaxial far-field stress, as shown in Fig. 1. The displacement field in the solid satisfies| (1 − 2ν) ∇2u + ∇(∇·u) = 0, | (1) |
 | ||
Fig. 1 Schematic diagram for uniaxial stretching of a single, incompressible droplet embedded in a linear-elastic solid. ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the length of the deformed droplet in the stretch direction. is the length of the deformed droplet in the stretch direction. | ||
For far-field boundary conditions, the stress in the solid σ is given by the applied uniaxial stress σzz = σ∞, σxx = σyy = 0 in cartesian coordinates. Stress and strain are related by
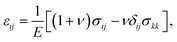 | (2) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (equal to twice the mean curvature, or the sum of the principal curvatures) via
(equal to twice the mean curvature, or the sum of the principal curvatures) viaσ·n = −pn + ϒ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) n n | (3) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) in terms of surface displacements are given in Appendix A – these are different from the expressions used in ref. 13 which ignored inclusion deformation and assumed that
in terms of surface displacements are given in Appendix A – these are different from the expressions used in ref. 13 which ignored inclusion deformation and assumed that ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = 2ϒ/R.14
= 2ϒ/R.14
We exploit symmetry and solve the problem in spherical polar co-ordinates by adopting as an ansatz the solution
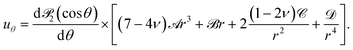 | (4) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 2 is the Legendre polynomial of order 2, and
2 is the Legendre polynomial of order 2, and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) through
through ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) will be determined from the boundary conditions.
will be determined from the boundary conditions.
Applying the far-field strain condition, we find that ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 0,
= 0, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = (1 − 2ν)εzz∞/3 and
= (1 − 2ν)εzz∞/3 and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = (1 + ν)εzz∞/3. Droplet incompressibility requires that
= (1 + ν)εzz∞/3. Droplet incompressibility requires that 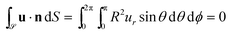 , where
, where ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is the boundary of the stretched droplet, and the area integral is evaluated using results from differential geometry summarised in Appendix A. This gives
is the boundary of the stretched droplet, and the area integral is evaluated using results from differential geometry summarised in Appendix A. This gives ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) = −(1 − 2ν)R3εzz∞/3. Finally, by applying the boundary condition (3) using eqn (2) to covert stresses to strains and displacements we obtain
= −(1 − 2ν)R3εzz∞/3. Finally, by applying the boundary condition (3) using eqn (2) to covert stresses to strains and displacements we obtain
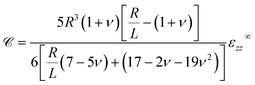 | (5) |
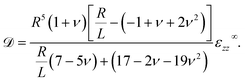 | (6) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) −
− ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) , eqn (4) gives us the exact displacement solutions. These also allow calculation of stresses in the solid: we convert displacements to strains (e.g.ref. 45) and then use eqn (2) to find the non-zero stress components σrr, σrθ, σθθ and σϕϕ.
, eqn (4) gives us the exact displacement solutions. These also allow calculation of stresses in the solid: we convert displacements to strains (e.g.ref. 45) and then use eqn (2) to find the non-zero stress components σrr, σrθ, σθθ and σϕϕ.
While these results are for uniaxial stress, they are readily extended to provide the solution for general far-field stresses. In the appropriate coordinate frame, the far-field stress matrix is diagonalisable so the only non-zero far-field stresses are σ1, σ2 and σ3. Then, from linearity of the governing equations, we can calculate the resulting displacements by simply summing the solutions for uniaxial far-field stresses σ1, σ2 and σ3.
A. Inclusion shape
While Eshelby's results are scale-free, surface tension makes the response of a liquid inclusion strongly size-dependent. We derive the equations describing the inclusion shapes in Appendix B. For large droplets, R ≫ L, the fluid droplet deforms more than the surrounding solid. In this limit, the droplet shape only depends on σ∞/E = εzz∞ and ν, in agreement with Eshelby's theory.1 However, as R approaches L, high interfacial curvatures are suppressed by surface tension. For R ≪ L, ur(R,θ) = 0 and the droplets remain spherical. This is visualized in Fig. 2 for a uniaxially-stressed solid where the far-field stress and strain are σ∞ = 0.3E and εzz∞ = 0.3, respectively. Here, the radial and polar displacements in the top two rows are measured relative to the far-field displacement field: ur∞ =![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) r + 2P2(cos
r + 2P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)
θ)![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) r and uθ∞ = P2′(cos
r and uθ∞ = P2′(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)
θ)![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) r.
r.
Changes in droplet shape are captured with an effective droplet strain εd = (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − 2R)/R = 2ur(R,0)/R, where
− 2R)/R = 2ur(R,0)/R, where ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the long-axis of the droplet. For an incompressible solid, eqn (4) gives
is the long-axis of the droplet. For an incompressible solid, eqn (4) gives
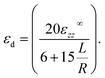 | (7) |
This is plotted in Fig. 3(a). In both extremes of droplet size, the droplet shape is independent of size. In the capillary-dominated regime (R ≪ L) the droplet stays spherical (εd = 0). In the large-droplet limit (R ≫ L), surface tension does not play a role, and Eshelby's results are recovered (εd = 10εxx∞/3). There is a smooth cross-over between these limits in the vicinity of R ∼ L. Surface tension makes significant changes to droplet shape for droplet radii up to about 100L.
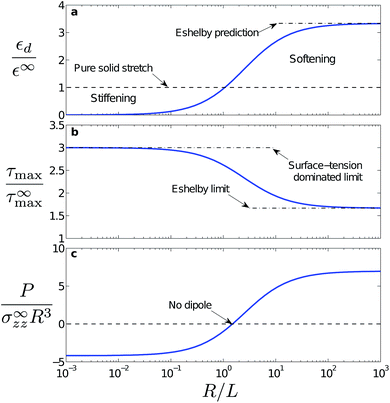 | ||
Fig. 3 Liquid inclusion characteristics as a function of size R/L for inclusions in an incompressible solid with an applied uniaxial far-field stress as shown in Fig. 1 (a) Droplet strain, εd = (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − 2R)/R divided by far-field strain ε∞ only depends on R/L. When R/L ≪ 1, surface tension dominates and there is no droplet deformation. When R/L ≫ 1, surface tension is negligible and the shape prediction is that of classical Eshelby theory – given by the dash-dotted line. The dashed line shows the material stretch, ( − 2R)/R divided by far-field strain ε∞ only depends on R/L. When R/L ≪ 1, surface tension dominates and there is no droplet deformation. When R/L ≫ 1, surface tension is negligible and the shape prediction is that of classical Eshelby theory – given by the dash-dotted line. The dashed line shows the material stretch, (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − 2R)/R = ε∞. (b) The shear-stress concentration factor at the inclusion tip (r = R, θ = 0). This corresponds to the highest shear stress in the solid around the inclusion (see Fig. 2, bottom row). Dash-dotted lines show surface-tension dominated and Eshelby limits: τmax/τmax∞ = 3, 5/3 respectively. (c) The far-field dipole caused around the inclusion. Note that this dipole changes sign at R = 1.5L, indicating the transition between inclusion stiffening and inclusion softening of the composite. − 2R)/R = ε∞. (b) The shear-stress concentration factor at the inclusion tip (r = R, θ = 0). This corresponds to the highest shear stress in the solid around the inclusion (see Fig. 2, bottom row). Dash-dotted lines show surface-tension dominated and Eshelby limits: τmax/τmax∞ = 3, 5/3 respectively. (c) The far-field dipole caused around the inclusion. Note that this dipole changes sign at R = 1.5L, indicating the transition between inclusion stiffening and inclusion softening of the composite. | ||
Although we only consider the uniaxial stress case above, the results can be generalised to the more general case of triaxial far-field strains. For example, for an incompressible solid in plane stress conditions (σ1, σ2 ≠ 0, σ3∞ = 0, as in our recent experiments34), we calculate the solution by the summation technique described earlier. This gives the length of the droplet in the 1-direction as
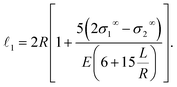 | (8) |
We recently compared this result to experimental measurements of individual liquid inclusions in soft, stretched solids. We found good agreement over a wide range of droplet sizes, substrate stiffnesses and applied strains.34
B. Stress focussing by inclusions
The macroscopic strength of composites can be reduced due to stress focusing by inclusions. According to the Tresca yield condition, the solid will yield when the shear stress exceeds a critical value τc. Fig. 2 (bottom row) shows the maximum shear stress, τmax, for an incompressible solid with a uniaxial far-field stress for various values of R/L. The maximum shear stress is greatest at the tip of the inclusion, and the value there increases significantly as R is reduced below L. In fact at the inclusion tip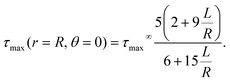 | (9) |
This is plotted in Fig. 3(b). There is a significant increase in shear-stress concentration as surface tension becomes more important with τmax(R,0) increasing from 5τmax∞/3 when R ≫ L, to 3τmax∞ when R ≪ L.
These results suggest that surface tension could weaken a soft composite when inclusions fall below a size ∼100L. This also means that the applied strain at which yielding is expected to occur is no longer independent of the size of the liquid inclusion, as would be predicted from Eshelby's results, but depends on the parameter R/L. These results hint at the potential role of surface tension for fracture mechanics in soft materials where a critical value is the crack-tip stress. The capillary-induced stress focussing seen here shows how surface tension could potentially significantly alter this value.46
C. Dipole signature of inclusions
At finite concentrations, inclusions interact at a distance through their far-field stresses. This can be important for determining mechanical properties of dilute composites (e.g.ref. 42 and 47). The far-field solutions are conveniently expressed by a multipole expansion.Here, inclusions appear as force dipoles in the far-field. From eqn (4), we find the leading order terms in the inclusion-induced displacements (ur − ur∞, uθ − uθ∞) are proportional to 1/r2. This corresponds to a force dipole in an elastic body
| Pij = Pẑiẑj + Peδij, | (10) |
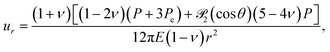 | (11) |
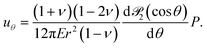 | (12) |
Thus, from comparison with eqn (4),
P = 24![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) πE(1 − ν)/(1 + ν), πE(1 − ν)/(1 + ν), | (13) |
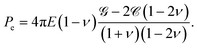 | (14) |
The first dipole, P, is a force dipole of two point forces on the z-axis which also act along the z-axis – i.e. parallel to the applied far-field stress. The second term Pe is an isotropic centre of expansion.48 When ν = 1/2, the displacement field due to Pe vanishes, and P = 8π![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) E.
E.
Intriguingly, the dipole strength, P, can be positive or negative. Fig. 3(c) shows the normalised dipole strength P/σ∞R3 of a liquid inclusion in incompressible solid with a uniaxial applied stress. For large inclusions (R > 1.5L), P > 0 and the dipole is a pair of outward pointing point forces. This increases solid displacements – consistent with a weak point in the solid. For small inclusions (R < 1.5L), P < 0 and so the dipole opposes the applied far-field stress, acting like a stiff point in the solid. The sign switch is clearly seen in the displacement fields of Fig. 2. At R = 1.5L, the inclusion has no effect on the far-field elasticity field and is effectively invisible (e.g., see ref. 49).
III. Soft composites
We have shown that the surface tension of a small liquid droplet in a soft linear elastic solid resists deformation imposed by far-field stretch. Therefore, we expect that the dispersion of small liquid droplets within a solid can increase its apparent macroscopic stiffness. We calculate the effective Young's modulus Ec of a composite containing a dilute quantity of monodisperse droplets by following Eshelby's original approach.1,13 First, we calculate the excess energy W due to the presence of a single inclusion when a solid is uniaxially stretched. Then, we consider uniaxial stretching of a dilute composite of noninteracting inclusions. If the applied stress is σzz = σ∞, the strain energy density of the composite is![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = (σ∞)2/(2E) + WΦ/(4πR3/3) = (σ∞)2/(2Ec), = (σ∞)2/(2E) + WΦ/(4πR3/3) = (σ∞)2/(2Ec), | (15) |
The excess energy due to the presence of a single elastic inclusion in a uniaxially-stressed solid is
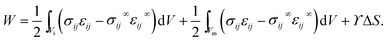 | (16) |
Here we assume that the inclusion is an elastic solid for generality – the droplet is the limiting case of zero shear modulus.
The volumes of the elastic matrix outside of the inclusion and the inclusion Vm and Vi, respectively, the far-field stresses/strains are σij∞ and εij∞ respectively, and the change in surface area of the droplet upon stretching is ΔS. Using the divergence theorem, the stress boundary condition (3), and the fact that in the far-field, σij∞ = σij,
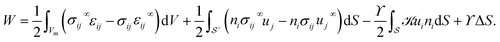 | (17) |
Integration on the matrix side of the droplet surface ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is denoted by
is denoted by ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) +. From eqn (2), the first term is zero, so W depends only upon displacements and stresses at the droplet surface. Using our earlier results (e.g.eqn (4)), along with second-order (in the displacement) versions of the expressions for n,
+. From eqn (2), the first term is zero, so W depends only upon displacements and stresses at the droplet surface. Using our earlier results (e.g.eqn (4)), along with second-order (in the displacement) versions of the expressions for n, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , dS and ΔS shown in Appendix A, we obtain W for the case of a uniaxial far-field stress σ∞:
, dS and ΔS shown in Appendix A, we obtain W for the case of a uniaxial far-field stress σ∞:
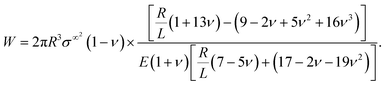 | (18) |
Finally, from eqn (15),
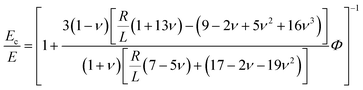 | (19) |
For an incompressible solid ν = 1/2 and we have
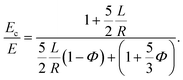 | (20) |
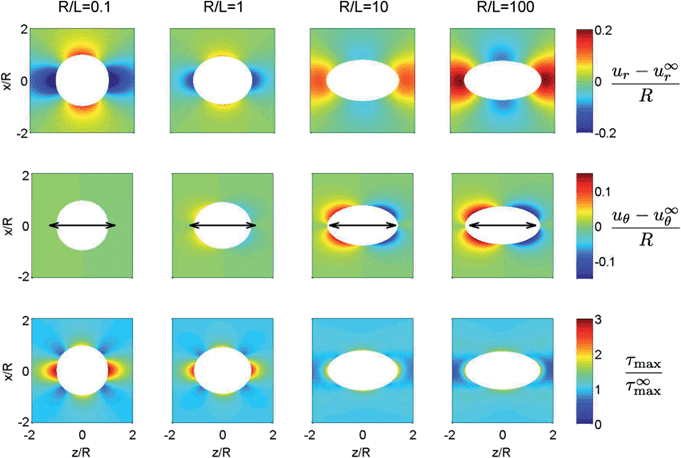
Fig. 4 plots the results of eqn (20) and shows the dramatic influence of capillarity on soft composite stiffness. When surface tension is negligible (R ≫ L), the composite becomes more compliant as the density of droplets increases – in exact agreement with Eshelby's prediction of Ec/E = (1 + 5Φ/3)−1 (dotted curve), and qualitatively agreeing with other classical composite laws (e.g.ref. 2 and 3). However Eshelby's predictions break down when R ≲ 100L. In fact, when R < 1.5L, increasing the density of droplets causes the solid to stiffen, consistent with the dipole sign-switching seen earlier. In the surface-tension dominated limit, R ≪ L, the droplets stay spherical, and we find the maximum achievable composite stiffness Ec = E/(1 − Φ) (dash-dotted curve). Note that the droplets do not behave like rigid particles in this limit, for which Ec = E/(1 − 5Φ/2) (ref. 1) (dashed curve). Although the droplets remain spherical due to capillarity, there are non-zero tangential displacements, unlike the case of rigid particles.
These results agree with experiments. Recently, we made soft composites of glycerol droplets embedded in soft silicone solids. In quantitative agreement with the theory, we saw stiffening of solids by droplets in compliant solids, and softening in stiffer solids.34 In the dilute limit (Φ → 0), eqn (20) matches with recent theoretical predictions (derived using the dipole approximation for inclusions in incompressible solids) that describe experimental measurements of shear moduli of emulsions containing monodisperse bubbles.35,42
IV. Conclusions
We have modified Eshelby's inclusion theory to include surface tension for liquid inclusions in a linear-elastic solid, giving both the microscopic behaviour and the macroscopic effects of inclusions in composites. We have shown that surface tension stiffens small inclusions, and focusses shear stresses at the inclusion tips. Thus composites with small, capillary-dominated inclusions will be stiffer but may be weaker. This stress-concentration illustrates the potentially strong role of surface tension in the failure of soft-solids, highlighting the relevance of this work to emerging fields like fracture mechanics and plasticity in soft materials (e.g.ref. 46, 50 and 51).Inclusions with surface tension can be viewed, at leading order, as elastic dipoles in a solid. The sign of the dipole captures the stiffening behaviour due to capillarity. Treating inclusions as dipoles also offers a simplified picture of inclusions that give the interactions between features in elastic bodies, and can streamline calculations of bulk composite properties via standard theories. The analytic theory presented for bulk composite stiffness, which incorporates the entire elastic field around inclusions, validates the dipole approach by recovering previous results for incompressible materials in the limit of dilute composites.35,42
Our work is applicable to a wide variety of soft material problems. Most obviously it can be directly applied to composites comprising soft materials such as gels and elastomers. As a specific example, we have shown how surface tension effects allow elastic cloaking, with inclusions of size R = 1.5L being mechanically invisible. Our work also has interesting uses in mechanobiology, as biological tissue is predominantly soft. For example, a recent study embedded droplets in biological tissue and observed their deformations to extract local anisotropic stresses.52 The coupling between microscopic and macroscopic stress also plays an important role in the tensional homeostasis of soft tissues.53,54 Although we have only considered liquid inclusions here our analysis can be repeated for more general soft composites with elastic inclusions in place of liquid droplets. In that case, we expect that similar capillary effects to those presented here will be seen whenever R ≲ 100ϒ/Ei, 100ϒ/Em with Ei/Em being the inclusion/matrix stiffnesses respectively.
Appendix
A. Differential geometry
To calculate the effect of surface tension on the shape of a droplet embedded in a soft solid, we need expressions for the normal to the droplet surface, its curvature, and surface area in terms of the surface displacements. We consider an initially spherical droplet with the position of its surface given by x = (R,0,0), and apply a uniaxial stretch so that x →x′ = (R + ur, uθ, 0). From axisymmetry, the ur, uθ are independent of the angle ϕ.We calculate the normal to the droplet surface, n, by taking the cross-product of the surface tangent vectors, ∂x′/∂θ and ∂x′/∂ϕ,55
 | (21) |
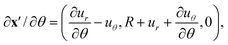 | (22) |
∂x′/∂ϕ = (0, 0, (R + ur)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + uθ θ + uθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). θ). | (23) |
At leading order in u we find
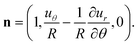 | (24) |
The droplet surface curvature, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , can be calculated from differential geometry using the first and second fundamental forms:55
, can be calculated from differential geometry using the first and second fundamental forms:55
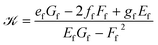 | (25) |
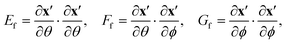 | (26) |
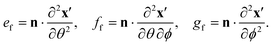 | (27) |
Thus, at leading order in u,
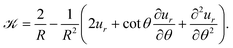 | (28) |
Using the results above, we also obtain the area element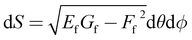 .55 At leading order in u,
.55 At leading order in u,
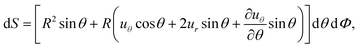 | (29) |
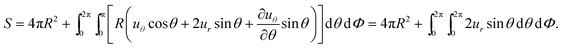 | (30) |
B. The shape of a uniaxially stretched droplet
We determine the shape of a uniaxially-stretched droplet by using the calculated expressions for![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) −
− ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) in eqn (4) to obtain the surface displacements:
in eqn (4) to obtain the surface displacements: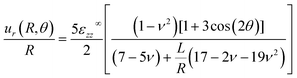 | (31) |
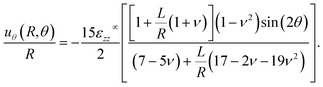 | (32) |
When L ≫ R, we see that radial displacements vanish, and the inclusions remain spherical. In the opposite limit, R ≫ L, the inclusion shape becomes independent of its size, as predicted by Eshelby's results.
Acknowledgements
We thank Peter Howell and Alain Goriely for helpful conversations. We are grateful for funding from the National Science Foundation (CBET-1236086) to ERD, the Yale University Bateman Interdepartmental Postdoctoral Fellowship to RWS and the John Simon Guggenheim Foundation, the Swedish Research Council, and a Royal Society Wolfson Research Merit Award to JSW.References
- J. D. Eshelby, Proc. R. Soc. London, Ser. A, 1957, 241, 376 CrossRef.
- Z. Hashin and S. Shtrikman, J. Mech. Phys. Solids, 1963, 11, 127 CrossRef.
- T. Mori and K. Tanaka, Acta Metall., 1973, 21, 571 CrossRef.
- R. Hill, J. Mech. Phys. Solids, 1963, 11, 357 CrossRef.
- B. Budiansky, J. Mech. Phys. Solids, 1965, 13, 223 CrossRef.
- J. R. Rice, J. Appl. Mech., 1968, 35, 379 CrossRef.
- B. Budiansky and R. J. O'Connell, Int. J. Solids Struct., 1976, 12, 81 CrossRef.
- T. Mura, Micromechanics of Defects in Solids, vol. 3, Springer, 1987 Search PubMed.
- J. Hutchinson, Proc. R. Soc. London, Ser. A, 1970, 319, 247 CrossRef CAS.
- M. Berveiller and A. Zaoui, J. Mech. Phys. Solids, 1978, 26, 325 CrossRef CAS.
- H. Kanamori and D. L. Anderson, Bull. Seismol. Soc. Am., 1975, 65, 1073 Search PubMed.
- P. Sharma and S. Ganti, J. Appl. Mech., 2004, 71, 663 CrossRef.
- F. Yang, J. Appl. Phys., 2004, 95, 3516 CrossRef CAS PubMed.
- H. L. Duan, J. Wang, Z. P. Huang and B. L. Karihaloo, Proc. R. Soc. A, 2005, 461, 3335 CrossRef.
- C. Y. Hui, A. Jagota, Y. Y. Lin and E. J. Kramer, Langmuir, 2002, 18, 1394 CrossRef CAS.
- A. Jagota, D. Paretkar and A. Ghatak, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051602 CrossRef.
- S. Mora, C. Maurini, T. Phou, J.-M. Fromental, B. Audoly and Y. Pomeau, Phys. Rev. Lett., 2013, 111, 114301 CrossRef.
- D. Paretkar, X. Xu, C.-Y. Hui and A. Jagota, Soft Matter, 2014, 10, 4084 RSC.
- S. Mora, T. Phou, J.-M. Fromental, L. M. Pismen and Y. Pomeau, Phys. Rev. Lett., 2010, 105, 214301 CrossRef.
- S. Mora, M. Abkarian, H. Tabuteau and Y. Pomeau, Soft Matter, 2011, 7, 10612 RSC.
- A. Chakrabarti and M. K. Chaudhury, Langmuir, 2013, 29, 6926 CrossRef CAS PubMed.
- D. L. Henann and K. Bertoldi, Soft Matter, 2014, 10, 709 RSC.
- R. W. Style and E. R. Dufresne, Soft Matter, 2012, 8, 7177 RSC.
- R. W. Style, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 066103 CrossRef.
- R. W. Style, Y. Che, S. J. Park, B. M. Weon, J. H. Je, C. Hyland, G. K. German, M. P. Power, L. A. Wilen, J. S. Wettlaufer and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12541 CrossRef CAS PubMed.
- N. Nadermann, C.-Y. Hui and A. Jagota, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10541 CrossRef CAS PubMed.
- J. B. Bostwick, M. Shearer and K. E. Daniels, Soft Matter, 2014, 10, 7361 RSC.
- S. Karpitschka, S. Das, B. Andreotti and J. Snoeijer, Dynamic Contact Angle of a Soft Solid, 2014, arXiv:arXiv:1406.5547 [physics.flu-dyn].
- K. Johnson, K. Kendall and A. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301 CrossRef CAS.
- R. W. Style, C. Hyland, R. Boltyanskiy, J. S. Wettlaufer and E. R. Dufresne, Nat. Commun., 2013, 4, 2728 Search PubMed.
- T. Salez, M. Benzaquen and E. Raphael, Soft Matter, 2013, 9, 10699 RSC.
- X. Xu, A. Jagota and C.-Y. Hui, Soft Matter, 2014, 10, 4625 RSC.
- Z. Cao, M. J. Stevens and A. V. Dobrynin, Macromolecules, 2014, 47, 3203 CrossRef CAS.
- R. W. Style, R. Boltyanskiy, B. Allen, K. E. Jensen, H. P. Foote, J. S. Wettlaufer and E. R. Dufresne, to appear in Nature Phys., preprint available at arXiv:1407.6424, 2014.
- L. Ducloue, O. Pitois, J. Goyon, X. Chateau and G. Ovarlez, Soft Matter, 2014, 10, 5093 RSC.
- H. L. Duan, X. Yi, Z. P. Huang and J. Wang, Mech. Mater., 2007, 39, 81 CrossRef PubMed.
- H. L. Duan, X. Yi, Z. P. Huang and J. Wang, Mech. Mater., 2007, 39, 94 CrossRef PubMed.
- S. Brisard, L. Dormieux and D. Kondo, Comput. Mater. Sci., 2010, 50, 403 CrossRef CAS PubMed.
- S. Brisard, L. Dormieux and D. Kondo, Comput. Mater. Sci., 2010, 48, 589 CrossRef CAS PubMed.
- C.-Y. Hui and A. Jagota, Langmuir, 2013, 29, 11310 CrossRef CAS PubMed.
- H. Duan, J. Wang, Z. Huang and B. Karihaloo, J. Mech. Phys. Solids, 2005, 53, 1574 CrossRef PubMed.
- J. F. Palierne, Rheol. Acta, 1990, 29, 204 CrossRef CAS.
- J. Wang, H. Duan, Z. Huang and B. Karihaloo, Proc. R. Soc. A, 2006, 462, 1355 CrossRef.
- R. W. Style, R. Boltyanskiy, G. K. German, C. Hyland, C. W. MacMinn, A. F. Mertz, L. A. Wilen, Y. Xu and E. R. Dufresne, Soft Matter, 2014, 10, 4047 RSC.
- L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, Theory of Elasticity, Pergamon Press, London, 3rd edn, vol. 7, 1986 Search PubMed.
- T. Liu, R. Long and C.-Y. Hui, Soft Matter, 2014, 10, 7723 RSC.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327 CrossRef CAS.
- A. Lurie and A. Belyaev, Theory of Elasticity, Springer, Berlin, 2005, p. 246 Search PubMed.
- G. W. Milton, M. Briane and J. R. Willis, New J. Phys., 2006, 8, 248 CrossRef.
- S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963 RSC.
- J. Cui, C. H. Lee, A. Delbos, J. J. McManus and A. J. Crosby, Soft Matter, 2011, 7, 7827 RSC.
- O. Campàs, T. Mammoto, S. Hasso, R. A. Sperling, D. O'Connell, A. G. Bischof, R. Maas, D. A. Weitz, L. Mahadevan and D. E. Ingber, Nat. Methods, 2014, 11, 183 CrossRef PubMed.
- R. Brown, R. Prajapati, D. McGrouther, I. Yannas and M. Eastwood, J. Cell. Physiol., 1998, 175, 323 CrossRef CAS.
- A. Zemel, I. Bischofs and S. Safran, Phys. Rev. Lett., 2006, 97, 128103 CrossRef CAS.
- E. Abbena, S. Salamon and A. Gray, Modern Differential Geometry of Curves and Surfacesand with Mathematica, Taylor & Francis, 2006 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |