Rapid determination of polarizability exaltation in fullerene-based nanostructures
M.
Swart
ab and
P. Th.
van Duijnen
c
aInstitució Catalana de Recerca i Estudis Avançats (ICREA), Pg. Lluís Companys 23, 08010 Barcelona, Spain. E-mail: marcel.swart@icrea.cat
bInstitut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, Campus Montilivi, 17071 Girona, Spain
cTheoretical Chemistry, Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: p.t.van.duijnen@rug.nl
First published on 5th November 2014
Abstract
The polarizability of fullerenes may be used in the design of nanostructures with specific properties and behaviour. Recent studies have been reported on the exaltation of polarizability, for which costly quantum-mechanical studies were needed. Here we report the results of Thole's polarizability model that correctly predicts the exaltation effect in a matter of seconds.
The C60 fullerene and its derivatives are widely being explored as building blocks for nanotechnology,1 such as in the design of photovoltaics2 or for charge-transfer states in organic semiconductors.1,2 One important property for these nanostructures is the polarizability, which determines the response to an external electric field. For this reason, Sabirov3,4 studied the polarizability of the C60 fullerene monomer and oligomers5,6 (n = 2–5) using Density Functional Theory (DFT) methods (see Fig. 1 for the structures).
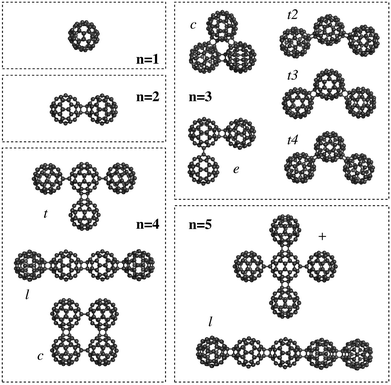 | ||
| Fig. 1 Nanostructures based on C60 fullerene oligomers (taken from ref. 3). | ||
He showed that for these oligomers the polarizability is not additive, the so-called exaltation of polarizability. For example, given in Table 1 are the calculated (DFT) molecular polarizabilities for C60 and its oligomers. Comparing the dimer with the monomer, one can note that the polarizability of the dimer (180.03 Å3) is 217.6% the value of the monomer (82.73 Å3). Of course, if the polarizability would have been additive, the dimer value should have been exactly twice as large as that of the monomer.
| DFT | Exalt.d | Thole | (dev.e) | Jensen | (dev.e) | |
|---|---|---|---|---|---|---|
| a In Å3. b PBE/3ζ, from ref. 3. c This work (in parentheses: relative deviation, %). d Exaltation of DFT molecular polarizability of (C60)n compared to n C60 monomers ([αn/nα1]; %). e Relative deviation (%) compared to DFT. f Used to obtain atomic polarizability for carbon. | ||||||
| C60 | 82.7 | 82.73 | (0.0f) | 82.73 | (0.0f) | |
| (C60)2 | 180.0 | +8.8 | 180.15 | (+0.1) | 179.08 | (−0.5) |
| e-(C60)3 | 276.4 | +11.4 | 276.32 | (0.0) | 274.18 | (−0.8) |
| t2-(C60)3 | 285.2 | +15.0 | 285.79 | (+0.2) | 282.92 | (−0.8) |
| t3-(C60)3 | 282.3 | +13.8 | 282.73 | (+0.2) | 280.08 | (−0.7) |
| t4-(C60)3 | 279.6 | +12.7 | 280.41 | (+0.3) | 277.88 | (−0.6) |
| c-(C60)3 | 281.2 | +13.3 | 275.50 | (−2.0) | 275.37 | (−2.0) |
| l-(C60)4 | 397.4 | +20.1 | 400.33 | (+0.7) | 394.91 | (−0.6) |
| c-(C60)4 | 376.4 | +13.8 | 375.79 | (−0.2) | 372.92 | (−0.9) |
| t-(C60)4 | 383.6 | +15.0 | 381.09 | (−0.7) | 376.99 | (−1.7) |
| l-(C60)5 | 510.7 | +23.5 | 515.35 | (+0.9) | 507.29 | (−0.7) |
| +-(C60)5 | 480.1 | +16.1 | 480.57 | (+0.1) | 475.54 | (−0.9) |
In the title of his 2013 paper,3 Sabirov expressed his surprise of the enhancement of the polarizability of the C60 dimer. However, almost a century ago Silberstein7,8 derived, analytically, expressions for the linear response of two classical polarizable spheres:
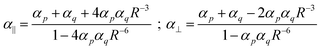 | (1) |
Eqn (1) shows directly that polarizabilities are not additive, and that even for isotropic starting polarizabilities, the total polarizability will be anisotropic (α∥ ≠ α⊥): we see that α∥ is larger, and α⊥ smaller than the sum of the separate polarizabilities. The relative increase comes from the positive feedback due to the head-to-tail orientation of the induced dipoles on p and q if the inducing field is parallel to the axis; in contrast, in the perpendicular direction the two parallel induced dipoles lead to negative feedback. Importantly, from eqn (1) we can see that if the distance R starts to approach the critical distance (4αpαq)1/6 the parallel component (α∥) goes to infinity and becomes negative for smaller distances. This unphysical behavior is referred to as the polarization catastrophe.
Let us first start with a simple model system. In the case of two equal polarizabilities, αp = αq = α, eqn (1) can be transformed into
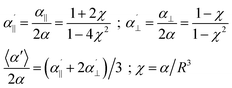 | (2) |
| R min | R | χ | α ∥/2α | α ⊥/2α | 〈α′〉/2α |
|---|---|---|---|---|---|
| a α = 1.0. | |||||
| 2.0 | 2.00 | 0.125 | 1.333 | 0.889 | 1.04 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| R/R crit (R crit ∼ 1.2599) | |||||
| 1.00006 | 1.26 | 0.4999 | 5320.1 | 0.667 | 1773.8 |
| 1.1 | 1.39 | 0.376 | 4.02 | 0.727 | 1.82 |
| 1.2 | 1.51 | 0.289 | 2.37 | 0.776 | 1.31 |
| 1.4 | 1.76 | 0.182 | 1.57 | 0.846 | 1.09 |
| 1.6 | 2.02 | 0.122 | 1.323 | 0.891 | 1.04 |
| 1.8 | 2.27 | 0.086 | 1.207 | 0.921 | 1.02 |
| 2.0 | 2.52 | 0.062 | 1.143 | 0.941 | 1.01 |
| 2.2 | 2.77 | 0.047 | 1.104 | 0.955 | 1.00 |
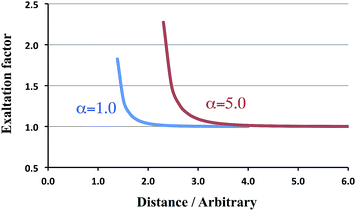
The following rows treat the more esoteric cases of ‘spheres’ or charge distributions that may overlap. For a distance of 1.26, which is slightly larger than Rcrit = (4α2)1/6, the α∥ component (in italics) is already past the singularity and returns from +∞. For larger distances the exaltation factor decreases until it becomes unity. We have collected in Fig. 2 the corresponding trend, together with the results for α = 5.0. From this figure it is immediately obvious that for the larger polarizability the exaltation factor increases too.
In order to prevent the polarization catastrophe, Thole developed a damping procedure9 for the dual-particle interaction to keep the resulting polarizability finite, based on previous work by e.g. Applequist.10,11 In an arbitrary collection of polarizabilities, the jth component of the induced dipole at a specific point p is given by:
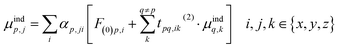 | (3) |
The induced dipole at a polarizable particle p depends on the external electric field F(0), and the fields of all elsewhere induced dipoles (t(2)). This interaction term t(2) is the usual (dipole-field) interaction tensor between two dipoles: 3rirj/R5 − δij/R3 (where ri and rj are components of the distance vector between points p and q, and R its length). We can rewrite eqn (3) into matrix form, by first bringing the polarizabilities (A) to the left-hand side, A−1M = F0 + T(2)M, and then the term with the interaction tensors T(2) as well, to give [A−1 − T(2)]M = F(0). By taking the inverse of the term in square brackets (B = [A−1 − T(2)]−1), we finally obtain a matrix equation that directly gives the induced dipoles as M = BF(0). The B-matrix therefore gives the molecular response to an electric field, i.e. it corresponds to the supermolecular polarizability, and can be reduced to a normal 3 × 3 polarizability tensor. Note that the t(2)-tensors contain only geometrical information. It is through the mutual orientation and distances that the polarizable particles respond locally differently in various parts of the structure.
The damping factors, to account for overlapping charge densities, lead to modified t(2) tensors,9,12 which in the end makes that the fullerene oligomers show alterations in the molecular polarizability values. The basic building block with which the large variation in polarizabilities can be reproduced, however, needs only one parameter per atom type: its polarizability in vacuo—αp in eqn (3)—which is independent of its ‘chemical environment’. The latter is in all cases absorbed in the T-blocks of B.
Recently we showed that by using Thole's model we obtained not only the molecular polarizabilities of small silicon clusters (Sin, with n = 3–10), but also the collective response of nanosized “bulk” (Si4950) systems.13 Hence, apart from expensive time-dependent DFT (TD-DFT)14,15 or Hessian calculations, the molecular polarizability can also be obtained rapidly and accurately using Thole's polarizability model.12,16
In order to apply this model to these oligomer fullerenes, we need an appropriate atomic polarizability. Therefore we have taken the molecular structure and polarizability of C60 from Sabirov's study3 and fitted the atomic polarizability of carbon (αC 16.002 a.u. = 2.3713 Å3), together with our fixed screening length of 2.1304 (a universal parameter for the width of the damping).12 Using this atomic polarizability we have computed the molecular polarizabilities of all fullerene oligomers of Fig. 1 using Thole's model. The results are given in Table 1.
The first thing that should be noticed is the remarkably excellent accuracy of Thole's model. For most of the oligomer polarizabilities we have been able to compute the molecular polarizability with an accuracy of 1% or often even much better. The only structure where the deviation is a little bit larger is c-(C60)3, but even then the deviation of 2.0% is very acceptable (and still small compared to the exaltation percentage of 13.3% with respect to the C60 monomer). Therefore, once again this is proof of the excellent behaviour of Thole's model.9,12 We also included the results with Jensen's dipole interaction model17,18 (IM-ERF, with αC 9.108 a.u. and ΦC 0.083; the polarizability was fitted here to reproduce the C60 value). Although the obtained polarizabilities are slightly different from the ones with Thole's model, the general trend is the same: we obtain very good agreement with the DFT values, both for the polarizability of the individual molecules and the corresponding exaltation. One aspect in the successful modeling of these nanostructures is of course the charge transfer that may occur from one fullerene to another (absent for the nanostructures studied here). There are several sophistications2,19–23 that can be used on top of the polarizability models used here to take this charge transfer into account.
Finally, an important thing to notice here is that the exaltation of the polarizability results directly from the structure of the fullerenes, or more specifically, the mutual orientation of the different polarizable particles. This brings us back to the Silberstein equation (eqn (1)), which showed that the polarizability parallel along the direction vector between two particles is increased, while the orthogonal value decreases. Although Silberstein showed this for a system of only two particles, it can be seen directly that the same effect still holds for nanosized systems. The best example for this are the larger oligomers: with n = 4 a substantial variation in the polarizability is observed for a number of different orientations. The largest value is found for the linear oligomer (see Fig. 1 and Table 1), followed by the t-form and finally the cyclic oligomer. The same happens for the pentamer where the linear form shows a larger polarizability than the “plus” form. Hence, Silberstein's equations still hold for nanostructures based on C60 fullerene oligomers.
Acknowledgements
The following organizations are thanked for financial support: the Ministerio de Ciencia e Innovación (MICINN, project number CTQ2011-25086/BQU), and the DIUE of the Generalitat de Catalunya (project number 2014SGR1202 and the XRQTC). Financial support from MICINN (Ministry of Science and Innovation, Spain) and the FEDER fund (European Fund for Regional Development) was provided by grant UNGI08-4E-003.Notes and references
- H. J. Bolink, E. Coronado, A. Forment-Aliaga, M. Lenes, A. La Rosa, S. Filippone and N. Martín, J. Mater. Chem., 2011, 21, 1382–1386 RSC.
- N. Gorczak, M. Swart and F. C. Grozema, J. Mater. Chem. C, 2014, 2, 3467–3475 RSC.
- D. S. Sabirov, RSC Adv., 2013, 3, 19430–19439 RSC.
- D. S. Sabirov, A. O. Terentyev and R. G. Bulgako, Phys. Chem. Chem. Phys., 2014, 16, 14594–14600 RSC.
- G.-W. Wang, K. Komatsu, Y. Murata and M. Shiro, Nature, 1997, 387, 583–586 CrossRef CAS PubMed.
- K. Komatsu, K. Fujiwara, T. Tanaka and Y. Murata, Carbon, 2000, 38, 1529–1534 CrossRef CAS.
- L. Silberstein, Philos. Mag., 1917, 33, 92–128 CrossRef CAS.
- L. Silberstein, Philos. Mag., 1917, 33, 521–533 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- J. Applequist, J. R. Carl and J. K. Fung, J. Am. Chem. Soc., 1972, 94, 2952 CrossRef CAS.
- J. Applequist, Acc. Chem. Res., 1977, 10, 79 CrossRef CAS.
- P. Th. van Duijnen and M. Swart, J. Phys. Chem. A, 1998, 102, 2399–2407 CrossRef CAS.
- P. Th. van Duijnen and M. Swart, J. Phys. Chem. C, 2010, 114, 20547–20555 CAS.
- S. J. A. van Gisbergen, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1995, 103, 9347 CrossRef CAS PubMed.
- S. J. A. van Gisbergen, V. P. Osinga, O. V. Gritsenko, R. van Leeuwen, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 3142–3151 CrossRef CAS PubMed.
- M. Swart, P. Th. van Duijnen and J. G. Snijders, J. Mol. Struct., 1999, 458, 11–17 CrossRef CAS.
- L. Jensen, P.-O. Åstrand, A. Osted, J. Kongsted and K. V. Mikkelsen, J. Chem. Phys., 2002, 116, 4001–4010 CrossRef CAS PubMed.
- L. Jensen, P.-O. Åstrand and K. V. Mikkelsen, J. Phys. Chem. B, 2004, 108, 8226–8233 CrossRef CAS.
- A. Mayer, Appl. Phys. Lett., 2005, 86, 153110 CrossRef PubMed.
- M. L. Olson and K. R. Sundberg, J. Chem. Phys., 1978, 69, 5400–5404 CrossRef CAS PubMed.
- H. S. Smalø, P.-O. Åstrand and A. Mayer, Mol. Phys., 2013, 111, 1470–1481 CrossRef.
- L. L. Jensen and L. Jensen, J. Phys. Chem. C, 2008, 112, 15697–15703 CAS.
- L. L. Jensen and L. Jensen, J. Phys. Chem. C, 2009, 113, 15182–15190 CAS.
| This journal is © The Royal Society of Chemistry 2015 |