Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic and optical properties of reduced graphene oxide
Mark
Lundie
a,
Željko
Šljivančanin
b and
Stanko
Tomić
*a
aJoule Physics Laboratory, University of Salford, Salford, UK. E-mail: s.tomic@salford.ac.uk; Tel: +44 (0)161 295 3847
bVinča Institute of Nuclear Sciences, Belgrade, Serbia
First published on 10th June 2015
Abstract
Controlled reduction of graphene oxide is an alternative and promising method to tune the electronic and optically active energy gap of this two-dimensional material in the energy range of the visible light spectrum. By means of ab initio calculations, based on hybrid density functional theory, that combine the Hartree–Fock method with the generalized gradient approximation (GGA), we investigated the electronic, optical, and radiative recombination properties of partially reduced graphene oxide, modelled as small islands of pristine graphene formed in an infinite sheet of graphene oxide. We predict that tuning of optically active gaps, in the wide range from ∼6.5 eV to ∼0.25 eV, followed by the electron radiative transition times in the range from ns to μs, can be effected by controlling the level of oxidization.
1 Introduction
The unique electronic properties of pristine graphene are highly desirable for a vast range of applications.1 Unfortunately, its semi-metallic nature greatly limits its utilisation in a number of these, not least photonics. For such a use, the existence of an optically active and preferably direct electronic band gap is essential.2The disruption of pristine graphene's two-dimensional (2D) network of sp2 hybridized bonds is typically exploited as a means of energy gap opening.3 This can be accomplished in a number of ways, including periodic lattice modulation, the formation of nano-ribbons4 or anti-dots,5,6 and patterned surface adsorption. The functionalization of graphene by surface adsorption of atomic oxygen,7,8 flourine,9 and hydrogen10,11 has been demonstrated experimentally to effect such an electronic modification. To date, hydrogenation of graphene has been the most common experimental approach toward energy gap formation.12 In this case, hydrogen's single 1s electron breaks the sp2 hybridized C–C double bond to form an sp3 hybridized bond, disrupting the π-electron network.
The modified Hummers method13,14 combines oxidation and sonification to convert graphite into graphene oxide (GO) and then the GO is exposed to reducing chemicals such as hydrazine.14 Since the produced graphene is only partially reduced15,16 its conductivity is considerably lower compared to that in high quality samples obtained through mechanical exfoliation of graphite.17 Even though it is still unsuitable for applications in high performance nano-electronics, reduced graphene oxide (rGO) is expected to be exploited in supercapacitors for energy storage, electrodes in Li-ion batteries or for transparent electrodes in solar cells.18,19
It turns out that the physical properties of rGO are very sensitive to the degree of reduction. For example a recent study by Eda et al.20 demonstrated that by changing the degree of reduction of GO the intensity of photoluminesence in rGO can be increased by a factor of ten compared to the value measured in as-synthesized GO samples. At variance with the insulating nature of fully oxidized graphene, rGO shows both insulating and conducting characters, depending on the percentage of oxygen left on the graphene sheet. The structure of rGO is usually described by nanometric sp2 graphitic islands separated by regions of oxidized graphene.17 The tendency of oxygen to agglomerate into highly oxidized domains surrounded by areas of pristine graphene has been recently demonstrated by first-principles and statistical calculations.21 Strong dependence of the electronic properties of graphene islands on their size opens up the prospect for efficient band gap engineering of this two-dimensional material.
An alternative approach to the harsh chemistry of “top-down” methods has been demonstrated by exposing graphene grown epitaxially on a SiC(001) surface to atomic oxygen under ultrahigh vacuum (UHV) conditions.22 The chemisorption of atomic oxygen in this “bottom-up” technique results only in the formation of epoxy functional groups, with no damage to the underlying honeycomb lattice. The process was shown to be reversible by annealing or desorption with a scanning tunnelling microscope (STM) tip. This leads to the prospect of producing GO with highly tunable properties.
Measurements of optical absorption taken during experiments with graphene oxide in aqueous suspension have shown interesting trends.23 Strong absorption is observed in the ultraviolet (UV) range of the spectrum, with absorption peaks shifting towards the visible range as the level of oxidation is increased.20,24 Photoluminescence emission in the infrared (IR) and visible ranges has also been observed in nanometre scale flakes of graphene oxide.25 Composite carbon-nanodot (CND)–GO structures have also demonstrated fluorescence quenching, attributed to sub-picosecond electron transfer processes.26
Computational modelling based on density functional theory (DFT) is able to provide a detailed description of different stages of graphene oxide reduction, which is not easily accessible even by the state-of-the-art experimental methods. In this paper, we present theoretical results from ab initio calculations focussing on the electronic and optical properties of GO and rGO. We based our study on the hybrid density functional theory, which has been shown to yield highly accurate estimates of optical properties of common semiconductor and simple oxide materials.27–30 After the Introduction, we describe the computational implementation of GO and rGO in the section Theoretical Considerations. In the same section, we briefly outline the derivation of the dipole matrix elements as implemented in the crystal code,31–33 and how they can be used to calculate the electron radiative transition times and absorption cross-section. In the Results and Discussion section, we present our theoretical results on GO and rGO, before we conclude our discussion in the final section.
2 Theoretical considerations
2.1 Methodology
Calculations were performed using DFT in localized Gaussian type orbital (GTO) formalism as implemented in the crystal code. Structural calculations were carried out at the GGA level using the renowned PBE exchange–correlation functional.34Since the GGA functionals are in general able to rather well describe the energetics of O adsorption on graphene, all formation energies of multiple O vacancies in the oxidized graphene layer reported here are calculated by applying the PBE exchange–correlation functional. However, it is well known that Kohn–Sham (KS) DFT inside local approximations alone is incapable of accurately predicting optical properties. As such, these properties were calculated using hybrid exchange with the PBE035 and B3LYP36 functionals, in which a fraction of 25% and 20%, respectively, of exact exchange calculated in the Hartree–Fock (HF) formalism is included.
Fully oxidized graphene was simulated using an irreducible rectangular unit cell with eight carbon atoms and four oxygen atoms. Partially oxidized graphene was modelled by removing oxygen adatoms from these cells to leave regions of free graphene. To prevent artificial Coulomb and quantum interactions between graphene islands due to periodic boundary conditions, modelling of rGO was carried out within a rectangular cell with 96 atoms in the graphene sub-lattice.
We exploit the properties of the localised basis set to treat a structure aperiodic in the z-direction without the need for introducing large vacuum regions. Atomic coordinates and cell parameters were relaxed using the BFGS algorithm, with an energy convergence tolerance of 10−8 Ha (∼10−7 eV) between optimization steps. The irreducible Brillouin zone (IBZ) was sampled using the Monkhorst–Pack scheme,37 with 4 k-points for geometry relaxation, and 130 k-points for electronic property calculations.
By using the GTO implementation of DFT, it is possible to use all-electron basis sets. To select a suitable basis set, the relaxed bond lengths and carbon–oxygen binding energies were compared to those calculated using projector-augmented wave (PAW) and plane-wave (PW) basis sets. The most suitable were found to be Dunning's correlation-consistent cc-pCVDZ sets.38 For carbon adjustment and reoptimization of the most diffuse orbital, a 2p polarization function was required, while for oxygen, no modification was necessary. Bond lengths were found to be within 0.1 Å and binding energies were within 0.01 eV in PAW and PW calculations.
2.2 Radiative properties
To examine the radiative properties of rGO we based our analysis on the optical dipole elements that we have calculated at the Γ point for all structures. Due to the large supercells employed, the band structures are almost dispersionless. The vertical transition probabilities under external radiation are given bydi→f = i∫dr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) ukf*(r)∇kuki(r), ukf*(r)∇kuki(r), | (1) |
dvi→f = i∫dr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) ukf*(r)∇kvuki(r), ukf*(r)∇kvuki(r), | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) = i∇k holds.40 From vertical transition probabilities given in eqn (1), the optical dipole matrix elements were obtained as:
= i∇k holds.40 From vertical transition probabilities given in eqn (1), the optical dipole matrix elements were obtained as:| pif = (Ef − Ei)di→f | (3) |
Radiative transition times between the highest occupied and lowest unoccupied states were calculated using the optical dipole matrix elements as given in eqn (3) and KS eigenvalues as:
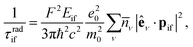 | (4) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ν and êν are the refractive index and light polarisation unit vectors along different Cartesian directions. The refractive index normal to the surface,
ν and êν are the refractive index and light polarisation unit vectors along different Cartesian directions. The refractive index normal to the surface, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) z is set to unity. Due to strong 3D confinement of the wavefunction in the case of all rGO structures (see Fig. 7) we assume a screening parameter for rGO of (4εGO + 2ε0)/(3εG + 2εGO + ε0), where ε0 = 1 is the vacuum permittivity, εG = 3.0 is the relative permittivity of graphene,42 and εGO is that of GO. For GO the screening parameter is equal to unity. The calculated dielectric tensor components for GO are listed below.
z is set to unity. Due to strong 3D confinement of the wavefunction in the case of all rGO structures (see Fig. 7) we assume a screening parameter for rGO of (4εGO + 2ε0)/(3εG + 2εGO + ε0), where ε0 = 1 is the vacuum permittivity, εG = 3.0 is the relative permittivity of graphene,42 and εGO is that of GO. For GO the screening parameter is equal to unity. The calculated dielectric tensor components for GO are listed below.
To assess the absorption properties of various GO and rGO structures we use the expression for the absorption cross-section:
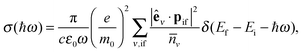 | (5) |
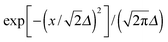 , defined by the phenomenological line broadening, Δ, set to 50 meV in all structures considered.
, defined by the phenomenological line broadening, Δ, set to 50 meV in all structures considered.
3 Results and discussion
3.1 Structural model and electronic properties of reduced graphene oxide
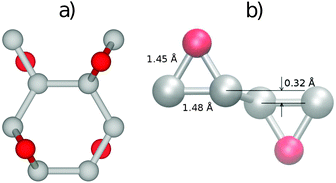
The most stable structure of fully oxidized graphene, Fig. 1(a), has a C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio of 2
O ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with alternating oxygen adsorption above and below the graphene lattice.43 Using the PBE-GGA exchange correlation functional for our structural analysis, we observe that the O adsorption in the bridge sites increases the distance between C atoms to 1.48 Å, which is 0.06 Å larger compared to the value found in pristine graphene. Since the calculated C–O bond-length is 1.45 Å, three atoms from the epoxy group form a nearly equilateral triangle, Fig. 1(b). The O binding energy of 3.25 eV per atom renders this structure highly stable. This adsorption geometry minimizes Coulomb repulsion between adsorbates, thereby increasing stability. Each oxygen atom forms an epoxy functional group with two carbon atoms, with bonding between the 2pz orbitals. This results in the rehybridization of the graphene lattice from sp2 to sp3, analogous to the type of bonding in diamond allotropes. The carbon atoms are displaced vertically from their positions in the hexagonal lattice of pristine graphene, relaxing the strain caused by the 2pz bond formation. The alternating oxygen coverage balances the effects of this buckling, making this structure considerably more stable than that with oxygen coverage only on one side.
1 with alternating oxygen adsorption above and below the graphene lattice.43 Using the PBE-GGA exchange correlation functional for our structural analysis, we observe that the O adsorption in the bridge sites increases the distance between C atoms to 1.48 Å, which is 0.06 Å larger compared to the value found in pristine graphene. Since the calculated C–O bond-length is 1.45 Å, three atoms from the epoxy group form a nearly equilateral triangle, Fig. 1(b). The O binding energy of 3.25 eV per atom renders this structure highly stable. This adsorption geometry minimizes Coulomb repulsion between adsorbates, thereby increasing stability. Each oxygen atom forms an epoxy functional group with two carbon atoms, with bonding between the 2pz orbitals. This results in the rehybridization of the graphene lattice from sp2 to sp3, analogous to the type of bonding in diamond allotropes. The carbon atoms are displaced vertically from their positions in the hexagonal lattice of pristine graphene, relaxing the strain caused by the 2pz bond formation. The alternating oxygen coverage balances the effects of this buckling, making this structure considerably more stable than that with oxygen coverage only on one side.
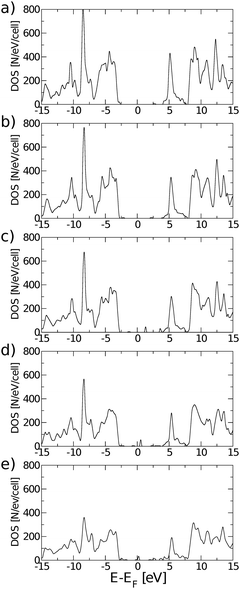
While chemical synthesis and reduction of GO produce considerable defects and leave a combination of carbonyl, carboxyl and hydroxyl groups in addition to the epoxy groups, the latter are dominant. In the following text we therefore refer to this purely epoxy functionalised structure as GO. However, the effect of the presence of OH groups on the electronic and optical properties of GO has been carefully examined, as described at the end of this subsection. The O adsorbates profoundly alter the electronic properties of the graphene layer as seen from the band structure and density of states (DOS) plots in Fig. 2. At variance with pristine graphene, GO is a wide band gap insulator. From PBE-GGA calculations we estimated the energy gap to be 4.09 eV at the Γ point. In order to improve the accuracy of the predicted gap, we proceeded with our analysis using the PBE0 and B3LYP hybrid functionals, giving the band gap values of 6.85 eV and 6.50 eV, respectively.
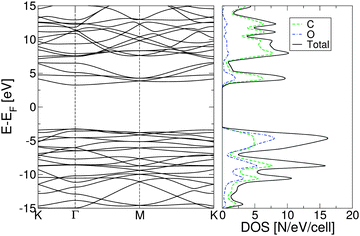 | ||
| Fig. 2 Electronic band structure of fully oxidized graphene (left) and total density of states (right), calculated using the PBE0 exchange correlation functional. | ||
The plot of the DOS projected onto O-2p and C-2p states (Fig. 2) suggests that the electrons occupying the highest valence bands are mainly from the O-2p states, while the electronic states of the conduction zones are predominantly of C-2p character. The energy gap opening in GO is also followed by an increase in the electron and hole effective masses. The GO structure shows a very anisotropic band structure around the Γ point, Fig. 2, as reflected in the effective masses at the bottom of the conduction band and at the top of the valence band. These are me* = 1.361(1.395)m0 and mh* = 0.558(0.597)m0 along the direction Γ → M, and me* = 0.399(0.417)m0 and mh* = 0.442(0.447)m0 along the direction Γ → K. The principal components of the elastic tensor are c11 = 245 Nm−1, c22 = 240 Nm−1, c12 = 25 Nm−1 and c66 = 110 Nm−1. By comparison, using the same basis set and methodology, we calculated the elastic constants of pristine graphene to be c11 = 357 Nm−1, c22 = 371 Nm−1, c12 = 51 Nm−1 and c66 = 137 Nm−1, the in-plane components of which compare well to the experimentally obtained value of 340 ± 50 Nm−1.44 This indicates that GO is substantially softer than pristine graphene, which can likely be attributed to the corrugation of the graphene sub-lattice upon O adsorption (Table 1).
| Γ [eV] | M [eV] | K [eV] |
|---|---|---|
| 6.850 (6.502) | 7.463 (7.073) | 7.358 (6.893) |
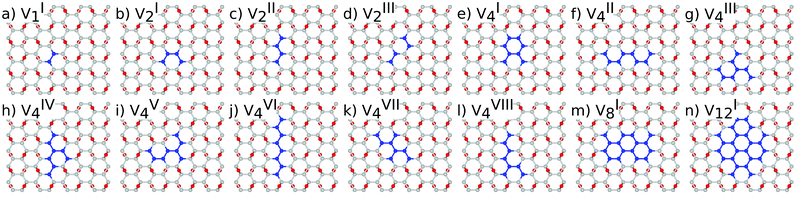
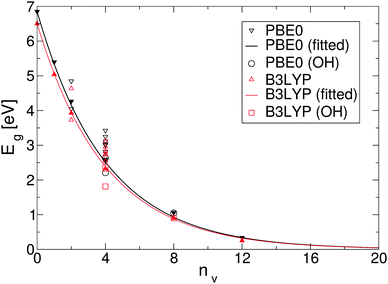
The reduction of GO proceeds by the removal of oxygen adsorbates, which results in carbon sp2 rehybridisation in the regions with oxygen-free C atoms, together with the local restoration of the flat honeycomb lattice. The segments of pristine graphene represent graphene quantum dots (GQDs) embedded into the GO layer. In this study we assumed that the GO reduction is not accompanied with the disruption of the honeycomb lattice, and thus the occurrence of point defects within the graphene layer was neglected. The reduced GO can then be considered as a 2D structure which contains GQDs of different sizes, randomly distributed across the GO surface. Using GO as the initial configuration, Fig. 1, we modelled different structural motifs present in partially reduced GO by removing a selected number of O atoms from the fully oxidized graphene sheet. The configurations produced upon removal of one, two, four, eight and twelve O atoms from the simulation cell are presented in Fig. 3. The smallest GQD is formed when a single O atom is removed from GO, Fig. 3(a). We calculated the O vacancy formation energy as 4.23 eV. This structure is accompanied with a reduction of the energy gap to 5.40 eV, a reduction of ∼1.45 eV compared to GO, due to the appearance of new electronic states. The energy gap values calculated with all three exchange–correlation functionals we used are given in Table 2. As is well known, PBE-GGA underestimates the realistic energy gaps and is given here just for a reference.
| E LUMO–EHOMO | |||
|---|---|---|---|
| n v | PBE | PBE0 | B3LYP |
| 1 | 3.238 | 5.397 | 5.038 |
| 2 | 2.502 | 4.264 | 3.927 |
| 4 | 1.249 | 2.594 | 2.327 |
| 8 | 0.372 | 1.056 | 0.902 |
| 12 | 0.000 | 0.338 | 0.258 |
Three different topologies with two adjacent O atoms removed from GO are presented in Fig. 3(b–d). The most stable is the configuration VI2 with two O vacancies along the armchair direction of the graphene lattice. Yet, the formation energies of the other two structures, calculated per missing O atom, differ by only 0.12 eV or less. The corresponding PBE0 energy gaps are in the range from 4.26 to 4.98 eV. We carefully inspected structures formed upon removal of four O adatoms from the surface. In total eight different configurations, presented in Fig. 3(e–l), were calculated. The most stable among studied structures is VI4, with a highly symmetric GQD left on the surface after four O atoms were desorbed, Fig. 3(e). The corresponding PBE0 energy gap is 2.59 eV. The formation energies of various topologies are presented in the Appendix, while the energy gaps of the energetically most favourable GQDs are listed in Table 2. The energy gaps vary approximately 1.0 eV among different topologies with four adjacent O vacancies (Table 7, see the Appendix).
Since the number of possible configurations with more than four neighbouring O atoms removed from the GO surface is progressively increasing, we restricted our study of larger GQDs to the two structures depicted in Fig. 3(m) and (n). The structure VI8 corresponds to a GQD with eight missing O adatoms, formed when the GQD in the configuration VI4 is enlarged twice along the armchair direction. The VI12 structure is a highly symmetric GQD with twelve O atoms being removed from the unit cell. The configurations VI8 and VI12 are included in this study with the aim to further confirm trends in the energy gap evolution with the size of the GQDs, found from a thorough examination of the rGO structures obtained upon removal of one, two and four O atoms from the GO layer.
As expected, the larger fraction of exact exchange energy incorporated in PBE0 results in the prediction of slightly larger gaps compared to those calculated using the B3LYP functional.45
To simplify understanding of the evolution of the energy gaps with respect to the number of removed O atoms, only the most energetically favourable GQDs with a given number of removed O atoms are compared. It turns out that the calculated energy gaps fit a very simple relationship, plotted in Fig. 4, based on the level of oxygen coverage:
| Eg(nv) ≈ Eg(0)exp(−0.25nv), | (6) |
Eigenstates of the GQDs and total DOS are plotted in Fig. 5 and 6, respectively. These clearly show the sp2 states localized on the GQDs, positioned at energies within the band gap of GO, which is the energy gap between the highest occupied and lowest unoccupied sp3 states.
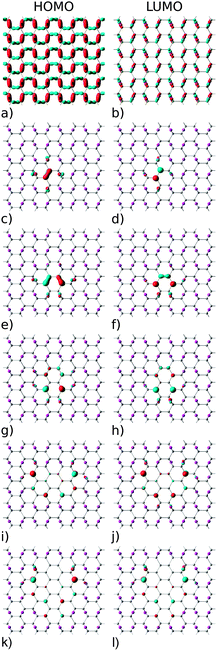
The electronic structure of reduced graphene oxide is readily explained by detailed inspection of the Bloch functions. Fig. 7(a) and (b) depict the HOMO and LUMO states of fully oxidized graphene, respectively, distinctly showing the sp3 hybridized bonds. By contrast, Fig. 7(c) and (d) illustrate the HOMO and the LUMO for the structure with one O atom removed, showing both to be largely localised on C atoms (node sites), but with partial contribution of p type orbitals from the four nearest neighbouring O atoms (bridge sites). Also evident is the reappearance of pristine graphene's characteristic sp2 hybridized π-bonds. Orbitals above the LUMO and below the HOMO are seen to be still of sp3 nature (not shown). According to Fig. 7 the HOMO and LUMO of all studied GQDs are mainly located at the edge of the C atoms. These electronic states of the three smallest quantum dots (Fig. 7c–h) are localized on the nearest neighbour C atoms and thus there is a strong overlap between the corresponding C-2pz orbitals which results in significant energy gap values. Since the frontier electronic states in larger GQDs (Fig. 7i–l) are to a large extent composed of the C-2pz orbitals centered on the atoms which are the second nearest neighbours, their weak overlapping is accompanied with small values of the energy gap.
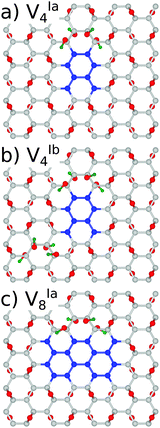
With a view to further justifying the model adopted, simulations were performed on a representative number of structures with hydroxyl groups present in addition to the epoxy motifs. To maintain the minimisation of repulsive Coulomb forces by even distribution of adsorbates above and below the graphene lattice, a single epoxy group was replaced by two hydroxyl groups and the epoxy groups were removed in pairs. The symmetry was deliberately preserved in structures VIa4 and VIa8, and broken in the case of VIb4, as shown in Fig. 8.
We have found the energy gaps predicted for the structures with the same symmetry, VIa4 and VIa8, differ only very slightly from the purely epoxy functionalised structures, as shown in Table 3. For VIa4 the difference is predicted by PBE0 (B3LYP) to be 36(37) meV, while for VIa8 it is 6(2) meV. The effect of the breaking of symmetry is much greater, with a calculated difference of 0.385(0.513) eV. This is in line with the calculations for the epoxy functionalised structures with different symmetries (see the Appendix, Table 7).
| E LUMO–EHOMO | |||
|---|---|---|---|
| Topology | PBE | PBE0 | B3LYP |
| VIa4 | 1.293 | 2.630 | 2.364 |
| VIb4 | 1.275 | 2.209 | 1.814 |
| VIa8 | 0.388 | 1.050 | 0.900 |
3.2 Optical properties of reduced graphene oxide
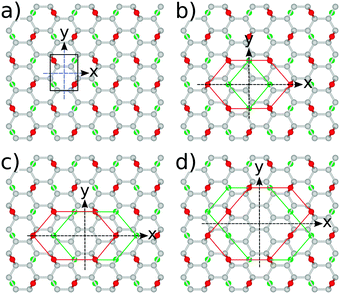
For all structures considered, i.e., GO and rGO with various numbers of O vacancies, nv, we examine whether the energy gap modulation with nv is also followed by changes in their optical activity. To examine this we use eqn (3), by setting uΓi(r) and uΓf(r) to HOMO and LUMO states, respectively. All rGO structures considered in this subsection are those with minimal total energy among configurations with the same number of removed O atoms and are all highly symmetric (Fig. 9). The correct values of optical matrix elements cannot be obtained unless the choice of the 2D unit cell also incorporates the point-group symmetry of the bulk.49,50 To ensure that this is the case, in all of our calculations we have aligned the “armchair” edge of the carbon sub-lattice along the x-axis. All calculations of optical properties were carried out on fully relaxed GO or rGO structures. We have observed that for all structures with minimal energy, which are also highly symmetric, relaxation preserves the perfect point group symmetry of motifs. As can be seen from Table 7 (see the Appendix), among structures with the same nv those with the highest vacancy formation energies are those with the unit cells of highest symmetry. As such, we have adopted only these cells for further analysis.As can be seen from Table 4, for all structures considered the HOMO–LUMO transitions are optically active at least in one polarization direction. If we ignore for the moment the structure with nv = 1, the general trend is that optical dipole matrix elements are reduced with increasing number of O vacancies, suggesting the reduced overlap between HOMO and LUMO states with nv. In order to explain the presence or the absence of transitions in particular polarization directions, we recall the arguments of group theory.51 Moving from a graphene ribbon (another C based structure with an energy gap) to fully oxidized GO the symmetry is reduced from C2v to Cy2, where the superscript denotes the principal axis [according to the orientation in Fig. 9(a)]. According to the character table for the Cy2 group the optically allowed transitions are either y or (z, x) polarized. Our results, Table 4, show only px polarization is bright suggesting by selection rule forbidden z-polarized transition. All other rGO structures with nv ≥ 2, stemming out from the energy minimisation procedure, are also Cy2, and show that both px and pz allowed dipole polarizations. All the other rGO configurations inside the same nv will break the symmetry in all three Cartesian directions and all polarisations will be optically allowed. However, the polarization parallel to the “armchair” direction will still be dominant. The remaining structure is that with nv = 1. There is only one such possible arrangement. The structure with nv = 1 is of Cz2 symmetry and according to group theory has either z or (x, y) polarized optically allowed transitions. Indeed, our results show that both px and py associated transitions are bright, while pz is dark. These interesting optical features open up possibilities for producing polarization sensitive optical devices by controlling the shape of voids of functionalized atoms, or by applying external strain or pressure on such structures in order to produce desirable reduction or restoration of symmetry.
| n v | p x [eV Å] | p y [eV Å] | p z [eV Å] |
|---|---|---|---|
| 0 | 3.880 (3.656) | 0 | 0 |
| 1 | 2.810 (2.662) | 3.090 (3.051) | 0 |
| 2 | 3.615 (3.355) | 0 | 0.673 (0.635) |
| 4 | 2.778 (2.510) | 0 | 0.366 (0.335) |
| 8 | 2.576 (2.248) | 0 | 0.126 (0.111) |
| 12 | 1.003 (0.784) | 0 | 0.022 (0.016) |
Table 4 contains dipole matrix elements at the fundamental gap calculated at Γ using the PBE0 and B3LYP exchange–correlation functionals, respectively. These are in the range between ∼1/3 and ∼1/10 of those for bulk III–V semiconductors commonly used in photonic applications. For a monolayer material, this is indicative of strong optical absorption.
As with the energy gaps, the addition of hydroxyl functional groups without altering the symmetry of the structure, VIa4 and VIa8, has only a negligible effect on the dipole matrix elements (compare Tables 5 and 7, appendix). The structure VIb4, being of only C1 point group symmetry, is optically active in all three polarisation directions. Compared to the highly symmetric structures, the optical activity is greatly weakened.
| Topology | p x [eV Å] | p y [eV Å] | p z [eV Å] |
|---|---|---|---|
| VIa4 | 2.803 (2.536) | 0 | 0.368 (0.336) |
| VIb4 | 0.424 (0.327) | 0.140 (0.160) | 0.187 (0.165) |
| VIa8 | 2.571 (2.248) | 0 | 0.142 (0.124) |
In order to calculate the absorption cross-section and radiative lifetimes, in addition to gain knowledge of the electronic structure and polarization direction selective dipole matrix elements, it is necessary to estimate accurately the dielectric properties. In a layered system, such as graphene or rGO, it is reasonable to expect the element of the dielectric tensor normal to the surface to be very close to the vacuum dielectric permittivity and significantly different to the in-plane components. Using time-dependent density functional theory (TD-DFT) in the linear response formalism,28,39,41 again with the PBE0 (B3LYP) exchange–correlation functionals, we have estimated the principal components of the dielectric tensor to be εxx = 1.261(1.291), εyy = 1.346(1.387), and εzz = 1.078(1.087). Due to the localized nature of the (Gaussian) basis set used, our approach is less sensitive to the choice of size of the embedding box in the z-direction.
From calculated HOMO–LUMO gaps, dipole matrix elements and dielectric constants, we estimated the electron radiative transition times for the most favourable structures considered, which are listed in Table 6. As expected with nv increasing both the gaps and dipole matrix elements decrease, contributing to the increase of τradif. It is interesting to note that by comparing other semiconducting material systems with the similar Eg ≈ 1 eV, like in InAs/GaAs QD's,52 in rGO with nv = 8, the radiative transition times are elevated to the ∼300 ns range (compared to ∼1–2 ns in inorganic semiconductor QDs with similar optical gaps).52 The large difference between our calculated radiative times and those reported for similar graphene based structures, albeit doped with nitrogen,53,54 can be attributed to very fast non-radiative processes that very likely take place in the actual structures measured. It has been already shown theoretically that the band gap opening and strong edge localization in graphene nanostructures lead to strong electron–phonon coupling, which may explain one such non-radiative process.6 Nevertheless, long radiative relaxation times could be of potential benefit to the electron transport processes in solar cells or photo-detectors, should suppression of non-radiative processes be achieved.55,56
| n v | τ radif [ns] |
|---|---|
| 0 | 11.40 (13.52) |
| 1 | 29.40 (33.52) |
| 2 | 48.02 (60.49) |
| 4 | 135.97 (185.54) |
| 8 | 394.05 (605.84) |
| 12 | 8138.31 (17547.80) |
| Topology | E f [eV] | E g [eV] | p x [eV Å] | p y [eV Å] | p z [eV Å] |
|---|---|---|---|---|---|
| VI1 | 4.231 | 5.397 | 2.811 | 3.090 | 0 |
| VI2 | 4.119 | 4.262 | 3.615 | 0.003 | 0.673 |
| VII2 | 4.132 | 4.048 | 2.389 | 4.486 | 0.613 |
| VIII2 | 4.231 | 4.985 | 2.977 | 0.037 | 0.144 |
| VI4 | 3.996 | 2.594 | 2.778 | 0 | 0.366 |
| VII4 | 4.074 | 3.424 | 2.884 | 1.924 | 0.790 |
| VIII4 | 4.051 | 3.112 | 4.466 | 0 | 0.296 |
| VIV4 | 4.062 | 3.247 | 3.533 | 1.663 | 0.191 |
| VV4 | 4.054 | 3.004 | 3.338 | 1.044 | 0.147 |
| VVI4 | 4.071 | 2.535 | 1.604 | 5.336 | 0.228 |
| VVII4 | 4.076 | 3.024 | 2.194 | 3.823 | 0.178 |
| VVIII4 | 4.060 | 2.816 | 2.368 | 3.280 | 0.194 |
| VI8 | 3.877 | 1.056 | 2.576 | 0 | 0.126 |
| VI12 | 3.865 | 0.338 | 1.003 | 0 | 0.021 |
Fig. 10 shows absorption cross-sections for all GQDs from PBE0 calculations, highlighting the dichroic nature of the material. In line with the dipole matrix elements presented in Table 4, the layer with one O vacancy, Fig. 9(a), has a similar absorption cross-section in the vicinity of the optical gap in both in-plane directions, while no absorption takes place in the z polarization direction. At higher energies y-polarized absorption dominates, with z-polarized absorption only becoming apparent at ∼8 eV. The behaviour of all structures with two or more O vacancies is qualitatively similar. After the first peak associated with the optical gap, with in-plane absorption, particularly in the y direction, again being dominant. Absorption at the optical gap is exclusively x-polarized in-plane and the evident weak z-polarized absorption falls off dramatically with the level of O reduction. These observations are in line with the previous assertion, based on Fig. 2, that the conduction region of the electronic structure is dominated by C-2p states. By extension, the absorption of z-polarized light can be largely attributed to that of O-2pz states higher in energy that do contribute to conduction. Again, taking into account that we are dealing with a single atomic layer, the optical absorption cross-section can be regarded as strong.
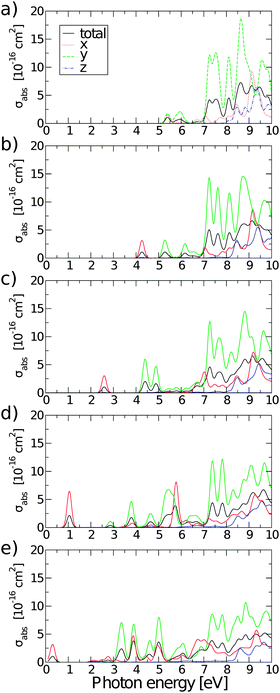 | ||
| Fig. 10 Polarisation selective and total absorption cross-sections of rGO structures with: (a) nv = 1, (b) nv = 2, (c) nv = 4, (d) nv = 8, and (e) nv = 12. | ||
4 Conclusions
Using ab initio calculations, we have demonstrated that effective tuning of the electronic and optical properties of oxidized graphene can be achieved by careful manipulation of the level of oxygen reduction. Combining density functional theory and time-dependent density functional theory with the PBE0 and B3LYP hybrid exchange–correlation functionals, it is possible to make quantitative predictions of these properties.The tuning of electronic and optical properties is effected by modification of the electronic structure so as to form islands of pristine graphene, or graphene quantum dots, within the GO sheet. The energy gap decreases with the number of O adatoms removed, or the dot diameter, allowing tuning through the ranges of UV, visible and IR light. The gap fits a simple exponential decay relation, eqn (6). We have also shown that rGO has a strong optical absorption cross-section when taking into consideration the fact that it is a monolayer material. Furthermore, the long radiative transition times may lead to favourable electron transport properties for charge separation and extraction of work in the case of photovoltaic and optoelectronic applications. The characteristics of this absorption can be controlled by the manipulation of the GQD symmetry, allowing for selection of the light polarization. This anisotropy of the optical response may also lead to applications in polarization sensitive optical devices.
Importantly, from our analysis of structure, VIb4, with OH groups we conclude that disruption of the symmetry of the quantum dot structures degrades the optical properties of rGO.
Appendix
Acknowledgements
The authors wish to thank the Royal Society, London, for the grants “Functionalized Graphene for Solar Cell Devices: insight from ab Initio Theory” and “High Performance Computing in Modelling of Innovative Photo-Voltaic Devices” and would like to acknowledge the contribution of COST Action MP1406 and The Great Britain Sasakawa Foundation. M. L. acknowledges the University of Salford, UK, for the award of Graduate Teaching Studentship. Ž. Š acknowledges financial support from Serbian Ministry of Education and Science under Grant No. 171033 and from the COST Action CM1104. The authors also thank B. G. Searle and L. Bernasconi for useful discussions.References
- K. Novoselov, A. Geim, S. Morozov, D. Jiang, Y. Zhang, S. Dubonos, I. Grigorieva and A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611–622 CrossRef CAS.
- L. Cao, S. Sahu, P. Anilkumar, C. Y. Kong and Y.-P. Sun, MRS Bull., 2012, 37, 1283–1289 CrossRef CAS.
- L. Pisani, J. A. Chan, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064418 CrossRef.
- T. G. Pedersen, C. Flindt, J. Pedersen, N. A. Mortensen, A.-P. Jauho and K. Pedersen, Phys. Rev. Lett., 2008, 100, 136804 CrossRef PubMed.
- V. M. Stojanović, N. Vukmirović and C. Bruder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165410 CrossRef.
- N. A. Vinogradov, K. Schulte, M. L. Ng, A. Mikkelsen, E. Lundgren, N. Mårtensson and A. B. Preobrajenski, J. Phys. Chem. C, 2011, 115, 9568–9577 CAS.
- R. Larciprete, S. Fabris, T. Sun, P. Lacovig, A. Baraldi and S. Lizzit, J. Am. Chem. Soc., 2011, 133, 17315–17321 CrossRef CAS PubMed.
- R. R. Nair, W. Ren, R. Jalil, I. Riaz, V. G. Kravets, L. Britnell, P. Blake, F. Schedin, A. S. Mayorov, S. Yuan, M. I. Katsnelson, H.-M. Cheng, W. Strupinski, L. G. Bulusheva, A. V. Okotrub, I. V. Grigorieva, A. N. Grigorenko, K. S. Novoselov and A. K. Geim, Small, 2010, 6, 2877–2884 CrossRef CAS PubMed.
- R. Balog, B. Jørgensen, J. Wells, E. Lægsgaard, P. Hofmann, F. Besenbacher and L. Hornekær, J. Am. Chem. Soc., 2009, 131, 8744–8745 CrossRef CAS PubMed.
- R. Balog, M. Andersen, B. Jørgensen, Z. Sljivancanin, B. Hammer, A. Baraldi, R. Larciprete, P. Hofmann, L. Hornekær and S. Lizzit, ACS Nano, 2013, 7, 3823–3832 CrossRef CAS PubMed.
- R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Laegsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekær, Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- T. Dufaux, J. Boettcher, M. Burghard and K. Kern, Small, 2010, 6, 1868–1872 CrossRef CAS PubMed.
- K. Erickson, R. Erni, Z. Lee, N. Alem, W. Gannett and A. Zettl, Adv. Mater., 2010, 22, 4467–4472 CrossRef CAS PubMed.
- C. Gomez-Navarro, R. T. Weitz, A. M. Bittner, M. Scolari, A. Mews, M. Burghard and K. Kern, Nano Lett., 2007, 7, 3499–3503 CrossRef CAS PubMed.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- W. Lu, P. Soukiassian and J. Boeckl, MRS Bull., 2012, 37, 1119–1124 CrossRef CAS.
- G. Eda, Y.-Y. Lin, C. Mattevi, H. Yamaguchi, H.-A. Chen, I.-S. Chen, C.-W. Chen and M. Chhowalla, Adv. Mater., 2010, 22, 505 CrossRef CAS PubMed.
- S. Zhou and A. Bongiorno, Sci. Rep., 2013, 3, 2484 Search PubMed.
- M. Z. Hossain, J. E. Johns, K. H. Bevan, H. J. Karmel, Y. T. Liang, S. Yoshimoto, K. Mukai, T. Koitaya, J. Yoshinobu, M. Kawai, A. M. Lear, L. L. Kesmodel, S. L. Tait and M. C. Hersam, Nat. Chem., 2012, 4, 305–309 CrossRef CAS PubMed.
- S. Niyogi, E. Bekyarova, M. Itkis, J. McWilliams, M. Hamon and R. Haddon, J. Am. Chem. Soc., 2006, 128, 7720–7721 CrossRef CAS PubMed.
- C. Y. Kong, W.-L. Song, M. J. Meziani, K. N. T. II, L. Cao, A. J. Farr, A. Anderson and Y.-P. Sun, J. Supercrit. Fluids, 2012, 61, 206–211 CrossRef CAS.
- X. Sun, Z. Liu, K. Welsher, J. T. Robinson, A. Goodwin, S. Zaric and H. Dai, Nano Res., 2008, 1, 203–212 CrossRef CAS PubMed.
- P. Yu, X. Wen, Y.-R. Toh, Y.-C. Lee, K.-Y. Huang, S. Huang, S. Shrestha, G. Conibeer and J. Tang, J. Mater. Chem. C, 2014, 2, 2894–2901 RSC.
- S. Tomić, B. Montanari and N. M. Harrison, Physica E, 2008, 40, 2125–2127 CrossRef.
- L. Bernasconi, S. Tomić, M. Ferrero, M. Rérat, R. Orlando, R. Dovesi and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195325 CrossRef.
- C. L. Bailey, L. Liborio, G. Mallia, S. Tomić and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205214 CrossRef.
- L. Liborio, G. Mallia and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245133 CrossRef.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL 09 Manual, 2009 Search PubMed.
- I. J. Bush, S. Tomić, B. G. Searle, G. Mallia, C. L. Bailey, B. Montanari, L. Bernasconi, J. M. Carr and N. M. Harrison, Proc. R. Soc. A, 2011, 467, 2112–2126 CrossRef CAS.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 1450–1459 CrossRef CAS PubMed.
- L. Bernasconi, M. Sprik and J. Hutter, J. Chem. Phys., 2003, 119, 12417–12431 CrossRef CAS.
- S. Tomić, L. Bernasconi, B. G. Searle and N. M. Harrison, J. Phys. Chem. C, 2014, 118, 14478–14484 Search PubMed.
- Y. Wang, V. W. Brar, A. V. Shytov, Q. Wu, W. Regan, H.-Z. Tsai, A. Zettl, L. S. Levitov and M. F. Crommie, Nat. Phys., 2012, 8, 653–657 CrossRef CAS.
- Ž. Šljivanaanin, A. S. Milošević, Z. S. Popović and F. R. Vukajlović, Carbon, 2013, 54, 482–488 CrossRef.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- S. Tomić and N. M. Harrison, AIP Conf. Proc., 2010, 1199, 65–66 CrossRef.
- A. D. Güçlü, P. Potasz and P. Hawrylak, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155445 CrossRef.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- K. A. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235–242 CrossRef CAS PubMed.
- K. Gundra and A. Shukla, Physica B, 2011, 406, 3538–3543 CrossRef CAS.
- K. Gundra and A. Shukla, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075413 CrossRef.
- M. S. Dresselhaus, G. Dresselhaus and A. Jorio, Group Theory, Springer, 2008 Search PubMed.
- S. Tomić, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195321 CrossRef.
- Y. Dai, H. Long, X. Wang, Y. Wang, Q. Gu, W. Jiang, Y. Wang, C. Li, T. H. Zeng, Y. Sun and J. Zeng, Part. Part. Syst. Charact., 2014, 31, 597–604 CrossRef CAS.
- D. Qu, M. Zheng, L. Zhang, H. Zhao, Z. Xie, X. Jing, R. E. Haddad, H. Fan and Z. Sun, Sci. Rep., 2014, 4, 5294 CAS.
- K. Nishikawa, Y. Takeda, T. Motohiro, D. Sato, J. Ota, N. Miyashita and Y. Okada, Appl. Phys. Lett., 2012, 100, 113105 CrossRef.
- S. Tomić, Appl. Phys. Lett., 2013, 103, 072112 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |