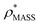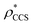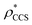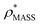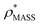EM∩IM: software for relating ion mobility mass spectrometry and electron microscopy data†
Matteo T.
Degiacomi
and
Justin L. P.
Benesch
Department of Chemistry, Physical & Theoretical Chemistry Laboratory, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: matteo.degiacomi@chem.ox.ac.uk; justin.benesch@chem.ox.ac.uk
First published on 23rd November 2015
Abstract
We present EM∩IM, software that allows the calculation of collision cross-sections from electron density maps obtained for example by means of transmission electron microscopy. This allows the assessment of structures other than those described by atomic coordinates with ion mobility mass spectrometry data, and provides a new means for contouring and validating electron density maps. EM∩IM thereby facilitates the use of data obtained in the gas phase within structural biology studies employing diverse experimental methodologies.
Ion mobility mass spectrometry (IM-MS) can be used to investigate the structure of large biomolecules and the complexes they assemble into.1–6 While the MS experiment provides a mass measurement, the IM dimension reports on the ability of an ion to traverse a region of low pressure that, depending on the experimental implementation,7,8 may be quantified through an orientationally averaged collision cross-section (CCS). The CCS can subsequently be exploited to validate existing atomic coordinates, assess differing candidate structures, or to guide model building directly.1–6
A number of different algorithms,9–14 tailored to specific applications, have been written to calculate the CCS of a given three-dimensional structure, allowing the relation of IM measurements to structures derived from X-ray crystallography, NMR spectroscopy, or atomic modelling.15–17 These algorithms are however limited to taking a coordinate file (e.g. pdb, or xyz format) that specifies the position in space of each constituent atom as input, meaning that detailed comparisons with structures displayed as volumes (e.g. density maps obtained by means of transmission electron microscopy, EM18,19) have not been possible. Here we present EM∩IM,‡ a computational tool that allows the display and interrogation of EM maps from the standpoint of IM-MS data. This allows the user to relate data from the two experimental techniques directly: allowing both the calculation of a CCS from an electron density map, and the exploitation of IM data to augment the interpretation of EM data.
An electron density map is typically a three-dimensional grid, with each voxel having a certain density value. In general, such a map is displayed as a volume demarcated by an isodensity surface, which is generated by specifying a contour-level, the lower electron density threshold (ρ*) for a voxel to be considered occupied. The more stringent this threshold is, the fewer voxels match the electron density criterion, and the smaller the resultant volume. Furthermore, as the electron density is typically anisotropic,18 changing the threshold can result in different shapes. Yet, despite its importance, defining the appropriate threshold is difficult, and particularly so for low resolution maps (>10 Å), where secondary structure elements are not readily identifiable.20
Our fundamental premise in designing EM∩IM was to allow calculation of mass and CCS, two physical quantities obtained in an IM-MS experiment, from an electron density map. The former is achieved simply based on the number of voxels exceeding a given electron density threshold and the voxel volume, converted into a mass using a protein density (typically 0.84 Da Å−3 (ref. 21)). To determine the CCS of an electron density map, EM∩IM converts it into a coordinate file in which hard-sphere pseudo-atoms are centred in voxels if they satisfy the given electron density threshold criterion. This approach returns a bead model similar to those generated by SEDI, an algorithm designed to generate high-resolution isodensity surfaces for small molecules.22 This coordinate file is then used to calculate a CCS using IMPACT,11 called directly from within the program, and adjusted using an empirical scaling factor to facilitate comparisons with experimental data.23
Our approach therefore provides the framework for displaying an EM map in a way that is consistent with mass and CCS data. To realise this, upon loading a map, EM∩IM performs mass and CCS calculations at a wide range of thresholds. The user is thereby able to retrieve the map that best matches experimental mass and/or CCS, or to explore the electron density as a function of IM-MS observables. EM∩IM incorporates a graphical user interface that allows the visualisation of the electron density and display of appropriate graphs, all of which can be exported in a variety of file formats.‡
CCS is a sensitive measure for contouring electron density maps
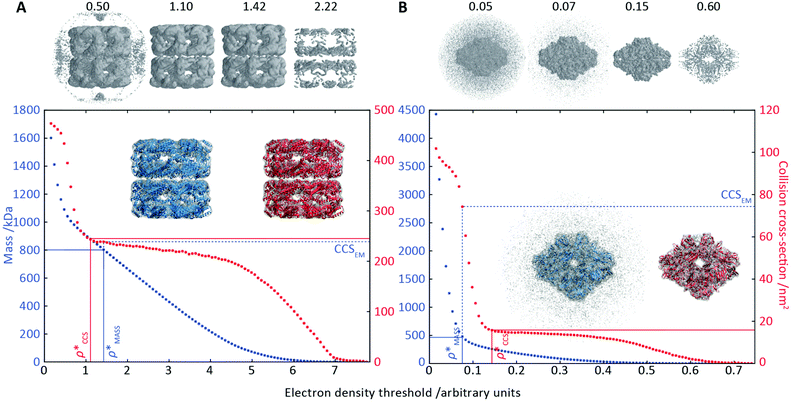
To illustrate the functionality of EM∩IM, we have examined density maps of GroEL (Fig. 1A: EMDB 1457, resolution 5.4 Å) and β-galactosidase (Fig. 1B: EMDB 2824, resolution 4.2 Å). For both proteins, the mass and CCS decrease as the threshold is increased, consistent with fewer voxels satisfying the minimum density requirement. At the extremes of these thresholds, the structures are clearly unrealistic, either missing density (at high ρ*) or including noise (at low ρ*) (Fig. 1, upper panels). However, at intermediate thresholds, the structures appear feasible yet differ noticeably in terms of overall size and shape.We used EM∩IM to determine the thresholds that reproduce the mass (801 kDa, solid blue line) and CCS (245 nm2, red) of GroEL as 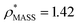 and
and 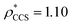 , respectively (Fig. 1A, lower panel). These ρ* values are similar, indicating that, given the mass, the CCS can in this case be estimated from the electron density to good accuracy (245 nm2, dashed blue line). Comparing the electron densities, returned by filtering either according to mass or CCS, to the GroEL crystal structure (PDB: 1SS8) reveals excellent correspondence in both cases (Fig. 1A, inset). A similar analysis for β-galactosidase returns thresholds of
, respectively (Fig. 1A, lower panel). These ρ* values are similar, indicating that, given the mass, the CCS can in this case be estimated from the electron density to good accuracy (245 nm2, dashed blue line). Comparing the electron densities, returned by filtering either according to mass or CCS, to the GroEL crystal structure (PDB: 1SS8) reveals excellent correspondence in both cases (Fig. 1A, inset). A similar analysis for β-galactosidase returns thresholds of 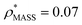 and
and 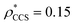 , based respectively on the known mass (465 kDa, solid blue line) and CCS (159 nm2, red) (Fig. 1B, lower panel). In this case, the ρ* values are very different: the electron density contoured according to mass corresponds to a very inaccurate CCS (743 nm2, dashed blue line) and gives a very poor fit to the crystal structure (PDB: 3IAP) (Fig. 1B, inset, left). Conversely, the density that is contoured according to CCS is in excellent agreement with the crystal structure (Fig. 1B, lower panel, right). It appears therefore that CCS is a more reliable means for obtaining a good electron density threshold than mass. This is likely due to mass being particularly prone to inaccuracies caused by regions of the protein not being well represented in the electron density, whereas the CCS is directly dependent on the demarcation of the molecular surface, rendering it extremely sensitive to noise in the electron density that appears outside the perimeter of the protein.
, based respectively on the known mass (465 kDa, solid blue line) and CCS (159 nm2, red) (Fig. 1B, lower panel). In this case, the ρ* values are very different: the electron density contoured according to mass corresponds to a very inaccurate CCS (743 nm2, dashed blue line) and gives a very poor fit to the crystal structure (PDB: 3IAP) (Fig. 1B, inset, left). Conversely, the density that is contoured according to CCS is in excellent agreement with the crystal structure (Fig. 1B, lower panel, right). It appears therefore that CCS is a more reliable means for obtaining a good electron density threshold than mass. This is likely due to mass being particularly prone to inaccuracies caused by regions of the protein not being well represented in the electron density, whereas the CCS is directly dependent on the demarcation of the molecular surface, rendering it extremely sensitive to noise in the electron density that appears outside the perimeter of the protein.
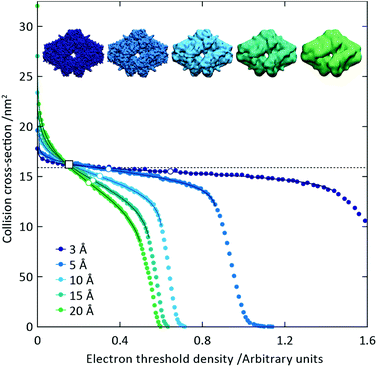
To capitalise on this sensitivity, we generated β-galactosidase maps at resolutions varying from 3 Å to 20 Å. For all resolutions, the CCS decreases rapidly as the threshold is increased, before reaching a plateau where it remains relatively constant, and then decreasing rapidly again (Fig. 2). The higher the resolution, the more “step-like” this trend appears, such that at 3 Å the CCS is largely invariant for the majority of the thresholds examined. By fitting a sigmoid function to the data we were able to determine the points of inflection (i.e. where the slope is least negative) for each resolution (Fig. 2, white circles). In all cases, these points of inflection occur at CCS values within 10% of each other and that calculated from the crystal structure (dashed line). Notably, the plots obtained for the different resolutions intersect with each other within a very narrow range, with the average intersection point (white square) occurring within 3% of the crystal structure CCS. Conversely, plots of mass versus threshold do not display similar features that might signpost the correct mass (Fig. S1†). These observations indicate that the CCS is an effective parameter for edge-detection within molecular volumes, and reveals potential routes for the coarse estimation of CCS from an EM map (and concomitantly determination of an appropriate threshold): either through determining the point of inflection within the trend of CCS as a function of threshold, by calculating points of intersection between plots obtained for down-sampled density maps.
Estimating the CCS using protein mass and electron density
In order to develop an improved means for estimating CCS from EM data, we simulated 35 electron density maps from crystal structures of proteins for which IM-MS data has been published, spanning a broad range of masses, CCSs, and electron density resolutions (Table S1†). For each of these, we computed both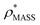 and
and 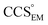 , the CCS estimated from the electron density map using
, the CCS estimated from the electron density map using 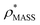 (as per the blue dashed lines, Fig. 1). For this synthetic data set, a plot of
(as per the blue dashed lines, Fig. 1). For this synthetic data set, a plot of 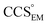 versus CCSX-RAY (that calculated from the crystal structures) reveals a linear correlation, with an average error of 8.2% (Fig. 3A and S2A†).
versus CCSX-RAY (that calculated from the crystal structures) reveals a linear correlation, with an average error of 8.2% (Fig. 3A and S2A†).
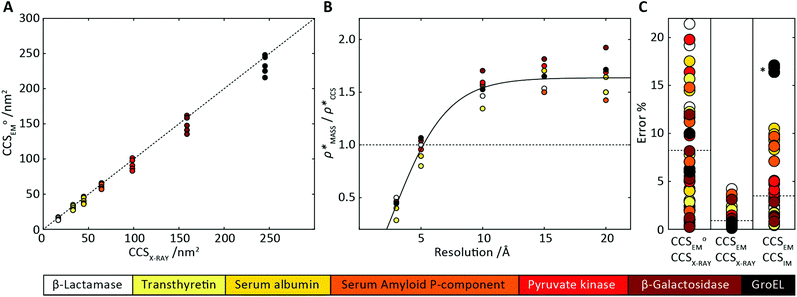 | ||
Fig. 3 Improving the prediction of CCS from mass. (A) Plot of CCSX-RAY and CCS estimated from protein mass via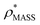 , , 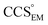 (Fig. 1), for 35 synthetic electron densities generated for a range of proteins of different size. The trend is linear, but with significant deviation from a 1 (Fig. 1), for 35 synthetic electron densities generated for a range of proteins of different size. The trend is linear, but with significant deviation from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence. (B) Examination of the data reveals that, at high resolutions, 1 correspondence. (B) Examination of the data reveals that, at high resolutions, 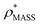 is smaller than is smaller than 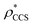 , with the opposite holding true at low resolution. Fitting their ratio with the sigmoid function , with the opposite holding true at low resolution. Fitting their ratio with the sigmoid function 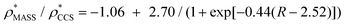 , allows for a correction in , allows for a correction in 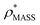 , and a resolution-calibrated CCS estimation, CCSEM. (C) When comparing , and a resolution-calibrated CCS estimation, CCSEM. (C) When comparing 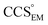 to CCSX-RAY, an average error (dashed line) of 8.2% is obtained (A). The same comparison for the corrected prediction, CCSEM return a much reduced average error of 1.2% and all maps having errors <5%. Comparing CCSEM to CCSIM shows that the experimental CCS of GroEL is poorly predicted, reflecting the collapsed gas phase conformation relative to the solution structure.25 Without these known outliers (*), the average error is 4.5%. This demonstrates that a calibrated use of mass is an effective means for extracting a CCS from an EM density, and that this CCSEM is accurate enough to identify conformations differing between solution and gas-phase measurements. to CCSX-RAY, an average error (dashed line) of 8.2% is obtained (A). The same comparison for the corrected prediction, CCSEM return a much reduced average error of 1.2% and all maps having errors <5%. Comparing CCSEM to CCSIM shows that the experimental CCS of GroEL is poorly predicted, reflecting the collapsed gas phase conformation relative to the solution structure.25 Without these known outliers (*), the average error is 4.5%. This demonstrates that a calibrated use of mass is an effective means for extracting a CCS from an EM density, and that this CCSEM is accurate enough to identify conformations differing between solution and gas-phase measurements. | ||
To examine the relationship between 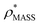 and
and 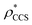 in more detail, we computed the ratio
in more detail, we computed the ratio 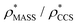 for each of the 35 maps, and plotted it as a function of the electron density resolution. A clear trend is observed (Fig. 3B): at high resolutions (≲5 Å), we find that
for each of the 35 maps, and plotted it as a function of the electron density resolution. A clear trend is observed (Fig. 3B): at high resolutions (≲5 Å), we find that 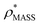 is typically smaller than
is typically smaller than 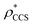 (i.e.
(i.e.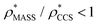 ), whereas the opposite is true at lower resolutions (≳5 Å). This means that
), whereas the opposite is true at lower resolutions (≳5 Å). This means that 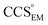 will be an overestimate of CCSX-RAY in the case of high resolution EM data, and an underestimate for low resolution EM data. To compensate for this phenomenon, we fitted the relationship between
will be an overestimate of CCSX-RAY in the case of high resolution EM data, and an underestimate for low resolution EM data. To compensate for this phenomenon, we fitted the relationship between 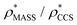 (Fig. 3B) to provide a means to rescale
(Fig. 3B) to provide a means to rescale 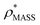 , and thereby obtain an improved estimate of CCS, CCSEM. Comparison of CCSEM with CCSX-RAY reveals a reduction in error to an average of 1.2% (Fig. 3C and S2B†). This error is less than the experimental uncertainties typical for CCS measurements,11,24 indicating that using a calibrated mass-defined threshold can lead to an acceptable CCS estimation as the basis for comparison between IM-MS and EM data. The scaling function, by virtue of being derived from a wide range of masses and resolutions, is general in its utility, however, the user could input alternatives derived from an appropriate calibration-set into EM∩IM to enable even lower error within a targeted window.
, and thereby obtain an improved estimate of CCS, CCSEM. Comparison of CCSEM with CCSX-RAY reveals a reduction in error to an average of 1.2% (Fig. 3C and S2B†). This error is less than the experimental uncertainties typical for CCS measurements,11,24 indicating that using a calibrated mass-defined threshold can lead to an acceptable CCS estimation as the basis for comparison between IM-MS and EM data. The scaling function, by virtue of being derived from a wide range of masses and resolutions, is general in its utility, however, the user could input alternatives derived from an appropriate calibration-set into EM∩IM to enable even lower error within a targeted window.
To test the selectivity of this approach, we compared CCSEM to published values obtained from IM-MS experiments,24 CCSIM (Fig. 2C). The average error is 4.5%, not including five outlying data points, all of which correspond to GroEL. This is in line with CCSIM and CCSX-RAY for this protein being known to differ, with the gas-phase conformation of GroEL being partially collapsed relative to that in solution.25 Our results demonstrate therefore that CCSEM is an informative measure, allowing the use of experimental CCS measurements to distinguish conformations different from those represented in a given EM density.
EM∩IM allows the validation of EM reconstructions
Motivated by the comparisons made with synthetic electron densities, to assess the practical utility of EM∩IM we tested our methodology on experimental EM data. For each of eleven GroEL and two β-galactosidase maps (generated by different research groups using different microscopes and different software pipelines, Table S2†) we computed CCSEM, and compared it to both the CCS obtained by IM-MS and that calculated from the proteins’ crystal structures. CCS estimation was generally poor: when using CCSX-RAY as reference, CCSEM of seven GroEL maps had errors <10%, but four had errors >20%, and both β-galactosidase predictions were incorrect by >60% (Fig. 4A). When tested against CCSIM, the majority of the predictions (not just GroEL, which can in this case be considered a negative control) had errors >20%, a level which is not commensurate with making useful comparisons between the two techniques.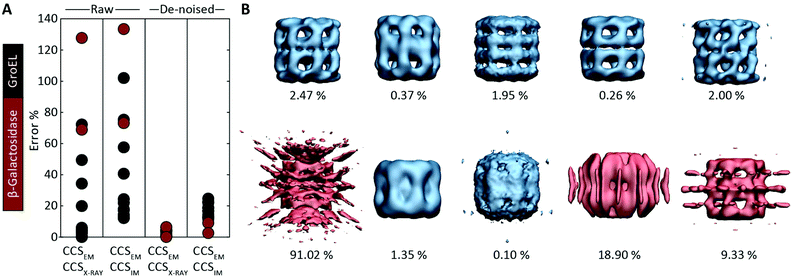 | ||
| Fig. 4 Application of CCSEM to assessing experimental electron densities. (A) Examining the relationship between CCSEM and both CCSX-RAY and CCSIM reveals very large errors. The same comparisons after using a de-noising filter implemented in EM∩IM results in vastly reduced errors, reflecting the selectivity observed in the synthetic data (Fig. 3C). (B) Comparison of CCSEM and CCSX-RAY for five correct (top) and five incorrect (bottom) GroEL initial models generated using various EM single-particle analysis algorithms.29 All of the correct reconstructions gave low errors (blue, percentage difference indicated), whereas three of the incorrect reconstructions gave large errors (red). This demonstrates the CCS measurements could be an effective means for validating or rejecting 3D models generated during EM data analysis. | ||
We hypothesised that these errors arise from the presence of noise, a common feature of experimental density maps (e.g.Fig. 1B),18 not present in our synthetic maps considered above (Fig. 2 and 3). To address this challenge, we implemented a de-noising filter in EM∩IM, based on a DBSCAN clustering algorithm.26,27 The filter acts to identify contiguous regions in the bead model obtained at the given threshold, with those regions containing less than 1% of the total beads being discarded (Fig. S3†). When we computed CCSEM on these de-noised maps we obtained excellent results: all predictions were within 7% of CCSX-RAY (Fig. 4A). When comparing to CCSIM, errors <8% were obtained for both β-galactosidase maps, while the GroEL maps yielded errors >12%. This mirrors the selectivity observed for the synthetic data (Fig. 3C), consistent with the CCSIM of GroEL being incompatible with the conformation in solution.25
Given the accuracy of our approach, we considered whether IM-MS data could in principle be useful for validating structural models obtained from EM data, an area of outstanding interest in the field.28 This challenge applies not only to the final reconstructions, but also to the initial models, which are generated early in the refinement process and can bias the resulting data processing.29 We analysed a set of ten alternative GroEL initial models, five of which are correct reconstructions, and five incorrect.29 We computed the CCSEM of each model, and compared them to the CCS determined from the GroEL crystal structure (Fig. 4B). For each of the correct reconstructions, the discrepancy in CCS was ≲2.5% (upper panel). Conversely, three of the five incorrect models had an error ≳10%, identifying them as poor representations of GroEL (lower panel). This test demonstrates therefore that CCS measurements could constitute an independent means to filter alternative reconstructions generated from EM data.
Conclusions
Here we have presented EM∩IM, software written to relate EM and IM data. We have shown that applying mass-based contouring to a de-noised electron density map allows CCS estimation within the error of a typical IM-MS experiment. Using GroEL and β-galactosidase as a test cases, we have demonstrated that this capability can be exploited such that experimental CCS values can compared directly to electron densities in order to ascertain conformational variations, as well as identifying inappropriate EM reconstructions. This opens the door to using CCS as an independent experimental means for validating EM models, a possibility that is attractive due to the relative universality and speed of the IM-MS experiment relative to other structural biology techniques.23Our work has highlighted how IM-MS and EM, though differing in the physical interactions between probe and molecule, are conceptually complementary techniques,4 a synergy that perhaps stems from both CCSs and EM reconstructions, broadly speaking, arising from the combination of orientationally averaged two-dimensional projections.30 We anticipate therefore that EM∩IM, and the approaches it enables, will be a useful addition to the growing list of hybrid methodologies that enable structural biology studies to capitalise on the benefits brought by employing multiple techniques.31,32
Acknowledgements
We thank: Erik Marklund (University of Oxford) for providing IMPACT11 as a library and, with Timothy Allison (University of Oxford), critical appraisal of the manuscript; Carlos Oscar Sorzano and Jose Maria Carazo (Spanish National Centre for Biotechnology) for providing the GroEL initial models;29 and Anthony Fitzpatrick (University of Cambridge) for helpful discussions. MTD is supported by the Swiss National Science Foundation, and JLPB is a Royal Society University Research Fellow.Notes and references
- A. Konijnenberg, A. Butterer and F. Sobott, Biochim. Biophys. Acta, 2013, 1834, 1239–1256 CrossRef CAS PubMed.
- M. Sharon, Science, 2013, 340, 1059–1060 CrossRef CAS PubMed.
- J. Snijder and A. J. Heck, Annu. Rev. Anal. Chem., 2014, 7, 43–64 CrossRef CAS PubMed.
- K. Thalassinos, A. P. Pandurangan, M. Xu, F. Alber and M. Topf, Structure, 2013, 21, 1500–1508 CrossRef CAS PubMed.
- T. Wyttenbach, N. A. Pierson, D. E. Clemmer and M. T. Bowers, Annu. Rev. Phys. Chem., 2014, 65, 175–196 CrossRef CAS PubMed.
- Y. Zhong, S. J. Hyung and B. T. Ruotolo, Expert Rev. Proteomics, 2012, 9, 47–58 CrossRef CAS PubMed.
- A. B. Kanu, P. Dwivedi, M. Tam, L. Matz and H. H. Hill Jr., J. Mass Spectrom., 2008, 43, 1–22 CrossRef CAS PubMed.
- J. L. P. Benesch, B. T. Ruotolo, D. A. Simmons and C. V. Robinson, Chem. Rev., 2007, 107, 3544–3567 CrossRef CAS PubMed.
- C. Bleiholder, T. Wyttenbach and M. T. Bowers, Int. J. Mass Spectrom., 2011, 308, 1–10 CrossRef CAS.
- C. Larriba and C. J. Hogan Jr., J. Comput. Phys., 2013, 251, 344–363 CrossRef CAS.
- E. G. Marklund, M. T. Degiacomi, C. V. Robinson, A. J. Baldwin and J. L. P. Benesch, Structure, 2015, 23, 791–799 CrossRef CAS PubMed.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef CAS.
- A. A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 1996, 261, 86–91 CrossRef CAS.
- G. Von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182–8192 CrossRef CAS.
- E. Jurneczko and P. E. Barran, Analyst, 2011, 136, 20–28 RSC.
- M. M. Maurer, G. C. Donohoe and S. J. Valentine, Analyst, 2015, 140, 6782–6798 RSC.
- C. Uetrecht, R. J. Rose, E. van Duijn, K. Lorenzen and A. J. Heck, Chem. Soc. Rev., 2010, 39, 1633–1655 RSC.
- E. V. Orlova and H. R. Saibil, Chem. Rev., 2011, 111, 7710–7748 CrossRef CAS PubMed.
- E. Nogales and S. H. Scheres, Mol. Cell, 2015, 58, 677–689 CrossRef CAS PubMed.
- C. Bajaj, S. Goswami and Q. Zhang, J. Struct. Biol., 2012, 177, 367–381 CrossRef CAS PubMed.
- H. Fischer, I. Polikarpov and A. F. Craievich, Protein Sci., 2004, 13, 2825–2828 CrossRef CAS PubMed.
- Y. Alexeev, D. G. Fedorov and A. A. Shvartsburg, J. Phys. Chem. A, 2014, 118, 6763–6772 CrossRef CAS PubMed.
- J. L. P. Benesch and B. T. Ruotolo, Curr. Opin. Struct. Biol., 2011, 21, 641–649 CrossRef CAS PubMed.
- M. F. Bush, Z. Hall, K. Giles, J. Hoyes, C. V. Robinson and B. T. Ruotolo, Anal. Chem., 2010, 82, 9557–9565 CrossRef CAS PubMed.
- C. J. Hogan Jr., B. T. Ruotolo, C. V. Robinson and J. Fernandez de la Mora, J. Phys. Chem. B, 2011, 115, 3614–3621 CrossRef PubMed.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), ed. E. Simoudis, J. Han and U. M. Fayyad, AAAI Press, Portland, Oregon, USA, 1996, vol. 96, pp. 226–231 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- R. Henderson, A. Sali, M. L. Baker, B. Carragher, B. Devkota, K. H. Downing, E. H. Egelman, Z. Feng, J. Frank, N. Grigorieff, W. Jiang, S. J. Ludtke, O. Medalia, P. A. Penczek, P. B. Rosenthal, M. G. Rossmann, M. F. Schmid, G. F. Schroder, A. C. Steven, D. L. Stokes, J. D. Westbrook, W. Wriggers, H. Yang, J. Young, H. M. Berman, W. Chiu, G. J. Kleywegt and C. L. Lawson, Structure, 2012, 20, 205–214 CrossRef CAS PubMed.
- C. O. Sorzano, J. Vargas, J. M. de la Rosa-Trevin, J. Oton, A. L. Alvarez-Cabrera, V. Abrishami, E. Sesmero, R. Marabini and J. M. Carazo, J. Struct. Biol., 2015, 189, 213–219 CrossRef CAS PubMed.
- A. J. Baldwin, H. Lioe, G. R. Hilton, L. E. Kay and J. L. P. Benesch, Structure, 2011, 19, 1855–1863 CrossRef CAS PubMed.
- G. C. Lander, H. R. Saibil and E. Nogales, Curr. Opin. Struct. Biol., 2012, 22, 627–635 CrossRef CAS PubMed.
- A. B. Ward, A. Sali and I. A. Wilson, Science, 2013, 339, 913–915 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5an01636c |
| ‡ EM∩IM is written in the Python programming language, and can be run using a graphical user interface (GUI) or from the command line, in Windows, Linux/Unix, and Mac OS X, all available for download at http://EMnIM.chem.ox.ac.uk/, together with documentation for usage and installation. |
| This journal is © The Royal Society of Chemistry 2016 |