Open Access Article
Open Access ArticleNanoplasmonic ruler to measure lipid vesicle deformation†
Joshua A.
Jackman
a,
Barbora
Špačková
b,
Eric
Linardy
a,
Min Chul
Kim
a,
Bo Kyeong
Yoon
a,
Jiří
Homola
b and
Nam-Joon
Cho
*ac
aSchool of Materials Science and Engineering and Centre for Biomimetic Sensor Science, Nanyang Technological University, 50 Nanyang Avenue 639798, Singapore. E-mail: njcho@ntu.edu.sg; Tel: +65-6592-7945
bInstitute of Photonics and Electronics, Academy of Science of the Czech Republic, Chaberska 57, Prague 8 18251, Czech Republic
cSchool of Chemical and Biomedical Engineering, Nanyang Technological University, 62 Nanyang Drive 637459, Singapore
First published on 1st October 2015
Abstract
A nanoplasmonic ruler method is presented in order to measure the deformation of adsorbed, nm-scale lipid vesicles on solid supports. It is demonstrated that single adsorbed vesicles undergo greater deformation on silicon oxide over titanium oxide, offering direct experimental evidence to support membrane tension-based theoretical models of supported lipid bilayer formation.
Vesicle fusion on solid supports mimics important biological phenomena and enables the fabrication of supported lipid bilayer (SLB) coatings for bionanotechnology applications.1–3 Numerous experimental and theoretical approaches have been developed in order to understand the vesicle fusion process, which involves vesicle adsorption, deformation, and rupture before molecular self-assembly promotes SLB formation.4–6 Nevertheless, fundamental questions remain unanswered in the vesicle-to-bilayer transformation. A classic example is the adsorption of small unilamellar vesicles onto silicon oxide versus titanium oxide. Theory predicts that adsorbed vesicles on titanium oxide would be more deformed and stressed due to an appreciably stronger lipid–substrate interaction.7–11 In turn, it is expected that adsorbed vesicles on titanium oxide are more likely to rupture and form SLBs. However, strikingly, the opposite is experimentally observed. SLBs efficiently form on silicon oxide, whereas adsorbed vesicles do not typically rupture on titanium oxide.10,12 Evidence to reconcile experiment and theory has been stymied by technical difficulties with detecting intermediate stages in the vesicle fusion process.13 The most challenging problem is to measure the deformation of adsorbed vesicles in the stage preceding vesicle rupture. Direct characterization of adsorbed vesicles with atomic force microscopy is hindered by the dynamic nature of the SLB formation process.14 Vesicle deformation remains a critical yet poorly understood step in the SLB formation process because it destabilizes the vesicles and makes them fusogenic and prone to rupture.15 Recently, we described a nanoplasmonic biosensing approach in order to detect the deformation of adsorbed, intact vesicles on titanium oxide.16 A similar concept was extended in order to measure the relative deformation of adsorbed vesicles on titanium oxide at different temperatures.17 Based on these foundation studies, the potential of nanoplasmonic biosensing to detect vesicle deformation is evident and suggests that vesicle deformation on different substrates can be directly compared. However, quantitative comparison of vesicle deformation on different substrates requires a delicate approach because the surface sensitivity of the plasmonic sensor depends on many factors and can vary from the bulk sensitivity or decay length of the electromagnetic field.18–23 Herein, we propose a nanoplasmonic ruler concept in order to compare vesicle deformation on silicon oxide- and titanium oxide-coated gold nanodisk arrays, offering direct experimental evidence to understand how vesicle deformation contributes to SLB formation.
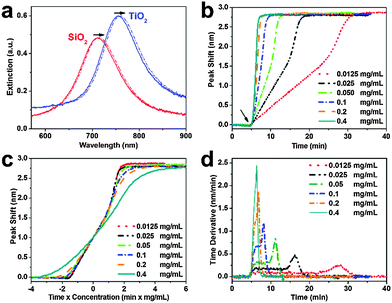
We first report characterization of the morphological and plasmonic properties of the experimental plasmonic substrates. Hole-mask colloidal lithography is employed to fabricate ca. 100 nm diameter gold nanodisks with ∼8% surface coverage and random arrangement on a glass substrate, followed by sputtering a 10 nm thick conformal dielectric layer of silicon oxide or titanium oxide on top of the substrate24 (Fig. 1a). Scanning electron microscopy experiments demonstrate that the coated nanodisks have approximately 120 nm diameter as expected (Fig. 1b). Aside from the material composition of the dielectric layer, the substrates are morphologically identical. Fig. 1c shows the calculated distribution of total electric field intensity at resonance for the representative case of silicon oxide-coated nanodisks. A similar result is obtained for titanium oxide-coated nanodisks. In both cases, the electromagnetic field is highly concentrated at the edges of the gold nanodisk and decreases from the vesicle–substrate contact proportionally to 1/(z + R*)3 where z is the coordinate perpendicular to the substrate surface (z = 0 corresponds to the vesicle–substrate contact). R* is the length scale characterizing the distance between the center of the nanodisk and vesicle–substrate contact;16 it includes the dielectric layer covering the nanoparticles and averaged length scale of a gold nanoparticle, and it is also proportional to the decay length of the electromagnetic field. Experimental extinction spectra of both nanostructures show close agreement with 3D finite-difference time-domain (FDTD) simulations (Fig. S1, ESI†). Taking into account the spatial distribution of the electromagnetic field as well as the spatial distribution of the refractive index of the vesicles, treated as a truncated sphere with a circular vesicle–substrate contact area of radius a and radius r* (see Fig. 1a), the LSPR shift due to vesicle adsorption onto the substrate can be expressed as
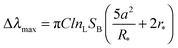 | (1) |
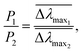 | (2) |
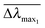 and
and 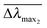 are normalized shifts of the resonance wavelength to the bulk sensitivities of the titanium oxide and silicon oxide substrates, respectively. The parameters SB and R* were determined from the spatial dependence of the sensitivity (Fig. 1d). The results show that SB is approximately 1.2 times higher for the titanium oxide-coated substrate than for the silicon oxide-coated substrate. The values of parameter R* for the two nanostructures differ only slightly (due to different optical thicknesses of the two dielectric layers covering the nanoparticles) and therefore we can assume that the decay length of the field of the two nanostructures are approximately the same and that the surface sensitivities can be compared in terms of bulk sensitivities.
are normalized shifts of the resonance wavelength to the bulk sensitivities of the titanium oxide and silicon oxide substrates, respectively. The parameters SB and R* were determined from the spatial dependence of the sensitivity (Fig. 1d). The results show that SB is approximately 1.2 times higher for the titanium oxide-coated substrate than for the silicon oxide-coated substrate. The values of parameter R* for the two nanostructures differ only slightly (due to different optical thicknesses of the two dielectric layers covering the nanoparticles) and therefore we can assume that the decay length of the field of the two nanostructures are approximately the same and that the surface sensitivities can be compared in terms of bulk sensitivities.
 | ||
| Fig. 1 Sensing properties of oxide-coated plasmonic gold nanodisks. (a) Schematic of the sensing scenario. (b) SEM micrograph of a silicon oxide-coated nanodisk array. Scale bar is 100 nm. (c) FDTD simulation of the total electric field intensity distribution at resonance. (d) FDTD simulation of surface sensitivity SS as a function of the thickness (D) of the layer within which the refractive index change occurs. Dots represents the results of the simulations, and the lines represent the fits to eqn (S2) in ESI.† (e) LSPR peak shift as a function of ΔRIU in glycerol/water mixtures. Linear fits show bulk RI sensitivity (nm/RIU). (f) LSPR peak shift as a function of time in response to SLB formation on the two substrates. Vesicles were added at t = 5 min. | ||
To compare the measurement sensitivities of the two plasmonic substrates, the bulk and surface sensitivities were experimentally determined. Bulk refractive index (RI) sensitivity experiments were conducted via titration of glycerol–water mixtures (0–35 wt% glycerol). In the measurement range, the peak shifts exhibited a linear dependence on the refractive index, and the corresponding slopes yielded the bulk RI sensitivities (Fig. 1e). The titanium oxide- and silicon oxide-coated substrates had bulk RI sensitivities of 123 and 94 nm per RIU, respectively. These values demonstrate that the titanium oxide-coated substrate has a 1.3-fold higher bulk RI sensitivity. To further compare surface sensitivities in the local environment, SLBs (∼4 nm thickness) were fabricated on the two substrates, well within the optical near field of the plasmonic nanodisks. The SLB on silicon oxide was formed using conventional 70 nm diameter zwitterionic 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid vesicles in 10 mM Tris buffer [pH 7.5] with 150 mM NaCl. In order to form an SLB on titanium oxide, it was necessary to use similar-size vesicles with a 50/50 mol% mixture of POPC and positively charged 1-palmitoyl-2-oleoyl-sn-glycero-3-ethylphosphocholine (POEPC) lipids.25 On both substrates, the baseline was recorded in buffer solution and the vesicles were added at t = 5 min (Fig. 1f, see arrow).The corresponding peak shifts for SLBs on the silicon oxide- and titanium oxide-coated substrates were 2.77 and 3.55 nm, respectively. Because the optical properties of SLBs are identical in both cases, we conclude that the titanium oxide-coated substrate has a 1.28-fold higher surface sensitivity than the silicon oxide-coated substrate. Together with the simulation results, the close agreement between the bulk and surface sensitivities of the two substrates supports that the measurement responses can be quantitatively compared by normalizing the peak shifts to bulk sensitivities. This verification enables us to perform identical vesicle adsorption experiments on the two substrates in a flow-through microfluidic configuration. While redshifts are observed for vesicle adsorption on both substrates, the magnitude of the shifts do not distinguish between SLB formation and strictly vesicle adsorption, motivating detailed kinetic analysis (Fig. 2a). In the rest of experiments, 70 nm diameter POPC lipid vesicles were exclusively used in order to obtain SLBs on silicon oxide and adsorbed vesicle layers on titanium oxide.
Vesicle adsorption, deformation, and rupture on silicon oxide-coated nanodisks were next tracked across a range of bulk lipid concentrations (0.0125–0.4 mg mL−1) (Fig. 2b). The initial rate of increase in the LSPR signal had a linear slope followed by rate acceleration, which is indicative of vesicle rupture after reaching a critical coverage of adsorbed vesicles.26 With increasing lipid concentration, the time scale of vesicle adsorption and rupture process was shorter. The final peak shift was 2.77 ± 0.12 nm independent of lipid concentration. In order to analyze the vesicle-to-bilayer structural transformation, the adsorption kinetics were also constructed as a function of ct where c is the bulk lipid concentration and t is time (Fig. 2c). As expected, the curves nearly overlap indicating that the structural transformation follows a similar sequence of steps at all tested concentrations.27 This finding verifies that the LSPR measurement technique is suitable for quantitative analysis of the SLB formation process within the tested concentration range (up to 0.2 mg mL−1 based on the experimental configuration).
To further scrutinize the kinetics of bilayer formation, the time derivative of the adsorption kinetics was plotted (Fig. 2d and Fig. S2, ESI†). During the initial adsorption stage, a constant rate of change in the LSPR signal was observed that varied according to the bulk lipid concentration. This constant rate arises from diffusion-limited irreversible adsorption of vesicles which is known to occur on both substrates.12,16,28 After reaching a critical surface coverage of adsorbed vesicles on the substrate, an acceleration in the rate occurred as adsorbed vesicles begin to fuse and rupture to form the SLB. The surface coverage of adsorbed vesicles at the critical coverage was calculated by taking into account the diffusion flux of vesicle adsorption to the substrate as well as the time interval from initial adsorption until rate acceleration began.16 Using this approach, the calculated surface coverage fraction was ∼0.22 at all lipid concentrations, which is in agreement with previous optical mass measurements.29 In order to confirm SLB formation, fluorescence recovery after photobleaching (FRAP) measurements were also performed (Fig. S3, ESI†).30
In parallel with the LSPR measurements described above on silicon oxide-coated nanodisks, similar experiments were conducted on titanium oxide-coated nanodisks. Specifically, the same batch of vesicles and identical flow conditions were used. In Fig. 3a, representative sensorgrams of 0.1 mg mL−1 lipid vesicle adsorption onto the two substrates are presented for comparison. On titanium oxide, vesicles adsorb until forming a saturated layer.32 Here, we focus on the initial linear rates of change in the LSPR signals (equivalent to the constant rate observed in the time derivative plots). Despite lower surface sensitivity, the experimentally-tracked initial rate on the silicon oxide substrate was larger even though the diffusion flux of vesicles to the substrate is equivalent on both substrates. To quantitatively compare the results obtained on the two substrates, the experimental data was normalized based on the bulk RI sensitivity and is presented in RI units (Fig. 3b). The explicit difference in the normalized rate of change in the LSPR signal is presented in Fig. 3c for the representative case. During the initial adsorption stage, the rate is ∼1.6-fold higher on silicon oxide. Similar results were also obtained at other lipid concentrations, and the average rate difference was 1.61 ± 0.07 across the different lipid concentrations (Fig. S4–S6, ESI†). The experimental data support that vesicle adsorption onto silicon oxide contributes to a greater rate of change in the LSPR signal.
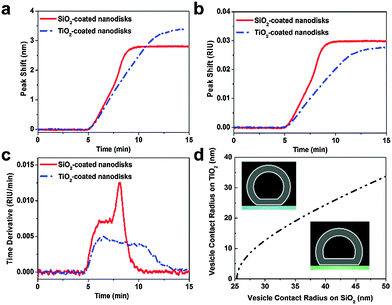 | ||
| Fig. 3 Nanoplasmonic ruler to measure lipid vesicle deformation. (a) Comparison of LSPR peak shifts as a function of time upon 0.1 mg mL−1 POPC lipid vesicle addition. (b) Normalized LSPR peak shifts from panel a according to the experimentally determined bulk RI sensitivity of each substrate (cf.Fig. 1e). (c) Time derivative of the normalized peak shift from panel b. (d) Calculated variation in contact radius of adsorbed vesicles on silicon oxide versus titanium oxide. | ||
To interpret this finding, we recall general equations that describe the effect of deformation of single vesicles on the LSPR signal17 and can be applied to analyse the experimental data obtained in the initial stage of vesicle adsorption on both substrates. If a single adsorbed vesicle is deformed, then its individual contribution to the corresponding LSPR signal will increase relative to a non-deformed adsorbed vesicle because lipids are, on average, nearer to the nanodisk.31 Here, we extend this model in order to measure the relative deformation of adsorbed vesicles on silicon oxide versus titanium oxide. Details of the calculations are provided in the ESI.† In line with the nanoplasmonic ruler concept, adsorbed vesicles on titanium oxide serve as a reference measurement in order to calculate the relative change in vesicle deformation on silicon oxide. While the exact degree of deformation for adsorbed vesicles on titanium oxide is not known, the corresponding signal enhancement can be calculated as a function of the vesicle contact radius which increases with increasing deformation. By taking into account that the signal enhancement for the adsorption of a single vesicle on silicon oxide is 1.61-fold greater than on titanium oxide, we calculate the corresponding vesicle contact radius. This approach allows us to compare the vesicle contact radii on titanium oxide and silicon oxide as presented in Fig. 3d. This analysis shows the trends in vesicle deformation on the two substrates, and indicates that the extent of vesicle deformation on silicon oxide is appreciably greater than on titanium oxide. Taking into consideration a membrane tension-based model to explain vesicle rupture, the calculations offer excellent agreement with past experimental observations that adsorbed vesicles on silicon oxide are more fusogenic than comparable vesicles on titanium oxide.
To understand the physical basis for the different behaviors of adsorbed vesicles on the two substrates, we recall that vesicle deformation is related to the vesicle–substrate contact energy.28,33 Extended-DLVO calculations9,26,34–36 have estimated the total interaction energy of vesicle–substrate attachment based on the van der Waals and double-layer electrostatic forces as well as the hydration force. A key factor, albeit without explicitly determined value, in this model is the magnitude of the hydration force.10,36 If the magnitude is assumed to be the same on both substrates, then calculations predict that the vesicle–substrate contact energy on titanium oxide is greater, which contrasts with the experimental results. With the first direct evidence of greater vesicle deformation on silicon oxide versus titanium oxide reported in this study, it is clear that the contact energy for adsorbed vesicles on silicon oxide is greater which conversely suggests that the hydration force is greater on titanium oxide. This finding is consistent with previous results discussed for peptide and protein adsorption,37,38 and supports that there is a close relationship between the various interfacial forces which govern adsorption processes. Collectively, the study presents a nanoplasmonic ruler method to measure vesicle deformation on solid supports. Based on this measurement approach, there is significant opportunity to further investigate the surface chemistry and interfacial science of SLBs and related systems.
This work was supported by the National Research Foundation (NRF-NRFF2011-01), the National Medical Research Council (NMRC/CBRG/0005/2012), and the Czech Science Foundation (contract # P205/12/G118). The authors thank Dr Olof Andersson and Dr Jeongeun Seo for technical assistance, and Dr Nicholas Scott Lynn for valuable discussions and comments.
Notes and references
- J. T. Groves and S. G. Boxer, Acc. Chem. Res., 2002, 35, 149–157 CrossRef CAS PubMed.
- E. T. Castellana and P. S. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS.
- A. Mashaghi, S. Mashaghi, I. Reviakine, R. M. Heeren, V. Sandoghdar and M. Bonn, Chem. Soc. Rev., 2014, 43, 887–900 RSC.
- C. Keller and B. Kasemo, Biophys. J., 1998, 75, 1397–1402 CrossRef CAS PubMed.
- P. S. Cremer and S. G. Boxer, J. Phys. Chem. B, 1999, 103, 2554–2559 CrossRef CAS.
- J. Pawłowski, J. Juhaniewicz, A. Güzeloğlu and S. Sek, Langmuir, 2015 DOI:10.1021/acs.langmuir.5b01331.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768 CrossRef CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- R. Tero, T. Ujihara and T. Urisu, Langmuir, 2008, 24, 11567–11576 CrossRef CAS PubMed.
- J. A. Jackman, G. H. Zan, Z. Zhao and N.-J. Cho, Langmuir, 2014, 30, 5368–5372 CrossRef CAS PubMed.
- E. N. Towns, A. N. Parikh and D. P. Land, J. Phys. Chem. C, 2015, 119, 2412–2418 CAS.
- E. Reimhult, F. Höök and B. Kasemo, Langmuir, 2003, 19, 1681–1691 CrossRef CAS.
- J. Andrecka, K. M. Spillane, J. Ortega-Arroyo and P. Kukura, ACS Nano, 2013, 7, 10662–10670 CrossRef CAS PubMed.
- H. Schönherr, J. M. Johnson, P. Lenz, C. W. Frank and S. G. Boxer, Langmuir, 2004, 20, 11600–11606 CrossRef PubMed.
- K. Dimitrievski, Langmuir, 2010, 26, 3008–3011 CrossRef CAS PubMed.
- J. A. Jackman, V. P. Zhdanov and N.-J. Cho, Langmuir, 2014, 30, 9494–9503 CrossRef CAS PubMed.
- E. Oh, J. A. Jackman, S. Yorulmaz, V. P. Zhdanov, H. Lee and N.-J. Cho, Langmuir, 2015, 31, 771–781 CrossRef CAS PubMed.
- K. M. Mayer and J. H. Hafner, Chem. Rev., 2011, 111, 3828–3857 CrossRef CAS PubMed.
- J. Li, J. Ye, C. Chen, L. Hermans, N. Verellen, J. Ryken, H. Jans, W. Van Roy, V. V. Moshchalkov and L. Lagae, Adv. Opt. Mater., 2015, 3, 176–181 CrossRef CAS.
- J. Li, J. Ye, C. Chen, Y. Li, N. Verellen, V. V. Moshchalkov, L. Lagae and P. Van Dorpe, ACS Photonics, 2015, 2, 425–431 CrossRef CAS.
- F. Mazzotta, T. W. Johnson, A. B. Dahlin, J. Shaver, S.-H. Oh and F. Höök, ACS Photonics, 2015, 2, 256–262 CrossRef CAS.
- L. Guo, J. A. Jackman, H.-H. Yang, P. Chen, N.-J. Cho and D.-H. Kim, Nano Today, 2015, 10, 213–239 CrossRef CAS.
- J. Jose, L. R. Jordan, T. W. Johnson, S. H. Lee, N. J. Wittenberg and S. H. Oh, Adv. Funct. Mater., 2013, 23, 2812–2820 CrossRef CAS.
- H. Fredriksson, Y. Alaverdyan, A. Dmitriev, C. Langhammer, D. S. Sutherland, M. Zäch and B. Kasemo, Adv. Mater., 2007, 19, 4297–4302 CrossRef CAS.
- A. Kunze, P. Sjövall, B. Kasemo and S. Svedhem, J. Am. Chem. Soc., 2009, 131, 2450–2451 CrossRef CAS PubMed.
- H. Z. Goh, J. A. Jackman, S.-O. Kim and N.-J. Cho, Small, 2014, 10, 4828–4832 CrossRef PubMed.
- C. Keller, K. Glasmästar, V. Zhdanov and B. Kasemo, Phys. Rev. Lett., 2000, 84, 5443 CrossRef CAS PubMed.
- V. Zhdanov, C. Keller, K. Glasmästar and B. Kasemo, J. Chem. Phys., 2000, 112, 900–909 CrossRef CAS.
- A. Mashaghi, M. Swann, J. Popplewell, M. Textor and E. Reimhult, Anal. Chem., 2008, 80, 3666–3676 CrossRef CAS PubMed.
- P. Jönsson, M. P. Jonsson, J. O. Tegenfeldt and F. Höök, Biophys. J., 2008, 95, 5334–5348 CrossRef PubMed.
- M. P. Jonsson, P. Jönsson, A. B. Dahlin and F. Höök, Nano Lett., 2007, 7, 3462–3468 CrossRef CAS PubMed.
- I. Reviakine, F. F. Rossetti, A. N. Morozov and M. Textor, J. Chem. Phys., 2005, 122, 204711 CrossRef PubMed.
- V. Zhdanov and B. Kasemo, Langmuir, 2001, 17, 3518–3521 CrossRef CAS.
- H. Nabika, A. Fukasawa and K. Murakoshi, Phys. Chem. Chem. Phys., 2008, 10, 2243–2248 RSC.
- J. A. Jackman, J.-H. Choi, V. P. Zhdanov and N.-J. Cho, Langmuir, 2013, 29, 11375–11384 CrossRef CAS PubMed.
- J. A. Jackman, S. R. Tabaei, Z. Zhao, S. Yorulmaz and N.-J. Cho, ACS Appl. Mater. Interfaces, 2014, 7, 959–968 Search PubMed.
- V. Zhdanov and B. Kasemo, Langmuir, 2001, 17, 5407–5409 CrossRef CAS.
- M. Mochizuki, M. Oguchi, S.-O. Kim, J. A. Jackman, T. Ogawa, G. Lkhamsuren, N.-J. Cho and T. Hayashi, Langmuir, 2015, 31, 8006–8012 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods, theoretical aspects, and characterization data. See DOI: 10.1039/c5cc06861d |
| This journal is © The Royal Society of Chemistry 2016 |