Two-dimensional polymers: concepts and perspectives

Abstract

Creation of polymers comprised of repeat units that can create topologically planar macromolecules (rather than linear) has been the topic of several recent studies in the field of synthetic polymer chemistry. Such novel macromolecules, known as 2D polymers, are the result of advanced synthetic methodology which allows creation of monolayer sheets with a periodic internal structure and functional groups placed at predetermined sites under mild conditions. Given the promising potentials of 2D polymers, this feature paper aims at discussing the concept of these novel macromolecules from a topological viewpoint in Section 1. This is followed by spotlighting the expected behavior of 2D polymers in the context of polymer physics (entropy elasticity, strength, percolation, and persistence) and polymer chemistry (copolymers and growth kinetics) in Section 2. Section 3 delineates synthetic and analytical matters associated with 2D polymers followed by a brief final section highlighting the potential of these sheet-like macromolecules for application purposes. We hope this article will trigger the interest of chemists, physicists and engineers to help develop this encouraging new class of materials further such that societally relevant applications will be accessible in the market soon.

---

Payam Payamyar

Payam Payamyar studied Polymer Engineering at Tehran Polytechnic in Iran before joining the Swiss Federal Institute of Technology (ETH Zurich) to pursue his PhD at the Department of Materials. His dissertation on characterization of two-dimensional (2D) polymers was carried out under the mentorship of Prof. A. Dieter Schlüter and was recognized by the ETH Medal. He is currently a postdoctoral researcher with a focus on determination of long-range structural order in 2D polymers by means of transmission electron microscopy (Dr Rolf Erni's group, EMPA Dübendorf). Alongside polymers, Payam is interested in the study of colloidal systems and glassy materials.

Benjamin T. King

Benjamin T. King is a professor of organic chemistry at the chemistry department of the University of Nevada, Reno, USA, since 2003. He studied chemistry at Northeastern University, Boston, USA, and received a PhD with Prof. Josef Michl at the University of Colorado, Boulder, USA. Thereafter he did a postdoc with Robert G Bergman at the University of California, Berkeley, USA. Since 2014 he is a R.C. Fuson professor at UNR and is now the chairman of the chemistry department. His research interests are in the area of organic and physical chemistry and recently also in the direction of materials chemistry.

Hans Christian Öttinger

Hans Christian Öttinger has been a professor of polymer physics at the Materials Department of ETH Zürich since 1996. He studied physics at the University of Freiburg, Germany, and received a PhD in 1983. After a postdoc position at the Rheology Research Center of the University of Wisconsin, Madison, USA (1986–87), he completed his habilitation at the University of Freiburg (1988) and then moved to ETH Zürich (1989). His research interests are in the area of nonequilibrium statistical thermodynamics and the emergence of irreversible phenomena.

A. Dieter Schlüter

A. Dieter Schlüter is a professor o polymer chemistry at the Materials Department of ETH Zürich since 2004. He studied chemistry and geophysics at the University of Munich and received a PhD in 1984. Thereafter he worked at the UC Berkeley, USA, the University of Durham, UK, MPI for Polymer Research, Mainz, Germany, Karlsruhe Institute of Technology, Germany, Free University of Berlin, Germany, and ETH Zürich. Since 2012 he is an elected member of the Swiss Academy of Engineering Sciences. His research interests are in the area of polymer synthesis.

---

Introduction

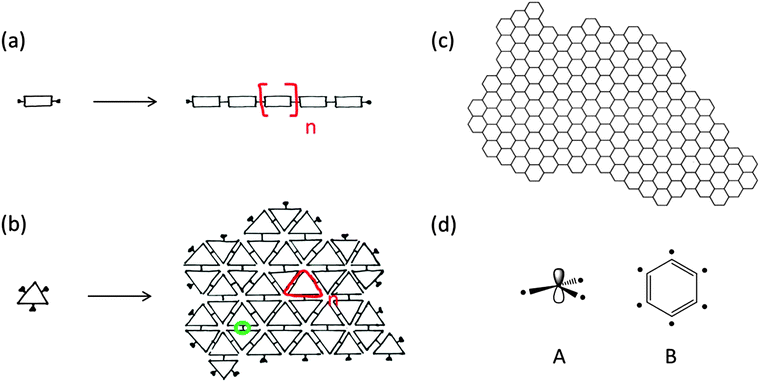
The existence of covalent macromolecules – also referred to as polymers – was proposed by Hermann Staudinger in the early 1920s.¹ For the time, the concept of polymers was considered inconceivable and important contemporaries of Staudinger opposed his views. Many were convinced of the role of weak intermolecular forces among small molecules as the cause of the properties observed for materials such as natural rubber. Staudinger, persistently, continued carrying out experiments that eventually showed the presence of macromolecules composed of small repetitive elements called as repeat units. A particularly suggestive experiment was hydrogenation of natural rubber through which he ruled out the relevance of π–π forces as the cause of the observed elasticity.² Repeat units are covalently attached to one another in a linear fashion resulting in chain-like backbones, which is the key structural feature of polymers (Fig. 1a). In 2015, almost 100 years later, this widespread disbelief in macromolecules that Staudinger encountered appears almost unimaginable: the yearly production of polymers has reached the order of 300 Mt and macromolecules have impacted everybody's daily life to a degree unforeseeable in the 1920s.³ It is thus not exaggerated to say that Staudinger's vision of long chain-like molecules has changed the world.

Fig. 1 (a) Sketch of a linear macromolecule composed of linearly attached repeat units represented by rectangular boxes. The number of repeat units and, thus, the length of the chain is given by the number n. (b) Sketch of a 2D polymer or a “molecular fisherman's net” composed of laterally connected, topologically planar repeat units represented by triangles. The expanse of the macromolecule is given by the number n, which is correlated to molecular weight. The circle marks one of the three covalent connections between repeat units. (c) Chemical structure of a small section of graphene with the double bonds omitted for clarity. (d) Two of the many possible repeat units to describe the entire expanse of a graphene sheet. (A) sp²-hybridized carbon atom and (B) benzene ring with six radical centers at its sp²-hybridized carbon atoms.

At this point we would like to leave the macromolecular chains behind for a moment despite their unrivalled importance and unchallenged beauty and rather enter into a discussion of polymers from a dimensionality point of view. We do so to shed light on the fact that polymers are not intrinsically limited to being chain-like, one dimensional structures and that their enormous success carries the danger of disguising the view for other spatial dimensions of the repeat units. Let us start the discussion of dimensionality by considering the great importance of 2D materials because of their spatial confinement along one axis of the space. Thin films are in fact famous for many scientific and applied purposes exactly because of such spatial confinement which triggers unique physical, chemical, electronic and mechanical properties. While confinement to two dimensions is thus the cause of many important features of materials, it does not provide a molecular scale perspective. By entering the world of polymers – where molecular precision is essential (consider e.g. the influence of tacticity in chiral polymers) – this shortcoming becomes even more evident. Therefore, we would like to attribute the dimensionality of polymers to their most basic building blocks, namely the repeat units. In fact, there are repeat units that can be attached to one another on a hypothetical planar scaffold rather than a line (Fig. 1b). A famous example of such nature is graphene (Fig. 1c) in which every sp²-hybridized carbon atom serves as a repeat unit with planar recurrence that results in a sheet-like macromolecule i.e. two-dimensional (2D) polymers (Fig. 1d). Graphene,⁴ boron nitride, dichalcogenides, and complex oxides⁵ have pushed the boundaries of electronics, optics and mechanics to new horizons, impressively showing the enormous potential that lies in two-dimensional extensions.

Despite the major progress made so far in the field of synthesis and characterization of 2D materials, it is still a major challenge to produce 2D polymers on a predetermined lateral scale (nm² up to m²) with avoidance of harsh thermolytic conditions^6,7 and instead with the use of the mild repertoires that organic-chemistry-based syntheses offer.⁸ As a famous example, the widely used synthesis of graphene on arbitrary aerial scales is achieved mainly upon oxidation of methane on copper substrates. However, upon thinking of structures different from graphene, one immediately notices the lack of synthetic recipes (harsh or mild) for making them on predetermined lateral scales.

The synthesis of 2D polymers⁸ through mild recipes was recently discovered⁹ and are likely to gain societal relevance. 2D polymers differ from those polymers discovered in the 1920s by the fact that their repeat units are not linearly connected to one another but rather laterally, resulting in a regular molecular shape similar to a fisherman's net (Fig. 1b). The above mentioned reports of their mild synthesis prove that 2D polymers are in principle accessible.^9–11 While this is exciting in itself, it also paves the way for many other questions with respect to their physics, mechanics, handling, chemical modification etc. Thus there are extremely interesting grounds to be explored both for synthesis and for application which stimulated us to discuss dimensionality aspects in polymer science more intensely in the present article.

This paper is composed of four sections which take the reader from a definition of 2D polymers up to their expected properties, syntheses approaches and their potential applications. Section 1 sets the stage by proposing a list of criteria according to which it can be decided whether or not a macromolecule qualifies as a 2D polymer. If for a particular example some of these criteria do not apply or could not yet experimentally be supported it is suggested to use the less stringent term 2D material instead of 2D polymer, which will also be explained in Section 1. Thereafter, Section 2 will discuss how the dimensionality of polymers impacts aspects such as entropy elasticity, theoretical strength, structural integrity, persistence size and copolymer structures and thus, provides insights into the peculiarities one faces upon entering the world of macromolecules with new dimensions. When presenting 2D polymers, it is of obvious importance to expand on the conditions under which their creation should take place. It cannot be neglected that despite the progress achieved so far, it is still a major challenge to produce covalent sheet-like materials and in particular 2D polymers meeting our definition with avoidance of harsh thermolytic conditions.^6,7 Just for recollection, the widely used synthesis of graphene is mainly based upon oxidation of methane on copper substrates at 1000 °C.⁶ Under such harsh conditions, rational synthetic design principles cannot meaningfully be applied and the fascinating option of tuning molecular structures including pore size, nature of functional groups and their placement, and segment flexibility between netpoints is missed out. It is this tuning of molecular structures which was the basis for the enormous success of the linear polymers and we are convinced that this creation of very different molecular structures will also be the key step towards a bright future of 2D polymers.

At this point organic chemistry steps in, which has the realization of covalent chemical structures from a blue print in its very center. If all the knowhow of this discipline is combined with the fundamentals of surface science, crystal engineering, and polymer chemistry major breakthroughs are to be expected for synthetic 2D polymers. This is what Section 3 mediates by highlighting the first rational syntheses of 2D polymers and related sheets. The strategies presented rest upon polymerization in layered single crystals and of monolayers at the air/water interface. A critical evaluation of these strategies ensures that the respective advantages and limitations become transparent. Section 3 also touches upon the recently developed simultaneous growth and crystallization approach leading to 2D Covalent Organic Frameworks (COFs) and discusses the potentials this interesting strategy has as another option for the synthesis of 2D polymers. Finally, Section 4 will briefly address potential fields of application as they are momentarily foreseen for 2D polymers. The current paper is limited in length and we therefore recommend the reader to also consult reviews on 2D polymers and closely related subjects that have recently appeared.^12–14

1. Two-dimensional polymers

Here, we would like to start by elaborating on the concept of dimensionality within polymers by borrowing ideas from polymer chemistry as well as mathematical topology. The growth reaction leading to chain-like macromolecules (e.g. polyethylene) occurs along a hypothetical line by the incorporation of monomers that have two binding sites (each carbon atom within the ethylene molecule). As we know from polymerization reaction, extension of the backbone does not necessarily need to follow a geometrical trajectory with a specific linear slope, but rather, it can freely pursue a topological line which could be bent or deformed similar to the conformational changes within a linear macromolecule. In such a case, we would like to refer to the macromolecular product as a “1D polymer” meaning that the repeat units in these polymers have a topologically linear extension in space. In topology, shapes similar to the letters “C” or “I” are identical as far as the transformations in between them do not include tearing or gluing.¹⁵ It is worth noting that even in the fully extended, all-trans conformation of a 1D polymer, e.g. polyethylene, the backbone does not follow a geometrically linear shape but rather a zigzag trajectory. Nevertheless, all the possible conformations of single-stranded polyethylene could topologically be regarded as 1D.

In the same context, one can also think of the attachment of topologically 2D repeat units (which must have at least three binding sites) such that the final polymer bears a sheet-like structure, similar to the “molecular fisherman's net” mentioned in the Introduction. In this context, it should be pointed out that topological objects in mathematics are continuous and solid constructs. Therefore, attribution of topology to repeat units has a component of mathematical idealization which should not undermine their discrete chemical structure. A well-known example of a polymer with topologically planar repeat units is graphene, in which every sp²-hybridized carbon atom formally serves as a laterally extended triply bonded repeat unit. In our view, such defect-free recurrence of repeat units will result in a 2D polymer.

It should be pointed out that based on our reference to dimensionality, confinement of 1D polymers in planar media¹⁶ or growth reactions that attach monomers with two binding sites in 2D confined geometries^17,18 cannot create 2D polymers. Neither of these cases could render a repeat unit with a lateral recurrence possible. In fact, in a physical sense, objects with a limited extension along one axis of coordinate (z) in comparison to other axes (x,y) could be considered as two-dimensional. However, the focus of this feature article is not on the mathematical notion but rather on macromolecular chemistry which deals with the recurrence of repeat units within a sheet.

Extension of repeat units on a topological plane is a notion which brings about experimentally assessable features that, in our view, lay the basis for a useful definition of a 2D polymer. Here, for the purpose of clarity, we would like to introduce the following five items as a check list for identification of a material as a 2D polymer. It is worth noting that there are other existing views on the definition of a 2D polymer.^12,13c,d,17 The five criteria are the following ones:

1. Planarity: 2D polymers are topologically planar sheets.

2. Repeat units: 2D polymers have repeat units rendering them crystalline in at least one conformation.

3. Covalent bonds: the repeat units of 2D polymers are connected by covalent bonds.

4. Thickness: 2D polymer molecules have the thickness of the constituent repeat unit (monolayers).

5. Separability: 2D polymers are strong enough to be free-standing under relevant gravitational conditions.

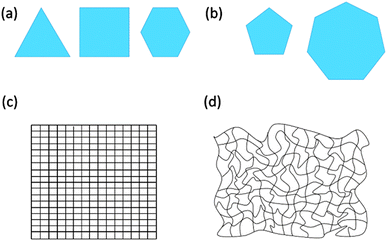
2D polymers consist of repeat units with which their entire expanse can be mapped. These repeat units can also be viewed as surface elements when considering 2D polymers under topological aspects. If such a sheet is placed on a metric, Cartesian plane it shows crystallinity. In other words, 2D polymers have at least one conformation in which they are crystalline. Achieving such crystallinity requires usage of monomers having 3, 4 or 6 binding sites (the edges of the polygons shown in Fig. 2a), while monomers with 5 or 7 binding sites cannot provide long-range periodicity (Fig. 2b). A criterion based on repeat units reflects the thinking of synthetic chemists, who dissect a polymer into such units prior to designing a monomer. This monomer is then converted into repeat units very much like the monomer ethylene is converted into the repeat unit ethane-1,2-diyl of polyethylene. After network formation and upon attaining the available degrees of freedom, the repeat units must not necessarily show geometrically periodic order. The requirement of at least one conformation in which the 2D polymer is crystalline is of relevance to “order detection”. Diffraction-based methods such as XRD require geometric periodicity. However, even if a 2D polymer sheet bears structural order among the constituent units, it might attain a conformation in which order detection by diffraction may turn impossible because of severe deviations from geometric periodicity (Fig. 2c and d).

Fig. 2 Simplified representation of monomers as filled geometric objects which are independently capable (a) and incapable (b) of forming 2D polymers. The edges of these objects are supposed to be the binding sites involved in polymerization. Monomers with 3-, 4-, and 6-fold symmetry (a) and objects 5- and 7-fold symmetry (b). Simplified representations of a 2D polymer in a conformation with and without geometric periodicity in (c) and (d), respectively.

Existence of covalent bonds as the binding chemistry between the repeat units qualifies 2D polymers as macromolecules. Carbon–carbon (CC) bonds as a specific type of this connectivity appear as a natural choice, while other element–element bonds are not excluded. The condition “covalent” can be generalized into any kind of bonding that ensures the durability of the product under the relevant ambient conditions.

2D polymers should be capable of being handled, manipulated and subjected to chemical modification as single entities in a reasonably wide window of conditions. This criterion establishes 2D polymers to be macromolecules in the common sense and is of relevance for structure proof while being the basis for practical use as single entities (Section 4).

The capability of a polymer in being isolated and handled as single entity is a key feature of a macromolecule. In the bulk of molten linear polymers, the individual chains reptate¹⁹ as individual entities relative to one another, this is the basis of melt flow. We require the same individuality for 2D polymers while noting that flow cannot be envisioned as intrinsic properties of such macromolecules. Instead, e.g. the osmotic pressure of 2D polymer solutions will depend upon whether individual sheets or sheet packages are dispersed. As will be seen later in the single crystal approach for synthesis of 2D polymers (Section 3.1), obtaining single sheets is also a final “structure” proof.

From this definition it is evident that 2D polymers are a sub-set of 2D materials. 2D materials may or may not have long range order (periodicity) within their individual layers and may or may not have persistent bonds between the individual constituents making up the layers. Furthermore, 2D materials^13,14 are not restricted to single layers but may well consist of several or even a large number of layers as long as the aspect ratio of the entire object remains large. Examples of 2D materials include metallic ultrathin films, monolayers of physically adsorbed organic molecules,²⁰ self-assembled peptoid layers^21,22 and, in principle, even monolayers of gases that form on surfaces. In this sense, 2D polymers are monolayered, periodic and covalent 2D materials.

Whenever a definition is proposed, the question of “is it needed?” arises. Being at the verge of what we foresee as a major development our answer to this question is a clear “yes”. Not only do the first reported examples meet the definition but, more importantly, looking at 2D polymers in a broader sense some of their properties and some of their applications will reflect the regularity on the molecular scale, while for other properties and other applications, the existence of topologically planar repeat units will not be so important. Section 4 addresses some potential fields of applications and it will point out where the periodicity of 2D polymers is expected to have a particular impact.

2. What to expect from two-dimensional polymers?

In the previous section, we aimed at providing a definition of 2D polymers by emphasizing not only on their sheet-like structure but, more importantly, on the confinement of the repeat units' recurrence in two dimensions. While sheet-like macromolecules are known for long times in the literature,^17,18,23,24 only upon establishment of an in-plane periodic order in their structure (at least in one conformation) one can pinpoint repeat units for them and categorize them as 2D polymers. As also mentioned earlier, 2D polymers are a subset of 2D materials. Accordingly, by virtue of such a hierarchy, they may manifest properties that are inherited both from ordered crystals as well as sheet-like structures. Here, we would like to discuss what is to be expected from the 2D polymers with respect to the fundamental mechanical, physical and chemical properties. A profound understanding of the expected properties of such molecules will pave the way for a more in-depth realization of their importance as a new class of materials. Accordingly, the purpose of this section is to employ the existing concepts in polymer science (e.g. viscoelasticity, gelation, glass transition, copolymers, and growth kinetics) to envision the potential properties of 2D polymers. We hope that the following discussion would trigger interest among experimental polymer scientists to explore this still far too rarely touched field.

2.1. Entropy elasticity

Unlike the energetic source of elasticity in solids made from small molecules, chain-like polymers that have high enough segmental mobility in the time scale of the experiment – exhibit entropy elasticity.²⁵ The driving force for this type of elasticity is to increase the available degrees of freedom in the polymer chains by enlarging the population of gauche-bonds. Accordingly, a stretched polymer chain will relax to its highest available degrees of freedom as shown in Fig. 3. This behavior could be seen either above glass transition temperature (T_g) or also under theta conditions. A very common example of this behavior can be witnessed in rubber bands where the linear chains between the cross-link points tend to rebound when released.

Fig. 3 Elastic stretching of 1D (top) and 2D polymer molecules (bottom).

As opposed to enthalpy elasticity, polymers with entropy elasticity show an increase in their elastic modulus upon increasing the temperature, which is a consequence of the enhanced segmental mobility and increased available degrees of freedom. It is worth noting that in one extreme case, when a 1D polymer molecule is trapped in its ultimate possible stretching – i.e. an all-trans chain – any further extension imposed on the molecule at that conformation will have an energetic cost in terms of changing bond angles.²⁶

Elasticity in 2D polymers is also composed of entropy and enthalpy contributions. Nevertheless, enthalpy elasticity plays a major role in the single-crystalline structure of 2D polymers. As similar to the fully stretched, zigzag conformation of 1D polymers (e.g. polyethylene), energy contribution of elasticity in 2D polymers would be pronounced in its already planar conformation, similar to the case of exposing a flat piece of paper to biaxial extension. In fact, elastic modulus of the nature-provided 2D polymer, graphene, is the highest measured value of a material (1 TPa).^27,28 As shown in Fig. 3, 2DPs also may undergo a “wrinkling” process with an increase in the population of their out-of-plane bonds. This conformation is entropically more favorable, but the significance of this source of elasticity is much smaller. Intrinsic ripples in suspended graphene is a well-known example of out-of-plane bonds.²⁹ The driving force to increase the available degrees of freedom in 2D polymers causes an enhancement in the population of the out-of-plane bonds which could lead to a temperature dependent modulus in solid or in theta-solvents.

2.2. Theoretical strength

For discussing the effect of dimensionality on strength, it would be beneficial to envision an experiment in which one end group of a 1D polymer molecule is attached to the tip of an atomic force microscope (AFM) while the other end group is adhered to a solid substrate. Upon pulling the chain, there will be a point of maximum extension after which the polymer would “tear” apart. For reaching the breaking point in the polymer, scission of one bond in the backbone is enough, e.g. a C–C bond in polyethylene. In this case, the strength of the polymer scales is with the energy of the broken bond in the backbone. Knowing this,^26,30,31 one can make a correlation between the dimensionality of the macromolecule with the energy required to make it fail. While for making a 1D polymer chain to break, scission of a single bond in its backbone is sufficient, this scission needs to cover a line of bonds in the case of 2DPs (e.g. graphene) and a plane in the case of 3D polymers³² (e.g. diamond). Thus, an N-dimensional polymer requires an N − 1 dimensional rupture in order to fail. This concept is schematically shown in Fig. 4.

Fig. 4 Structural failure in an N-dimensional polymer requires an N − 1 dimensional defect.

2.3. Percolation in synthesis

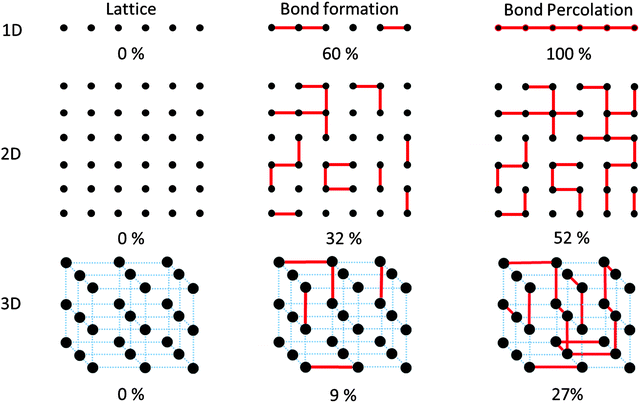
The most basic characteristics of polymers, e.g. universality and free volume, arise from connectivity between the repeat units that lie in a hypothetical spatial lattice.³³ One fundamental aspect is the relation between fidelity of connections (i.e. the degree of conversion P) and integrity of the product. Consider the monomers to sit on a 1D, 2D or 3D lattice as shown in Fig. 5. The first connectivity between the neighboring monomers in any of these lattices follows a linear attachment pattern. But as the growth continues, a linear bond sitting on e.g. the 2D lattice of monomers grows into clusters with non-integer mathematical dimensions (d) such that 1 < d < 2. For the case of a 3D monomer lattice, the clusters grow to dimensions in the range of 1 < d < 3. The lesson to be learned from this consideration for synthetic chemistry is the importance of reaching full conversion in order to create the desired dimensionality.

Fig. 5 Ordered lattice of monomers as shown by black circles in 1D, 2D and 3D space. Hypothetical covalent bonds between the monomers is shown by red-colored lines. The bonds could be made either horizontally or vertically only along axes of the Cartesian coordinate. Bond formation above the bond percolation threshold creates clusters in the lattice that have long-range order. The numbers marked under each lattice indicate the fraction of the formed bonds with respect to all the producible bonds.

In order to reach a perfect 1D, 2D or 3D polymer within this lattice, it is important to reach 100% conversion in the monomers for the purpose of reaching a perfect covalent network with long range periodicity in the end.^34,35 Nevertheless, chemical reactions do not always provide 100% conversion. Therefore, it is important to understand which minimum degree of conversion is required to provide a meaningful cluster size that can end up in 1D, 2D or 3D polymers. On a practical level, connectivity of the repeat units offers certain physical functions e.g. transport between the interconnected lattice sites. Such transports would include energy and charge transport along the backbone as well as stress transfer within the effective force field of the polymer chain. Fulfilling such physical tasks requires the formation of a minimum level of connectivity in the lattice of the unreacted monomers by reaching a certain level of monomer conversion into a polymer.³⁶ However, when it comes to minimum required conversion for realization of clusters that may end up being as 1D, 2D or 3D polymers, one needs to use the language of percolation theory which will be discussed in the following.

Fig. 5 shows an incremental process of bond formation among unreacted monomers (black dots) that are sitting in lattices with 1, 2 and 3 dimensions with linear, square shaped and cubic structures, respectively. Each lattice, in order to convert to its corresponding N-dimensional polymer, needs to reach a certain level of connectivity between any two subsets of lattice sites. Please note that the formation of each connection is treated as an independent, random process. In the case of the 1D lattice of unreacted monomers, in order to create a cross talk between two random monomers (e.g. the first one and the last one), there is a need for the formation of all the possible bonds in the network. Only then, a 1D connection between the lattice sites will be formed. In the 2D squared lattice, the formation of a path that attaches e.g. the upper lattice line to the lower one requires the formation of at least half of the potential bonds that could be created. In this case, only when 50% of monomer conversion is reached (within a random bond formation process) the first cross-talk between the lattice lines at the top and bottom will be formed.^34,35 The minimum value which is required to form a cluster of bonds that attaches two locations of a lattice to one another is called “bond percolation threshold”.³⁷ It is worth mentioning that reaching conversion values above the percolation threshold is by no means a criterion for creation of structurally perfect networks. Nevertheless, it provides a measure for the minimum required random monomer conversion such that a structure would start, then on, showing a certain dimensionality. In the case of 2D lattices, the percolation threshold has been determined for many lattice patterns including the Archimedean lattices. As one practical example, there is minimally required conversion such that a 2D network would exhibit mechanical elasticity (rigidity percolation threshold)³⁸ or free-standing nature. Only after reaching conversions above this value, a 2D network can have a finite non-zero elastic modulus. In fact, a free standing polymer film has certainly overcome its rigidity percolation threshold.

As it is shown in Fig. 5, reaching bond percolation threshold in a 3D cubic lattice requires conversions above 24.88%.^34,35Table 1 shows the value of bond percolation threshold (p_c) and the mathematical dimensionality of the clusters (d_f) that are formed at p_c.

Table 1 Monomers sitting on a D-dimensional lattice with respective linear, squared or cubic packing and their corresponding bond percolation threshold (p_c) and the cluster dimension (d_f)

D	p c (%)	d f
1	100	1
2	50	1.896
3	24.88	2.523

---

The decreasing trend of the bond percolation threshold with respect to the increased dimensionality is of enormous importance. Practically, this means that reaching certain physical functions in materials with reduced spatial dimensions requires higher values of conversions and thereby the significance of choosing growth reactions with 100% yield becomes more evident. Another example is a classical problem witnessed in polymer synthesis upon formation of macromolecular networks when gelation takes place in the reaction medium. Given the lower values of bond percolation threshold in 3D space, covalent gelation could be witnessed more often in the synthesis of 3D cross-linked networks.

2.4. Persistence size

For linear macromolecules, there are specific configurational constraints based on which the nth bond along the backbone is attached to the (n − 1)th bond. The backbone, in fact, grows based on the prerequisites dictated by the bonding configurations. Therefore, geometrical coordinates of the nth repeat unit in space could be tracked back to the location of the first repeat unit. However, if a hypothetical observer travels along the backbone with a step size as large as the “persistence length”, then the trajectory of this motion would attain a random walk nature and the hypothetical chain made from its trajectory would be a freely-jointed chain with no configurational constraints (Fig. 6). In fact, the persistence length indicates the step size based on which the bonding memory is cleared. The higher the rigidity of the backbone, the larger the corresponding persistence length. The perception of the term persistence length is largely due to Werner Kuhn.³⁹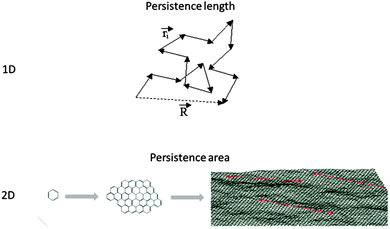

Fig. 6 Travelling along the backbone of a 1D polymer by the step size as large as the persistence length (r_i) results in a freely jointed chain. R represents the end-to-end distance. In the molecular size range between benzene and graphene, persistence area defines the threshold after which a 2D oligomer turns into a 2D polymer. Graphene image taken from ref. 40 with permission.

Configurational constraints are far more restrictive for 2DPs given the nature of the growth which is simultaneously pursuing two dimensions. Accordingly, while the expanse of a 2D polymer might not completely lose its memory during the growth of the sheet, it may undergo a transition to another scaling regime. As a more practical example, the transition between benzene, nano-graphene and graphene would be determined by the persistence area as shown in Fig. 6.

2.5. Copolymer

Copolymers fulfill a distinguished purpose in macromolecular chemistry. Properties that they offer lie in a window defined by their corresponding homopolymers and can be adjusted by incorporating the necessary fraction of the respective repeat units. The unexplored field of synthetic 2D copolymers⁴¹ is not excluded from this paradigm. If the prerequisites for symmetry elements of the monomers in terms of their ability to tile cover a surface are met and if there is no conflicting mismatch between the lateral sizes of the monomers, one can then overcome the first challenge in the formation of 2D copolymers, namely monomer selection and design.

One of the important elements in the kinetics of 2D copolymer synthesis is the relation between mole-fraction of the monomer mixture (f_i) and the corresponding repeat units in the copolymer (F_i). Such correlations are mathematically developed for the kinetics of linear copolymerization through chain growth reactions as achieved by the well-known statistical model of Mayo–Lewis.⁴² For 2D copolymers there is so far no such model to the best of our knowledge.

Another notable feature of 2D copolymers is the spatial distribution of repeat units within their structure.^41,43 Based on the function that the 2D copolymer is aimed to serve, it could potentially be made to form either of the following four types of copolymers, depending on the morphology of the phase segregation namely block, gradient, random and alternating. These types are schematically shown in Fig. 7. It should be pointed out that the first criterion for the definition of 2D polymers does not hold true for the images a–c represented in Fig. 7. For convenience, we propose to nevertheless stick to the term copolymers as it is commonly referred to in the case of linear copolymers. The alternating copolymer in Fig. 7d matches our definition precisely.

Fig. 7 Cartoon representation of various types of 2D copolymers made from two types of hypothetical repeat units (grey and dark). Block, gradient, random and alternating copolymers are shown in (a), (b), (c) and (d), respectively. Image taken from ref. 8 with permission.

2.6. Growth reaction

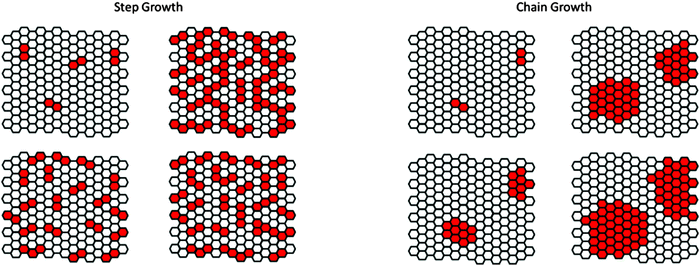
Similar to the growth kinetics of 1D polymers, 2D macromolecules can also grow either by step-growth or chain-growth kinetics. Ideally, step-growth 2D polymerization would proceed by random dimerization of the neighboring monomers that are sitting in a crystalline lattice. A local dimerization event should neither promote nor inhibit dimerization of the neighboring sites such that the randomness criterion is fulfilled. An example of such type is shown as a cartoon representation in Fig. 8 where a step growth reaction has formed dimers, trimers, tetramers etc. within the crystalline matrix of the not-yet reacted monomers (a solid solution of reacted dimers in monomers).

Fig. 8 Step growth and chain growth kinetics of polymerization in 2D array of monomers. Lattice sites specified with a white color code represent the unreacted monomers while the red colors exhibit the reacted (polymerized) sites. Chain growth polymerization follows a nucleation and growth mechanism.

In the chain-growth scenario, an initiator activates a certain number of monomers in their respective ordered lattice. Thereby, within each activated site, a subset of the closest neighboring monomers would be activated through which the reaction front propagates towards the rest of the lattice. As depicted in Fig. 8, initiation sites account to the formation of clusters that grow across their periphery to percolate throughout the whole structure.

3. Synthetic two-dimensional polymers

As a result of the successful synthesis of 2D polymers by mild recipes, the desire for creation of these materials is not anymore facing the question of feasibility.^9–11,44 Nowadays, the challenges are lying on a more specific level. Easier to access monomers, structural elucidation, optimization of crystallization, facile accessibility of monolayers, and freedom of choice in monolayer size along with copolymerization and post-polymerization reactions are currently in the to-do list of the chemists with regard to 2D polymers. Addressing the above mentioned challenges would not be possible without exploring all the potential strategies for creating 2D polymers. While a handful of strategies are in fact encouraging (e.g. organization in smectic phases^17,18 and solution^45,46) here we would like to present three selected approaches for which we foresee particularly promising future. The common theme of all these efforts lies on the order of formation and crosslinking. Advantages and disadvantages of each method will be discussed and the perspectives lying ahead of each approach will briefly be touched.

3.1. Single crystal to single crystal

This method is based on topochemical polymerization of monomers that are preorganized in lamellar⁹ or quasi-lamellar⁴⁴ single crystals. Each layer within the crystal is composed of monomers that sit next to each other and are ready to undergo polymerization. The neighboring layers are separated through solvent molecules or free volume such that there is little chance for cross-talks (e.g. bond formation) between the neighboring layers. Therefore, the growth reaction is likely to proceed in a 2D medium without the danger of creating a 3D random network. Polymerization needs to be carried out by the least disturbance of the crystal parameters e.g. unit cell dimensions. It is therefore preferable to employ reactions that are not associated with mass transport. Also, given that bond formation upon polymerization can cause shrinkage (or expansion) of the van der Waals distances, it is important to design the monomer such that it could accommodate local contractions (expansions) and thus avoid the crack formation within the crystal. This issue will be addressed in the following.

After achieving the polymer product at the end of the reaction, the single layers (2D polymers) can be isolated through exfoliation techniques. The success in isolation of polymer monolayers is dependent on the nature of the secondary forces that glue the polymer layers to each other in the crystal and also on the structural defects within the monomer single crystal. Some of the defects can potentially result in reactions that induce bonds between the polymer layers which are undesirable for creation of single sheet 2D polymers. This is why we require 2D polymers to be isolable as single sheets (Section 1, third criterion of the definition). There is no better way to rule out interlayer connectivity but isolating a single layer from the crystal.

In an ideal synthesis case of 2D polymers through single crystal approach, the exfoliated single layers of polymer should have the same lateral size as the original monomer single crystal. In other words, if monomer single crystals can be transformed into polymer single crystals and exfoliated with no loss in the lateral size of the individual layers, then an ideal synthesis of 2D polymers by this technique is achieved. Defects in the single crystal and also the chemical nature of the growth reaction are the two factors which will determine the chances of success in fulfilling this task. Mosaicity and defects such as twinning, interstitials, voids and grain boundaries are existing within a single crystal⁴⁷ and could hinder an ideal synthesis of a 2D polymer. It is therefore helpful to optimize the crystallization procedure and to also use monomer structures with high rigidity in order to achieve a high quality crystal. The information about the nature of the potential defects within a single crystal is hidden in the width of the X-ray Bragg peaks and also in the diffuse X-ray scattering that are recorded from an XRD pattern of the monomer or polymer single crystal.^48–50

Structural changes that the monomer crystal will experience during the course of the polymerization can induce mechanical stresses. The extent of these stresses will determine whether or not cracks occur in the crystal and if the long-range periodicity will be present in the final polymer. A single crystal to single crystal transformation from the monomer to the polymer will take place only if the expansion/contraction of the unit cell is kept minimal upon polymerization.⁵¹ Structural changes of the monomers along the mechanistic pathway (and their respective energy levels) that lead to the polymer will be important in reaching the final product as single crystal form. Higher levels of mechanical stress can result in products with polycrystalline structure. In this case, the chances for isolation of monolayers of 2D polymers with large aerial size from the mother crystal will be slim. Therefore, the challenge of designing the monomer and the growth reaction has to consider minimal induction of mechanical stress on the original single crystal.⁸

In 2012, a synthetic 2D polymer meeting the above definition was reported,⁹ shortly thereafter followed by a similar study from the King group.⁴⁴ The first synthesis was achieved through photochemical [4+2]-cycloaddition of anthrylene and ethynylene moieties from a rigid macrocyclic monomer 1 with three-fold symmetry (Fig. 9). The structure of the monomer single crystal was resolved by X-ray diffraction where a close proximity of the neighboring monomers (Schmidt distance⁵²) rendered the photochemistry possible. Photopolymerization was studied by fluorescence and Raman spectroscopy and the exfoliation of the polymer sheets was achieved down to single layer. However, due to the small size of the crystalline domains capable of coherent diffraction, connectivity of the polymer was demonstrated by electron diffraction patterns rather than X-ray.

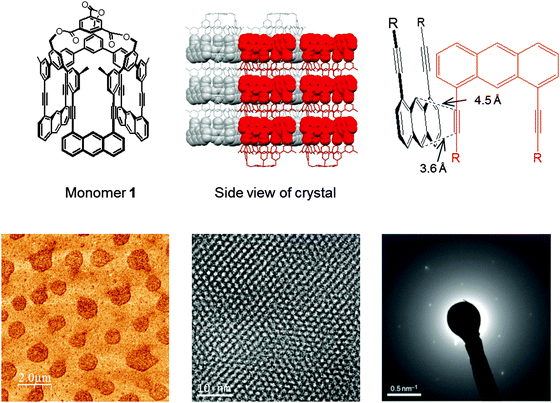Fig. 9 Featuring an example of a structurally characterized 2D polymer according to the definition provided in this article. For another early example, see ref. 44. Top row: Monomer structure and monomer packing in the single crystal. Critical distance between neighboring monomers ensuring the desired reaction between the acteylene unit of one monomer with the opposing anthracene unit of the other monomer. Bottom row: (left) AFM height image of exfoliated single sheets. (center) Wiener-filtered TEM image of a polymer sheet package proving the existence of an ordered array of laterally connected, topologically planar repeat units. (right) Electron diffraction pattern of the monomer crystals. Images taken from ref. 9 with permission.

Efforts on extending the size of the single crystalline domains in the polymer achieved success in 2014 by two reports of the King and Schlüter groups that made the use of anthracene [4+4]-cycloaddition within the single crystals of two different monomers. Both studies resulted in a polymer single crystal (Fig. 10). Kissel et al. showed the polymerization to take place through two consecutive steps of dimerization all within a single crystal which provided a mechanistic insight into the reaction pathway.¹¹ The exfoliation of the 2D polymer resulted in single layers. The example introduced by Kory et al. offers a large scale synthesis of the monomer. Besides, it was unique given that the retro-reaction could also be brought about while the entire sequence of polymerization and depolymerization was performed by maintaining the single crystalline state (Fig. 10).¹⁰ Both polymer and monomer single crystals contain the polar solvent 2-cyanopyridine and belong to the chiral and polar space group R3. They may therefore show e.g. piezoelectric and ferroelectric properties. It shall be pointed out here that the single crystal approach potentially offers structure analysis by X-ray diffraction which is a relatively easy to apply analysis method. Particularly at the beginning of the research into 2D polymers, unequivocal structure analysis was considered particularly important a task. As we will see in Section 3.2 structure analysis turns much more challenging when not working with single crystals.

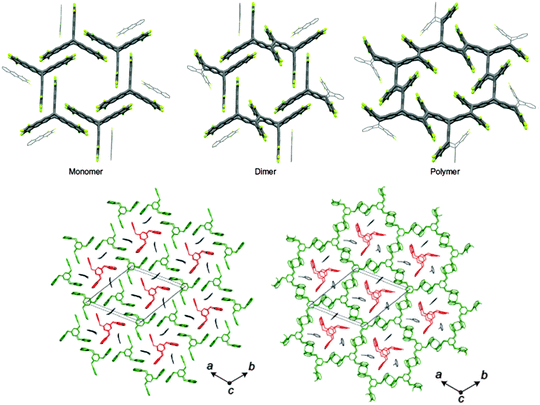Fig. 10 Single crystal to single crystal transformation of trifunctional monomers into the corresponding 2D polymers. Top: Sequence of XRD structures showing how a monomer structure is converted into a 2D polymer through an intermediate state in which the monomers are dimerized. Taken from ref. 11. Bottom: Similar transformation with another monomer (green) whereby the polymerization process takes place around a template formed from unused monomers (red) and solvent molecules (black). Interestingly the latter polymerization is fully reversible. In both cases the polymerization is brought about by anthracene dimerization whereby the long axis of the anthracene lies in (top) and stands vertically on the drawing plane (bottom), respectively. Images taken from ref. 10 and 11 with permission.

While crystal sizes as large as mm-range are reported for organic compounds, improving the size of the exfoliated sheets remains a practical challenge which needs further attention. Although mm-sized crystals are suitable for laboratory characterization purposes, they may not be sufficient for all possible applications and therefore there is a need for improvement of the accessible crystal sizes. To the best of our knowledge, the largest available synthetic polymer single crystals are reported for 1D polymers of bis(indenone) which is made from its respective monomer single crystal with needle shaped crystals as large as few centimeters.⁵³ This work, however, does not address the issue of mosaicity.

3.2. Interface (air/water)

Another suitable medium for pre-organizing monomers prior to polymerization is the surface of solid substrates and liquids. Polycrystalline substrates have abundantly been used for syntheses of organic sheets through physical⁵⁴ or chemical adsorption⁵⁵ of the reactive molecules on solid substrates. However, challenges associated with the incorporation of a laterally connected repeat unit within these films over a macroscopic scale have not yet been sufficiently addressed. Lattice mismatch between monomer geometry and substrate lattice, polycrystalline nature of substrates causing the formation of smaller domains and difficulties with detachment of the final product from the substrate are some of the challenges to be mastered in this direction.

Surfaces of liquids, in particular water, provide a possibly more promising option for synthesizing 2D polymers⁵⁶ and similar sheet-like entities.⁵⁷ Not only does the amorphous nature of water circumvent problems with the lattice mismatch of surface with monomer size to start with, but also the low surface-roughness of water (root mean-square of about 3 Å)⁵⁸ extends over large areas and provides a unique advantage in regard to achieving the required preorganization of monomers.⁵⁹ Additionally, order formation within a plane can take place because of monomer mobility on the fluid medium offering the possibility of defect healing. Amphiphilic molecules were repeatedly shown to achieve periodic order on scales much larger than molecular dimensions.⁶⁰ Accordingly, using the surface of water has the potential of overcoming the current shortcomings of the single crystal approach in the synthesis of 2D polymers namely the limited lateral size of the obtained polymer sheets.

Amphiphilicity facilitates the formation of a Langmuir film on the surface of water and is used to make sure that the monomers present the growth units to their neighbors all at the some altitude above the interface. Monomer thickness less than 1 nm will help with structural analyses, e.g., by STM. While it is possible to record images from molecules thicker than 1 nm by this method,^61,62 it is beneficial to use thinner molecules for high resolution imaging.⁶³ Furthermore, high mass ratio of binding sites within the monomer will help with an improved signal-to-noise ratio for spectroscopic analyses of polymerization reaction. Regarding the aspect of binding forces between monomers, minimal attractive forces among them will hinder the formation of nucleation sites for crystallization at the interface. Very much like in regular crystallization, the number of nuclei will eventually determine the crystal size. At an interface, ideally the crystal size translates into the domain size. Thus, a limited number of nucleation sites is advantageous in regard to reaching large domains (for a discussion on the well-defined behavior of the two-dimensional phase, please refer to ref. 64). Crystalline domains with limited sizes are among the shortcomings of the air/water interface approach in the synthesis of 2D polymers.⁸ Micron sized domains made by perfluorinated amphiphiles are presently among the largest achieved domains made at an air/water interface.⁶⁵

Despite the long history of Langmuir films,^66,67 there are only few reports where monomers were employed at the air/water interface whose molecular structures are potentially capable of bringing about controlled lateral growth. Before entering into the three cases which we consider the most advanced ones, it shall be mentioned that Michl et al. had reported fascinating initial experiments towards laterally extended structures at a mercury/air interface.⁶⁸ They unfortunately did not meet with much success but in retrospect appear rather farsighted. The first of the three cases to expand upon concerns monolayer metal–organic networks,^69–71 several of which give mechanically coherent monolayer sheets capable of being spanned over holes (fifth criterion in the definition of 2D polymers in Section 1). They fulfill several criteria of the above check list; however, in all instances unravelling of the molecular structure is still to be achieved. This seemingly simple statement of the yet untouched structure has such an importance in the field of 2D polymers that we will use it as an opportunity to explain in a few sentences what the differences between the single crystal and the interfacial approaches are. Provided appropriate monomer packing, the former approach furnishes 2D polymers ideally in the form of single crystals. While this limits the sheets lateral expanse and eventually requires exfoliation (which can be tedious), it has the enormous plus that structure analysis is straight forward. For reasonably sized crystals simple in-house XRD is sufficient to prove the molecular structure of 2D polymers within a matter of a day. This is in sharp contrast to the interfacial approach where one obtains single sheets of practically unlimited lateral dimensions with obviously no need for any exfoliation step. The price to be paid for these pluses, however, is the structure analysis of the sheets obtained, and this can turn into a real nightmare. This is why for products of this approach we suggest to use the term monolayer 2D material until the structure analysis is completed and it can be decided whether or not the sheet qualifies as a 2D polymer (at least in domains). Structure analysis may require in the order of a year. Further below in this section, we will briefly touch on some aspects of monolayer analytics but will keep this brief for space limitations of the paper.

The second case refers to the amphiphilic monomer 2 (Fig. 11a) and related compounds with anthracene and 1,8-diazanathracene growth units.^41,57,72 Such monomers can easily be spread at the air/water interface and subsequently polymerized by photochemical treatment. Within a matter of few hours a covalent monolayer sheet can be synthesized which is strong enough to support its own weight when spanned over 20 × 20 m²-sized holes. The disappearance of excimer emission suggests complete consumption of growth sites but does not prove order formation. Further structural evidence is presently being accumulated but its completion will require substantially more time. The third and last case regards the report by Murray et al. with the synthesis of a covalent monolayer sheet (by employing monomer 3 in Fig. 11d) for at least small parts of which, crystallinity was shown (by STM) to have been reached at the air/water interface. Also here anthracene dimerization was the key to success though in rather different geometry.⁵⁶ These two cases will be referred to again further below when analytical issues will be discussed.

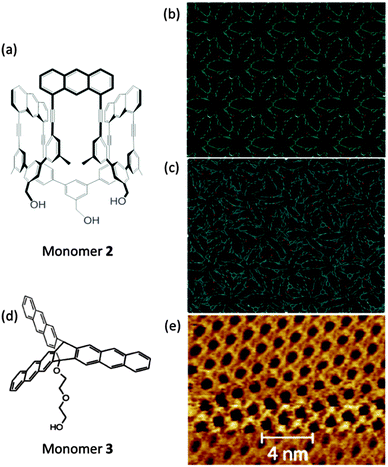Fig. 11 Polymerizations at an air/water interface. (a) Structure of amphiphilic monomer 2 with three anthracene units mediating photochemically induced lateral growth. (b) Hypothetical structure of a sheet obtained from monomer 2 using the crystal structure of a congener molecule from ref. 9 after treatment with energy minimization by DFT simulations in a vacuum and at room temperature. The image shows a periodic structure with repeat units. The hydroxyl groups are depicted in red. (c) In a vacuum DFT calculations of the energy-minimized conformation of the structure shown in (b) reflecting densification which is achieved by the sheet assuming disordered conformation. (d) Structure of monomer 3 with three anthracene blades and a hydrophilic chain at the central triptycene moiety's bridgehead. (e) STM image under 1-phenyloctane of the monolayer polymerized at the air/water interface exhibiting order on the molecular level. (e) Is taken from ref. 56 with permission.

As mentioned, the most challenging obstacle in this context is the need to employ an arsenal of partially complex analytical tools in order to unequivocally establish a molecular structure. Difficulties rise from the miniscule quantity of mass incorporated into monolayers which bring about the issue of a low signal-to-noise ratio in most of the analytical experiments.

Accordingly, special measures need to be taken into account when it comes to structural investigation. Nowadays there are a handful of monolayer-sensitive spectroscopy and microscopy methods available in order to gain insight into the structure of monolayers. Infra-red reflection absorption spectroscopy (IR-RAS), tip-enhanced Raman spectroscopy (TERS), fluorescence and UV/Vis absorption spectroscopy, Brewster angle microscopy, ellipsometry, X-ray photoelectron spectroscopy (XPS) along with scanning tunneling (STM, UHV-STM), electron and light microscopies (TEM, cryo-TEM, SEM, and OM) neutron reflectivity (NR), X-ray reflectivity (XRR), X-ray absorption spectroscopy (XAS = NEXAFS), X-ray magnetic dichroism (XMCD), and high resolution AFM are among the available methods for this purpose. Not all methods can be usefully applied to all sheets. It is of enormous importance to pay attention to the necessities dictated by the analytical techniques when it comes to monomer design. Apart from the structural rigidity as mentioned in the design of the monomers for single crystal approach, there is a need for the monomer to be amphiphilic, thinner than 1 nm and with highest possible mass ratio of the binding sites to the rest of the monomer. Also the binding forces among the monomers will play a role for a successful synthesis of 2D polymers. In the following, these individual characteristics will be discussed.

Geometric changes associated with the growth reaction are also very important in the synthesis of 2D polymers at an air/water interface. Reactions with the least lateral shrinkage/expansion will help with minimal disturbance of the monolayer structure upon polymerization. Furthermore, reactions that will result in products that have an IR or Raman active out-of-plane bond will be advantageous for analytical spectroscopies that have surface selection rules (IR-RAS and TERS). A first report employing TERS for a covalent monolayer made by a polymerization of a three-fold symmetry monomer is available. The product has no out-of-plane polarizability though.⁴³ At this point we come back to the second and third case introduced above because they provide valuable further insights into what needs to be considered to increase chances for a successful interfacial synthesis of 2D polymers. Fig. 11b shows a model for how the sheet created form monomer 2 might look like. One realizes the regularity in this hypothetical structure and can identify repeat units. If this structure in a DFT calculation in a vacuum is allowed to minimize its potential energy, the structure in Fig. 11c is obtained. Not only does this structure lack any regularity in 2D, it even partially departs into the third dimension. Thus, even if the connectivity between monomers is regular, the minimum energy conformation the sheets attain may be disordered. This is not a trivial point. Conformationally disordered but otherwise perfectly periodic sheets would not give rise to Bragg reflections in grazing incidence scattering experiments. This could falsely lead to conclude that a particular sheet is not a 2D polymer. The lesson to be learned from this is that structure analysis has to be done in the biaxially strained state or that monomer design has to contain an element creating shape persistency in the product. This is the point where the third case comes into discussion. Murray et al.⁵⁶ use the three-fold symmetric monomer 3 with triptycene core and anthraceno blades. Consulting a molecular model shows that this monomer should give rise to a particularly rigid network after polymerization which ought not to spontaneously contract. And in fact, after photo-irradiation of the monolayer of 3 at the air/water interface internal periodicity could locally be proved by STM. A small mismatch between the expected and observed lattice sizes still needs attention in future. Nevertheless, this is the first evidence for 2D order formation in a Langmuir sheet used for the synthesis of 2D polymers and thus an important step. In-depth spectroscopic analyses of the bonds that are formed upon polymerization are to be conducted for corroborating the structural perfection. The upcoming challenges further lie in the investigation of the domain sizes and exploring ways how to increase them.

3.3. Covalent organic frameworks

Covalent organic frameworks (COFs) were synthesized by Yaghi et al. and others in an attempt to achieve novel mesoporous materials based on cross-linked polymers with long-range periodicity.⁷³ The key feature of COF synthesis is the simultaneous occurrence of crystallization and bond formation processes, that is in distinct contrast to the above two approaches where “order formation” and “polymerization” steps are well separated from one another. In terms of the nature of the bonds involved in COF synthesis, this key feature requires them to be reversible. Sheets composed of, e.g., CC-bonds are therefore not within this method's scope in the first place. While COF synthesis is attractively simple, steering both processes such that defects are avoided and large crystals are obtained is still an almost insurmountable challenge. Nevertheless, layered COFs – known as 2D COFs – may become quite useful with respect to the synthesis of 2D polymers in the future despite the challenges with crystal growth.⁷⁴ A major challenge in the COF approach to 2D polymers is their exfoliation into individual sheets and structural characterization. Nevertheless, COFs appear to be a viable approach.^75–77Fig. 12 shows a prominent example for a 2D COF which was reported in 2005. The synthesis involves dehydration reaction between 1,4-benzenediboronic acid and hexahydroxytriphenylene and is claimed to result in stacked multilayers. The individual sheets are held together by boronic esters. Open issues include how to overcome microcrystallinity and how to identify and quantify eventual crystal defects. Another problem associated with the use of COFs for synthesizing 2D polymers is their expected sensitivity to exfoliation. By virtue of the method the bonds created during COF formation are reversible. Examples are boronic esters, boroxines, imines or hydrazines. However, these bonds not only are reversible but also prone to hydrolysis. Therefore, chemical stability of single COF sheets might be at risk under ambient conditions when entropy-driven hydrolysis could result in sheet decomposition. Dichtel et al. and Zamora et al. have systematically studied and confirmed the integrity of 2D COFs after exfoliation in thicknesses down to few layers, however, not to single sheets so far.^78–80 In this context it is noted that Dichtel et al. have discovered a method to grow 20–200 nm thin COF layers on graphene.⁷⁶ This is an interesting development for various reasons and might be a starting point for exfoliation of larger COF sheets.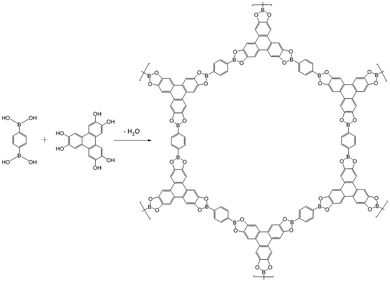

Fig. 12 Synthesis of a 2D COF by dehydration reaction between 1,4-benzenediboronic acid and hexahydroxytriphenylene.⁷³

At the end of this section, we would like to point out that there is progress in terms of single crystalline COFs. Wuest et al. used weak trans-azodioxy bonds (bond dissociation energy 20–30 kcal mol⁻¹) in a reversible growth reaction and reached a single crystal structure of a 3D COF.⁸¹ To the best of our knowledge, there is so far only two reported cases of single crystalline COFs which both concern 3D systems and therefore have no direct bearing on 2D polymers.^81,82 Nevertheless there seems to be leeway for development.

4. About processing and applications

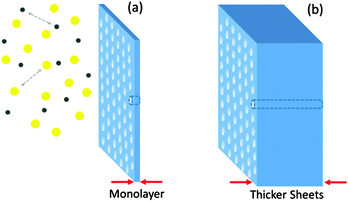
It is perhaps still early for composing a section on how to process 2D polymers and what applications they may find. The entire field is still in its infancy and therefore providing more than few speculative comments is difficult. Yet, many questions are being raised towards this direction. 2D polymers are increasingly recognized as structurally novel – a key basis for new and exciting applications. Comparing with the enormous development that 1D polymers experienced, it is not exaggerated to predict a bright future to this subclass of 2D materials, supposed easy and cost-effective solutions can be found. Processing of 2D polymers will be concerned with shaping them into useful artifacts and exploring their characteristics. Various processing routes are available to start with. Among them are, of course, the in situ creation of the 2D polymers (for which no example exists yet), either directly onto surfaces, or possibly within the melt of a bulk polymer. Other schemes include solid-state processing, which was successfully employed to shape a wide spectrum of organic semi-conductors⁸³ as it is not expected that traditional melt-processing will be an option. Finally, appropriately functionalized 2D polymers can be molecularly dispersed (i.e. dissolved), not only for characterization purposes (Section 2.4), but also to facilitate solution processing, as for instance in doctor blading, spin coating, and ink-jet printing In addition, once soluble 2D polymers are in hand, their binary or tertiary blends with linear polymers would make an attractive opportunity. The various artifacts created with 2D polymers may include molecular coatings, multi-layer sheets, and blends with linear polymers in film and fiber form. Among the many properties to be investigated are wear and scratch resistance. The latter property is especially intriguing, as it is expected that due to the numerous contact loci of 2D polymers on appropriate surfaces, molecular adhesion will be outstanding. Objects made by blending 2D polymers with bulk polymers will be a further attractive research target, again for their mechanical behavior as above, but also as to whether the 2D polymer “objects” have the ability to enhance nucleation and crystal growth of crystallizable polymers – a much sought after property. Furthermore, barrier properties of blends of 2D polymers and bulk polymers in the form of biaxially oriented films will receive attention.

At this point we would like to come back to the aspect raised at the very end of Section 2 on whether it is the sheet nature of 2D polymers that matters or rather the order in the sheet's internal molecular structure. In the applications raised so far, we believe it will be more the object character of a 2D polymer that matters and not so much the molecular structure, except for the fact that, of course, too many defects in a sheet (Section 2.3, Percolation in synthesis) will impact the sheet's overall properties such as bending modulus, adhesion and the like. The molecular structure and its precision become more important when the optical and/or electrical characteristics of 2D polymers are of relevance or these materials shall be used as ultrathin membranes for gas separation. This last aspect shall be expanded upon a bit further. Considering that the monomers used in the synthesis of 2D polymers are inherently porous, the final macromolecule is also porous (in the non-collapsed conformation). The pore size depends on the monomer structure and the conformation the corresponding repeat units assume within the network. Given their regular structure, 2D polymers exhibit a monodisperse pore size distribution. This is unique compared to other membrane materials and renders them ideal candidates for membrane applications.^84,85 The pore size plays a crucial role in separation. For example, hydrogen atoms need a time range of 10⁹ years to permeate across graphene while positively charged protons have high permeation across this naturally occurring 2D polymer.⁸⁶ Separation of gas mixtures is another example of this type for which gas dynamics can be harnessed by a rational selection of the polymer pore size for reaching optimum selectivity.

Membranes with smaller thickness values are particularly suitable given the higher flux of the gas across the membrane which may result in a faster separation process. For separation purpose, classical Knudsen flow conditions are applicable in which the pore size of the membrane is equal or smaller than the mean free path of the gas molecule. Based on the gas dynamic calculations, in the Knudsen flow regime, the flux of the gas across the membrane becomes inversely proportional to the square-root of the molar mass of the gas which serves as the principle for separation.⁸⁷Fig. 13a shows a schematic representation of ultra-separation where the thin nature of the 2D polymer assures high permeation flux (in contrast to Fig. 13b) and the separation process is achieved by Knudsen flow in which the polymer pore size is smaller than the mean-free-path of the gas. It should be pointed out that calculations based on the Knudsen regime are classical simulations and their accuracy has to be compared with the quantum mechanical models.

Fig. 13 Two types of gas molecules as shown by yellow and black dots are exposed to two membranes with various thicknesses but the same pore size. Porous films could separate the gasses by mechanisms similar to Knudsen diffusion. 2D polymers are inherently porous materials that could be used for gas separation purposes. Their monolayer thickness (a) has a higher flux of gas, compared to thicker sheets (b), which is of importance for faster gas separation.

Conclusion

Based on initial successful cases, this article aims at delineating an emerging research direction in new 2D materials – 2D polymers. It provides criteria for identifying 2D polymers and differentiating them from linear polymers, as well as from other 2D materials. It also provides insights into analytical problems and where these new macromolecules will have impact and will gain importance in the future. These latter aspects particularly apply to their physics (establishing the differences between common linear polymers and 2D polymers in terms of, e.g., scaling behavior and universality), as well as engineering aspects, including the creation of useful devices, blends, or coated surfaces with these materials. Together with a yet-to-be initiated application-driven research activity, polymer physics and engineering will lay the foundation for the future of 2D polymers, which, because of the novelty of their structures, we expect to be bright and prosperous. This article is also to be understood as an encouragement to synthetic chemists to enter the field, since the creation of 2D polymers, is obviously a necessity before their importance can be assessed and their impact felt. Many more structurally different variants of 2D polymers are now needed for which the ingenuity and inspiration of chemists is crucial. Now that the proof of principle has been established, such an activity will, of course, increasingly be subjected to the pressures of high efficiency, high perfection, simplicity and low cost.

At this point we draw the readers' attention to the perhaps surprising observation that common synthetic polymers such as polyethylene or Teflon are structurally simpler than their natural counterparts e.g. the proteins, DNA and polysaccharides, while in two dimensions this is the opposite. Naturally occurring graphite layers or layered silicates are simpler than the first synthetic 2D polymers presented here. When thinking about new monomer structures and new polymerization reactions, it is therefore suggested not only to think differently but also more simply. Is not there a feasible path to be discovered, somewhere within the still rather virgin territory of 2D polymers, that will lead to atomically flat, structurally simple representatives, such as graphene or its fully hydrogenated congener graphane? In regard to the latter, we mention a Gedanken experiment recently put forward by Roald Hoffmann, Ithaca, who hypothesizes about the creation of graphane from an array of dearomatized benzenes (cyclohexa-1,3,5-trienes) based on the higher stability of this hydrocarbon sheet relative to benzene.⁸⁸ The challenge in such thoughts lies in the fact that their realization requires a kind of thinking that is far away from the norm in synthetic chemistry. This is also illustrated by a recent study exploring the structural space available to carbon monoxide depending on pressure.⁸⁹ Under certain conditions, this compound, which is a gas at ambient pressure and therefore not considered a natural choice for 2D polymer synthesis, can be converted into layered structures!

Finally, we briefly return to the aspect of structural periodicity, which was proposed in this and earlier articles as a useful criterion in defining 2D polymers. Some properties of sheets depend upon whether their internal structure is periodic or not. Periodicity thus is and remains key. It would nevertheless be of interest and also appealing to think in terms of non-periodic, monolayer 2D materials. Fig. 14 shows some examples. The momentum generated by the present gold-rush mood in sheet synthesis should be used to explore such macromolecules as well in order to explore the entire field of covalent, monolayer sheets more broadly. In our assessment, however, non-periodic 2D macromolecules (without going into any detail here) will likely be more complicated to synthesize and analyze compared to 2D polymers. Yet another fascinating thought, which is probably even further up the scale of complexity, is to approach monolayer 2D materials from knitting micrometer-sized molecular carpets with e.g. Turkish or Persian knots from linear polymers.⁹⁰ Synthetic chemistry offers great and fascinating challenges. The prospect of a host of exciting properties and applications for 2D polymers and other 2D macromolecules provide the stimulus to take on these challenges.

Fig. 14 Examples of two-dimensional sheets which cannot be represented by a regular array of repeat units (left: irregular network; center: Penrose tiling; right: inspired by the Dutch painter P. Mondrian). Irregular 2D networks like the one shown on the left side are to be understood such that the netpoints and the linear segments connecting them are created from branched molecules (the latter netpoints) and differently long segments in a predetermined, controlled fashion. They are not to be understood as the result of incomplete reactions between monomers that failed to give a 2D polymer.

Acknowledgements

ADS and BTK cordially thank the many coworkers, who with their very engaged work and creative intellectual input have invaluably contributed to achieving the nucleus of what in a few years from now will be the field of 2D polymers. Their names are given in the references. There are several colleagues and collaborators the authors would like to cordially thank for a wonderful and fruitful period of interaction while establishing the field of flat macromolecules. For space reasons we will only mention Profs. Gerhard Wegner, Mainz, and Josef Michl, Boulder and Prague, who were the early mentors of ADS and BTK, respectively, and showed constant interest in the developments described here as well as Prof. Yoshito Tobe, Osaka, for exchange of ideas on how to synthesize 2D polymers. We thank Gregor Hofer, ETHZ, for carefully reading the manuscript. PP thanks ETHZ for financial support through the grant ETH-26 10-2.

Notes and references

1. H. Staudinger, Ber. Dtsch. Chem. Ges., 1920, 53, 1073–1085.
2. “Hermann Staudinger Foundation of Polymer Science - Landmark - American Chemical Society,” can be found under http://www.acs.org/content/acs/en/education/whatischemistry/landmarks/staudingerpolymerscience.html, 1999.
3. Plastics – the Facts 2014. An analysis of European plastics production, demand and waste data, can be found under http://www.plasticseurope.org/, 2014.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
5. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
6. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
7. C. D. Simpson, J. D. Brand, A. J. Berresheim, L. Przybilla, H. J. Räder and K. Müllen, Chem. – Eur. J., 2002, 8, 1424–1429.
8. J. Sakamoto, J. Van Heijst, O. Lukin and A. D. Schlüter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069.
9. P. Kissel, R. Erni, W. B. Schweizer, M. D. Rossell, B. T. King, T. Bauer, S. Götzinger, A. D. Schlüter and J. Sakamoto, Nat. Chem., 2012, 4, 287–291.
10. M. J. Kory, M. Wörle, T. Weber, P. Payamyar, S. W. van de Poll, N. Trapp and A. D. Schlüter, Nat. Chem., 2014, 6, 779–784.
11. P. Kissel, D. J. Murray, W. J. Wulftange, V. J. Catalano and B. T. King, Nat. Chem., 2014, 6, 774–778.
12. J. W. Colson and W. R. Dichtel, Nat. Chem., 2013, 5, 453–465.
13. (a) X. Zhuang, Y. Mai, D. Wu, F. Zhang and X. Feng, Adv. Mater., 2014, 27, 403–427; (b) M. Lackinger, Polym. Int., 2015, 64, 1073–1078; (c) Y. Zang, T. Aoki, M. Teraguchi, T. Kaneko, L. Ma and H. Jia, Polym. Rev., 2015, 55, 57–89; (d) K. Baek, I. Hwang, I. Roy, D. Shetty and K. Kim, Acc. Chem. Res., 2015, 48, 2221–2229; (e) C. E. Boott, A. Nazemi and I. Manners, Angew. Chem., Int. Ed., 2015 DOI:10.1002/anie.201502009; (f) S.-L. Cai, W.-G. Zhang, R. N. Zuckermann, Z.-T. Li, X. Zhao and Y. Liu, Adv. Mater., 2015, 27, 5762–5770.
14. R. Mas-Ballesté, C. Gómez-Navarro, J. Gómez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30.
15. P. L. Shick, Topology, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2007.
16. G. Wegner, Thin Solid Films, 1992, 216, 105–116.
17. S. I. Stupp, S. Son, H. C. Lin and L. S. Li, Science, 1993, 259, 59–63.
18. S. I. Stupp, S. Son, L. S. Li, H. C. Lin and M. Keser, J. Am. Chem. Soc., 1995, 117, 5212–5227.
19. P. G. de Gennes, J. Chem. Phys., 1971, 55, 572–579.
20. (a) K. Tahara, H. Yamaga, E. Ghijsens, K. Inukai, J. Adisoejoso, M. O. Blunt, S. De Feyter and Y. Tobe, Nat. Chem., 2011, 3, 714–719; (b) C.-A. Palma, A. Ciesielski, M. A. Öner, G. Schaeffer, J.-M. Lehn, J. V. Bartha and P. Samori, Chem. Commun., 2015 10.1039/C5CC07204B.
21. B. Sanii, T. K. Haxton, G. K. Olivier, A. Cho, B. Barton, C. Proulx, S. Whitelam and R. N. Zuckermann, ACS Nano, 2014, 8, 11674–11684.
22. E. J. Robertson, G. K. Olivier, M. Qian, C. Proulx, R. N. Zuckermann and G. L. Richmond, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13284–13289.
23. G. Gee, Trans. Faraday Soc., 1936, 32, 187.
24. G. Gee and E. K. Rideal, J. Chem. Soc., 1937, 772.
25. L. H. Sperling, Introduction To Physical Polymer Science, John Wiley & Sons, Inc., Hoboken, New Jersey, 2006.
26. J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487.
27. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
28. G. H. Lee, R. C. Cooper, S. J. An, S. Lee, A. van der Zande, N. Petrone, A. G. Hammerberg, C. Lee, B. Crawford, W. Oliver, J. W. Kysar and J. Hone, Science, 2013, 340, 1073–1076.
29. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60–63.
30. G. H. Michler and F. J. Balta-Calleja, Mechanical Properties of Polymers Based on Nanostructure and Morphology, CRC Press Taylor & Francis, Boca Raton, Florida, 2005.
31. M. M. Caruso, D. A. Davis, Q. Shen, S. A. Odom, N. R. Sottos, S. R. White and J. S. Moore, Chem. Rev., 2009, 109, 5755–5798.
32. A polymer whose repeat units would have spatially regular 3D connectivity, like diamond.
33. P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca and London, 1979.
34. S. Torquato and Y. Jiao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032149.
35. R. Parviainen, J. Phys. A: Math. Theor., 2007, 40, 9253–9258.
36. G. Odian, Principles of Polymerization, John Wiley & Sons, Inc., 2002.
37. A. A. Dietrich Stauffer, Introduction to Percolation Theory, Taylor & Francis, London and Philadelphia, 1994.
38. S. Feng and P. Sen, Phys. Rev. Lett., 1984, 52, 216–219.
39. W. Kuhn, Kolloid Z., 1934, 68, 2–15.
40. A. Fasolino, J. H. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858–861.
41. P. Payamyar, M. Servalli, T. Hungerland, A. P. Schütz, Z. Zheng, A. Borgschulte and A. D. Schlüter, Macromol. Rapid Commun., 2015, 36, 151–158.
42. F. R. Mayo and F. M. Lewis, J. Am. Chem. Soc., 1944, 66, 1594–1601.
43. L. Opilik, P. Payamyar, J. Szczerbinski, A. P. Schütz, M. Servalli, T. Hungerland, A. D. Schlüter and R. Zenobi, ACS Nano, 2015, 9, 4252–4259.
44. R. Bhola, P. Payamyar, D. J. Murray, B. Kumar, A. J. Teator, M. U. Schmidt, S. M. Hammer, A. Saha, J. Sakamoto, A. D. Schlüter and B. T. King, J. Am. Chem. Soc., 2013, 135, 14134–14141.
45. K. Baek, G. Yun, Y. Kim, D. Kim, R. Hota, I. Hwang, D. Xu, Y. H. Ko, G. H. Gu, J. H. Suh, C. G. Park and B. J. Sung, J. Am. Chem. Soc., 2013, 135, 6523–6528.
46. (a) T. Y. Zhou, F. Lin, Z.-T. Li and X. Zhao, Macromolecules, 2013, 46, 7745–7752; (b) K. Baek, G. Yun, Y. Kim, D. Kim, R. Hota, I. Hwang, D. Xu, Y. Ho Ko, G. Ho Gu, J. H. Suh, C. G. Park, B. J. Sung and K. Kim, J. Am. Chem. Soc., 2013, 135, 6523–6528.
47. A. A. Kelly and K. M. Knowles, Crystallography and Crystal Defects., John Wiley & Sons, 2012.
48. Studying defects in single crystals is however not straight forward due to their small mass fraction within the crystal. It requires analysis of the diffuse part of the scattering (not the Bragg reflections) which is non-trivial and can only be done if brilliant X-ray beams are available. We nevertheless consider it crucial to go through this analysis to gain an in-depth understanding of the crystal defects when interpreting the results of the exfoliation process.
49. T. Weber and A. Simonov, Z. Kristallogr., 2012, 227, 238–247.
50. T. R. Welberry and B. D. Butler, Chem. Rev., 1995, 95, 2369–2403.
51. G. Wegner, Makromol. Chem., 1972, 154, 35–48.
52. G. M. J. Schmidt, Pure Appl. Chem., 1971, 27, 647–678.
53. L. Dou, Y. Zheng, X. Shen, G. Wu, K. Fields, W.-C. Hsu, H. Zhou, Y. Yang and F. Wudl, Science, 2014, 343, 272–277.
54. (a) L. Lafferentz, V. Eberhardt, C. Dri, C. Africh, G. Comelli, F. Esch, S. Hecht and L. Grill, Nat. Chem., 2012, 4, 215–220; (b) X.-H. Liu, C.-Z. Guan, S.-Y. Ding, W. Wang, H.-J. Yan, D. Wang and L.-J. Wan, J. Am. Chem. Soc., 2013, 135, 10470–10474; (c) Q. Fan, T. Wang, L. Liu, J. Zhao, J. Zhu and J. M. Gottfried, J. Chem. Phys., 2015, 142, 101906.
55. K. Tahara, J. Adisoejoso, K. Inukai, S. Lei, A. Noguchi, B. Li, W. Vanderlinden, S. De Feyter and Y. Tobe, Chem. Commun., 2014, 50, 2831–2834.
56. D. J. Murray, D. D. Patterson, P. Payamyar, R. Bhola, W. Song, M. Lackinger, A. D. Schlüter and B. T. King, J. Am. Chem. Soc., 2015, 137, 3450–3453.
57. P. Payamyar, K. Kaja, C. Ruiz-Vargas, A. Stemmer, D. J. Murray, C. J. Johnson, B. T. King, F. Schiffmann, J. Vandevondele, A. Renn, S. Götzinger, P. Ceroni, A. Schütz, L. T. Lee, Z. Zheng, J. Sakamoto and A. D. Schlüter, Adv. Mater., 2014, 26, 2052–2058.
58. A. Braslau, M. Deutsch, P. S. Pershan and A. H. Weiss, Phys. Rev. Lett., 1985, 54, 114–117.
59. R. Koitz, M. Iannuzzi and J. Hutter, J. Phys. Chem. C, 2015, 119, 4023–4030.
60. V. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819.
61. K. Edinger, A. Goelzhaeuser, K. Demota, C. Woell and M. Grunze, Langmuir, 1993, 9, 4–8.
62. G. E. Poirier, Chem. Rev., 1997, 97, 1117–1128.
63. J. A. A. W. Elemans, I. De Cat, H. Xu and S. De Feyter, Chem. Soc. Rev., 2009, 38, 722–736.
64. J. Israelachvili, Langmuir, 1994, 10, 3774–3781.
65. T. Kaindl, J. Oelke, A. Pasc, S. Kaufmann, O. V. Konovalov, S. S. Funari, U. Engel, A. Wixforth and M. Tanaka, J. Phys.: Condens. Matter, 2010, 22, 285102.
66. B. Franklin, W. Brownrigg and M. Farish, Philos. Trans. R. Soc. London, 1774, 64, 445–460.
67. I. Langmuir, J. Am. Chem. Soc., 1917, 39, 1848–1906.
68. J. Michl and T. F. Magnera, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4788–4792.
69. T. Bauer, Z. Zheng, A. Renn, R. Enning, A. Stemmer, J. Sakamoto and A. D. Schlüter, Angew. Chem., Int. Ed., 2011, 50, 7879–7884.
70. Z. Zheng, C. S. Ruiz-Vargas, T. Bauer, A. Rossi, P. Payamyar, A. Schütz, A. Stemmer, J. Sakamoto and A. D. Schlüter, Macromol. Rapid Commun., 2013, 34, 1670–1680.
71. R. Sakamoto, K. Hoshiko, Q. Liu, T. Yagi, T. Nagayama, S. Kusaka, M. Tsuchiya, Y. Kitagawa, W.-Y. Wong and H. Nishihara, Nat. Commun., 2015, 6, 6713.
72. Y. Chen, M. Li, P. Payamyar, Z. Zheng, J. Sakamoto and A. D. Schlüter, ACS Macro Lett., 2014, 3, 153–158.
73. A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170.
74. B. Lukose, A. Kuc and T. Heine, Chem. – Eur. J., 2011, 17, 2388–2392.
75. E. L. Spitler and W. R. Dichtel, Nat. Chem., 2010, 2, 672–677.
76. J. W. Colson, A. R. Woll, A. Mukherjee, M. P. Levendorf, E. L. Spitler, V. B. Shields, M. G. Spencer, J. Park and W. R. Dichtel, Science, 2011, 332, 228–231.
77. S. Jin, T. Sakurai, T. Kowalczyk, S. Dalapati, F. Xu, H. Wei, X. Chen, J. Gao, S. Seki, S. Irle and D. Jiang, Chem. – Eur. J., 2014, 8602, 14608–14613.
78. D. N. Bunck and W. R. Dichtel, J. Am. Chem. Soc., 2013, 135, 14952–14955.
79. I. Berlanga, M. L. Ruiz-González, J. M. González-Calbet, J. L. G. Fierro, R. Mas-Ballesté and F. Zamora, Small, 2011, 7, 1207–1211.
80. I. Berlanga, R. Mas-Ballesté and F. Zamora, Chem. Commun., 2012, 48, 7976–7978.
81. D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830–834.
82. Y. Zhang, J. Su, H. Furukawa, Y. Yun, F. Gándara, A. Duong, X. Zou and O. M. Yaghi, J. Am. Chem. Soc., 2013, 135, 16336–16339.
83. M. A. Baklar, A. Kumar, E. B. Domingo, M. Campoy-Quiles, K. Feldman, L. Yu, P. Wobkenberg, J. Ball, R. M. Wilson, I. McCulloch, T. Kreouzis, M. Heeney, T. Anthopoulos, P. Smith and N. Stingelin, Adv. Mater., 2010, 22, 3942–3947.
84. T. Rodenas, I. Luz, G. Prieto, B. Seoane, H. Miro, A. Corma, F. Kapteijn, I. X. F. X. Llabres and J. Gascon, Nat. Mater., 2015, 14, 48–55.
85. K. Celebi, J. Buchheim, R. M. Wyss, A. Droudian, P. Gasser, I. Shorubalko, J.-I. Kye, C. Lee and H. G. Park, Science, 2014, 344, 289–292.
86. S. Hu, M. Lozada-Hidalgo, F. C. Wang, A. Mishchenko, F. Schedin, R. R. Nair, E. W. Hill, D. W. Boukhvalov, M. I. Katsnelson, R. A. W. Dryfe, I. V. Grigorieva, H. A. Wu and A. K. Geim, Nature, 2014, 516, 227–230.
87. M. Vargas, S. Naris, D. Valougeorgis, S. Pantazis and K. Jousten, Vacuum, 2014, 109, 385–396.
88. R. Hoffmann, Am. Sci., 2011, 99, 116–119.
89. J. Sun, D. D. Klug, C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2011, 106, 145502.
90. E. Mußotter, The Carpet as Artifact, Concept & Metaphor, can be found under http://arthist.net/archive/8765, 2014.

---