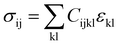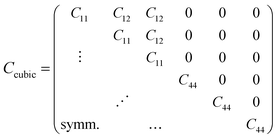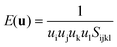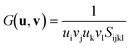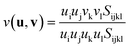Discovering connections between terahertz vibrations and elasticity underpinning the collective dynamics of the HKUST-1 metal–organic framework†
Matthew R.
Ryder
ab,
Bartolomeo
Civalleri
c,
Gianfelice
Cinque
b and
Jin-Chong
Tan
*a
aDepartment of Engineering Science, University of Oxford, Parks Road, Oxford OX1 3PJ, UK. E-mail: jin-chong.tan@eng.ox.ac.uk
bDiamond Light Source, Harwell Campus, Didcot, Oxford OX11 0DE, UK
cDepartment of Chemistry, NIS Interdepartmental Centre and INSTM Reference Centre, University of Turin, via Pietro Giuria 7, 10125 Torino, Italy
First published on 22nd January 2016
Abstract
We employed a combination of theoretical and experimental techniques to study the metal–organic framework (MOF)-mechanics central to the paddle-wheel Cu3(BTC)2 porous structure, commonly designated as HKUST-1. Lattice dynamics of the hybrid framework at below 18 THz were measured by means of Raman and synchrotron far-infrared spectroscopy, and systematically correlated to collective vibrational modes computed from ab initio density functional theory (DFT). We have identified a number of intriguing low-energy framework vibration mechanisms, reminiscent of the ‘trampoline-like’ deformations and new oscillatory motions associated with Cu paddle-wheel ‘molecular rotors’. The three independent single-crystal elastic constants of the HKUST-1 (i.e. C11, C12 and C44) were calculated using the DFT approach, taking into account the effects of dispersion corrections. We established the full elasticity solutions accompanying detailed deformation mechanisms that control its anisotropic mechanical properties, ranging from the Young's and shear moduli to linear compressibility and Poisson's ratio. Our results support the notion that the co-existance of soft modes and intrinsic shear distortions connected to the THz lattice dynamics dictate a range of anomalous elastic phenomena, for example: negative Poisson's ratio (auxeticity), negative thermal expansion (NTE), and exceedingly low shear moduli properties.
1. Introduction
Metal–organic frameworks (MOFs)1 are contemporary nanoporous solids with vast structural versatility,2 giving rise to highly tunable physical and chemical functionalities.3 The current trend is rapidly shifting from purely chemical structure discovery to development of potential applications to afford commercial use in industry, engineering, and value-added products.4 In fact, research into potential applications of MOFs is no longer limited to gas separations, carbon capture and adsorption,5 but expanding into many innovative domains encompassing optoelectronics6 and lighting,7 biomedicine,8 heterogeneous catalysis9 and chemical sensing.10The basic mechanical properties11–13 and material toughness,14,15 in conjunction with long-term structural, moisture and chemical stability of MOFs are central for manufacturing,16 shaping17 and scaling up, all of which underpinning successful deployment of aforementioned applications in many diverse technological settings. The emerging field of “MOF-mechanics”,13,18,19 particularly concerning the effects of elevated pressure (i.e. hydrostatic compression) on the structural transformation and chemical response of MOFs is an area of intense study.20,21 Tunability of MOF mechanical properties made possible through isoreticular design and construction,22 host–guest interactions,23 and chemical modification24 is another topic of current interest. Given the flexible nature of open frameworks25 attributed to compliant metal coordination environments bridged by organic linkages, they offer exciting new opportunities to yield unusual elastic response (i.e. mechanical metamaterials)26 which are rare in conventional materials, for example: negative linear compressibility (NLC), negative Poisson's ratio (NPR or auxeticity), and negative thermal expansion (NTE).18,19,21 Large elastic anisotropy of MOFs are notable,18,27 and this property could have important consequences on both mechanical and thermal stability determining the robustness of porous frameworks against structural destabilization,28 irreversible plastic deformation11,29 and amorphization.30
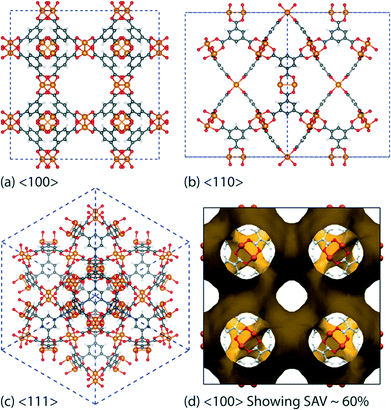
Low-frequency lattice modes—called “terahertz (THz) vibrations”31 have recently been demonstrated to be prevalent in the family of zeolitic MOFs.32 These collective modes detected at THz frequencies have been identified to have a major influence for triggering a range of intriguing lattice dynamics, particularly gate opening and breathing phenomena dictating influx and release of absorbents, soft modes and shear-induced deformations that might be the source of framework destabilization and collapse. While the structural dynamics of certain MOFs have been studied before,33 there is no detailed work connecting the behaviour of THz dynamics and elastic anisotropy to facilitate understanding of basic core mechanisms of MOFs. In this paper, we described the use of Raman and synchrotron far-infrared spectroscopy techniques in combination with ab initio density functional theory (DFT), to pinpoint and elucidate low-energy vibrational modes and associated deformation mechanisms detected in the paddle-wheel HKUST-1 [Cu3(BTC)2; BTC = benzene-1,3,5-tricarboxylic acid]34 porous framework structure (Fig. 1).
2. Experimental & theoretical methods
2.1 Experimental methodology
Infrared (IR) absorption spectra of HKUST-1 were recorded at the Multimode InfraRed Imaging and Microspectroscopy (MIRIAM) Beamline B22 at Diamond Light Source. Diamond synchrotron was operating in standard user mode, hence 900 bunches filling pattern for a total circulating current of 300 mA with top-up every 10 min (with electron beam lifetime of 18 hours). The spectrum was obtained under vacuum using a Bruker Vertex 80 V Fourier Transform Infrared (FTIR) interferometer equipped with a DLaTGS detector, operating at a resolution of 1 cm−1 and utilising a 6 μm Mylar broad-band multilayer beamsplitter. The specific beamsplitter used allowed for excellent spectra to be obtained in the region <600 cm−1 (∼20 THz). The IR spectra were acquired in ca. 2 minutes for best signal-to-noise ratio. In addition, the data set was recorded at room temperature via single-bounce Attenuated Total Reflection (ATR). Specifically, HKUST-1 powder was placed on top of a diamond ATR crystal and held in position by pressure applied on a high-density polyethylene (HDPE) disk. The Synchrotron IR beam therefore enters the ATR crystal from the bottom at an angle of 45° and is totally reflected at the interface of the crystal and the sample, then redirected by a 45° mirror to a detector. The absorption spectrum is thus measured as a modulation of this reflected light due to the evanescent wave penetrating the specimen at the diamond surface.Raman spectra were recorded using a Bruker Senterra confocal microscope with a 50× objective with high numerical aperture 0.8. Operating with a 532 nm excitation laser at 50 mW and via a 50 μm aperture setting, a resolution 6–9 cm−1 was dictated by the 1200 lines per mm grating and the spectral range of ∼4000 cm−1 to 40 cm−1 by the edge filter. Spectra were detected by an Andor deed depleted Si CCD Peltier cooled at −80 °C.
2.2 Computational methodology
We performed ab initio density functional theory (DFT) calculations using the periodic code CRYSTAL14.35 Gaussian-type atom-centred all-electron basis sets were used consisting of 2880 basis functions for all of the HKUST-1 calculations (see ESI†). The ferromagnetic cubic geometry of HKUST-1 was optimised at the B3LYP and B3LYP-D levels of theory by relaxation of both the lattice parameters and atomic coordinates. We also calculated the elastic properties of the antiferromagnetic phase36 for completeness, and the values differed by less than 1% on average with the greatest difference being 2%. To ensure the optimised structures were accurate the convergence criteria of the route mean square (RMS) of the gradient and the displacement were increased, from the default values of 0.0003 a.u. and 0.0012 a.u. to 0.0002 a.u. and 0.0004 a.u., respectively. In addition, the self-consistent field (SCF) convergence threshold was also improved from 10–7 a.u. to 10–10 a.u on the total energy and tighter tolerances for the evaluation of two-electron integrals were used.The single-crystal elastic constants of the elasticity matrix (tensor) were calculated using the numerical first derivative of the analytic cell gradients.37 These values correspond to the independent elastic stiffness coefficients, Cij.38 The unique coefficients were obtained via the method of deforming the optimised structure, using a three-point formula, in the symmetrically required directions of both positive and negative amplitudes. These particular deformations correspond to tensile and compressive strains required to obtain the elastic response. The magnitude of each individual strain deformation is defined as 1%, ensuring the response is in the purely elastic region. The mechanical properties were calculated via tensorial analysis implemented in Mathematica39 and the ElAM code.40
The vibrational frequencies at the gamma point were obtained by slightly displacing the optimised structure, with respect to the 3 N atomic coordinates, to allow for numerical differentiation of the analytical first derivatives, hence producing the mass-weighted Hessian matrix.41 The intensities of the IR-active modes were calculated via numerical differentiation, using the Berry phase approach.42 More specifically, the atomic Born tensors were evaluated via the derivation of the dipole moment with respect to the atomic displacements. This equates to the polarization differences between the optimised and the displaced structures and is equivalent to the time-integrated transient current that flows through the material during the vibrations. The intensities of the Raman-active modes were calculated analytically via Coupled Perturbed Hartree–Fock (CPHF) theory43 and corrected for the experimental parameters of a laser frequency of 532 nm and a temperature of 293 K.
3. Results and discussion
3.1 Vibrational motions present in HKUST-1
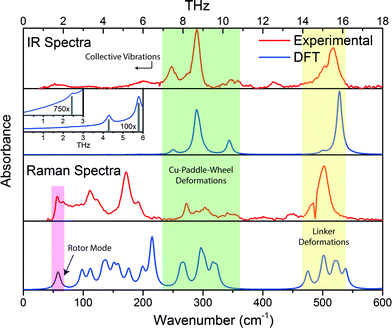
The vibrational modes located in the mid-infrared (MIR) region are simply due to the common chemical vibrational motions of any system containing organic moieties. These motions are well characterised and understood and are the result of bond stretching and bending. Even in hybrid materials, such as MOFs, the variations from the isolated organic linkers are minor. However, the low energy vibrations located in the far-infrared (FIR) region are not as trivial to explain, and this is due to them no longer originating from isolated molecular motions but instead involve the collective motion of the framework (lattice vibrations).32 In HKUST-1, particularly interesting lattice vibrations were detected to lie in the region of under 600 cm−1 (<18 THz) and involve contributions varying from Cu-paddle-wheel deformations, indicative of possible molecular rotor potentials,44 to organic linker movements which could explain the phenomenon of negative thermal expansion (NTE) experimentally confirmed in HKUST-1.45Herein we have compared the experimental and theoretical IR-active and Raman-active vibrational motions identified in the region less than 18 THz. As can be seen from Fig. 2, the agreement is very good for both IR and Raman spectra. To gain a full physical understanding of the lattice dynamics of HKUST-1, we calculated the theoretical vibrational spectra using DFT, at the B3LYP level of theory with and without corrections for dispersion. B3LYP has been augmented with the Grimme DFT-D246 empirical atom–atom pairwise -C6ij/Rij6 dispersion correction as modified for solids.47 Due to the high cubic symmetry present in HKUST-1 there are not that many unique vibrational modes in this important region, specifically we determined respectively 12 and 25 unique IR and Raman active motions located under 600 cm−1. It is worth mentioning, however, that many of the modes are triply degenerate, due to the symmetry of the framework and in addition, there are also 44 unique non-optically active vibrational motions in the same spectral region. In the next section, we will summarise all of the IR and Raman active modes and highlight some of the non-optically active modes that are of significant interest to the framework elastic properties and its anisotropy discussed after.
3.2 Distinct regions of THz vibrational modes of HKUST-1
Altogether HKUST-1 has 81 unique vibrational motions located under 600 cm−1, all of which are summarised in the ESI. The majority are due to the deformational movements of either the organic linker moieties or the inorganic Cu-centric paddle wheel units but can be grouped into distinctive spectral regions, and there are many interesting motions located in the low-energy region under 100 cm−1. Specifically, the vibrational modes can be characterised into the following regions, working from the higher energy modes downwards:• above 530 cm−1 (>16 THz) are Cu–O stretching motions;
• modes lying within 400–530 cm−1 (ca. 12–16 THz) are in-plane and out-of-plane aromatic ring deformations;
• 100–400 cm−1 modes (ca. 3–12 THz) are various combinations of ‘paddle-wheel’ deformations and linker rotational motions. These oscillatory deformations mainly consist of Cu–O stretching, O–Cu–O bending, and an interesting Cu–Cu buckling motion similar to vibrational buckling motions in small organic molecules.48 Another interesting observation in this region, are modes where the symmetry of the displacements result in a swelling or ‘breathing’ appearance of the Cu-based paddle-wheel unit. These particular motions are all Raman-active and located around 3.4 and 6.4 THz, (112, 214 and 215 cm−1), with the lowest energy example exhibiting the strongest structural deformation effect;
• modes under 100 cm−1 (<3 THz) are associated with collective framework vibrations, including ‘trampoline-like’ motions, paddle-wheel rotors, and symmetric collective motions that could explain the source of anomalous mechanical behaviour.
3.3 Noteworthy collective vibrations
We have discovered 8 unique collective vibrations of significant interest each originating from three specific classes of motion. The first interesting motion can be described as ‘trampoline-like’ deformation and is depicted in Fig. 3. There are four vibrational modes demonstrating this particular motion, located at 58, 81, 94 and 98 cm−1 (from 1.7 to 3 THz) corresponding to the Raman, IR, non-optically active, and Raman-active modes, respectively. The IR and non-active motions are primarily just the movement of the organic linker in a trampoline-like fashion but the Raman-active ones are more distinct. This is due to the symmetry of the mode located at 98 cm−1, resulting in a breathing effect of the organic–inorganic cluster. In addition, the lower-energy Raman active mode at 58 cm−1 also shows the second class of motion, involving a rotation of the paddle-wheel unit simultaneously (Fig. 4). This particular combination of motions are analogous to modes that have been suggested experimentally to drive negative thermal expansion (NTE).45 The previous work45 showed thermal ellipsoids suggesting the ‘trampoline-like’ motion at a temperature range of 100–404 K and also proposed that the liberation of the aromatic rings and twisting of the ‘paddle-wheel’ unit also contribute to the expansion upon thermal stimulus.45 All of these low-energy deformations have been demonstrated in full in our work, with the indication that NTE can be driven by a combination of THz vibrational motions. Such NTE phenomenon is possibly also linked to the other non-active modes (located at 16, 20, 63 and 78 cm−1), showing translational and rotating motions of the organic linker and Cu-based paddle-wheel which are all located in the important low-energy (THz) region, see summary in Table 1. It is also worth noting that similar motions have been suggested to be the source of NTE in other less complex MOF materials, such as the cubic MOF-5.49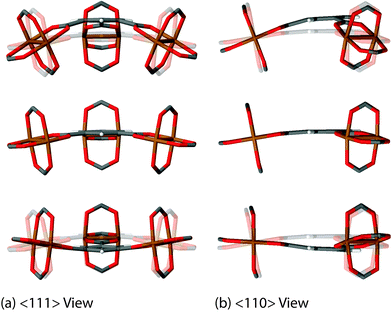 | ||
| Fig. 3 Low-energy collective vibration, located at 81 cm−1 (2.4 THz), viewed down the (a) <111> and (b) <110> directions, showing a ‘trampoline-like’ motion linked to negative thermal expansion (NTE). Videos of the motions are available in the ESI.† | ||
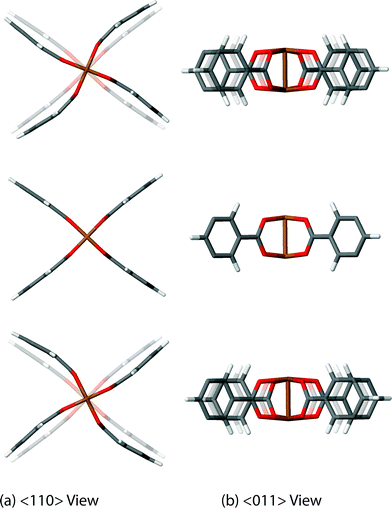 | ||
| Fig. 4 Low-energy collective vibration, located at 58 cm−1 (1.7 THz), viewed down the (a) <110> and (b) <011> directions, showing a rotor motion of the Cu-based paddle-wheel moiety. Videos of the motions are available in the ESI.† | ||
| Mode | Activity | IRREPa | Description | |
|---|---|---|---|---|
| (cm−1) | (THz) | |||
| a IRREP = Irreducible representation; Non = non-optically active mode. | ||||
| 16.32 | 0.49 | Non | F2u | Strong paddle wheel deformation and translational motion (symmetric cluster rotation) |
| 20.43 | 0.61 | Non | Eu | Strong paddle wheel deformation and translational motion |
| 58.07 | 1.74 | Raman | F2g | Strong paddle wheel rotation with organic linker trampoline-like motion |
| 63.17 | 1.89 | Non | F2u | Paddle wheel deformation and translational motion with organic linker rotating |
| 78.28 | 2.35 | Non | Bg | Paddle wheel deformation with organic linker rotating (symmetric cluster rocking) |
| 81.47 | 2.44 | IR | F1u | Organic linker trampoline-like motion |
| 94.15 | 2.82 | Non | Bu | Organic linker trampoline-like motion |
| 98.41 | 2.95 | Raman | Ag | Organic linker trampoline-like motion (symmetric cluster breathing) |
The second intriguing class of collective dynamics already mentioned above is the strong paddle-wheel rotor shown to be linked to the Raman-active mode at 58 cm−1 (1.7 THz). This particular motion is of high interest as it could suggest the possibility of utilising the mechanism for potential ‘molecular’ rotor applications.50 This is a topical area of research with some examples in MOFs starting to appear.44,51 However, most work done on MOFs has concentrated on the use of the organic linkers which is dissimilar from the rotation attributed to the metal–containing units, such as the rotor dynamics identified here regarding the paddle-wheel of HKUST-1.
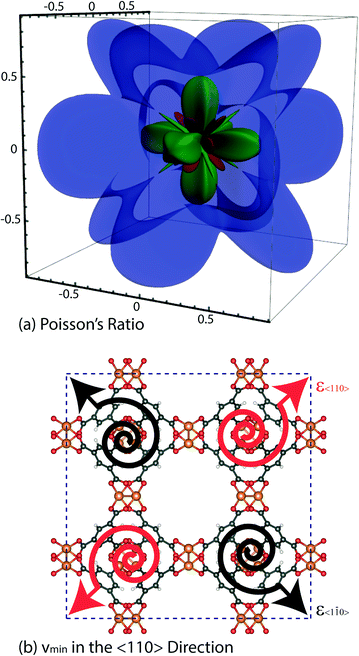
The final exciting vibrational motion revealed from our work is less trivial to describe in words, but videos of its structural dynamics can be seen in the ESI† to aid in the conceptualisation. In principle, the motions fully involve the collective framework and the organic–inorganic cluster, briefly mentioned when discussing the Raman-active mode at 98 cm−1 (∼3 THz). There are other modes in HKUST-1 whose dynamics are reminiscent of this motion, although they are more due to the symmetry of the mode resulting in the effect of synchronous cluster dynamics. Examples other than the Raman-active mode discussed, are a non-active cluster rocking motion located 78 cm−1 (2.3 THz) and this is accompanied by another non-active higher energy cluster rocking motion at 138 cm−1 (∼4 THz). However, the most exciting cluster-linked motion is the non-active mode at 16 cm−1, which is the lowest energy vibrational mode of HKUST-1 found at ca. 0.5 THz. This particular motion involves a combination of rocking and translational dynamics resulting in the rotation of the linker–paddle-wheel 4-noded cluster. The rotational movement of the cluster could reveal the nature of the mechanism behind anomalous elastic behaviour present in the material, specifically the directional auxetic response (negative Poisson's ratio), discussed in more detail later in this work.
3.4 Single-crystal elastic constants of HKUST-1
The vibrational motions discussed so far can be intrinsically linked to the mechanical behaviour of HKUST-1, especially its elastic response. We therefore, have calculated the single-crystal elastic constants using DFT and via tensorial analysis can obtain the related mechanical properties, i.e. Young's modulus, shear modulus, linear compressibility and Poisson's ratio. The link between the elastic constants and the mechanical response is from Hooke's law being related to stress σ and strain ε (both second-rank tensors) in the following equation:38where Cijkl represents the symmetric fourth-rank elasticity tensor connecting stress to strain. HKUST-1 only has three unique elastic constants (see Table 2), due to having a cubic symmetry and the symmetric elasticity matrix (stiffness tensor) therefore is:
The diagonal coefficient C11 represents the framework stiffness along each of the three principal crystal axes, i.e. a, b, and c (due to them being equal) under uniaxial strain. The other diagonal coefficient C44 is the shear stiffness measuring angular distortion against a shear deformation. The off-diagonal coefficient C12 signifies the tensile–tensile coupling between any two orthonormal axes. Importantly, the mechanical properties discussed in the next section are calculated from the inversion of the elasticity matrix, known as the compliance matrix (S) in accordance to:
| Sijkl = Cijkl−1 |
| Functional | C 11 | C 12 | C 44 |
|---|---|---|---|
| B3LYP | 27.719 | 25.722 | 5.399 |
| B3LYP-D | 27.539 | 25.476 | 5.273 |
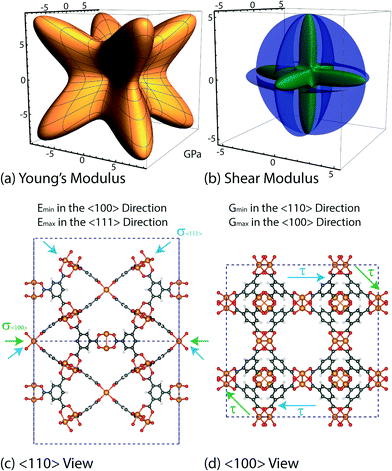
3.5 Framework elastic anisotropy under uniaxial and angular deformations
The elastic anisotropy of HKUST-1 can be witnessed when examining the 3-D directional Young's and shear moduli (see Fig. 6 and Table 3). Firstly the Young's modulus is simply the ratio of uniaxial stress over strain and can be obtained via tensorial analysis of the compliance matrix through the following equation, depending on a unit vector u: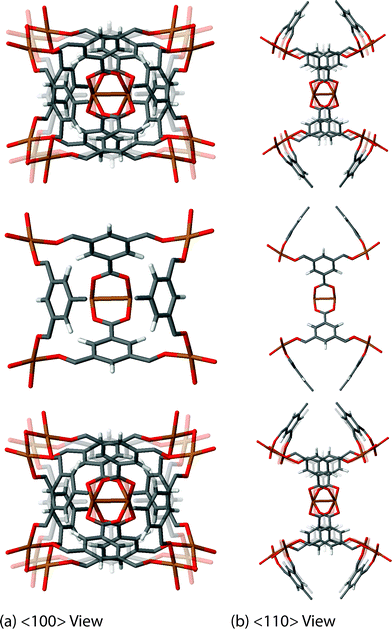 | ||
| Fig. 5 Low-energy collective vibration, located at 16 cm−1 (0.5 THz), viewed down the (a) <100> and (b) <110> directions, showing a cluster rotation mechanism, linked to auxeticity. Videos of the motions are available in the ESI.† | ||
| Elastic property | B3LYP | B3LYP-D | |
|---|---|---|---|
| Young's modulus, E (GPa) | E max | 15.15 | 14.81 |
| E min | 2.96 | 3.05 | |
| A E = Emax/Emin | 5.12 | 4.86 | |
| Shear modulus, G (GPa) | G max | 5.40 | 5.27 |
| G min | 1.00 | 1.03 | |
| A G = Gmax/Gmin | 5.40 | 5.12 | |
| Linear compressibility, β (TPa−1) | β | 12.63 | 12.74 |
| Poisson's ratio, ν | ν max | 1.21 | 1.19 |
| ν min | −0.31 | −0.28 | |
| Zener anisotropy, A | 5.41 | 5.11 | |
| Acoustic velocities(km s−1) | max | 6.18 | 6.14 |
| min | 5.62 | 5.59 |
Both the minimum and maximum Young's moduli of HKUST-1 can be easily explained from a structure–property relationship. The origin of Emax (15 GPa) is related to compression in the direction of the planarity of the aromatic rings. The link between deforming aromatic rings of the organic linker and the direction of Emax has also been detected for ZIF and MIL framework structures.18,52 In the case of HKUST-1 these maxima are located along the <111> axes. Another intriguing uniaxial property is the minimum Young's moduli, Emin (see Fig. 6). The minimum is located along the <001> axes and can be related to only partial reinforcement of the linker–paddle-wheel–linker (L–PW–L) moiety oriented along each axes. The L-PW-L unit does not provide as much mechanical rigidity as the single-linker reinforcement that has been recently found in our work on the Zr-based MIL-140 series and hence we see an Emin of just 3 GPa.52
Moving on to the angular rigidity of HKUST-1, we evaluate the shear modulus which can similarly be straightforwardly explained via structure–property relationships. Unlike the uniaxial directions of the 3-D Young's modulus surface, the shear modulus depends on an additional unit vector v and hence the representation shown in Fig. 6, depicts the maximum (blue) and minimum response (green) resulting from angular deformations in the respective directions. As per the single unit vector equation shown earlier, the shear modulus is also derived from the compliance matrix but via the following two unit vector equation:
Due to the cubic symmetry the maximum and minimum values (Gmax and Gmin) are located in multiple directions, with Gmax lying along each principal crystallographic axes <100> whereas Gmin is present in the <110> direction. This logically is due to the nodes inclusive of flexible organic components allowing for deformation upon shear strain more easily than the inorganic-based paddle-wheel on its own. This effect is illustrated very clearly in Fig. 6, where the different nodes are highlighted.
Before moving on to more complex elastic behaviour, it is worth noting that due to the cubic space group of HKUST-1, the linear compressibility (β) response of the framework upon hydrostatic compression is isotropic, unlike all of the other mechanical properties discussed in this work (Table 3). The magnitude of β is calculated to be 12.74 TPa−1 at the B3LYP-D level of theory using the following equation:
| β(u) = uiujSijkl |
3.6 Auxetic behaviour and Poisson's ratio (ν)
An interesting elastic property of HKUST-1 is the Poisson's ratio, where in certain crystalline directions a negative value has been predicted, indicating an auxetic response. As per the shear modulus discussed before, the Poisson's ratio depends on two unit vectors (u, v) and hence the 3-D representation (Fig. 7) is again limited to the maxima and minima in each direction. This instance however, due to the auxetic directions, the maximum is depicted as blue and minimum as green and red for positive and negative values, respectively. The value of the Poisson's ratio represents the ratio of the transverse strain to the axial strain under uniaxial deformation and is obtained from the following equation:The minima values, vmin and the auxetic response of −0.3, are located in the <110> direction, with the corresponding transverse in the <1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0> direction. The mechanism behind this particular response is non-trivial to explain but could be linked to the dynamics of the inorganic–organic clusters highlighted in Fig. 5, rotating upon being stretched to allow for the elongation in the transverse direction instead of the intuitive and more common response of contraction. The suggested mechanism shows the complex nature of the origins for anomalous elastic behaviour in MOFs, as new candidates for mechanical metamaterials.53 This is also a good example of why these particular calculations and studies are vital to obtain an accurate structure–property relationship at the atomic level between the framework in question and highlighting the complex 3-D directionally dependent elastic properties.
0> direction. The mechanism behind this particular response is non-trivial to explain but could be linked to the dynamics of the inorganic–organic clusters highlighted in Fig. 5, rotating upon being stretched to allow for the elongation in the transverse direction instead of the intuitive and more common response of contraction. The suggested mechanism shows the complex nature of the origins for anomalous elastic behaviour in MOFs, as new candidates for mechanical metamaterials.53 This is also a good example of why these particular calculations and studies are vital to obtain an accurate structure–property relationship at the atomic level between the framework in question and highlighting the complex 3-D directionally dependent elastic properties.
3.7 Bulk modulus and polycrystalline mechanical properties
The stability under uniform hydrostatic compression of a given material can be quantified by the bulk modulus (K). In this work, we used the Voigt–Reuss–Hill (VRH) average as the theoretical value of the bulk modulus, which equates to the numerical average of the Voigt and Reuss methods that assume a uniform strain, and uniform stress respectively. The value obtained at the B3LYP level of theory was 26 GPa, which is in reasonable agreement with the literature.54 However, as the calculated values are based on ideal polycrystalline materials assuming no residual solvent or defects, it is logical to expect experimental values would be relatively higher.The other VRH averaged polycrystalline properties (Table 4) are the isotropic analogues of the mechanical response discussed above but with the added benefit of replicating more realistically the conditions of bulk materials used for many potential applications. For example, the values can be helpful to approximate the elastic properties of randomly oriented polycrystalline MOF coatings.15,55 We established that the polycrystalline average Poisson's ratio of HKUST-1 is positive (νVRH = 0.45) despite exhibiting a significant degree of auxeticity (νmin = −0.28) in single crystal form.
| DFT functional | K VRH | E VRH | G VRH | νVRH |
|---|---|---|---|---|
| B3LYP | 26.39 | 8.10 | 2.80 | 0.45 |
| B3LYP-D | 26.16 | 8.07 | 2.78 | 0.45 |
4. Conclusions
We demonstrated the connections that can be made between vibrational modes of a framework material and its mechanical properties. Ab initio density functional theory (DFT) was employed to calculate and explain the important vibrational motions, structural dynamics and elastic properties of HKUST-1. Importantly, the vibrational calculations provide insights into significant vibrational modes including ‘trampoline-like’ motions, paddle-wheel rotors, and soft modes32,56 linked to symmetric collective mechanisms, which could explain the origin of auxeticity and negative thermal expansion (NTE) of HKUST-1 evidenced in certain crystallographic directions. In addition to the negative Poisson's ratio, a full analysis of the elastic properties was demonstrated explaining the structure–property relationships underlying the mechanics of the Cu-based MOF. Our theoretical approach coupled with experimental spectroscopy provide new understandings of the basic molecular mechanisms underlying lattice dynamics surrounding the elastic (in)stability of the paddle-wheel based framework material. It is also important to note that, the elucidated THz vibrational methodologies could be used to gain a deeper understanding of the fundamental mechanisms applicable to entirely new applications, for example: MOF host–guest interactions underpinning uptake-release sensing, molecular-scale ‘structural health’ integrity monitoring and framework diagnostics, and rotor dynamics for energy transduction. To summarise, our findings highlight that many of the mechanical mechanisms behind the anomalous elasticity of MOF materials are yet to be fully understood. In particular, we hope that further experimental studies will be performed on HKUST-1 to confirm the level of anisotropy, with regards to the DFT predicted directional dependant Young's modulus, shear modulus and Poisson's ratio.Acknowledgements
M. R. R. would like to thank the UK Engineering and Physical Sciences Research Council (EPSRC) for a DTA postgraduate scholarship and also an additional scholarship from the Science and Technology Facilities Council (STFC) CMSD Award 13-05. We thank Dr. B. Van de Voorde, KU Leuven for provision of sample. We thank Diamond Light Source for access to the MIRIAM beamline B22 (Proposal SM9388). The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (http://dx.doi.org/10.5281/zenodo.22558). We are also grateful to the SCARF cluster at the Rutherford Appleton Laboratory for provision of additional computing resources.References
- H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS PubMed; J. C. Tan and B. Civalleri, CrystEngComm, 2015, 17, 197–198 RSC.
- A. K. Cheetham, C. N. Rao and R. K. Feller, Chem. Commun., 2006, 4780–4795 RSC; M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675–702 CrossRef CAS PubMed.
- G. Férey, Chem. Soc. Rev., 2008, 37, 191–214 RSC; A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed; H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- J. Caro, Curr. Opin. Chem. Eng., 2011, 1, 77–83 CrossRef CAS; P. Silva, S. M. Vilela, J. P. Tome and F. A. Almeida Paz, Chem. Soc. Rev., 2015, 44, 6774–6803 RSC; M. R. Ryder and J. C. Tan, Mater. Sci. Technol., 2014, 30, 1598–1612 CrossRef; M. Gaab, N. Trukhan, S. Maurer, R. Gummaraju and U. Müller, Microporous Mesoporous Mater., 2012, 157, 131–136 CrossRef.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T. H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781 CrossRef CAS PubMed; M. P. Suh, H. J. Park, T. K. Prasad and D. W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef PubMed.
- V. Stavila, A. A. Talin and M. D. Allendorf, Chem. Soc. Rev., 2014, 43, 5994–6010 RSC.
- Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed.
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Ferey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268 CrossRef CAS PubMed; W. Cai, C. C. Chu, G. Liu and Y. X. Wang, Small, 2015, 11, 4806–4822 CrossRef PubMed.
- A. H. Chughtai, N. Ahmad, H. A. Younus, A. Laypkov and F. Verpoort, Chem. Soc. Rev., 2015, 44, 6804–6849 RSC.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125 CrossRef CAS PubMed; A. K. Chaudhari, I. Han and J. C. Tan, Adv. Mater., 2015, 27, 4438–4446 CrossRef PubMed; I. Stassen, M. Styles, T. Van Assche, N. Campagnol, J. Fransaer, J. Denayer, J. C. Tan, P. Falcaro, D. De Vos and R. Ameloot, Chem. Mater., 2015, 27, 1801–1807 CrossRef.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- W. Li, S. Henke and A. K. Cheetham, APL Mater., 2014, 2, 123902 CrossRef.
- J. C. Tan, B. Civalleri, A. Erba and E. Albanese, CrystEngComm, 2015, 17, 375–382 RSC.
- E. M. Mahdi and J. C. Tan, J. Membr. Sci., 2016, 498, 276–290 CrossRef CAS; N. W. Khun, E. M. Mahdi, S. Q. Ying, T. Sui, A. M. Korsunsky and J. C. Tan, APL Mater., 2014, 2, 124101 CrossRef; B. Van de Voorde, I. Stassen, B. Bueken, F. Vermoortele, D. De Vos, R. Ameloot, J.-C. Tan and T. D. Bennett, J. Mater. Chem. A, 2015, 3, 1737–1742 Search PubMed.
- I. Buchan, M. R. Ryder and J. C. Tan, Cryst. Growth Des., 2015, 15, 1991–1999 CAS; B. Van de Voorde, R. Ameloot, I. Stassen, M. Everaert, D. De Vos and J. C. Tan, J. Mater. Chem. B, 2013, 1, 7716–7724 Search PubMed.
- M. D. Allendorf and V. Stavila, CrystEngComm, 2015, 17, 229–246 RSC.
- D. Bazer-Bachi, L. Assié, V. Lecocq, B. Harbuzaru and V. Falk, Powder Technol., 2014, 255, 52–59 CrossRef CAS.
- M. R. Ryder and J. C. Tan, Dalton Trans., 2016 10.1039/C5DT03514G (In Press).
- J. M. Ogborn, I. E. Collings, S. A. Moggach, A. L. Thompson and A. L. Goodwin, Chem. Sci., 2012, 3, 3011 RSC.
- S. C. McKellar and S. A. Moggach, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 587–607 CrossRef CAS PubMed; A. J. Graham, J. C. Tan, D. R. Allan and S. A. Moggach, Chem. Commun., 2012, 48, 1535–1537 RSC; P. Zhao, T. D. Bennett, N. P. Casati, G. I. Lampronti, S. A. Moggach and S. A. Redfern, Dalton Trans., 2015, 44, 4498–4503 RSC.
- P. Serra-Crespo, A. Dikhtiarenko, E. Stavitski, J. Juan-Alcaniz, F. Kapteijn, F. X. Coudert and J. Gascon, CrystEngComm, 2015, 17, 276–280 RSC.
- J. C. Tan, T. D. Bennett and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9938–9943 CrossRef CAS PubMed; W. Li, A. Thirumurugan, P. T. Barton, Z. Lin, S. Henke, H. H. Yeung, M. T. Wharmby, E. G. Bithell, C. J. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2014, 136, 7801–7804 CrossRef PubMed; J. C. Tan, P. Jain and A. K. Cheetham, Dalton Trans., 2012, 41, 3949–3952 RSC.
- S. Henke, W. Li and A. K. Cheetham, Chem. Sci., 2014, 5, 2392–2397 RSC.
- R. J. Marshall, S. L. Griffin, C. Wilson and R. S. Forgan, J. Am. Chem. Soc., 2015, 137, 9527–9530 CrossRef CAS PubMed.
- G. Ferey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399 RSC.
- J. N. Grima and R. Caruana-Gauci, Nat. Mater., 2012, 11, 565–566 CrossRef CAS PubMed.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502 CrossRef CAS PubMed; J. C. Tan, J. D. Furman and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 14252–14254 CrossRef PubMed.
- J. C. Tan, B. Civalleri, C. C. Lin, L. Valenzano, R. Galvelis, P. F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502 CrossRef CAS PubMed; T. D. Bennett, J. Sotelo, J. C. Tan and S. A. Moggach, CrystEngComm, 2015, 17, 286–289 RSC; W. Zhou, H. Wu and T. Yildirim, Chem. Phys. Lett., 2010, 499, 103–107 CrossRef.
- K. Banlusan, E. Antillon and A. Strachan, J. Phys. Chem. C, 2015, 119, 25845 Search PubMed; V. Ishwar Hegde, J.-C. Tan, U. V. Waghmare and A. K. Cheetham, J. Phys. Chem. Lett., 2013, 4, 3377–3381 CrossRef CAS PubMed.
- T. D. Bennett, P. J. Saines, D. A. Keen, J. C. Tan and A. K. Cheetham, Chem. – Eur. J., 2013, 19, 7049–7055 CrossRef CAS PubMed; T. D. Bennett, J. C. Tan, Y. Yue, E. Baxter, C. Ducati, N. J. Terrill, H. H. M. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079 CrossRef PubMed.
- G. N. Greaves, F. Meneau, O. Majerus, D. G. Jones and J. Taylor, Science, 2005, 308, 1299–1302 CrossRef CAS PubMed.
- M. R. Ryder, B. Civalleri, T. D. Bennett, S. Henke, S. Rudić, G. Cinque, F. Fernandez-Alonso and J. C. Tan, Phys. Rev. Lett., 2014, 113, 215502 CrossRef PubMed.
- J. Nishida, A. Tamimi, H. Fei, S. Pullen, S. Ott, S. M. Cohen and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18442–18447 CrossRef CAS PubMed; N. Lock, M. Christensen, Y. Wu, V. K. Peterson, M. K. Thomsen, R. O. Piltz, A. J. Ramirez-Cuesta, G. J. McIntyre, K. Noren, R. Kutteh, C. J. Kepert, G. J. Kearley and B. B. Iversen, Dalton Trans., 2013, 42, 1996–2007 RSC; W. Zhou and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 180301(R) CrossRef; V. K. Peterson, G. J. Kearley, Y. Wu, A. J. Ramirez-Cuesta, E. Kemner and C. J. Kepert, Angew. Chem., Int. Ed., 2010, 49, 585–588 CrossRef PubMed.
- S. S. Chui, S. M. Lo, J. P. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- D. Tiana, C. H. Hendon and A. Walsh, Chem. Commun., 2014, 50, 13990–13993 RSC.
- W. F. Perger, J. Criswell, B. Civalleri and R. Dovesi, Comput. Phys. Commun., 2009, 180, 1753–1759 CrossRef CAS; A. Erba, A. Mahmoud, R. Orlando and R. Dovesi, Phys. Chem. Miner., 2014, 41, 151–160 CrossRef.
- J. F. Nye, Physical Properties of Crystals, Clarendon Press, Oxford, 1985, p. 1957 Search PubMed.
- Wolfram Research Inc., Mathematica, 2015 Search PubMed.
- A. Marmier, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Comput. Phys. Commun., 2010, 181, 2102–2115 CrossRef CAS.
- F. Pascale, C. M. Zicovich-Wilson, F. L. Gejo, B. Civalleri, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 888–897 CrossRef CAS PubMed; C. M. Zicovich-Wilson, F. Pascale, C. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 1873–1881 CrossRef PubMed; B. Civalleri, F. Napoli, Y. Noel, C. Roetti and R. Dovesi, CrystEngComm, 2006, 8, 364–371 RSC.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL14 User's Manual, University of Torino, Torino, 2014 Search PubMed.
- L. Maschio, B. Kirtman, M. Rerat, R. Orlando and R. Dovesi, J. Chem. Phys., 2013, 139, 164101 CrossRef PubMed; L. Maschio, B. Kirtman, M. Rerat, R. Orlando and R. Dovesi, J. Chem. Phys., 2013, 139, 164102 CrossRef PubMed.
- A. Comotti, S. Bracco, T. Ben, S. L. Qiu and P. Sozzani, Angew. Chem., Int. Ed., 2014, 53, 1043–1047 CrossRef CAS PubMed.
- Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929–8932 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410 RSC.
- A. Buonaugurio, J. Graham, A. Buytendyk, K. H. Bowen, M. R. Ryder, Z. G. Keolopile, M. Haranczyk and M. Gutowski, J. Chem. Phys., 2014, 140, 221103 CrossRef PubMed.
- L. H. Rimmer, M. T. Dove, A. L. Goodwin and D. C. Palmer, Phys. Chem. Chem. Phys., 2014, 16, 21144–21152 RSC.
- M. Peplow, Nature, 2015, 525, 18–21 CrossRef CAS PubMed.
- V. N. Vukotic, C. A. O'Keefe, K. Zhu, K. J. Harris, C. To, R. W. Schurko and S. J. Loeb, J. Am. Chem. Soc., 2015, 137, 9643–9651 CrossRef CAS PubMed; A. Comotti, S. Bracco, P. Valsesia, M. Beretta and P. Sozzani, Angew. Chem., Int. Ed., 2010, 49, 1760–1764 CrossRef PubMed; M. Inukai, T. Fukushima, Y. Hijikata, N. Ogiwara, S. Horike and S. Kitagawa, J. Am. Chem. Soc., 2015, 137, 12183–12186 CrossRef PubMed.
- M. R. Ryder and J. C. Tan, Unpublished work on the elasticity of isoreticular MIL structures, 2015 Search PubMed.
- L. R. Meza, A. J. Zelhofer, N. Clarke, A. J. Mateos, D. M. Kochmann and J. R. Greer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11502–11507 CrossRef CAS PubMed; R. Gatt, L. Mizzi, J. I. Azzopardi, K. M. Azzopardi, D. Attard, A. Casha, J. Briffa and J. N. Grima, Sci. Rep., 2015, 5, 8395 CrossRef PubMed.
- K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2008, 130, 10524–10526 CrossRef CAS PubMed.
- A. Betard and R. A. Fischer, Chem. Rev., 2012, 112, 1055–1083 CrossRef CAS PubMed.
- P. A. Fleury, Annu. Rev. Mater. Sci., 1976, 6, 157–180 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Lattice parameters, basis set information, descriptions of all THz vibrational modes, and videos of selected collective vibrations. See DOI: 10.1039/c5ce02347e |
| This journal is © The Royal Society of Chemistry 2016 |