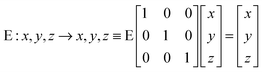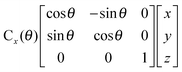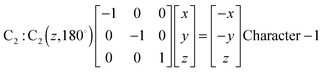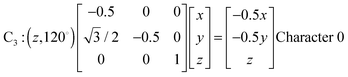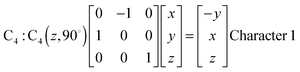Classical group theory adapted to the mechanism of Pt3Ni nanoparticle growth: the role of W(CO)6 as the “shape-controlling” agent†
Received
25th August 2015
, Accepted 13th November 2015
First published on 16th November 2015
Abstract
Classical group theory was applied to prove the Pt3Ni crystallographic transformation from Platonic cubic to Archimedean cuboctahedral structures and the formation of Pt3Ni polypods. The role of W(CO)6 as a shape-controlling agent is discussed with respect to the crystallographic features of the clusters and superstructures generated as control samples.
The colloidal Pt and Pt-based alloys are very important catalysts in chemical and electrochemical processes, including hydrogenation,1 isomerization,2 photocatalytic splitting of water,3 oxygen reduction4 or methanol oxidation.5 It has been proven that all Pt-catalysed reactions are sensitive to the crystallographic structure,6 electronic structure7 and surface atomic arrangement8 of the catalyst and can be controlled by tuning the composition and shape of nanoparticles. This molecular-scale engineering control generates catalysts with desired and improved functions and is attained in many different ways, such as the surface-energy and surfactant-governed growth,9 diffusion-limited growth,10 atom or particle-mediated growth,11 defects in seed-induced anisotropic growth,12 chemical etching of colloidal particles,13 electrochemistry-driven synthesis,14 or by using carbonyl-containing organometallics as reducing agents.15 Among those listed, relatively unexplored is the last one, especially important for the fabrication of ultra-fine metal nanoparticles (particle size less than 20 nm) with desired shapes.16 In this method the rate of metal nucleation during particle growth is controlled by a foreign element (metallic or ion) generated in situ during the thermal decomposition of e.g. carbonyls (W16 and Mn17). Taking the W(CO)6-mediated synthesis of colloidal Pt as an example, at the critical temperature, the W0 generated from W(CO)6 can reduce Pt(acac)2 to Pt atoms according to the equilibrium: Pt2+ + W0 ↔ Wn+ + Pt0.18 The tungsten ions may further accumulate locally with variable concentration and influence Pt growth. In such a case the Pt(acac)2-to-W0 concentration interplay has a strong effect on the Pt0 seed development. The Pt crystal growth will also be strongly affected by the operating temperature and reaction time, and also by the presence of a surfactant or an additional reducing agent, as is in the case of Mn2(CO)10-mediated synthesis of Pt nanocrystals.17 Assuming that the reaction temperature is close to carbonyl decomposition (but does not exceed) and the chemical reduction of the Pt cation is predominant, the second possible mechanism of Pt growth that involves carbonyl groups as the building units for Pt metal (not foreign metal or cation) is expected. This process implicates a mechanism, known as the oriented attachment,19 in which atoms are preferentially arranged towards specific crystallographic directions of the building units. This occurs in order to minimize the interfacial energy (in other words, atoms will be preferentially attached to facets with the highest surface energy or surface area).20 This method is an excellent way of synthesis of the ordered superstructures composed of many individual nanocrystals that share common crystallographic planes. Such structures possess scattering properties similar to those of single crystals.20a In this study we aim to synthesize Pt3Ni clusters or superstructures, which, depending on the synthesis conditions, can be generated with controllable features, owing to the presence of the tungsten carbonyl, the shape-controlling agent. The role of metal carbonyl in nanocluster/superstructure synthesis under various conditions (variable temperature, concentration, type of solvent, reaction time, etc.) has been already demonstrated,16 providing very important insights in the optimization of the process that delivers nano-objects with desired architectures. Our approach is to correlate the carbonyl structure with the collective symmetric configurations of metallic nanoparticles using theoretical assumptions. The proposed analysis is based on generalized group theory applied to the point group mutual for interacting (carbonyl – the shape controlling agent) and resulting species (metal nanoparticles). With respect to the theoretical arguments, we will prove that irreducible representations responsible for an excitation of translational modes in Cartesian coordinates can be defined by simple geometrical considerations based on a point group character tables, and without advanced numerical computations. Based on HR-TEM observations the Pt3Ni cluster has cuboctahedral features (Oh group20b). Thus the formation of such structures can be assumed as the transformation from Platonic cubic into Archimedean cuboctahedral arrangement. Furthermore, the same formalism is applied to study the combination of the hierarchical arrays composed of a large number of nanoparticles (Pt3Ni polypods). The details regarding the synthesis procedure for cuboctahedral Pt3Ni and polypods with elemental mapping are provided in the ESI.†
Theoretical assumption based on group theory
Energy can be considered as a sum of electronic, translational, rotational and vibrational elements.21 Energy generated by heat uptake/release (during the temperature change in the system) is defined as the random mode of translational kinetic energy in solids and random mode of rotational and translational fractions in gases composed of many atoms.21 With respect to this, when heat is applied to the molecule/ion/atom (e.g., during the temperature-dependent synthesis of metal particles) its translational modes are excited, resulting in an initiation of the structural transformations.
Fig. 1 represents the W(CO)6 octahedral crystal incorporated into a cube defined by 48 symmetry operations that are categorized by classes: E, 8C3, 6C4, 6C2, 3C2 (= C42), i, 6S4, 8S6, 3σh, and 6σd.22 Also, since cube and octahedron belong to the point group Oh, they both have the same set of symmetry operations.22 As a result, each can be generated from the other by cutting corners, e.g., irregular polyhedron, which is an intermediate structure, and is called cuboctahedron (and is also affiliated to Oh symmetry). The matrixes that are necessary to create an irreducible representation are listed below:23a
| | 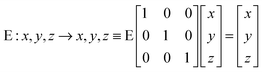 | (1) |
| | 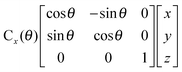 | (2) |
| | 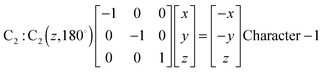 | (3) |
| | 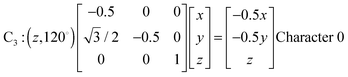 | (4) |
| | 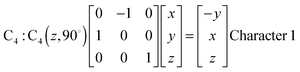 | (5) |
The matrices for various C
2, C
3 and C
4 rotations (as they affect general points:
x,
y,
z) will give directly characters for T
1 irreducible representation (
Table 1). The numbers marked in red are counterparts for the calculation of characters of matrix representations in
Table 1.
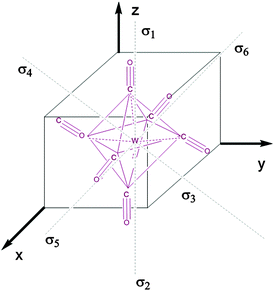 |
| | Fig. 1 The projection of the octahedral symmetry group (Oh) applied to the W(CO)6 crystal with marked σ bonds. | |
Table 1 Character table of the octahedral point group22
| O |
E |
8C3 |
6C2′ |
6C4 |
3C2 = (C4)2 |
Linear functions, rotations |
| A1 |
+1 |
+1 |
+1 |
+1 |
+1 |
— |
| A2 |
+1 |
+1 |
−1 |
−1 |
+1 |
— |
| E |
+2 |
−1 |
0 |
0 |
+2 |
— |
| T1 |
+3 |
0 |
−1 |
+1 |
−1 |
(x, y, z) (Rx, Ry, Rz) |
| T2 |
+3 |
0 |
+1 |
−1 |
−1 |
— |
The main excitation exhibits in T1 irreducible representation that causes the propagation of translational energy modes towards xz, yz and z directions. This excitation event is responsible for the elongation of the specific crystal faces in a face centred cubic (fcc), resulting in the formation of cuboctahedron. The calculations are restricted to the O group hence it represents only the translational part of the Oh group.
It is assumed a priori that after applying heat, the Brownian motions of atoms participating in the crystal growth will increase. This leads to the imposition of the Oh group to just O, which makes the calculation more restricted and simplified.
(a) Cube-to-cuboctahedra transition
The transformation of cube-to-cuboctahedron is illustrated in Fig. 2. It is predicted that the contact edges of octahedron (tungsten hexacarbonyl) are centres of excitation where the corresponding cubic crystals grow (also in the direction where the edges overlap). As proven by both theoretical and experimental studies, under similar synthesis conditions, the face-centred cubic Pt3Ni clusters are favourable. The Pt3Ni{111} family of crystallographic planes become thermodynamically the most stable (as it is the most electrochemically stable23b and the most catalytically active crystallographic facet of the Pt3Ni cluster23c,d). This promotes a rapid elimination of other Pt3Ni planes (leading in the presence of carbonyl to Pt3Ni octahedra). The formation of cuboctahedron from the cube is promoted in the presence of metal carbonyl16 and this transition can be initiated in different ways. One will be the etching of the cube, followed by dissolution in the 〈111〉 directions. It can also be the elongation of the cube towards 〈111〉 directions.24 In terms of geometry, the octahedron is a dual polyhedron with respect to cube, which means that the vertices of the octahedron correspond to the faces of the cube. This explains the formation of the octahedron through the etching of the cube. In such a case, the vertex-to-vertex distance of the octahedron would be equal to the length of the edge. The cube is also a dual polyhedron with respect to the octahedron, taking into account the contrast that the cuboctahedron can grow from cubes. In fact, the cube grows initially into an octahedron; therefore the vertex-to-vertex distance of the octahedron is two times longer than the length of the cube edge. Based on this assumption, the possible explanation of cube-to-octahedron evolution is that at lower operating temperatures the metal carbonyl will act as the crystal seed for the epitaxial growth of Pt3Ni cuboctahedron and at higher temperatures (above W(CO)6 decomposition) the metal (or metal ion) will selectively stabilize the Pt(111) species. In the latest case the W0 acts as the reducing agent in Pt2+ + 2e− = Pt0 process. Here, the Pt0 will occupy the position of galvanically replaced W0, similar to that for Mn2(CO)10-assisted synthesis.17 Mn2CO10 belongs to D4d group symmetry and W(CO)6 to Oh. The nucleation step controlled by either tungsten hexacarbonyl or dimanganese decacarbonyl starts with the elongation of x, y and z axes (Fig. 1). An excitation of the specific modes resulting in the growth along these directions is similar for both symmetries. Although the point groups are different for these carbonyls, both can initiate elongations of the same modes as discussed by other groups.25,26 As confirmed experimentally in this work, if the process is not quenched, a sub-sequential growth of Pt3Ni polypods takes place. This was accomplished by annealing the reaction vessel at 230 °C for several hours (Fig. 3).
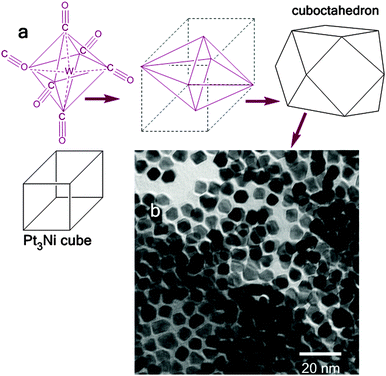 |
| | Fig. 2 Comparison between face centred cube, cuboctahedron and tungsten hexacarbonyl with the point group Oh (a) together with the TEM image of Pt3Ni structures synthetized in this work (b). | |
 |
| | Fig. 3 The formation of Pt3Ni polypods from cuboctahedral particles (a) and the corresponding TEM image (b). | |
(b) Formation of “porous crystals” (polypods)
For branched metal nanocrystals (tetrapods, octapods, multipods, and hyper-branched nanocrystals), the common synthetic control is a low carbonyl-to-Pt(acac)2 ratio and/or long reaction time.27 Under these experimental conditions the porous crystal growth will be affected by the interplay of carbonyl-to-Pt0 seed local concentration. At the operating temperature of 230 °C, carbonyl is depleted before all Pt precursors are reduced to Pt0, resulting in local gradients of the seed concentration (sometimes called “Pt0 monomer”). These metal monomers are captured by corners of the metal nanocrystals. Due to the local Pt0 depletion, more monomers are generated around the corners and thus corners grow faster. This phenomenon is described as “branch instability” and explains the crystal growth of porous metallic structures such as snow crystals.28 The growth of multipods initiated by the local gradient concentration can be classified as a four-step process that includes (steps are graphically displayed in Fig. 3a): the formation of quasi-octapods (step 1), the transition of quasi octapods to etched octapods (step 2), the transition of etched octapods to porous nanocrystals (step 3) and the growth of porous nanocrystals (step 4), as projected in Fig. 3. During the first phase, the quasi-octapods are generated from single cuboctahedral crystals. During this process faster growth on the {111} facets than on the {100} leads to prolongation along 〈111〉. In the second step, the arms of quasi-octapods grow along 〈111〉, whereas the centre of the {100} facets has been reduced (etched), resulting in the formation of etched-octapods. This process intensifies in step 3: longer branches are generated simultaneously with the intensive etching of the core, resulting in ultra-porous nanocrystals (step 4 in Fig. 3a).
Conclusions
The growth and the shape transformation of Pt3Ni particles and porous Pt3Ni superstructures are discussed with respect to the role of W(CO)6 as the shape controlling agent. The transition of Pt3Ni cubes into cuboctahedral in the kinetically controlled regime (temperature dependent) can proceed according to two mechanisms. First assumes the epitaxial crystal growth over the metal carbonyl template that occurs below the thermal decomposition of W(CO)6. The second path follows the reduction of Pt2+ with W0 associated with the preferential Pt0 occupation in the position of galvanically replaced tungsten. The theoretical calculations with assumptions for the Oh group symmetry proved the crystallographic orientation of Pt3Ni. Furthermore, the formation of Pt3Ni polypod superstructures from cuboctahedral crystals via core crystal etching and the elongation of crystal corners toward the 〈111〉 directions were discussed and correlated with experimental results (porous structures that were generated at higher temperatures or during extended reaction time). Since Pt-based alloys have great application potential in catalysis or the structure-sensitive reactions we believe that this theoretical approach provides some insights into the design of other multimetallic systems and highlights the important role of shape controlling additives.
Acknowledgements
We thank Dr Stephanie Höppener for TEM imaging and Carl Zeiss Foundation for the financial support.
Notes and references
- X. Li, B. Li, M. Cheng, Y. Du, X. Wang and P. Yang, J. Mol. Catal. A: Chem., 2008, 284, 1 CrossRef CAS.
- B. Rezaei, M. Mokhtaranpour and A. A. Ensafi, Int. J. Hydrogen Energy, 2015, 40, 6754 CrossRef CAS.
- F. Mauriello, E. Garrone, M. G. Musolino, R. Pietrapaolo and B. Onida, J. Mol. Catal. A: Chem., 2010, 328, 27 CrossRef CAS.
- N. V. Long, T. D. Hien, T. Asaka, M. Ohtaki and M. Nogami, Int. J. Hydrogen Energy, 2011, 36, 8478 CrossRef.
- M. C. Figueirendo, J. Solla-Gullón, F. J. Vidal-Iglesias, M. Nisula, J. M. Feliu and T. Kallio, Electrochem. Commun., 2015, 55, 47 CrossRef.
- E. Florez, F. Mondragon and F. Illas, Surf. Sci., 2012, 606, 1010 CrossRef CAS.
- M. D. Kane, F. S. Roberts and S. L. Anderson, Int. J. Mass Spectrom., 2015, 377, 263 CrossRef CAS.
- L. C. Wang, C. Y. Huang, C. Y. Chang, W. C. Lin and K. J. Chao, Microporous Mesoporous Mater., 2008, 110, 451 CrossRef CAS.
- S. K. Mehta, S. Kumar and M. Gradzielski, J. Colloid Interface Sci., 2011, 360, 497 CrossRef CAS PubMed.
- L. Ottaviano, P. Parisse, V. Grossi and M. Passacantando, J. Non-Cryst. Solids, 2010, 356, 2076 CrossRef CAS.
- T. Wang, S. Li, M. Jia, C. Guo and J. Hu, Colloids Surf., A, 2013, 434, 229 CrossRef CAS.
- L. Han, P. Cui, H. He, H. Liu, Z. Peng and J. Yang, J. Power Sources, 2015, 286, 488 CrossRef CAS.
- Y. Zheng, Y. Wang, S. Wang and C. H. A. Huan, Colloids Surf., A, 2006, 277, 27 CrossRef CAS.
- M. Radtke, S. Stumpf, B. Schröter, S. Höppener, U. S. Schubert and A. Ignaszak, Tetrahedron Lett., 2015, 56, 4048 CrossRef.
- Y. Luo, J. M. Mora-Hernández, L. A. Estudilo-Wong, E. M. Arce-Estrada and N. Alonso-Vante, Electrochim. Acta, 2015, 173, 771 CrossRef CAS.
- J. Zhang, H. Yang, J. Fang and S. Zou, Nano Lett., 2010, 10, 638 CrossRef CAS PubMed.
- Y. Kang, J. B. Pyo, X. Ye, R. E. Diaz, T. R. Gordon, E. A. Stach and B. Murray, ACS Nano, 2013, 7, 645 CrossRef CAS PubMed.
- J. Zhang and J. Fang, J. Am. Chem. Soc., 2009, 131, 18543 CrossRef CAS PubMed.
- K. A. Fichthorn, Chem. Eng. Sci., 2015, 121, 10 CrossRef CAS.
-
(a) C. Luna, E. D. Barriga-Castro and R. Mendoza-Reséndez, Acta Mater., 2014, 66, 405 CrossRef CAS;
(b)
D. Bonchev, Chemical Group Theory: Techniques and Applications, Taylor & Francis, 1995, ISBN-10: 2884490345 Search PubMed.
-
P. Atkins and J. de Paula, Physical Chemistry, OUP Oxford, 9th edn, 2010, ISBN-13: 978-1429218122 Search PubMed.
-
F. A. Cotton, Chemical Applications of Group Theory, Wiley-Interscience, 3rd edn, 2003, ISBN-10: 0471510947 Search PubMed.
-
(a)
G. H. Wagniére, On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image, John Wiley & Sons, 2007, ISBN: 978-3-90639-038-3 Search PubMed;
(b)
J. Fang and J. Zhang, US Pat., US8741801 B2, 2014 Search PubMed;
(c) V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, S. A. Lucas and N. M. Markovic, Science, 2007, 315, 493 CrossRef CAS PubMed;
(d) N. Todoroki, Y. Lijima, R. Takahashi, Y. Asakimori and T. Wadayama, J. Electrochem. Soc., 2013, 160, F591 CrossRef CAS.
- S. C. Yang, F. Hong, L. Q. Wang, S. W. Guo, X. P. Song, B. J. Ding and Z. M. Yang, J. Phys. Chem. C, 2010, 114, 203 CAS.
- A. Gholami and A. Reza Ashrafi, Indian J. Chem., 2008, 47A, 225 CAS.
- J. B. Westmore, K. J Fisher and G. D. Willett, Int. J. Mass Spectrom., 1999, 182–183, 53 CrossRef.
- L. Xiong and T. He, Electrochem. Commun., 2006, 8, 1671 CrossRef CAS.
- J. Gravner and D. Griffeath, Phys. D, 2008, 237, 385 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05060j |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.