Open Access Article
Open Access ArticleThe elastic–plastic transition in nanoparticle collisions
Emmanuel N.
Millán
a,
Diego R.
Tramontina
ab,
Herbert M.
Urbassek
*c and
Eduardo M.
Bringa
a
aCONICET and Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Cuyo, Mendoza, 5500 Argentina
bInstituto de Bioingeniería, Universidad de Mendoza, Mendoza, M5502BZ Argentina
cPhysics Department and Research Center OPTIMAS, University Kaiserslautern, Erwin-Schrödinger-Straße, D-67663 Kaiserslautern, Germany. E-mail: urbassek@rhrk.uni-kl.de; Web: http://www.physik.uni-kl.de/urbassek/
First published on 5th October 2015
Abstract
When nanoparticles (NPs) collide with low velocities, they interact elastically in the sense that – besides their fusion caused by their mutual van-der-Waals attraction – no defects are generated. We investigate the minimum velocity, vc, necessary for generating defects and inducing plasticity in the NP. The determination of this elastic–plastic threshold is of prime importance for modeling the behavior of granular matter. Using the generic Lennard-Jones interaction potential, we find vc to increase strongly with decreasing radius. Current models do not agree with our simulations, but we provide a model based on dislocation emission in the contact zone that quantitatively describes the size dependence of the elastic–plastic transition.
I. Introduction
Colliding nanoparticles (NPs) interact at small impact velocities elastically while plastic deformation occurs at larger velocities. The critical velocity, vc, which separates these two regimes is of prime importance for modeling the consequences of the impact; it is a basic ingredient to all discrete-element models that treat granular collisions on a mesoscopic scale,1–4 since plastic processes provide a novel route of dissipation of collision energy not present in the elastic regime. The elastic–plastic limit is decisive in such diverse areas as in materials processing of granular matter5 and dust collisions in astrophysical contexts, such as debris disks and protoplanetary disk atmospheres.6,7 Experimentally, the determination of vc is not easy, and experimenters prefer to determine the restitution coefficient or the bouncing velocity (the smallest velocity required for a NP to bounce off a wall rather than to stick to it); they then refer these quantities or changes therein to vc.Early estimates of vc assume this quantity to depend only on the mass density, the plastic yield strength and the elastic moduli.8,9vc was therefore assumed to be independent of the NP size, apart form the fact that the yield strength itself may increase for small NPs due to confinement effects. However, recently it has become possible for experiments to directly explore NPs under load. Thus it was shown that the elastic properties of NPs are basically the same as the bulk elastic properties in the case of Al NPs,10 but may deviate strongly in the case of Au or Ag NPs.11,12 Plasticity, on the other hand, can be significantly different at the nanoscale. Plastic deformation in nanoscale systems is being studied in a variety of conditions such as under nanoindentation,13,14 in nanopillars,15 nanowhiskers,16 nanoclusters,17,18 or in adhesive contacts,19 and it is often related to plasticity of nanograins in polycrystals,20 or plasticity arising from nanoscale defects like nanovoids.21,22 Recent microscopy techniques allow to view dislocations, stacking faults and twins in sub-10 nm NPs.23 To give but two examples of recent findings, experiments by Zheng et al.24 demonstrate that partial dislocations emitted from the surface dominate plasticity in sub-10 nm Au NPs, and Chrobak et al.14 point at a change of the mechanism of plasticity from a phase-transition to a dislocation-dominated regime in Si.
Complementary to experiments, molecular dynamics (MD) simulation provides a method to determine the processes occurring in NPs at the atomistic scale. Because of the simplicity of the setup, NP collisions have been frequently studied, and results on the restitution coefficient,25 NP bouncing off a surface or off other NPs,26,27 grain mixing,28 fragmentation,29,30 and the occurrence of inelastic processes31 have been reported. An analysis of the dislocation generation has been lacking up to now, with the exception of Han et al.32 who explored the interplay of collision inelasticity and dislocation generation by studying the reflection of NPs off a rigid wall.
In this paper we study the onset of plasticity in NP collisions and set up a correlation between NP size and the critical velocity for plastic yield, vc.
II. Method
We employ a generic interatomic interaction potential, the Lennard-Jones (LJ) potential, which has been frequently used in the past to model NP collisions.25–27,29,31 The plastic behavior of LJ solids has been thoroughly studied, in particular under shock loading and the dislocation activity in LJ solids has been found to be typical of that of fcc crystals.1,39,40 LJ potentials are characterized by their well depth ε and the length parameter σ. The potential is cut-off at rc = 2.5σ. Data will be reported in reduced LJ units. Table 1 specifies these units for three materials: Ar, water and Ag. The NPs are built by carving spheres of radius R from a perfect fcc structure. The number of atoms, N, in a NP is connected to its radius by R = 0.607 × N1/3 or N = 4.47 × R3. We study NPs in the range of N = 103 to 106, equivalent to R = 6.1 to 61. Here we focus on central (collinear) collisions between identical NPs. The relative orientation between the colliding NPs has been varied; the quantitative results shown are averages of up to 1000 orientations.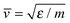 , time
, time  , temperature, T = ε/kB, and pressure,
, temperature, T = ε/kB, and pressure, ![[p with combining overline]](https://www.rsc.org/images/entities/i_char_0070_0305.gif) = ε/σ3, where kB is Boltzmann's constant
= ε/σ3, where kB is Boltzmann's constant
| ε (meV) | σ (Å) | m (amu) |
![[v with combining overline]](https://www.rsc.org/images/entities/i_char_0076_0305.gif) (m s−1) (m s−1) |
![[t with combining overline]](https://www.rsc.org/images/entities/i_char_0074_0305.gif) (ps) (ps) |
![[T with combining overline]](https://www.rsc.org/images/entities/i_char_0054_0305.gif) (K) (K) |
![[p with combining overline]](https://www.rsc.org/images/entities/i_char_0070_0305.gif) (MPa) (MPa) |
|
|---|---|---|---|---|---|---|---|
| Ar | 10.32 | 3.41 | 39.95 | 158 | 2.16 | 119.8 | 41.6 |
| H2O | 30.7 | 2.725 | 18.02 | 404 | 0.675 | 358.4 | 242.7 |
| Ag | 345 | 2.644 | 107.87 | 555 | 0.476 | 4028 | 2986 |
The molecular dynamics code LAMMPS41 is used to perform the simulations. We employ a time step of 0.001. The simulations are carried out in the constant energy ensemble, for an initial temperature of T = 0.1. The NPs are started to undergo a central collision with initial relative velocity v. We pursue the simulations for more than 105 time steps (equivalent to a final time beyond 100 in LJ units) to ensure a reasonable relaxation of the grains after their collision. VMD (visual molecular dynamics)42 and OVITO43 are used to view the simulation results. The generated defects are tracked using the dislocation extraction algorithm (DXA)44,45 and the crystal analysis tool (CAT).46
III. Results
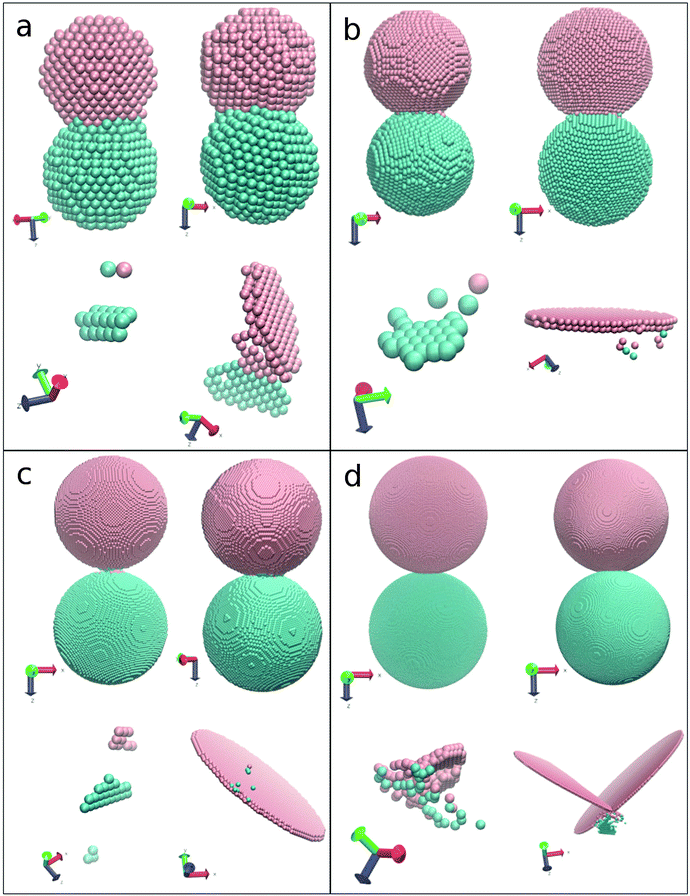
Fig. 1 gives an overview over the processes that occur upon the collision of 2 identical NPs. Here the colors cyan and pink characterize from which NP atoms originate and thus allow to identify the amount of atom transfer (mixing) during the collision. The defects produced by the large stress in the contact area are partial dislocations.47 They travel rapidly through the NPs such that at the end of the collision, when the snapshots of Fig. 1 are taken, they already swept through the entire NP. Thus the dislocations have actually vanished from the NPs but left behind the trace of their glide through the crystal: steps at the surface – clearly seen for instance in Fig. 1(c) – and a changed sequence of lattice planes in the crystal interior, called stacking faults (SFs). Such SF planes appear prominently in golden color in Fig. 1. If several SFs are produced in consecutive planes, a nanotwin is formed, such as that seen in Fig. 1(c). For certain events around vc, we observe production of transient SFs which do not reach the opposite surface, and can be reabsorbed leaving defect-free grains at the end of the simulation, as noted before.30,32Fig. 1 demonstrates that at small velocity, the NPs merely stick together, as the collision energy is dissipated by excitation of phonons and creation of heat; the attractive forces then do not allow the 2 NPs to separate again. At higher velocity, the pressure created in the contact area is large enough to create dislocations; these lead to the SF planes characterizing the induced defects. Clearly their orientation is dictated by the crystallography of the 2 NPs. At still higher velocity, abundant plasticity has been created – showing up in the intersecting SF planes, Fig. 1(c), that originated by dislocations moving along various glide systems – that virtually fills out the entire volume of the NP. Finally, at the largest velocity the 2 NPs are shattered and besides several larger fragments, a large number of monomers have been created.
We note that we occasionally do see bouncing of the 2 NPs; it occurs around vc, when the velocity is high enough to allow the 2 NPs to separate again after the collision but small enough that plasticity does not yet dominate energy dissipation.26
A. Plasticity at the threshold
Fig. 2 shows the atomistic structure of defects formed around the critical velocity. For 4 different NP sizes – varying from N = 103 to 106 – collision velocities slightly above and below the respective vc were chosen and typical defect structures are shown. Again the colors pink and cyan differentiate between the 2 NPs from which the atoms originate. Here defect atoms are not shown in golden color but in the color of the NP they belong to. While below the critical velocity, only embryonic features are seen – amorphous or plate-like strongly constrained structures – above vc full SF platelets spanning the entire NP have formed. This demonstrates that already slightly above vc plasticity is characterized by the formation of volume-spanning planar defects. Dislocations generally nucleate directly at the contact area; from there they expand until they span the entire NP. In Fig. 2(c) it is seen that the formation of planar defects is accompanied by slip leading to steps on the surface. Note that the number of defects generated in the two colliding NPs can differ strongly; this underlines the importance of the NP orientation on the creation of crystal defects.B. Existing models for critical velocity
We extract the critical velocity vc from our series of simulations by using the criterion that the number of defect atoms has reached a level of 0.5% of the total number of atoms in the NPs. For the two smallest cluster sizes used here, a threshold of 5% was used instead. In all cases, these criteria agree with the rapid rise in the curves of defects versus velocity for a given radius. Our data are averages of collisions using different NP orientations for each radius. A large variation exists in the number of defects generated in NPs of the same R and v if the crystalline orientations of the 2 colliding NPs are different, but 10–100 different orientations are enough to provide a stable mean and standard deviation, and going to 1000 events did not change our results even for the smallest clusters. The data are displayed in Fig. 3 and show that for large NPs vc levels off at 0.1, while it increases strongly with decreasing sphere radius, reaching vc = 0.55 for the smallest NPs studied, R = 3.9.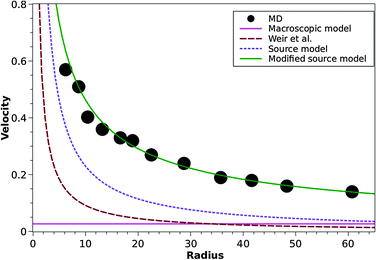 | ||
| Fig. 3 Plastic threshold, vc, as a function of NP radius, R. Symbols: our MD data. Lines provide available models: the macroscopic model, eqn (1), the model by Weir and McGavin, eqn (2), the simple source model, eqn (7), and our novel modified source model, eqn (9). The error in vc is smaller than the symbol size. | ||
The critical velocity for plasticity in the collision between two crystalline NPs is highly orientation-dependent, since it is related to the critical resolved shear stress in glide planes. In this study, a large number of collision orientations has been considered to average out this effect; the averaging is analogous to what happens in NP collision experiments due to the difficulty of tuning collision orientations at the nanoscale. This orientation dependence leads to a considerable spread in the number of defects for a given velocity and radius; for velocities in the vicinity of vc the standard deviation of the defect distribution amounts to around 50% of the average value. However, due to our large number of simulations the error of the average value in vc reduces to only around 10%. We note that there are certain experimental settings where cluster orientation could become important – such as the compression of NPs of well controlled orientation48 – and this might lead to different estimates of the critical stress for plasticity initiation.
There are only few models available in the literature that discuss the elastic–plastic transition in NP collisions. The oldest and most often used model predicts vc to show no explicit dependence on size.8,9,49,50 For two equal spheres it reads
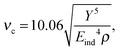 | (1) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ∼ ν/R, which may reach values of up to 0.1 for our smallest NPs. While materials constants, and in particular the yield strength Y, do depend on
∼ ν/R, which may reach values of up to 0.1 for our smallest NPs. While materials constants, and in particular the yield strength Y, do depend on ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , this dependence cannot explain any R dependence of the critical velocity, since
, this dependence cannot explain any R dependence of the critical velocity, since ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) does not change significantly at the contact interface in the NP collisions considered here. In addition we will use the theoretical strength for Y, which provides a reasonable upper bound also at high strain rates.
does not change significantly at the contact interface in the NP collisions considered here. In addition we will use the theoretical strength for Y, which provides a reasonable upper bound also at high strain rates.
Quesnel et al.51 calculated for a LJ fcc solid a density of ρ = 1.08485. In the same paper they recommend isotropic values for the elastic properties – as determined from an appropriate averaging over the elastic constants – of E = 100 and ν = 0.25, resulting in Eind = 107. For further use, we note that the shear modulus is G = 40 and the bulk modulus is K = 67. Taking Y = G/10 = 4 for a defect-free single crystal,52eqn (1) gives vc = 0.027. This is considerably smaller than our MD results, even for the largest NPs studied here. We note, however, that in a recent study of LJ NPs oriented such that they meet with their (100) facets Takato et al.27 found a larger macroscopic value of vc = 0.16 based on eqn (1), caused in particular by the larger G – and hence yield strength Y – of crystals in this direction.
There exists no theory for the increase of vc with decreasing R; however a number of models have been set up for related quantities. Thus several models have been set up for the rebound velocity, vr, which measures the minimum velocity necessary for NPs to bounce off each other; at lower velocities they stick. The rebound velocity is thought to be related to the critical velocity for plastic failure. Rennecke and Weber53 provide measurements of vr for Ag NPs with sizes between 10 and 100 nm rebounding from flat surfaces, and observed a strong increase of vr with decreasing particle size R. They show that a model by Wang and Kasper,54 which assumes completely elastic rebound, strongly underestimates the rebound velocity. However, the model by Weir and McGavin55 is approached for the smallest particles sizes. This model assumes complete plastic failure during the contact and predicts rebound to occur above
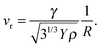 | (2) |
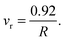 | (3) |
C. Source models
We will consider here dislocation emission from the high-pressure contact region as the origin of plasticity. Inspired by the concept of the Frank–Read source,47,57 we consider a dislocation to become emitted from the high-stress contact zone if the stress surpasses a value of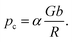 | (4) |
Since dislocation emission is governed by the applied stress, we need to convert the NP collision velocity v to pressure by using the Hugoniot relation, which relates the pressure p in a shocked material to the velocity of the piston driving the shock, up, and the velocity of the shock wave, us:
| p = ρupus = ρv(cl + sv) ≅ ρvcl. | (5) |
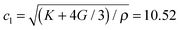 , and eqn (5) reads
, and eqn (5) reads| p = 11.41v. | (6) |
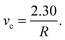 | (7) |
However, our MD simulations show that dislocations nucleate in the contact zone area, and hence the contact zone radius, ac, should be used in eqn (4) rather than the entire NP radius. The physical picture here is the following: if a dislocation line of length 2ac – spanning the contact area – has been generated, the high stress in the contact zone will drive it out into the NP, provided the line tension of the dislocation does not prevent it. At a critical stress of αGb/ac the dislocation will become unstable, leave the contact area and span the entire NP. Tanaka et al.26 showed that the collisions of LJ NPs can be reasonably well described by the JKR theory of adhesive contact mechanics.61 This theory determines the contact radius as
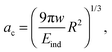 | (8) |
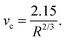 | (9) |
IV. Conclusions
In summary, our simulations show that the velocity – and hence the stress – necessary to generate dislocations in a NP increases with decreasing NP radius R proportional to 1/R2/3. Our data can be quantitatively modeled by our modified source model which assumes dislocations to be emitted from the contact area if the stress in the contact area becomes larger than the dislocation line tension. This model not only correctly reproduces the 1/R2/3 dependence of the critical velocity, but provides also a quantitatively correct description of the data obtained for the LJ NPs.Already slightly above the critical velocity, volume-spanning planar defects (stacking-fault planes) are generated. The formation of nanotwins enclosed between pairs of SF planes is another typical outcome of the plastic activity slightly above the critical velocity.
These results have immediate consequences on the sticking and bouncing behavior of NPs since plasticity forms the dominant mode of energy dissipation in NPs. In addition, they influence the coefficient of restitution. The data presented here provides basic information to enter into granular-dynamics codes and is also relevant for nanotechnology applications using NPs, since plasticity can modify their properties.62 Finally, as shown here, plastic slip leads to the generation of surface steps on the NPs, which may advantageously alter their properties for chemical processes such as, e.g., catalysis.
In future work, the effect of non-central collisions needs be addressed as well as the peculiarities of specific materials that may not be well captured by the generic Lennard-Jones model. While metal clusters are of interest in basic research, collisions of quartz and water ice clusters are of immense relevance in astrophysics and planetary sciences. Finally it will be interesting to investigate how collisions between already collided (i.e., pre-damaged) NPs differ from collisions of the single-crystalline clusters studied here.
Acknowledgements
E.M., D.T. and E.M.B. thank support from a SeCTyP project and PICT2009-0092. E.M. and D.T. acknowledge support from CONICET. H.M.U. has been supported by the Deutsche Forschungsgemeinschaft via Sonderforschungsbereich 926.References
- B. L. Holian and P. S. Lomdahl, Science, 1998, 280, 2085 CrossRef CAS PubMed.
- C. Dominik and H. Nübold, Icarus, 2002, 157, 173 CrossRef.
- K. Wada, H. Tanaka, T. Suyama, H. Kimura and T. Yamamoto, Astrophys. J., 2011, 737, 36 CrossRef.
- C. Ringl, E. M. Bringa, D. S. Bertoldi and H. M. Urbassek, Astrophys. J., 2012, 752, 151 CrossRef.
- J. Duran, Sands, powders, and grains: an introduction to the physics of granular materials, Springer Verlag, 2000 Search PubMed.
- A. Gáspár, G. H. Rieke and Z. Balog, Astrophys. J., 2013, 768, 25 CrossRef.
- A. E. Glassgold, J. Najita and J. Igea, Astrophys. J., 2004, 615, 972 CrossRef CAS.
- A. Chokshi, A. G. G. M. Tielens and D. Hollenbach, Astrophys. J., 1993, 407, 806 CrossRef.
- C. Thornton and Z. Ning, Powder Technol., 1998, 99, 154 CrossRef CAS.
- V. Juvé, A. Crut, P. Maioli, M. Pellarin, M. Broyer, N. Del Fatti and F. Vallée, Nano Lett., 2010, 10, 1853 CrossRef PubMed.
- K.-I. Saitoh and Y. Yonekawa, J. Adv. Mech. Des. Syst. Manuf., 2010, 4, 405 Search PubMed.
- J. Sun, L. He, Y.-C. Lo, T. Xu, H. Bi, L. Sun, Z. Zhang, S. X. Mao and J. Li, Nat. Mater., 2014, 13, 1007 CrossRef CAS PubMed.
- D. Mordehai, M. Kazakevich, D. J. Srolovitz and E. Rabkin, Acta Mater., 2011, 59, 2309 CrossRef CAS.
- D. Chrobak, N. Tymiak, A. Beaber, O. Ugurlu, W. W. Gerberich and R. Nowak, Nat. Nanotechnol., 2011, 6, 480 CrossRef CAS PubMed.
- D. Jang, X. Li, H. Gao and J. R. Greer, Nat. Nanotechnol., 2012, 7, 594 CrossRef CAS PubMed.
- A. Sedlmayr, E. Bitzek, D. S. Gianola, G. Richter, R. Mönig and O. Kraft, Acta Mater., 2012, 60, 3985 CrossRef CAS.
- L. M. Hale, D.-B. Zhang, X. Zhou, J. A. Zimmerman, N. R. Moody, T. Dumitrica, R. Ballarini and W. W. Gerberich, Comput. Mater. Sci., 2012, 54, 280 CrossRef CAS.
- A. Tolvanen and K. Albe, Beilstein J. Nanotechnol., 2013, 4, 173 CrossRef CAS PubMed.
- N. Pradeep, D.-I. Kim, J. Grobelny, T. Hawa, B. Henz and M. R. Zachariah, Appl. Phys. Lett., 2007, 91, 203114 CrossRef.
- Y. T. Zhu, X. Z. Liao and X. L. Wu, Prog. Mater. Sci., 2012, 57, 1 CrossRef CAS.
- V. A. Lubarda, Int. J. Plast., 2011, 27, 181 CrossRef.
- Y. Tang, E. M. Bringa and M. A. Meyers, Acta Mater., 2012, 60, 4856 CrossRef CAS.
- C.-C. Chen, C. Zhu, E. R. White, C.-Y. Chiu, M. C. Scott, B. C. Regan, L. D. Marks, Y. Huang and J. Miao, Nature, 2013, 496, 74 CrossRef CAS PubMed.
- H. Zheng, A. Cao, C. R. Weinberger, J. Y. Huang, K. Du, J. Wang, Y. Ma, Y. Xia and S. X. Mao, Nat. Commun., 2010, 1, 144 CrossRef PubMed.
- H. Kuninaka and H. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031309 CrossRef PubMed.
- H. Tanaka, K. Wada, T. Suyama and S. Okuzumi, Prog. Theor. Phys. Suppl., 2012, 195, 101 CrossRef.
- Y. Takato, S. Sen and J. B. Lechman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 033308 CrossRef PubMed.
- M. M. Mariscal, S. A. Dassie and E. P. M. Leiva, J. Chem. Phys., 2005, 123, 184505 CrossRef PubMed.
- M. Kalweit and D. Drikakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 235415 CrossRef.
- N. Ohnishi, E. M. Bringa, B. A. Remington, G. Gilmer, R. Minich, Y. Yamaguchi and A. G. G. M. Tielens, J. Phys.: Conf. Ser., 2008, 112, 042017 CrossRef.
- S.-C. Jung, J.-G. Bang and W.-S. Yoon, J. Aerosol Sci., 2012, 50, 26 CrossRef CAS.
- L. B. Han, Q. An, S. N. Luo and W. A. Goddard III, Mater. Lett., 2010, 64, 2230 CrossRef CAS.
- A. Michels, H. Wijker and H. K. Wijker, Physica, 1949, 15, 627 CrossRef CAS.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151 CrossRef CAS.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular theory of gases and liquids, Wiley, New York, 1967 Search PubMed.
- D. T. W. Lin and C.-K. Chen, Acta Mech., 2004, 173, 181 CrossRef.
- T. Halicioglu and G. M. Pound, Phys. Status Solidi A, 1975, 30, 619 CrossRef CAS.
- P. Guan, D. R. Mckenzie and B. A. Pailthorpe, J. Phys.: Condens. Matter, 1996, 8, 8753 CrossRef CAS.
- T. Hatano, Phys. Rev. Lett., 2004, 93, 085501 CrossRef PubMed.
- D. Tanguy, M. Mareschal, P. S. Lomdahl, T. C. Germann, B. L. Holian and R. Ravelo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144111 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117 CrossRef CAS , http://lammps.sandia.gov/.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef , http://www.ovito.org/.
- A. Stukowski and K. Albe, Modell. Simul. Mater. Sci. Eng., 2010, 18, 085001 CrossRef.
- A. Stukowski, V. V. Bulatov and A. Arsenlis, Modell. Simul. Mater. Sci. Eng., 2012, 20, 085007 CrossRef.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2012, 20, 045021 CrossRef.
- J. P. Hirth and J. Lothe, Theory of dislocations, Wiley, New York, 2nd edn, 1982 Search PubMed.
- W.-Z. Han, L. Huang, S. Ogata, H. Kimizuka, Z.-C. Yang, C. Weinberger, Q.-J. Li, B.-Y. Liu, X.-X. Zhang and J. Li, et al. , Adv. Mater., 2015, 27, 3385 CrossRef CAS PubMed.
- R. M. Davies, Proc. R. Soc. London, Ser. A, 1949, 197, 416 CrossRef.
- K. L. Johnson, Contact mechanics, Cambridge University Press, Cambridge, 1985 Search PubMed.
- D. J. Quesnel, D. S. Rimai and L. P. DeMejo, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 6795 CrossRef CAS.
- A. Kelly and N. H. Macmillan, Strong Solids, Clarendon Press, Oxford, 3rd edn, 1986 Search PubMed.
- S. Rennecke and A. P. Weber, J. Aerosol Sci., 2013, 58, 135 CrossRef CAS.
- H.-C. Wang and G. Kasper, J. Aerosol Sci., 1991, 22, 31 CrossRef CAS.
- G. Weir and P. McGavin, Proc. R. Soc. London, Ser. A, 2008, 464, 1295 CrossRef.
- J. Q. Broughton and G. H. Gilmer, Acta Metall., 1983, 31, 845 CrossRef CAS.
- M. A. Meyers and K. K. Chawla, Mechanical behavior of materials, Cambridge University Press, Cambridge, 2nd edn, 2010 Search PubMed.
- V. B. Shenoy, R. V. Kukta and R. Phillips, Phys. Rev. Lett., 2000, 84, 1491 CrossRef CAS PubMed.
- A. K. Nair, E. Parker, P. Gaudreau, D. Farkas and R. D. Kriz, Int. J. Plast., 2008, 24, 2016 CrossRef CAS.
- T. C. Germann, B. L. Holian, P. S. Lomdahl and R. Ravelo, Phys. Rev. Lett., 2000, 84, 5351 CrossRef CAS PubMed.
- D. Maugis, Contact, adhesion and rupture of elastic solids, Springer, Berlin, 2000 Search PubMed.
- H. Portales, N. Goubet, L. Saviot, S. Adichtchev, D. B. Murray, A. Mermet, E. Duval and M.-P. Pileni, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14784 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |