Ab initio variational predictions for understanding highly congested spectra: rovibrational assignment of 108 new methane sub-bands in the icosad range (6280–7800 cm−1)†
Michaël
Rey
*a,
Andrei V.
Nikitin
bc,
Alain
Campargue
de,
Samir
Kassi
de,
Didier
Mondelain
de and
Vladimir G.
Tyuterev
a
aGroupe de Spectrométrie Moléculaire et Atmosphérique, UMR CNRS 7331, BP 1039, F-51687, Reims Cedex 2, France. E-mail: michael.rey@univ-reims.fr
bLaboratory of Theoretical Spectroscopy, Institute of Atmospheric Optics, SB RAS, 634055 TOMSK, Russia
cLaboratory of Quantum Mechanics of Molecules and Radiative Processes, Tomsk State University, 36 Lenin Avenue, 634050 Tomsk, Russia
dUniv. Grenoble Alpes, LIPhy, F-38000 Grenoble, France
eCNRS, LIPhy, F-38000 Grenoble, France
First published on 12th November 2015
Abstract
A detailed study of methane spectra in the highly congested icosad range of 6280–7800 cm−1 has been performed using global variational calculations derived from accurate ab initio potential energy and dipole moment surfaces. About 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 12CH4 lines of the WKLMC line lists recorded at 80 and 296 K using very sensitive laser techniques (DAS, CRDS) have been rovibrationally assigned from first principles predictions. Overall, a total of 7436 upper energy levels were determined. Among the 20 bands and the 134 sub-levels contained in the icosad system, 20 and 108 have been identified for the first time, respectively. The assigned transitions represent 98% of the sum of the experimental intensity at 80 K. This work demonstrates for the first time how accurate first principles global calculations allow assigning complicated spectra of a molecule with more than 4 atoms.
000 12CH4 lines of the WKLMC line lists recorded at 80 and 296 K using very sensitive laser techniques (DAS, CRDS) have been rovibrationally assigned from first principles predictions. Overall, a total of 7436 upper energy levels were determined. Among the 20 bands and the 134 sub-levels contained in the icosad system, 20 and 108 have been identified for the first time, respectively. The assigned transitions represent 98% of the sum of the experimental intensity at 80 K. This work demonstrates for the first time how accurate first principles global calculations allow assigning complicated spectra of a molecule with more than 4 atoms.
1 Introduction
Radiative properties of methane are of crucial importance for various domains of science and applications, including chemistry, combustion, and climate changes.1 Methane is the most abundant hydrocarbon in the Earth's atmosphere acting as a greenhouse gas.2 It also affects the ozone layer depletion.1 The knowledge of methane spectroscopy in a wide frequency range is of major importance for environmental sciences and for the modeling of various planetary atmospheres (e.g. Titan3–5) as well as for other astrophysical applications.6–8 Together with other elementary hydrocarbon molecules, methane dominates the opacity of some brown dwarfs and asymptotic-giant-branch (AGB) stars and is considered among “standard” building blocks for carbon-rich atmospheres of many exoplanets.9A lot of efforts have been conducted during more than 35 years for the assignments and analyses of rotationally resolved methane spectra in the infrared range (see ref. 10–17 and references therein). The corresponding vibration–rotation patterns are known to be very complicated because of numerous intra-mode couplings due to degeneracies and accidental resonances.11,16 Because of the high tetrahedral Td symmetry of the CH4 molecule, the vibrational levels exhibit a so-called polyad structure11,16,18,19 characterized by the polyad number P = 2(υ1 + υ3) + υ2 + υ4 where υi are the normal mode vibrational quantum numbers. All assignments and modeling of high-resolution experimental spectra available in the literature have been performed using effective polyad models11,16,18,20 involving empirically-fitted parameters. Up to now, the rotationally resolved analyses covered the “forbidden” and “allowed” transitions for the vibrational ground state (GS, P = 0)21 (0–200 cm−1), the dyad (P = 1)10 (1000–1800 cm−1), the pentad (P = 2)12 (2200–3300 cm−1), the octad (P = 3)13,15 (3700–4800 cm−1), and the tetradecad (P = 4)16,17,22 (4800–6300 cm−1) ranges. In the next P = 5 polyad (icosad, 6280–7700 cm−1), only the lower edge part between 6287 and 6550 cm−1 involving the 5ν4 and 4ν4 + ν2 band systems have been analyzed by Nikitin et al.14 At higher wavenumber ranges, several experimental line-by-line methane measurements have been published by Fourier Transform Spectroscopy (FTS),23–25 Cavity-Ring-Down spectra (CRDS),26–29 Direct Absorption Spectroscopy (DAS)30–34 and Intra-Cavity-Laser Spectroscopy (ICLAS).35,36 Part of these raw data has been included in the recent edition HITRAN-2012 spectroscopic database37,38 but almost no rotationally resolved analyses are available above 6550 cm−1 except for the ν2 + 2ν3 band by Manca et al.,39 the 3ν3 band by Pierre et al.25 and for few vibrational bands reported from Zurich FTS spectra at 80 K.40 This is because an empirical determination of resonance coupling parameters in the frame of effective spectroscopic models is extremely difficult, in particular for high methane polyads involving numerous overlapping sub-bands. Of relevance for the present work, a complete jet-cooled spectrum of methane in the range 7050–7350 cm−1 has been measured in a jet at 28 K and in a bulk at 81 K, leading to the accurate determination of a number of low state rotational J values (≤4).41,42 For completeness, let us mention some rovibrational assignments obtained from jet spectra in the region of the 3ν1 + ν3 band near 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.43,44
000 cm−1.43,44
On the other hand, there has been recently considerable progress in accurate ab initio calculations of the methane PES45–50 and DMS.51–53 Various methods of variational calculations have been reported.46,50,54–61 But to our knowledge, first principles intensity predictions have not yet been directly employed for the line-by-line assignment of crowded spectra which were considered as intractable with standard effective models.
The question which we investigate in this work is then whether sufficiently accurate rotationally resolved variational predictions can be used both for line positions and intensities to directly assign complicated spectrum patterns of a five-atomic molecule in a high-energy range. To this end, we apply here for the first time a variational method to the assignment of experimental laser spectra of methane in the icosad range. The icosad system contains 20 bands with 134 sub-bands. Among them, only 3 bands with 23 sub-bands have been analyzed up to now.14,39 The motivation for this study is then twofold: first, the information on assigned transitions could be directly used in various applications for which the conditions are different from those of laboratory recordings. Second, this will provide an extremely accuracy-demanding validation both for the state-of-the-art PES and DMS and for the method of global spectral calculations. This is in turn crucial for improving high-temperature line lists60–65 for astrophysical applications (opacity of exoplanets, brown dwarfs, cool stars, etc.).
2 Experimental line list from high-sensitivity laser spectroscopy
The experimental line list considered for the present analysis is the part of the WKLMC (Wang, Kassi, Leshchishina, Mondelain, Campargue) empirical list at 80 K, corresponding to the icosad (6280–7600 cm−1), as provided in ref. 28. Because of the spectral congestion of the room temperature methane spectrum in the icosad region (about 20 lines per cm−1), low temperature recordings are highly suitable for rotational assignments. The WKLMC list for natural methane at 80 K (about 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 measured absorption lines) was constructed in Grenoble by laser absorption spectroscopy between 5850 and 7920 cm−1. High sensitivity differential laser absorption spectroscopy (DAS)30–34 and CW-Cavity Ring Down Spectroscopy (CRDS) were used in the strong absorbing regions and in the 1.58 μm26 and 1.28 μm27 window, respectively. A WKLMC line list was also constructed at room temperature (about 55
000 measured absorption lines) was constructed in Grenoble by laser absorption spectroscopy between 5850 and 7920 cm−1. High sensitivity differential laser absorption spectroscopy (DAS)30–34 and CW-Cavity Ring Down Spectroscopy (CRDS) were used in the strong absorbing regions and in the 1.58 μm26 and 1.28 μm27 window, respectively. A WKLMC line list was also constructed at room temperature (about 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 absorption lines measured at 296 K). The 296 K list is reproduced in the HITRAN2012 database.38 In the lists at 80 and 296 K, the lines of the CH3D66 and 13CH4 isotopologues present in “natural” methane were systematically identified by visual comparison with DAS spectra of the corresponding highly enriched species recorded under the same temperature conditions. The combination of the WKLMC lists at 80 and 296 K allow applying the so-called “2-Temperature-method” which consists in deriving the lower state energy level, Eemp, of a given transition from the ratio of the intensities of the corresponding line measured at two temperatures.26,31 The accuracy of the method was checked from the propensity of the derived lower state empirical Jemp values to be close to integers.26,27,33,34,67 As illustrated below, the knowledge of the lower state J value provides a useful information for full rovibrational assignment. The WKLMC list at 80 K which accounts empirically for the temperature dependence of cold band line intensities has already allowed for significant progress in the analysis of the near infrared spectra of various planetary objects, in particular Titan.34,68–70
200 absorption lines measured at 296 K). The 296 K list is reproduced in the HITRAN2012 database.38 In the lists at 80 and 296 K, the lines of the CH3D66 and 13CH4 isotopologues present in “natural” methane were systematically identified by visual comparison with DAS spectra of the corresponding highly enriched species recorded under the same temperature conditions. The combination of the WKLMC lists at 80 and 296 K allow applying the so-called “2-Temperature-method” which consists in deriving the lower state energy level, Eemp, of a given transition from the ratio of the intensities of the corresponding line measured at two temperatures.26,31 The accuracy of the method was checked from the propensity of the derived lower state empirical Jemp values to be close to integers.26,27,33,34,67 As illustrated below, the knowledge of the lower state J value provides a useful information for full rovibrational assignment. The WKLMC list at 80 K which accounts empirically for the temperature dependence of cold band line intensities has already allowed for significant progress in the analysis of the near infrared spectra of various planetary objects, in particular Titan.34,68–70
In the presently studied 6280–7600 cm−1 spectral interval, the WKLMC list of methane at 80 K28 is formed from CRDS data of ref. 26 and 27 and DAS data of ref. 33 (see Fig. 1 of ref. 28). For the forthcoming analysis, we excluded lines identified as CH3D and 13CH4 together with lines observed at 296 K and artificially added to the WKLMC list at 80 K (these lines were marked “A” in the ESI† attached to ref. 28). Note that near the borders of the analysed region, 13CH4 lines were not identified in the WKLMC list at 80 K and the resulting “cleaned” 12CH4 list may include a few 13CH4 lines.
3 Theory
Ab initio calculations for small molecules have helped resolving many issues related to spectral analyses in high energy ranges (see for example ref. 72–79 and references therein). Various implementations of variational methods exist in the literature,55,80–83 however this issue remains particularly challenging when increasing the number of atoms.84–86 In the case of five-atomics, global rotationally resolved spectral calculations in high energy ranges are known to be extremely demanding.60,61The present work is devoted to the complicated icosad system (methane polyad P = 5) composed of 20 bands which are split into 134 vibrational sublevels due to the high tetrahedral symmetry as listed below
| 5ν4(A1, E, 2F1, 4F2)/ν2 + 4ν4(2A1, 2A2, 4E, 3F1, 3F2)/ν1 + 3ν4(A1, F1, 2F2)/2ν2 + 3ν4(A, E, 4F1, 5F2)/ν3 + 3ν4/(2A1, A2, 3E, 3F1, 4F2)/2ν1 + ν4(F2)/ν1 + ν2 + 2ν4(A1, A2, 2E, F1, F2)/ν2 + ν3 + 2ν4(A1, A2, 2E, 5F1, 5F2)3ν2 + 2ν4(2A1, 2A2, 4E, 2F1, 2F2)/ν1 + ν3 + ν4(A1, E, F1, F2)/ν1 + 2ν2 + ν4(F1, 2F2)/2ν1 + ν2(E)/2ν3 + ν4(A1, E, 2F1, 3F2)/2ν2 + ν3 + ν4(2A1, A2, 3E, 3F1, 3F2)/ν1 + ν2 + ν3(F1, F2)/4ν2 + ν4(2F1, 3F2)/ν1 + 3ν2(A1, A2, E)/ν2 + 2ν3(A1, A2, 2E, F1, F2)/3ν2 + ν3(2F1, 2F2)/5ν2(A1, A2, 2E) |
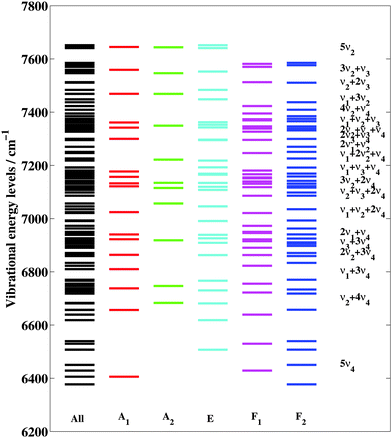
Each sub-band is characterized by the principal vibrational normal mode quantum numbers v1v2v3v4, by the symmetry irreducible representations of the Td group (C = A1, A2, E, F1 and F2) and by the corresponding ranking numbers. The complexity of the icosad vibrational structure is illustrated in Fig. 1 where the 134 vibrational sub-bands are sorted by increasing energy in different columns according to their symmetry. Among these 134 sub-bands, 43 are infrared active with F2 upper-state vibrational symmetry; the others become active through multiple resonances and intensity transfers. The effects of the tetrahedral vibrational splitting are clearly apparent. With superposed rotational patterns, this results in additional vibrational-rotational splittings and in highly congested spectra, even at low temperature.
All previous analyses10–17 of methane spectra have revealed that appropriate theoretical tools11,87,88 fully accounting for high-symmetry properties were necessary for the investigation of the corresponding complex perturbations. For the same reason, a symmetry-adapted version of variational calculations has been developed56,89,90 based on the formalism of the irreducible tensor operators (ITO).20 A full account of the symmetry properties permits us (i) to reduce the dimension of the symmetry blocks in the Hamiltonian matrix and (ii) to avoid a proliferation of redundant components for degenerate states and for the corresponding operator products. It is also beneficial for handling strict degeneracies and selection rules, particularly in the case of transitions among highly excited vibration–rotation states and high temperature spectra.
In order to be consistent with conventional spectroscopic assignments, the normal mode representation was employed in this work. As a first step, the full nuclear normal mode Eckart-frame Hamiltonian91 has been constructed in the ITO form59,90 using the 9-dimensional (9D) PES. In all calculations, we used the ab initio based potential by Nikitin et al.48 for which the previous comparisons have shown the best available agreement with experiment for rotational levels48,92 and for vibrational band centers.71 This surface will be referred to hereafter as NRT (Nikitin–Rey–Tyuterev) PES. Contrary to empirical spectroscopic models that deal with finite-dimensional matrices, the first-principles variational calculations face the well-known problem of the basis set convergence, which becomes a computational challenge in the case of elevated energy states with nine coupled vibrational degrees of freedom. To make the calculations feasible and to drastically reduce the cost of computation without almost loss of precision, a series of reduction/compression techniques were applied both to the Hamiltonian and basis functions. The reduced Hamiltonian contains much less number of ITO terms and allows avoiding non-physical features of power series expansions as described in ref. 59, 90 and 93. It is partitioned in order to solve the nuclear motion Schroedinger equation in two steps. In the initial step, the optimized vibrational sub-space (VSS) spanned by primitive symmetry-adapted normal modes basis functions was defined.59,93 In the next step, the rovibrational matrices at all J and C values were built from a more realistic basis of anharmonically coupled wavefunctions using the projection-compression technique.59,93,94 For this work, to properly converge the J = 0 energy levels, the F(15) basis of ref. 71 was used. For example, the F2 symmetry block has 105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 basis functions. If the VSS compression is not applied, the rovibrational problem would not be manageable e.g. the (J = 8, F2) block size is of 1
888 basis functions. If the VSS compression is not applied, the rovibrational problem would not be manageable e.g. the (J = 8, F2) block size is of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771
771![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276. When applying the VSS projection, only 1591 and 2767 vibrational functions corresponding to the reduced basis sets F(8) (for 14 ≤ J ≤ 19) and F(9) (for 0 ≤ J ≤ 13), respectively, were selected from F(15): see ref. 71 for the definition of F(8) and F(9). The size of the symmetry block (J = 8, F2) now drastically reduces to 44
276. When applying the VSS projection, only 1591 and 2767 vibrational functions corresponding to the reduced basis sets F(8) (for 14 ≤ J ≤ 19) and F(9) (for 0 ≤ J ≤ 13), respectively, were selected from F(15): see ref. 71 for the definition of F(8) and F(9). The size of the symmetry block (J = 8, F2) now drastically reduces to 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844, that is the rovibrational problem is scaled by 1:4
844, that is the rovibrational problem is scaled by 1:4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.
0.
By applying the VSS procedure, the vibrational band centers at this step could be refined or replaced by observed ones when available. In this way, all rotational calculations are done with ab initio Hamiltonian and DMS, but vibration–rotation resonances are better described. The latter ones are very sensitive to energy distances among upper ro-vibrational levels of the same symmetry belonging to various nearby bands. Using the VSS approach we can considerably reduce the errors in these distances as a large part of the uncertainties associated with the band centers determinations is removed. The advantage of this approach is that all elementary ITO matrix elements expressed in primitive basis functions are computed analytically without loss of precision.
Line strength calculations were performed using the purely ab initio NRT DMS52 also converted to the normal mode ITO representation and the Hamiltonian eigenvectors. All technical details of the variational method as well as convergence tests both for line positions and line intensities can be found in the previous studies.59,71 Theoretical line lists computed in this way for the icosad bands71 contain about 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 transitions for T = 80 K and 194
100 transitions for T = 80 K and 194![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 transitions for T = 296 K with the intensity cut-off of 10−29 cm−1 per molecule cm−2 upto Jmax = 15.
500 transitions for T = 296 K with the intensity cut-off of 10−29 cm−1 per molecule cm−2 upto Jmax = 15.
4 Assignment of the 12CH4 experimental line list (6280–7800 cm−1)
On a bird's-eye view, the overall agreement with the spectrum simulated from the WKLMC list at 80 K is excellent as illustrated in Fig. 2. But the detailed line-by-line assignment is still a challenging task, particularly for weak and interfering transitions.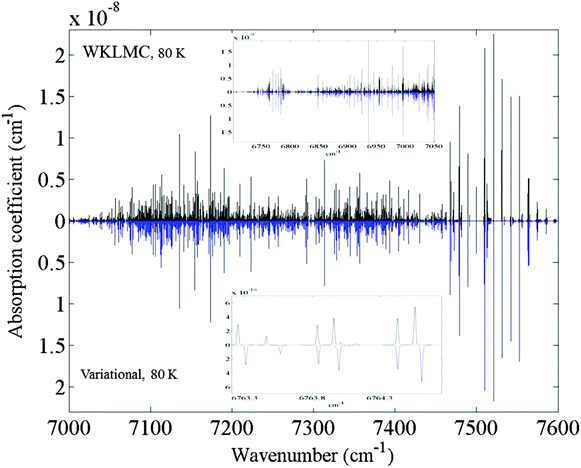 | ||
| Fig. 2 The absorption of 12CH4 in the icosad region: overview comparison of the 80 K spectra using the experimental WKLMC list28 and the ab initio variationally computed list.71 A Doppler profile (HWHM = 0.005 cm−1) was used for the simulation, with a pressure of 1 Torr. The upper inset shows the low energy edge of the icosad. The zoom presented on the lower inset illustrates the quality of the agreement. | ||
Among the 134 sub-band centers of the icosad, prior to this work, only 9 have been reliably determined14,39 from rovibrational analyses of experimental spectra. The VSS procedure permitted shifting of the calculated band centers to the known empirically derived values. The results of the analyses for the corresponding line systems were quite easily confirmed and extended. For the other sub-bands, the assignment remained quite laborious requiring several iterations except for the strongest lines which could be surely matched in many cases (see the inset in Fig. 2). Empirically determined Jemp values included in the WKLMC list28 were helpful as an initial starting point. But this did not provide neither upper vibrational states nor symmetry types. Examination of the error trends of ab initio predictions for a series of overtone and combination bands in lower polyads also provided useful hints. In the next step, the comparison of theoretical and experimental line lists for 80 K and for 296 K gave initial assignments for some rovibrational series that were further checked by extended combination differences complemented by intensity (Obs.-Calc.) matching criteria. Consistent temperature dependence between measured and predicted lines was also an important assignment criterion. Series of assignments were carried out from the comparison of the intensity ratios I(80 K)/I(296 K) for both experimental and theoretical spectra while some ambiguous lines were discarded from combination differences. Over 6000 icosad transitions were assigned in this step. Typical deviations for weak rovibrational lines at a blown up scale are shown in a zoom in Fig. 2. Even very weak transitions have been assigned during this work. For example in the inset of Fig. 2, two tiny transitions found in the experimental spectrum at 6764.125 and 6764.008 cm−1 have been assigned using the theoretical list provided in the ESI.† They correspond to the transitions 3F1 ← 3F2 of the ν2 + 4ν4(F1) sub-band and 6A1 ← 5A2 of the ν3 + 3ν4(F2) sub-band, respectively.
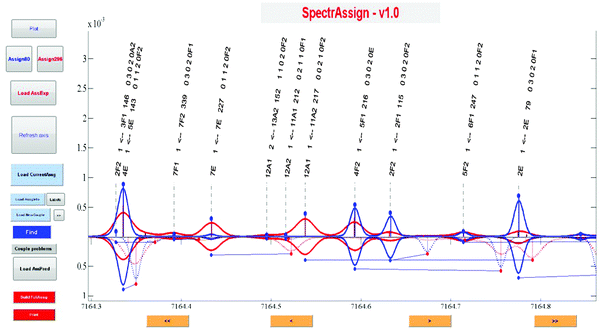
In the next step, some vibrational band centers were deduced and a new calculation was performed by replacing the J = 0 centers in the VSS procedure to refine predictions. It is worth noticing that no fits were performed in this work. Other band centers were then deduced iteratively by refining variational J = 0 energy levels from line positions involving J > 1 transitions and by computing the corresponding synthetic spectrum, and so on. A dedicated graphical interface (SpectrAssign) was developed to facilitate the assignment procedure (see Fig. 3) where 80 K and 296 K spectra are plotted in blue and red, respectively. The visual comparison of spectral simulations based on the WKLMC list (upper panel) and the variational list (bottom panel) allows the assignment of strong absorption lines at 80 K (or 296 K). Then, the intensity of the assigned lines is extrapolated at 296 K (or 80 K) on the basis of their rovibrational assignment and validated by comparison to the WKLMC simulation.
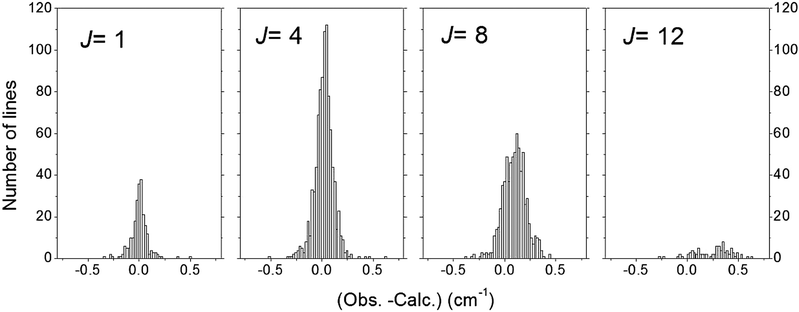
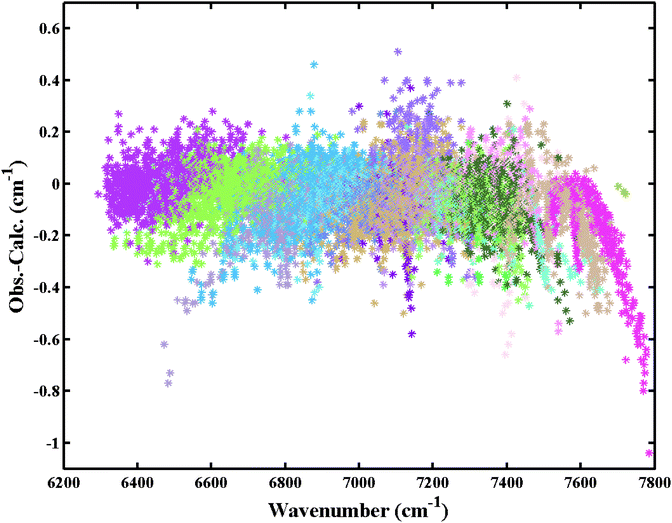
Finally, a set of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 transitions belonging to 20 bands and 131 icosad sub-bands of 12CH4 were assigned. The overview of the assigned lines is shown in Fig. 4. The assignment statistics including the number of assigned lines per band and per sub-band are given in Fig. 5. The obtained (Obs.-Calc.) line position differences are illustrated in Fig. 6 for several J values of the upper energy levels.
055 transitions belonging to 20 bands and 131 icosad sub-bands of 12CH4 were assigned. The overview of the assigned lines is shown in Fig. 4. The assignment statistics including the number of assigned lines per band and per sub-band are given in Fig. 5. The obtained (Obs.-Calc.) line position differences are illustrated in Fig. 6 for several J values of the upper energy levels.
 | ||
| Fig. 4 Overview of the assigned transitions in the icosad region of 12CH4 at 80 K. Different bands are plotted with different colors. | ||
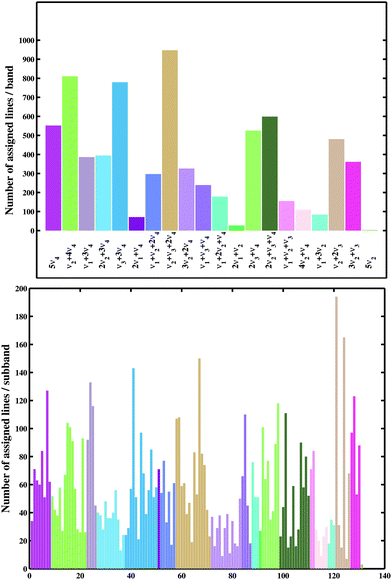 | ||
| Fig. 5 Number of assigned lines by the band (top) and by the sub-band (bottom) in increasing energy. | ||
It is instructive to compare the final lower state J values for the assigned transitions with approximated empirical determinations from the “2-Temperature method” in ref. 26 and 31 using estimations for Boltzmann temperature population. According to Fig. 7, 87% of the rounded Jemp values agree with our assignments. Most of the disagreements of the prior Jemp determination with our more rigorous assignments correspond to weak or blended lines, in particular high J transitions with very small intensity at 80 K. A few disagreements also concern strong lines corresponding to unresolved doublets, the previously reported Jemp value being an intermediate between the correct J values of the two components.
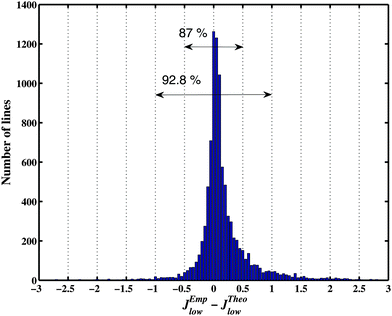 | ||
| Fig. 7 Comparison of theoretical assigned Jlow,theo values with the approximate two-temperature Jemp determination.26,31 | ||
5 Comparisons with previous studies
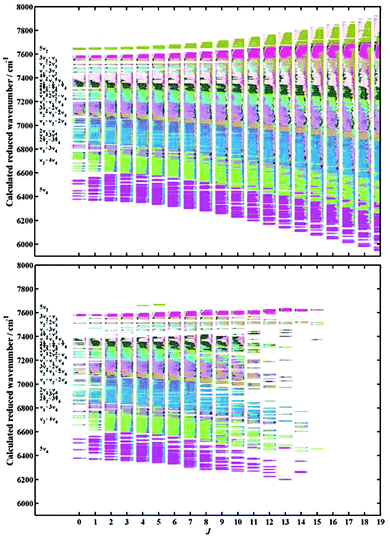
From the assigned lines, we were able to deduce 7436 vibration–rotational upper state levels without any fitting procedures. In Fig. 8, we compare the entire set of theoretical icosad levels up to J = 15 with experimentally determined ones. The corresponding errors of our initial theoretical rovibrational energy predictions are shown in Fig. 9. Actually, the largest outliers can be organized in five distinct groups with similar absolute mean errors![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) : (I)
: (I) ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = −0.7 cm−1 at around 6490 cm−1 corresponding to high-J values (>11) of the ν1 + 3ν4 band. (II) The outliers at 7140 cm−1 (
= −0.7 cm−1 at around 6490 cm−1 corresponding to high-J values (>11) of the ν1 + 3ν4 band. (II) The outliers at 7140 cm−1 (![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = −0.5 cm−1) come from the series J = 8, 9 and 10 of the 2ν1 + ν4 band while (III) those at around 7200 cm−1 (
= −0.5 cm−1) come from the series J = 8, 9 and 10 of the 2ν1 + ν4 band while (III) those at around 7200 cm−1 (![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = +0.4 cm−1) are mid-J values (J = 3–6) of ν1 + ν3 + ν4(F1) which is strongly mixed with the other components of ν1 + ν3 + ν4 and with 3ν2 + 2ν4via Coriolis couplings. (IV) Around 7400 cm−1 (
= +0.4 cm−1) are mid-J values (J = 3–6) of ν1 + ν3 + ν4(F1) which is strongly mixed with the other components of ν1 + ν3 + ν4 and with 3ν2 + 2ν4via Coriolis couplings. (IV) Around 7400 cm−1 (![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = −0.6 cm−1), the outliers come from the series J = 2–5 of the 4ν2 + ν4 band where the three F2 components are strongly mixed altogether and consequently the corresponding energy levels are very difficult to converge. (V) Finally the outliers at 7780 correspond to the series J = 10–15 of the 3ν2 + ν3 band for which the F1–F2 sublevels are strongly mixed. For the groups (I), (II) and (V), a J dependence could be derived from the errors but however would require a careful analysis. To this end, we plan to improve the calculation of the corresponding line positions by least-squares fit using effective Hamiltonian models for which matrices are finite dimensional.
= −0.6 cm−1), the outliers come from the series J = 2–5 of the 4ν2 + ν4 band where the three F2 components are strongly mixed altogether and consequently the corresponding energy levels are very difficult to converge. (V) Finally the outliers at 7780 correspond to the series J = 10–15 of the 3ν2 + ν3 band for which the F1–F2 sublevels are strongly mixed. For the groups (I), (II) and (V), a J dependence could be derived from the errors but however would require a careful analysis. To this end, we plan to improve the calculation of the corresponding line positions by least-squares fit using effective Hamiltonian models for which matrices are finite dimensional.
The empirical centers of sub-bands deduced from the present analysis are given in column 2 of Table 1. Among the 131 sub-band centers, 34 levels of symmetry F2 are determined with experimental accuracy (0.0015 cm−1) from P(1) transitions. The other ones have been deduced from J → 0 extrapolations of low-J energy levels. Their accuracy may be estimated to be ∼0.1–0.4 cm−1. But for 5 of them, low-J transitions were not assigned and the number of assignments was not sufficiently large for a reliable J → 0 extrapolation. For these sub-bands, we give in Table 1 variational predictions obtained from the NRT PES.48 Only the 5ν2 “dipole-forbidden” band system that does not have infrared active F2 vibrational upper state components remains almost missing (just 4 transitions found) as it is extremely weak and overlapping with the next P = 6 polyad (Triacontad). For completeness, the theoretical value of the 5ν2 sub-band center is provided in Table 1.
| Band | Emp. valuesi | Emp.-NRT PES (normal coord.)a | Emp.-NRT PES (curv. coord.)b | Emp.-WCc | Emp.-ExoMold | Emp.-Heffe |
|---|---|---|---|---|---|---|
| The columns give the discrepancies between the empirically determined band centersi and theoretical calculated values:a Calc. 1: variationally predicted from the NRT PES48 and normal coordinates as in ref. 71.b Calc. 2: variationally predicted from the refined NRT PES and curvilinear coordinates.58c Calc. 3: reported by Wang and Carrington (WC)49 from empirically fitted PES.d Calc. 4: from the ExoMol 10 to 10 project.60 Downloaded from http://www.exomol.com/ (August, 2015).e Calc. 5: obtained from an empirical effective Hamiltonian model.40f Values obtained from P(1) transitions.g Assigned but values fixed from Calc. 1.h Not assigned; values fixed from Calc. 1.i The estimated accuracy of the experimental values is 10−3 cm−1 when determined from an observed P(1) transition and 0.1–0.4 cm−1 in other cases. | ||||||
| 5ν4(F2) | 6377.53 | 0.41 | −0.52 | −1.35 | −34.56 | 3.92 |
| 5ν4(A1) | 6405.89 | 0.10 | −0.35 | −1.37 | −30.48 | |
| 5ν4(F1) | 6429.20 | 0.26 | −0.49 | −0.67 | −30.39 | |
| 5ν4(F2) | 6450.060f | −0.30 | −0.59 | −1.29 | −26.53 | −0.18 |
| 5ν4(E) | 6507.37 | 0.11 | 0.01 | −0.50 | −17.66 | |
| 5ν4(F2) | 6507.554f | 0.10 | −0.04 | −0.50 | −20.05 | −3.77 |
| 5ν4(F1) | 6529.74 | 0.01 | −0.19 | −0.63 | −18.79 | |
| 5ν4(F2) | 6539.182f | −0.27 | −0.19 | −0.94 | −15.70 | 0.76 |
| ν 2 + 4ν4(E) | 6617.50 | −0.78 | −1.16 | −1.03 | −22.83 | |
| ν 2 + 4ν4(F1) | 6638.52 | −0.63 | −0.97 | −0.97 | −16.18 | |
| ν 2 + 4ν4(A1) | 6655.88 | −0.78 | −1.32 | −0.45 | −30.57 | |
| ν 2 + 4ν4(F2) | 6657.092f | −0.17 | −0.60 | −0.96 | −23.98 | −1.76 |
| ν 2 + 4ν4(E) | 6680.93 | −0.32 | −0.54 | −0.94 | −28.86 | |
| ν 2 + 4ν4(A2) | 6682.82 | −0.37 | −0.68 | −0.93 | −14.03 | |
| ν 2 + 4ν4(F2) | 6717.991f | −0.18 | −0.42 | −0.17 | −17.01 | 2.38 |
| ν 2 + 4ν4(F1) | 6722.00 | −0.15 | −0.17 | −0.61 | −17.18 | |
| ν 2 + 4ν4(E) | 6729.60 | −0.57 | −0.75 | −0.32 | −19.92 | |
| ν 2 + 4ν4(F2) | 6733.105f | −0.40 | −0.50 | −0.58 | −15.57 | 1.32 |
| ν 2 + 4ν4(A1) | 6737.79 | −0.04 | −0.17 | −0.28 | −14.32 | |
| ν 2 + 4ν4(A2) | 6746.23 | −0.51 | −0.34 | −0.97 | −15.61 | |
| ν 2 + 4ν4(F1) | 6755.38 | −0.06 | −0.12 | −0.61 | −16.47 | |
| ν 2 + 4ν4(E) | 6766.23 | −0.31 | −0.17 | −0.81 | −15.48 | |
| ν 1 + 3ν4(F2) | 6769.194f | −1.03 | −0.16 | −1.65 | −26.61 | −9.39 |
| ν 1 + 3ν4(A1) | 6809.40 | −0.68 | 0.07 | −1.17 | −11.53 | |
| ν 1 + 3ν4(F1) | 6822.30 | −0.31 | 0.03 | −1.26 | −13.78 | |
| ν 1 + 3ν4(F2) | 6833.190f | −0.43 | −0.11 | −1.64 | −20.82 | −4.58 |
| ν 3 + 3ν4(F2) | 6858.707f | −0.64 | −0.14 | −0.53 | −12.42 | −1.72 |
| ν 3 + 3ν4(E) | 6862.74 | −0.07 | −0.02 | −0.22 | −10.64 | |
| ν 3 + 3ν4(F1) | 6862.85 | −0.12 | 0.08 | −0.25 | −7.64 | |
| ν 3 + 3ν4(A1) | 6863.10 | −0.55 | −0.31 | −1.17 | −12.45 | |
| 2ν2 + 3ν4(F2) | 6869.793f | −0.89 | −1.37 | −0.32 | −23.91 | −3.33 |
| 2ν2 + 3ν4(F1) | 6889.68 | −0.75 | −1.08 | −0.68 | −21.12 | |
| ν 3 + 3ν4(F2) | 6897.383f | −0.02 | 0.03 | −0.18 | −12.40 | −4.06 |
| 2ν2 + 3ν4(F2) | 6905.60 | −0.58 | −0.92 | −0.57 | −13.96 | |
| ν 3 + 3ν4(E) | 6908.80 | −0.16 | 0.14 | −0.04 | −5.52 | |
| ν 3 + 3ν4(F2) | 6910.383f | −0.11 | 0.10 | −0.18 | −19.21 | −1.87 |
| ν 3 + 3ν4(F1) | 6915.18 | 0.19 | 0.27 | 0.05 | −8.35 | |
| ν 3 + 3ν4(A2) | 6918.55 | 0.14 | 0.11 | 0.09 | −60.60 | |
| ν 3 + 3ν4(F1) | 6921.58 | −0.24 | 0.04 | −0.40 | −52.53 | |
| ν 3 + 3ν4(A1) | 6922.07 | −0.11 | −0.12 | −0.61 | −49.80 | |
| ν 3 + 3ν4(F2) | 6924.967f | −0.01 | 0.03 | −0.34 | −45.72 | −0.87 |
| ν 3 + 3ν4(E) | 6925.67 | −0.30 | −0.16 | −0.88 | −57.71 | |
| 2ν2 + 3ν4(E) | 6938.40 | −0.39 | −0.50 | −0.54 | −16.52 | |
| 2ν2 + 3ν4(F2) | 6940.051f | −0.65 | −1.01 | −0.39 | −17.01 | 5.90 |
| 2ν2 + 3ν4(A1) | 6940.10 | −0.36 | −0.54 | −0.22 | −13.60 | |
| 2ν2 + 3ν4(F1) | 6945.16 | −0.74 | −0.94 | −0.24 | −15.01 | |
| 2ν2 + 3ν4(F1) | 6949.70 | −0.39 | −0.72 | −0.14 | −13.80 | |
| 2ν2 + 3ν4(F2) | 6962.42 | −0.28 | −0.36 | −0.48 | −15.74 | |
| 2ν2 + 3ν4(F1) | 6972.86g | |||||
| ν 1 + ν2 + 2ν4(E) | 6990.01 | −0.70 | −0.43 | −1.03 | −27.93 | |
| 2ν2 + 3ν4(F2) | 6992.582f | −0.36 | −0.33 | −0.71 | −14.48 | −1.37 |
| ν 1 + ν2 + 2ν4(F1) | 7020.43 | −0.67 | −0.28 | −0.87 | −15.74 | |
| ν 1 + ν2 + 2ν4(A1) | 7024.03 | −0.26 | −0.45 | −0.61 | −19.57 | |
| ν 1 + ν2 + 2ν4(F2) | 7035.180f | −0.16 | −0.03 | −0.88 | −14.98 | −3.32 |
| ν 1 + ν2 + 2ν4(E) | 7045.69 | −0.24 | −0.05 | −1.26 | −19.11 | |
| ν 1 + ν2 + 2ν4(A2) | 7056.56 | −0.40 | −0.02 | −1.41 | −18.58 | |
| 2ν1 + ν4(F2) | 7085.637f | −0.33 | 0.04 | 0.69 | −8.58 | −7.39 |
| ν 2 + ν3 + 2ν4(F1) | 7085.73 | 0.07 | 0.31 | 1.00 | −14.79 | |
| ν 2 + ν3 + 2ν4(F2) | 7097.915f | −0.06 | −0.13 | 0.32 | −21.04 | 0.11 |
| ν 2 + ν3 + 2ν4(E) | 7107.28 | −0.71 | −0.29 | 0.40 | −19.53 | |
| ν 2 + ν3 + 2ν4(A2) | 7114.54 | −0.59 | −0.40 | 0.18 | 3.54 | |
| ν 2 + ν3 + 2ν4(F2) | 7116.385f | −0.20 | −0.12 | 0.38 | 9.18 | −2.05 |
| ν 2 + ν3 + 2ν4(F1) | 7118.05g | |||||
| 3ν2 + 2ν4(E) | 7118.40 | −1.01 | −1.37 | 0.55 | −24.30 | |
| 3ν2 + 2ν4(A1) | 7120.74 | −0.60 | −0.78 | 0.72 | −26.27 | |
| ν 2 + ν3 + 2ν4(F2) | 7121.90 | 0.25 | 0.05 | 0.63 | −17.49 | 0.73 |
| ν 2 + ν3 + 2ν4(F1) | 7130.90 | −0.15 | −0.14 | −0.07 | −40.27 | |
| ν 2 + ν3 + 2ν4(F2) | 7131.135f | −0.10 | −0.11 | 0.05 | −34.85 | −1.01 |
| ν 2 + ν3 + 2ν4(A1) | 7132.50 | −0.04 | −0.55 | 0.48 | 0.96 | |
| 3ν2 + 2ν4(A2) | 7133.69 | −0.76 | −1.19 | −0.07 | −23.27 | |
| ν 2 + ν3 + 2ν4(E) | 7134.00 | −0.02 | −0.02 | 0.09 | −15.25 | |
| ν 2 + ν3 + 2ν4(F1) | 7139.23 | −0.17 | −0.11 | 0.02 | −47.06 | |
| ν 2 + ν3 + 2ν4(F2) | 7141.50 | −0.12 | −0.18 | −0.09 | −31.34 | |
| ν 2 + ν3 + 2ν4(F1) | 7151.02 | −0.20 | −0.03 | 0.16 | 6.67 | |
| 3ν2 + 2ν4(F1) | 7153.84 | −0.87 | −1.18 | −0.26 | −13.55 | |
| ν 1 + ν3 + ν4(A1) | 7157.16 | 0.14 | 0.20 | 0.68 | 2.41 | |
| ν 1 + ν3 + ν4(F2) | 7158.128f | −0.11 | 0.10 | 0.69 | 12.95 | 3.40 |
| ν 1 + ν3 + ν4(E) | 7164.60 | −0.53 | −0.24 | 0.28 | 55.64 | |
| ν 1 + ν3 + ν4(F1) | 7165.60 | −1.04 | −0.71 | −0.44 | 32.51 | |
| 3ν2 + 2ν4(E) | 7168.00 | −0.83 | −1.22 | 0.01 | −12.99 | |
| 3ν2 + 2ν4(F2) | 7168.422f | −0.60 | −0.94 | −0.11 | −13.09 | 1.98 |
| 3ν2 + 2ν4(A1) | 7176.10 | −0.93 | −1.32 | −0.44 | −12.84 | |
| 3ν2 + 2ν4(F1) | 7180.00 | −0.53 | −0.93 | −0.17 | −13.71 | |
| 3ν2 + 2ν4(F2) | 7191.05 | −0.57 | −1.03 | −0.29 | −11.13 | |
| 3ν2 + 2ν4(E) | 7191.85 | −0.63 | −0.87 | −0.19 | −14.09 | |
| 3ν2 + 2ν4(E) | 7217.40 | −0.56 | −0.73 | −0.51 | −13.33 | |
| 3ν2 + 2ν4(A2) | 7221.10 | −0.56 | −0.81 | −0.47 | −12.76 | |
| ν 1 + 2ν2 + ν4(F2) | 7225.433f | −0.30 | −0.51 | −0.17 | −27.96 | −7.77 |
| ν 1 + 2ν2 + ν4(F1) | 7246.01 | −0.29 | −0.29 | −0.66 | −12.60 | |
| 2ν3 + ν4(F2) | 7250.542f | −0.16 | 0.00 | −0.07 | 26.75 | −11.04 |
| ν 1 + 2ν2 + ν4(F2) | 7269.442f | −0.24 | −0.12 | −0.61 | −11.35 | 6.66 |
| 2ν1 + ν2(E) | 7295.20 | 0.20 | 0.38 | 1.03 | −4.67 | |
| 2ν3 + ν4(E) | 7295.50 | −1.02 | −1.05 | −0.57 | −11.54 | |
| 2ν3 + ν4(F1) | 7295.80 | −0.07 | −0.09 | 0.26 | −12.68 | |
| 2ν3 + ν4(F2) | 7299.443f | −0.12 | −0.08 | 0.55 | −0.19 | 0.65 |
| 2ν3 + ν4(A1) | 7299.45 | −0.19 | −0.02 | 0.35 | 34.62 | |
| 2ν2 + ν3 + ν4(F1) | 7326.25 | −0.15 | −0.32 | 1.11 | −15.85 | |
| 2ν2 + ν3 + ν4(F2) | 7331.053f | −0.23 | −0.37 | 0.85 | −7.82 | 0.46 |
| 2ν3 + ν4(F2) | 7337.55 | −0.26 | −0.20 | 0.12 | −7.04 | |
| 2ν3 + ν4(F1) | 7338.16 | −0.19 | −0.11 | 0.31 | −36.02 | |
| 2ν2 + ν3 + ν4(A1) | 7341.60 | −0.44 | −0.91 | 0.05 | 0.78 | |
| 2ν2 + ν3 + ν4(E) | 7342.10 | −0.25 | −0.68 | 0.22 | −2.81 | |
| 2ν2 + ν3 + ν4(F2) | 7346.006f | −0.28 | −0.29 | 0.57 | −7.94 | −1.85 |
| 2ν2 + ν3 + ν4(F1) | 7346.46 | −0.19 | −0.30 | 0.74 | −22.36 | |
| 2ν2 + ν3 + ν4(A2) | 7348.85 | −0.20 | −0.48 | 0.26 | −11.93 | |
| 2ν2 + ν3 + ν4(E) | 7352.20 | −0.28 | −0.45 | −0.01 | −2.96 | |
| 2ν2 + ν3 + ν4(A1) | 7360.80 | −0.39 | −0.40 | 0.02 | −4.69 | |
| 2ν2 + ν3 + ν4(E) | 7362.16g | |||||
| 2ν2 + ν3 + ν4(F2) | 7365.401f | −0.36 | −0.33 | 0.63 | −18.17 | −2.75 |
| 2ν2 + ν3 + ν4(F1) | 7368.88 | −0.35 | −0.29 | 0.20 | −17.45 | |
| ν 1 + ν2 + ν3(F1) | 7373.16 | −0.21 | −0.18 | 0.75 | 21.50 | |
| ν 1 + ν2 + ν3(F2) | 7374.246f | −0.60 | −0.55 | 0.73 | 5.07 | 6.10 |
| 4ν2 + ν4(F2) | 7384.108f | −0.71 | −1.05 | 0.46 | −7.12 | 4.09 |
| 4ν2 + ν4(F1) | 7394.20 | −0.89 | −1.51 | 0.13 | −10.45 | |
| 4ν2 + ν4(F2) | 7408.20 | −0.77 | −1.40 | −0.01 | −10.56 | |
| 4ν2 + ν4(F1) | 7422.30 | −0.69 | −1.34 | −0.02 | −10.67 | |
| 4ν2 + ν4(F2) | 7436.30 | −0.84 | −1.52 | −0.13 | −10.51 | |
| ν 1 + 3ν2(E) | 7447.52 | −0.74 | −0.72 | 0.24 | −43.53 | |
| ν 1 + 3ν2(A2) | 7468.21 | −0.37 | −0.37 | −0.64 | −7.07 | |
| ν 1 + 3ν2(A1) | 7468.50 | −0.39 | −0.38 | −0.70 | −6.66 | |
| ν 2 + 2ν3(E) | 7483.67 | −0.09 | −0.26 | −0.01 | 51.04 | |
| ν 2 + 2ν3(F2) | 7510.338f | −0.10 | −0.19 | 0.44 | −1.45 | −0.99 |
| ν 2 + 2ν3(F1) | 7512.26 | −0.21 | −0.27 | 0.43 | −12.46 | |
| ν 2 + 2ν3(A2) | 7546.49g | |||||
| ν 2 + 2ν3(E) | 7552.23 | −0.20 | −0.24 | 0.92 | ||
| ν 2 + 2ν3(A1) | 7559.00 | −0.27 | −0.29 | 18.21 | ||
| 3ν2 + ν3(F1) | 7569.51 | −0.56 | −0.72 | −6.96 | ||
| 3ν2 + ν3(F2) | 7575.858f | −0.51 | −0.66 | −5.39 | 0.76 | |
| 3ν2 + ν3(F1) | 7580.90 | −0.49 | −0.67 | −7.11 | ||
| 3ν2 + ν3(F2) | 7584.513f | −0.62 | −0.86 | −6.48 | −2.10 | |
| 5ν2(E) | 7640.81h | |||||
| 5ν2(A2) | 7643.78h | |||||
| 5ν2(A1) | 7644.89h | |||||
| 5ν2(E) | 7651.68g | |||||
| rms error (cm−1) | 0.45 | 0.60 | 0.65 | 22.10 | 2.66 | |
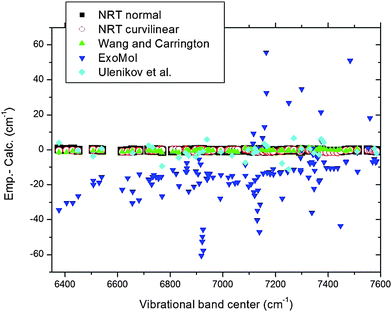
The third column of Table 1 gives the empirical discrepancies between our sub-band centers (vibrational levels) and the variationally predicted levels71 from the NRT PES using the ITO normal mode technique. This PES has been originally obtained by extended ab initio calculations with a subsequent scaling of four quadratic parameters to empirical fundamental band frequencies.48 The fourth column gives the differences with the variational calculations derived from the exact kinetic energy operator (EKO) and essentially the same NRT PES slightly refitted with the curvilinear redundant coordinates approach (“6A angular basis”).58 Column 5 gives the (Emp.-Calc.) differences with variational calculations reported by Wang and Carrington (WC).49 These authors used their empirically fitted PES obtained by adjusting ab initio PES of Schwenke45 to previously known experimental band centers up to the Tetradecad range. Column 6 corresponds to comparisons with “ExoMol 10to10” methane energies (http://www.exomol.com/) also obtained from ab initio based empirically fitted PES of Yurchenko et al.60 generated with the TROVE variational code.83 Finally the last column corresponds to a comparison with the calculations by Ulenikov et al.40 that used the empirical effective Hamiltonian model. In the latter case the set of reported icosad levels is not complete since only the F2 components are reported.
The overview comparison between the different approaches presented in Fig. 10 illustrate the excellent agreement between the experimental sub band centers and the NRT and WC variational calculations (RMS of 0.45 and 0.65 cm−1, respectively). Much larger differences (up to 10 cm−1) are noted for the values provided by Ulenikov et al.40 while ExoMol predictions60 differ by up to 60 cm−1. Note that NRT and WC gave accurate isotopic predictions as well. In the case of NRT, a comparison of isotopic methane spectra93–95 with available experimental band centers gave a similar error. In a recent work, Masát et al.42 reported positions of lines 16 R(0) transitions unambiguously identified by applying the 2-Temperature method to jet at 25 K and bulk spectra at 80 K. All but one R(0) of the icosad transitions identified in ref. 42 are presently confirmed. The only R(0) line at 7152.7215 cm−1 which was not correctly assigned42 belongs in fact to 13CH4 in natural abundance in the methane sample of ref. 28.
 | ||
| Fig. 10 Differences between the empirical values of the 12CH4 sub band centers of the icosad and theoretical values calculated using different approaches: pure ab initio NRT,58,71 Wang and Carrington,49 ExoMol60 and Ulenikov et al.40 | ||
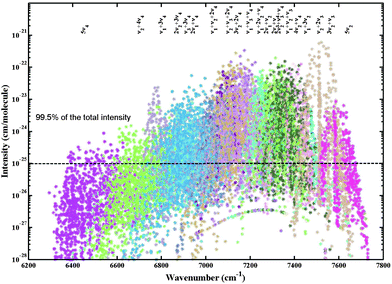
Examples of comparison for the simulated spectra of our variational predicted list and the theoretical ExoMol 10to10 list60 with experimental 80 K and 296 K WKLMC spectra28 are shown in Fig. 11. The assigned lines form a representative sample of the total icosad band system in terms of intensities. A comparison of the integrated intensities for the assigned lines between the WKLMC lists28 at T = 80 K and our variational predictions are given in Table 2. The 12CH4 assigned transitions represent more than 98% of the total integrated intensity. For the cold spectrum at 80 K, over 98% of the strong transitions (I ≥ 10−23 cm per molecule) are assigned while for medium lines, over 2/3 of the transitions are assigned: 85% with I ≥ 10−24 cm per molecule and 65% with I ≥ 10−25 cm per molecule.
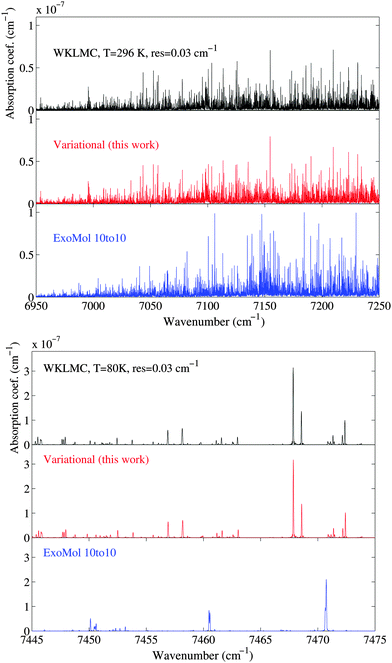 | ||
| Fig. 11 Comparison of the absorption spectrum in the icosad region between our variational ab initio calculations, the ExoMol “10to10” list60 and the experimental WKLMC line list28 at T = 80 and 296 K. The spectra are computed with a line profile at a resolution of 0.03 cm−1. | ||
| v 1 v 2 v 3 v 4 | WKLMC28 (W) | Theory (T) | (%) | Nb. lines |
|---|---|---|---|---|
| 0005 | 2.22 × 10−23 | 2.31 × 10−23 | −4.4 | 998 |
| 0013 | 1.06 × 10−21 | 1.02 × 10−21 | 4.2 | 1461 |
| 0021 | 4.52 × 10−21 | 4.65 × 10−21 | −2.9 | 907 |
| 0104 | 1.16 × 10−22 | 1.20 × 10−22 | −3.9 | 1441 |
| 0112 | 8.38 × 10−21 | 8.13 × 10−21 | 3.0 | 1702 |
| 0120 | 9.52 × 10−21 | 9.43 × 10−21 | 0.9 | 994 |
| 0203 | 2.65 × 10−22 | 2.61 × 10−22 | 1.4 | 653 |
| 0211 | 5.93 × 10−21 | 5.44 × 10−21 | 8.3 | 1121 |
| 0302 | 2.24 × 10−21 | 2.15 × 10−21 | 4.0 | 553 |
| 0310 | 1.95 × 10−22 | 2.01 × 10−22 | −3.1 | 578 |
| 0401 | 1.24 × 10−21 | 1.06 × 10−21 | 13.9 | 193 |
| 0500 | 6.54 × 10−27 | 7.18 × 10−27 | −9.7 | 4 |
| 1003 | 4.66 × 10−22 | 4.42 × 10−22 | 5.4 | 657 |
| 1011 | 3.78 × 10−21 | 3.55 × 10−21 | 5.9 | 386 |
| 1102 | 6.61 × 10−22 | 6.64 × 10−22 | −0.4 | 529 |
| 1110 | 9.78 × 10−22 | 9.08 × 10−22 | 7.1 | 306 |
| 1201 | 1.51 × 10−21 | 1.60 × 10−21 | −6.5 | 296 |
| 1300 | 4.09 × 10−23 | 4.13 × 10−23 | −1.0 | 117 |
| 2001 | 9.11 × 10−22 | 9.37 × 10−22 | −2.9 | 116 |
| 2100 | 4.13 × 10−23 | 3.72 × 10−23 | 9.9 | 43 |
| ∑ | 4.19 × 10−20 | 4.07 × 10−20 | 2.9 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 055 |
6 Assigned line lists of 12CH4 transitions in the icosad range
As the result of this work, we provide two line lists of the icosad ← GS 12CH4 transitions in the range 6280–7800 cm−1. The first one is the theoretical variationally computed list, in which band centers are empirically corrected using the VSS shift procedure. Except for this band center optimization, all ro-vibrational interactions were calculated here from the full normal-mode Eckart frame Hamiltonian using the NRT PES48 and the line intensities from the corresponding wave functions and ab initio NRT DMS52 following the method described in ref. 59 and 71. After applying the VSS band center shift corrections, the RMS error with respect to the assigned sample of experimental line positions is 0.14 cm−1. This improved theoretical list is complete and contains 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097 transitions for icosad ← GS upto J = 15 with the intensity cut-off of 10−29 cm per molecule at 80 K and 194
097 transitions for icosad ← GS upto J = 15 with the intensity cut-off of 10−29 cm per molecule at 80 K and 194![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 transitions at 296 K with the same intensity cut-off. The second one is the WKLMC experimental line list28 for natural methane, in which all quantum assignments (≡13
488 transitions at 296 K with the same intensity cut-off. The second one is the WKLMC experimental line list28 for natural methane, in which all quantum assignments (≡13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055) obtained in this work were inserted. This extended experimental list contains 45
055) obtained in this work were inserted. This extended experimental list contains 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255 transitions at 80 K in the range 6280–7800 cm−1 and 36
255 transitions at 80 K in the range 6280–7800 cm−1 and 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 transitions at 296 K. The entire files are provided in the ESI.†
650 transitions at 296 K. The entire files are provided in the ESI.†
7 Discussion and conclusion
More than 35 years have been necessary to achieve sufficiently complete vibration–rotation assignments of 32 cold band systems of the main 12CH4 isotopologue involving 106 sub-bands. This required a tedious interval-by-interval fitting process using the effective empirical model approach that faced problems of explosive proliferation of adjustable parameters11,15,16 and ambiguity issues.96–98 Here we doubled the number of assigned sub-bands that belong to the highest presently analyzed wavenumber range. Over 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 transitions of 108 new sub-bands (among 111 icosad bands unknown prior this study) were rovibrationally assigned in congested experimental spectra. The assigned lines shown in Fig. 4 represent 98% of the total 12CH4 opacity in the icosad range at 80 K. If the intensity cutoff of 10−24 cm per molecule is applied to the assigned lines at 80 K, then 3310 transitions will be involved, giving 96.5% of the total integrated intensity. For the cutoff of 10−25 cm per molecule, we retain 7000 transitions with 99.5% of the total integrated intensity. At 296 K, we obtain the corresponding samples of 93.7% and 99.6%. Concerning the scatter in the position errors, if we select lines with Obs.-Calc. errors < |0.2| cm−1, this gives us 94.2% of the total intensity and for the line sample with Obs.-Calc. errors < |0.4| cm−1, 99% of the intensity is included.
000 transitions of 108 new sub-bands (among 111 icosad bands unknown prior this study) were rovibrationally assigned in congested experimental spectra. The assigned lines shown in Fig. 4 represent 98% of the total 12CH4 opacity in the icosad range at 80 K. If the intensity cutoff of 10−24 cm per molecule is applied to the assigned lines at 80 K, then 3310 transitions will be involved, giving 96.5% of the total integrated intensity. For the cutoff of 10−25 cm per molecule, we retain 7000 transitions with 99.5% of the total integrated intensity. At 296 K, we obtain the corresponding samples of 93.7% and 99.6%. Concerning the scatter in the position errors, if we select lines with Obs.-Calc. errors < |0.2| cm−1, this gives us 94.2% of the total intensity and for the line sample with Obs.-Calc. errors < |0.4| cm−1, 99% of the intensity is included.
This breakthrough was possible due to the new level of accuracy and completeness of first principles predictions of high-resolution infrared spectra. Various theoretical ingredients were necessary for this work. Convergence of global nuclear motion calculations in twelve degrees of freedom to the spectroscopic accuracy was a challenging issue requiring efficient reduction-compression basis set techniques59 and a full account of symmetry.90 Using our ab initio based PES, this permitted generating line positions up to J = 15 with typical errors of ∼0.1–1 cm−1 only. Such a high accuracy of variationally predicted energy levels up to five vibrational quanta was mandatory for reliable calculations of wave functions that have a big impact on line intensities. Our convergence tests have shown that even relatively small errors in dense energy patterns could result in large outliers in line strengths due to resonance intensity transfer (a well-known resonance borrowing effect for so called unstable lines77,99). By using our variational wave functions and the purely ab initio NRT DMS, it was possible to obtain almost experimental accuracy for strong lines, agreement for interval-by-interval integrated intensities being nearly perfect. The global integrated intensity (Obs.-Calc.) deviation for the entire set of assigned icosad lines is less than 3% that is not far from the experimental uncertainty (see Table 2). This work represents a new step forward in the computational spectroscopy for five-atomic molecules highlighting the importance of quantum chemistry and of efficient variational methods for high-resolution applications.
We provide two types of methane line lists at 80 K and 296 K. One is a theoretical list for pure 12CH4 (pure ab initio intensities and J-dependencies in lines positions) with empirically corrected bands centers using the VSS technique. This list fulfills the completeness criteria for the considered temperatures: full description of the T-dependence for low level populations and all dipole-allowed transitions up to a requested intensity cutoff. In view of excellent intensity agreement with experiment this list could be suitable for medium resolution planetology applications since the average error in line positions is about ∼0.14 cm−1. The second one was obtained by the insertion of our assignments to the experimental WKLMC list28 for natural methane that meets accuracy requirements for high-resolution applications: ∼0.001–0.003 cm−1 for measured line positions. It contains still unassigned weak lines and lines of 13CH4 and CH3D in natural abundance but is less complete than the theoretical list for 12CH4, particularly for high-J transitions. A precise characterizing of resonance mixing effects for remaining weak transitions and eventual isotopic lines will require further investigations.
In the future work, we plan to extend this study to achieve both completeness and accuracy. This will be based on new interval-by-interval effective mixed contact transformation-models combining ab initio derived resonance coupling elements with empirical optimization of diagonal parameters as was discussed by Tyuterev et al.77 for lower polyads. This more enhanced analysis is already well advanced at the lower edge 6300–6800 cm−1 of the icosad system100 allowing on the one hand a confirmation of the present assignments and on the other hand improving the calculated line accuracy to an rmf value of 0.005 cm−1 by a locally focused empirical fit. We also plan to extend this work as well as the previous ones by the generation of line lists with similar accuracy in larger temperature and wavenumber ranges. This would meet quite urgent needs for assignments of high-T experimental measurements for numerous astrophysical applications.
Acknowledgements
This work was carried out in the frame of the Laboratoire International Associé SAMIA (Spectroscopie d'Absorption des Molécules d'Intéret Atmosphérique) between CNRS (France) and RFBR (Russia). The support from Tomsk State University Academic D. Mendeleev funding program, from IDRIS/CINES computer centre of France and of the ROMEO computer centre Reims-Champagne-Ardenne is acknowledged. A part of this work was performed in the frame of the LabexOSUG@2020 (ANR10 LABX56).References
- O. Boucher, P. Friedlingstein, B. Collins and K. P. Shine, Environ. Res. Lett., 2009, 4, 044007 CrossRef.
- M. Khalil, Annu. Rev. Energy Environ., 1999, 24, 645–661 CrossRef.
- L. A. Sromovsky, P. M. Fry, V. Boudon, A. Campargue and A. Nikitin, Icarus, 2012, 218, 1–23 CrossRef CAS.
- E. Lellouch, B. Sicardy, C. de Bergh, H. U. Kaufl, S. Kassi and A. Campargue, Astron. Astrophys., 2009, 495, 963–974 CrossRef.
- P. G. J. Irwin, R. de, C. Courtin, B. Bezard, N. A. Teanby and G. R. Davis, et al. , Icarus, 2012, 220, 369–382 CrossRef CAS.
- T. Nakajima, B. R. Oppenheimer, S. R. Kulkarni, D. A. Golimowski, K. Matthews and S. T. Durrance, Nature, 1995, 378, 463–465 CrossRef CAS.
- B. R. Oppenheimer, S. R. Kulkarni, K. Matthews and T. Nakajima, Science, 1995, 270, 1478–1479 CAS.
- M. R. Swain, P. Deroo, C. A. Griffith, G. Tinetti, A. Thatte, G. Vasisht, P. Chen, J. Bouwman, I. J. Crossfield, D. Angerhausen, C. Afonso and T. Henning, Nature, 2010, 463, 637–639 CrossRef CAS PubMed.
- R. Hu and S. Seager, Astrophys. J., 2014, 784, 63 CrossRef.
- J. P. Champion, J. C. Hilico, C. Wenger and L. R. Brown, J. Mol. Spectrosc., 1989, 133, 256–272 CrossRef CAS.
- J. P. Champion, M. Loëte and G. Pierre, Spherical Top Spectra, Academic Press, San Diago, 1992 Search PubMed.
- J. C. Hilico, J. P. Champion, S. Toumi, V. G. Tyuterev and S. A. Tashkun, J. Mol. Spectrosc., 1994, 168, 455–476 CrossRef CAS.
- S. Albert, S. Bauerecker, V. Boudon, L. R. Brown, J.-P. Champion, M. Loëte, A. V. Nikitin and M. Quack, Chem. Phys., 2009, 356, 131–146 CrossRef CAS.
- A. V. Nikitin, X. Thomas, L. Regalia, L. Daumont, P. Von der Heyden, V. Tyuterev, L. Wang, S. Kassi and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 28–40 CrossRef CAS.
- L. Daumont, A. V. Nikitin, X. Thomas, L. Régalia, P. Von der Heyden, V. Tyuterev, M. Rey, V. Boudon, C. Wenger, M. Loëte and L. R. Brown, J. Quant. Spectrosc. Radiat. Transfer, 2013, 116, 101–109 CrossRef CAS.
- A. V. Nikitin, V. Boudon, C. Wenger, S. Albert, L. R. Brown, S. Bauerecker and M. Quack, Phys. Chem. Chem. Phys., 2013, 15, 10071–10093 RSC.
- A. V. Nikitin, X. Thomas, L. Régalia, L. Daumont, M. Rey, S. A. Tashkun, V. Tyuterev and L. R. Brown, J. Quant. Spectrosc. Radiat. Transfer, 2014, 138, 116–123 CrossRef CAS.
- V. Boudon, M. Rey and M. Loëte, J. Quant. Spectrosc. Radiat. Transfer, 2006, 98, 394–404 CrossRef CAS.
- V. Tyuterev, S. Tashkun, M. Rey, R. Kochanov, A. Nikitin and T. Delahaye, J. Phys. Chem. A, 2013, 117, 13779–13805 CrossRef CAS PubMed.
- A. V. Nikitin, J. P. Champion and V. G. Tyuterev, J. Mol. Spectrosc., 1997, 182, 72–84 CrossRef CAS.
- V. Boudon, O. Pirali, P. Roy, J. B. Brubach, L. Manceron and J. Vander Auwera, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 1117–11129 CrossRef CAS.
- A. V. Nikitin, O. M. Lyulin, S. N. Mikhailenko, V. I. Perevalov, N. N. Filippov, I. M. Grigoriev, I. Morino, Y. Yoshida and T. Matsunaga, J. Quant. Spectrosc. Radiat. Transfer, 2015, 154, 63–71 CrossRef CAS.
- L. Brown, J. Quant. Spectrosc. Radiat. Transfer, 2005, 96, 251–270 CrossRef CAS.
- S. Béguier, A. W. Liu and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2015, 166, 6–12 CrossRef.
- G. Pierre, J. C. Hilico and C. De Bergh, J. Mol. Spectrosc., 1980, 82, 379–393 CrossRef CAS.
- L. Wang, S. Kassi, A. W. Liu, S. M. Hu and A. Campargue, J. Mol. Spectrosc., 2010, 261, 41–52 CrossRef CAS.
- D. Mondelain, S. Kassi, L. Wang and A. Campargue, Phys. Chem. Chem. Phys., 2011, 13, 7985–7996 RSC.
- A. Campargue, O. Leshchishina, L. Wang, D. Mondelain and S. Kassi, J. Mol. Spectrosc., 2013, 291, 16–22 CrossRef CAS.
- S. Béguier, S. Kassi and A. Camparue, J. Mol. Spectrosc., 2015, 308–309, 1–5 CrossRef.
- S. Kassi, B. Gao, D. Romanini and A. Campargue, Phys. Chem. Chem. Phys., 2008, 10, 28–34 RSC.
- B. Gao, S. Kassi and A. Campargue, J. Mol. Spectrosc., 2009, 253, 55–63 CrossRef CAS.
- E. Sciamma O'Brien, S. Kassi, B. Gao and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 951–963 CrossRef.
- D. Wang, L. Mondelain, S. Kassi and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2011, 113, 47–57 CrossRef.
- A. Campargue, L. Wang, D. Mondelain, S. Kassi, B. Bézard, E. Lellouch, A. Coustenis, C. D. Bergh, M. Hirtzig and P. Drossart, Icarus, 2012, 219, 110–128 CrossRef CAS.
- K. Singh and J. J. O'Brien, J. Quant. Spectrosc. Radiat. Transfer, 1995, 54, 607–619 CrossRef CAS.
- J. J. O'Brien and C. Hong, J. Quant. Spectrosc. Radiat. Transfer, 2002, 75, 323–350 CrossRef.
- L. R. Brown, K. Sung, D. C. Benner, V. M. Devi, V. Boudon, T. Gabard, C. Wenger, A. Campargue, O. Leshchishina, S. Kassi, D. Mondelain, L. Wang, L. Daumont, L. Régalia, M. Rey, X. Thomas, V. G. Tyuterev, O. M. Lyulin, A. V. Nikitin, H. M. Niederer, S. Albert, S. Bauerecker, M. Quack, J. J. O'Brien, I. E. Gordon, L. S. Rothman, H. Sasada, A. Coustenis, M. A. H. Smith, T. Carrington, X. G. Wang, A. W. Mantz and P. T. Spickler, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 201–219 CrossRef CAS.
- L. S. Rothman, I. E. Gordon, Y. Babikov, A. Barbe, D. Chris Benner, P. F. Bernath, M. Birk, L. Bizzocchi, V. Boudon, L. R. Brown, A. Campargue, K. Chance, E. A. Cohen, L. H. Coudert, V. M. Devi, B. J. Drouin, A. Fayt, J. M. Flaud, R. R. Gamache, J. J. Harrison, J. M. Hartmann, C. Hill, J. T. Hodges, D. Jacquemart, A. Jolly, J. Lamouroux, R. J. Le Roy, G. Li, D. A. Long, O. M. Lyulin, C. J. Mackie, S. T. Massie, S. Mikhailenko, H. S. P. Müller, O. V. Naumenko, A. V. Nikitin, J. Orphal, V. Perevalov, A. Perrin, E. R. Polovtseva, C. Richard, M. A. H. Smith, E. Starikova, K. Sung, S. Tashkun, J. Tennyson, G. C. Toon, V. Tyuterev and G. Wagner, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 4–50 CrossRef CAS.
- C. Manca Tanner and M. Quack, Mol. Phys., 2012, 110, 2111–2135 CrossRef.
- O. N. Ulenikov, E. S. Bekhtereva, S. Albert, S. Bauerecker, H. M. Niederer and M. Quack, J. Chem. Phys., 2014, 141, 234302 CrossRef CAS PubMed.
- O. Votava, M. Masát, S. Pracna, P. Kassi and A. Camparue, Phys. Chem. Chem. Phys., 2010, 12, 3145–3155 RSC.
- M. Masát, D. Pracna, P. Mondelain, S. Kassi, A. Camparue and O. Votava, J. Mol. Spectrosc., 2013, 291, 9–15 CrossRef.
- K. Boraas, Z. Lin and J. Reilly, J. Chem. Phys., 1994, 100, 7916–7927 CrossRef CAS.
- A. Campargue, D. Permogorov and R. Jost, J. Chem. Phys., 1995, 102, 5910–5916 CrossRef CAS.
- D. W. Schwenke and H. Partridge, Spectrochim. Acta, Part A, 2001, 57, 887–895 CrossRef CAS.
- D. W. Schwenke, Spectrochim. Acta, Part A, 2002, 58, 849–861 CrossRef.
- R. Marquardt and M. Quack, J. Phys. Chem. A, 2004, 108, 3166–3181 CrossRef CAS.
- A. V. Nikitin, M. Rey and V. G. Tyuterev, Chem. Phys. Lett., 2011, 501, 179–186 CrossRef CAS.
- X. G. Wang and T. Carrington, J. Chem. Phys., 2014, 141, 154106 CrossRef PubMed.
- M. Majumder, S. Hegger, R. Dawes, S. Manzhos, X. G. Wang, T. Carrington Jr., J. Li and H. Guo, Mol. Phys., 2015, 113, 1823–1833 CrossRef CAS.
- P. Cassam-Chenaï and J. Liévin, J. Chem. Phys., 2012, 136, 174309 CrossRef PubMed.
- A. V. Nikitin, M. Rey and V. G. Tyuterev, Chem. Phys. Lett., 2013, 565, 5–11 CrossRef CAS.
- S. N. Yurchenko, J. Tennyson, R. J. Barber and W. Thiel, J. Mol. Spectrosc., 2013, 291, 69–76 CrossRef CAS.
- E. Mátyus, G. Czakó, B. T. Sutcliffe and A. G. Császár, J. Chem. Phys., 2007, 127, 084102 CrossRef PubMed.
- J. M. Bowman, T. Carrington and H. D. Meyer, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- A. V. Nikitin, M. Rey, J. P. Champion and V. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 1034–1042 CrossRef CAS.
- X. G. Wang and T. Carrington Jr., J. Chem. Phys., 2013, 138, 104106 CrossRef PubMed.
- A. V. Nikitin, M. Rey and V. Tyuterev, J. Chem. Phys., 2015, 142, 094118 CrossRef CAS PubMed.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2013, 15, 10049–10061 RSC.
- S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2014, 440, stu326 CrossRef.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, Astrophys. J., 2014, 789, 2 CrossRef.
- R. Nassar and P. Bernath, J. Quant. Spectrosc. Radiat. Transfer, 2003, 82, 279–292 CrossRef CAS.
- J. Thiévin, R. Georges, S. Carles, B. Abdessamad, B. Rowe and J. P. Champion, J. Quant. Spectrosc. Radiat. Transfer, 2008, 108, 2027–2036 CrossRef.
- R. J. Hargreaves, C. A. Beale, L. Michaux, M. Irfan and P. F. Bernath, Astrophys. J., 2012, 757, 46 CrossRef.
- R. J. Hargreaves, C. A. Beale, L. Michaux, M. Irfan and P. F. Bernath, Astrophys. J., 2013, 774, 89 CrossRef.
- Y. Lu, D. Mondelain, S. Kassi and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 2683–2697 CrossRef CAS.
- L. Wang, S. Kassi, A. W. Liu, S. M. Hu and A. Campargue, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 937–951 CrossRef CAS.
- C. De Bergh, R. Courtin, B. Bézard, A. Coustenis, E. Lellouch, M. Hirtzig, P. Rannou, P. Drossart, A. Campargue, S. Kassi, L. Wang, V. Boudon, A. Nikitin and V. Tyuterev, Planet. Space Sci., 2012, 61, 85–98 CrossRef CAS.
- M. Hirtzig, B. Bézard, E. Lellouch, A. Coustenis, C. de Bergh, P. Drossart, A. Campargue, V. Boudon, V. Tyuterev, P. Rannou, T. Cours, S. Kassi, A. Nikitin, D. Mondelain, S. Rodriguez and S. Le Mouélic, Icarus, 2013, 226, 470–486 CrossRef CAS.
- J. Bailey, L. Ahlsved and V. S. Meadows, Icarus, 2011, 213, 218–232 CrossRef CAS.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2015, 164, 207–220 CrossRef CAS.
- H. Partridge and D. W. Schwenke, J. Chem. Phys., 1997, 106, 4618–4639 CrossRef CAS.
- A. G. Császár, E. Mátyus, T. Szidarovszky, L. Lodi, N. F. Zobov, S. V. Shirin, O. L. Polyansky and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 1043–1064 CrossRef.
- X. Huang, D. W. Schwenke, S. A. Tashkun and T. J. Lee, J. Chem. Phys., 2012, 136, 124311 CrossRef PubMed.
- A. V. Nikitin, M. Rey and V. G. Tyuterev, J. Mol. Spectrosc., 2014, 305, 40–47 CrossRef CAS.
- O. L. Polyansky, N. F. Zobov, S. Viti, J. Tennyson, P. F. Bernath and L. Wallace, Science, 1997, 277, 346–348 CrossRef CAS PubMed.
- V. G. Tyuterev, R. V. Kochanov, S. A. Tashkun, F. Holka and P. G. Szalay, J. Chem. Phys., 2013, 139, 134307 CrossRef PubMed.
- V. Tyuterev, R. Kochanov, A. Campargue, S. Kassi, D. Mondelain, A. Barbe, E. Starikova, M. R. De Backer, P. G. Szalay and S. Tashkun, Phys. Rev. Lett., 2014, 113, 143002 CrossRef PubMed.
- X. Huang, R. S. Freedman, S. A. Tashkun, D. W. Schwenke and T. J. Lee, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 134–146 CrossRef CAS.
- D. W. Schwenke, J. Phys. Chem., 1996, 100, 2867–2884 CrossRef CAS.
- J. C. Light and T. Carrington Jr., Adv. Chem. Phys., 2000, 114, 263–310 CrossRef.
- M. Rey and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2007, 9, 2538–2548 RSC.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- S. Carter, A. R. Sharma and J. M. Bowman, J. Chem. Phys., 2012, 137, 154301 CrossRef PubMed.
- J. M. L. Martin, T. J. Lee, P. R. Taylor and J. P. François, J. Chem. Phys., 1995, 103, 2589–2602 CrossRef CAS.
- T. Delahaye, A. V. Nikitin, M. Rey, P. G. Szalay and V. G. Tyuterev, J. Chem. Phys., 2014, 141, 104301 CrossRef PubMed.
- V. Boudon, J. P. Champion, T. Gabard, M. Loëte, F. Michelot, G. Pierre, M. Rotger, C. Wenger and M. Rey, J. Mol. Spectrosc., 2004, 228, 620–634 CrossRef CAS.
- B. I. Zhilinskii, V. I. Perevalov and V. G. Tyuterev, Method of Irreducible Tensorial Operators in the Theory of Molecular Spectra, Nauka (in Russian), Novosibirsk, 1984 Search PubMed.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, Mol. Phys., 2010, 108, 2121–2135 CrossRef CAS.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Chem. Phys., 2012, 136, 244106 CrossRef PubMed.
- J. K. G. Watson, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- P. Cassam-Chena, Y. Bouret, M. Rey, S. A. Tashkun, A. V. Nikitin and V. Tyuterev, Int. J. Quantum Chem., 2012, 112, 2201–2220 CrossRef.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Chem. Phys., 2014, 141, 044316 CrossRef PubMed.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Phys. Chem. A, 2015, 119, 4763–4779 CrossRef CAS PubMed.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Mol. Spectrosc., 2013, 291, 85–97 CrossRef CAS.
- V. I. Perevalov, V. Tyuterev and B. I. Zhilinskii, Chem. Phys. Lett., 1984, 104, 455–461 CrossRef CAS.
- V. I. Perevalov, V. Tyuterev and B. I. Zhilinskii, J. Mol. Spectrosc., 1985, 111, 1–19 CrossRef CAS.
- V. Tyuterev, J. P. Champion, G. Pierre and V. I. Perevalov, J. Mol. Spectrosc., 1986, 120, 49–78 CrossRef CAS.
- L. Lodi and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 850–858 CrossRef CAS.
- A. V. Nikitin, M. Rey, S. Tashkun, S. Kassi, D. Mondelain, A. Campargue and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2016, 168, 207–216 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05265c |
| This journal is © the Owner Societies 2016 |