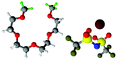Bulk nanostructure of the prototypical ‘good’ and ‘poor’ solvate ionic liquids [Li(G4)][TFSI] and [Li(G4)][NO₃]

Abstract

The bulk nanostructures of a prototypical ‘good’ solvate ionic liquid (SIL) and ‘poor’ SIL have been examined using neutron diffraction and empirical potential structure refinement (EPSR) simulated fits. The good SIL formed by a 1 : 1 mixture of lithium bis(trifluoromethylsulfonyl)imide (Li[TFSI]) in tetraglyme (G4), denoted [Li(G4)][TFSI], and the poor SIL formed from a 1 : 1 mixture of lithium nitrate (Li[NO₃]) in G4, denoted [Li(G4)][NO₃], have been studied. In both SILs there are strong Lewis acid–base interactions between Li⁺ and ligating O atoms. However, the O atoms coordinated to Li⁺ depend strongly on the counter anion present. Li⋯O coordination numbers with G4 are 2–3 times higher for [Li(G4)][TFSI] than [Li(G4)][NO₃], and conversely the Li⋯O anion coordination number is 2–3 times higher in [Li(G4)][NO₃]. In both solvates the local packing of Li around G4 O atoms are identical but these interactions are less frequent in [Li(G4)][NO₃]. In both SILs, Li⁺ has a distribution of coordination numbers and a wide variety of different complex structures are present. For [Li(G4)][NO₃], there is a significant proportion uncoordinated G4 in the bulk; ∼37% of glyme molecules have no Li⋯O contacts and each G4 molecule coordinates to an average of 0.5 Li⁺ cations. Conversely, in [Li(G4)][TFSI] only ∼5% of G4 molecules lack Li⋯O contacts and G4 molecules coordinates to an average of 1.3 Li⁺ cations. Li⁺ and G4 form polynuclear complexes, of the form [Li_x(G4)_y]^x+, in both solvates. For [Li(G4)][TFSI] ∼35% of Li⁺ and G4 form 1 polynuclear complexes, while only ∼10% of Li⁺ and G4 form polynuclear complexes in [Li(G4)][NO₃].

---

Introduction

Ionic liquids (ILs) are pure salts with low melting temperatures (<100 °C).¹ ILs have garnered significant research attention for a wide variety of applications,^2–13 but especially as next generation solvents in electrochemical devices.^7,14–20 Many studies have investigated IL–lithium salt solutions, with a view to producing high performance electrolytes^{17,19,21–25} with wide electrochemical windows and liquid stability temperature ranges.^15,20 However, low lithium (Li) transference numbers and solubility of electrode materials are recurrent problems in IL-based electrolytes. Solvate ILs (SILs) are an emerging class of ionic liquids with the potential to circumvent these problems.¹⁹

SILs are a sub-class of ILs, consisting of a metal cation bound to a stoichiometric quantity of coordinating ligands via strong Lewis acid–base interactions that yield stable complex cations and counter ions in the bulk. The first known examples of SILs consisted of aqua cations in inorganic hydrate melts.²⁶ However, perhaps the most widely studied SILs utilise oligoethers (glymes) with metal salts.^22,23,27 Research into glyme-based SILs owes much of its growth to investigations of Li-salt:polyethylene oxide (PEO) rubbery electrolytes.²⁸ It was found that particular salt:PEO mixtures produced low melting, highly conductive amorphous phases in the “crystallinity gap” regions of the phase diagrams.²⁹ Many stoichiometric mixtures of glymes and lithium salts form crystalline complexes, and a variety of crystal structures have been elucidated.^30–33 Notably, many of these solvate complexes melt near room temperature.²⁹ These melts have been identified as SILs, and closely conform to a rigorous set of criteria characteristic of SILs.³⁴

Interactions between Li⁺ and solvating glyme molecules strongly influence the thermal^22,27,34 and electrochemical^19,24,27,34 stability of lithium–glyme solvates. Moreover, the solvation and coordination environment of Li⁺ controls bulk transport^{23,24,27,34,35} of Li⁺ and its behaviour at electrode interfaces.^18,36 Understanding the coordination environment of Li⁺ in the bulk of SILs is critical for practical applications. Li⁺ has a complex coordination chemistry, forming complexes with coordination numbers between 2 to 8 in solution, and crystalline phases.³⁷ 4–6 coordinate structures are much more common while 2 and 3 coordinate structures are rare.^19,38 Li⁺ has coordination numbers of ca. 4 in both pure molten Li[TFSI]³⁹ and Li[NO₃].⁴⁰ Li⁺ coordination numbers of six are preferred in crystalline structures³⁷ including glyme-based solvates^30–33 and crystalline Li[NO₃].⁴¹ Crystalline Li[TFSI],⁴² however, is 4 coordinate. In glyme-based solvates, the make-up of the Li⁺ coordination shell is controlled by the relative Lewis basicity of the glyme and the counter anion present.³⁴ Higher anion basicity leads to fewer Li⋯glyme contacts and a greater number of Li⋯anion contacts. In the case of high Lewis basicity anions, strong Li⋯anion interactions preclude Li⋯glyme interactions, leading to significant proportions of uncoordinated (“free”) glyme in solution.²⁵

The presence of ‘free’ glyme is key consideration for solvate systems. SILs that are comprised of almost purely ionic species are defined as ‘good’ while SILs that are mixture of ionic and molecular species are categorised as ‘poor’, with an equilibria of complex cations and dissociated Li⁺ cations and glyme molecules.³⁴ Strong complexation between Li⁺ and the glyme produces stable [Li(glyme)]⁺ complex cations, producing a good SIL. Conversely, a ‘poor’ SIL is characterised by stronger interactions between Li⁺ and its counter anion, reducing the prevalence of [Li(glyme)]⁺ complexes and promoting free, uncoordinated glyme in solution.

Here, the bulk structure of two 1 : 1 lithium salt : glyme mixtures have been elucidated using isotopically labelled contrast variation neutron diffraction in conjunction with empirical potential structure refinement (EPSR) fits. EPSR compares simulated and experimental diffraction structure factors, iteratively refining the simulation against the measured data to faithfully reproduce the atom–atom correlations in the system. This means the simulated atomic level structure can be commented on with confidence. Equimolar mixtures of lithium bis(trifluoromethane)sulfonimide (Li[TFSI]) with tetraethylene glycol dimethyl ether (G4) ([Li(G4)][TFSI]) and lithium nitrate (LiNO₃) with G4 ([Li(G4)][NO₃]) were selected as prototypical ‘good’ and ‘poor’ SILs respectively. These systems are interrogated to determine how the coordination environment of Li⁺ differs in a good SIL compared to a poor SIL. The effect of the anion species on the coordination numbers and coordination geometry around Li⁺, the geometry of ligand⋯Li⁺ interactions, distribution of complexes formed, including both mono and polynuclear complexes and the proportion of free glyme present in solution, is examined.

Method

Synthesis of deuterated tetraglyme isotopomers

Chemicals and reagents of the highest grade were purchased from Sigma-Aldrich and used without further purification. Solvents used in the synthesis of deuterated glymes were purchased from Sigma-Aldrich Chemical Co., Merck and Fronine Laboratory Supplies and were purified by literature methods. When solvent mixtures were used as an eluent, the proportions are given by volume. NMR spectroscopy solvents were purchased from Cambridge Isotope Laboratories Inc. and were used without further purification. Thin-layer chromatography (TLC) was performed on Fluka Analytical silica gel aluminium sheets (25 F254). Davisil® silica gel (LC60Å 40–63 micron) was used for bench-top flash column chromatography and prepacked silica cartridges were used for REVELERIS™ flash chromatography. Deuterated tetraglyme isotopomers were synthesised via the reaction scheme given in Fig. 1. A full description of the synthesis of the tetraglyme isotopomers and their respective intermediates is given in the (ESI†).

Fig. 1 Reaction scheme for the synthesis of the HC₃O(CD₂CD₂O)₄CH₃ (d₁₆-G4) and DC₃O(CD₂CD₂O)₄CD₃ (d₂₂-G4) isotopologues of tetraglyme. The D₃CO(CH₂CH₂O)₄CD₃ (d₆-G4), isotopologue was prepared from hydrogenous 8 using the reaction conditions given in viii. The purified products were then used to prepare isotopomeric contrasts of the solvate ionic liquids for neutron diffraction measurements.

The percentage deuteration of the product tetraglyme isotopologues were characterised using enhanced resolution – mass spectroscopy (ER-MS), ¹H NMR (400 MHz), ¹³C NMR (100 MHz), and ²H NMR (61.4 MHz). The overall percent deuteration of the molecules was calculated by via ER-MS using the isotope distribution analysis of the different isotopologues by analysing the area under each MS peak which corresponds to a defined number of deuterium atoms. The contribution of the carbon-13 (natural abundance) to the value of the area under each [X + 1] MS signal is subtracted based on the relative amount found in the protonated version. In a typical analysis we measure the C-13 natural abundance contribution by running ER-MS of the protonated version (or estimate it by ChemDraw software) and use this value in our calculation using an in-house developed method that subtracts this contribution from each MS signal constituting the isotope distribution. ¹H NMR (400 MHz), ¹³C NMR (100 MHz), and ²H NMR (61.4 MHz) spectra were recorded on a Bruker 400 MHz spectrometer at 298 K. Chemical shifts, in ppm, were referenced to the residual signal of the corresponding solvent. Deuterium NMR spectroscopy was performed using the probe’s lock channel for direct observation.

Preparation of solvate ionic liquids

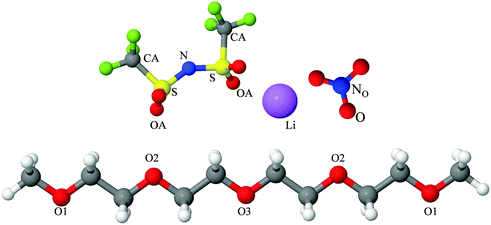
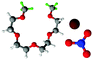
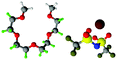
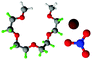
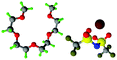
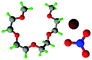
Fully hydrogenous tetraethylene glycol dimethyl ether, aka tetraglyme, (G4) (Sigma Aldrich, ≥99%), lithium nitrate (Sigma Aldrich, ≥99%) and lithium bis(trifluoromethane)sulfonimide (Li[TFSI]) (Sigma, ≥99%) were used as received. H, d₆, d₁₆, and d₂₂ contrasts for [Li(G4)][TFSI] and [Li(G4)][NO₃] were prepared by dissolving equimolar quantities of LiNO₃ or Li[TFSI] in the appropriate G4 samples. Prior to synthesis of the glyme solvate ionic liquids, the pure salts used were dried in an oven at 120 °C for 24 hours. The salt–G4 mixtures were stirred at 60 °C for 8 hours under N₂ atmosphere to ensure the lithium salts were completely dissolved and thoroughly mixed with the G4. Fig. 2 gives the structure of G4, nitrate and TFSI⁻ and the atom labels used. Table 1 shows the structure and deuteration of the [Li(G4)][TFSI] and [Li(G4)][NO₃] isotopomers prepared.

Fig. 2 Structure and atomic labels for the bis(trifluromethanesulfonyl)imide, TFSI⁻, anion (top left); lithium cation, Li⁺, (top centre); nitrate anion, NO₃⁻, (top right) and tetraethylene glycol dimethyl ether aka tetraglyme, G4, (bottom).

Table 1 Structure and names of isotopomeric contrasts for 1 : 1 lithium salt : tetraglyme (G4) solvates for which neutron diffraction spectra were recorded. Hydrogen atoms are coloured white and deuterium atoms are highlighted green, carbon atoms are grey, oxygen atoms are red, nitrogen atoms are blue, sulphur atoms are yellow, and fluorine atoms are brown

[Li(G4)][TFSI]		[Li(G4)][NO3]
Contrast	Name	Contrast	Name
	H-[Li(G4)][TFSI]		H-[Li(G4)][NO3]
	d6-[Li(G4)][TFSI]		d6-[Li(G4)][NO3]
	d16-[Li(G4)][TFSI]		d16-[Li(G4)][NO3]
	d22-[Li(G4)][TFSI]		d22-[Li(G4)][NO3]

---

Neutron diffraction spectra were collected for all isotopomeric SIL samples (Table 1) using the SANDALS time-of-flight spectrometer at the ISIS pulsed neutron and muon source, Rutherford Appleton Laboratory, UK. The SNADALS instrument has an incident wavelength range of 0.05–4.5 Å, and covers a Q range of 0.05–50 Å⁻¹.⁴³ For the measurements, samples were contained in chemically inert, ‘null scattering’, Ti_0.68Zr_0.32 flat plate cells with internal geometries of 1 × 35 × 35 mm, with a wall thickness of 1 mm sealed with PTFE O-rings. Samples were maintained at a temperature of 298 K using a recirculating heater (Julabo FP50) for the duration of the diffraction experiments. Diffraction measurements were made on each of the empty sample containers, the empty spectrometer, and a 3.1 mm thick vanadium standard sample to enable instrument calibration and data normalisation. The net run time for each measurement was ca. 8 hours. Reduction of raw scattering data was performed using the GUDRUN software package as described in the ATLAS manual.⁴⁴ During data reduction, corrections including normalisation to the incident neutron flux, absorption and multiple scattering corrections, Ti–Zr can subtraction and normalisation to absolute units by dividing the measured differential cross section by the scattering of a vanadium standard of known thickness were performed. Fits to the normalised diffraction data were produced using empirical potential structure refinement (EPSR) simulations.^45,46 The simulation used Lennard-Jones 12-6 and electrostatic potentials, truncated at 12 Å. Previously reported potential values were used for the potential parameters for tetraglyme molecules⁴⁷ and lithium,⁴⁸ bis(trifluoromethanesulfonyl)imide⁴⁹ and nitrate⁵⁰ ions. For both systems the spectra for all four isotopomers were fit simultaneously.

Results and discussion

The measured neutron diffraction data, S(Q), for four contrasts of [Li(G4)][TFSI] and [Li(G4)][NO₃] are shown in Fig. 3A and B respectively. A preliminary comparison of the S(Q) functions for the two solvates reveals important differences between the two liquids. The d₆ and d₂₂ contrasts for [Li(G4)][TFSI] have low Q peaks, located at 0.95 and 0.65 Å⁻¹ respectively, which are absent in the corresponding contrasts for [Li(G4)][NO₃]. These peaks indicate the presence of regular repeating structures in the bulk with characteristic lengths of 6.6 Å and 9.7 Å. The smaller of these repeat lengths, characterised by the weak peak in the d₆ contrast, is consistent with the combined packing dimension of the Li⁺ cation⁵¹ and TFSI⁻ anion⁵² while the larger repeat length is slightly greater than the packing dimension expected for an [Li(G4)][TFSI] ion pair calculated using the molecular weight and density of the solvate, assuming a cubic packing geometry.^36,53 This suggests the presence of complexes larger than a simple 1 : 1 lithium : glyme complex cation, i.e. polynuclear complexes, which have been previously suggested.^19,39 The primary peak found between 1 and 2 Å⁻¹ in all contrasts for both solvates is consistently at higher Q for [Li(G4)][NO₃] than for [Li(G4)][TFSI], indicating smaller bulk repeat spacings. This can be attributed to two factors. Firstly, the nitrate anion is much smaller than TFSI⁻ and secondly, the local Li⁺ solvation environment is expected to be significantly different in the two liquids.

Fig. 3 SANDALS neutron diffraction data and EPSR derived fits for (A) 1 : 1 mole fraction lithium bis(trifluoromethane)sulfonimide in tetraglyme, [Li(G4)][TFSI] and (B) 1 : 1 lithium nitrate in tetraglyme, [Li(G4)][NO₃]. Coloured dots show the experimentally measured S(Q) and the black lines the EPSR derived fits.

Extracting detailed structural information from the experimentally measured diffraction spectra, S(Q), is difficult without the aid of supporting simulations. This is because the S(Q) is a complex sum of scatting contributions from multiple atom–atom correlations, which produce both positive and negative going peaks.^54–58 Accurately modelling S(Q) functions is difficult as there are almost invariably more partial site–site radial distribution functions than independent diffraction data sets. Constraining atom–atom arrangements by defining optimised molecular geometries, preventing unrealistic atom–atom overlap and fixing the bulk atomic density to its known value (calculated from the measured bulk density) ensures only physically plausible structures are produced. Additionally, in the case of neutron diffraction, contrast variation using isotopic substitution of deuterium for hydrogen highlights specific atom–atom correlations contributing to the total S(Q). Simultaneously fitting multiple isotopomeric contrasts with a single model structure affords greater confidence in the simulated structure factors. The EPSR simulated fits produced for both [Li(G4)][TFSI] and [Li(G4)][NO₃] (solid black lines in Fig. 3) show good agreement with the measured S(Q) (open circles in Fig. 3) for all four contrasts.

Fig. 4 presents snapshots of the front faces of the equilibrated simulation boxes corresponding to the fits presented in Fig. 3. Close examination of the snapshot presented for [Li(G4)][TFSI] reveals Li⁺ cations (green spheres) solvated by G4 molecules, separated from TFSI⁻. In addition, Li⁺ cations can be seen interacting with both G4 and TFSI⁻ simultaneously. Conversely, in [Li(G4)][NO₃] relatively few Li⁺ cations are obviously solvated exclusively by G4 in the snapshot. This suggests that Li⋯glyme interactions are much more abundant in [Li(G4)][TFSI] than in [Li(G4)][NO₃], where Li⋯anion interactions dominate. Differences in Li⁺ coordination environments for the two solvates can be clearly seen in Fig. 4C and D where only the cations are plotted. For the [Li(G4)][TFSI] (Fig. 4C) Li⁺ cations are uniformly distributed throughout the simulation box. However, for [Li(G4)][NO₃] (Fig. 4D) Li⁺ cations are less uniformly distributed, with evidence of cation clustering, producing Li⁺ enriched and Li⁺ depleted regions. The interactions producing these structural differences are quantified by examining g_ij(r) functions, coordination numbers, spherical density functions (SDF) and cluster distributions extracted from the simulation boxes for the two solvates.

Fig. 4 Snapshot of fitted bulk structure for [Li(G4)][TFSI] (left hand column) and [Li(G4)][NO₃] (right hand column) equilibrated at 298 K. Each simulation box contains 300 ion pairs. (A) Shows all [Li(G4)][TFSI] atoms; 300 G4, 300 Li⁺ and 300 TFSI⁻. (B) Shows all [Li(G4)][NO₃] atoms; 300 G4, 300 Li⁺ and 300 NO₃⁻. (C) Shows the 300 Li⁺ in [Li(G4)][TFSI] and (D) shows the 300 Li⁺ in [Li(G4)][NO₃]. H atoms are shown in white, C atoms in grey, N atoms in blue, O atoms in red, F atoms in brown, S atoms in yellow and Li atoms in green.

g _ij(r) correlation functions for [Li(G4)][TFSI] are given in Fig. 5 and for [Li(G4)][NO₃] in Fig. 6. Both [Li(G4)][TFSI] and [Li(G4)][NO₃] have very pronounced Li⋯O g_ij(r) correlations due to strong Lewis acid–base interactions between Li⁺ and O atoms on G4 and counter anions. However, the strongest Li⋯O interactions differ markedly between [Li(G4)][TFSI] and [Li(G4)][NO₃]. In [Li(G4)][TFSI], all Li⋯O correlations with G4 oxygen atoms (Li⋯O₁, Li⋯O₂ and Li⋯O₃) have very strong sharp peaks at 1.90 Å. Additionally, the Li⋯O correlation with the TFSI⁻ anion has a strong, sharp peak at 2.0 Å. However the Li⋯O correlation with TFSI⁻ is weaker than the Li⋯O₁ and Li⋯O₂ correlations and of comparable intensity to the Li⋯O₃ correlation with G4. Caution must be taken when comparing g_ij(r) functions peak intensities for atom–atom pairs with different bulk atomic densities because distributions are normalised to this bulk density, giving a value of 1 at wide separations. The calculated coordination numbers (cf.Table 2) are a better guide for this type of comparison. The g_ij(r) functions are a useful guide for determining the atom–atom separations for atom–atom correlations and identifying particularly strong interactions. [Li(G4)][NO₃] has similar Li⋯O correlation peaks. However, in [Li(G4)][NO₃], Li⋯O correlations with the nitrate anion have far more intense g_ij(r) peaks than Li⋯O correlations with G4 O atoms. The dissimilar g_ij(r) peak intensities between [Li(G4)][TFSI] and [Li(G4)][NO₃] reveal markedly different Li⁺ coordination environments in the two liquids.

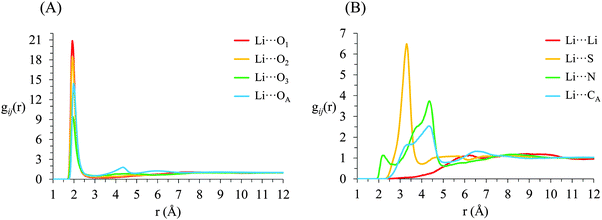Fig. 5 Key g_ij(r) functions for [Li(G4)][TFSI]. (A) Gives Li⁺⋯O correlations (B) gives Li⁺⋯anion and Li⁺⋯Li⁺ correlations.

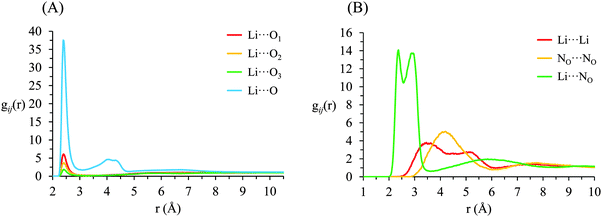Fig. 6 Key g_ij(r) functions for [Li(G4)][NO₃]. (A) Gives Li⁺⋯O correlations (B) gives Li⁺⋯anion, anion⋯anion and Li⁺⋯Li⁺ correlations.

Table 2 Coordination numbers for Li⋯O_X atom–atom pairs in [Li(G4)][TFSI] and [Li(G4)][NO₃] derived from the EPSR modelled interionic partial radial g_ij(r) data. Coordination numbers were calculated over 0.00–3.25 Å, corresponding to the first local minima in the respective Li⋯O_Xg_ij(r) functions

	[Li(G4)][TFSI]	[Li(G4)][NO3]
Li⋯O1	1.00	0.49
Li⋯O2	0.94	0.35
Li⋯O3	0.33	0.09
Li⋯Oanion	1.72	4.39
Li⋯Oglyme	2.27	0.93
Li⋯OTotal	3.99	5.32

---

Li⁺⋯anion correlations (Fig. 5B) in [Li(G4)][TFSI] confirm Li⁺ interacts with the anion preferentially through its O atoms, the Li⋯O_A peak is much more intense than any other correlations between Li⁺ and anion atoms. Additionally, a pronounced peak is present in the Li⋯S g_ij(r) function at 3.33 Å which is 1.35 Å higher than the Li⋯O_Ag_ij(r) peak. This distance is comparable to the S=O_A bond length (1.442 Å), indicating roughly linear S–O_A⋯Li arrangements are preferred. Conversely, Li⁺⋯anion correlation for [Li(G4)][NO₃] (Li⋯N_O in Fig. 6B) is much stronger than the Li⁺⋯anion correlations for [Li(G4)][TFSI]. This reveals Li⁺ interacts with the nitrate anion much more strongly than with the TFSI⁻ anion.

The Li⋯N_Og_ij(r) function has two pronounced, closely separated peaks at 2.73 and 2.94 Å. The close peaks indicate that nitrate anions complex Li⁺ in two different geometries in [Li(G4)][NO₃]. Nitrate is known to complex in two distinct fashions – as a monodentate ligand, interacting with a metal centre through one of its O atoms, and as a bidentate ligand, interacting with a metal centre through two of its O atoms.⁵⁹ These two different binding methods result in different Li⋯N_O distances. In [Li(G4)][TFSI] there is no evidence in the g_ij(r) functions of TFSI⁻ anions binding Li⁺ cations in a bidentate fashion.

The Li⋯Li g_ij(r) functions for [Li(G4)][TFSI] and [Li(G4)][NO₃] are markedly different. In [Li(G4)][TFSI], the Li⋯Li g_ij(r) function lacks a well-defined peak and slowly reaches its bulk value by approximately 6 Å. This indicates that the strong lithium⋯glyme interactions, evident in the Li⁺⋯O_glymeg_ij(r) functions, produces stable complex cations which favour larger average Li⋯Li separations. Conversely, for [Li(G4)][NO₃], a pronounced peak is present at 3.5 Å, indicating much Li⁺ is densely packed in [Li(G4)][NO₃]. This denser Li⋯Li packing, coupled with exceptionally strong Li⋯O and Li⋯N_Og_ij(r) correlations, indicates that Li⁺ and NO₃⁻ partially segregate from the solvating G4 molecules. This is visibly evident in the snapshot given in Fig. 4D, where regions slightly enriched in Li⁺ can be seen. Phase segregation of Li⁺ and NO₃⁻ has been observed in previous simulations,³⁹ and attributed in part to difficulties in accurately modelling polarisation of the nitrate anion when it coordinates with Li⁺. However, the present results indicate that the predicted partial segregation of Li⁺ and NO₃⁻ from G4 is not an artefact and does indeed occur in the [Li(G4)][NO₃] system.

Fig. 7 gives spherical density function (SDF) plots produced for Li⋯O correlations with anion O atoms in [Li(G4)][TFSI] and [Li(G4)][NO₃]. SDF plots give three dimensional reconstructions of the corresponding g_ij(r) functions, depicting the spatial distribution of Li⁺ around the selected O atoms. The SDF plots in Fig. 7A and B show the packing of Li⁺ around nitrate in [Li(G4)][NO₃]. The two closely separated peaks in the Li⋯N_Og_ij(r) function (Fig. 6B) indicate the nitrate anion binds to Li⁺ in both monodentate and bidentate geometries, and the Li@N_O SDF plots confirm this. At low separations, 0.0–2.6 Å, (Fig. 7A) three Li⁺ density lobes are symmetrically distributed about the nitrate anion, in plane with the anion and between its O atoms. These lobes are due to the nitrate anion coordinating to Li⁺ in a bidentate fashion. The SDF plot for larger Li⋯N_O separations, 2.6–3.5 Å, (Fig. 7B) has three Li⁺ density lobes, each coaxial with the N–O bonds. These lobes corresponds to monodentate Li⋯nitrate complexation interactions. The SDF plot in Fig. 7C shows the packing of Li⁺ around TFSI⁻ O atoms in [Li(G4)][TFSI]. The SDF distribution is calculated with the highlighted S atom at the centre of the plot. (Distributions are the same for both anion S atoms). Li⁺ closely associates with the O atoms of TFSI⁻, coaxial with the S=O bonds. This reveals that TFSI⁻ anions bind with Li⁺ cations in a monodentate fashion. However, TFSI⁻ anions may simultaneously bind to more than one Li⁺ cation (i.e. bridging between cations).

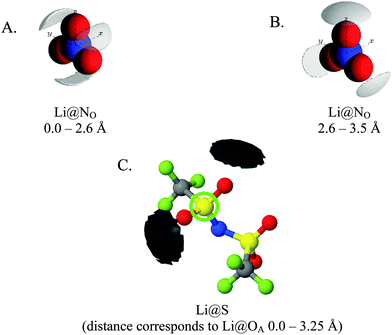Fig. 7 SDF plots for Li⁺ cations around (A) nitrate N atoms at short separations, corresponding to the first peak in the corresponding Li⋯N_Og_ij(r) function given in Fig. 6B; (B) nitrate N atoms at larger separations, corresponding to the second peak in the corresponding Li⋯N_Og_ij(r) function given in Fig. 6B; (C) the highlighted TFSI⁻ S atom, using radial separations that correspond to a Li⋯O_A separation of 0.0–3.25 Å and capturing the Li⋯O_A peak in the corresponding g_ij(r) function given in Fig. 5B. All SDF plots show the 20% isosurface.

Fig. 8 presents SDF plots for Li⁺ around G4 O atoms; A and B give the SDF distribution for Li⁺ cations around the O₂ atoms (highlighted by green circles) of representative G4 molecules taken from the respective simulation boxes for [Li(G4)][NO₃] and [Li(G4)][TFSI], while C and D give the general local geometry of Li⋯O interactions with G4 O atoms. It is important to stress is that the G4 molecules presented in Fig. 8 are representative of average interactions only. In the bulk G4 molecules freely rotate, adopting a distribution of conformers. Free rotation of G4 and the exchange of O atoms coordinated to Li⁺ means the exact geometry of a [Li(G4)]⁺ complex is time dependant. The distribution of Li⋯O interactions is discussed in greater detail below. For reference, corresponding plots for other O atoms are presented in the ESI† in Fig. S23 and S24.

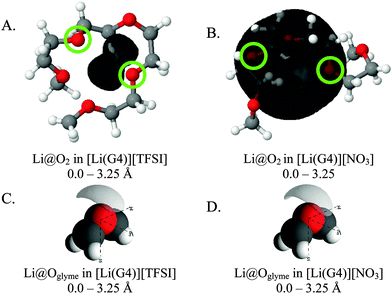Fig. 8 SDF plots for Li⁺ cations around (A) G4 O₂ atoms (highlighted by green circles) in [Li(G4)][TFSI], distances used corresponding to the first peak in the corresponding Li⋯O₂g_ij(r) function given in Fig. 5A; (B) G4 O atoms in [Li(G4)][TFSI], distances used corresponding to the first peaks in the corresponding Li⋯O_glymeg_ij(r) functions given in Fig. 5A; (C) G4 O₂ atoms (highlighted by green circles) in [Li(G4)][NO₃], distances used corresponding to the first peak in the corresponding Li⋯O₂g_ij(r) function given in Fig. 6A; (D) G4 O atoms in [Li(G4)][NO₃], distances used corresponding to the first peaks in the corresponding Li⋯O_glymeg_ij(r) functions given in Fig. 6A. All SDF plots show the 20% isosurface.

For [Li(G4)][TFSI], SDF plot shows that the distribution of Li⁺ cations about the G4 O₂ atoms (indicated by the black shaded density lobe in Fig. 8A) is concentrated, located immediately adjacent to the two O₂ atoms. Conversely, for [Li(G4)][NO₃] the distribution is quite diffuse (Fig. 8B). This is because Li⁺ and O₂ atoms in [Li(G4)][NO₃] are not as strongly correlated as in [Li(G4)][TFSI], which translates to weaker Li⋯O interactions with G4 and less regular packing.

The general local geometry of Li⋯O coordination interactions is given in Fig. 8C and D for [Li(G4)][NO₃] and [Li(G4)][TFSI] respectively. The geometry of this interaction is identical in both solvates. In both systems, Li⁺ packs adjacent to the G4 O atoms, opposite to the O bonded –CH₂– groups. While the local geometry of Li⋯O_glyme interactions is identical in both [Li(G4)][NO₃] and [Li(G4)][TFSI], g_ij(r) functions and coordination numbers show that these interactions are far less frequent in [Li(G4)][NO₃].

Li⋯O coordination numbers corresponding to the first g_ij(r) peaks are given in Table 2 for both [Li(G4)][TFSI] and [Li(G4)][NO₃]. Li⋯O coordination numbers with G4 are 2–3 times higher for [Li(G4)][TFSI] than [Li(G4)][NO₃]. Conversely, the Li⋯O anion coordination number is 2–3 times higher in [Li(G4)][NO₃]. This confirms that lithium⋯glyme interactions predominate in [Li(G4)][TFSI] while lithium⋯anion interactions are dominant in [Li(G4)][NO₃] as is indicated by the g_ij(r) functions presented in Fig. 5 and 6. This is in agreement with both experimental findings and recent MD simulations.^39,60

In [Li(G4)][TFSI], the EPSR simulations show that Li⁺ is coordinated by an average of 2.27 G4 O atoms and 1.73 TFSI⁻ O atoms, giving a total coordination number of 4.00. This contrasts with the Li⋯O coordination numbers obtained by other simulations. In the MD/ab initio simulations by Tsuzuki et al.,⁶⁰ Li⁺ is coordinated by an average of 4.5 G4 O atoms and 0.5 TFSI⁻ O atoms (total coordination number of 5.0), whereas in the MD simulations by Shimizu et al.³⁹ Li⁺ is coordinated by an average of 3.9 G4 O atoms and 1.9 TFSI⁻ O atoms (total coordination number of 5.8).

All simulations agree that G4 O atoms displace TFSI⁻ O atoms in [Li(G4)][TFSI], such that the Li⁺ coordination shell is dominated by glyme O atoms. Such displacement generally yields systems with a greater total Li⋯O coordination numbers: in pure crystalline Li[TFSI], Li⁺ is tetrahedrally coordinated by four oxygen atoms from four different TFSI⁻ anions,⁴² whereas in crystalline [Li(glyme)][TFSI] systems, the total Li⋯O coordination numbers frequently increase to 5 or 6.^32,33 The total coordination numbers in the corresponding liquid systems are generally slightly lower (e.g., in liquid Li[TFSI] at 530 K, the Li⋯O coordination number is 3.72³⁹ instead of the above-cited value of 4 for the solid phase).

The different Li⋯O coordination numbers from the previous simulations and the EPSR fits to the neutron diffraction data in this work reflect the different types of solvate structures obtained using distinctive models: the torsionally unhindered glyme molecules used in the MC/EPSR simulations are less prone to wrap around a given Li⁺ and coordinate it in a polydentate fashion (cf.Fig. 7 below). This yields Li–G4 solvates that suffer more competition from the anions and are thus coordinated to more TFSI⁻ O atoms. On the other hand, the parameterization of glyme molecules performed by the Tsuzuki et al.⁶⁰ took into account ab initio geometries of [Li(G4)][TFSI] complexes, where the Li⁺ coordination shell is dominated by glyme O atoms from a single glyme molecule. Such strong and polydentate solvation by the glyme molecules inhibits the coordination of TSFI⁻ O atoms. The MD simulations by Shimizu et al.³⁹ used torsionally-hindered glyme molecules parameterized by a general force-field and show a situation where the competition between glyme and TFSI⁻ for the complexation of Li⁺ yields a wide distribution of solvates with distinct coordination numbers. The versatility and dynamics of such a distribution probably accounts for the larger total coordination numbers observed in this last model. The EPSR fits are refined against, and must ultimately fit, the four scattering spectra obtained for different isotopic contrasts. Thus, the EPSR coordination numbers are experimentally validated in ways that the pure simulations are not (or at least not to the same extent³⁹).

In [Li(G4)][NO₃], each Li⁺ cation is coordinated by an average of 0.93 G4 and 4.39 nitrate O atoms donated by 2.69 nitrate anions (calculated from the Li⋯N_Og_ij(r) function in Fig. 6B). In crystalline LiNO₃ lithium cations are octahedrally coordinated by 6 NO₃⁻ anions,⁴¹ converse to the tetrahedral arrangement produced with the much larger TFSI⁻ anion. Li⋯NO₃ associations are diminished in the molten state, with each Li⁺ cation interacting with an average of 4 nitrate anions via their O atoms,^40,61 similar to the situation in to pure crystalline and molten Li[TFSI]. Far fewer Li⋯NO₃ associations are displaced by the addition of G4 in [Li(G4)][NO₃] compared to [Li(G4)][TFSI]. The overwhelming preference for Li⋯anion interactions is consistent with segregation of Li⁺ and NO₃⁻, as is apparent by the Li⁺ rich regions in the simulation snapshot given in Fig. 4. The Li⋯Li g_ij(r) functions for [Li(G4)][NO₃] confirm that Li⋯Li are associated in this poor solvate.

As the number of Li–O contacts with G4 increase around a cation, the attraction between Li⁺ and the coordinating O atom decreases.³⁵ The weaker attractions are the result of the negative charges on coordinating O atoms progressively weakening the electric field around Li⁺, weakening the electrostatic and ion–dipole interactions responsible for Li–O binding as more O atoms coordinate to the cation. This produces longer Li–O distances for each additional O atom coordinated to Li⁺. However, coulombic interactions with anions stabilize [Li(G4)]⁺ with multiple Li–O contacts, allowing good SILs to form. The difference between a good and a poor SIL then depends on whether [Li(G4)]–anion interactions stabilize the complex (as with the TFSI⁻ anion), or the anion displaces precludes interactions with G4 (as with the nitrate anion).

The difference between Li⁺ coordination shells in [Li(G4)][TFSI] and [Li(G4)][NO₃] is thus due to the relative Lewis basicity of G4, TFSI⁻ and nitrate. The Lewis basicity of ligands can be compared by their Gutmann donor number (DN)⁶² which is defined as the negative enthalpy value for formation of a 1 : 1 adduct with a standard Lewis acid. A large DN value corresponds to a high Lewis basicity, and therefore Li⁺ coordinating power. DN values have been reported for G4 (69.4 kJ mol⁻¹),⁶³ TFSI⁻ (22.5 kJ mol⁻¹)⁶³ and nitrate (87.9 kJ mol⁻¹)⁶⁴ showing that their relative coordination power follows the order of TFSI⁻ < G4 < NO₃⁻.⁶⁵ Consequently, nitrate complexes Li⁺ more strongly than G4 in [Li(G4)][NO₃]. Conversely, TFSI⁻ forms weaker complex with Li⁺ than G4 and is displaced from the Li⁺ coordination shell in [Li(G4)][TFSI]. Thus Lewis basicity can be used to indicate whether a given glyme–lithium salt combination will form a “good” or a “poor” SIL.³⁴

The above g_ij(r) functions and coordination numbers describe the average Li⁺ coordination shell in [Li(G4)][TFSI] and [Li(G4)][NO₃]. However, the instantaneous coordination environment for any given Li⁺ cation in the two solvates can vary widely. Fig. 9 gives the coordination number probability distributions, p(n), for Li⋯O linkages in [Li(G4)][TFSI] and [Li(G4)][NO₃], describing the probability of a cation having a specific coordination number, n, for each Li⋯O pair. The coordination environments in both [Li(G4)][TFSI] and [Li(G4)][NO₃] can vary markedly from cation to cation. While G4 O atoms contribute most to the Li⁺ coordination shell in [Li(G4)][TFSI], the TFSI⁻ anion also contributes significantly. Similarly, in [Li(G4)][NO₃], there are an appreciable number of Li⋯O linkages with G4 despite the dominance of nitrate anions in the Li⁺ coordination shell.

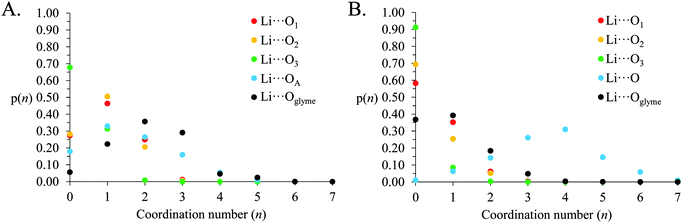Fig. 9 Coordination number probability distributions for Li⋯O linkages in (A) [Li(G4)][TFSI] and (B) [Li(G4)][NO₃].

In [Li(G4)][TFSI] the Li⋯O coordination number with G4 readily varies between 0 and 5. However, coordination numbers of 2–3 are preferred, with just over 70% of all Li⁺ cations having 2 or more contacts with G4 O atoms. Conversely, ∼5% of Li⁺, at any time, are found uncoordinated to G4. The Li⋯O coordination number with TFSI⁻ varies between 0 and 4, with 0–2 the most probable. The Li⁺ coordination environment in [Li(G4)][NO₃] also fluctuates. The number of nitrate anion O atoms coordinated to Li⁺ varies between 0 and 7, with 3 and 4 most frequently encountered. The number of G4 O atoms about Li⁺ is between 0 and 4, although numbers of 0 and 1 are most common, with only ∼24% of Li⁺ having more than 1 Li⋯O contact with G4, and ∼37% of Li⁺ lacking any Li⋯O contacts with G4. However, there is 1 glyme O atom present in the average coordination environment of Li⁺ in [Li(G4)][NO₃] which affords solubility of the Li[NO₃] salt in G4 despite the Li⋯nitrate connectivity in the bulk liquid.

A key consideration for categorising SILs good or poor is the percentage of free glyme in the solvate, i.e. the fraction of glyme molecules which lack coordination interactions with Li⁺. A good SIL is characterised by strong complexation between the metal cation and the glyme, forming stable [Li(glyme)]⁺ complex cations.³⁴ The size and distribution of complexes formed is also of interest. The number of ions and G4 molecules in a complex is variable, and both G4 and the counter anions can bridge between Li⁺ cations to produce poly nuclear complexes.

Cluster analysis has been performed for [Li(G4)][TFSI] and [Li(G4)][NO₃] to determine the proportion of free glyme and give insight into the distribution of complexes formed in both solvates. A G4 molecule was designated as coordinated to a Li⁺ cation if any of its O atoms were found to be within 3.25 Å of the Li⁺ cation (this distance corresponds to the first local minima in the Li⋯O g_ij(r) functions involving G4 O atoms in Fig. 5 and 6). The analysis performed considers any two G4 and/or Li⁺ cations to be a part of a single complex if they are joined by an uninterrupted chain of Li⋯O linkages between Li⁺ and G4 as defined above. This allows the proportion of [Li(G4)₂]⁺ and [Li₂(G4)]²⁺, and higher, complexes to be determined in addition to the proportion of free glyme present.

In [Li(G4)][TFSI] ∼5% of G4 molecules lack Li⋯O so are ‘free’ glyme. This agrees remarkably well with the estimation of free glyme concentration in [Li(G4)][TFSI] using Raman spectroscopy,²⁵ and with the predictions of recent MD simulations for this solvate³⁹ but is higher than the free glyme concentration determined electrochemically²⁵ for [Li(G4)][TFSI] of 0.29%. The activation energy for charge transfer processes at an Li/Li⁺ electrode for SILs are controlled by the energy required to break the final Li–O contact between Li⁺ and a solvating glyme molecule.²² This means that the electrochemical approach will be sensitive to [Li(G4)]⁺ complexes with few Li–O contacts while the Raman method is sensitive only to complexes with multiple Li–O contacts.

The average number of Li⁺ cations interacting with all O atoms for a G4 molecule for [Li(G4)][TFSI] is 1.30. This suggests that most G4 molecules interact with only one Li⁺ cation, while some G4 molecules interact with multiple Li⁺ cations. The cluster analysis performed indicates ∼60% of Li : G4 complexes exist as 1 : 1 complexes, resembling lithium–crown ether complexes, as suggested by ab inito calculations,³⁵ however the number of Li⋯O contacts between Li⁺ and G4 in the complexes determined here are, on average, lower and more variable than predicted.³⁵ An additional ∼20% of the Li⁺ and G4 in the system participate in [Li(G4)₂]⁺ and [Li₂(G4)]²⁺ complexes while a further ∼15% of the Li⁺ and G4 form complexes of the form [Li_x(G4)_y]^x+ where x + y = 4. These poly-nuclear complexes are the reason the average number of Li⁺ cations coordinated to each G4 molecule is higher than one.

In [Li(G4)][NO₃], ∼37% of glyme molecules lack Li⋯O contacts and can be considered as ‘free’ glyme. This fraction is markedly lower than the fraction determined from Raman spectroscopy²⁵ and recent MD simulations.³⁹ However, the degree of Li⋯O contacts with G4 in this solvate is low, cf. the coordination number distributions in Fig. 9. The average number of Li⁺ cations coordinated to each G4 molecule is only 0.51 which is a function of the high fraction of free G4 in the bulk and low overall average number of Li⁺ cations coordinated to each G4 molecule. This means the exchange time for G4 complexed to Li⁺ will be markedly shorter in [Li(G4)][NO₃] than [Li(G4)][TFSI]. Short exchange times coupled with low Li⋯O connectivity between Li⁺ and G4 in [Li(G4)][NO₃] means that the percentage of free glyme predicted from Raman spectroscopy will be significantly higher than the ∼37% determined by these EPSR fits. Cluster analysis also reveals that only about 5% of Li⁺ and G4 in [Li(G4)][NO₃] participate in complexes of the form [Li(G4)₂]⁺ and [Li₂(G4)]²⁺, while only a further 5% in complexes of the form [Li_x(G4)_y]^x+ where x + y = 4. This is in stark contrast to the much higher fraction of poly-nuclear complexes present in [Li(G4)][TFSI]. This is due to markedly lower coordination numbers for Li⋯O contacts between Li⁺ and G4 in [Li(G4)][NO₃] compared to [Li(G4)][TFSI]. This means the degree of connectivity between G4 and Li⁺ is much lower and G4 does not extensively displace nitrate anions coordinated Li⁺ in [Li(G4)][NO₃]. Consequently, the proportion of [Li(G4)]⁺ complexes in the nitrate solvate containing multiple Li⋯O contacts between G4 and Li⁺ is small.

The formation of [Li(G4)]⁺ complex cations in SILs results in reduced diffusion coefficients for Li⁺ compared to what may be expected for an unsolvated Li⁺.^22,34 The formation of poly-nuclear clusters could further reduce the Li⁺ self-diffusion coefficient. However, only a relatively small fraction of the Li⁺ is found in poly-nuclear clusters at any time, and these are only weakly associated. This means the diffusion coefficient for Li⁺ in the system is probably not strongly impacted by the presence of poly-nuclear clusters. The apparent measured diffusion coefficient for Li⁺ will be the average for Li⁺ in both 1 : 1 and poly-nuclear complexes, as is seen for example by NMR.²²

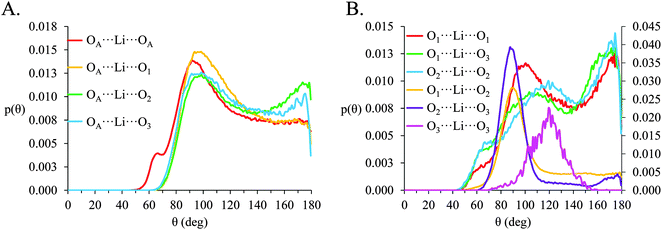
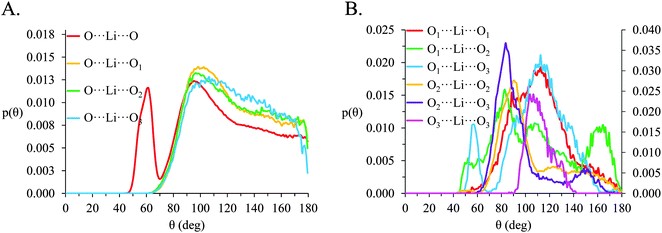
SDF plots cannot be produced for packing atoms around Li⁺ as there is no way to define and distinguish a privileged set of axis about the spherical ion. However, atom-triplet angle distributions for O⋯Li⋯O triplets allow the spatial packing of O atoms around Li⁺ to be deduced. Atom-triplet angle distributions for [Li(G4)][TFSI] and [Li(G4)][NO₃] are given in Fig. 10 and 11 respectively.

Fig. 10 Normalized angle probability distributions (p(θ)) for O⋯Li⋯O atom-triplets in [Li(G4)][TFSI] calculated for r values corresponding to the first local minima in the corresponding g_ij(r) data. (A) Gives p(θ) for O_anion⋯Li⋯O_anion atom and O_anion⋯Li⋯O_glyme triplets and (B) gives p(θ) for O_glyme⋯Li⋯O_glyme atom triplets, note that the O₁⋯Li⋯O₂, O₂⋯Li⋯O₃ and O₃⋯Li⋯O₃ distributions are plotted on a secondary axis for clarity.

Fig. 11 Normalized angle probability distributions (p(θ)) for O⋯Li⋯O atom-triplets in [Li(G4)][NO₃] calculated for r values corresponding to the first local minima in the corresponding g_ij(r) data. (A) gives p(θ) for O_anion⋯Li⋯O_anion and O_anion⋯Li⋯O_glyme atom triplets and (B) gives p(θ) for O_glyme⋯Li⋯O_glyme atom triplets, note that the O₁⋯Li⋯O₂, O₂⋯Li⋯O₃ and O₃⋯Li⋯O₃ distributions are plotted on a secondary axis for clarity.

In [Li(G4)][NO₃], a sharp pronounced peak is present in the angle distribution for the O⋯Li⋯O triplet at ca. 60°. This peak corresponds to the Li⁺ bound to nitrate in a bidentate fashion, producing a sharp angle between the two closely spaced O atoms on the anion and the bound Li⁺ cation. A similar, but much smaller shoulder at ca. 60° is also observed in the O_A⋯Li⋯O_A triplet in [Li(G4)][TFSI]. This shoulder is due to the TFSI⁻ O atoms bound to the same S atom both falling within the radial limit used to calculate the angle distribution. However, the Li⋯O_Ag_ij(r) function (Fig. 4A) and the corresponding SDF plot (Fig. 7C) do not show any features consistent with TFSI⁻ binding Li⁺ in a bidentate fashion like the nitrate anion, meaning the shoulder seen in the O_A⋯Li⋯O_A angle distribution is an artefact of the angle distribution calculation.

In both [Li(G4)][NO₃] and [Li(G4)][TFSI] triplets involving O atoms adjacent on the G4 chain (i.e. O₁⋯ Li⋯O₂ and O₂⋯ Li⋯O₃) produce sharp, well-defined peaks at ca. 85–90°. This is because the molecular bonding between O₁, O₂ and O₃ atoms on the same G4 chain physically constrain their coordination geometry around Li⁺, necessarily producing a sharp, well defined peak in the angle distribution. The O₁⋯ Li⋯O₂ and O₂⋯ Li⋯O₃ angle distributions also have finite probabilities at higher angles (>100°) which is the result of O atoms from different G4 molecules coordinating Li⁺ in polynuclear complexes as detected by cluster analysis. However, the probability for these interactions is much lower as the close proximity of O₁ to O₂ and O₂ to O₃ on the G4 chain make it far more likely that neighbouring O atoms on G4 will chelate a common Li⁺ cation. This is the origin of the chelate effect for glymes, favouring coordination by O atoms from the same G4 chain. The chelate effect has already been shown to be important in lithium–glyme solvates.²⁴ In both [Li(G4)][NO₃] and [Li(G4)][TFSI], the O₃⋯Li⋯O₃ angle distributions also have strong sharp peaks at ca. 120°. Each G4 molecule only has one O₃ atom defined, meaning this angle distribution represents Li⁺ cations coordinated O atoms from two G4 molecules. The well-defined peak is for the O₃⋯ Li⋯O₃ angle distribution is the result of steric hindrance about the G4 O₃ atoms, constraining packing of the O₃ atoms around the Li⁺ cation.

In [Li(G4)][NO₃] the O⋯Li⋯O and O⋯Li⋯O_glyme distributions have maxima at ca. 90–100° while the O_glyme⋯Li⋯O_glyme distributions peak at ca. 80–90°, 110–120° and 160–170°. Atom-triplet angle distributions involving only G4 O atoms have sharper peaks than either the O_anion⋯Li⋯O_anion or O_anion⋯Li⋯O_glyme triplets. However, there is greater variation in the peak positions observed. These distributions, together with an average Li⋯O 5–6 in [Li(G4)][NO₃], are consistent with the formation of distorted 5 coordinate trigonal bipyramidal Li⁺ complexes, and distorted 6 coordinate octahedral Li⁺ complexes. The angle distributions for [Li(G4)][NO₃] generally have peaks sharper than for [Li(G4)][TFSI]. This is attributed to strong complexation between Li⁺ and the nitrate anion, which means a smaller portion of the Li⁺ coordination sphere is available for glyme oxygens, leading to smaller, tighter angle distributions. In [Li(G4)][TFSI] the O_A⋯Li⋯O_A, O_A⋯Li⋯O_glyme and O_glyme⋯Li⋯O_glyme angle distributions all have maxima at ca. 110–120° while the O_glyme⋯Li⋯O_glyme distributions also have peaks at ca. 170–180° in addition to the peaks at ca. 90° for O atoms adjacent each other on the G4 chain. Li⁺ has an average coordination number of 4 in [Li(G4)][TFSI]. Taken with the calculated O⋯Li⋯O angle distributions for this solvate, these angle distribution indicate distorted tetrahedral geometries are commonly encountered for Li⁺ in [Li(G4)][TFSI].

Torsional angles for O–C–C–O dihedrals in [Li(G4)][TFSI] and [Li(G4)][NO₃] are given in Fig. 12. Differences in the proportion of free glyme and the degree of Li⋯O_glyme connectivity between [Li(G4)][TFSI] and [Li(G4)][NO₃] produces differing torsional angle distributions along the G4 chains. In [Li(G4)][TFSI] gauche/cis O–C–C–O rotamers are favoured. In this conformation, O atoms are eclipsed or slightly staggered. In this conformation, G4 O atoms are appropriately oriented to interact with a common Li⁺ cation. The dihedral distribution for [Li(G4)][TFSI] is the result of a high proportion of stable [Li(G4)]⁺ complexes in this solvate. Conversely, in [Li(G4)][NO₃] there is no strong preference for any given rotamer. This the consequence of a high proportion of free glyme and the limited degree of Li⋯O_glyme connectivity in [Li(G4)][NO₃], meaning Li⋯G4 complexation does not create an energetic bias toward specific rotamers as it does in [Li(G4)][TFSI].

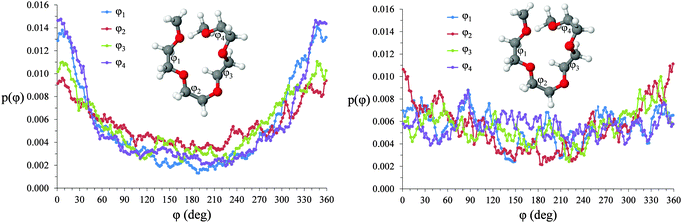Fig. 12 Torsional angle distributions for O–C–C–O dihedrals in (A) [Li(G4)][TFSI] and (B) [Li(G4)][NO₃].

Conclusion

In both [Li(G4)][TFSI] and [Li(G4)][NO₃], the strongest atom–atom correlations in the bulk are between Li⁺ cations and O atoms. These correlations are due to strong Lewis acid–base interactions between Li⁺ and ligating O atoms. However, the O atoms which form the Li⁺ coordination shell differ greatly depending on the counter anion present. Li⋯O coordination numbers with G4 are 2–3 times higher for [Li(G4)][TFSI] than [Li(G4)][NO₃], and the Li⋯O anion coordination number is 2–3 times higher in [Li(G4)][NO₃]. This difference in the coordination numbers between the two systems is a consequence of the relative Lewis basicities of TFSI⁻ and NO₃⁻ compared to G4. The more basic nitrate anion coordinates Li⁺ more strongly than G4, meaning Li⋯O anion interactions dominate in [Li(G4)][NO₃]. Conversely, the less basic TFSI⁻ anion is readily displaced by G4, meaning Li⋯O G4 interactions dominate in [Li(G4)][TFSI]. In both solvates the local geometry of Li⋯O G4 interactions are identical but they are much less frequent in [Li(G4)][NO₃]. Nitrate anions in [Li(G4)][NO₃] coordinate Li⁺ in both monodentate and bidentate geometries. TFSI⁻, however, does not bind Li⁺ in a bidentate fashion.

In [Li(G4)][NO₃], strong Li⋯O anion interactions and low number of Li⋯O G4 interactions produce Li⁺ rich and Li⁺ depleted regions in the bulk. Conversely, strong Li⋯O G4 interactions in [Li(G4)][TFSI] generates stable complex cations, with Li⁺ well solvated and uniformly distributed in the bulk. For [Li(G4)][NO₃], weaker Li⋯O G4 interactions also means that there is 37% free glyme in the bulk and low overall connectivity between Li⁺ and G4; each G4 molecule is coordinated to an average of 0.5 Li⁺ cations. In [Li(G4)][TFSI] only ∼5% of G4 molecules lack Li⋯O contacts with Li⁺ and G4 molecules are coordinated to an average of 1.3 Li⁺ cations.

In [Li(G4)][TFSI] the Li⋯O_glyme coordination numbers vary between 0 and 5. However, coordination numbers of 2–3 are preferred, while the Li⋯O coordination number with TFSI⁻ varies between 0 and 4, with 0–2 the most probable. In [Li(G4)][NO₃] the number of nitrate anion O atoms coordinated to Li⁺ varies between 0 and 7, with numbers of 3 and 4 favoured. The number of G4 O atoms about Li⁺ varies between 0 and 4, although 0 and 1 are most common. The distribution of coordination numbers is accompanied by a distribution of complex clusters in both solvates. In [Li(G4)][TFSI] ∼20% of the Li⁺ and G4 in the system participate in [Li(G4)₂]⁺ and [Li₂(G4)]²⁺ complexes while a further ∼15% of the Li⁺ and G4 form complexes of the form [Li_x(G4)_y]^x+ where x + y = 4. These poly-nuclear complexes are the reason the average number of Li⁺ cations coordinated to each G4 molecule is higher than one. Conversely, only about 5% of Li⁺ and G4 in [Li(G4)][NO₃] participate in complexes of the form [Li(G4)₂]⁺ and [Li₂(G4)]²⁺, while only a further 5% in complexes of the form [Li_x(G4)_y]^x+ where x + y = 4.

Acknowledgements

TM thanks the University of Newcastle for a PhD stipend. RA thanks the ARC for a Future Fellowship. This research was supported by an ARC Discovery Project and an ISIS beamtime grant. Financial support provided by Fundação para a Ciência e Tecnologia (FCT) through projects FCT-ANR/CTM-NAN/0135/2012, PTDC/QUI-QUI/117340/2010 and UID/QUI/00100/2013. K. S. acknowledges post-doctoral grant SFRH/BPD/94291/2013. The National Deuteration Facility is partially funded by the National Collaborative Research Infrastructure Strategy, an initiative of the Australian Federal Government.

References

1. F. Endres and S. Z. El Abedin, Phys. Chem. Chem. Phys., 2006, 8, 2101–2116.
2. R. A. Asencio, E. D. Cranston, R. Atkin and M. W. Rutland, Langmuir, 2012, 28, 9967–9976.
3. J. J. Segura, A. Elbourne, E. J. Wanless, G. G. Warr, K. Voitchovsky and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 3320–3328.
4. R. Atkin, N. Borisenko, M. Drüschler, F. Endres, R. Hayes, B. Huber and B. Roling, J. Mol. Liq., 2014, 192, 44–54.
5. A. J. Page, A. Elbourne, R. Stefanovic, M. A. Addicoat, G. G. Warr, K. Voïtchovsky and R. Atkin, Nanoscale, 2014, 6, 8100–8106.
6. H. Li, R. J. Wood, M. W. Rutland and R. Atkin, Chem. Commun., 2014, 50, 4368–4370.
7. R. Hayes, N. Borisenko, B. Corr, G. B. Webber, F. Endres and R. Atkin, Chem. Commun., 2012, 48, 10246–10248.
8. P. L. Short, Chemical and egineering news, 2006, 84, 7.
9. M. E. Van Valkenburg, R. L. Vaughn, M. Williams and J. S. Wilkes, Thermochim. Acta, 2005, 425, 181–188.
10. R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974–4975.
11. H. M. Yau, S. T. Keaveney, B. J. Butler, E. E. L. Tanner, M. S. Guerry, S. R. D. George, M. H. Dunn, A. K. Croft and J. B. Harper, Pure Appl. Chem., 2013, 85, 1979–1990.
12. T. Welton, Chem. Rev., 1999, 99, 2071–2083.
13. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
14. F. Endres, ChemPhysChem, 2002, 3, 144–154.
15. M. Galinski, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580.
16. N. Borisenko, S. Z. El Abedin and F. Endres, ChemPhysChem, 2012, 13, 1736–1742.
17. K. Fujii, H. Hamano, H. Doi, X. D. Song, S. Tsuzuki, K. Hayamizu, S. Seki, Y. Kameda, K. Dokko, M. Watanabe and Y. Umebayashi, J. Phys. Chem. C, 2013, 117, 19314–19324.
18. H. Moon, R. Tatara, T. Mandai, K. Ueno, K. Yoshida, N. Tachikawa, T. Yasuda, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 20246–20256.
19. C. Zhang, A. Yamazaki, J. Murai, J.-W. Park, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 17362–17373.
20. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629.
21. Y. Umebayashi, H. Harnano, S. Seki, B. Minofar, K. Fujii, K. Hayamizu, S. Tsuzuki, Y. Kameda, S. Kohara and M. Watanabe, J. Phys. Chem. B, 2011, 115, 12179–12191.
22. K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2011, 115, 18384–18394.
23. K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331.
24. C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144–5153.
25. K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257.
26. C. A. Angell, J. Electrochem. Soc., 1965, 112, 1224–1227.
27. T. Mandai, K. Yoshida, S. Tsuzuki, R. Nozawa, H. Masu, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2015, 119, 1523–1534.
28. S. Lascaud, M. Perrier, A. Vallee, S. Besner, J. Prudhomme and M. Armand, Macromolecules, 1994, 27, 7469–7477.
29. W. A. Henderson, J. Phys. Chem. B, 2006, 110, 13177–13183.
30. W. A. Henderson, N. R. Brooks, W. W. Brennessel and V. G. Young, Chem. Mater., 2003, 15, 4679–4684.
31. W. A. Henderson, N. R. Brooks and V. G. Young, Chem. Mater., 2003, 15, 4685–4690.
32. W. A. Henderson, F. McKenna, M. A. Khan, N. R. Brooks, V. G. Young and R. Frech, Chem. Mater., 2005, 17, 2284–2289.
33. D. Brouillette, D. E. Irish, N. J. Taylor, G. Perron, M. Odziemkowski and J. E. Desnoyers, Phys. Chem. Chem. Phys., 2002, 4, 6063–6071.
34. T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772.
35. S. Tsuzuki, W. Shinoda, S. Seki, Y. Umebayashi, K. Yoshida, K. Dokko and M. Watanabe, ChemPhysChem, 2013, 14, 1993–2001.
36. B. McLean, H. Li, R. Stefanovic, R. J. Wood, G. B. Webber, K. Ueno, M. Watanabe, G. G. Warr, A. Page and R. Atkin, Phys. Chem. Chem. Phys., 2015, 17, 325–333.
37. U. Olsher, R. M. Izatt, J. S. Bradshaw and N. K. Dalley, Chem. Rev., 1991, 91, 137–164.
38. Y. Kameda, Y. Umebayashi, M. Takeuchi, M. A. Wahab, S. Fukuda, S.-i. Ishiguro, M. Sasaki, Y. Amo and T. Usuki, J. Phys. Chem. B, 2007, 111, 6104–6109.
39. K. Shimizu, A. A. Freitas, R. Atkin, G. G. Warr, P. A. FitzGerald, H. Doi, S. Saito, K. Ueno, Y. Umebayashi, M. Watanabe and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2015, 17, 22321–22335.
40. A. K. Adya, G. W. Neilson, I. Okada and S. Okazaki, Mol. Phys., 1993, 79, 1327–1350.
41. X. Wu, F. R. Fronczek and L. G. Butler, Inorg. Chem., 1994, 33, 1363–1365.
42. J. L. Nowinski, P. Lightfoot and P. G. Bruce, J. Mater. Chem., 1994, 4, 1579–1580.
43. C. Benmore and A. K. Soper, The SANDALS manual: A Guide to performing experiments on the small angle neutron diffractometer for amorphous and liquid samples at ISIS, 1998.
44. A. K. H. W. S. H. A. C. Soper, ATLAS: analysis of time-of-flight diffraction data from liquid and amorphous samples, Rutherford Appleton Laboratory, Didcot, 1989.
45. A. K. Soper, Chem. Phys., 1996, 202, 295–306.
46. A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204.
47. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
48. R. Hayes, S. A. Bernard, S. Imberti, G. G. Warr and R. Atkin, J. Phys. Chem. C, 2014, 118, 21215–21225.
49. J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898.
50. J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047.
51. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
52. T. Carstens, R. Gustus, O. Höfft, N. Borisenko, F. Endres, H. Li, R. J. Wood, A. J. Page and R. Atkin, J. Phys. Chem. C, 2014, 118, 10833–10843.
53. R. G. Horn, D. F. Evans and B. W. Ninham, J. Phys. Chem., 1988, 92, 3531–3537.
54. H. K. Kashyap, J. J. Hettige, H. V. R. Annapureddy and C. J. Margulis, Chem. Commun., 2012, 48, 5103–5105.
55. H. K. Kashyap, C. S. Santos, R. P. Daly, J. J. Hettige, N. S. Murthy, H. Shirota, E. W. Castner and C. J. Margulis, J. Phys. Chem. B, 2013, 117, 1130–1135.
56. H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838–16846.
57. C. S. Santos, N. S. Murthy, G. A. Baker and E. W. Castner, J. Chem. Phys., 2011, 134.
58. J. J. Hettige, H. K. Kashyap, H. V. R. Annapureddy and C. J. Margulis, J. Phys. Chem. Lett., 2013, 4, 105–110.
59. R. Han and G. Parkin, J. Am. Chem. Soc., 1991, 113, 9707–9708.
60. S. Tsuzuki, W. Shinoda, M. Matsugami, Y. Umebayashi, K. Ueno, T. Mandai, S. Seki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 126–129.
61. T. Yamaguchi, I. Okada, H. Ohtaki, M. Mikami and K. Kawamura, Mol. Phys., 1986, 58, 349–364.
62. V. Gutmann, Coord. Chem. Rev., 1976, 18, 225–255.
63. K. M. Abraham, J. Electrochem. Soc., 2015, 162, A3021–A3031.
64. E. P. Buchikhin, A. M. Chekmarev and N. A. Bobyrenko, Russ. J. Inorg. Chem., 2011, 56, 1088–1093.
65. M. Schmeisser, P. Illner, R. Puchta, A. Zahl and R. van Eldik, Chem. – Eur. J., 2012, 18, 10765.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00176a

---