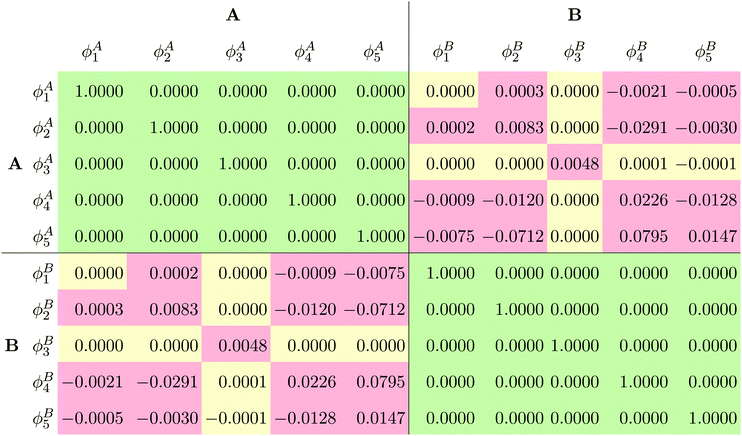Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
No need for external orthogonality in subsystem density-functional theory†
Jan P.
Unsleber
a,
Johannes
Neugebauer
*a and
Christoph R.
Jacob
 *b
*b
aTheoretische Organische Chemie, Organisch-Chemisches Institut and Center for Multiscale Theory and Computation, Westfälische Wilhelms-Universität Münster, Corrensstraße 40, 48149 Münster, Germany. E-mail: j.neugebauer@uni-muenster.de
bInstitute of Physical and Theoretical Chemistry, TU Braunschweig, Hans-Sommer-Straße 10, 38106 Braunschweig, Germany. E-mail: c.jacob@tu-braunschweig.de
First published on 15th February 2016
Abstract
Recent reports on the necessity of using externally orthogonal orbitals in subsystem density-functional theory (SDFT) [Annu. Rep. Comput. Chem., 8, 2012, 53; J. Phys. Chem. A, 118, 2014, 9182] are re-investigated. We show that in the basis-set limit, supermolecular Kohn–Sham-DFT (KS-DFT) densities can exactly be represented as a sum of subsystem densities, even if the subsystem orbitals are not externally orthogonal. This is illustrated using both an analytical example and in basis-set free numerical calculations for an atomic test case. We further show that even with finite basis sets, SDFT calculations using accurate reconstructed potentials can closely approach the supermolecular KS-DFT density, and that the deviations between SDFT and KS-DFT decrease as the basis-set limit is approached. Our results demonstrate that formally, there is no need to enforce external orthogonality in SDFT, even though this might be a useful strategy when developing projection-based DFT embedding schemes.
1 Introduction
Quantum-chemical subsystem and embedding methods (for recent reviews, see, e.g., ref. 1–4) allow for an efficient treatment of complex chemical systems. For approaches based on density-functional theory (DFT), one can distinguish two different strategies that allow for a formally exact subsystem treatment. Such formally exact approaches are particularly relevant because they can serve as a starting point for multiscale methods combining wavefunction-based quantum-chemical methods with DFT (wavefunction-in-DFT embedding methods).5–10Firstly, subsystem density-functional theory (SDFT)11,12 and frozen-density embedding (FDE)13 are based on a partitioning of the total electron density ρ(r) into (possibly overlapping) subsystem electron densities. The embedding potential obtained by reformulating Kohn–Sham-DFT (KS-DFT) in terms of these subsystem electron densities contains a contribution of the nonadditive kinetic energy, which can either be approximated13,14 or treated exactly by reconstructing the embedding potential leading to a certain target density.15–18 It is widely believed that with such an exact treatment of the nonadditive kinetic energy, SDFT and FDE will exactly reproduce the total electron density from supermolecular KS-DFT calculations.2,4,19
Secondly, the partitioning can also be achieved by assigning the KS-like orbitals to different subsystems. To this end, non-local projection techniques are used to ensure orthogonality of the subsystem orbitals, so that the non-additive kinetic energy vanishes.20 Hence, no approximate functionals for this energy component need to be introduced and the use of potential reconstruction techniques is not required. It can be demonstrated that such projection-based embedding calculations are exactly equivalent to supermolecular KS-DFT calculations.20
The question of orthogonality between the different subsystem orbitals (“external orthogonality”) is recently causing some apparent confusion in the literature. Hoffmann and co-workers have questioned that SDFT is formally exact.21,22 Instead, they argue that an exact treatment of the nonadditive kinetic energy alone does not suffice to make SDFT equivalent to KS-DFT, but that it is mandatory to enforce the external orthogonality of the subsystem orbitals. Also Chulhai and Jensen have picked up the argument, based on the work by Hoffmann and co-workers, that non-additive kinetic-energy potentials as used in SDFT and FDE may lead to incorrect results even for the exact kinetic-energy functional.23 If these arguments were correct, the two apparent conclusions are: (i) if external orthogonality is not enforced, even the exact non-additive kinetic-energy potential will give incorrect results, and (ii) if external orthogonality is enforced, this potential is exactly zero and SDFT becomes equivalent to projection-based embedding schemes. Hence, there would be no reason whatsoever to attempt constructing approximate non-additive kinetic energy potentials or to develop numerical schemes for the reconstruction of accurate embedding potentials.
In this work, we re-investigate the question whether or not external orthogonality is mandatory for an exact SDFT treatment. First, in Section 2 we reconsider the analysis given in ref. 21 and 22 to formally address this question. In a second step, we study this question on the basis an analytical example in Section 3 and on the basis of numerical results obtained with reconstructed potentials, which are derived from exact relations for the non-additive kinetic-energy potential, in Section 4. We conclude from our results in Section 5.
2 Theory
In (supermolecular) KS-DFT, the ground-state electron density is obtained as,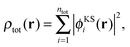 | (1) |
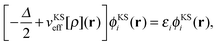 | (2) |
In the following, we will consider the special case of SDFT for two subsystems (A and B), which already introduces all the basic questions that may arise in the more general case of arbitrarily many subsystems. The goal of SDFT is then to find electron densities for these two subsystems ρA and ρB which add up to the correct total electron density ρ,
| ρtot(r) = ρA(r) + ρB(r). | (3) |
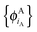 and
and 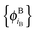 , as
, as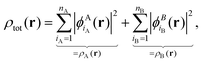 | (4) |
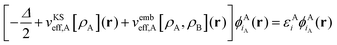 | (5) |
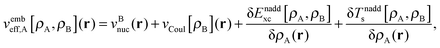 | (6) |
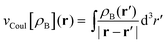 is the Coulomb potential of the frozen electron density ρB, Enaddxc [ρA,ρB] = Exc[ρtot] − Exc[ρA] − Exc[ρB] is the nonadditive exchange–correlation energy and Tnadds[ρA,ρB] = Ts[ρtot] − Ts[ρA] − Ts[ρB] is the nonadditive kinetic energy.
is the Coulomb potential of the frozen electron density ρB, Enaddxc [ρA,ρB] = Exc[ρtot] − Exc[ρA] − Exc[ρB] is the nonadditive exchange–correlation energy and Tnadds[ρA,ρB] = Ts[ρtot] − Ts[ρA] − Ts[ρB] is the nonadditive kinetic energy.
FDE is generally understood to be exact – in the sense that the sum of the subsystem densities, ρA(r) + ρB(r) is equal to the total electron density ρtot(r) from a supermolecular KS-DFT calculation [cf.eqn (3)] – if the following conditions are fulfilled:
(1) The contribution of the nonadditive kinetic energy Tnadds[ρA,ρB] to the embedding potential is treated exactly, for instance by using analytical potential reconstruction techniques.24,25 Numerical schemes for the reconstruction of the embedding potential15–18 might introduce errors due to the inaccuracies of optimized effective potential algorithms, in particular if finite basis sets are used.26
(2) The exchange–correlation energy is treated consistently in all calculations by using the same approximate functional in the supermolecular calculation, the subsystem calculations, and when evaluating the embedding potential.
(3) The KS(-like) equations for the supermolecule [eqn (2)] and for subsystem A [eqn (5)] are solved exactly, i.e., without introducing a finite basis set for the orbitals. To which extent this condition can be relaxed will be discussed in the following.
(4) All appearing densities, most importantly ρA(r) = ρtot − ρB(r), are noninteracting vs-representable. In particular, the frozen density ρB(r) must be chosen such that ρB(r) ≤ ρtot(r) holds at every point in space. This condition can be relaxed in SDFT, where the densities of both subsystems are updated iteratively in freeze-and-thaw cycles.27 For a detailed discussion, see ref. 2 and 19. Here, we will assume that this condition is fulfilled and not elaborate further on this rather intricate point.
In ref. 21 and 22, Hoffmann and co-workers argue that SDFT and FDE can only be exact if the additional condition that the KS-like orbitals of subsystem A and B, 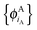 and
and 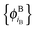 , are externally orthogonal, is fulfilled. They base their argument on the assertion that for SDFT to be exact, the supermolecular KS orbitals {ϕKSi} must be contained in the subspace spanned by the subsystem orbitals
, are externally orthogonal, is fulfilled. They base their argument on the assertion that for SDFT to be exact, the supermolecular KS orbitals {ϕKSi} must be contained in the subspace spanned by the subsystem orbitals 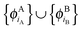 . That is, they assume that it must be possible to expand the supermolecular KS orbitals in the basis of the subsystem orbitals.
. That is, they assume that it must be possible to expand the supermolecular KS orbitals in the basis of the subsystem orbitals.
However, all that is required for SDFT to be exact is that the supermolecular density can be obtained, but not necessarily the supermolecular KS orbitals. Thus, the question is rather whether it is possible that the two different expansions of eqn (1) and of eqn (4) result in exactly the same total electron density, i.e.,
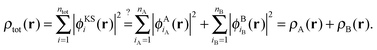 | (7) |
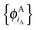 and
and 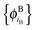 of internally orthogonal subsystem orbitals. For FDE, the frozen density ρB(r) and the set of orbitals
of internally orthogonal subsystem orbitals. For FDE, the frozen density ρB(r) and the set of orbitals 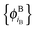 are given and the question becomes whether there is a set
are given and the question becomes whether there is a set 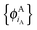 so that this equation can be fulfilled. As we require that for FDE the complementary ρA(r) is noninteracting vs-representable, this is equivalent to the SDFT case. In the following, we use
so that this equation can be fulfilled. As we require that for FDE the complementary ρA(r) is noninteracting vs-representable, this is equivalent to the SDFT case. In the following, we use 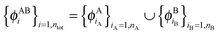 for the combined set of subsystem orbitals.
for the combined set of subsystem orbitals.
Following the analysis in ref. 21 and 22, we proceed by creating an explicitly orthonormalized combined set of subsystem orbitals for subsystems A and B, {![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) orthi}, with
orthi}, with
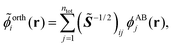 | (8) |
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) ij = 〈ϕABi|ϕABj〉 is the overlap matrix of the combined set of subsystem orbitals. Note that so far there is no reason to assume that these orthonormalized subsystem orbitals {
ij = 〈ϕABi|ϕABj〉 is the overlap matrix of the combined set of subsystem orbitals. Note that so far there is no reason to assume that these orthonormalized subsystem orbitals {![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) orthi} span the same subspace as the supermolecular KS orbitals {ϕKSi}.
orthi} span the same subspace as the supermolecular KS orbitals {ϕKSi}.
The sum of the subsystem densities [right-hand side of eqn (7)] can now be expressed as,21
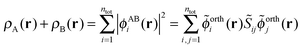 | (9) |
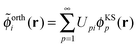 | (10) |
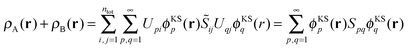 | (11) |
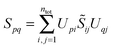 . For SDFT to be exact, this has to be equal to the left-hand side of eqn (7), that is,
. For SDFT to be exact, this has to be equal to the left-hand side of eqn (7), that is,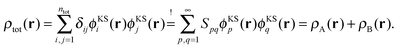 | (12) |
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) = I, i.e., if and only if the subsystem orbitals are externally orthogonal. This step is at the heart of the arguments of Hoffmann and coworkers in ref. 21 and 22.
= I, i.e., if and only if the subsystem orbitals are externally orthogonal. This step is at the heart of the arguments of Hoffmann and coworkers in ref. 21 and 22.
However, this conclusion can only be drawn if the set of orbital products {ϕKSpϕKSq}p,q=1,∞ is linearly independent. It is well known that for a complete basis set of the one-electron Hilbert space, the corresponding product basis set is linearly dependent. For a proof, we refer to the clear presentation by Görling et al. in Appendix A of ref. 28.
Specifically, since the supermolecular KS orbitals {ϕKSp}p=1,∞ form a complete basis, the set of orbital products {ϕKSpϕKSq}p,q=1,∞ must be linearly dependent. Therefore, there is a non-trivial solution of the equation
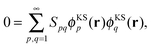 | (13) |
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) ≠ I, i.e., for the case of subsystem orbitals that are not externally orthogonal. Thus, we conclude that the arguments for enforcing external orthogonality in SDFT given in ref. 21 and 22 do not hold in the basis-set limit. Even for incomplete basis sets, (near) linear dependencies in the orbital products may still occur.28
≠ I, i.e., for the case of subsystem orbitals that are not externally orthogonal. Thus, we conclude that the arguments for enforcing external orthogonality in SDFT given in ref. 21 and 22 do not hold in the basis-set limit. Even for incomplete basis sets, (near) linear dependencies in the orbital products may still occur.28
3 An analytical example
It can be demonstrated that SDFT is able to exactly reproduce the supermolecular density with subsystem orbitals that are not externally orthogonal for a simple analytical model, which has been previously introduced by Savin and Wesolowski.24 To this end, we consider a closed-shell four-electron system, in which the supermolecular electron density is given by,| ρtot(r) = 2|ϕKS1(r)|2 + 2|ϕKS2(r)|2. | (14) |
As an extreme case, we consider a decomposition of the total densities into equal subsystem densities,
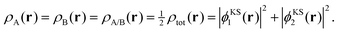 | (15) |
| ρA(r) = 2|ϕA1(r)|2 and ρB(r) = 2|ϕB1(r)|2, | (16) |
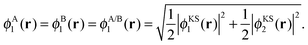 | (17) |
The potential in the KS-like equations for the subsystems A and B that leads to the required subsystem densities is analytically given by,2,24
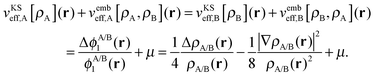 | (18) |
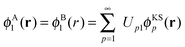 | (19) |
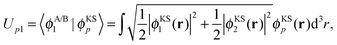 | (20) |
4 Numerical examples
4.1 Basis-set limit
To investigate an example with more than two orbitals, we turn to the argon atom as a test case, because for atoms the KS equations can easily be solved numerically on a grid, which provides results close to the basis-set limit.As total density ρKStot(r), we choose the one obtained in a KS-DFT calculation performed with the ADF program package29,30 using the BP86 exchange–correlation functional31,32 and a QZ4P Slater-type orbital basis set.33
We partition this total density into two closed-shell subsystem densities by defining
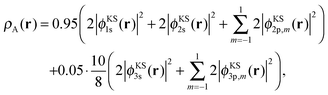 | (21) |
| ρB(r) = ρKStot(r) − ρA(r). | (22) |
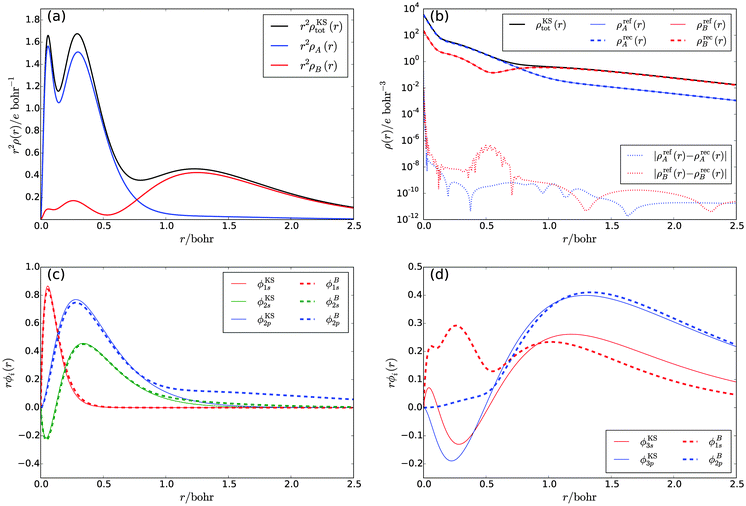
By construction, these subsystem densities are both non-negative at any point in space and each integrates to an integer number of electrons (nA = 10 and nB = 8). The radial densities r2ρKStot(r), r2ρA(r), and r2ρB(r) are shown in Fig. 1a.
To verify that these two subsystem densities can each be represented in terms of subsystem orbitals, we performed a reconstruction of the KS potentials vs[ρA] and vs[ρB] that yield the target densities ρA(r) and ρB(r), respectively, in a fully numerical solution of the KS equations on a logarithmic radial grid of 400 points. The modified van Leeuwen–Baerends algorithm34 used for the potential reconstruction as well as the computational details of the numerical solution of the KS equations are described in ref. 26 and 35.
It turns out to be possible to reconstruct the subsystem densities almost exactly. A comparison of the reference and the reconstructed subsystem densities as well as their difference on a logarithmic scale are shown in Fig. 1b. The integrated density difference, defined as
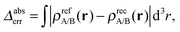 | (23) |
The subsystem orbitals for subsystems A and B are shown in Fig. 1c and d, respectively, alongside the corresponding supersystem KS orbitals. For subsystem A, the density as defined by eqn (21) is mainly composed of the five lowest supersystem KS orbitals ϕKS1s, and ϕKS2s, ϕKS2p (three degenerate orbitals), with a small admixture of the remaining orbitals. Consequently, the subsystem orbitals are very similar to the supersystem ones, with the deviations being caused by the admixture of small 3s- and 3p-orbital contributions in the subsystem density. On the other hand, the density of subsystem B is composed of the four orbitals ϕKS3s and ϕKS3p (three degenerate orbitals), with a small admixture of the remaining orbitals. In the subsystem calculation, this density needs to be reproduced by the ground-state orbitals ϕB1s and ϕB2p. Hence, in contrast to the corresponding supersystem KS orbitals, the radial parts of the subsystem orbitals are nodeless and large differences occur in the region from r = 0.0 bohr to r = 0.7 bohr.
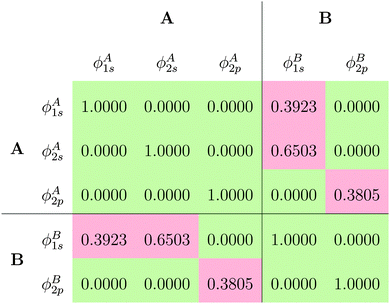
The fact that for both subsystem A and subsystem B the lowest s- and p-orbitals are each nodeless leads to a significant overlap between the subsystem orbitals, as can be seen from the overlap matrix ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) of the subsystem orbitals shown in Table 1. Thus, the subsystem orbitals are not externally orthogonal. Nevertheless, the sum of the subsystem densities reproduces the total density exactly. Of course, the s- and p-orbitals of the different subsystems are still mutually orthogonal because of the atomic symmetry of the specific test case considered here.
of the subsystem orbitals shown in Table 1. Thus, the subsystem orbitals are not externally orthogonal. Nevertheless, the sum of the subsystem densities reproduces the total density exactly. Of course, the s- and p-orbitals of the different subsystems are still mutually orthogonal because of the atomic symmetry of the specific test case considered here.
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) of the subsystem orbitals obtained for the Ar atom test case
of the subsystem orbitals obtained for the Ar atom test case
In summary, our results show that if the KS-like equations for the subsystems are solved numerically on a grid to avoid errors introduced by a finite basis set, a total density can be reproduced exactly as a sum of subsystem densities, even if the subsystem orbitals are not externally orthogonal. This confirms that SDFT is indeed exact if all the conditions listed in Section 2 are fulfilled, without the need to enforce external orthogonality.
4.2 Finite basis sets
Finally, we also want to investigate the case in which both the supermolecular KS-DFT calculation and the subsystem calculations are performed using a finite basis set for expanding the supermolecular and the subsystem orbitals. This is the scenario in which SDFT is usually applied in practical calculations. With finite basis sets, the linear dependence of the orbital products is not guaranteed. With small basis sets, the orbital product can in general be expected to be linearly independent.28 As discussed in Section 2, in this case the arguments of ref. 21 and 22 hold and it will not be possible to express the supermolecular density as a sum of two subsystem densities unless the subsystem orbitals are externally orthogonal. However, as the basis set gets larger, (near) linear dependencies of the orbital products will appear.We consider one of the test cases investigated in ref. 22, an NH3⋯NH3 complex (see Fig. 2), which can be partitioned into two NH3 subsystems. All calculations have been performed using the ADF program package29,30 and its FDE implementation,36 in combination with the PyADF scripting framework.37 In all of the subsystem calculations a supermolecular integration grid was used to ensure the transferability of the results. All subsystem calculations use the full supermolecular basis set [FDE(s)], i.e., ghost basis functions on the atoms of the frozen subsystem are included. The PW91 exchange–correlation functional38,39 has been used in all calculations.
First, a supermolecular KS-DFT calculation using a finite Slater-type orbital basis set has been performed to obtain a supermolecular reference density ρKStot(r). Subsequently, SDFT using accurate reconstructed embedding potentials were performed to investigate to which extent it is possible to reproduce the supermolecular density as a sum of two subsystem densities when using the same finite basis set in the subsystem calculations.
These accurate SDFT calculations have been done as follows: in the initial iteration, the densities ρ(0)A(r) and ρ(0)B(r) calculated for the isolated subsystems A and B, respectively, are used as initial guess for the subsystem densities. In the n-th iteration, the kinetic-energy component of the embedding potentials for subsystem A and B are then reconstructed as16,41
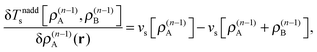 | (24) |
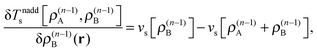 | (25) |
Such a freeze-and-thaw procedure ensures that both subsystem densities are noninteracting vs-representable and thus alleviates the shortcomings of the approach used in ref. 16 (see also ref. 44 and 45), where a frozen density constructed from localized orbitals was used. Since both subsystem densities are optimized, it should result in a pair of subsystem densities ρA(r) and ρB(r) that minimizes the total energy functional E[ρA + ρB].
The accuracy of the sum of the resulting subsystem densities ρA(r) + ρB(r) compared to the supermolecular density ρKStot(r) can be measured as,
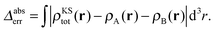 | (26) |
| DZP | ATZP | ET-pVQZ | |
|---|---|---|---|
| SumFrag | 0.1134 | 0.1208 | 0.1203 |
| SDFT/PW91k | 0.0344 | 0.0356 | 0.0358 |
| SDFT/RecPot | 0.0046 | 0.0047 | 0.0025 |
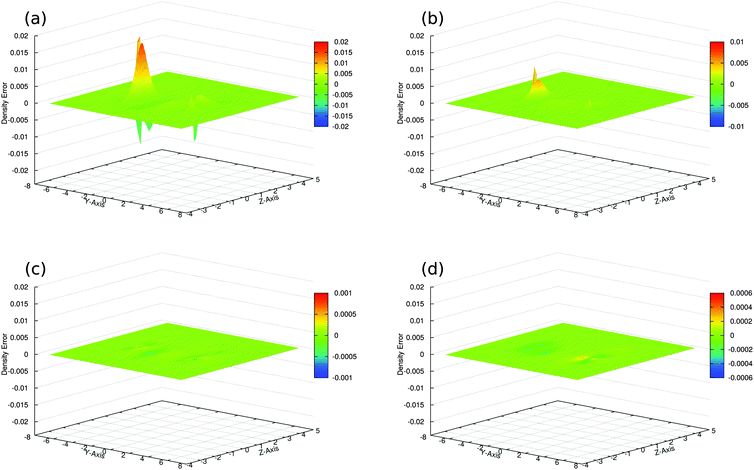
We find that in the SDFT calculations with reconstructed potentials (SDFT/RecPot, Fig. 3c), the sum of the subsystem densities is not identical to the supermolecular density, but approaches it closely. This is the case already with the small DZP Slater-type orbital basis set33 and when using the ATZP Slater-type orbital basis set.33,40 In fact, the integrated density error of 0.0046 electrons and 0.0047 electrons with DZP and ATZP, respectively, is one order of magnitude smaller that in an SDFT calculation in which the the nonadditive kinetic energy was approximated using the PW91k46 kinetic-energy functional (SDFT/PW91k, Fig. 3b) and almost two orders of magnitude smaller than for the sum of the densities from KS-DFT calculations for the isolated subsystems (SumFrag, Fig. 3a). When repeating the calculations with a larger ET-pVQZ Slater-type orbital basis set,47 the discrepancy is further reduced (Fig. 3d). This suggest that when approaching the basis-set limit, it becomes possible to reproduce the supermolecular density as a sum of subsystem densities.
In order to evaluate the external orthogonality of the subsystem orbitals, the overlap matrix ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) of the subsystem orbitals from the SDFT/RecPot calculation with the ET-pVQZ basis set is shown in Table 3. Indeed, the overlap of the subsystem orbitals is non-zero, i.e., the subsystem orbitals that can closely reproduce the supermolecular density are not externally orthogonal.
of the subsystem orbitals from the SDFT/RecPot calculation with the ET-pVQZ basis set is shown in Table 3. Indeed, the overlap of the subsystem orbitals is non-zero, i.e., the subsystem orbitals that can closely reproduce the supermolecular density are not externally orthogonal.
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) of the subsystem orbitals obtained in the SDFT/RecPot calculation with the ET-pVQZ basis set for NH3⋯NH3. Yellow cells are numerically non-zero
of the subsystem orbitals obtained in the SDFT/RecPot calculation with the ET-pVQZ basis set for NH3⋯NH3. Yellow cells are numerically non-zero
In summary, with finite basis sets, it is in general not possible to exactly reproduce the supermolecular KS-DFT density as a sum of two subsystem densities. However, as the size of the basis set is increased and the basis-set limit is approached, the discrepancies decrease and with basis sets of reasonable size it is possible to reproduce the supermolecular density rather accurately. While most of the remaining difference in the densities is most likely due to the use of a finite basis set, a part could also be caused by inaccuracies of the numerical potential reconstruction algorithm, such as the use of a finite basis set for the potential in the Wu-Yang method.
It should also be noted that with finite basis sets, both the supermolecular KS-DFT and the SDFT calculation are affected by a basis set error. Even though both calculations minimize the total energy functional E[ρtot], the space of the possible densities is different since different expansions of the density are used. We would argue that it is not a priori possible to decide which expansion will result in the more accurate total density. If we assume that the supermolecular KS-DFT/ET-pVQZ calculation gives results close to the basis-set limit, both the supermolecular KS-DFT and the SDFT/RecPot calculation in the smaller ATZP basis set exhibit a similar basis set error: the integrated density error Δabserr when comparing the supermolecular KS-DFT/ATZP calculation to the one in the larger ET-pVQZ basis set is 0.1315 electrons, whereas when comparing the sum of the SDFT/RecPot subsystem densities in the ATZP basis set to the supermolecular KS-DFT/ET-pVQZ density the integrated difference density Δabserr is 0.1322 electrons. However, a more systematic investigation of the basis set errors will be necessary to decide whether in a finite basis set, supermolecular KS-DFT or SDFT calculations yield results closer to the basis-set limit.
5 Conclusion
Our results demonstrate that recent claims21–23 that SDFT can only be exact if the external orthogonality of the subsystem orbitals is enforced are not justified. In fact, our analysis reveals that such claims are based on the assumption that the products of linearly independent orbitals are themselves linearly independent. This assumption is not true in the basis-set limit, and might also not hold for many finite basis sets used in practical calculations because (near) linear dependencies of orbital products appear.We have illustrated our analysis by demonstrating for the analytically solvable case of a two-orbital system that the sum of subsystem densities arising from mutually non-orthogonal subsystem orbitals can exactly reproduce a supermolecular KS-DFT density. The same has been shown, within numerical accuracy, for a many-orbital atom when solving the KS-like equations for the subsystems in the basis-set limit. For calculations in a finite basis set, we could show that a supermolecular density can be approached closely by the sum of subsystem densities, with the differences decreasing as the basis-set limit is approached.
However, for finite basis sets in which the products of basis functions are indeed linearly independent, the arguments given in ref. 21 and 22 do hold and external orthogonality is needed to reproduce the supermolecular density exactly. Thus, the minimization of the total energy functional E[ρtot] is performed with respect to different spaces of possible densities in SDFT and in KS-DFT. However, it is not clear which one will result in the density that yields a lower total energy (and is thus closer to the basis-set limit) if the nonadditive kinetic energy is evaluated exactly. This question is complicated by the fact that in SDFT, the subsystem densities of externally orthogonal subsystem orbitals cannot be expected to be vs-representable.16,24 Therefore, the supermolecular KS-DFT ground state density will not be accessible in SDFT, whereas the SDFT ground-state density might not be accessible in KS-DFT.
Alternatively, one can, of course, use subsystem approaches that are not based on a partitioning of the total density, but on a partitioning of the KS orbital space.20 With such approaches, supermolecular KS-DFT and subsystem calculations will result in exactly the same density, even with finite basis sets. This can be achieved by enforcing the external orthogonality of the subsystem orbitals by using projection operators. It must be noted that in this case the nonadditive kinetic energy vanishes, and its contribution to the embedding potential is replaced by the projection operator enforcing the external orthogonality. Using both a projection operator and an (approximate) nonadditive kinetic-energy contribution in the embedding potential will introduce additional errors because of double counting.22
Acknowledgements
J. P. U and J. N. acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) through IRTG 2027.References
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- C. R. Jacob and J. Neugebauer, WIREs Comput. Mol. Sci., 2014, 4, 325–362 CrossRef CAS.
- A. Krishtal, D. Sinha, A. Genova and M. Pavanello, J. Phys.: Condens. Matter, 2015, 27, 183202 CrossRef PubMed.
- T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928 CrossRef CAS PubMed.
- N. Govind, Y. A. Wang, A. J. R. da Silva and E. A. Carter, Chem. Phys. Lett., 1998, 295(1-2), 129–134 CrossRef CAS.
- N. Govind, Y. A. Wang and E. A. Carter, J. Chem. Phys., 1999, 110(16), 7677–7688 CrossRef CAS.
- T. A. Wesolowski, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 012504 CrossRef.
- A. S. P. Gomes and C. R. Jacob, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 222–277 RSC.
- F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775 CrossRef CAS PubMed.
- T. Dresselhaus and J. Neugebauer, Theor. Chem. Acc., 2015, 134, 97 CrossRef.
- G. Senatore and K. R. Subbaswamy, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5754 CrossRef CAS.
- P. Cortona, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(16), 8454–8458 CrossRef.
- T. A. Wesolowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050–8053 CrossRef CAS.
- T. A. Wesolowski, J. Chem. Phys., 1997, 106(20), 8516–8526 CrossRef CAS.
- O. Roncero, M. P. de Lara-Castells, P. Villarreal, F. Flores, J. Ortega, M. Paniagua and A. Aguado, J. Chem. Phys., 2008, 129, 184104 CrossRef CAS PubMed.
- S. Fux, C. R. Jacob, J. Neugebauer, L. Visscher and M. Reiher, J. Chem. Phys., 2010, 132, 164101 CrossRef PubMed.
- J. D. Goodpaster, N. Ananth, F. R. Manby and T. F. Miller III, J. Chem. Phys., 2010, 133, 084103 CrossRef PubMed.
- C. Huang, M. Pavone and E. A. Carter, J. Chem. Phys., 2011, 134, 154110 CrossRef PubMed.
- T. A. Wesolowski, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszczynski, World Scientific, Singapore, 2006, vol. 10, pp. 1–82 Search PubMed.
- F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, III, J. Chem. Theory Comput., 2012, 8, 2564–2568 CrossRef CAS PubMed.
- Y. G. Khait and M. R. Hoffmann, Annu. Rep. Comput. Chem., 2012, 8, 53–70 CAS.
- P. K. Tamukong, Y. G. Khait and M. R. Hoffmann, J. Phys. Chem. A, 2014, 118, 9182–9200 CrossRef CAS PubMed.
- D. V. Chulhai and L. Jensen, J. Chem. Theory Comput., 2015, 11, 3080–3088 CrossRef CAS PubMed.
- A. Savin and T. A. Wesolowski, in Advances in the Theory of Atomic and Molecular Systems, ed. P. Piecuch, J. Maruani, G. Delgado-Barrio and S. Wilson, Springer, Dordrecht, 2009, pp. 311–326 Search PubMed.
- P. de Silva and T. A. Wesolowski, J. Chem. Phys., 2012, 137, 094110 CrossRef PubMed.
- C. R. Jacob, J. Chem. Phys., 2011, 135, 244102 CrossRef PubMed.
- T. A. Wesolowski and J. Weber, Chem. Phys. Lett., 1996, 248, 71–76 CrossRef CAS.
- A. Görling, A. Heßelmann, M. Jones and M. Levy, J. Chem. Phys., 2008, 128, 104104 CrossRef PubMed.
- Amsterdam density functional program Theoretical Chemistry, Vrije Universiteit, Amsterdam, 2015.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22(9), 931–967 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- R. van Leeuwen and E. J. Baerends, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 2421–2431 CrossRef CAS.
- K. Boguslawski, C. R. Jacob and M. Reiher, J. Chem. Phys., 2013, 138, 044111 CrossRef PubMed.
- C. R. Jacob, J. Neugebauer and L. Visscher, J. Comput. Chem., 2008, 29, 1011–1018 CrossRef CAS PubMed.
- C. R. Jacob, S. M. Beyhan, R. E. Bulo, A. S. P. Gomes, A. W. Götz, K. Kiewisch, J. Sikkema and L. Visscher, J. Comput. Chem., 2011, 32(10), 2328–2338 CrossRef CAS PubMed.
- J. P. Perdew, in Electronic Structure of Solids, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, pp. 11–20 Search PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- D. P. Chong, Mol. Phys., 2005, 103, 749–761 CrossRef CAS.
- C. R. Jacob, S. M. Beyhan and L. Visscher, J. Chem. Phys., 2007, 126, 234116 CrossRef PubMed.
- Q. Wu and T. Van Voorhis, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 024502 CrossRef.
- T. Heaton-Burgess and W. Yang, J. Chem. Phys., 2008, 129, 194102 CrossRef PubMed.
- T. A. Wesolowski, J. Chem. Phys., 2011, 135, 027101 CrossRef PubMed.
- S. Fux, C. R. Jacob, J. Neugebauer, L. Visscher and M. Reiher, J. Chem. Phys., 2011, 135, 027102 CrossRef.
- A. Lembarki and H. Chermette, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 5328–5331 CrossRef CAS.
- D. P. Chong, E. van Lenthe, S. van Gisbergen and E. J. Baerends, J. Comput. Chem., 2004, 25, 1030 CrossRef CAS PubMed.
Footnote |
| † Dedicated to Professor Evert Jan Baerends on the occasion of his 70th birthday. |
| This journal is © the Owner Societies 2016 |