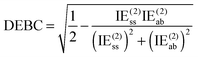Open Access Article
Open Access ArticleThe S66x8 benchmark for noncovalent interactions revisited: explicitly correlated ab initio methods and density functional theory†
Brina
Brauer‡
a,
Manoj K.
Kesharwani‡
a,
Sebastian
Kozuch
 b and
Jan M. L.
Martin
*a
b and
Jan M. L.
Martin
*a
aDepartment of Organic Chemistry, Weizmann Institute of Science, 76100 Rehovot, Israel. E-mail: gershom@weizmann.ac.il; Fax: +972 8 934 3029
bDepartment of Chemistry, Ben-Gurion University of the Negev, 84105 Beer-Sheva, Israel
First published on 1st March 2016
Abstract
The S66x8 dataset for noncovalent interactions of biochemical relevance has been re-examined by means of MP2-F12 and CCSD(F12*)(T) methods. We deem our revised benchmark data to be reliable to about 0.05 kcal mol−1 RMS. Most levels of DFT perform quite poorly in the absence of dispersion corrections: somewhat surprisingly, that is even the case for the double hybrids and for dRPA75. Analysis of optimized D3BJ parameters reveals that the main benefit of dRPA75 and DSD double hybrids alike is the treatment of midrange dispersion. dRPA75-D3BJ is the best performer overall at RMSD = 0.10 kcal mol−1. The nonlocal VV10 dispersion functional is especially beneficial for the double hybrids, particularly in DSD-PBEP86-NL (RMSD = 0.12 kcal mol−1). Other recommended dispersion-corrected functionals with favorable price/performance ratios are ωB97X-V, and, surprisingly, B3LYP-D3BJ and BLYP-D3BJ (RMSDs of 0.23, 0.20 and 0.23 kcal mol−1, respectively). Without dispersion correction (but parametrized for midrange interactions) M06-2X has the lead (RMSD = 0.45 kcal mol−1). A collection of three energy-based diagnostics yields similar information to an SAPT analysis about the nature of the noncovalent interaction. Two of those are the percentages of Hartree–Fock and of post-MP2 correlation effects in the interaction energy; the third, CSPI = [IE(2)ss − IE(2)ab]/[IE(2)ss + IE(2)ab] or its derived quantity DEBC = CSPI/(1 + CSPI2)1/2, describes the character of the MP2 correlation contribution, ranging from 0 (purely dispersion) to 1 (purely other effects). In addition, we propose an improved, parameter-free scaling for the (T) contribution based on the Ecorr[CCSD-F12b]/Ecorr[CCSD] and Ecorr[CCSD(F12*)]/Ecorr[CCSD] ratios. For Hartree–Fock and conventional DFT calculations, full counterpoise generally yields the fastest basis set convergence, while for double hybrids, half-counterpoise yields faster convergence, as previously established for correlated ab initio methods.
Introduction
Noncovalent interactions have great importance in many areas of research, particularly in chemistry and biological science.1,2 In biomolecules, noncovalent interactions play a major role in determining their structure and reactivity: hydrogen bonding, π stacking, and dispersion interactions are among the most important noncovalent interactions.All present-day computational methods capable of handling biomolecules with thousands of atoms, such as molecular mechanics force fields (e.g.ref. 3) and semiempirical methods (e.g., ref. 4 and 5), are highly approximated and heavily parametrized. Ideally, parametrization of such approximate methods would be based on experimental observations; in practice, this is an intractable problem as experimental data are not available in sufficient quantity or in isolation from various environmental or dynamical effects that cannot easily be included in the approximate method during the many evaluation cycles required for parametrization. Highly accurate ab initio computational data represent a convenient alternative.
From a SAPT (symmetry-adapted [intermolecular] perturbation theory) perspective (see ref. 6–8 for recent reviews), the interaction energy of a noncovalent dimer can be decomposed into four main components: exchange repulsion (Eexc), electrostatic attraction (Eelst), induced electrostatic interactions (Eind), and dispersion forces (Edisp). The balance of their relative importance changes between different types of systems,9 as well as with distance, but dispersion (which is a long-range electron correlation effect) matters in all of them: indeed, in certain systems (such as noble gas dimers or alkane dimers) it is the glue that holds the dimer together at all. Electron correlation however also contributes in higher order to induced and electrostatic forces, particularly at shorter distances. To sum up, no accurate treatment of long-range correlation effects is possible without accounting for electron correlation.10
Coupled-cluster correlated methods with sufficiently large basis sets are known to accurately reproduce these interactions, but their high computational cost and massive resource demands limit their use to small benchmark systems.
Such benchmark data, for a representative set of small systems, do enable the validation and/or calibration of less demanding, more approximate methods, such as density functional theory.
In the past decade, a number of databases have been proposed for noncovalent interactions. An early one that has been used in the parametrization of a number of empirical density functionals is S22,11 which are 22 noncovalent complexes ranging from water and methane dimers to the adenine–thymine base pair (both Watson–Crick and stacked). Its ab initio reference data were recently comprehensively revised.12
In order to have a broader set that is more representative of interactions one might see in biomolecules, Hobza and coworkers assembled a larger S66 set9,13 of 66 noncovalent pairs, generated from 14 monomers in various combinations. The selection of monomers was based on their frequency as motifs or functional groups in the most commonly found biomolecules. The S66 set was designed with a balance in mind between electrostatic dominated (hydrogen bonding), dispersion dominated (including π stacking), and mixed-influenced complexes. Single hydrogen bonds, aromatic–aliphatic, and aliphatic–aliphatic interactions are also incorporated into the S66 set, which were not adequately covered by the narrower S22 dataset.
In an actual biomolecule, such interactions would not necessarily occur near the equilibrium inter-monomer separation, but at the separation dictated by the geometry of the system (e.g., by the secondary structure of the protein). Hence, the Hobza group extended the S66 set by considering each dimer at eight different inter-monomer separations: 0.90re, 0.95re, re, 1.05re, 1.10re, 1.25re, 1.5re, and 2re, where re is the equilibrium distance (the monomers were separated out without further geometry optimization). Thus, the S66x8 dataset was created, which is the subject of the present investigation. A full listing of the systems, together with the final recommended values obtained in the present work, is presented in Table 1. Reference geometries were taken “as is” from the Benchmark Energy and Geometry Database (http://www.begdb.com).14
| 0.90re | 0.95re | 1.00re | 1.05re | 1.10re | 1.25re | 1.50re | 2.00re | |
|---|---|---|---|---|---|---|---|---|
| Hydrogen bonding | ||||||||
| 01 water⋯water | 4.659 | 4.954 | 4.951 | 4.768 | 4.487 | 3.473 | 2.113 | 0.872 |
| 02 water⋯MeOH | 5.293 | 5.630 | 5.634 | 5.434 | 5.119 | 3.967 | 2.394 | 0.955 |
| 03 water⋯MeNH2 | 6.577 | 6.937 | 6.929 | 6.689 | 6.315 | 4.932 | 2.982 | 1.143 |
| 04 water⋯peptide | 7.748 | 8.149 | 8.153 | 7.907 | 7.514 | 6.023 | 3.844 | 1.442 |
| 05 MeOH⋯MeOH | 5.396 | 5.787 | 5.824 | 5.644 | 5.337 | 4.172 | 2.538 | 1.015 |
| 06 MeOH⋯MeNH2 | 7.067 | 7.550 | 7.603 | 7.385 | 7.005 | 5.517 | 3.352 | 1.277 |
| 07 MeOH⋯peptide | 7.784 | 8.270 | 8.330 | 8.116 | 7.737 | 6.228 | 3.668 | 1.104 |
| 08 MeOH⋯water | 4.684 | 5.032 | 5.063 | 4.901 | 4.629 | 3.611 | 2.208 | 0.909 |
| 09 MeNH2⋯MeOH | 2.862 | 3.078 | 3.063 | 2.917 | 2.704 | 1.984 | 1.104 | 0.396 |
| 10 MeNH2⋯MeNH2 | 3.724 | 4.113 | 4.165 | 4.016 | 3.756 | 2.793 | 1.309 | 0.390 |
| 11 MeNH2⋯peptide | 5.009 | 5.409 | 5.453 | 5.277 | 4.976 | 3.230 | 1.413 | 0.460 |
| 12 MeNH2⋯water | 6.834 | 7.272 | 7.300 | 7.070 | 6.688 | 5.234 | 3.158 | 1.199 |
| 13 peptide⋯MeOH | 5.811 | 6.224 | 6.278 | 6.109 | 5.810 | 4.646 | 2.970 | 1.315 |
| 14 peptide⋯MeNH2 | 6.938 | 7.446 | 7.536 | 7.360 | 7.021 | 5.639 | 3.567 | 1.498 |
| 15 peptide⋯peptide | 8.204 | 8.696 | 8.767 | 8.569 | 8.204 | 6.728 | 4.457 | 1.793 |
| 16 peptide⋯water | 4.801 | 5.150 | 5.191 | 5.044 | 4.790 | 3.825 | 2.468 | 1.139 |
| 17 uracil⋯uracil (BP) | 16.229 | 17.358 | 17.583 | 17.214 | 16.473 | 13.350 | 8.462 | 3.380 |
| 18 water⋯pyridine | 6.527 | 6.918 | 6.928 | 6.701 | 6.336 | 4.965 | 3.026 | 1.195 |
| 19 MeOH⋯pyridine | 6.944 | 7.445 | 7.520 | 7.324 | 6.963 | 5.525 | 3.403 | 1.343 |
| 20 AcOH⋯AcOH | 17.970 | 19.228 | 19.469 | 19.049 | 18.219 | 14.736 | 9.289 | 3.611 |
| 21 AcNH2⋯AcNH2 | 15.335 | 16.375 | 16.559 | 16.188 | 15.476 | 12.544 | 8.054 | 3.020 |
| 22 AcOH⋯uracil | 18.421 | 19.632 | 19.877 | 19.488 | 18.697 | 15.325 | 9.953 | 4.179 |
| 23 AcNH2⋯uracil | 18.182 | 19.310 | 19.557 | 19.217 | 18.501 | 15.386 | 10.320 | 4.691 |
| π stacking | ||||||||
| 24 benzene⋯benzene (π–π) | 0.105 | 2.016 | 2.725 | 2.813 | 2.607 | 1.578 | 0.515 | 0.072 |
| 25 pyridine⋯pyridine (π–π) | 1.201 | 3.111 | 3.809 | 3.865 | 3.607 | 2.396 | 0.990 | 0.246 |
| 26 uracil⋯uracil (π–π) | 7.976 | 9.640 | 9.976 | 9.590 | 8.848 | 6.217 | 3.196 | 1.034 |
| 27 benzene⋯pyridine (π–π) | 0.602 | 2.636 | 3.358 | 3.414 | 3.159 | 2.012 | 0.752 | 0.155 |
| 28 benzene⋯uracil (π–π) | 3.492 | 5.222 | 5.741 | 5.604 | 5.144 | 3.363 | 1.412 | 0.271 |
| 29 pyridine⋯uracil (π–π) | 3.679 | 6.170 | 6.847 | 6.637 | 6.039 | 3.937 | 1.824 | 0.552 |
| 30 benzene⋯ethene | 0.111 | 1.027 | 1.350 | 1.366 | 1.237 | 0.692 | 0.183 | 0.006 |
| 31 uracil⋯ethene | 2.519 | 3.209 | 3.365 | 3.235 | 2.966 | 2.009 | 0.951 | 0.262 |
| 32 uracil⋯ethyne | 2.708 | 3.507 | 3.702 | 3.571 | 3.281 | 2.232 | 1.054 | 0.278 |
| 33 pyridine⋯ethene | 0.765 | 1.541 | 1.808 | 1.799 | 1.651 | 1.030 | 0.374 | 0.049 |
| London dispersion complexes | ||||||||
| 34 pentane⋯pentane | 2.919 | 3.674 | 3.820 | 3.651 | 3.337 | 2.257 | 1.066 | 0.278 |
| 35 neopentane⋯pentane | 1.913 | 2.542 | 2.651 | 2.518 | 2.282 | 1.516 | 0.711 | 0.191 |
| 36 neopentane⋯neopentane | 1.484 | 1.758 | 1.790 | 1.698 | 1.551 | 1.060 | 0.512 | 0.139 |
| 37 cyclopentane⋯neopentane | 1.669 | 2.299 | 2.443 | 2.354 | 2.161 | 1.482 | 0.716 | 0.194 |
| 38 cyclopentane⋯cyclopentane | 2.301 | 2.894 | 3.038 | 2.893 | 2.621 | 1.731 | 0.804 | 0.211 |
| 39 benzene⋯cyclopentane | 2.143 | 3.243 | 3.584 | 3.492 | 3.193 | 2.094 | 0.918 | 0.199 |
| 40 benzene⋯neopentane | 1.859 | 2.683 | 2.909 | 2.824 | 2.591 | 1.729 | 0.786 | 0.196 |
| 41 uracil⋯pentane | 3.932 | 4.792 | 4.934 | 4.689 | 4.163 | 2.508 | 1.012 | 0.228 |
| 42 uracil⋯cyclopentane | 3.146 | 4.062 | 4.221 | 4.001 | 3.615 | 2.352 | 1.052 | 0.263 |
| 43 uracil⋯neopentane | 2.954 | 3.684 | 3.782 | 3.566 | 3.217 | 2.102 | 0.955 | 0.244 |
| 44 ethene⋯pentane | 1.647 | 1.966 | 1.987 | 1.861 | 1.674 | 1.093 | 0.497 | 0.123 |
| 45 ethyne⋯pentane | 1.045 | 1.563 | 1.698 | 1.638 | 1.490 | 0.966 | 0.421 | 0.098 |
| 46 peptide⋯pentane | 3.814 | 4.264 | 4.298 | 4.096 | 3.775 | 2.662 | 1.212 | 0.298 |
| Mixed influence complexes | ||||||||
| 47 benzene⋯benzene (TS) | 1.657 | 2.603 | 2.898 | 2.853 | 2.643 | 1.804 | 0.856 | 0.237 |
| 48 pyridine⋯pyridine (TS) | 2.547 | 3.336 | 3.566 | 3.489 | 3.255 | 2.328 | 1.206 | 0.384 |
| 49 benzene⋯pyridine (TS) | 2.099 | 3.064 | 3.354 | 3.291 | 3.056 | 2.134 | 1.075 | 0.345 |
| 50 benzene⋯ethyne (CH-π) | 1.847 | 2.636 | 2.865 | 2.800 | 2.593 | 1.802 | 0.903 | 0.277 |
| 51 ethyne⋯ethyne (TS) | 1.203 | 1.464 | 1.516 | 1.456 | 1.341 | 0.934 | 0.463 | 0.135 |
| 52 benzene⋯AcOH (OH-π) | 4.002 | 4.613 | 4.737 | 4.583 | 4.283 | 3.156 | 1.722 | 0.564 |
| 53 benzene⋯AcNH2 (NH-π) | 3.849 | 4.320 | 4.408 | 4.270 | 4.008 | 3.005 | 1.668 | 0.492 |
| 54 benzene⋯water (OH-π) | 2.766 | 3.186 | 3.250 | 3.121 | 2.896 | 2.105 | 1.160 | 0.419 |
| 55 benzene⋯MeOH (OH-π) | 3.403 | 4.014 | 4.168 | 4.057 | 3.804 | 2.813 | 1.542 | 0.526 |
| 56 benzene⋯MeNH2 (NH-π) | 2.457 | 3.051 | 3.209 | 3.109 | 2.861 | 1.960 | 0.951 | 0.267 |
| 57 benzene⋯peptide (NH-π) | 3.756 | 4.978 | 5.313 | 5.183 | 4.825 | 3.458 | 1.837 | 0.632 |
| 58 pyridine⋯pyridine (CH-N) | 2.989 | 3.970 | 4.259 | 3.973 | 3.517 | 2.226 | 1.041 | 0.287 |
| 59 ethyne⋯water (CH-O) | 2.608 | 2.873 | 2.907 | 2.807 | 2.634 | 2.003 | 1.182 | 0.461 |
| 60 ethyne⋯AcOH (OH-π) | 4.364 | 4.844 | 4.908 | 4.727 | 4.414 | 3.263 | 1.776 | 0.559 |
| 61 pentane⋯AcOH | 2.741 | 2.938 | 2.913 | 2.761 | 2.544 | 1.812 | 0.802 | 0.177 |
| 62 pentane⋯AcNH2 | 3.193 | 3.538 | 3.540 | 3.353 | 3.072 | 2.140 | 1.061 | 0.283 |
| 63 benzene⋯AcOH | 2.691 | 3.581 | 3.798 | 3.660 | 3.354 | 2.260 | 1.040 | 0.271 |
| 64 peptide⋯ethene | 2.599 | 2.952 | 2.994 | 2.862 | 2.641 | 1.869 | 0.890 | 0.194 |
| 65 pyridine⋯ethyne | 3.701 | 4.048 | 4.104 | 3.980 | 3.755 | 2.888 | 1.694 | 0.627 |
| 66 MeNH2⋯pyridine | 3.435 | 3.870 | 3.964 | 3.852 | 3.623 | 2.724 | 1.516 | 0.502 |
Several studies have been published regarding the performance of lower ab initio, DFT and double-hybrid DFT methods using S66 and/or S66x8 as a benchmark.15–20 Those results use the originally reported CCSD(T)/CBS calculated interaction energies as the reference. Those were based on extrapolated MP2 limits combined with additive “high-level corrections” (HLCs) – that is, CCSD(T)-MP2 differences – in the meager aug-cc-pVDZ basis set. Hobza and coworkers13 re-evaluated the HLCs for just S66 (which is almost, but not quite, equivalent to the 1.0re ‘slice’ of S66x8): the RMSD (root mean square difference) between the original9 and revised13 sets is 0.10 kcal mol−1, with the individual largest positive difference of 0.32 kcal mol−1 for acetic acid dimer, and largest negative difference of 0.12 kcal mol−1 for benzene-uracil. While this may not sound like a great deal, we shall show below that this is comparable with the accuracy of the best DFT methods available nowadays.
In reference to originally reported S66 and S66x8 database, Grimme and coworkers17 have assessed the performance of several DFT methods, also have tested their own developed dispersion-correction schemes DFT-D3 and DFT-D3BJ. Aragó et al.15 and Yu16 have considered the S66 database to evaluate the efficacy of nonlocal van der Waals corrections for the double-hybrid DFT and spin-component-scaled double-hybrid DFT methods, respectively. The Hobza group18 themselves have evaluated the performance of the MP2 variants for noncovalent interactions of the S66 benchmark set.
Basis set convergence of orbital-based CCSD(T) is quite slow, debilitatingly so in fact, for our purposes. Explicitly correlated21,22 (in practice nowadays, F12)23 approaches offer succor here: for many applications, we can expect a gain of 2–3 angular momentum steps.24–26 Furthermore,26,27 it has been reported that the combination of cc-pVDZ-F12 HLCs (high-level corrections, defined as the CCSD(T)-F12–MP2-F12 difference) with larger-basis MP2-F12 energetics yields excellent results for noncovalent interactions.
In this paper, we are reporting a revision of the reference interaction energies for the S66x8 dataset by means of explicitly correlated MP2 and coupled cluster methods. These interaction energy data will then be used to evaluate the performance of various wavefunction ab initio and density functional, as well as double-hybrid density functionals, which are fifth-rung DFT functionals from one perspective and occupy the twilight zone between wavefunction and DFT methods from another. In most cases, performance of DFT methods for noncovalent interactions is very poor unless dispersion corrections are included: both molecular mechanics-like corrections and nonlocal dispersion functionals will be considered in this work. The issue of BSSE (basis set superposition error) for explicitly correlated methods was considered in an earlier study26 and will be re-examined here for all methods.
Computational details
All calculations were performed on the Faculty of Chemistry cluster at the Weizmann Institute of Science. Most wavefunction-based ab initio calculations were carried out using MOLPRO 2012.1,28 while Turbomole29 6.6 was employed for some MP3-F12 calculations. The density functional calculations were performed using either the Gaussian 09 Rev. D.01 package,30 or primarily for the double hybrids a locally modified version of ORCA.31 The latter was primarily used for the double hybrids, owing to the availability of the RI-MP2 (resolution of the identity MP2) method,32,33 approximation for the MP2-like step.For conventional, orbital-based, ab initio calculations we mostly employed correlation-consistent34–37 basis sets. In general, we combined diffuse-function augmented sets aug-cc-pVnZ (n = D, T, Q, 5) on nonhydrogen atoms with the underlying regular cc-pVnZ basis sets on hydrogen. This practice has been denoted variously in the literature as aug′-cc-pVnZ by Del Bene,38 A′VnZ by ourselves, hanZ (“heavy-augmented”) by the Hobza group,13 heavy-aug-cc-pVnZ by the Sherrill group,39 and (with a calendric pun) jul-cc-pVnZ by Papajak & Truhlar.40
For some of the ab initio calculations, and all of the DFT calculations, we employed the Weigend–Ahlrichs basis sets41 def2-QZVP, def2-TZVPP, def2-TZVP and def2-SVP, as well as the diffuse-function augmented def2-QZVPD basis set.42 In ORCA, we employed the corresponding auxiliary basis sets43 for simultaneously fitting Coulomb and exchange, and the associated RI-MP2 auxiliary basis sets44 for the double-hybrid calculations in ORCA. The Weigend–Ahlrichs family seeks to strike a balance between the requirements of DFT and wavefunction ab initio calculations, and was therefore deemed especially appropriate for the double hybrids.
Single-point explicitly correlated CCSD(T)(F12*), CCSD(T)-F12b and RI-MP2-F12 calculations were carried out using the cc-pVnZ-F12 (where n = D, T, Q) basis sets of Peterson et al.45 in conjunction with the associated auxiliary and complementary auxiliary (CABS) basis sets.46,47 The cc-pVnZ-F12 family was specifically developed with explicitly correlated calculations.
For some calibration calculations, the even larger cc-pV5Z-F12 basis set27 was employed, which effectively corresponds to the basis set limit. Here, we employed a combination of Weigend's aug-cc-pV5Z/JKFIT basis set43 for the Coulomb and exchange elements and Hättig's aug-cc-pwCV5Z/MP2FIT basis set44 for both the RI-MP2 parts and for the CABS.
As recommended in ref. 48, the geminal exponents were set to β = 0.9 for cc-pVDZ-F12 and β = 1.0 for cc-pVTZ-F12 and cc-pVQZ-F12; for cc-pV5Z-F12 we used β = 1.2 as specified in ref. 27. The SCF component was improved through the “CABS correction”.49,50
For the (T) term, which does not benefit from the F12, we considered three different corrections for basis set expansion: (a) the Marchetti–Werner approximation,51,52 denoted CCSD(T*)-F12b, in which the (T) contribution is scaled by the Ecorr[MP2-F12]/Ecorr[MP2] correlation energy ratio; (b) analogues, denoted CCSD(Tb) and CCSD(Tc), in which the respective Ecorr[CCSD-F12b]/Ecorr[CCSD] and Ecorr[CCSD(F12*)]/Ecorr[CCSD] ratios were substituted; and (c) uniform scaling of the (T) contributions, denoted CCSD(Ts)-F12b,27 in which the (T) contributions are multiplied by constant scaling factors of 1.1413 for cc-pVDZ-F12 and 1.0527 for cc-pVTZ-F12 (Table 3 in ref. 27). Options (a) and (b) are not strictly size-consistent, but can be rendered so by applying the dimer Ecorr[MP2-F12]/Ecorr[MP2], Ecorr[CCSD-F12b]/Ecorr[CCSD], viz. Ecorr[CCSD(F12*)]/Ecorr[CCSD] ratios also to the monomers: this is indicated by the notation CCSD(T*sc), CCSD(Tbsc), and CCSD(Tcsc), respectively.
As byproducts of the MP2 and MP2-F12 calculations, we also obtain spin-component-scaled varieties such as SCS-MP2-F12,53–55 SCS(MI)MP2, and S2-MP2.56
The following DFT functionals were considered (grouped by rung on the Perdew57 “Jacob's Ladder”):
• on the second (GGA) rung, BP86,58,59 BLYP,58,60 and PBE;61
• on the third (meta-GGA) rung, TPSS,62 and M06L;63
• on the fourth (occupied-orbital dependent) rung, the hybrid64 functionals B3LYP,60,65,66 B3PW91,65,67 PBE0,68 TPSS0,69,70 APF,71 M06,63 and M06-2X;63 as well as the range-separated hybrids M11,72 CAM-B3LYP,73 LC-ωPBE,74 ωB97X-D3,75 and ωB97X-V.76
• and on the fifth (virtual-orbital dependent) rung, the double hybrids B2PLYP,77 B2GP-PLYP,78 and the spin component scaled double hybrids DSD-PBEP86,79 DSD-PBEPBE,80 and DSD-PBEB9580 methods. The dRPA75 method81 represents approaches with correlation based on the random phase approximation (RPA).82
Further, we have also considered the following types of empirical dispersion corrections (for a review see ref. 83) for DFT energies:
(a) Grimme's 2006 version, denoted by the suffix “-D2” using Grimme's expression
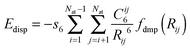 | (1) |
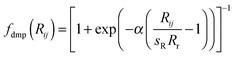 | (2) |
(b) Grimme's DFT-D386,87 version with Becke–Johnson damping, denoted by the suffix “-D3BJ”
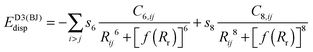 | (3) |
Where parameters were not available from the literature, or from Prof. Grimme's website, we have optimized them ourselves against our best S66x8 reference data, using an adaptation of the BOBYQA (Bound Optimization BY Quadratic Approximation) optimization program of Powell.88
In addition to these molecular mechanics-like corrections, we have also considered the Vydrov–van Voorhis (VV10) “nonlocal” (NL) dispersion functional,89 in which an a posteriori correction is obtained from the electron density. The required short-range attenuation parameter, b, used for various DFT-NL calculations were obtained from ref. 90 for the conventional DFT functionals and optimized in our group for the DSD double hybrids: the various values are listed in Table 1 of ref. 91 These calculations were carried out using its implementation in ORCA.
The values for DSD-PBEP86-NL and B2GP-PLYP-NL given there differ slightly from those obtained earlier16 from calculations uncorrected for basis set superposition error; even with the def2-QZVP basis set, the basis set superposition error in a double hybrid is significant enough that this makes a difference for b of as much as one unit.91
Symmetry-adapted perturbation theory calculations were carried out using the implementation (ref. 39 and references therein) in a prerelease version of PSI 4.92
For the purposes of basis set extrapolation, we employed a two-point expression of the form 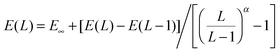 , in which α is taken from Table 2. We wish to point out that all of the various expressions for two-point extrapolation are mathematically equivalent (see, e.g., ref. 93), and have merely converted them to a single form for convenience. Extrapolations of SCF and correlation energies were always performed separately; in the F12 calculations, the SCF component was taken from the largest basis set calculation.
, in which α is taken from Table 2. We wish to point out that all of the various expressions for two-point extrapolation are mathematically equivalent (see, e.g., ref. 93), and have merely converted them to a single form for convenience. Extrapolations of SCF and correlation energies were always performed separately; in the F12 calculations, the SCF component was taken from the largest basis set calculation.
| {T,Q} | {Q,5} | {5,6} | ||
|---|---|---|---|---|
| a Given for comparison; not used in the present work. | ||||
| SCF | 7.6070 | 8.7042 | 9.6897 | Karton and Martin93 |
| SCF alternatea | 5.1507 | 10.3626 | 12.2568 | Schwenke94 |
| MP2 | 2.5313 | 2.7399 | 2.8349 | Hill et al.,48 Table 8 |
| MP2 alternatea | 2.5672 | 2.7028 | 2.7771 | Ranasinghe & Petersson,95 eqn (11) |
| CCSD | 3.0840 | 3.2711 | 3.1937 | Schwenke94 |
| CCSD-MP2 | 2.0926 | 2.2459 | 2.3546 | Ranasinghe & Petersson,95 Fig. 6 |
| (T) | 2.9988 | 3.6018 | 3.2279 | Schwenke94 |
| (T) alternatea | 3.3950 | 3.3723 | 3.3266 | Ranasinghe & Petersson,95 eqn (12) |
| MP2-F12 | 4.3548 | 5.0723 | N/A | {T,Q} Hill et al.,48 Table 9; {Q,5} this work |
| CCSD-F12b | 4.5960 | 6.0642 | N/A | {T,Q} Hill et al.,48 Table 10; {Q,5} this work |
| (T) post F12 | 2.8950 | {T,Q} Hill et al.,48 Table 11 | ||
The cc-pV{Q,5}Z-F12 extrapolation exponents in the present work were obtained by following, to the letter, the optimization procedure for the cc-pV{T,Q}Z-F12 exponents detailed in ref. 48.
Calibration of the reference method
Choice of the MP2-F12 reference level
For the smaller, earlier, S22 dataset of noncovalent interactions, a revised set of benchmark data was reported by Marshall, Burns, and Sherrill (MBS).12 Aside from total CCSD(T) limit interaction energies given in the paper itself, HLCs (high-level corrections) are given in Table S1 of that paper's ESI, and MP2 limits were extracted as the difference. These correspond to counterpoise-corrected AV{Q,5}Z basis set extrapolation.Thus, we are able to consider performance for the MP2 basis set limit and for the HLC in isolation.
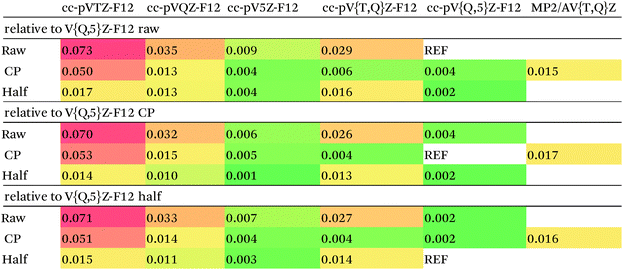
Our counterpoise-corrected DF-MP2-F12/cc-pVQZ-F12 interaction energies differ from the MBS estimated MP2 limits by just 0.01 kcal mol−1. This increases to 0.02 kcal mol−1 upon cc-pV{T,Q}Z-F12 extrapolation: for the corresponding raw and half-counterpoise values, RMSDs are 0.053 and 0.036 kcal mol−1, respectively.
Calculating DF-MP2-F12/cc-pVTZ-F12 and DF-MP2-F12/cc-pVQZ-F12 energies for the entire S66x8 set proved technically quite feasible, both with and without counterpoise correction. We may conclude that the MP2 component is not the accuracy-limiting factor.
In previous studies25,27 where comparison with the even larger cc-pV5Z-F12 basis set27 was possible, it was concluded that half-counterpoise came closest to the basis set limit.
With considerable effort, we were able to obtain DF-MP2-F12/cc-pV5Z-F12 interaction energies for the 1.0re slice of S66x8 (which has slightly different geometries than the S66 set – particularly for π stacks). The RMS counterpoise correction at that level is just 0.010 kcal mol−1. Between raw and counterpoise cc-pV{Q,5}Z-F12 extrapolated values – which should ideally be identical – the RMS difference drops even further to 0.004 kcal mol−1. (As noted in the Methods section, the extrapolation exponent in Table 2, 5.0723, was obtained in the present work, and the MP2-F12 correlation component was extrapolated in isolation and combined with the largest basis set HF + CABS component. For the smaller cc-pV{T,Q}Z-F12 sequence, the extrapolation exponent 4.3548 was taken from ref. 48, cf.Table 2.)
Error statistics for smaller basis sets can be found in Table 3. The counterpoise-corrected {T,Q}-F12 values deviate from the corresponding {Q,5}-F12 limits by just 0.004 kcal mol−1 RMS; for half-counterpoise, this increases to 0.013 kcal mol−1 relative to counterpoise {Q,5}-F12, or 0.014 kcal mol−1 relative to half-counterpoise {Q,5}-F12 limits. If we were to dispense with extrapolation entirely, half-counterpoise cc-pVQZ-F12 appears to have a slight edge over full counterpoise, and a definite one over the raw values: in fact, half-counterpoise cc-pVTZ-F12 is found to be preferred over raw cc-pVQZ-F12.
We finally chose full-counterpoise MP2-F12/cc-pV{T,Q}Z-F12 extrapolation as the MP2 component for our benchmark data. Based on the statistics given in Table 3, we conservatively estimate the accuracy of our MP2 limits to be better than 0.01 kcal mol−1.
For comparison, the conventional, counterpoise-corrected MP2/aug-cc-pV{T,Q}Z values used by the Hobza group as the MP2 component of the S66x8 benchmark data in the Benchmark Energy and Geometry Database (http://www.begdb.com)14 were recalculated in the present work. They differ from our best reference values by 0.017 kcal mol−1 RMS.
Choice of the high-level correction, i.e., CCSD(T)-MP2 contribution
The crucial factor affecting performance will be the choice of approximation to the (T) connected triple excitations (see Methods section). RMSDs for the HLCs of the S22 set are presented in Table 4.
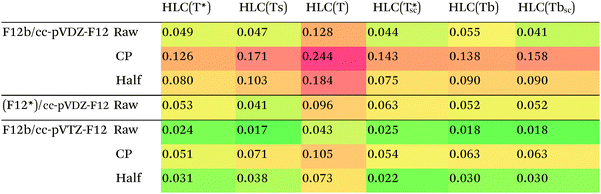
For the subset, we find that HLC(Ts)/cc-pVTZ-F12 has an RMSD of less than 0.02 kcal mol−1 from the MBS reference data. With the said basis set, there is little to choose between HLC(Ts), HLC(Tbsc), and HLC(T*sc) – or the non-size-consistent variant HLC(T*), for that matter – as the difference between the RMSDs is less than the presumed uncertainty in the reference data.
Counterpoise correction on the HLC appears to be unhelpful, which is useful considering its computational cost for larger systems. (Counterpoise calculations typically require disabling symmetry.)
For the smaller cc-pVDZ-F12 basis sets, the raw HLCs are definitely preferred over counterpoise and half-counterpoise. Among the size-consistent options, (Tbsc) and (Ts) seem to have an edge over (T*sc), with there again being little to choose between (Tbsc) and (Ts). In our experience,27 with cc-pVTZ-F12 and larger basis sets, CCSD-F12b and the more rigorous CCSD(F12*),96 a.k.a. CCSD-F12c, method yield nearly identical results, but with the cc-pVDZ-F12 basis set, CCSD(F12*) may offer an edge for some applications.25 For the S22 set, we cannot distinguish between the F12b and (F12*) approaches based on the RMSD for HLC alone. We do note, however, that the CCSD-MP2 parts of (F12*)/cc-pVDZ-F12 are considerably closer (RMSD = 0.019 kcal mol−1) to the available F12b/cc-pVTZ-F12 values than the F12b/cc-pVDZ-F12 counterparts (RMSD = 0.044 kcal mol−1).
For the entire S22 set, conventionally computed HLCs with different basis sets are available from the ESI of ref. 12 and 97. The lowest RMSD from the MBS reference data, 0.04 kcal mol−1, is found for counterpoise-corrected CCSD(T)/aug-cc-pV{D,T}Z.
Let us consider the CCSD-MP2 differences with the cc-pVDZ-F12 basis set in isolation. Here we do not have to contend with the different (T) options: our two available choices are CCSD(F12*)-MP2-F12 and CCSD-F12b-MP2-F12. The most significant differences between them are seen for systems with multiple hydrogen bonds, such as 17 (uracil dimer Watson–Crick), 20 (acetic acid dimer), 21 (acetamide dimer), 22 (acetic acid-uracil), and 23 (acetamide-uracil), for each of which the difference exceeds 0.100 kcal mol−1 at equilibrium or compressed geometries. As expected, these differences are greatly reduced for stretched geometries and effectively dwindle to nothing at 2.0re.
(F12*)-F12b differences are smaller, but still some what significant, for π stacks and mixed-influence complexes, but effectively negligible for London complexes.
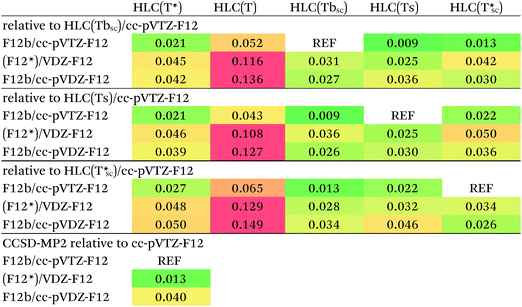
Which is more correct? At great computational expense and following multiple failures due to Linux kernel tuning issues, we were able to perform CCSD(T)-F12b/cc-pVTZ-F12 calculations for a subset of 58 out of 66 systems at the 1.0re geometries. The subset consists of all systems except the London complexes 35 and 37–43. The CCSD-MP2 differences in the dissociation energies, obtained as a by-product, should be quite close to the basis set limit. The [CCSD(F12*)-MP2-F12]/cc-pVDZ-F12 agrees with those to 0.013 kcal mol−1 RMS (Table 5), compared to 0.040 kcal mol−1 for [CCSD-F12b-MP2-F12]/cc-pVDZ-F12. We have hence decided to err on the side of rigor, and to favor CCSD(F12*) over CCSD-F12b, as we have at present no realistic prospect of carrying out CCSD-F12b/cc-pVTZ-F12 calculations for the entire S66x8 dataset.
Performance of different (T) scaling procedures for the HLCs of the 58-system subset has been compared in Table 5. First, we note that they all yield very similar values for the cc-pVTZ-F12 basis set: HLC(Tbsc) differs from HLC(Ts) by less than 0.01 kcal mol−1 RMS, and by just 0.013 kcal mol−1 from HLC(T*sc). As generally HLC(Ts) < HLC(Tbsc) < HLC(T*sc), we have somewhat arbitrarily selected the middle values HLC(Tbsc)/cc-pVTZ-F12 for comparison, but another choice would not have led to qualitatively different conclusions.
Second, HLC(Tbsc)/cc-pVDZ-F12, HLC(Tcsc)/cc-pVDZ-F12, and (Ts) from (F12*)/cc-pVDZ-F12 or F12b/cc-pVDZ-F12 all agree with those values to 0.025–0.042 kcal mol−1 RMS, with a possible slight advantage for (F12*)/cc-pVDZ-F12 over F12b/cc-pVDZ-F12. The RMSDs of HLC(Ts)(F12*)/cc-pVDZ-F12 and HLC(Tcsc)(F12*)/cc-pVDZ-F12 however are essentially identical, hence no meaningful choice between them can be made from the numbers alone. On the other hand, while (Ts) contains a single empirical parameter (the ‘one size fits all’ scaling factor), (Tbsc) and (Tcsc) contain none at all and instead elicit everything from ab initio calculations for the actual system at hand. For want of a realistic option to use larger basis sets, we therefore decided on HLC(Tcsc)/cc-pVDZ-F12, i.e., with the triples scaled by the Ecorr[CCSD(F12*)]/Ecorr[CCSD] ratio, as our final choice for the reference data. For the 58-system subset, the HLC(Tcsc)/cc-pVDZ-F12 combination agrees to 0.031 kcal mol−1 RMS with the cc-pVTZ-F12 data, compared to 0.09 kcal mol−1 for the counterpoised conventional [CCSD(T)-MP2]/aug-cc-pVDZ HLCs used in the original S66x8 paper, which we reconstructed by recalculating their counterpoised MP2/aug-cc-pV{T,Q}Z components and subtracting from the total S66x8 values.
Counterpoise corrections for lower-level methods
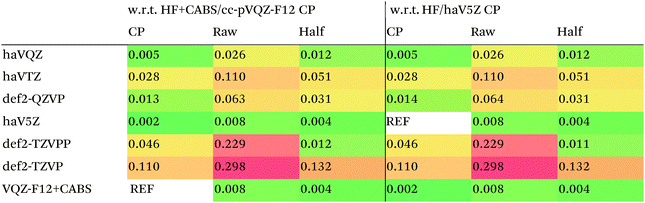
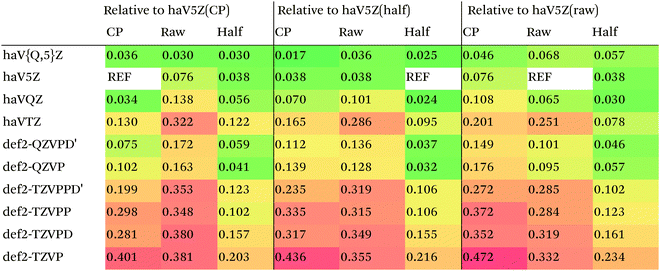
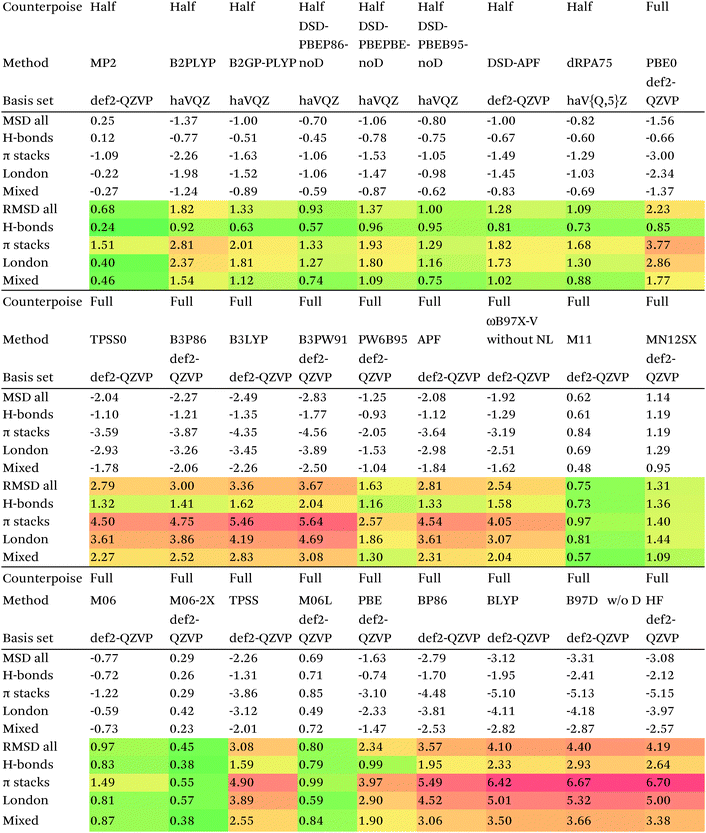
We then are faced with not only the choice of basis set for the lower-level methods, but also the choice of counterpoise correction. It is fairly well-known (e.g., ref. 98) that, for noncovalent interactions, uncorrected dissociation energies approach the basis set limit from above, and counterpoise-corrected ones from below: the half–half counterpoise method, i.e., the average of raw and counterpoise interaction energies, then immediately suggests itself. In ref. 99 it was shown that half-counterpoise generally comes closest to the basis set limit for orbital-based wavefunction ab initio calculations. In ref. 26 we showed that this is also generally the case for explicitly correlated methods, except perhaps for large basis sets like cc-pVQZ-F12 and especially cc-pV5Z-F12, where full counterpoise may be more appropriate but the counterpoise corrections in any case become insignificant.At the HF level, things are rather different. For def2-TZVPP, half-counterpoise appears to have an edge over full counterpoise, but for all larger basis sets full counterpoise “carries the day”, with an RMSD as small as 0.005 kcal mol−1 for the haVQZ basis set, and 0.013 kcal mol−1 for def2-QZVP (Table 6). It hardly matters whether one uses the CABS-corrected HF/cc-pVQZ-F12 or the orbital HF/haV5Z as references: the counterpoise-corrected values for both differ by no more than 0.002 kcal mol−1 RMS.
As can be seen in Table 6, HF/def2-QZVP with full counterpoise is quite close to the basis set limit, HF/haVQZ even closer.
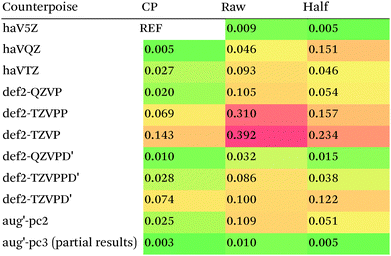
What about DFT functionals below rung five? We considered the example of PBE0. Somewhat arbitrarily, we chose haV5Z with full counterpoise correction as the reference: the difference with half-counterpoise in the same basis set amounts to just 0.005 kcal mol−1 RMSD (Table 7). For essentially all basis sets considered, full counterpoise is clearly the best of the three options, except that for def2-QZVPD′ the gap with half-counterpoise is quite narrow. At any rate, the RMSD of 0.02 kcal mol−1 for def2-QZVP is considered small enough that we can use it for benchmark purposes.
Summing up: for Hartree–Fock and DFT functionals, we will use full counterpoise and a basis of def2-QZVP or better quality.
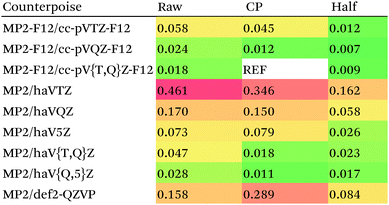
For MP2, it appears even haVQZ is not adequate to reach the basis set limit, but haV{T,Q}Z extrapolation with full counterpoise does succeed. Half-counterpoise haV5Z comes reasonably close without extrapolation, as does haV{Q,5}Z without counterpoise. In contrast, with the explicitly correlated approach, even MP2-F12/cc-pVTZ-F12 is already within 0.01 kcal mol−1 RMS if half-counterpoise is applied (Table 8). At any rate, as reported by Burns et al.99 for conventional correlated calculations and our group26 for explicitly correlated ones, half-counterpoise is unambiguously preferred.
This finally leaves the double hybrids, where one might expect behavior to be intermediate between MP2 and PBE0. For basis sets def2-QZVP and larger, we can expect the Kohn–Sham part to be converged, which leaves the MP2-like component as the dominant factor in basis set convergence for double hybrids.
Based on the results given in Table 9, we have selected half-counterpoise with the haVQZ basis set as our basis set of choice, with def2-QZVP with half-counterpoise as a fallback. With smaller Weigend–Ahlrichs41 basis sets, half-counterpoise is again unequivocally preferred, justifying the design decisions taken in ref. 79, 80 and 84.
Results and discussion
Wavefunction ab initio results
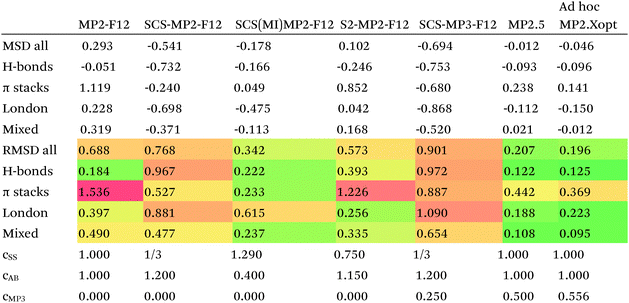
Since so much work on weak interactions has historically focused on hydrogen bonds (and, to a lesser extent, London dispersion), it is received wisdom in much of the quantum chemical community that MP2 is a “high-level ab initio” treatment for noncovalent interactions. In fact, for the S66x8 dataset with the cc-pVQZ-F12 basis set (half counterpoise), the RMSD is a somewhat disappointing 0.69 kcal mol−1 (Table 10). Some things become clearer if we break the results down by categories: hydrogen bonds (systems 1–23), π stacks (systems 24–33), London dispersion complexes (systems 34–46), and mixed-influence (systems 47–66). We then see that MP2 has an excellent RMSD = 0.18 kcal mol−1 for hydrogen bonds, a tolerable 0.40 kcal mol−1 for London complexes, and an appalling 1.54 kcal mol−1 for π stacks. It has been known for some time (e.g., ref. 100 and 101) that π–π interactions at the MP2 level are severely overestimated due to the dispersion component of the 2nd-order energy effectively corresponding to uncoupled Hartree–Fock dispersion (ref. 102; see also ref. 103).SCS-MP2 mostly remedies the issue for π stacks, at the expense of degraded performance for London complexes and especially hydrogen bonds. SCS(MI)MP2, optimized for weak interactions, yields fairly poor results for London complexes, but very good to excellent results for the rest of S66x8, at the expense of general thermochemistry. The quasi-first principles S2-MP256 trades off some of the great performance for hydrogen bonds for better results in the other categories, still yielding unacceptable pi complexes. Similar to a wrinkle in a carpet larger than the room, the error of parametrized MP2 can be moved from one category to another, but never fully removed. Ad hoc fitting of SCS-MP2 yielded c2ab = 0.339, c2ss = 1.429, RMSD = 0.285 kcal mol−1, somewhat better than the similar SCS(MI)MP2.
Moving on to higher-cost methods, third-order corrections E3 were evaluated in MP3(F12*)/cc-pVDZ-F12 calculations using Turbomole and added in to half-counterpoise MP2-F12/cc-pVQZ-F12 and spin-component-scaled variants thereof. SCS-MP3 in fact is found to perform worse than SCS-MP2. MP2.5 on the other hand,104 – averaging between MP2 and MP3, which typically err on opposite sides of the true number – yields a rather pleasing RMSD = 0.21 kcal mol−1, with especially outstanding performance for H-bonds and mixed-influence complexes, while π stacks are still acceptable at 0.44 kcal mol−1. Ad hoc refitting of c3 yields a very modest further improvement in RMSD, while additionally refitting c2ss and c2ab is found to be statistically insignificant.
As an aside, Hesselmann proposed105 the MP2C method, in which the dispersion part was removed from MP2 and replaced by its TDDFT counterpart. Basis set limit extrapolated MP2C values for the S66 set (i.e., just the equilibrium geometry slice of S66x8) have been reported in ref. 106: the RMSD from their reference data was given as 0.13 kcal mol−1.
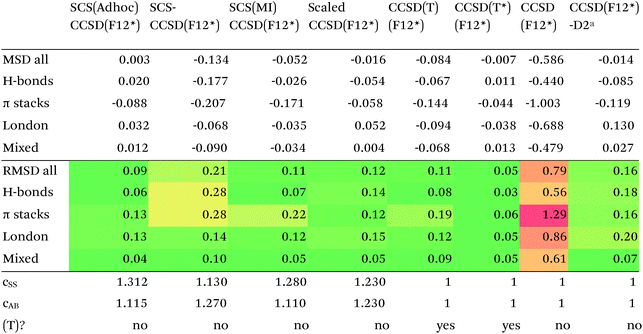
Turning now to CCSD(F12*), we find that it actually performs worse than MP2-F12. SCS-CCSD(F12*) greatly improves things, and SCS(MI)CCSD(F12*) especially so (Table 11). Ad hoc minimization of RMSD with respect to css and cab yields coefficients fairly close to SCS(MI)CCSD(F12*), yet simply scaling the CCSD(F12*) correlation energy by a factor of 1.23 seems to work nearly as well, as does adding a Grimme D2 dispersion correction with s6 = 0.225 (see discussion below together with dRPA75).
| Errors relative to CCSD(Tcsc)-F12c/cc-pVDZ-F12. cc-pVDZ-F12 basis set throughout.a s6 = 0.225. |
|---|
|
At the request of a reviewer, we consider the effect of the new data on the intermolecular separations. In the original S66 paper, the intermolecular separations were obtained by quartic interpolation on the {0.90, 0.95, 1.00, 1.05, 1.10}re data points in S66x8 for each complex. We have repeated this procedure for both the original S66x8 data obtained from www.http://begdb.com and for the present revised data in Table 1. The minimum-energy intermolecular separations from both datasets are compared in the master data spreadsheet in the ESI,† while the Cartesian coordinates corresponding to them are also made available in .xyz format in the ESI.†
By and large, the higher level of theory in the present data (particularly for the HLC) does not translate into dramatic geometry changes: the separations change by −0.00074re on average (the revised geometries being slightly shorter than the originals), 0.00246re mean absolute difference, and 0.00285re RMS difference. The largest differences are +0.0066re for benzene⋯ethene (system 30) and −0.0063re for pyridine⋯ethyne (system 65). Generally speaking, the revised data lead to stretching for the pi stacks and contraction for the hydrogen bonds, with mixed behavior seen for the remaining systems.
How consequential are these geometry differences for the total energy? We evaluated DF-SCS(MI)MP2-F12/cc-pVTZ-F12 energies at both sets of geometries: the RMS difference between the total energies over the S66 systems was found to be just 0.004 kcal mol−1. This is immaterial for all but the highest-accuracy work – and then one would wish to optimize monomer geometries at a higher level as well.
Performance of density functional methods
For straight MP2 this drops to 0.68 kcal mol−1, which would be a lot better if it weren't for the poor performance for π stack (RMSD = 1.5 kcal mol−1). MP2 actually holds its own quite well for H-bonds (0.24 kcal mol−1) and reasonably well for London and mixed complexes.
By far the best performer without any dispersion correction is M06-2X, at RMSD = 0.43 kcal mol−1. M06 has over twice that error (0.95 kcal mol−1). At 0.74 and 1.30 kcal mol−1, respectively, M11 and M12 do not offer relief either.
Simple double hybrids perform fairly poorly, RMSD = 1.82 kcal mol−1 for B2PLYP and 1.33 kcal mol−1 for B2GP-PLYP. The DSD-noD functionals are in the 0.9–1.4 kcal mol−1 range, and thus arguably “do not earn their keep”, since they are outperformed by straight MP2.
Very recently, Kallay and coworkers proposed81 the dRPA75 functional, in which the correlation is obtained from a dRPA (direct random phase approximation,107 a.k.a. drCCD or direct ring coupled cluster82,108) with all doubles calculation in a set of orbitals involving a mixture of 75% Hartree–Fock-like exchange and 25% PBE exchange. Using the haVTZ basis set, RMSD without counterpoise correction is a deceptively low 0.37 kcal mol−1; this rises to 0.77 kcal mol−1 for def2-QZVP, 0.71 kcal mol−1 for haVQZ, 0.89 kcal mol−1 for haV5Z, and 1.09 kcal mol−1 at the haV{Q,5}Z extrapolated limit. At the basis set limit, raw and counterpoise-corrected values agree tolerably well, yet one manifestly sees very slow basis set convergence akin to a conventional wavefunction method.
| a Obtained in the present work by minimization of S66x8 RMSD. |
|---|
|
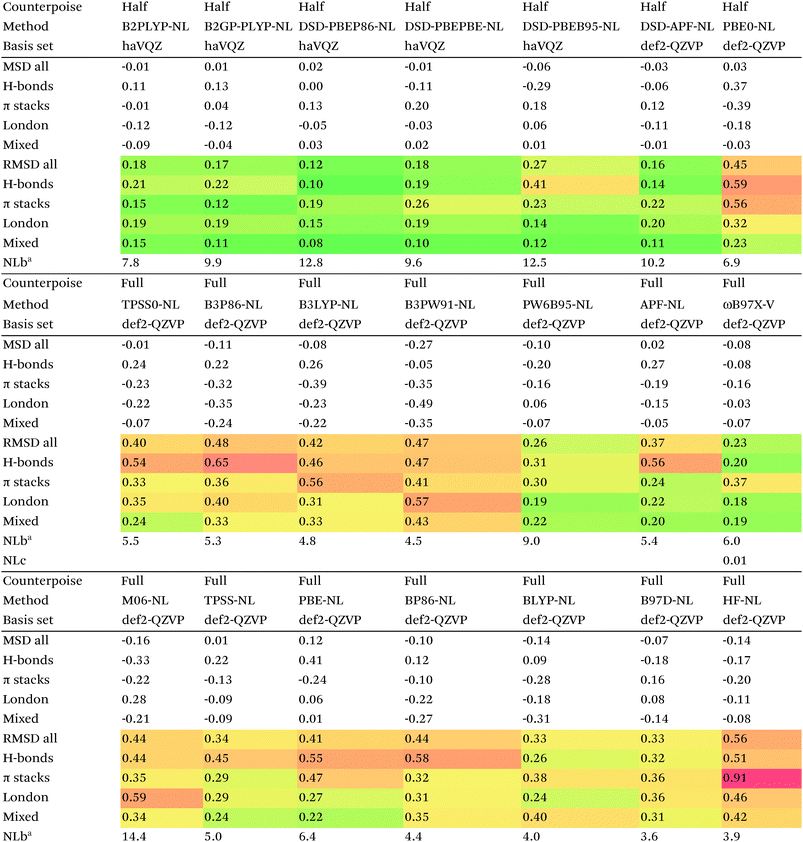
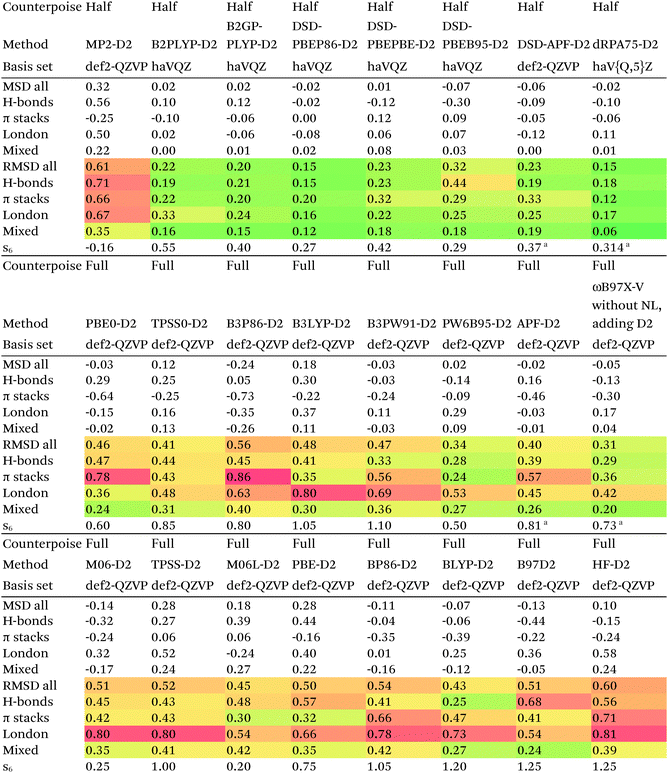
Of the simple double hybrids, both B2PLYP-D2 and B2GP-PLYP-D2 exhibit excellent performances (RMSD = 0.22 and 0.20 kcal mol−1, respectively, even including π stack dimers). DSD-PBEP86-D2 yields the best result of all the D2-corrected functionals, at RMSD = 0.15 kcal mol−1.
The most significant improvement is seen for dRPA75. At the half-counterpoise haV{Q,5}Z limit, adding a D2 correction with s6 = 0.314 leads to RMSD = 0.15 kcal mol−1, which changes the performance of dRPA75 from mediocre to best of class. A partial rationale is offered by considering the statistical correlation between (Tb) and the D2 correction: for the entire S66x8 set, R2 = 0.92. This is perhaps not surprising, from an SAPT perspective, in view of the importance of fourth-order (T) in the correction to the dispersion energy. dRPA can, after all, be seen as an approximation to CCSD. By way of further illustration, we considered adding D2 corrections to CCSD(F12*) itself, which leads to s6 = 0.225 and RMSD = 0.156 kcal mol−1, not dissimilar to dRPA75-D2.
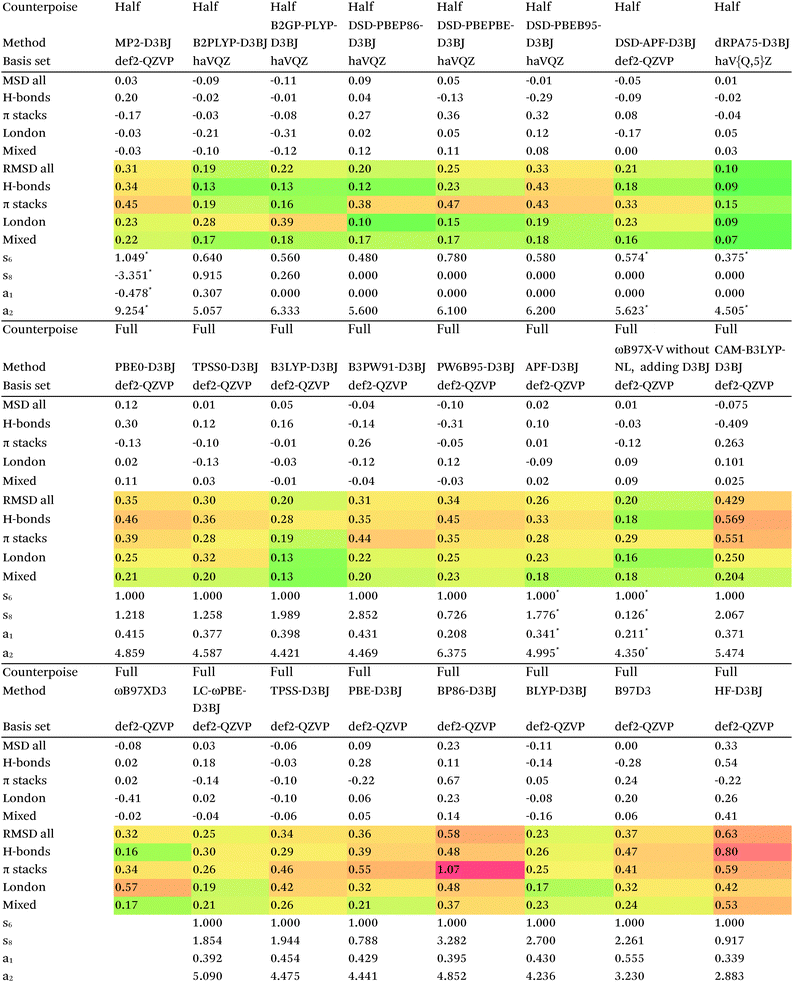
Switching from D2 to the more sophisticated D3BJ empirical correction improves statistics for virtually all the GGAs, meta-GGAs, and hybrids. (The two exceptions are straight HF – which could be regarded as a “hybrid” with 100% exact exchange and null correlation – and PW6B95.) For BLYP-D3BJ, for instance, an amazingly low RMSD = 0.23 kcal mol−1 is obtained, while B3LYP-D3BJ yields essentially the same performance to within the uncertainty of the reference dataset (Table 14). Several other functionals can attain values around 0.3 kcal mol−1, such as TPSS0-D3BJ and B3PW91-D3BJ.
| D3BJ parameters taken from http://www.thch.uni-bonn.de/tc/downloads/DFT-D3/functionalsbj.html except where indicated by (*), which were optimized in this work, and for DSD double hybrids, taken from ref. 80. |
|---|
|
The APF functional71 (RMSD = 0.26 kcal mol−1 for APF-D3BJ) was designed to be more or less “dispersion-free”: specifically, it consists of a linear combination of B3PW91 and PBE0 chosen such that the dissociation curve of Ne2 (a paradigmatically dispersion-bound system) is as close to the repulsive Hartree–Fock results as possible. D3BJ parameters were fitted in this work: noteworthy is the large positive s8 coefficient. The latter corresponds to an additional correction in the medium-range region. For perspective, we also fitted D3BJ parameters for straight MP2, and found a large negative s8 = −3.35, corresponding to RMSD = 0.31 kcal mol−1. For additional perspective, we fitted D3BJ parameters for dRPA75, and found that RMSD dropped to 0.10 kcal mol−1 with both a1 and s8 constrained to zero. No statistically significant change was seen when relaxing the s8 = 0 constraint. In other words, while dRPA75 does not recover all long-range dispersion, it appears to recover the intermediate range.
Exploring this point a little further, we considered fitting M06-D3BJ. No stable fit could be obtained unless the constraints a1 = s8 = 0 were applied, in which case RMSD dropped to 0.40 kcal mol−1. It thus appears that the main benefit of M06 over conventional hybrid GGAs is likewise in the intermediate-distance region (vide supra).
What about the double hybrids? While for B2PLYP-D3BJ, s8 = 0.91 and thus quite nontrivial, for B2GP-PLYP-D3BJ s8 = 0.26 and a1 = 0.00, corresponding to RMSD = 0.23 kcal mol−1. For DSD-PBEP86-D3BJ, on the other hand, a stable fit required setting s8 = a1 = 0.00: this pattern repeats itself across all the DSD double hybrids. Effectively, this means that, for weak interactions, (a) the principal benefit of double hybrids and RPA correlation alike is correction in the intermediate distance region; (b) since straight MP2 overcorrects in that region, this needs to be tempered by either including higher-order correlation (as in dRPA75 or MP2.5) or by throttling the MP2 correlation term (as happens in double hybrids). We attempted replacing the dRPA correlation term in dRPA75 by an MP2-like term, and found qualitatively the same behavior as for ordinary MP2.
Overall, for the double hybrids, improvements from using D3BJ instead of D2 are marginal at best, while DSD-PBEP86-D2 even outperforms DSD-PBEP86-D3BJ. We note that, aside from the s8 term being effectively absent (or not fittable at a statistically significant level), a large part of dispersion is already covered by the MP2-like terms.
We optimized a new DSD double hybrid based on the APF “dispersion-free” hybrid, with the idea that this would eliminate some double-counting. It yields a respectable RMSD = 0.23 kcal mol−1, which is however no improvement over DSD-PBEP86-NL.
dRPA75-D3BJ, with s6 = 0.3754, a2 = 4.5048, a1 = s8 = 0, improves further (to 0.10 kcal mol−1) on the already outstanding performance of dRPA75-D2.
In a very recent benchmark study on the conformer energies of the proteinogenic amino acids, we noted excellent performance of the uncorrected dRPA75/def2-QZVP method, RMSD = 0.21 kcal mol−1 (Boltzmann-weighted, TB = 1000 K) or 0.37 kcal mol−1 (unit weights). We re-evaluated these statistics using dRPA75-D2/def2-QZVP and dRPA75-D3BJ/def2-QZVP. With the D2 dispersion correction, statistics for the conformer set actually were degraded to 0.42 (Boltzmann) and 0.70 (unit weights) kcal mol−1. The D3BJ correction, on the contrary, improved the statistics to 0.14 (Boltzmann) and 0.32 (unit weights) kcal mol−1, comparable to the best performers in that paper. It was previously shown (e.g., see ref. 109 and 110 for alkanes) that midrange dispersion interactions are very important in conformer equilibria, and that D2 is often more of a hindrance than a help for these properties owing to the form of the cutoff function; D3BJ, on the other hand, does not exhibit this problem.110 As we have shown earlier in the manuscript that unassisted dRPA75 already works well in the medium distance range, adding D2 for conformer equilibria amounts to “fixing what ain't broke”.
Concerning range-separated double hybrids, we note that Head-Gordon's recent “survival of the fittest/most transferable” ωB97X-V (0.23 kcal mol−1), which involves NL as its dispersion component, is actually slightly improved by replacing NL with a custom-fitted D3BJ. This may prove useful for codes in which no implementation of NL is available. While CAM-B3LYP-D3BJ does considerably worse than B3LYP-D3BJ, LC-ωPBE-D3BJ well outperforms both PBE-D3BJ and PBE0-D3BJ.
We now turn to the Vydrov–Van Voorhis89 “nonlocal” (NL) dispersion correction. This correction effectively only has a single adjustable parameter NLb, which governs short-range attenuation. There are no atomic parameters, as this information is extracted a posteriori from the calculated electron density.
For many functionals such as PBE, PBE0, TPSS0, BLYP, B3LYP, and B3PW91, NL actually performs worse than D3BJ, while for TPSS the two appear to be of the same quality. For BP86, B97D, HF, and PW6B95, it clearly is superior to D3BJ, besides having the obvious advantage that no atomic parameters are required at all (Table 15).
Among the simple double hybrids, NL does marginally better than D2 and D3BJ for B2GP-PLYP (RMSD = 0.17 kcal mol−1).
Yu16 proposed adding the correction to spin-component scaled double hybrids. His optimization procedure neglects the quite considerable BSSE in the S66 series: in the framework of our recent study on amino acid conformers91 we reoptimized his proposed restriction parameters: these are the ones used in the present work.
In relative terms, it may well be the DSD double hybrids that benefit most. For DSD-PBEP86-NL, RMSD drops to just 0.12 kcal mol−1, coupled with the excellent performance of DSD-PBEP86 for thermochemical and kinetic properties79,80 as well as for vibrational frequencies.111 But also for DSD-PBEPBE-NL (0.18 kcal mol−1), DSD-APF-NL (0.16 kcal mol−1), and to a lesser extent for DSD-PBEhB95-NL (0.27 kcal mol−1) significant improvements over the corresponding D3BJ functionals were seen. The π-stacking complexes benefit most, their RMS errors typically being about halved.
The DSD-APF-NL functional, which yielded the second best performance, was actually created by simply applying 0.411*DSD-PBE+(1-0.411)*DSD-BPW91, each with parameters taken from ref. 80
Functionals of the form DSD-XC-NL not only appear to have excellent performance, but they come with two additional advantages: (1) there is no need for an elaborate set of atomic dispersion parameters; (2) the method is no longer open to the criticism that it involves “adulterating” an electronic structure method with Lennard-Jones type corrections.
The advantages of NL for double hybrids are not evident if only equilibrium values (i.e., S66) are considered: it is at compressed geometries that they yield their greatest benefits.
The original D3BJ parameters for the DSD functionals were optimized using half-counterpoise with the relatively small def2-TZVP basis set, mostly from the S22 and Grubbs catalyst benchmarks. We considered performance when refitting against the present S66x8 data. For DSD-PBEP86-D3BJrefit, we obtain RMSD = 0.158 kcal mol−1 for s6 = 0.468 and a2 = 5.857, which closes some of the gap with DSD-PBEP86-NL but not all of it. For DSD-PBEPBE-D3BJ, RMSD = 0.193 kcal mol−1 is statistically indistinguishable from the DSD-PBEPBE-NL number; the revised parameters are s6 = 0.518 and a2 = 4.846. For DSD-PBEhB95-D3BJ, refitting yields s6 = 0.263 and a somewhat anomalous a2 = 3.360, with RMSD = 0.204 kcal mol−1 actually better than DSD-PBEhB95-NL.
How does the substitution of NL for D3BJ affect performance for other test sets, such as barrier heights, atomization energies, and the like? We considered the six training sets used in parametrizing the original functionals. The results can briefly be summarized as implying that D3BJ and NL yield results of similar quality considering the residual uncertainty in the reference values. It therefore appears to pass the “above all, do no harm” test.
On the other hand, D3BJ is available in several additional codes beyond ORCA, and derivatives are trivial to implement (unlike for NL).
SAPT results and a proposed new noncovalent character index
From a SAPT perspective, the SCF component of the interaction energy can be decomposed as follows:39,112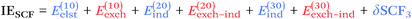 | (4) |
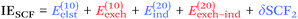 | (5) |
The second-order component can be decomposed as:39,112
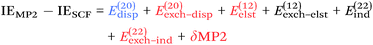 | (6) |
For the third-order terms, eqn (6:35) of Chalasinski and Szczesniak102 implies that
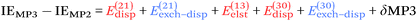 | (7) |
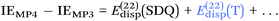 | (8) |
At the two least expensive levels of SAPT, SAPT0 and SAPT2, the interaction energy can be decomposed as:
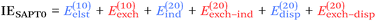 | (9) |
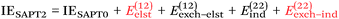 | (10) |
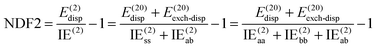 | (11) |
NDF2 can be computed from an MP2 and an SAPT0 calculation in the same basis set. However, let us now consider the following variable that just requires an MP2 or RI-MP2 calculation:
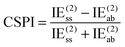 | (12) |
Over the S66x8 set, with the haVTZ basis set, we found that NDF2 and CSPI (correlation spin polarization index) have a squared correlation coefficient of no less than 0.991 (see Table S1 in ESI†). We may therefore safely conclude that they contain the same chemical information.
For a system where the interaction energy is dominated by E(20)disp, CSPI will approach zero; in systems where non-dispersion factors play a role in the correlation part of the interaction energy, CSPI will depart from zero. However, for highly stretched systems, absolute values of the same-spin and opposite component may be so small that CSPI suddenly flips sign. In order to avoid this problem, we will instead consider
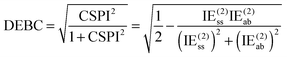 | (13) |
However, at very long distance in systems dominated by nondispersion effects (e.g., acetic acid dimer), IE(2) will be negligible compared to IESCF and hence DEBC may not be very informative anymore. We will instead consider two additional indices. One is the fraction of the interaction energy accounted for at the Hartree–Fock level
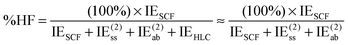 | (14) |
For systems dominated by electrostatic effects (e.g., H2O dimer at long distance), %HF will approach 100%; for systems where the primary HF-level component is exchange repulsion (e.g. alkane dimers), %HF will be negative.
A second index is the fraction of the interaction energy accounted for by post-MP2 correlation effects:
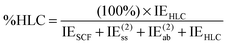 | (15) |
This index will typically be low for systems dominated by electrostatic effects. For systems dominated by London dispersion (e.g., alkane dimers), it is empirically found to be small as well, since an error compensation appears to take place between neglect of (attractive) connected triple excitations and neglect of (typically repulsive) third- and fourth-order double excitations. In the S66x8 set, large values of %HLC are seen for π-stacking interactions.
In short, by consideration of three indices derived from the calculated interaction energy, one can infer the dominant interaction type in a system even without resorting to SAPT calculations.
A complete tabulation, complete with the Hobza disp/elec ratio9 of values for all the S66x8 systems is given in the ESI.† In Table 16, we present data for some representative systems.
| NDF2 | CSPI | DEBC | Hobza ratio disp/(elec + ind) | %HF | %HLC | IE (kcal mol−1) | |
|---|---|---|---|---|---|---|---|
| H-bond⋯(CH3COOH)2 | |||||||
| 20⋯0.90re | 2.656 | 1.046 | 0.723 | 0.166 | 80.5 | −2.0 | −17.970 |
| 20⋯0.95re | 2.515 | 1.037 | 0.720 | 0.170 | 85.0 | −2.2 | −19.228 |
| 20⋯1.00re | 2.440 | 1.045 | 0.723 | 0.173 | 87.9 | −2.4 | −19.469 |
| 20⋯1.05re | 2.417 | 1.068 | 0.730 | 0.176 | 90.1 | −2.6 | −19.049 |
| 20⋯1.10re | 2.439 | 1.105 | 0.742 | 0.178 | 91.8 | −2.8 | −18.219 |
| 20⋯1.25re | 2.760 | 1.322 | 0.798 | 0.180 | 95.4 | −3.1 | −14.736 |
| 20⋯1.50re | 4.841 | 2.467 | 0.927 | 0.167 | 99.3 | −3.2 | −9.289 |
| 20⋯2.00re | −6.091 | −3.304 | 0.957 | 0.126 | 105.1 | −2.9 | −3.611 |
| π-stack (C6H6)2 parallel displaced | |||||||
| 24⋯0.90re | 0.028 | −0.067 | 0.067 | 1.535 | −185.2 | 53.8 | −0.105 |
| 24⋯0.95re | 0.020 | −0.061 | 0.061 | 2.062 | −111.4 | 39.5 | −2.016 |
| 24⋯1.00re | 0.014 | −0.056 | 0.056 | 2.869 | −75.9 | 32.5 | −2.725 |
| 24⋯1.05re | 0.008 | −0.052 | 0.051 | 4.229 | −55.9 | 28.5 | −2.813 |
| 24⋯1.10re | 0.003 | −0.048 | 0.048 | 6.930 | −43.7 | 26.1 | −2.607 |
| 24⋯1.25re | −0.014 | −0.042 | 0.042 | −18.003 | −28.1 | 22.7 | −1.578 |
| 24⋯1.50re | −0.043 | −0.044 | 0.044 | −4.045 | −29.5 | 21.7 | −0.515 |
| 24⋯2.00re | −0.083 | −0.064 | 0.064 | −2.242 | −53.0 | 23.1 | −0.072 |
| π-stack (uracil)2 stacked | |||||||
| 26⋯0.90re | 0.174 | 0.045 | 0.045 | 0.963 | −68.1 | 18.4 | −7.976 |
| 26⋯0.95re | 0.167 | 0.054 | 0.054 | 1.069 | −23.4 | 12.8 | −9.640 |
| 26⋯1.00re | 0.164 | 0.064 | 0.064 | 1.157 | −0.4 | 9.8 | −9.976 |
| 26⋯1.05re | 0.164 | 0.075 | 0.074 | 1.220 | 13.7 | 8.0 | −9.590 |
| 26⋯1.10re | 0.166 | 0.086 | 0.086 | 1.255 | 23.2 | 6.7 | −8.848 |
| 26⋯1.25re | 0.193 | 0.128 | 0.127 | 1.209 | 40.1 | 4.4 | −6.217 |
| 26⋯1.50re | 0.301 | 0.227 | 0.222 | 0.927 | 55.7 | 2.5 | −3.196 |
| 26⋯2.00re | 0.840 | 0.647 | 0.543 | 0.521 | 77.9 | −0.4 | −1.034 |
| London (n-pentane)2 | |||||||
| 34⋯0.90re | 0.079 | −0.015 | 0.015 | 2.216 | −268.8 | 11.3 | −2.919 |
| 34⋯0.95re | 0.064 | −0.014 | 0.014 | 2.804 | −138.9 | 5.9 | −3.674 |
| 34⋯1.00re | 0.053 | −0.013 | 0.013 | 3.575 | −85.8 | 3.8 | −3.820 |
| 34⋯1.05re | 0.043 | −0.012 | 0.012 | 4.601 | −57.4 | 2.7 | −3.651 |
| 34⋯1.10re | 0.034 | −0.011 | 0.011 | 5.982 | −40.3 | 2.1 | −3.337 |
| 34⋯1.25re | 0.017 | −0.008 | 0.008 | 14.297 | −16.0 | 1.7 | −2.257 |
| 34⋯1.50re | 0.003 | −0.005 | 0.005 | 185.803 | −4.7 | 2.2 | −1.066 |
| 34⋯2.00re | −0.003 | −0.003 | 0.003 | −42.381 | −2.6 | 3.5 | −0.278 |
| π-stack plus dipole–quadrupole: (C6H6)2 T-shaped | |||||||
| 47⋯0.90re | 0.082 | −0.018 | 0.018 | 1.470 | −135.8 | 35.8 | −1.657 |
| 47⋯0.95re | 0.076 | −0.010 | 0.010 | 1.735 | −70.7 | 25.3 | −2.603 |
| 47⋯1.00re | 0.072 | −0.004 | 0.004 | 2.014 | −39.0 | 20.3 | −2.898 |
| 47⋯1.05re | 0.070 | 0.003 | 0.003 | 2.290 | −20.4 | 17.3 | −2.853 |
| 47⋯1.10re | 0.070 | 0.009 | 0.009 | 2.539 | −8.3 | 15.5 | −2.643 |
| 47⋯1.25re | 0.072 | 0.027 | 0.027 | 2.955 | 10.7 | 12.8 | −1.804 |
| 47⋯1.50re | 0.088 | 0.052 | 0.052 | 2.668 | 23.2 | 11.4 | −0.856 |
| 47⋯2.00re | 0.136 | 0.095 | 0.095 | 1.783 | 34.6 | 9.9 | −0.237 |
| Mixed-influence: (C6H6)⋯H2O | |||||||
| 54⋯0.90re | 0.194 | 0.048 | 0.048 | 0.732 | −30.3 | 14.9 | −2.766 |
| 54⋯0.95re | 0.206 | 0.063 | 0.063 | 0.739 | 5.9 | 10.5 | −3.186 |
| 54⋯1.00re | 0.221 | 0.080 | 0.080 | 0.731 | 25.5 | 8.2 | −3.250 |
| 54⋯1.05re | 0.241 | 0.099 | 0.099 | 0.711 | 38.0 | 6.8 | −3.121 |
| 54⋯1.10re | 0.266 | 0.121 | 0.120 | 0.680 | 46.9 | 5.9 | −2.896 |
| 54⋯1.25re | 0.374 | 0.203 | 0.199 | 0.558 | 63.3 | 4.5 | −2.105 |
| 54⋯1.50re | 0.717 | 0.439 | 0.402 | 0.375 | 78.0 | 3.7 | −1.160 |
| 54⋯2.00re | 4.515 | 2.948 | 0.947 | 0.193 | 92.7 | 3.2 | −0.419 |
First, let us consider the acetic acid dimer with its strong double hydrogen bond. The Hobza ratio is solidly in the electrostatic range. CSPI and therefore DEBC are large, %HLC is close to zero, and as the dimer is pulled apart, the %SCF in the interaction energy approach is 100%. At long distance, the interaction energy indeed behaves similar to the R−3 power law expected for dipole–dipole electrostatic interactions.
Next, the stacked benzene dimer. Here, we find a small negative CSPI and a large HLC fraction. The HF fraction is negative throughout, consisting effectively of exchange repulsion. Long-range behavior is in fact not dissimilar to the R−5 expected for a quadrupole–quadrupole interaction.
For the stacked uracil dimer, we see something similar at short range, but at longer distances we see HLC becoming fairly unimportant, CSPI rising, and HF capturing an increasing positive fraction of the interaction energy. This reflects that, unlike the benzene dimer, there is a dipole–dipole interaction at longer distances in the uracil dimer.
For pentane dimer, CSPI stays small throughout, as does the %HLC. The HF contribution is repulsive but tapers off quickly at long distances, where the behavior is dominated by the London interaction.
In the mixed-influence benzene–water complex, on the other hand, CSPI is near zero at short distances but goes up at long distances (where a dipole–quadrupole interaction dominates), while the HLC fraction is substantial at short distances but tapers off to near zero at longer ones, and the HF fraction is small at short distances but approaches unity in the long-distance regime.
Conclusions
We have presented a revision of the S66x8 dataset by means of explicitly correlated methods, combining basis set limit MP2-F12 energies with CCSD(Tcsc)-F12b/cc-pVDZ-F12 high level corrections. Based on assessments for smaller datasets, we deem our results reliable to about 0.05 kcal mol−1 RMS. The RMS deviation from the original S66x8 reference data is 0.11 kcal mol−1, comparable to the performance of the best DFT levels considered here.Most levels of DFT perform quite poorly in the absence of dispersion corrections: somewhat surprisingly, that is even the case for the double hybrids and for dRPA75. Even the simple D2 empirical dispersion leads to substantial improvement, especially for dRPA75-D2 (s6 = 0.31, RMSD = 0.13 kcal mol−1) and for DSD-PBEP86-D2 (s6 = 0.27, RMSD = 0.15 kcal mol−1). Below the fifth rung, ωB97X-V without NL, adding D2 is seen as the best performer (s6 = 0.73, RMSD = 0.31 kcal mol−1).
The D3BJ correction leads to further improvements for GGAs and hybrids, much less so for fifth-rung functionals. (D3BJ parameters for a number of additional functionals were optimized in this work.) Significantly, the optimized s8 coefficient for the R−8 term is close to zero for the double hybrids and dRPA75, or needs to be fixed at zero to get a stable fit. In contrast, for the APF functional (which is constructed to be dispersion-free on average), s6 = 1.776, while for MP2, s6 = −3.351. This illustrates that the primary benefit of fifth-rung functionals for noncovalent interactions lies in the handling of medium-range interactions: in straight MP2, overcorrection takes place in that region, which is remedied in the case of dRPA75-D3BJ by higher-order correlation corrections, and in the double hybrids by the use of a mixture of GGA and KS-MP2 correlation. dRPA75-D3BJ actually falls below the RMSD = 0.10 kcal mol−1 threshold. B3LYP-D3BJ performs surprisingly well at RMSD = 0.20 kcal mol−1.
Considering S66x8 in tandem with the amino acid conformers illustrates why it is worthwhile to consider multiple benchmarks for evaluation lower-level methods: dRPA75-D3BJ performs well on both sets, dRPA75 and dRPA75-D2 each on only one set.
A nonlocal (Vydrov–Van Voorhis 2010, or VV10) correlation model performs less well than D3BJ for some GGAs and hybrids, while it is superior for the double hybrids, particularly for DSD-PBEP86-NL, with RMSD = 0.12 kcal mol−1. Among the range-separated hybrids, ωB97X-V stands out, with RMSD = 0.23 kcal mol−1.
A caveat is due here: the benchmark study in the present paper only concerns noncovalent interactions and any conclusions reached about the performance of specific DFT methods are not necessarily applicable to other properties. It is however worth mentioning that one of the best performers for the S66x8 benchmark, namely the DSD-PBEP86-D3BJ double hybrid,79,80 also was found to yield outstanding performance for general thermochemistry79,80 and reaction barrier heights,79,80 as well as for vibrational frequencies.111 The same remarks apply, to a lesser extent, for the B2GP-PLYP-D2 double hybrid.78 The computational surcharge for such approaches is actually fairly modest if the RI-MP2 (resolution of the identity MP2) method32,33 can be used for the MP2-like step.
Informative as SAPT may be about the character of a given interaction, a collection of three energetically based indices offer similar information. Two of those are the percentages of Hartree–Fock and of post-MP2 correlation effects in the interaction energy: the third
In the context of CCSD(T)-F12b calculations, we propose (Tb), namely an improved, parameter-free scaling for the (T) contribution based on the Ecorr[CCSD-F12b]/Ecorr[CCSD] rather than the Ecorr[MP2-F12]/Ecorr[MP2] ratio. Similarly, we propose (Tc) for CCSD(F12*)(T) calculations, where the scaling is done by the Ecorr[CCSD(F12*)]/Ecorr[CCSD] ratio instead.
Regarding the accuracy of wavefunction ab initio methods, the several flavors of MP2 and SCS-MP2 methods have again shown that they can be parametrized for a specific kind of interaction, but at the cost of degrading the other interactions. While MP3 overcorrects, MP2.5, averaging the MP2 and MP3 values, yields excellent performance. Uncorrected CCSD yields no adequate return for the additional computational effort: similar to dRPA75, however, adding in a D2 correction to compensate for the missing (T) results in an excellent RMSD = 0.16 kcal mol−1 (for s6 = 0.228); even further improvement at zero added cost is possible through SCS(MI)CCSD, or even simple overall scaling of the CCSD correlation energy.
Finally, with the relatively small cc-pVDZ-F12 basis set, CCSD(F12*) has a small but significant edge over CCSD-F12b, particularly for multiply H-bonded systems.
Acknowledgements
MKK acknowledges a Feinberg Graduate School postdoctoral fellowship. This research was supported by the Israel Science Foundation (grant 1358/15), the Minerva Foundation, the Lise Meitner-Minerva Center for Computational Quantum Chemistry, and a grant from the Yeda-Sela Initiative (Weizmann Institute of Science). The authors would like to thanks Profs. Leeor Kronik (Weizmann Institute of Science), Amir Karton (U. of Western Australia, Perth), and Martin Suhm (U. of Göttingen, Germany) for helpful discussions.References
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CrossRef CAS.
- K. E. Riley and P. Hobza, Acc. Chem. Res., 2013, 46, 927–936 CrossRef CAS PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- B. P. Martin, C. J. Brandon, J. J. P. Stewart and S. B. Braun-Sand, Proteins: Struct., Funct., Bioinf., 2015, 83, 1427–1435 CrossRef CAS PubMed.
- G. Jansen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 127–144 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 304–326 CrossRef CAS.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272 CrossRef CAS.
- J. Rezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
- I. G. Kaplan, Intermolecular Interactions, John Wiley & Sons, Ltd, Chichester, UK, 2006 Search PubMed.
- P. Jurecka, J. Sponer, J. Cerný and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- M. S. Marshall, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2011, 135, 194102 CrossRef PubMed.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3466–3470 CrossRef.
- J. Řezáč, P. Jurečka, K. E. Riley, J. Černý, H. Valdes, K. Pluháčková, K. Berka, T. Řezáč, M. Pitoňák, J. Vondrášek and P. Hobza, Collect. Czech. Chem. Commun., 2008, 73, 1261–1270 CrossRef , see also: http://www.begdb.com.
- J. Aragó, E. Ortí and J. C. Sancho-García, J. Chem. Theory Comput., 2013, 9, 3437–3443 CrossRef PubMed.
- F. Yu, J. Chem. Theory Comput., 2014, 10, 4400–4407 CrossRef CAS PubMed.
- L. Goerigk, H. Kruse and S. Grimme, ChemPhysChem, 2011, 12, 3421–3433 CrossRef CAS PubMed.
- K. E. Riley, J. A. Platts, J. Řezáč, P. Hobza and J. G. Hill, J. Phys. Chem. A, 2012, 116, 4159–4169 CrossRef CAS PubMed.
- J. A. Platts, J. G. Hill, K. E. Riley, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 330–337 CrossRef CAS PubMed.
- M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 4249–4255 CrossRef CAS PubMed.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- S. Ten-no, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef CAS.
- K. A. Peterson, D. A. Dixon and H. Stoll, J. Phys. Chem. A, 2012, 116, 9777–9782 CrossRef CAS PubMed.
- J. M. L. Martin and M. K. Kesharwani, J. Chem. Theory Comput., 2014, 10, 2085–2090 CrossRef CAS PubMed.
- B. Brauer, M. K. Kesharwani and J. M. L. Martin, J. Chem. Theory Comput., 2014, 10, 3791–3799 CrossRef CAS PubMed.
- K. A. Peterson, M. K. Kesharwani and J. M. L. Martin, Mol. Phys., 2015, 113, 1551–1558 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselman, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. M. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, Version 2012.1, a Package of Ab Initio Programs, University of Cardiff Chemistry Consultants (UC3), Cardiff, Wales, UK, 2012, see also: http://https://www.molpro.net Search PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 91–100 CrossRef , see also: http://www.turbomole.com.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Rev. D01., Gaussian, Inc., Wallingford, CT, 2012, see also: http://www.gaussian.com Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS , see also: http://https://orcaforum.cec.mpg.de.
- F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340 CrossRef CAS.
- R. A. Kendall and H. A. Früchtl, Theor. Chem. Acc., 1997, 97, 158–163 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 7410 CrossRef CAS.
- J. E. Del Bene, J. Phys. Chem., 1993, 97, 107–110 CrossRef CAS.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59 RSC.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, Chem. Phys. Lett., 2009, 476, 303–307 CrossRef CAS.
- J. G. Hill, K. A. Peterson, G. Knizia and H.-J. Werner, J. Chem. Phys., 2009, 131, 194105 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- J. Noga and J. Šimunek, Chem. Phys., 2009, 356, 1–6 CrossRef CAS.
- O. Marchetti and H.-J. Werner, Phys. Chem. Chem. Phys., 2008, 10, 3400 RSC.
- O. Marchetti and H.-J. Werner, J. Phys. Chem. A, 2009, 113, 11580–11585 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095 CrossRef CAS.
- A. Szabados, J. Chem. Phys., 2006, 125, 214105 CrossRef PubMed.
- S. Grimme, L. Goerigk and R. F. Fink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 886–906 CrossRef CAS.
- R. F. Fink, J. Chem. Phys., 2010, 133, 174113 CrossRef PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Tao, J. Perdew, V. Staroverov and G. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 13298–13307 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- S. Grimme, J. Phys. Chem. A, 2005, 109, 3067–3077 CrossRef CAS PubMed.
- M. M. Quintal, A. Karton, M. A. Iron, A. D. Boese and J. M. L. Martin, J. Phys. Chem. A, 2006, 110, 709–716 CrossRef CAS PubMed.
- A. Austin, G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. Throssell, J. Chem. Theory Comput., 2012, 8, 4989–5007 CrossRef CAS PubMed.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886 CrossRef CAS PubMed.
- S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107 RSC.
- S. Kozuch and J. M. L. Martin, J. Comput. Chem., 2013, 34, 2327–2344 CAS.
- P. D. Mezei, G. I. Csonka, A. Ruzsinszky and M. Kállay, J. Chem. Theory Comput., 2015, 11, 4615–4626 CrossRef CAS PubMed.
- H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084 CrossRef.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. D. Powell, The BOBYQA algorithm for bound constrained optimization without derivatives (DAMPT Report 2009/NA06), Department of Applied Mathematics and Theoretical Physics, University of Cambridge, UK, 2009, see also: http://en.wikipedia.org/wiki/BOBYQA [Retrieved February 29, 2016].
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- M. K. Kesharwani, A. Karton and J. M. L. Martin, J. Chem. Theory Comput., 2016, 12, 444–454 CrossRef CAS PubMed.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565 CrossRef CAS.
- A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2005, 115, 330–333 CrossRef.
- D. W. Schwenke, J. Chem. Phys., 2005, 122, 14107 CrossRef PubMed.
- D. S. Ranasinghe and G. A. Petersson, J. Chem. Phys., 2013, 138, 144104 CrossRef PubMed.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- T. Takatani, E. G. Hohenstein, M. Malagoli, M. S. Marshall and C. D. Sherrill, J. Chem. Phys., 2010, 132, 144104 CrossRef PubMed.
- A. Halkier, H. Koch, P. Jørgensen, O. Christiansen, I. M. B. Nielsen and T. Helgaker, Theor. Chem. Acc., 1997, 97, 150–157 CrossRef CAS.
- L. A. Burns, M. S. Marshall and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 49–57 CrossRef CAS PubMed.
- A. Hesselmann, J. Chem. Phys., 2008, 128, 144112 CrossRef PubMed.
- R. A. DiStasio, G. von Helden, R. P. Steele and M. Head-Gordon, Chem. Phys. Lett., 2007, 437, 277–283 CrossRef CAS.
- G. Chałasiński and M. M. Szcześniak, Mol. Phys., 1988, 63, 205–224 CrossRef.
- A. Szabo and N. S. Ostlund, J. Chem. Phys., 1977, 67, 4351 CrossRef CAS.
- R. Sedlak, K. E. Riley, J. Rezáč, M. Pitoňák and P. Hobza, ChemPhysChem, 2013, 14, 698–707 CrossRef CAS PubMed.
- M. Pitoňák and A. Heßelmann, J. Chem. Theory Comput., 2010, 6, 168–178 CrossRef PubMed.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2014, 10, 1359–1360 CrossRef PubMed.
- J. Toulouse, W. Zhu, A. Savin, G. Jansen and J. G. Ángyán, J. Chem. Phys., 2011, 135, 084119 CrossRef PubMed.
- G. E. Scuseria, T. M. Henderson and D. C. Sorensen, J. Chem. Phys., 2008, 129, 231101 CrossRef PubMed.
- D. Gruzman, A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 11974–11983 CrossRef CAS PubMed.
- J. M. L. Martin, J. Phys. Chem. A, 2013, 117, 3118–3132 CrossRef CAS PubMed.
- M. K. Kesharwani, B. Brauer and J. M. L. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714 CrossRef CAS PubMed.
- R. M. Parrish, T. M. Parker and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 4417–4431 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Spreadsheet with revised reference interaction energies for the S66x8 dataset, interaction energies at various levels of theory and SAPT results; Cartesian coordinates (66 structures, XMol .xyz format) for the interpolated minimum geometries. See DOI: 10.1039/c6cp00688d |
| ‡ Equally contributing first authors. |
| This journal is © the Owner Societies 2016 |