Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Planar vs. three-dimensional X62−, X2Y42−, and X3Y32− (X, Y = B, Al, Ga) metal clusters: an analysis of their relative energies through the turn-upside-down approach†‡
Ouissam
El Bakouri
a,
Miquel
Solà
*a and
Jordi
Poater
*bcd
aInstitut de Química Computacional i Catàlisi (IQCC) and Departament de Química, Universitat de Girona, Campus Montilivi, 17071 Girona, Catalonia, Spain. E-mail: miquel.sola@udg.edu
bDepartament de Química Inorgànica i Orgànica & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, Martí i Franquès 1-11, 08028 Barcelona, Catalonia, Spain. E-mail: jordi.poater@gmail.com
cDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling, Vrije Universiteit Amsterdam, De Boeleaan 1083, NL-1081HV Amsterdam, The Netherlands
dInstitució Catalana de Recerca i Estudis Avançats (ICREA), Pg. Lluís Companys 23, 08010 Barcelona, Catalonia, Spain
First published on 11th March 2016
Abstract
Despite the fact that B and Al belong to the same group 13 elements, the B62− cluster prefers the planar D2h geometry, whereas Al62− favours the Oh structure. In this work, we analyse the origin of the relative stability of D2h and Oh forms in these clusters by means of energy decomposition analysis based on the turn-upside-down approach. Our results show that what causes the different trends observed is the orbital interaction term, which combined with the electrostatic component do (Al62− and Ga62−) or do not (B62−) compensate the higher Pauli repulsion of the Oh form. Analysing the orbital interaction term in more detail, we find that the preference of B62− for the planar D2h form has to be attributed to two particular molecular orbital interactions. Our results are in line with a dominant delocalisation force in Al clusters and the preference for more localised bonding in B metal clusters. For mixed clusters, we have found that those with more than two B atoms prefer the planar structure for the same reasons as for B62−.
Introduction
The electronic distribution of nanosized molecular clusters can be very different from that of the bulk state.1 In fact, metals can exhibit isolating behaviour when reduced to small particles. Since the electronic properties of nanoparticles are quite different from those of the bulk, molecular clusters are expected to have a variety of electronic applications, such as single-electron transistors, diodes, and quantum dots.2–4 The properties of clusters are profoundly affected by the type of bonding they have. For some of these clusters one can expect an intermediate situation between covalent and metallic bonding. As modern technologies evolve towards the nanoscale, it becomes more important to have a more precise understanding of the bonding in these species to better tune their properties.Among clusters, those made by group 13 atoms are particularly important.5 Both B and Al belong to the same group 13, and thus present a similar electronic structure, [He]2s22p1 and [Ne]3s23p1, respectively. However, when they form small clusters, B clusters adopt a planar conformation as the equilibrium structure;6–9 whereas Al clusters present a three-dimensional (3D) closed shape.10–13 The most relevant examples are B62− and Al62− clusters, which were obtained experimentally as lithium salts in the form of LiB6− and LiAl6−.14–16 B62− adopts a planar D2h geometry in its low-lying singlet state, whereas the Al62− cluster is octahedral. Both shapes of the metal clusters are kept when lithium salts are formed.
The chemical bonding of B62− and Al62− has been widely analysed in previous studies.14,17,18 In particular, Alexandrova et al.18 highlighted the fact that B62− is able to 2s–2p hybridize and to form 2-center–2-electron (2c–2e) B–B covalent localised bonds. On the other hand, 3s–3p hybridisation in the Al62− cluster is more difficult due to larger s–p energy separation, which hampers the formation of directional covalent Al–Al bonds.19 In this case, bonding comes from the combination of radial and tangential p-orbitals that result in extensive delocalisation.20 Indeed, the Al62− cluster displays octahedral aromaticity,14,21 whereas planar D2h B62− is considered σ- and π-antiaromatic.17,18,22,23 Thus, as pointed out by Alexandrova et al.,18,24–26 covalent and delocalised bonding shows opposite effects in determining the molecular structure of many clusters. Huynh and Alexandrova analysed the whole series BnAl6−n2− (n = 0–6), from B62− till Al62− by substituting one B by Al each time, concluding that covalent bonding is a resilient effect that governs the cluster shape more than delocalisation does. Indeed, the planar structure of B62− persists until n = 5, the reason being the strong tendency to form 2c–2e B–B bonds in case the cluster contains two or more B atoms.18 Similar results were reported by Fowler and Ugalde in larger clusters of group 13. In particular, these authors found that B13+ prefers a planar conformation27 in contrast to Al13−,28 which adopts an icosahedral geometry. Interestingly, in closo boranes and substituted related species, like B6H62− or B12I122−, the delocalised 3D structure is preferred. However, successive stripping of iodine in B12I122− leads to a B12 planar structure with some localised 2c–2e B–B bonds.29,30 Similarly, for B6Hn− clusters, the clusters are planar for n ≤ 3 and become tridimensional for n ≥ 4.31
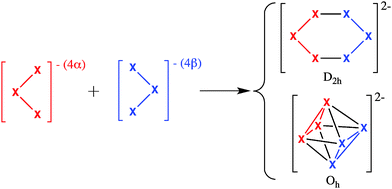
As can be seen in Scheme 1, both 2D D2h planar and 3D Oh geometries for X62− (X = B, Al) can be obtained joining the same two X3− cluster fragments.14,17 Therefore, X62− species in D2h and Oh geometries are particularly suitable for an energy decomposition analysis (EDA)32–35 based on the turn-upside-down approach.36–39 In this approach, two different isomers are formed from the same fragments and the bonding energy is decomposed into different physically meaningful components using an EDA. Differences in the energy components explain the reasons for the higher stability of the most stable isomer. For instance, using this method we provided an explanation of why the cubic isomer of Td geometry is more stable than the ring structure with D4h symmetry for (MX)4 tetramers (X = H, F, Cl, Br, and I) if M is an alkalimetal and the other way round if M belongs to group 11 transition metals.38 Therefore, the application of this type of analysis to B62− and Al62− clusters will disclose the factors that make the planar D2h structure more stable for boron and the octahedral one for aluminium. As said before, boron clusters favour localised covalent bonds whereas aluminium clusters prefer a more delocalised bonding. With the present analysis, we aim to provide a more detailed picture of the reasons for the observed differences. The analysis will be first applied to the above referred B62− and Al62− clusters, and then further complemented with Ga62−. Finally, X2Y42− and X3Y32− (X, Y = B, Al, Ga) mixed clusters in their distorted D2h planar and 3D D4h geometries will also be discussed.
Computational methods
All Density Functional Theory (DFT) calculations were performed using the Amsterdam Density Functional (ADF) program.40 The molecular orbitals (MOs) were expanded in a large uncontracted set of Slater type orbitals (STOs) of triple-ζ quality for all atoms (TZ2P basis set). The 1s core electrons of boron, 1s–2p of aluminium, and 1s–3p of gallium were treated by the frozen core approximation. Energies and gradients were computed using the local density approximation (Slater exchange and VWN correlation) with non-local corrections for exchange (Becke88) and correlation (Lee–Yang–Parr 1988) included self-consistently (i.e. the BLYP functional). D3(BJ) dispersion corrections by Grimme were also included in the functional (i.e. BLYP-D3(BJ) functional).41–44 Analytical Hessians were computed to confirm the nature of the located minima at the same level of theory.Relative energies between the planar and 3D species were also calculated using the Gaussian 09 program45 at the coupled cluster level46 with single and double excitation (CCSD)47 and with triple excitation treated perturbatively (CCSD(T))48 using Dunning's correlation consistent augmented triple-ζ (aug-cc-pVTZ)49,50 at optimised BLYP-D3(BJ)/TZ2P molecular geometries.
The bonding energy corresponding to the formation of X62− for both D2h and Oh symmetries from two anionic quintet tetraradicals, fragment 1 (αααα) + fragment 2 (ββββ) (see Scheme 1), is made up of two major components (eqn (1)):
| ΔE = ΔEdist + ΔEint | (1) |
| ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp | (2) |
In bond-energy decomposition,51–53 open-shell fragments were treated with spin-unrestricted formalism but, for technical reasons, spin-polarisation was not included. This error causes the studied bond to become in the order of a few kcal mol−1 too strong. To facilitate a straightforward comparison, the EDA results were scaled to match exactly the regular bond energies (the correction factor is consistently in the range 0.97–0.98 in all model systems and does therefore not affect trends). A similar scheme based on the same EDA approach was used by Frenking and coworkers54,55 and by some of us36,37,56 to estimate the strength of π-cyclic conjugation in typical (anti)aromatic organic compounds and in metallabenzenes and metallacyclopentadienes.
Let us mention here that, as already mentioned in the introduction, some of the analysed metal clusters exist experimentally as lithium salts.14–16 On the other hand, these dianionic systems are unstable against the ejection of an electron. However, their molecular and electronic structure is very similar to that of their corresponding lithium salts, which justifies the analysis of the chemical bonding of these doubly charged systems, as it is not affected by the presence of a lithium cation.
Finally, the metalloaromaticity57 of these clusters was evaluated at the BLYP/aug-cc-pVDZ level of theory with the optimized BLYP-D3(BJ)/TZ2P geometries by means of multicentre electron sharing indices (MCIs).58–60 MCIs provide a measure of electron sharing among the atoms considered,59 in the present case the six atoms that form each of the clusters studied. MCI values have been calculated using the ESI-3D program.61,62
Results and discussion
We first focus on the homoatomic X62− metal clusters with X = B, Al, and Ga. The optimized Oh and D2h geometries at the BLYP-D3(BJ)/TZ2P level are depicted in Fig. 1 with the main bond lengths and angles. As expected, B–B bond lengths (1.536–1.768 Å) are much shorter than those for Al–Al (2.574–2.912 Å) and Ga–Ga (2.526–2.898 Å). The similar Al–Al and Ga–Ga distances in X62− metal clusters (X = Al, Ga) are not unexpected given the similar van der Waals radii of these two elements.63 In addition, the X–X bond length connecting the two equivalent X3− fragments in Oh clusters is longer than in the D2h systems.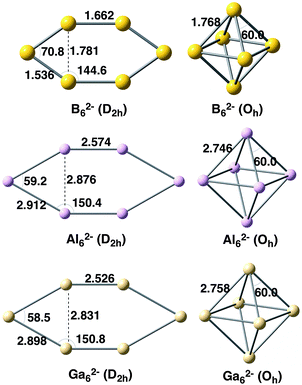 | ||
| Fig. 1 Geometries of X62− metal clusters analysed with D2h and Oh symmetries. Distances in Å and angles in degrees. | ||
Table 1 encloses the energy differences between Oh and D2h clusters. For B62−D2h symmetry is more stable than Oh by 67.5 kcal mol−1, the latter not being a minimum.18 Meanwhile the opposite trend is obtained in the other two metal clusters, for which Oh is lower in energy by 15.8 (Al62−) and 9.3 kcal mol−1 (Ga62−) than D2h structures. These trends are confirmed by higher level CCSD(T)/aug-cc-pVTZ single point energy calculations at the same BLYP-D3(BJ)/TZ2P geometries (values also enclosed in Table 1). The relative energies of B62−, Al62−, and Ga62− between Oh and D2h symmetries are now −38.7, +44.8 and +46.6 kcal mol−1, respectively. CCSD(T) values systematically favour Oh as compared to D2h structures by about 20–30 kcal mol−1. However, the qualitative picture remains the same.
| Clusters | BLYP-D3(BJ)/TZ2Pa | CCSD(T)/aug-cc-pVTZb | MCIc | ||||
|---|---|---|---|---|---|---|---|
| O h | D 2h | O h | D 2h | O h | D 2h | ||
| a B2Ga42− (D2h) has not been obtained because optimization breaks the symmetry; whereas B3Al32− and B3Ga32− (Oh) have not been obtained because the strength of the B3 unit causes the systems to be planar and to avoid a 3D geometry. b Single point energy calculations at BLYP-D3(BJ)/TZ2P geometries. c MCI calculated at the BLYP/aug-cc-pVDZ level of theory with the BLYP-D3(BJ)/TZ2P optimized geometries. d Local minima. e One imaginary frequency. f One small imaginary frequency due to numerical integration problems. g Two imaginary frequencies. h Three imaginary frequencies. | |||||||
| X62− | B62− | 67.5e | 0.0d | 38.7 | 0.0 | 0.062 | −0.052 |
| Al62− | 0.0d | 15.8e | 0.0 | 44.8 | 0.077 | 0.068 | |
| Ga62− | 0.0f | 9.3f | 0.0 | 46.6 | 0.083 | 0.071 | |
The aromaticity of these X62− metal clusters was evaluated by means of the MCI electronic criterion. The six-membered MCIs are enclosed in Table 1. In all cases, the Oh system is more aromatic than the D2h one, in agreement with the larger electronic delocalisation of the former, as discussed in the Introduction.21 MCI values confirm the octahedral aromaticity21 of Oh Al62− and the antiaromatic character of D2h B62−.17,18,22,23 Interestingly, MCI values point out the clear aromatic character of all 3D clusters that do not contain boron (MCI = 0.074–0.077); whereas mixed B2Al42−, Al2B42−, and Ga2B42−D4h clusters containing boron atoms are less aromatic (MCI = 0.032–0.047). For planar structures, there are basically two groups of clusters. First, the group formed by B62− and B2Al42− has eight valence electrons distributed in two π-MOs and two σ-MOs (vide infra). Therefore, having four π-electrons and four σ-electrons, they are σ- and π-antiaromatic species. Second, the group formed by Al62−, Ga62−, Al2B42−, Al2Ga42−, Ga2B42−, and Ga2B42− have eight valence electrons distributed in one π-MO and three σ-MOs (vide infra) and, therefore, they are σ- and π-aromatic species.
With the aim to obtain a deeper insight into the origin of 2D to 3D relative energies an energy decomposition analysis was performed, following the reaction presented in Scheme 1. As pointed out above, both systems can be constructed from two identical X3− anionic fragments, both in their quintet state in order to form the corresponding new bonds. Three of these bonds are of σ character, two tangential (σT) and one radial (σR), and one π character (see Fig. 2). It must be pointed out that, very recently, Mercero et al. have proven the multiconfigurational character of some of the lowest-lying electronic states of Al3−.19 In the case of the quintet state of Al3−, which is the fragment used in our calculations, the authors showed that the electronic configuration of the four valence electrons is also derived from the occupation of two σ-type tangential and one σ-type radial molecular orbitals arising from the 3px and 3py atomic orbitals, and one π-type orbital arising from the 3pz ones. This quintet state was found to be dominated by one-single configuration with a coefficient of 0.92 in the multiconfigurational wavefunction.19 Moreover, the energy difference between the ground state and the quintet state was almost the same when computed at DFT or at the MCSCF levels of theory.19 This seems to indicate that DFT methods give reasonable results for this quintet state. Finally, the T1 test64 applied to clusters collected in Table 1 was found to be always less than 0.045, thus indicating the relatively low multiconfigurational character of these species. It is commonly accepted that CCSD(T) produces acceptable results for T1 values as high as 0.055.65
The different terms of the EDA for B62−, Al62−, and Ga62− clusters are enclosed in Table 2. First we notice that the total bonding energies (ΔE) are much larger for B62− than for Al62− or Ga62−. For the former, ΔE are −100.2 (Oh) and −179.5 kcal mol−1 (D2h), whereas for the two latter are in between −19.0 and −38.1 kcal mol−1. This trend correlates with the shorter B–B bond lengths mentioned above. Table 2 also encloses the relative EDA energies between the two clusters. The B3− fragment taken from the B62− system in its D2h symmetry is the one that suffers the largest deformation, i.e. the largest change in geometry with respect to the fully relaxed B3− cluster in the quintet state (ΔEdist = 12.5 kcal mol−1), whereas the rest of the systems present small values of ΔEdist (0.0–1.7 kcal mol−1). However, differences in ΔE are not due to distortion energies (indeed ΔEdist values follow the opposite trend as ΔE), but to interaction energies (ΔEint).
| B62− | Al62− | Ga62− | |||||||
|---|---|---|---|---|---|---|---|---|---|
| D 2h + D2h → D2h | O h + Oh → Oh | Δ(ΔE) | D2h + D2h → D2h | O h + Oh → Oh | Δ(ΔE) | D 2h + D2h → D2h | O h + Oh → Oh | Δ(ΔE) | |
| ΔEint | −192.0 | −101.4 | −90.6 | −20.7 | −39.8 | 19.1 | −19.1 | −31.0 | 11.9 |
| ΔEPauli | 533.5 | 735.3 | −201.8 | 225.7 | 348.0 | −122.3 | 269.6 | 384.5 | −114.9 |
| ΔVelstat | −239.0 | −291.9 | 52.9 | −96.3 | −166.5 | 70.2 | −138.0 | −207.5 | 69.5 |
| ΔEoi | −483.4 | −542.8 | 59.4 | −146.9 | −217.4 | 70.5 | −146.7 | −203.4 | 56.7 |
| ΔEdisp | −3.2 | −2.1 | −1.1 | −3.2 | −3.9 | 0.7 | −4.0 | −4.7 | 0.6 |
| ΔEdist | 12.5 | 1.3 | 11.2 | 0.0 | 1.7 | −1.7 | 0.1 | 1.4 | −1.3 |
| ΔE | −179.5 | −100.2 | −79.3 | −20.7 | −38.1 | 17.4 | −19.0 | −29.6 | 10.6 |
Thus, we focus on the decomposition of ΔEint into ΔEPauli, ΔVelstat, ΔEoi, and ΔEdisp terms. As a general trend, in all three X62− clusters ΔEPauli is larger for the Oh than the D2h cluster (Δ(ΔEPauli) = −201.8, −122.3, and −114.9 kcal mol−1 for B62−, Al62−, and Ga62−, respectively), so making it less stable. The overlaps between doubly occupied MOs are larger in the more compact Oh structure that, consequently, has larger ΔEPauli. The larger difference in ΔEPauli between the Oh and D2h structures in the case of B62− as compared to Al62− and Ga62− is attributed to the particularly short B–B distances that increase the overlap between doubly occupied MOs of each B3− fragment. At the same time, the Oh form presents larger (more negative) electrostatic interactions (Δ(ΔVelstat) = 52.9, 70.2, and 69.5 kcal mol−1 for B62−, Al62−, and Ga62−, respectively). It is usually the case that higher destabilising Pauli repulsions go with larger stabilising electrostatic interactions. The reason has to be found in the fact that both interactions increase in the absolute value when electrons and nuclei are confined in a relatively small space. The electrostatic interaction together with orbital interaction (Δ(ΔEoi) = 59.4, 70.5, and 56.7 kcal mol−1 for B62−, Al62−, and Ga62−, respectively) terms favour the Oh structure. However, in the case of Oh B62−, Δ(ΔVelstat) and Δ(ΔEoi) cannot compensate Δ(ΔEPauli), which causes the D2h system to be the lowest in energy. The opposite occurs for Al62− and Ga62−. Finally, the dispersion term almost does not affect the relative energies, as the difference in dispersion is only in the order of ca. 1.0 kcal mol−1. Therefore, what causes the different trend observed for B62− on one side, and Al62− and Ga62− on the other side is basically the ΔEoi term, which combined with the ΔVelstat component does (Al62− and Ga62−) or does not (B62−) compensate the higher ΔEPauli of the Oh form.
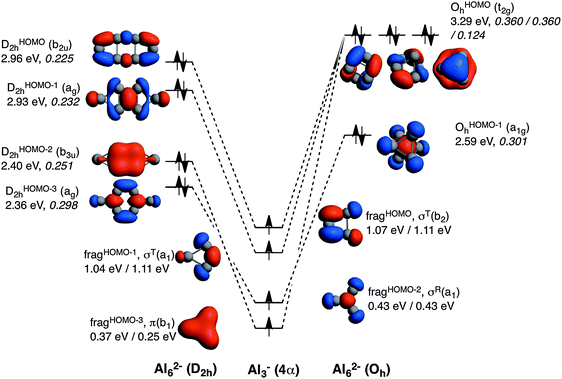
The comparison of the MOs diagrams of B62− and Al62−, built from their X3− fragments, justify the trends of ΔEoi (see Fig. 2 and 3). Both D2h and Oh clusters are built from the same fragments; the only difference is that the two tangential fragHOMO(σT(b2)) and fragHOMO−1(σT(a1)) MOs of Al3− are degenerate when obtained from Al62− in its Oh geometry, whereas they are not when generated from the D2h system, although they still are very close in energy. As discussed from the EDA, Oh is more stable than D2h because of more stabilizing electrostatic and orbital interactions, which compensate its larger Pauli repulsion. Fig. 2 also encloses the overlaps for the interactions between the four SOMOs of the Al3− fragments to form the MOs of the metal clusters in both geometries. We take the Al3− fragments in their quintet states with three unpaired σ- and one unpaired π-electrons, all of them with spin α in one fragment and β in the other. A more negative ΔEoi in Oh Al62− is justified from the larger 〈SOMO|SOMO〉 overlaps, especially for t2gOHOMOah and OHOMObh (0.360 compared to 0.225 and 0.232 for b2uDHOMO2h and agDHOMO−12h, respectively). D2h only presents a larger overlap for the π fragment orbital (0.251 for b3uDHOMO−22h and 0.124 for t2gOHOMOch). Meanwhile both of them have almost the same overlap for the combination of the radial MO (σR) fragment (fragHOMO−2), with 〈SOMO|SOMO〉 = 0.298 and 0.301 for agDHOMO−32h and OHOMO−1h, respectively. Overall, the higher orbital interaction term of the Oh system can be explained by the larger 〈SOMO|SOMO〉 overlaps of two of the t2g delocalised molecular orbitals for this cluster (see Fig. 2). The energies of the occupied MOs of Al62− formed are higher than those of the Al3− SOMOs because we move from a monoanionic fragment to a dianionic molecule.
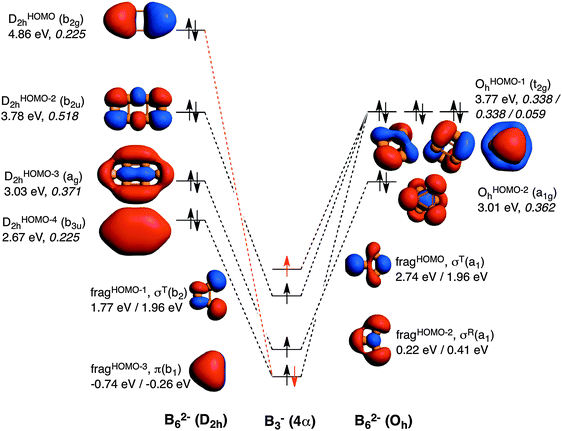
Now it is the turn to visualize the MOs of B62−. The fragments for B3− are the same as those for Al3− (see Fig. 3). However, the first difference appears in the MOs for B62− with D2h symmetry. In this case, it would be more reasonable to build the MOs of this molecule from two triplet (not quintet) B3− fragments. The reason is the different occupation of the MOs when compared to the D2h Al62− species. In D2h B62−, the HOMO corresponds to the antibonding π MO. To reach doubly occupied bonding (b3uDHOMO−42h) and antibonding (b2gDHOMO2h) π MOs, the π MO (fragHOMO−3) should be doubly occupied. Furthermore, the tangential σT(a1) fragHOMO does not participate in any occupied MO of this metal cluster and only generates virtual MOs. Consequently, MOs of B62− are better formed from two B3− fragments in their triplet state (see red electron in Fig. 3). On the other hand, B62− with Oh follows the same trend as Al62−, and in this case the same SOMOs in their quintet state are involved. At this point, it is worth mentioning that, as pointed out by Mercero et al., due to the strong multiconfigurational character of this species, one must be cautious with the electronic configuration, especially for the triplet state, as radial and tangential MOs are very close in energy.19
To make results comparable, Table 2 gathers the EDA of Oh and D2h B62− from two B3− fragments in their quintet states. Also in this case ΔEoi is more favourable for Oh than for D2h, however, at a lower extent when compared to Al62−. There are two main reasons for such a decrease of the strength of ΔEoi in Oh compared to D2h. First, and more importantly, because the DHOMO−22h formed presents a much larger 〈SOMO|SOMO〉 overlap than t2gOHOMO−1h (0.518 in the former vs. 0.338 in the latter). In particular, this DHOMO−22h MO contributes to the 2c–2e B–B localised bonds that are related to the larger covalent character of this structure. And second, because the π-interaction between the two π SOMO fragments is much larger in the case of D2h (0.225 vs. 0.059 for D2h and Oh, respectively). Nevertheless, these two more favourable orbital interactions are not enough to surpass the ΔEoi term of the Oh cluster. However, as compared to Al62−, for B62− the Δ(ΔEoi) term favours the Oh system to a less extent and cannot compensate the higher ΔEPauli term of the Oh form, thus making the planar geometry to be more stable in this case. This is related to the determinant force of the formed covalent bonding, involving more localised MOs than for Al62−. Such a larger covalent component in B62− is also supported by the covalent character of the interaction between the two fragments calculated as % covalency = (ΔEoi/(ΔEoi + ΔVelstat + ΔEdisp)) × 100. This formula results in B62−: 65–67% (Oh, D2h), Al62−: 56–60% (Oh, D2h), and Ga62−: 49–51% (Oh, D2h); thus confirming again the larger covalency found in B62−.
Finally, as done usually in the turn-upside-down approach,36–39,56,66,67 instead of building X62− in Oh symmetry from the corresponding two X3− fragments obtained from the Oh structure, we can build the Oh system from two X3− fragments extracted from the X62− cluster in D2h symmetry, and viceversa (see Tables S2–S4 in the ESI‡). The main conclusions remain unaltered and confirm that the D2h structures suffer a lower Pauli repulsion whereas those of Oh symmetry have more favourable electrostatic and orbital interactions. The interplay between the Pauli repulsion on the one hand and electrostatic and orbital interactions on the other determines the most favorable symmetry in each case.
Just to conclude this section, we must point out that the whole EDA and turn-upside-down analyses were performed with fragments in their quintet state. However, as we commented before this is not the most reasonable way to build B62− in D2h symmetry. Table S5 (ESI‡) contains the EDA for Oh and D2h B62− systems using B3− fragments in their triplet states. Results show that although the different terms are larger in the absolute value, the trends discussed above are not affected, and the D2h cluster is favoured mainly because of smaller Pauli repulsions.
Mixed metal clusters
In this section, we analyse the X2Y42− clusters with X, Y = B, Al, Ga and X ≠ Y (see Fig. 4). The relative energies of the planar and 3D forms are also enclosed in Table 1. In all cases, the D2h system is preferred when the cluster incorporates four B atoms; otherwise the 3D D4h geometry is the lowest in energy. In particular, the D2h symmetry is much more stable for Al2B42− and Ga2B42− by 66.9 and 79.4 kcal mol−1, respectively. On the other hand, when B is not the predominant atom, the D4h cluster is more stable by about 9–16 kcal mol−1. As for the homoatomic metal clusters, at the CCSD(T) level, the same trend is obtained, although the D4h system is stabilized with respect to the D2h one by 20–30 kcal mol−1. It is important to note that the D4h and D2h systems are not always the most stable for the X2Y42− clusters. For instance, for Al2B42−, a C2 geometry is the most stable form and, for B2Al42−, a C2v structure is the lowest in energy.18 However, we are not interested here in finding the most stable structure for each cluster but to discuss the reasons why in some cases 2D clusters are preferred over 3D and the other way round. Finally, Al3Ga32− also prefers an Oh geometry by 13.2 kcal mol−1. Unfortunately, this latter relative energy cannot be compared to those of B3Al32− or B3Ga32− because the strength of the localised bonding between three B atoms prevents the optimization of their 3D structures. In this context, it is worth mentioning that Alexandrova and coworkers26 found in X3Y3 (X = B, Al, Ga; Y = P, As) clusters that the lighter elements prefer 2D structures, whereas the heavier ones favour 3D geometries.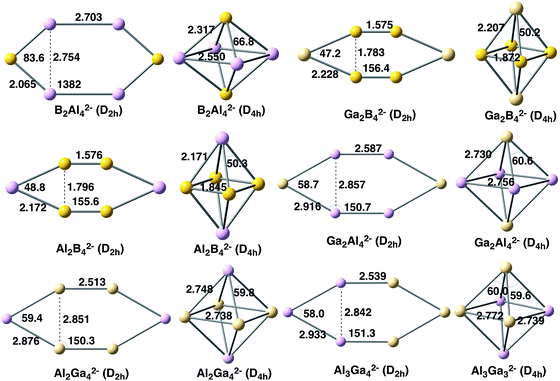 | ||
| Fig. 4 Geometries of mixed metal clusters analysed with planar and 3D geometries. Distances in Å and angles in degrees. | ||
The EDA was also performed for this series of six mixed metal clusters (see Table 3) with the aim to further understand the determinant force towards the most stable cluster. For the X2Y42− clusters, the EDA was carried out taken YXY− fragments in their quintet states. For Al3Ga32−, the fragments were Al3− and Ga3− in the quintet state too. For those systems for which the out-of-plane geometry is the most stable, the combination of more favourable electrostatic and orbital interactions, even though presenting larger Pauli repulsion, gives the explanation to the trend observed. This is the same behaviour already discussed above for both Al62− and Ga62− systems. On the other hand, when D2h symmetry is the cluster lower in energy, as for Al2B42− and Ga2B42− metal clusters, even though the D4h system presents more stable electrostatic interaction, now the orbital interactions in combination with less unfavourable Pauli repulsion favour the D2h symmetry. This latter behaviour differs from that of B62−, for which the orbital interactions also favour the Oh symmetry, thus making Pauli repulsion the determinant factor towards the preference for planar D2h B62−.
| ΔEint | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ||
|---|---|---|---|---|---|---|
| B2Al42− | D 4h | −52.1 | 440.1 | −202.7 | −285.7 | −3.9 |
| D 2h | −40.4 | 243.4 | −98.1 | −182.5 | −3.3 | |
| ΔE | 11.7 | −196.7 | 104.6 | 103.2 | 0.6 | |
| Al2B42− | D 4h | −75.1 | 584.0 | −251.7 | −404.1 | −3.3 |
| D 2h | −139.6 | 556.6 | −238.6 | −454.5 | −3.3 | |
| ΔE | −64.6 | −27.4 | 13.2 | −50.4 | 0.0 | |
| Al2Ga42− | D 4h | −35.0 | 381.2 | −201.0 | −210.6 | −4.6 |
| D 2h | −19.2 | 283.1 | −147.1 | −151.4 | −3.8 | |
| ΔE | 15.8 | −98.1 | 53.8 | 59.3 | 0.8 | |
| Ga2B42− | D 4h | −83.8 | 590.4 | −262.5 | −408.2 | −3.5 |
| D 2h | −157.5 | 540.0 | −225.6 | −468.6 | −3.2 | |
| ΔE | −73.7 | −50.4 | 36.8 | −60.4 | 0.3 | |
| Ga2Al42− | D 4h | −38.4 | 370.1 | −188.0 | −216.1 | −4.3 |
| D 2h | −20.6 | 218.0 | −90.8 | −144.4 | −3.6 | |
| ΔE | 17.8 | −152.0 | 97.3 | 71.7 | 0.8 | |
| Al3Ga32− | D 3h | −36.8 | 381.0 | −197.8 | −215.7 | −4.2 |
| C 3v | −20.7 | 254.4 | −122.8 | −148.7 | −3.6 | |
| ΔE | 16.1 | −126.6 | 75.0 | 67.0 | 0.6 | |
Conclusions
In previous studies,18 the preference of B62− for the planar D2h geometry and of Al62− for the 3D Oh one was justified by the inclination for localised covalent bonding in the former cluster and delocalised bonding in the latter. These two effects point in opposite directions. In the present work, we go one-step further by showing that the preference of B62− for the planar D2h form is due to two particular molecular orbital interactions. From one side the DHOMO−12h(b2u) formed from two tangential SOMO σT(b2) orbitals. This orbital is related to localised covalent bonding, and has a much more important weight in B62− than in Al62−, proving the dominant localised covalent character in the former. And the second determinant interaction is that of π character. In the case of OHOMO−1h(t2g) for B62−, its formation from two π SOMO orbitals is much less favourable than for Al62−. This result is in line with a dominant delocalisation force in Al clusters and more localised bonding in B metal clusters. For mixed clusters, we have found that those with more than two B atoms prefer the planar structure for same reasons discussed for B62−.Acknowledgements
This work was supported by the Ministerio de Economía y Competitividad (MINECO) of Spain (Project CTQ2014-54306-P) and the Generalitat de Catalunya (project 2014SGR931, Xarxa de Referència en Química Teòrica i Computacional, ICREA Academia 2014 prize for M.S., and grant No. 2014FI_B 00429 to O. E. B.). The EU under the FEDER grant UNGI10-4E-801 (European Fund for Regional Development) has also funded this research. J. P. thanks the National Research School Combination-Catalysis (NRSC-C), and The Netherlands Organization for Scientific Research (NWO/CW and NWO/NCF). The authors are grateful to Dr Ferran Feixas for fruitful discussions.References
- Y. Hu, T. J. Wagener, Y. Gao, H. M. Meyer and J. H. Weaver, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3037–3044 CrossRef CAS.
- B. Wang, H. Wang, H. Li, C. Zeng, J. G. Hou and X. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 035403 CrossRef.
- V. Torma, T. Reuter, O. Vidoni, M. Schumann, C. Radehaus and G. Schmid, ChemPhysChem, 2001, 2, 546–548 CrossRef CAS PubMed.
- R. N. Barnett, C. L. Cleveland, H. Häkkinen, W. D. Luedtke, C. Yannouleas and U. Landman, Eur. Phys. J. D, 1999, 9, 95–104 CrossRef CAS.
- S. Aldridge and A. J. Downs, The Group 13 Metals Aluminium, Gallium, Indium and Thallium: Chemical Patterns and Peculiarities, John Wiley & Sons, Ltd, Chichester, 2011 Search PubMed.
- A. N. Alexandrova, K. A. Birch and A. I. Boldyrev, J. Am. Chem. Soc., 2003, 125, 10786–10787 CrossRef CAS PubMed.
- A. N. Alexandrova and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3588–3592 CrossRef CAS PubMed.
- A. N. Alexandrova, A. I. Boldyrev, H.-J. Zhai and L.-S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866 CrossRef CAS.
- H.-J. Zhai, A. N. Alexandrova, L.-S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2003, 42, 6004–6008 CrossRef CAS PubMed.
- A. I. Boldyrev and L.-S. Wang, Chem. Rev., 2005, 105, 3716–3757 CrossRef CAS PubMed.
- A. E. Kuznetsov, K. A. Birch, A. I. Boldyrev, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 300, 622–625 CrossRef CAS PubMed.
- A. E. Kuznetsov, A. I. Boldyrev, H.-J. Zhai, X. Li and L.-S. Wang, J. Am. Chem. Soc., 2002, 124, 11791–11801 CrossRef CAS PubMed.
- X. Li, A. E. Kuznetsov, H.-F. Zhang, A. Boldyrev and L.-S. Wang, Science, 2001, 291, 859–861 CrossRef CAS PubMed.
- A. E. Kuznetsov, A. I. Boldyrev, H.-J. Zhai, X. Li and L.-S. Wang, J. Am. Chem. Soc., 2002, 124, 11791–11801 CrossRef CAS PubMed.
- O. C. Thomas, W.-J. Zheng, T. P. Lippa, S.-J. Xu, S. A. Lyapustina and K. H. Bowen, J. Chem. Phys., 2001, 114, 9895–9900 CrossRef CAS.
- A. N. Alexandrova, A. I. Boldyrev, H.-J. Zhai and L.-S. Wang, J. Chem. Phys., 2005, 122, 054313 CrossRef PubMed.
- A. N. Alexandrova, A. I. Boldyrev, H.-J. Zhai, L.-S. Wang, E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2003, 107, 1359–1369 CrossRef CAS.
- M. T. Huynh and A. N. Alexandrova, J. Phys. Chem. Lett., 2011, 2, 2046–2051 CrossRef CAS.
- J. M. Mercero, E. Matito, F. Ruipérez, I. Infante, X. Lopez and J. M. Ugalde, Chem. – Eur. J., 2015, 21, 9610–9614 CrossRef CAS PubMed.
- C. Corminboeuf, C. S. Wannere, D. Roy, R. B. King and P. v. R. Schleyer, Inorg. Chem., 2006, 45, 214–219 CrossRef CAS PubMed.
- O. El Bakouri, M. Duran, J. Poater, F. Feixas and M. Solà, Phys. Chem. Chem. Phys., 2016 10.1039/c5cp07011b.
- J. Ma, Z. Li, K. Fan and M. Zhou, Chem. Phys. Lett., 2003, 372, 708–716 CrossRef CAS.
- L.-M. Yang, J. Wang, Y.-H. Ding and C.-C. Sun, Phys. Chem. Chem. Phys., 2008, 10, 2316–2320 RSC.
- A. N. Alexandrova, Chem. Phys. Lett., 2012, 533, 1–5 CrossRef CAS.
- A. N. Alexandrova, M. J. Nayhouse, M. T. Huynh, J. L. Kuo, A. V. Melkonian, G. Chavez, N. M. Hernando, M. D. Kowal and C.-P. Liu, Phys. Chem. Chem. Phys., 2012, 14, 14815–14821 RSC.
- A. N. Alexandrova, M. R. Nechay, B. R. Lydon, D. P. Buchan, A. J. Yeh, M.-H. Tai, I. P. Kostrikin and L. Gabrielyan, Chem. Phys. Lett., 2013, 588, 37–42 CrossRef CAS.
- J. E. Fowler and J. M. Ugalde, J. Phys. Chem. A, 2000, 104, 397–403 CrossRef CAS.
- J. E. Fowler and J. M. Ugalde, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 383–388 CrossRef CAS.
- P. Farràs, N. Vankova, L. L. Zeonjuk, J. Warneke, T. Dülcks, T. Heine, C. Viñas, F. Teixidor and D. Gabel, Chem. – Eur. J., 2012, 18, 13208–13212 CrossRef PubMed.
- M. R. Fagiani, L. Liu Zeonjuk, T. K. Esser, D. Gabel, T. Heine, K. R. Asmis and J. Warneke, Chem. Phys. Lett., 2015, 625, 48–52 CrossRef CAS.
- J. K. Olson and A. I. Boldyrev, J. Phys. Chem. A, 2013, 117, 1614–1620 CrossRef CAS PubMed.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS.
- M. El-Hamdi, W. Tiznado, J. Poater and M. Solà, J. Org. Chem., 2011, 76, 8913–8921 CrossRef CAS PubMed.
- M. El-Hamdi, O. El Bakouri El Farri, P. Salvador, B. A. Abdelouahid, M. S. El Begrani, J. Poater and M. Solà, Organometallics, 2013, 32, 4892–4903 CrossRef CAS.
- M. El-Hamdi, M. Solà, G. Frenking and J. Poater, J. Phys. Chem. A, 2013, 117, 8026–8034 CrossRef CAS PubMed.
- R. Islas, J. Poater, E. Matito and M. Solà, Phys. Chem. Chem. Phys., 2012, 14, 14850–14859 RSC.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02 ed., Gaussian, Inc., Pittsburgh, PA, 2009 Search PubMed.
- J. Cizek, J. Chem. Phys., 1966, 45, 4256–4266 CrossRef CAS.
- G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, in Rev. Comput. Chem., ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- F. M. Bickelhaupt, A. Diefenbach, S. P. de Visser, L. J. de Koning and N. M. M. Nibbering, J. Phys. Chem. A, 1998, 102, 9549–9553 CrossRef CAS.
- C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed.
- I. Fernández and G. Frenking, Faraday Discuss., 2007, 135, 403–421 RSC.
- I. Fernández and G. Frenking, Chem. – Eur. J., 2007, 13, 5873–5884 CrossRef PubMed.
- R. Islas, J. Poater and M. Solà, Organometallics, 2014, 33, 1762–1773 CrossRef CAS.
- F. Feixas, E. Matito, J. Poater and M. Solà, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 105–122 CrossRef CAS.
- P. Bultinck, R. Ponec and S. Van Damme, J. Phys. Org. Chem., 2005, 18, 706–718 CrossRef CAS.
- F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434–6451 RSC.
- J. Poater, M. Duran, M. Solà and B. Silvi, Chem. Rev., 2005, 105, 3911–3947 CrossRef CAS PubMed.
- E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2005, 122, 014109 CrossRef PubMed.
- E. Matito, ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning, Institute of Computational Chemistry and Catalysis, Girona, 2006, http://iqc.udg.es/~eduard/ESI Search PubMed.
- S. Alvarez, Dalton Trans., 2013, 42, 8617–8636 RSC.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, S23, 199–207 Search PubMed.
- J. M. L. Martin, in Energetics of Stable Molecules and Reactive Intermediates, ed. M. S. Minas da Piedade, Kluwer Academic Publishers, Dordrecht, 1999, vol. 535, pp. 373–417 Search PubMed.
- J. Poater, R. Visser, M. Solà and F. M. Bickelhaupt, J. Org. Chem., 2007, 72, 1134–1142 CrossRef CAS PubMed.
- E. Díaz-Cervantes, J. Poater, J. Robles, M. Swart and M. Solà, J. Phys. Chem. A, 2013, 117, 10462–10469 CrossRef PubMed.
Footnotes |
| † This work is dedicated to Prof. Evert Jan Baerends as a proof of our admiration for his brilliant contributions to chemistry and of our gratitude for helping us to understand chemistry better. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01109h |
| This journal is © the Owner Societies 2016 |