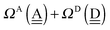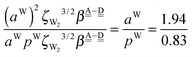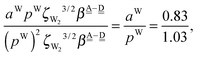Electronic origin of the dependence of hydrogen bond strengths on nearest-neighbor and next-nearest-neighbor hydrogen bonds in polyhedral water clusters (H2O)n, n = 8, 20 and 24†
Received
14th April 2016
, Accepted 22nd June 2016
First published on 28th June 2016
Abstract
The influence of the nearest neighbor and next-nearest neighbor water molecules on the strength of the hydrogen (H) bonds was examined for the polyhedral clusters of cubic (H2O)8, dodecahedral (H2O)20 and tetrakaidecahedral (H2O)24 cages. The relative stability and the characteristics of the H bond networks are also studied. The charge-transfer (CT) and dispersion interaction terms of every pair of H bonds are evaluated using perturbation theory based on the locally-projected molecular orbitals (LPMO PT). Every water molecule and every H-bonded pair in these polyhedral clusters are classified by the types of the neighbor molecules and H bonds. The relative binding energies among the polyhedral clusters are grouped by these classifications. The optimized O⋯O distances, which are strongly correlated with the calculated pairwise CT terms, are dependent on the 49 sub-groups of the H bonds determined by the type of the neighbor molecules. The electronic origin of this dependence is analyzed using Mulliken's charge-transfer theory, and employing a few assumptions, the analytical formulas for the contribution of the CT terms to the H bond energy are derived.
Introduction
Among the finite size of pure water clusters, the polyhedral forms exhibit some unique features. The cubic cage of (H2O)8 consists of 6 four-membered rings (46),1 the dodecahedral cage of (H2O)20 consists of 12 five-membered rings (512),1,2 and the tetrakaidecahedral cage of (H2O)24 consists of 12 five-membered rings and 2 six-membered rings (51262).1,3 There are several graph theoretical studies for water clusters,1,4–9 and some are specific for polyhedral forms, and the others are more general. These studies showed that there are 14 distinct isomers of the cubic cage of (H2O)8, while there are 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 symmetry-distinct configurations for the dodecahedral cage of (H2O)20,1,5 and 3
026 symmetry-distinct configurations for the dodecahedral cage of (H2O)20,1,5 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043
043![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 for the tetrakaidecahedral cage of (H2O)24.3,6 Every water molecule in these polyhedral clusters participates in three hydrogen bonds (H bonds) to neighbors; one hydrogen-donating OH and two hydrogen-accepting O⋯H (hereafter, this type of water is called daa),2,10–15 or two hydrogen-donating OH and one hydrogen-accepting O⋯H (dda). Anick called them F and L, respectively.7,8 Water dda (F) has a “free” OH, often called a dangling OH bond. The polyhedral cages consist of n/2 dda and n/2 daa water molecules.7 Therefore, there are only four types of hydrogen bonds in the polyhedral clusters, viz. daa⇐daa, daa⇐dda, dda⇐daa, and dda⇐dda. Among them, the bond dda⇐daa is the strongest.16–18 Smith and Dang called the bonds “defect” if both of the neighbor pair are either dda or daa, suggesting that dda⇐dda and daa⇐daa are weaker than the other types of pairs.1,2 Because of the fixed arrangement of the oxygen atoms among numerous distinct isomers and the restricted types of the hydrogen bonds in the clusters, the polyhedral water clusters are ideal to probe the characteristics of the hydrogen bonded networks and the factors determining the strength of the H bonds. The above four types of H bonds are further sub-grouped by the types of the neighboring water molecules. One of the ways is to use the “topological index” of an H bond ξ,19 which is defined as a sum of the number of dd neighbors at the H donor and the number of aa neighbors at the H acceptor. The index ranges from 0 to 4. Thus, there are 20 subsets of the types of the H bonds. Anick used the index in his analysis of the calculated OH harmonic frequencies, and further classified the H bonds by introducing the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor; their values are 0 if the neighbor (secondary) water is daa, and 1 if the neighbor water is dda.8,20,21 With this classification, there are 49 sub-groups of the H bonds (see below). Using these descriptors, he demonstrated that the H bond distances can be fitted linearly. He further extended the models to include the influence from the ternary water molecules.
836 for the tetrakaidecahedral cage of (H2O)24.3,6 Every water molecule in these polyhedral clusters participates in three hydrogen bonds (H bonds) to neighbors; one hydrogen-donating OH and two hydrogen-accepting O⋯H (hereafter, this type of water is called daa),2,10–15 or two hydrogen-donating OH and one hydrogen-accepting O⋯H (dda). Anick called them F and L, respectively.7,8 Water dda (F) has a “free” OH, often called a dangling OH bond. The polyhedral cages consist of n/2 dda and n/2 daa water molecules.7 Therefore, there are only four types of hydrogen bonds in the polyhedral clusters, viz. daa⇐daa, daa⇐dda, dda⇐daa, and dda⇐dda. Among them, the bond dda⇐daa is the strongest.16–18 Smith and Dang called the bonds “defect” if both of the neighbor pair are either dda or daa, suggesting that dda⇐dda and daa⇐daa are weaker than the other types of pairs.1,2 Because of the fixed arrangement of the oxygen atoms among numerous distinct isomers and the restricted types of the hydrogen bonds in the clusters, the polyhedral water clusters are ideal to probe the characteristics of the hydrogen bonded networks and the factors determining the strength of the H bonds. The above four types of H bonds are further sub-grouped by the types of the neighboring water molecules. One of the ways is to use the “topological index” of an H bond ξ,19 which is defined as a sum of the number of dd neighbors at the H donor and the number of aa neighbors at the H acceptor. The index ranges from 0 to 4. Thus, there are 20 subsets of the types of the H bonds. Anick used the index in his analysis of the calculated OH harmonic frequencies, and further classified the H bonds by introducing the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor; their values are 0 if the neighbor (secondary) water is daa, and 1 if the neighbor water is dda.8,20,21 With this classification, there are 49 sub-groups of the H bonds (see below). Using these descriptors, he demonstrated that the H bond distances can be fitted linearly. He further extended the models to include the influence from the ternary water molecules.
Recently, one of the present authors (S.I.) has developed the perturbation theory based on the locally projected molecular orbital (LPMO PT) and applied it to several molecular clusters.22,23 The zero-order energy is exactly free of Basis Set Superposition Error (BSSE) with any basis set, and because of the proper definition of the excited orbitals, the perturbation correction is approximately BSSE-free.24 By using the augmented basis functions, and by adding the dispersion (Disp) terms properly, the method provides reasonably accurate binding energies for H bonded clusters, halogen bonded dimers and weak charge-transfer (CT) complexes.23,25 One of the advantages of this method is that the contribution to the interaction energy from the CT terms can be expressed by a sum of the terms of every pair of H bonded molecules as the contributions from the Disp terms are. The pairwise terms of the CT and Disp terms in the water clusters have been shown to be strongly correlated with the H bond distance in water clusters,26,27 and they have been used as an alternative measure of the strength of the H bonds in analyzing the H bonded networks in (H2O)20 and (H2O)25.27 The present paper is an extension of these previous studies to representative polyhedral water clusters.
With the aid of the CT term of each H bond, the electronic origins of the dependence of the H bond strength on the types of the neighboring waters and on the H bond networks are elucidated. To analyze them, we adopt the classical model theory of the charge-transfer (electron-donor–aceptor) interaction proposed by Mulliken.28 The wave function for an H bond 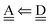 is given by
is given by
| | 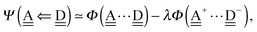 | (1) |
where
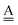
and
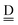
stand for the hydrogen acceptor and donor.
29–31 The electron donor orbital is the non-bonding orbital of the hydrogen acceptor water molecule
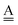
, and the electron acceptor orbital is the anti-bonding σ
OH* of the hydrogen donor water molecule
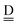
. These frontier molecular orbitals, which participate the CT electronic configurations, undergo changes by the neighboring H bonds. Based on a few simple assumptions, the analytical forms of the CT contributions to the H bond energy of 49 sub-groups defined by Anick
8,21 are derived, and they are well correlated with the H bond distances and with the calculated CT terms, averaged over all of cube isomers of (H
2O)
8 and over 13 most stable dodecahedral (H
2O)
20. The model theory can be extended to any H bonded networks, which are found in more complicated caged clusters than in the polyhedral clusters.
The goals of the present study are (1) to demonstrate that the strength of H bonds is influenced by the types of the other two neighbor H bonds in the polyhedral water clusters and that accordingly, there are 49 sub-grouped H bonds, whose strengths are distinct from those of the others, and (2) to elucidate the electronic origin of this dependence in terms of the Mulliken's CT theory. (3) Besides, the relative stability among the isomers is related to the different numbers of the sub-grouped H bonds in the isomers.
Theoretical and computational procedure
The binding energy and pairwise energy
The perturbation expansion theory based on the locally projected molecular orbital (LPMO PT) has been previously developed by one of the authors.22,23,25,32–34 Here we describe only a few salient features that pertain to the current discussion. The zero order wave function ΨLPMO for a molecular cluster is a single Slater determinant constructed from sets of strictly local MOs variationally determined by a coupled set of Hartree–Fock equations. The equations are derived under the strong constraint that the occupied MOs for each molecule are expanded only with the basis sets placed on that molecule. The zero and first order wave function is| | 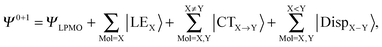 | (2) |
where |LEX〉 stands for the single excitations within molecule X and |CTX→Y〉 stands for the single excitations from molecule X to Y, whereas |DispX−Y〉 denotes for the double excitations of the dispersion type. When the number of molecules in the cluster is larger than 3, the required computation time up to the single excitation PT calculation is much shorter than for the supermolecule HF calculation. This expansion is made possible by defining the locally projected excited MOs, most of which are expanded in terms of the basis sets on each molecule X.24 The binding energy of the clusters is defined as| | 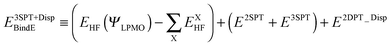 | (3) |
| | 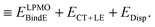 | (4) |
The first parenthesis in eqn (3) represents the binding energy evaluated by LPMO, and defines the energy ELPMOBindE, which contains the electrostatic and exchange-repulsion terms and a part of induction terms. The second parenthesis in eqn (3) is the second and third order correction PT contribution from the single excitations, which is expressed by the sums| | 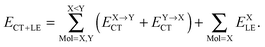 | (5) |
The contribution from the local excitations is non-zero only at the third order and always much smaller than the CT terms, because the occupied LPMOs are canonical within each molecule. In other words, ELPMOBindE does contain most of the induction terms, which are defined by the second order perturbation theory expanded in terms of the products of the wave functions of the isolated monomers. According to the previous literature,35–37 the induction terms are the contribution from the products in which one of the wave functions of the monomers is for the excited state, and the dispersion terms are that from the products in which two of the wave functions are for the excited states. The polarization terms are the sum of both. Under this formalism, the CT terms are a part of the induction terms, but note that ELPMOBindE in our theory does not contain the CT terms, which are separately evaluated by the second and third order PT as ECT+LE. By using the MC+BS (monomer-centered plus basis sets), which allows that the excited orbitals are delocalized over molecules, the SAPT could evaluate the CT contribution.37 In the polarizable model functions such as TTM2-R,38 the atomic (not molecular) centered polarizability might be able to effectively include the CT contributions. The term ELPMOBindE in eqn (3) is the dominant term in the binding energy. The LPMO wave function ΨLPMO is a single Slater determinant, and in that sense, it is a kind of the supermolecule wave function. Therefore, the decomposition of ELPMOBindE to the sum of electrostatic, exchange-repulsion, and induction terms requires further model calculations, and in particular, for the clusters of many molecules, the analysis is not straightforward.
The CT term for a pair of water molecules is used to identify the H bond. Because the clusters studied in the present study are of polyhedral form, the O–O distance or O–HO distance can be used as the criteria of the H bond, as often used. In the previous studies,26 the CT criteria helped to find the weak H bonds in some complex cage structures of water clusters and to locate the cyclic networks. Subsequently, the hydrogen bonding matrix HB, defined by Miyake and Aida,9 is constructed from the digraph for the cluster.4 By manipulating the matrix, the types of the water molecules and of the hydrogen bonds are identified. To analyze the clusters, a code was developed with python3/numpy.
Computational details
The geometries of cubic water clusters (H2O)8 were optimized with the MP2/aug-cc-pVDZ level in the present study. For (H2O)20 we used the thirteen isomers optimized by Xantheas at the MP2/aug-cc-pVDZ level,39 which are among a larger set of isomers determined by empirical potential energy functions. The isomers of tetrakaidecahedral (H2O)24 are the 20 most stable ones, optimized at the DFT/B3LYP/aug-cc-pVDZ level.40 A few additional higher lying stable isomers are selected for comparison.
The calculations were carried out using the in-house ab initio MO package, MOLYX, on a local Mac Pro and on the SGI UV2000 at the RCCS, Okazaki Research facilities of National Institutes of Natural Science (NINS). The required computer resources for (H2O)24/aug-cc-pVDZ on the SGI UV2000 were 32 cores (16G memory each) and 236 h 42 m cpu (11 h 05 m wall) time for LPMO 3SPT + Disp. The present code is partially parallelized using OpenMP.
Results and discussion
Relative energies
The relative energies of the polyhedral cages of (H2O)n isomers for n = 8, 20 and 24 studied in the present work are shown in Fig. 1. Table 1 compares the relative (with respect to the most stable isomer) binding energies of all of the cube (H2O)8 isomers evaluated by eqn (4) of LPMO PT, and by the MP2 method. The energy in the third column is evaluated by replacing the HF energy with EHF(ΨLPMO) + E2SPT + E3SPT in eqn (3). In previous studies,23,34,41 the evaluated energy is shown to be close to the counterpoise (CP) corrected HF binding energy if the augmented basis functions are used. By adding the dispersion term EDisp as in eqn (4), E3SPT+DispBindE comes close to the approximately CP corrected HF plus MP2 binding energy EapprCP_HF+MP2. For instance, E3SPT+DispBindE/aug-cc-pVDZ for Cl−(H2O) and Cl−(H2O)2 is −62.0 and −125.5 kJ mol−1, respectively.41 The corresponding EapprCP_HF+MP2/aug-cc-pVxZ binding energies are −57.6 (x = D), −61.2 (x = T), −62.1 (x = Q) and −62.5 (x = 5) kJ mol−1 for Cl−(H2O),42 and −112.7 (x = D), −125.3 (x = T), −114.3 (x = Q) kJ mol−1 for Cl−(H2O)2.41
 |
| | Fig. 1 Relative binding energy of polyhedral water clusters of (H2O)n. (a) n = 8, (b) n = 20, and (c) n = 24. See text and Table 4 for A, B, C and D in (c). | |
Table 1 Relative energies (kJ mol−1) of the cubic isomers of (H2O)8
| Isomera |
E
3SPT+DispBindE (eqn (4)) |
E
apprCP_HF+MP2BindE
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
E
HF+MP2BindE
|
dda(s,t)c |
See Fig. 2 for the labelling of isomers. The first number is the number of the dda⇐daa pairs, Mdda⇐daa (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) bFL), and the second is the ordering of the binding energy.
The HF binding energy is replaced with ELPMOBindE + ECT+LE in eqn (4).
The number of dda(s,t) type waters; (s,t) = (0,3), (1,2), (2,1), (3,0). daa(s,t) = dda(t,s). See text. bFL), and the second is the ordering of the binding energy.
The HF binding energy is replaced with ELPMOBindE + ECT+LE in eqn (4).
The number of dda(s,t) type waters; (s,t) = (0,3), (1,2), (2,1), (3,0). daa(s,t) = dda(t,s). See text.
|
| 4-1 |
0.0 |
0.0 |
0.0 |
4,0,0,0 |
| 4-2 |
0.32 |
0.07 |
0.16 |
4,0,0,0 |
| 2-1 |
12.51 |
12.09 |
12.42 |
0,4,0,0 |
| 2-2 |
12.76 |
12.27 |
12.71 |
0,4,0,0 |
| 2-3 |
16.65 |
16.84 |
17.43 |
1,2,1,0 |
| 2-4 |
16.66 |
16.50 |
17.04 |
1,2,1,0 |
| 2-5 |
16.89 |
17.07 |
17.71 |
1,2,1,0 |
| 2-6 |
16.99 |
16.12 |
16.44 |
1,2,1,0 |
| 1-1 |
26.37 |
26.49 |
27.44 |
0,2,2,0 |
| 1-2 |
27.01 |
27.03 |
28.20 |
0,2,2,0 |
| 1-3 |
27.10 |
26.68 |
27.48 |
0,2,2,0 |
| 1-4 |
30.93 |
30.83 |
31.73 |
0,3,0,1 |
| 0-1 |
42.07 |
44.19 |
46.02 |
0,0,4,0 |
| 0-2 |
42.10 |
44.40 |
46.26 |
0,0,4,0 |
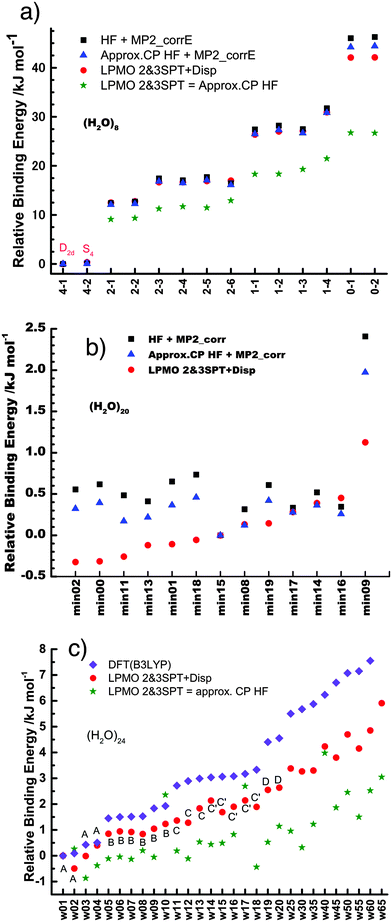
Table 1 and Fig. 1a clearly show that in terms of the stability there are four groups of the cubic (H2O)8 isomers, whose Schlegel diagrams are given in Fig. 2.43 The corresponding ball-and-stick figures are given in ESI.†Fig. 3 shows the correlation between the CT and dispersion (Disp) terms and the O⋯O distance for every pair of the H bonds in all cubic (H2O)8 isomers and in the thirteen dodecahedral (H2O)20 isomers studied. The plots distinguish four types of the H bonds, viz. daa⇐daa, daa⇐dda, dda⇐daa, and dda⇐dda; for each type. The strongest H bonds are of the dda⇐daa type, as previously reported.8,10,12,17,44 By proposing the ‘Strong–Weak-Effective-Bond’ (SWEB), Kirov, Fanourgakis and Xantheas classified the H bonds on the surface of polyhedral water clusters to five groups, namely t1d, t1a, c2, c0 and c1a.44 Their classification was based on the relative orientations as well as the connectivity to neighbors. As shown in Fig. 3, the present four types correspond to theirs except that our daa⇐dda includes both t1a and c1a. Similarly, Chihaia et al. classified the H bonds in the buckyball water clusters to five types.3 By explicitly counting the types of the neighboring water molecules, Kuo et al. defined the “topological index” ξ for H bonds as a sum of the number of dd neighbors at the H donor and the number of aa neighbors at the H acceptor.19,21 The index was shown to be related to the H bond distance. Anick further classified the H bonds by introducing the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor; there are 49 sub-groups of H bonds,8,20 which are more explicitly analyzed below in detail. The binding energy of the clusters is correlated with the types of the H bonds in the cluster.
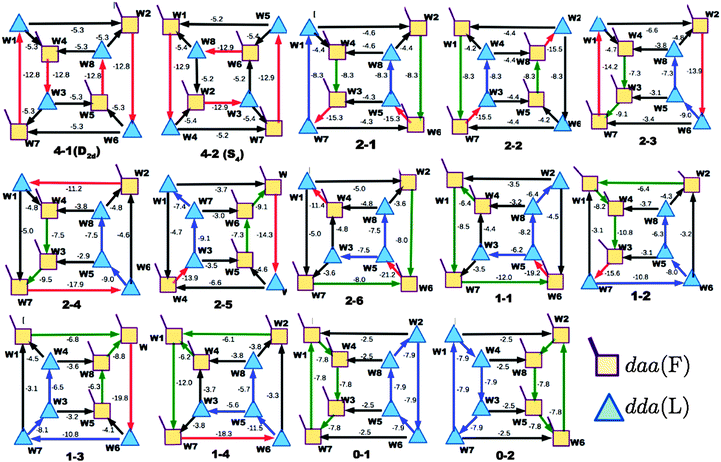 |
| | Fig. 2 Schlegel diagrams of all of cubic (H2O)8 isomers. The triangles are dda waters, and the squares are daa waters. See the corresponding ball-and-stick figures in ESI.† | |
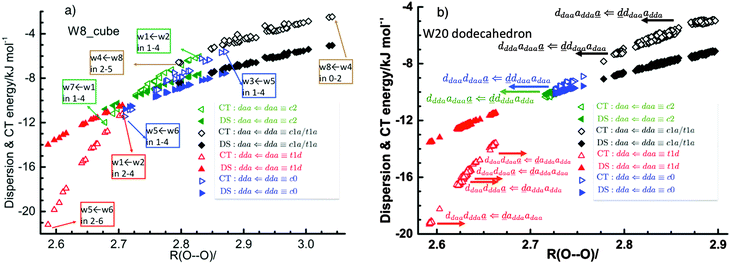 |
| | Fig. 3 Correlation of the charge-transfer energy EX,YCT and dispersion EX,YDisp energies per H bond for (a) cubic (H2O)8 and (b) dodecahedral (H2O)20 with the O⋯O bond distance/Å. | |
The first column of Table 1 is the label of the cubic (H2O)8 isomers; the first number of the label is the number of the pairs, Mdda⇐aad, of dda⇐daa, which is the strongest among the four types of the H bonds. The total binding energies are grouped by Mdda⇐daa, which is equivalent to parameter bFL defined by Anick.8 He demonstrated that the total energy of the cube isomers is linear to bFL.
Among the isomers of Mdda⇐daa = 2, the first two isomers, which have the mirror-imaged isomers, are more stable than the next four isomers. To examine the cause of the difference among the M = 2 isomers, the dda water molecules are further sub-grouped by the types of three nearest neighbor water molecules as dda(s,t) with (s,t) = (0,3), (1,2), (2,1), or (3,0), where (s,t) implies that the water molecule bonds to s water molecules of the dda type and t water molecules of the daa type. The list (0,4,0,0) implies that isomers 2-1 and 2-2 have four dda(1,2). Their Schlegel diagrams show that every (triangle) dda molecule has one triangle dda and two squares daa as the neighbor molecules. The number of dda(2,1) waters is equivalent to aTh of Anick,8 who showed that larger aTh clusters are less stable. The next four isomers share the common list (1,2,1,0). Among the isomers of Mdda⇐daa = 1, the first three of them have the common list (0,2,2,0), and their binding energies are quite close to each other.
This dependence of the relative stability on the list of the sub-groups of water molecules in the cluster is the consequence of the strong dependence of the H bond strength on the pairs of neighboring molecules. To demonstrate it clearly, some of the pairs of the H bonds are explicitly indicated in Fig. 3.
Interestingly, the fitted function in the early work by McDonald et al.1 successfully distinguished Mdda⇐daa from that of the other types of pairs, but failed to differentiate among the isomers of the same Mdda⇐daa.
All dodecahedral (H2O)20 and tetrakaidecahedral (H2O)24 cage isomers studied are a family of Mdda⇐daa = 7 and 9, respectively, as reported earlier. They are only those of the most stable isomers,2,20,45,46 therefore, the lists of the sub-groups of water molecules are (4,6,0,0) for (H2O)20 and (6,6,0,0) for (H2O)24 in the present study. As mentioned in the Introduction, there is a large number of isomers, which belong to the other lists.
Effect of the next-nearest-neighbor hydrogen bonds
In polyhedral water clusters, there are seven types of H donors and of H acceptors, depending on the types of two neighboring waters.8Fig. 4 depicts these seven types of H donors and H acceptors. When a dda water (triangle in Fig. 2 and 4) is a hydrogen donor for a hydrogen bond, this water has an H donating to a neighbor water and an HO accepting from a neighbor water. Because the neighbor waters are either dda or daa, as shown in the first row of Fig. 4, there are four types of the hydrogen donors of dda depending on the types of waters at the other end of the neighbor hydrogen bonds. Symbol ![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa implies that the hydrogen donor,
dddaadaa implies that the hydrogen donor, ![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) da, donates a H atom to a neighbor dda water and accepts a H atom from a neighbor daa water. As shown in the second row of Fig. 4, when daa (square) is the hydrogen donor for a hydrogen bond, this water should have two H atoms accepting from the neighboring waters, and there are three types of the hydrogen donor daa in polyhedral water clusters. Similarly, when a dda water is the hydrogen acceptor in a hydrogen bond, as shown in the third row of Fig. 4, there are three types of hydrogen acceptors, depending on the neighbor waters. On the other hand, when a daa water is a hydrogen acceptor, the fourth row of Fig. 4 shows that there are four types of the hydrogen acceptors. Symbol dddaddda
da, donates a H atom to a neighbor dda water and accepts a H atom from a neighbor daa water. As shown in the second row of Fig. 4, when daa (square) is the hydrogen donor for a hydrogen bond, this water should have two H atoms accepting from the neighboring waters, and there are three types of the hydrogen donor daa in polyhedral water clusters. Similarly, when a dda water is the hydrogen acceptor in a hydrogen bond, as shown in the third row of Fig. 4, there are three types of hydrogen acceptors, depending on the neighbor waters. On the other hand, when a daa water is a hydrogen acceptor, the fourth row of Fig. 4 shows that there are four types of the hydrogen acceptors. Symbol dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) implies that the hydrogen acceptor is dda, donating a H atom to two dda waters. Thus, if two neighbor waters of both of the hydrogen donor and acceptor waters are taken into account, there are 49 types of H bonds as shown in Fig. 4.8
implies that the hydrogen acceptor is dda, donating a H atom to two dda waters. Thus, if two neighbor waters of both of the hydrogen donor and acceptor waters are taken into account, there are 49 types of H bonds as shown in Fig. 4.8
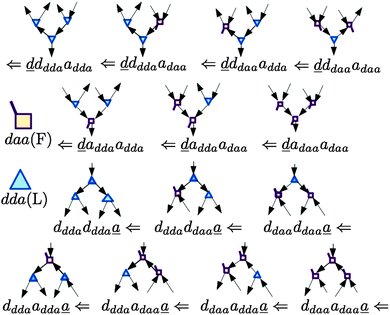 |
| | Fig. 4 Seven types of the hydrogen donors and acceptors. The upper seven hydrogen donors correspond to the column in Tables 2 and 3, and the lower seven hydrogen acceptors correspond to the row. | |
These 49 sub-groups of the hydrogen bonds are same with those characterized by the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor by Anick.20 The average hydrogen bond length R(O⋯O) and the CT term for each type of the hydrogen bonds are given in Table 2 for (H2O)8 and in Table 3 for (H2O)20. In Table 2, the “topological index”, ξ, of Kuo et al. is given in square brackets.19 The values in the tables are the averaged ones over all isomers studied; note that for (H2O)8 all of the possible polyhedral isomers are studied, but for (H2O)20 only the most stable thirteen isomers are examined. Therefore, the averaged value for the H bond types for (H2O)20 is favored for the strong H bonds, and therefore, Table 3 lacks some of the H bond sub-groups found in Table 2. The corresponding table for (H2O)24 is very similar to Table 3 for (H2O)20. Because the clusters of (H2O)24 were optimized at the DFT/B3LYP/aug-cc-pVDZ level, while the clusters of (H2O)8 and (H2O)20 were optimized at the MP2/aug-cc-pVDZ level, the direct numerical comparison is not meaningful.
Table 2 The CT energy (kJ mol−1) and O⋯O distance (Å) for the hydrogen bond types in cube (H2O)8 isomers.a In each pair of H-bond types, the first line is the number of cases of the pairs and the topological index ξ in square brackets. The second and third lines are the averaged CT energy and O⋯O distance with the standard deviation in parentheses
| |
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda d
daa
a
dda
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
dda
daa d
dda
daa
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda d
daa
a
dda
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
daa d
daa
a
daa
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda a
dda
a
dda
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa a
dda
a
daa
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
daa
a
daa a
daa
a
daa
|
|
See Fig. 4 for the types of hydrogen donors and of acceptors.
|
d
dda
d
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
0 |
0 |
0 |
1, [0] |
0 |
1, [1] |
1, [0] |
|
|
|
|
|
−11.45(0.00) |
|
−19.22(0.00) |
−21.18(0.00) |
|
|
|
|
|
2.710(0.00) |
|
2.605(0.00) |
2.587(0.00) |
d
daa
d
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
0 |
1, [2] |
10, [2] |
5, [1] |
2, [3] |
7, [2] |
1, [1] |
|
|
|
−8.21(0.00) |
−7.93(0.05) |
−9.77(0.86) |
−13.93(0.01) |
−16.20(1.20) |
−19.84(0.00) |
|
|
|
2.778(0.00) |
2.799(0.003) |
2.744(0.020) |
2.665(0.001) |
2.635(0.011) |
2.597(0.00) |
d
daa
d
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
2, [4] |
3, [3] |
6, [3] |
4, [2] |
10, [4] |
2, [3] |
0 |
|
|
−5.65(0.00) |
−7.09(0.61) |
−6.91(0.51) |
−8.31(0.02) |
−12.54(0.62) |
−14.29(0.05) |
|
|
|
2.868(0.000) |
2.803(0.020) |
2.826(0.017) |
2.776(0.001) |
2.685(0.010) |
2.658(0.002) |
|
|
|
d
dda
a
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
0 |
1, [1] |
5, [1] |
18, [0] |
4, [2] |
5, [1] |
1, [0] |
|
|
|
−4.61(0.00) |
−4.76(0.05) |
−5.46(0.40) |
−8.31(0.03) |
−9.93(0.88) |
−11.99(0.00) |
|
|
|
2.869(0.000) |
2.890(0.003) |
2.844(0.016) |
2.758(0.005) |
2.718(0.020) |
2.678(0.000) |
d
dda
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
1, [3] |
3, [2] |
5, [2] |
1, [1] |
3, [3] |
1, [2] |
0 |
|
|
−3.14(0.00) |
−4.02(0.41) |
−4.16(0.35) |
−4.99(0.00) |
−7.59(0.54) |
−8.77(0.00) |
|
|
|
2.985(0.000) |
2.910(0.024) |
2.921(0.021) |
2.868(0.000) |
2.778(0.016) |
2.745(0.000) |
|
d
daa
a
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
4, [3] |
5, [2] |
16, [2] |
5, [1] |
6, [3] |
10, [2] |
0 |
|
|
−3.16(0.02) |
−3.93(0.47) |
−4.10(0.34) |
−4.82(0.15) |
−6.87(0.50) |
−7.92(0.23) |
|
|
|
2.976(0.007) |
2.908(0.025) |
2.923(0.021) |
2.871(0.005) |
2.796(0.016) |
2.762(0.006) |
|
d
daa
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
11, [4] |
1, [3] |
4, [3] |
0 |
2, [4] |
0 |
0 |
|
|
−2.63(0.22) |
−3.09(0.00) |
−3.55(0.07) |
|
−6.12(0.00) |
|
|
|
|
3.028(0.019) |
2.965(0.000) |
2.965(0.005) |
|
2.826(0.000) |
|
|
Table 3 The CT energy (kJ mol−1) and O⋯O distance (Å) for the hydrogen bond types in dodecahedral (H2O)20 isomers
| H-donora |
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
dda
a
daa d
dda
a
daa
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda d
daa
a
dda
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
adaa d
daa
adaa
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda a
dda
a
dda
|
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa a
dda
a
daa
|
| H-acceptora |
|
See Fig. 4 for the types of hydrogen donors and of acceptors.
|
d
daa
d
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
|
|
|
−16.19 |
−19.13 |
|
|
|
|
2.627 |
2.594 |
|
|
d
daa
d
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
|
|
−9.59 |
−14.14 |
−16.01 |
|
|
|
2.735 |
2.654 |
2.627 |
|
|
d
dda
a
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
−6.01 |
−6.24 |
−7.07 |
−9.98 |
|
| 2.833 |
2.838 |
2.800 |
2.725 |
|
|
|
d
dda
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
−5.16 |
−5.15 |
−6.16 |
|
|
| 2.877 |
2.885 |
2.838 |
|
|
|
|
d
daa
a
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
|
−5.01 |
−5.05 |
−5.92 |
|
|
| 2.877 |
2.888 |
2.841 |
|
|
As shown in Table 2, the standard deviations both for the CT terms and O⋯O distances are small. The largest ones in cubic isomers (H2O)8 are 0.47 kJ mol−1 and 0.025 Å for ddaaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa (the number of cases is 5). For (H2O)20, the largest standard deviations are 0.46 kJ mol−1 and 0.008 Å, respectively, for ddaaddda
dddaadaa (the number of cases is 5). For (H2O)20, the largest standard deviations are 0.46 kJ mol−1 and 0.008 Å, respectively, for ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa (the total number of cases is 26).
dddaadaa (the total number of cases is 26).
Tables 2 and 3 are split to four blocks of dda⇐daa, dda⇐dda, daa⇐daa, and daa⇐dda; which correspond to four symbols in Fig. 3. In each block, smaller ξs (the values in square brackets) are for larger CT terms and shorter H bond distances. The “defect” H bonds, as defined by Smith and Dang,2 are those in the upper left and lower right blocks in tables.
The large distribution of the plots for the same types of the H bonds found in Fig. 3 results from the dependence of the H bond strength on the types of two neighbor water molecules.
Table 4 shows the average CT energy and O⋯O distance for four of the strongest types of the H bonded pairs in the (H2O)24 isomers in Fig. 1(c), where the first 20 isomers are labeled A, B, C, C′ and D. Their stability is grouped by the number of the H bonded pair sub-groups. The most stable isomers (A) have three ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda, and the next group (B) has two.
addaadda, and the next group (B) has two.
Table 4 Characteristics of tetrakaidecahedral (H2O)24 isomers
Charge-transfer theory of Mulliken
Tables 2–4 clearly show that the strength of an H bond is influenced from the types of the two other neighbor waters of the H donor and H acceptor molecules. To further look for the electronic structure origin of this finding, we adopt the classical model theory of the charge-transfer (electron-donor–acceptor) interaction by Mulliken.29–31
The wave function for an H bond is given by eqn (1), where, for instance, 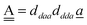 and
and 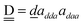 . By assuming a weak interaction, the mixing coefficient is approximately given [Assumption A] as
. By assuming a weak interaction, the mixing coefficient is approximately given [Assumption A] as
| | 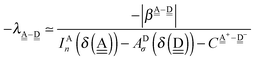 | (6) |
where
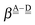
is the resonance integral and
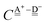
the Coulomb attraction term. The effective ionization energy of the donor orbital,
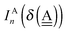
, and the electron affinity of the acceptor orbital,
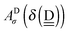
, are assumed to be functions of the net charges,
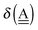
and
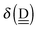
, of the molecules [Assumption B]. Recently Xu and coworkers computationally demonstrated the linear dependence of the ionization energy and electron affinity on a small fractional charge,
47 using their double hybrid DFT.
48 The following linear forms
| | IAn(δ) = IW0 + ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) Wδ Wδ | (7) |
are used in Assumption B. The linear coefficients
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) W
W and
ãW are positive, because the electron is more tightly bound as the system is more positive. By inserting
eqn (7) and (8) into
eqn (6) and by assuming the change is small, the coefficient can be expanded as
| | 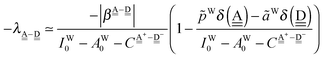 | (9) |
| | 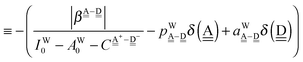 | (10) |
| | 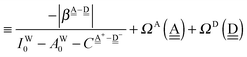 | (11) |
The second line defines the positive parameters,
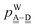
and
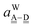
, whereas the third line defines the characteristic factors
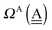
of the H acceptor and
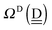
of the H donor.
Effective net charges for the Frontier orbitals
The simplest hydrogen bond is a water dimer, W⇐W, which can be thought of as a reference system for the chains of H bonds. The net charge δ of both molecules is zero, and thus Ω = 0. The coefficient is| | 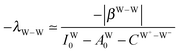 | (12) |
This simplest H bond induces the net charge −ζW2 on the H donor water molecule and +ζW2 on the H acceptor water molecule, This change of the net charge influences a new H bond. For instance, suppose that a water molecule is H-bonded to the H donor side of the water dimer as (Wa⇐Wda)⇐Wd. To estimate the strength of the new H bond Wda⇐Wd, the change of the ionization energy of the non-bonding orbital in Wda should be taken into account. Here, the Effective Net Charge for the Frontier Orbital (ENCFO), δ(Wda), on water Wda is assumed to be equal to −ζW2, because molecule Wda is the hydrogen donor and the electron acceptor in the water dimer. Accordingly, the ionization energy IAn(δ) in eqn (6) for the new hydrogen bond, Wda⇐Wd, is changed as in eqn (7). Thus, the CT coefficient for the new H bond, eqn (6), is| | 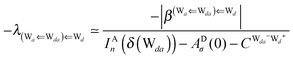 | (14) |
where δ(Wda) = −ζW2. By using eqn (10) and (13)| | 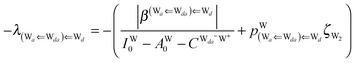 | (15) |
Thus, the ENCFO of molecule ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d in the chain is
d in the chain is| | δ((Wa⇐Wda)⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) = −(−λ(Wa⇐Wda)⇐Wd)2 d) = −(−λ(Wa⇐Wda)⇐Wd)2 | (16) |
For further analysis, the formulas are simplified by reducing the subscripts. The resonance integral 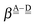 is an exponentially decaying function of R(O⋯O), and the Coulomb term
is an exponentially decaying function of R(O⋯O), and the Coulomb term 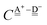 is proportional to the inverse of R(O–O). As Tables 2 and 3 show, R(O–O) varies depending on the pairs of the H donor and acceptor. But for the time being, we adopt an ambitious Assumption C that
is proportional to the inverse of R(O–O). As Tables 2 and 3 show, R(O–O) varies depending on the pairs of the H donor and acceptor. But for the time being, we adopt an ambitious Assumption C that 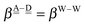 and
and 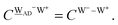 By neglecting the higher order of ζW2, we have
By neglecting the higher order of ζW2, we have| | δ((Wa⇐Wda)⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) = −(ζW2 + 2pWζW23/2) d) = −(ζW2 + 2pWζW23/2) | (17) |
So when molecule ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d becomes an H acceptor to a new H bond, its effective net charge for the frontier orbital (ENCFO) is negative, and its ionization energy decreases, and thus it becomes a better electron donor (H acceptor).
d becomes an H acceptor to a new H bond, its effective net charge for the frontier orbital (ENCFO) is negative, and its ionization energy decreases, and thus it becomes a better electron donor (H acceptor).
The next H bond arrangement examined is ((Wa⇐)2Wdda)⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d, which is a part of dddaddda
d, which is a part of dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) as shown in Fig. 4. Because molecule Wdda has two donating OH, two of the σOH* orbitals accept the electron from the H acceptor molecules, and δ(Wdda) = −2ζW2, if the two σOH* orbitals do not interfere with each other (Assumption D). Thus we have
as shown in Fig. 4. Because molecule Wdda has two donating OH, two of the σOH* orbitals accept the electron from the H acceptor molecules, and δ(Wdda) = −2ζW2, if the two σOH* orbitals do not interfere with each other (Assumption D). Thus we have
| | δ(((Wa⇐)2Wdda)⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) ≃ −(ζW2 + 4pWζW23/2) d) ≃ −(ζW2 + 4pWζW23/2) | (18) |
The H acceptor
dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
has two of the above chain as ((W
a⇐)
2W
dda)
2⇐
![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d
d. Again by assuming no interference of the H bonds, we obtain the ENCFO and the characteristic factor for the hydrogen acceptor water of row-1 in
Table 2 as
δ(dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = δ(((Wa⇐)2Wdda)2⇐ ) = δ(((Wa⇐)2Wdda)2⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) ≃ −2(ζW2 + 4pWζW23/2) d) ≃ −2(ζW2 + 4pWζW23/2) |
ΩA(dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = −pWδ(dddaddda ) = −pWδ(dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +2pW(ζW2 + 4pWζW23/2) (row-1) ) ≃ +2pW(ζW2 + 4pWζW23/2) (row-1) |
Another chain of the type ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wda⇐Wd) is examined, where the H acceptor of a water dimer, Wda⇐Wd, is an H donor in the new H bond. In eqn (6),
a⇐(Wda⇐Wd) is examined, where the H acceptor of a water dimer, Wda⇐Wd, is an H donor in the new H bond. In eqn (6), 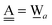 and
and 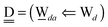 . Therefore, the CT coefficient is
. Therefore, the CT coefficient is
| | 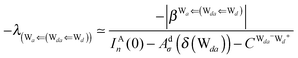 | (19) |
| | 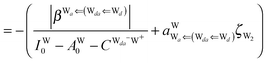 | (20) |
where
δ(W
da) =
ζW2 is used. The ENCFO of the end water of the chain under the above assumptions is
| | δ(![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wda⇐Wd)) ≃ +(ζW2 + 2aWζW23/2) a⇐(Wda⇐Wd)) ≃ +(ζW2 + 2aWζW23/2) | (21) |
and this chain is found in the rightest chain of four types of the hydrogen acceptors at the bottom of
Fig. 4. From
eqn (17) and (21), the ENCFO cannot be the net charges of molecules in the chain water trimer, W⇐W⇐W, because the sum of the two terms are not zero, unless
pW =
aW. The ENCFO, therefore, is the hypothetical quantity to estimate the changes of the ionization energy and the electron affinity in Mulliken's CT theory.
For chain ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdd⇒Wa),
a⇐(Wdd⇒Wa), 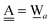 and
and 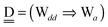 . Therefore, δ(Wdd) = −ζW2. Thus, for a branched chain
. Therefore, δ(Wdd) = −ζW2. Thus, for a branched chain ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdda(⇐Wd)(⇒Wa)), which is found at the right half of dddaadda
a⇐(Wdda(⇐Wd)(⇒Wa)), which is found at the right half of dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) in Fig. 4,
in Fig. 4,
| | | δ(Wdda) ≃ +ζW2 − ζW2 = 0 | (22) |
Thus,
| | 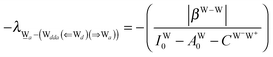 | (23) |
and
| | δ(![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdda(⇐Wd)(⇒Wa))) a⇐(Wdda(⇐Wd)(⇒Wa))) | (24) |
| | = (−λ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a−(Wdda(⇐Wd)(⇒Wd))) = ζW2 a−(Wdda(⇐Wd)(⇒Wd))) = ζW2 | (25) |
By combining
eqn (25) with
eqn (18), we have for
dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
,
| | δ(dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = −(ζW2 + 4pWζW23/2) + ζW2 ) = −(ζW2 + 4pWζW23/2) + ζW2 | (26) |
| | ΩA(dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +4(pW)2ζW23/2 (row-4) ) ≃ +4(pW)2ζW23/2 (row-4) | (28) |
By repeating the above procedure, we have
ΩA(ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +2pW(ζW2 + 2pWζW23/2) (row-2) ) ≃ +2pW(ζW2 + 2pWζW23/2) (row-2) |
ΩA(ddaaddaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 2pWζW2 (row-3) ) ≃ 2pWζW2 (row-3) |
ΩA(dddaadaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 4pW(pW − aW)ζW23/2 (row-5) ) ≃ 4pW(pW − aW)ζW23/2 (row-5) |
ΩA(ddaaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 0 (row-6) ) ≃ 0 (row-6) |
ΩA(ddaaadaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ −4pWaWζW23/2 (row-7) ) ≃ −4pWaWζW23/2 (row-7) |
In the study on the cubic isomers of X−(H2O)7 (X = F and Cl),41 the ENCFO of the ligand water molecule (L), which is also induced by the chain of the hydrogen bonds, was derived. The procedure to obtain the formulas for 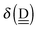 was same with the above one, by replacing “L” in X−(H2O)741 with “D”. The characteristic factors
was same with the above one, by replacing “L” in X−(H2O)741 with “D”. The characteristic factors 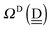 of the H donor in Tables 2 and 3 are
of the H donor in Tables 2 and 3 are
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa) ≃ 2aW(ζW2 + 4aWζW23/2) (column-7) adaaadaa) ≃ 2aW(ζW2 + 4aWζW23/2) (column-7) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadaa) ≃ 2aW(ζW2 + 2aWζW23/2) (column-6) addaadaa) ≃ 2aW(ζW2 + 2aWζW23/2) (column-6) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) ≃ 2aWζW2 (column-5) addaadda) ≃ 2aWζW2 (column-5) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadaa) ≃ 4(aW)2ζW23/2 (column-4) ddaaadaa) ≃ 4(aW)2ζW23/2 (column-4) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadda) ≃ 0 (column-3) ddaaadda) ≃ 0 (column-3) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa) ≃ −4aW(pW − aW)ζW23/2 (column-2) dddaadaa) ≃ −4aW(pW − aW)ζW23/2 (column-2) |
ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadda) ≃ −4aWpWζW23/2 (column-1) dddaadda) ≃ −4aWpWζW23/2 (column-1) |
The charge-transfer term in the Mulliken theory is
| | 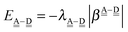 | (29) |
| | 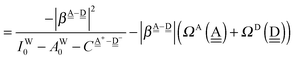 | (30) |
The relations
| | | ΩA for upper row > ΩA for lower row | (31) |
| | | ΩD for right column > ΩD for left column | (32) |
hold if
pW ≳
aW > 0. The CT terms shown in
Tables 2 and 3 are consistent with these relations for
ΩA and
ΩD with a very few exceptions between columns 3 and 2, and between rows 5 and 6 in
Table 2.
The large step between the fifth column (![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) and the fourth column (
addaadda) and the fourth column (![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadaa) corresponds to the well-known empirical rule that the daa water is a better H donor than the dda molecule. The step between the third row (ddaaddda
ddaaadaa) corresponds to the well-known empirical rule that the daa water is a better H donor than the dda molecule. The step between the third row (ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) and the fourth row (dddaadda
) and the fourth row (dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) also corresponds to the rule that dda is a better H acceptor. The four blocks in Tables 2 and 3 result from the linear term ζW2 in ΩA and ΩD.
) also corresponds to the rule that dda is a better H acceptor. The four blocks in Tables 2 and 3 result from the linear term ζW2 in ΩA and ΩD.
The sum 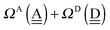 is a measure of the strength of the hydrogen bonds. For instance, among the dda⇐daa bonds, the sum for the strongest bond is
is a measure of the strength of the hydrogen bonds. For instance, among the dda⇐daa bonds, the sum for the strongest bond is
ΩA(dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) + ΩD( ) + ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa) = 2(pW + aW)ζW2 + 8((pW)2 + (aW)2)ζW23/2 adaaadaa) = 2(pW + aW)ζW2 + 8((pW)2 + (aW)2)ζW23/2 |
while the sum for the weakest one is
ΩA(ddaaddaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) + ΩD( ) + ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) = 2(pW + aW)ζW2 addaadda) = 2(pW + aW)ζW2 |
As is seen in
Table 2, the hydrogen bond length of
dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
⇐
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa
adaaadaa is shorter by 0.1 Å than that of
ddaaddaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
⇐
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda
addaadda, and the difference in the CT term is as large as 8.64 kJ mol
−1. Similarly, the dependence of the H bond strength on Kuo's topological index
ξ within each of four blocks is elucidated by the sum
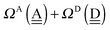
; the coefficient of
ζW23/2 is related with the topological index
ξ.
To further demonstrate the relation between the sum of the characteristic factors, 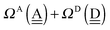 , and the CT terms and O⋯O distances, a matrix is constructed by extracting the columns and rows of Tables 2 and 3, and is shown in Fig. 5. Because all the parameters are safely assumed to be positive and ζ < 1, the large CT terms and short O⋯O distances strongly are correlated with the sum. If pW ≈ aW, the matrix of
, and the CT terms and O⋯O distances, a matrix is constructed by extracting the columns and rows of Tables 2 and 3, and is shown in Fig. 5. Because all the parameters are safely assumed to be positive and ζ < 1, the large CT terms and short O⋯O distances strongly are correlated with the sum. If pW ≈ aW, the matrix of 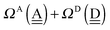 becomes approximately symmetric, and Fig. 5 numerically shows that it is nearly symmetric.
becomes approximately symmetric, and Fig. 5 numerically shows that it is nearly symmetric.
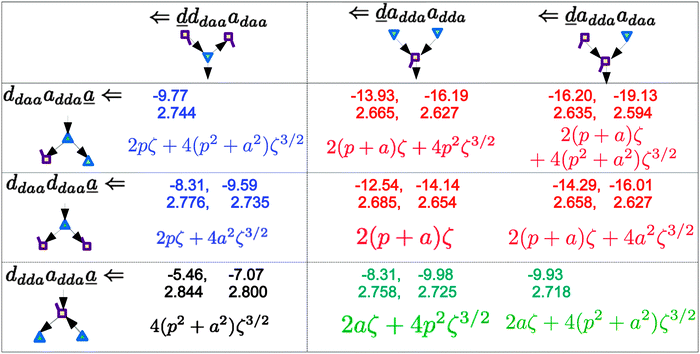 |
| | Fig. 5 Comparison of the sum of the characteristic factors, 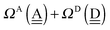 , for some of the typical hydrogen donor and acceptor pairs with the CT term/kJ mol−1 (the upper value) and the O⋯O distance per Å. The left and right values are for (H2O)8 and for (H2O)20, respectively. The subscripts and superscripts in the equations in text are deleted. , for some of the typical hydrogen donor and acceptor pairs with the CT term/kJ mol−1 (the upper value) and the O⋯O distance per Å. The left and right values are for (H2O)8 and for (H2O)20, respectively. The subscripts and superscripts in the equations in text are deleted. | |
The differences of the characteristic factors for columns 7 and 6, and for columns 6 and 5 in Table 2 are 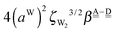 . The corresponding numerical differences are [1.95, 3.64, *, 2.06, *, *] and [*, 2.27, 1.75, 1.62, 1.18, 1.05] kJ mol−1, respectively, from the top row, where “*” implies that no data are available in Table 2. The averaged value (the standard deviation) of these two differences is 1.94 (0.80) kJ mol−1. Similarly, the difference of the characteristic factors for rows 2 and 1 and for rows 3 and 2 is
. The corresponding numerical differences are [1.95, 3.64, *, 2.06, *, *] and [*, 2.27, 1.75, 1.62, 1.18, 1.05] kJ mol−1, respectively, from the top row, where “*” implies that no data are available in Table 2. The averaged value (the standard deviation) of these two differences is 1.94 (0.80) kJ mol−1. Similarly, the difference of the characteristic factors for rows 2 and 1 and for rows 3 and 2 is 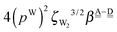 . The corresponding numerical differences in Table 2 are [1.34, 3.02, *, 1.68, *, *] and [*, 1.91, 1.35, 1.46, 1.03, 1.12] kJ mol−1, respectively, from the rightest of rows. The average value (standard deviation) of two differences is 1.61 (0.63) kJ mol−1. The other examples are seen in the differences of the characteristic factors for columns 3 and 1 and for rows 7 and 6; both of them are
. The corresponding numerical differences in Table 2 are [1.34, 3.02, *, 1.68, *, *] and [*, 1.91, 1.35, 1.46, 1.03, 1.12] kJ mol−1, respectively, from the rightest of rows. The average value (standard deviation) of two differences is 1.61 (0.63) kJ mol−1. The other examples are seen in the differences of the characteristic factors for columns 3 and 1 and for rows 7 and 6; both of them are 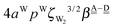 . The corresponding numerical difference values in Table 2 are [*, *, 1.25, *, 0.88, 0.94, 0.92] kJ mol−1 between columns 3 and 1 from the top, and [*, *, 0.75, *, 0.55, 0.84, 0.53] kJ mol−1 between rows 7 and 6 from the right. The average value (standard deviation) of two differences is 0.83 (0.23) kJ mol−1. Although the standard deviations are not small, we may safely claim that these numerical tests qualitatively support the model derived from Mulliken's CT theory. But, if the product
. The corresponding numerical difference values in Table 2 are [*, *, 1.25, *, 0.88, 0.94, 0.92] kJ mol−1 between columns 3 and 1 from the top, and [*, *, 0.75, *, 0.55, 0.84, 0.53] kJ mol−1 between rows 7 and 6 from the right. The average value (standard deviation) of two differences is 0.83 (0.23) kJ mol−1. Although the standard deviations are not small, we may safely claim that these numerical tests qualitatively support the model derived from Mulliken's CT theory. But, if the product 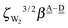 are assumed to be common for all of the above cases, the ratio aW/pW could be estimated as
are assumed to be common for all of the above cases, the ratio aW/pW could be estimated as
which shows that the simple assumption is broken down. The refinement of the model is required to include the influence from the change of the H bond distance.
In Fig. 5, the values for (H2O)8 (left numbers in each box) and (H2O)20 (right) are compared with each other. The strengthening of the hydrogen bonds in (H2O)20 with respect to (H2O)8 is evident. One possible cause is the size of the ring structure; five membered rings in (H2O)20 and four membered rings in (H2O)8, resulting in less strain in the ring structure for (H2O)20 than for (H2O)8. However, the above analysis based on Mulliken's CT theory strongly supports an alternative cause, namely that the longer lengths of the hydrogen bond chains in (H2O)20 influence the hydrogen bond strength. As shown above, the change in ENCFO propagates positively or negatively through the long hydrogen bonded chain. In his regression analysis,21 Anick added the parameters of the contribution from the ternary water molecules (next-nearest neighbors), and Recently Akase and Aida examined the type and size dependence of the dipole moment of a water molecule in various geometric configurations of water clusters (H2O)n, n = 2–10,15 using the all-atom polarizable model potential, TTM2-R.49 The dipole moments of dda and daa waters do slowly converge up to n = 8. This finding supports that the difference between (H2O)8 and (H2O)20 in Tables 2 and 3 and in Fig. 5 results from the size dependence of the CT interaction and of the hydrogen bond strength. Similarly Bakó and Mayer reported the collective effects on the dipole moments caused by “non-immediate environment” in water clusters.50 It suggests that the regression analysis for a set of the water clusters should have better carried out with a constant size, to avoid the unintentional statistical errors,1,8,12,20,51 unless the lengths of the H bonded networks are taken into account.
Concluding remarks
The influence of the neighbor and next-neighbor water molecules on the strength of the H bonds was examined for the polyhedral clusters of (H2O)8, (H2O)20 and (H2O)24. The polyhedral water clusters are suitable for the study, because they have only two types of molecules, either dda type or daa type, and they are further sub-grouped by the types of three neighbor (H-bonded) molecules as dda(s,t) and daa(s,t), s + t = 3. The stability of the isomers is related with the numbers of the eight sub-grouped molecules. In these clusters there are four types of the H bonds, and they are further divided to 49 sub-types of the H bonds when the neighbors of each of the H donor and H acceptor water molecules are taken into account. The H bond strengths are classified by these 49 sub-types. Based on the Mulliken's CT theory, the formulas for the CT contribution to the H bond energy are derived, and they explain the sub-type dependence of the H bond strength. This model theory can be extended to any H bonded networks of water molecules, and the works are in progress for hundreds of isomers of (H2O)8 and (H2O)12, which include various H bonded networks.52 The model theory with properly determined parameters could help to improve the empirical potential functions containing the influence of the H bonded chains and networks.
Acknowledgements
The work is partially supported by the Grant-in-Aid for Science Research of JSPS (S.I.). Part of this work was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences at Pacific Northwest National Laboratory. Battelle operates the Pacific Northwest National Laboratory for the US Department of Energy (S. S. X.). S. I. acknowledges Prof. H. Matsuzawa and Dr C. Ishibashi for their helpful discussion on the H bond analysis.
References
- S. McDonald, L. Ojamae and S. J. Singer, J. Phys. Chem. A, 1998, 102, 2824–2832 CrossRef CAS.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 101, 7873–7881 CrossRef CAS.
- V. Chihaia, S. Adams and W. F. Kuhs, Chem. Phys., 2004, 297, 271–287 CrossRef CAS.
- W. C. Radhakrishnan and T. P. Herndon, J. Phys. Chem, 1991, 95, 10609–10617 CrossRef.
- J.-L. Kuo, J. V. Coe, S. J. Singer, Y. B. Band and O. Lars, J. Chem. Phys., 2001, 114, 2527–2540 CrossRef CAS.
- M. V. Kirov, J. Struct. Chem., 2002, 43, 790–797 CrossRef CAS.
- D. J. Anick, THEOCHEM, 2002, 587, 87–96 CrossRef CAS.
- D. J. Anick, THEOCHEM, 2002, 587, 97–110 CrossRef CAS.
- T. Miyake and M. Aida, Chem. Phys. Lett., 2006, 427, 215–220 CrossRef CAS.
- U. Buck, I. Ettischer, M. Melzer, V. Buck and J. Sadlej, Phys. Rev. Lett., 1998, 80, 2578–2581 CrossRef CAS.
- J. Brudermann, M. Melzer, U. Buch, K. Kazimirski, J. Sadlej and V. Bush, J. Chem. Phys., 1999, 110, 10649–10652 CrossRef CAS.
- J. Sadlej, Chem. Phys. Lett., 2001, 333, 485–492 CrossRef CAS.
- M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134–1137 CrossRef CAS PubMed.
- J.-W. Shin, N. I. Hammer, E. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. Duncan, R. A. Christle and K. D. Jordan, Science, 2004, 304, 1137–1140 CrossRef CAS PubMed.
- D. Akase and M. Aida, J. Phys. Chem. A, 2014, 118, 7911–7924 CrossRef CAS PubMed.
- S. S. Xantheas, Chem. Phys., 2000, 258, 225–231 CrossRef CAS.
- K. Ohno, M. Okimura, N. Akai and Y. Katsumoto, Phys. Chem. Chem. Phys., 2005, 7, 3005–3014 RSC.
-
S. Yoo and S. S. Xantheas, in Handbook of Computational Chemistry, ed. J. Leszczynski, Springer, 2012, pp. 761–792 Search PubMed.
- J.-L. Kuo, C. V. Ciobanau, L. Ojamae, I. Shavitt and S. J. Singer, J. Chem. Phys., 2003, 118, 3583–3588 CrossRef CAS.
- D. J. Anick, J. Chem. Phys., 2003, 119, 12442–12455 CrossRef CAS.
- D. J. Anick, J. Phys. Chem. A, 2006, 110, 5135–5143 CrossRef CAS PubMed.
- S. Iwata and T. Nagata, Theor. Chem. Acc., 2006, 116, 137–144 CrossRef.
- S. Iwata, J. Chem. Phys., 2011, 135, 0941011 CrossRef PubMed.
- T. Nagata and S. Iwata, J. Chem. Phys., 2004, 120, 3555–3563 CrossRef CAS PubMed.
- S. Iwata, Phys. Chem. Chem. Phys., 2012, 14, 7787–7794 RSC.
- S. Iwata, P. Bandyopadhyay and S. S. Xantheas, J. Phys. Chem. A, 2013, 117, 6641–6651 CrossRef CAS PubMed.
- S. Iwata, Phys. Chem. Chem. Phys., 2014, 16, 11310–11317 RSC.
-
R. S. Mulliken and W. B. Person, Molecular Complexes, Wiley Interscience, NY, 1969 Search PubMed.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811–824 CrossRef CAS.
- K. Nukazawa, J. Tanaka and S. Nagakura, J. Phys. Soc. Jpn., 1953, 8, 792–793 CrossRef.
- H. Tsubomura, Bull. Chem. Soc. Jpn., 1954, 27, 445–450 CrossRef CAS.
- S. Iwata, Chem. Phys. Lett., 2006, 431, 204–209 CrossRef CAS.
- S. Iwata, J. Phys. Chem. B, 2008, 112, 16104–16109 CrossRef CAS PubMed.
- S. Iwata, J. Phys. Chem. A, 2010, 114, 8697–8704 CrossRef CAS PubMed.
-
I. G. Kaplan, in Types of Intermolecular Interactions: Qualitative Picture, ed. S. Wilson, Wiley Interscience, NY, 2003, ch. 6, vol. 3, pp. 161–181 Search PubMed.
-
I. G. Kaplan, Intermolecular Interactions, John Wiley & Sons, Ltd., 2006 Search PubMed.
-
K. Jeziorski and B. Szalewicz, in Symmetry-adaptive Perturbation Theory, ed. S. Wilson, Wiley Interscience, NY, 2003, ch. 9, vol. 3, pp. 232–277 Search PubMed.
- C. J. Burnham and S. S. Xantheas, J. Chem. Phys., 2002, 116, 1500–1510 CrossRef CAS.
- S. S. Xantheas, Can. J. Chem. Eng., 2012, 90, 843–853 CrossRef CAS.
- S. Yoo, M. V. Kilov and S. S. Xantheas, J. Am. Chem. Soc., 2009, 131, 7564–7566 CrossRef CAS PubMed.
- C. Ishibashi, S. Iwata, K. Onoe and H. Matsuzawa, J. Phys. Chem. A, 2015, 119, 10241–10253, DOI:10.1021/acs.jpca.5b07244.
- S. S. Xantheas, J. Chem. Phys., 1996, 104, 8821–8824 CrossRef CAS.
- V. Schlegel, Verhandlungen der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher, 1883, 44, 343 Search PubMed.
- M. V. Kirov, G. S. Fanourgakis and S. S. Xantheas, Chem. Phys. Lett., 2008, 461, 180–188 CrossRef CAS.
- L. Lenz and A. Ojamae, Chem. Phys. Lett., 2006, 418, 361–367 CrossRef.
- D. J. Anick, J. Chem. Phys., 2010, 132, 164311 CrossRef PubMed.
- I. Y. Zhang and X. Xu, Phys. Chem. Chem. Phys., 2012, 14, 12554–12570 RSC.
- I. Y. Zhang and X. Xu, Int. Rev. Phys. Chem., 2011, 30, 115–160 CrossRef CAS.
- S. S. Xantheas, C. J. Burnham and R. J. Harrison, J. Chem. Phys., 2002, 116, 1493–1499 CrossRef CAS.
- I. Bakó and I. Mayer, J. Phys. Chem. A, 2016, 120, 631–638 CrossRef PubMed.
- L. Lenz and A. Ojamae, Phys. Chem. Chem. Phys., 2005, 07, 1905–1911 RSC.
- D. Akase, M. Aida, K. Ohno and S. Iwata, PacifiChem, 2015 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The xyz files (cubic_W8.xyz.zip) the ball-and-stick figures for the cubic (H2O)8 are available. See DOI: 10.1039/c6cp02487d |
| ‡ Visiting Professor, 2012–2016. |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 symmetry-distinct configurations for the dodecahedral cage of (H2O)20,1,5 and 3
026 symmetry-distinct configurations for the dodecahedral cage of (H2O)20,1,5 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043
043![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 for the tetrakaidecahedral cage of (H2O)24.3,6 Every water molecule in these polyhedral clusters participates in three hydrogen bonds (H bonds) to neighbors; one hydrogen-donating OH and two hydrogen-accepting O⋯H (hereafter, this type of water is called daa),2,10–15 or two hydrogen-donating OH and one hydrogen-accepting O⋯H (dda). Anick called them F and L, respectively.7,8 Water dda (F) has a “free” OH, often called a dangling OH bond. The polyhedral cages consist of n/2 dda and n/2 daa water molecules.7 Therefore, there are only four types of hydrogen bonds in the polyhedral clusters, viz. daa⇐daa, daa⇐dda, dda⇐daa, and dda⇐dda. Among them, the bond dda⇐daa is the strongest.16–18 Smith and Dang called the bonds “defect” if both of the neighbor pair are either dda or daa, suggesting that dda⇐dda and daa⇐daa are weaker than the other types of pairs.1,2 Because of the fixed arrangement of the oxygen atoms among numerous distinct isomers and the restricted types of the hydrogen bonds in the clusters, the polyhedral water clusters are ideal to probe the characteristics of the hydrogen bonded networks and the factors determining the strength of the H bonds. The above four types of H bonds are further sub-grouped by the types of the neighboring water molecules. One of the ways is to use the “topological index” of an H bond ξ,19 which is defined as a sum of the number of dd neighbors at the H donor and the number of aa neighbors at the H acceptor. The index ranges from 0 to 4. Thus, there are 20 subsets of the types of the H bonds. Anick used the index in his analysis of the calculated OH harmonic frequencies, and further classified the H bonds by introducing the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor; their values are 0 if the neighbor (secondary) water is daa, and 1 if the neighbor water is dda.8,20,21 With this classification, there are 49 sub-groups of the H bonds (see below). Using these descriptors, he demonstrated that the H bond distances can be fitted linearly. He further extended the models to include the influence from the ternary water molecules.
836 for the tetrakaidecahedral cage of (H2O)24.3,6 Every water molecule in these polyhedral clusters participates in three hydrogen bonds (H bonds) to neighbors; one hydrogen-donating OH and two hydrogen-accepting O⋯H (hereafter, this type of water is called daa),2,10–15 or two hydrogen-donating OH and one hydrogen-accepting O⋯H (dda). Anick called them F and L, respectively.7,8 Water dda (F) has a “free” OH, often called a dangling OH bond. The polyhedral cages consist of n/2 dda and n/2 daa water molecules.7 Therefore, there are only four types of hydrogen bonds in the polyhedral clusters, viz. daa⇐daa, daa⇐dda, dda⇐daa, and dda⇐dda. Among them, the bond dda⇐daa is the strongest.16–18 Smith and Dang called the bonds “defect” if both of the neighbor pair are either dda or daa, suggesting that dda⇐dda and daa⇐daa are weaker than the other types of pairs.1,2 Because of the fixed arrangement of the oxygen atoms among numerous distinct isomers and the restricted types of the hydrogen bonds in the clusters, the polyhedral water clusters are ideal to probe the characteristics of the hydrogen bonded networks and the factors determining the strength of the H bonds. The above four types of H bonds are further sub-grouped by the types of the neighboring water molecules. One of the ways is to use the “topological index” of an H bond ξ,19 which is defined as a sum of the number of dd neighbors at the H donor and the number of aa neighbors at the H acceptor. The index ranges from 0 to 4. Thus, there are 20 subsets of the types of the H bonds. Anick used the index in his analysis of the calculated OH harmonic frequencies, and further classified the H bonds by introducing the descriptors (t1P,t1Q) for the H acceptor and (t2P,t2Q) for the H donor; their values are 0 if the neighbor (secondary) water is daa, and 1 if the neighbor water is dda.8,20,21 With this classification, there are 49 sub-groups of the H bonds (see below). Using these descriptors, he demonstrated that the H bond distances can be fitted linearly. He further extended the models to include the influence from the ternary water molecules.
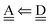 is given by
is given by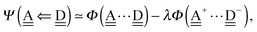
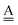 and
and 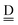 stand for the hydrogen acceptor and donor.29–31 The electron donor orbital is the non-bonding orbital of the hydrogen acceptor water molecule
stand for the hydrogen acceptor and donor.29–31 The electron donor orbital is the non-bonding orbital of the hydrogen acceptor water molecule 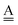 , and the electron acceptor orbital is the anti-bonding σOH* of the hydrogen donor water molecule
, and the electron acceptor orbital is the anti-bonding σOH* of the hydrogen donor water molecule 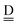 . These frontier molecular orbitals, which participate the CT electronic configurations, undergo changes by the neighboring H bonds. Based on a few simple assumptions, the analytical forms of the CT contributions to the H bond energy of 49 sub-groups defined by Anick8,21 are derived, and they are well correlated with the H bond distances and with the calculated CT terms, averaged over all of cube isomers of (H2O)8 and over 13 most stable dodecahedral (H2O)20. The model theory can be extended to any H bonded networks, which are found in more complicated caged clusters than in the polyhedral clusters.
. These frontier molecular orbitals, which participate the CT electronic configurations, undergo changes by the neighboring H bonds. Based on a few simple assumptions, the analytical forms of the CT contributions to the H bond energy of 49 sub-groups defined by Anick8,21 are derived, and they are well correlated with the H bond distances and with the calculated CT terms, averaged over all of cube isomers of (H2O)8 and over 13 most stable dodecahedral (H2O)20. The model theory can be extended to any H bonded networks, which are found in more complicated caged clusters than in the polyhedral clusters.
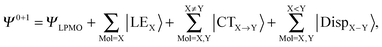
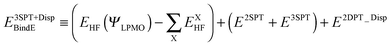
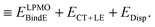
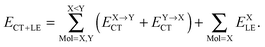

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) bFL), and the second is the ordering of the binding energy.
b The HF binding energy is replaced with ELPMOBindE + ECT+LE in eqn (4).
c The number of dda(s,t) type waters; (s,t) = (0,3), (1,2), (2,1), (3,0). daa(s,t) = dda(t,s). See text.
bFL), and the second is the ordering of the binding energy.
b The HF binding energy is replaced with ELPMOBindE + ECT+LE in eqn (4).
c The number of dda(s,t) type waters; (s,t) = (0,3), (1,2), (2,1), (3,0). daa(s,t) = dda(t,s). See text.


![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa implies that the hydrogen donor,
dddaadaa implies that the hydrogen donor, ![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) da, donates a H atom to a neighbor dda water and accepts a H atom from a neighbor daa water. As shown in the second row of Fig. 4, when daa (square) is the hydrogen donor for a hydrogen bond, this water should have two H atoms accepting from the neighboring waters, and there are three types of the hydrogen donor daa in polyhedral water clusters. Similarly, when a dda water is the hydrogen acceptor in a hydrogen bond, as shown in the third row of Fig. 4, there are three types of hydrogen acceptors, depending on the neighbor waters. On the other hand, when a daa water is a hydrogen acceptor, the fourth row of Fig. 4 shows that there are four types of the hydrogen acceptors. Symbol dddaddda
da, donates a H atom to a neighbor dda water and accepts a H atom from a neighbor daa water. As shown in the second row of Fig. 4, when daa (square) is the hydrogen donor for a hydrogen bond, this water should have two H atoms accepting from the neighboring waters, and there are three types of the hydrogen donor daa in polyhedral water clusters. Similarly, when a dda water is the hydrogen acceptor in a hydrogen bond, as shown in the third row of Fig. 4, there are three types of hydrogen acceptors, depending on the neighbor waters. On the other hand, when a daa water is a hydrogen acceptor, the fourth row of Fig. 4 shows that there are four types of the hydrogen acceptors. Symbol dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) implies that the hydrogen acceptor is dda, donating a H atom to two dda waters. Thus, if two neighbor waters of both of the hydrogen donor and acceptor waters are taken into account, there are 49 types of H bonds as shown in Fig. 4.8
implies that the hydrogen acceptor is dda, donating a H atom to two dda waters. Thus, if two neighbor waters of both of the hydrogen donor and acceptor waters are taken into account, there are 49 types of H bonds as shown in Fig. 4.8

![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda
d
daa
a
dda
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
dda
daa
d
dda
daa
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda
d
daa
a
dda
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
daa
d
daa
a
daa
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda
a
dda
a
dda
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa
a
dda
a
daa
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
daa
a
daa
a
daa
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
dda
a
daa
d
dda
a
daa
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
a
dda
d
daa
a
dda
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) d
daa
adaa
d
daa
adaa
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda
a
dda
a
dda
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa
a
dda
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa (the number of cases is 5). For (H2O)20, the largest standard deviations are 0.46 kJ mol−1 and 0.008 Å, respectively, for ddaaddda
dddaadaa (the number of cases is 5). For (H2O)20, the largest standard deviations are 0.46 kJ mol−1 and 0.008 Å, respectively, for ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa (the total number of cases is 26).
dddaadaa (the total number of cases is 26).![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda, and the next group (B) has two.
addaadda, and the next group (B) has two.![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa
a
dda
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda
a
dda
a
dda
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
daa
a
dda
a
daa
![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif)
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) a
dda
a
dda
a
dda
a
dda
 and
and 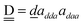 . By assuming a weak interaction, the mixing coefficient is approximately given [Assumption A] as
. By assuming a weak interaction, the mixing coefficient is approximately given [Assumption A] as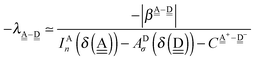
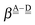 is the resonance integral and
is the resonance integral and 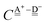 the Coulomb attraction term. The effective ionization energy of the donor orbital,
the Coulomb attraction term. The effective ionization energy of the donor orbital, 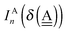 , and the electron affinity of the acceptor orbital,
, and the electron affinity of the acceptor orbital, 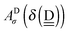 , are assumed to be functions of the net charges,
, are assumed to be functions of the net charges, 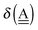 and
and 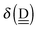 , of the molecules [Assumption B]. Recently Xu and coworkers computationally demonstrated the linear dependence of the ionization energy and electron affinity on a small fractional charge,47 using their double hybrid DFT.48 The following linear forms
, of the molecules [Assumption B]. Recently Xu and coworkers computationally demonstrated the linear dependence of the ionization energy and electron affinity on a small fractional charge,47 using their double hybrid DFT.48 The following linear forms![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) Wδ
Wδ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) W and ãW are positive, because the electron is more tightly bound as the system is more positive. By inserting eqn (7) and (8) into eqn (6) and by assuming the change is small, the coefficient can be expanded as
W and ãW are positive, because the electron is more tightly bound as the system is more positive. By inserting eqn (7) and (8) into eqn (6) and by assuming the change is small, the coefficient can be expanded as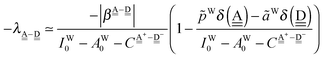
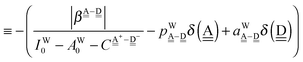
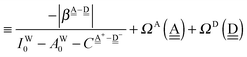
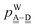 and
and 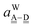 , whereas the third line defines the characteristic factors
, whereas the third line defines the characteristic factors 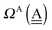 of the H acceptor and
of the H acceptor and 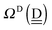 of the H donor.
of the H donor.
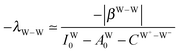
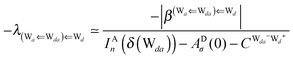
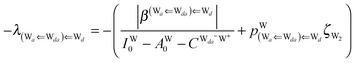
![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d in the chain is
d in the chain is![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) = −(−λ(Wa⇐Wda)⇐Wd)2
d) = −(−λ(Wa⇐Wda)⇐Wd)2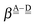 is an exponentially decaying function of R(O⋯O), and the Coulomb term
is an exponentially decaying function of R(O⋯O), and the Coulomb term 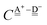 is proportional to the inverse of R(O–O). As Tables 2 and 3 show, R(O–O) varies depending on the pairs of the H donor and acceptor. But for the time being, we adopt an ambitious Assumption C that
is proportional to the inverse of R(O–O). As Tables 2 and 3 show, R(O–O) varies depending on the pairs of the H donor and acceptor. But for the time being, we adopt an ambitious Assumption C that 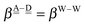 and
and 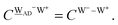 By neglecting the higher order of ζW2, we have
By neglecting the higher order of ζW2, we have![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) = −(ζW2 + 2pWζW23/2)
d) = −(ζW2 + 2pWζW23/2)![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d becomes an H acceptor to a new H bond, its effective net charge for the frontier orbital (ENCFO) is negative, and its ionization energy decreases, and thus it becomes a better electron donor (H acceptor).
d becomes an H acceptor to a new H bond, its effective net charge for the frontier orbital (ENCFO) is negative, and its ionization energy decreases, and thus it becomes a better electron donor (H acceptor).
![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d, which is a part of dddaddda
d, which is a part of dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) as shown in Fig. 4. Because molecule Wdda has two donating OH, two of the σOH* orbitals accept the electron from the H acceptor molecules, and δ(Wdda) = −2ζW2, if the two σOH* orbitals do not interfere with each other (Assumption D). Thus we have
as shown in Fig. 4. Because molecule Wdda has two donating OH, two of the σOH* orbitals accept the electron from the H acceptor molecules, and δ(Wdda) = −2ζW2, if the two σOH* orbitals do not interfere with each other (Assumption D). Thus we have![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) ≃ −(ζW2 + 4pWζW23/2)
d) ≃ −(ζW2 + 4pWζW23/2)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) has two of the above chain as ((Wa⇐)2Wdda)2⇐
has two of the above chain as ((Wa⇐)2Wdda)2⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d. Again by assuming no interference of the H bonds, we obtain the ENCFO and the characteristic factor for the hydrogen acceptor water of row-1 in Table 2 as
d. Again by assuming no interference of the H bonds, we obtain the ENCFO and the characteristic factor for the hydrogen acceptor water of row-1 in Table 2 as![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = δ(((Wa⇐)2Wdda)2⇐
) = δ(((Wa⇐)2Wdda)2⇐![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) d) ≃ −2(ζW2 + 4pWζW23/2)
d) ≃ −2(ζW2 + 4pWζW23/2)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = −pWδ(dddaddda
) = −pWδ(dddaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +2pW(ζW2 + 4pWζW23/2) (row-1)
) ≃ +2pW(ζW2 + 4pWζW23/2) (row-1)![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wda⇐Wd) is examined, where the H acceptor of a water dimer, Wda⇐Wd, is an H donor in the new H bond. In eqn (6),
a⇐(Wda⇐Wd) is examined, where the H acceptor of a water dimer, Wda⇐Wd, is an H donor in the new H bond. In eqn (6), 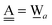 and
and 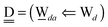 . Therefore, the CT coefficient is
. Therefore, the CT coefficient is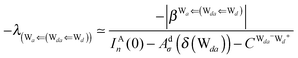
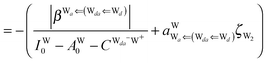
![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wda⇐Wd)) ≃ +(ζW2 + 2aWζW23/2)
a⇐(Wda⇐Wd)) ≃ +(ζW2 + 2aWζW23/2)![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdd⇒Wa),
a⇐(Wdd⇒Wa), 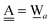 and
and 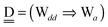 . Therefore, δ(Wdd) = −ζW2. Thus, for a branched chain
. Therefore, δ(Wdd) = −ζW2. Thus, for a branched chain ![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdda(⇐Wd)(⇒Wa)), which is found at the right half of dddaadda
a⇐(Wdda(⇐Wd)(⇒Wa)), which is found at the right half of dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) in Fig. 4,
in Fig. 4,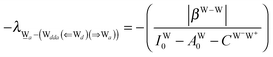
![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a⇐(Wdda(⇐Wd)(⇒Wa)))
a⇐(Wdda(⇐Wd)(⇒Wa)))![[W with combining low line]](https://www.rsc.org/images/entities/char_0057_0332.gif) a−(Wdda(⇐Wd)(⇒Wd))) = ζW2
a−(Wdda(⇐Wd)(⇒Wd))) = ζW2![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ,
,![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) = −(ζW2 + 4pWζW23/2) + ζW2
) = −(ζW2 + 4pWζW23/2) + ζW2![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +4(pW)2ζW23/2 (row-4)
) ≃ +4(pW)2ζW23/2 (row-4)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ +2pW(ζW2 + 2pWζW23/2) (row-2)
) ≃ +2pW(ζW2 + 2pWζW23/2) (row-2)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 2pWζW2 (row-3)
) ≃ 2pWζW2 (row-3)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 4pW(pW − aW)ζW23/2 (row-5)
) ≃ 4pW(pW − aW)ζW23/2 (row-5)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ 0 (row-6)
) ≃ 0 (row-6)![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) ≃ −4pWaWζW23/2 (row-7)
) ≃ −4pWaWζW23/2 (row-7)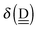 was same with the above one, by replacing “L” in X−(H2O)741 with “D”. The characteristic factors
was same with the above one, by replacing “L” in X−(H2O)741 with “D”. The characteristic factors 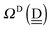 of the H donor in Tables 2 and 3 are
of the H donor in Tables 2 and 3 are![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa) ≃ 2aW(ζW2 + 4aWζW23/2) (column-7)
adaaadaa) ≃ 2aW(ζW2 + 4aWζW23/2) (column-7)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadaa) ≃ 2aW(ζW2 + 2aWζW23/2) (column-6)
addaadaa) ≃ 2aW(ζW2 + 2aWζW23/2) (column-6)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) ≃ 2aWζW2 (column-5)
addaadda) ≃ 2aWζW2 (column-5)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadaa) ≃ 4(aW)2ζW23/2 (column-4)
ddaaadaa) ≃ 4(aW)2ζW23/2 (column-4)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadda) ≃ 0 (column-3)
ddaaadda) ≃ 0 (column-3)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadaa) ≃ −4aW(pW − aW)ζW23/2 (column-2)
dddaadaa) ≃ −4aW(pW − aW)ζW23/2 (column-2)![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) dddaadda) ≃ −4aWpWζW23/2 (column-1)
dddaadda) ≃ −4aWpWζW23/2 (column-1)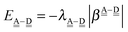
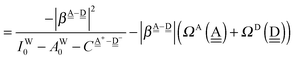
![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) and the fourth column (
addaadda) and the fourth column (![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) ddaaadaa) corresponds to the well-known empirical rule that the daa water is a better H donor than the dda molecule. The step between the third row (ddaaddda
ddaaadaa) corresponds to the well-known empirical rule that the daa water is a better H donor than the dda molecule. The step between the third row (ddaaddda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) and the fourth row (dddaadda
) and the fourth row (dddaadda![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) also corresponds to the rule that dda is a better H acceptor. The four blocks in Tables 2 and 3 result from the linear term ζW2 in ΩA and ΩD.
) also corresponds to the rule that dda is a better H acceptor. The four blocks in Tables 2 and 3 result from the linear term ζW2 in ΩA and ΩD.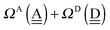 is a measure of the strength of the hydrogen bonds. For instance, among the dda⇐daa bonds, the sum for the strongest bond is
is a measure of the strength of the hydrogen bonds. For instance, among the dda⇐daa bonds, the sum for the strongest bond is![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) + ΩD(
) + ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa) = 2(pW + aW)ζW2 + 8((pW)2 + (aW)2)ζW23/2
adaaadaa) = 2(pW + aW)ζW2 + 8((pW)2 + (aW)2)ζW23/2![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ) + ΩD(
) + ΩD(![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda) = 2(pW + aW)ζW2
addaadda) = 2(pW + aW)ζW2![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) adaaadaa is shorter by 0.1 Å than that of ddaaddaa
adaaadaa is shorter by 0.1 Å than that of ddaaddaa![[a with combining low line]](https://www.rsc.org/images/entities/i_char_0061_0332.gif) ⇐
⇐![[d with combining low line]](https://www.rsc.org/images/entities/i_char_0064_0332.gif) addaadda, and the difference in the CT term is as large as 8.64 kJ mol−1. Similarly, the dependence of the H bond strength on Kuo's topological index ξ within each of four blocks is elucidated by the sum
addaadda, and the difference in the CT term is as large as 8.64 kJ mol−1. Similarly, the dependence of the H bond strength on Kuo's topological index ξ within each of four blocks is elucidated by the sum 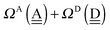 ; the coefficient of ζW23/2 is related with the topological index ξ.
; the coefficient of ζW23/2 is related with the topological index ξ.
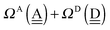 , and the CT terms and O⋯O distances, a matrix is constructed by extracting the columns and rows of Tables 2 and 3, and is shown in Fig. 5. Because all the parameters are safely assumed to be positive and ζ < 1, the large CT terms and short O⋯O distances strongly are correlated with the sum. If pW ≈ aW, the matrix of
, and the CT terms and O⋯O distances, a matrix is constructed by extracting the columns and rows of Tables 2 and 3, and is shown in Fig. 5. Because all the parameters are safely assumed to be positive and ζ < 1, the large CT terms and short O⋯O distances strongly are correlated with the sum. If pW ≈ aW, the matrix of 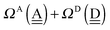 becomes approximately symmetric, and Fig. 5 numerically shows that it is nearly symmetric.
becomes approximately symmetric, and Fig. 5 numerically shows that it is nearly symmetric.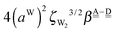 . The corresponding numerical differences are [1.95, 3.64, *, 2.06, *, *] and [*, 2.27, 1.75, 1.62, 1.18, 1.05] kJ mol−1, respectively, from the top row, where “*” implies that no data are available in Table 2. The averaged value (the standard deviation) of these two differences is 1.94 (0.80) kJ mol−1. Similarly, the difference of the characteristic factors for rows 2 and 1 and for rows 3 and 2 is
. The corresponding numerical differences are [1.95, 3.64, *, 2.06, *, *] and [*, 2.27, 1.75, 1.62, 1.18, 1.05] kJ mol−1, respectively, from the top row, where “*” implies that no data are available in Table 2. The averaged value (the standard deviation) of these two differences is 1.94 (0.80) kJ mol−1. Similarly, the difference of the characteristic factors for rows 2 and 1 and for rows 3 and 2 is 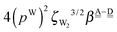 . The corresponding numerical differences in Table 2 are [1.34, 3.02, *, 1.68, *, *] and [*, 1.91, 1.35, 1.46, 1.03, 1.12] kJ mol−1, respectively, from the rightest of rows. The average value (standard deviation) of two differences is 1.61 (0.63) kJ mol−1. The other examples are seen in the differences of the characteristic factors for columns 3 and 1 and for rows 7 and 6; both of them are
. The corresponding numerical differences in Table 2 are [1.34, 3.02, *, 1.68, *, *] and [*, 1.91, 1.35, 1.46, 1.03, 1.12] kJ mol−1, respectively, from the rightest of rows. The average value (standard deviation) of two differences is 1.61 (0.63) kJ mol−1. The other examples are seen in the differences of the characteristic factors for columns 3 and 1 and for rows 7 and 6; both of them are 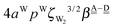 . The corresponding numerical difference values in Table 2 are [*, *, 1.25, *, 0.88, 0.94, 0.92] kJ mol−1 between columns 3 and 1 from the top, and [*, *, 0.75, *, 0.55, 0.84, 0.53] kJ mol−1 between rows 7 and 6 from the right. The average value (standard deviation) of two differences is 0.83 (0.23) kJ mol−1. Although the standard deviations are not small, we may safely claim that these numerical tests qualitatively support the model derived from Mulliken's CT theory. But, if the product
. The corresponding numerical difference values in Table 2 are [*, *, 1.25, *, 0.88, 0.94, 0.92] kJ mol−1 between columns 3 and 1 from the top, and [*, *, 0.75, *, 0.55, 0.84, 0.53] kJ mol−1 between rows 7 and 6 from the right. The average value (standard deviation) of two differences is 0.83 (0.23) kJ mol−1. Although the standard deviations are not small, we may safely claim that these numerical tests qualitatively support the model derived from Mulliken's CT theory. But, if the product 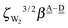 are assumed to be common for all of the above cases, the ratio aW/pW could be estimated as
are assumed to be common for all of the above cases, the ratio aW/pW could be estimated as