Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transport properties of hierarchical micro–mesoporous materials†‡
Daniel
Schneider
,
Dirk
Mehlhorn
,
Philipp
Zeigermann
,
Jörg
Kärger
and
Rustem
Valiullin
*
Faculty of Physics and Earth Sciences, University of Leipzig, Leipzig, Germany. E-mail: valiullin@uni-leipzig.de
First published on 13th January 2016
Abstract
Adding mesopore networks in microporous materials using the principles of hierarchical structure design is recognized as a promising route for eliminating their transport limitations and, therefore, for improving their value in technological applications. Depending on the routes of physico-chemical procedures or post-synthesis treatments used, very different geometries of the intentionally-added transport mesopores can be obtained. Understanding the structure–dynamics relationships in these complex materials with multiple porosities under different thermodynamical conditions remains a challenging task. In this review, we summarize the results obtained so far on experimental and theoretical studies of diffusion in micro-mesoporous materials. By considering four common classes of bi-porous materials, which are differing by the inter-connectivities of their sup-spaces as one of the most important parameter determining the transport rates, we discuss their generic transport properties and correlate the results delivered by the equilibrium and non-equilibrium techniques of diffusion measurements.
1 Introduction
The economical value of using microporous materials in a great variety of practical applications may hardly be overestimated. Their different properties, such as favourable chemical activity or molecular selectivity, originating from a specific organization of their crystalline structure containing well-ordered voids of molecular dimensions, are widely exploited in chemistry, medicine, energy transformation and storage, and environmental protection.1–4 It has long been recognized, however, that exactly the existence of strong confinements, giving on one hand rise to the prosperous material properties, can simultaneously severely affect their performance in the respective processes due to the extremely slow mass transfer through micropores.5 The latter has several unfavourable consequences, such as slowing down of the overall process operations and the formation of unwanted by-products. That is why different strategies for improving transport properties of microporous solids have been developed over the last decades. There are, essentially, three different routes for transport enhancement, i.e. for attaining enhanced exchange rates of the molecules between the space of micropores and the surroundings: (i) by a reduction of the crystal sizes, (ii) by operating with larger micropores and (iii) by incorporating mesopores into the space of micropores as additional, low-resistance transport pathways.Although conceptually attractive, the viability of the first option is often limited by technological difficulties accompanying synthesis and handling of small (nano)crystals, the linear dimension of which should often lie in the range of hundreds or even tens of nanometres.6 Similarly, despite a significant progress done in the synthesis of zeolites with extra-large pores7,8 (exceeding typically 12-membered ring) and MOFs,9–11 it is recognized that the thus attained transport improvement is penalized by decreased chemical activity and thermal stability. Therefore, the third option, namely the development of porous materials with combined micro-, meso- and even macro-porosities, is nowadays considered to be the most promising route for developing economically-valuable crystalline porous materials with optimized mass transfer properties and chemical functionality.12–24
Technologically, these materials can be obtained either via various post-synthetic treatments, such as desilication or dealumination, or by soft- or hard-templating during the material synthesis, with subsequent template removal, or in a mixed route.25–33 Clearly, depending on the approach used and the details, under which a particular material is obtained, quite diverse geometries of the imbedded mesopore space may result, ranging from isolated voids of mesoscalic dimension to mesoporous channels traversing the whole microporous crystal. In turn, different pore geometries may, depending on the operation conditions and the nature of the guest compounds under consideration, lead to notably different mass transfer patterns. Very importantly, the simplest strategies, such as to incorporate as much transport mesopores as possible, may fail due to, e.g., the reduction of the micropore space where the reaction steps shall ultimately occur.34 These situations will be encountered for the processes where the micropore confinement is an ultimate prerequisite. On the other hand, for catalytic processes profiting from the accessibility of the active sites, the creation of a large mesopore surface readily accessible for bulky molecules may substantially contribute to the overall process efficiency.22,35 Optimization of the processes by profiting from the pore space hierarchies is thus a complex, multi-dimensional task during which a large variety of different phenomena has to be complementarily taken into account.36–40 It is, therefore, more and more recognized that, in addition to detailed structural information evidencing the incorporation of mesopores,41 transport properties of newly synthesized hierarchical materials should simultaneously be provided as a guide for theoretical modelling and process engineering.38,42–50
For materials solely containing micro- or mesopores, general aspects of the intra-crystalline mass transfer are well understood and this knowledge is amply sufficient for the process engineering purposes. Detailed descriptions of diffusion processes in these materials may be found in numerous text-books and reviews.5,51–54 Transport phenomena become, however, increasingly complicated for porous solids which combine micro- and mesopores.55–59 Here, in addition to the already rich dynamics in the individual building blocks of the composite materials, the by far more intricate molecular exchange between these blocks may further complicate the overall mass transfer processes, often to an intractable extent. Notably, the exchange patterns may be determined by not only thermodynamic conditions, but also by the occurrence of additional transport resistances, the impact of which is finding more and more evidences.60,61 For the class of hierarchical materials discussed here, the molecular exchange, whose microscopic details are crucial for the understanding of the macroscopic dynamics, typically takes place between regions of nanoscalic dimensions. Due to this fact, molecular exchange processes occurring on this length- and time-scales can hardly be directly assessed by any experimental technique available so far. This complicates any deeper insight into molecular transport in these materials. Computer modelling approaches based on realistic models of porous solids with multiple porosities and of underlying physics, capturing microscopic details of fluid coexistence between different porosity domains and the elementary steps of molecular propagations therein, become therefore increasingly important.46,62,63
Depending on the routes of chemical synthesis or post-synthesis treatment, very different geometries of the intentionally-added transport pores can be obtained. They may give rise to quite different transport properties of the resulting porous materials. The purposeful design of hierarchical pore systems for meeting specific application-oriented criteria demands, therefore, a deeper understanding of their structure–dynamics relationships. Their complexity makes experimental exploration of mass transfer patterns in these materials a challenging task with a particular task to establish a common basis for the analysis and comparison of experimental data obtained using different analytical techniques.64 One of the goals of the present contribution is, therefore, to provide a general scheme for the prediction of transport properties of hierarchical porous materials. Among them, the main focus will be on bi-porous, micro-mesoporous materials as the most widely used ones, leaving a large pool of other types of hierarchical assemblies for a future account.65–74
2 Diffusion in porous materials
2.1 Basics of diffusion
Quite generally, the methods of transport characterization may be subdivided into two classes, viz. equilibrium and non-equilibrium techniques.75 In the first category, information on mass transfer is only accessible if a distinction between different molecules is possible. The category of non-equilibrium experiments may further be subdivided into experiments operating under transient conditions (where the information on mass transfer is attained by studying the rate of equilibration) and non-equilibrium experiments operating under boundary conditions that ensure stationary conditions. In this case, information on mass transfer is contained in the fluxes (flux measurements) or in the integral (uptake) or spatially-resolved (micro-imaging) concentrations. In all details the underlying principles of these experimental approaches are reviewed in numerous text-books and reviews.5,53,75,76 Therefore, for the sake of conciseness, in what follows we recollect only the most essential points in an amount just enough to follow the rest of this review.If a spatial gradient ∂c/∂x in the concentration of particles, as shown schematically in Fig. 1a, is created, this will lead to the occurrence of the particle flux j. For near-equilibrium conditions, j is just linearly proportional to the gradient:77
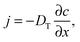 | (1) |
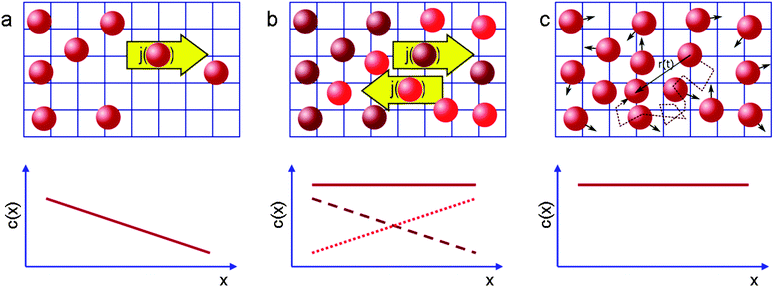 | ||
| Fig. 1 Schematic representation of the measurement of diffusion processes (a) in the presence and (b and c) in the absence of macroscopic concentration gradients (full lines in the lower graphs). In (b) diffusion is probed by following the (counter-)flux of differently labelled molecules (brown, red), in (c) by recording the displacement of the individual molecules. This image has been reproduced with permission from ref. 53, published by Royal Society of Chemistry. | ||
In that case, conventionally the transport characteristics are probed by recording the rate of molecular uptake or release following a stepwise change of the concentration c of the guest molecules in the surrounding atmosphere. In the context of the present work, such concentration jumps will lead to the establishment of the concentration gradient within the porous particles, which will equilibrate via diffusion. Assuming that mass transfer in the porous material under study can be adequately described by an effective diffusivity Deff (to which we shall refer in detail in the subsequent chapters), this diffusivity can easily be obtained by matching the solution of the corresponding diffusion equation (Fick's 2nd law)
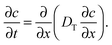 | (2) |
The latter results as the combination of eqn (1) with the law of mass conservation
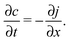 | (3) |
It has to be noted that an exact solution of eqn (2) is only possible if the initial and boundary conditions are exactly defined. While the former ones can easily be controlled in the experiment, the latter ones are not so easy to quantify. Thus, the boundary conditions as given by the particle size and shape, can, for the majority of real materials, hardly be shaped in mathematical expressions. Secondly, the boundary conditions are determined by the permeabilities at the particle boundaries, which are a topic of controversial discussions.
Under such conditions it is useful to exploit the method of the statistical moments78 and to introduce, as a measure of the time constant of molecular uptake and release, the first statistical moment T defined by the relation
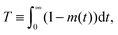 | (4) |
Here, 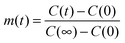 , with C(t) denoting the total amount adsorbed by a porous body at time t. For converting this time constant T to the diffusivity DT, assumptions on the particle geometry are needed.79 For example, for a spherical uniform particle of radius R it holds
, with C(t) denoting the total amount adsorbed by a porous body at time t. For converting this time constant T to the diffusivity DT, assumptions on the particle geometry are needed.79 For example, for a spherical uniform particle of radius R it holds
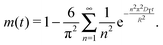 | (5) |
By inserting eqn (5) into eqn (4), the relation for the first statistical moment T of uptake is obtained as
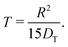 | (6) |
Thus, by recording the uptake curve during filling of the model system (or during adsorption experiments), the uptake diffusion coefficient can be calculated. Alternatively, also the short-time uptake data may be used to assess the diffusivities. In this case, by expanding eqn (5) into a series, the leading term remains as
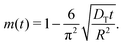 | (7) |
This approach ensures a very high accuracy in the initial range of uptake or release, with deviations of less than 1% for 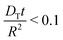 .80 One has to be aware, however, that this is only true if uptake can be assumed to be controlled by a single diffusivity. This may not be the case for hierarchical materials. Thus, if spherical particles with a core–shell organization of their inner structure are considered, then eqn (5) does not hold anymore and shall be modified correspondingly.81,82 The clarification of this point will be in the focus of this review.
.80 One has to be aware, however, that this is only true if uptake can be assumed to be controlled by a single diffusivity. This may not be the case for hierarchical materials. Thus, if spherical particles with a core–shell organization of their inner structure are considered, then eqn (5) does not hold anymore and shall be modified correspondingly.81,82 The clarification of this point will be in the focus of this review.
The working principles of the techniques operating at equilibrium conditions are exemplified in Fig. 1b and c. In the spirit of Fig. 1b, the diffusion equation can be applied to two sub-ensembles of molecules. These two ensembles of identical particles are chosen to provide two identical concentration gradients opposing each other. Once again, the respective diffusivities, which are commonly referred to as self-diffusivities and are denoted as D0, can be obtained via Fick's law. In the absence of any specific interactions between the particles, i.e. with DT in eqn (1) being a sole function of the concentration difference, but not the absolute concentration, the diffusivities DT and D0 obtained for two situations exemplified by Fig. 1a and b will obviously coincide.
2.2 Microscopic view of diffusion
So far we have discussed diffusion only in the context of macroscopic fluxes without referring to underlying microscopic processes resulting in matter redistribution. This connection, which has been suggested as early as in 1905,83 can be done by considering the trajectories of individual molecules shown in Fig. 1c. By recording them for sufficiently long intervals of time and by performing their statistical analysis it may be shown that, on considering displacements in a certain direction, the square displacement x2 averaged over large molecular ensembles grows linearly with the observation time t (possible deviations from this law84 are beyond the topic of this introduction). Most importantly, the proportionality coefficient D0,| 〈x2〉 = 2D0t, | (8) |
Eqn (8) allows for a microscopic understanding of diffusivity. A crucial prerequisite for obtaining eqn (8) is the Markovian character of the displacements on the timescale t considered.85 In simple words, if any trajectory is subdivided onto shorter sub-trajectories each of a duration τ0, the displacements l0 associated with two adjacent sub-trajectories must be uncorrelated. In this case, the diffusivity D0 in eqn (8) turns out to be
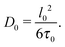 | (9) |
All underlying microscopic mechanisms of diffusion become now encoded in l0, τ0, and in the mechanisms providing randomization of the trajectories.
In the context of the present work, one may encounter several situations relevant for diffusion in homogeneous phases, i.e. in phases where there is only one diffusion mechanism present. The most simple case is represented by gases in which molecules perform ballistic flights. Here, effective randomization of the trajectories is provided by the binary molecular collisions. Under this condition, it is natural to associate the sub-trajectories mentioned in the preceding paragraph with the periods of free flights between the collisions. With the common knowledge from gas-kinetic theory one may easily show that the diffusivity in this case is given by Dgas = λ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /3, where
/3, where ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) is the average thermal velocity. If one considers a rarified gas in a porous material at pressures resulting in the mean free path λ in bulk gas at other identical conditions being much longer than the characteristic pore size in the material under study, the randomization is exclusively determined by the collisions with the pore walls. This process is commonly referred to as Knudsen diffusion. The Knudsen diffusivity DK = d
is the average thermal velocity. If one considers a rarified gas in a porous material at pressures resulting in the mean free path λ in bulk gas at other identical conditions being much longer than the characteristic pore size in the material under study, the randomization is exclusively determined by the collisions with the pore walls. This process is commonly referred to as Knudsen diffusion. The Knudsen diffusivity DK = d![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /3, which may be obtained using eqn (9) assuming cylindrical pore shape and the pore diameter d and by considering diffusive reflections at the pore walls, is often used as an estimate of the gas diffusion rates in porous materials.86,87 More dense gases in which λ ∼ d may be treated analogously by considering two randomization mechanisms provided by molecular collisions and collisions with the pore walls.
/3, which may be obtained using eqn (9) assuming cylindrical pore shape and the pore diameter d and by considering diffusive reflections at the pore walls, is often used as an estimate of the gas diffusion rates in porous materials.86,87 More dense gases in which λ ∼ d may be treated analogously by considering two randomization mechanisms provided by molecular collisions and collisions with the pore walls.
Situation becomes more complicated in liquids. Here one may consider the diffusion process as matter redistribution driven by thermally activated molecular hops to the free volumes created in the liquid. Thus, l0 can be associated with the hop length which is of the order of molecular diameter. The hop directions already between two subsequent hops of a selected molecule may reasonably well be considered being uncorrelated. In contrast to gases, however, estimating τ0 is far from being trivial and is out of the scopes of this review. For our purposes it is enough to note that τ0 is much shorter than the time scale of the experimental techniques covered in this work.
An analogous view on the diffusion process is applicable for micro- and mesoporous materials in which the guest molecules are homogeneously distributed. In microporous zeolitic materials one may consider the hops between the adjacent cages in the zeolite framework. Once again the driving mechanism is the thermal energy which is also responsible for randomization. It should, however, be noted that specific pore architecture may lead to several effects. Thus the hop probabilities, which are proportional to τ0−1, as well as the hop lengths may be different in different directions, giving thus rise to a macroscopic diffusion anisotropy (the diffusivity becomes thus a matrix). Another phenomenon which may emerge due to structural features is the occurrence of a local persistency in the molecular hopes. Similarly, molecules close to the pore walls in liquid-filled mesopores may exhibit correlations in the hop directions. Under these conditions, it is always possible to consider, instead of single hop events, the combination of several of them until the memory in subsequent displacements will be lost. As long as such coarsening procedure ensures that τ0 ≪ t, on the time scale of the experiment diffusion will be described by a constant diffusivity. This approach will in what follows used to introduce the effective diffusivity for situations in which different diffusion mechanisms may combine in the systems under study.
2.3 Diffusion in inhomogeneous environments
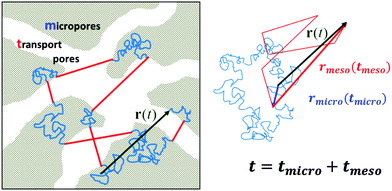
In contrast to bulk liquids or molecules in purely micro- or mesoporous materials, in porous solids comprising several porosities the molecules may alternate in position between the different sub-spaces. Under equilibrium conditions, maintenance of equilibrium between the fluid phases in the different pore spaces (this means the balance between molecular fluxes from micro- to mesopores and from meso- to micropores) requires molecular exchange between micro- and mesopores to be a function of the fluid densities in the micro- and mesopore spaces, which profoundly becomes important under gas phase operation. Indeed, because at already very low pressures of the surrounding atmosphere the micropores are completely occupied by the guest molecules,88 for the pressures below the onset of the capillary condensation in the mesopores the exchange between the micro- and mesopore spaces will almost exclusively be controlled by the gas density in the mesopores. The latter is determined by the particular details of the phase equilibria as defined by the adsorption isotherm.89To rationalize the conditions under which mass transfer in partially filled porous media can be enhanced due to molecular flights in the gaseous phase, let us consider molecular trajectories composed of periods in which the molecules perform erratic hops in micropores and periods of propagations in the gaseous phase in mesopores. An example of such a trajectory is shown in Fig. 2 for a large microporous crystal containing cylindrical worm-chain-like interconnected pores of mesoscalic dimension as a model system. The analysis performed in what follows is, however, generally valid for arbitrary geometries of the microporous regions and mesopore spaces, irrespective of the inter-connectivity of the mesopore space. Moderate gas pressures in the surrounding gas atmosphere, below saturated vapor pressure, are considered. The mean-free path in the bulk gas notably exceeds, under such conditions, the mesopore dimensions. Thus, after diffusing in the micropore spaces and leaving into the mesopores, the molecules will perform Knudsen flights. This means they experience ballistic flights until they hit the pore wall again and get adsorbed.
A sufficiently long trajectory, for which the distance between its initial and final positions notably exceeds the characteristic length scale of a porous material (being of the order of a few mesopore sizes), can be considered as a stochastic one. Thus, to quantify the effective diffusivity Deff associated with such trajectories, one may use the three-dimensional version of the Einstein law, eqn (8), 〈r2(t)〉 = 6Defft. By collecting the displacements in the two different phases separately, but keeping their order within each phase unchanged, the overall displacement r(t) in this equation can be expanded to the sum of the combined displacements rmicro(tmicro) in the micropores and in the transport mesopores rmeso(tmeso). Here tmicro and tmeso refer to the time spans spent by a tracer particle in the micro- and mesopore spaces, respectively, and t = tmicro + tmeso. Thus, Deff may be obtained as
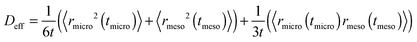 | (10) |
Because the displacements in the micro- and mesopore spaces are not correlated, in most situations the last term in eqn (10) safely can be neglected. By formally introducing the effective diffusivities associated with the sub-trajectories in the micro- and mesopores as
 | (11) |
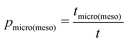 , eqn (10) can now, quite generally, be written as
, eqn (10) can now, quite generally, be written as| Deff = pmicroDmicro + pmesoDmeso | (12) |
Eqn (12), referred to as the generalized fast-exchange equation,93 constitutes a key equation for the assessment of the overall transport properties of a hierarchical pore system. In this respect, it is instructive to elaborate briefly on the meaning of all parameters in this equation.
By their definition and due to the principle of microscopic reversibility, pmicro and pmeso turn out to be equal to the relative fractions of molecules in the micro- and mesopore spaces (pmicro + pmeso = 1). Notably, these two quantities are unambiguously determined by the thermodynamic conditions considered.94
The next quantity, Dmicro, the diffusivity in the sub-space with the slowest transport, can reasonably well be associated with the diffusivity D0,micro in an infinitely extended microporous material. Under certain conditions, namely for very low gas pressures when mass transfer through the mesopore space is negligibly small, this diffusivity has to be corrected for the tortuosity τ of the microporous space, i.e. Dmicro = D0,micro/τ. Indeed, due to exclusion of mass transfer through the mesopores, they act as impermeable obstacles rendering the molecular pathways more tortuous. The most interesting and intuitively not quite easily comprehensible meaning has the parameter Dmeso to which we shall refer in more detail in the next section.
To illustrate this, let us consider a molecule which has just entered a domain of condensed liquid in the micropores after performing a Knudsen flight (see inset in Fig. 3). Due to the laws of diffusion, it will return back to the same liquid–gas interface with a higher probability rather than to similar interfaces formed by other domains of the gaseous phase. Now, if the probability plg is relatively high, this molecule will leave the liquid domain in close proximity of the point, where it has been adsorbed. The flight direction will be centered around the normal to the interface at that point. That means that the flight directions between two subsequent flight events will be statistically anti-correlated. Let us, in what follows, refer to this transport regime as the ‘anti-correlated Knudsen regime’. In the limiting case of extremely high escape probability plg from the liquid into the gaseous phase, the molecule will predominantly perform back-and-forth flights leading to a very slow growth of the mean square displacements acquired in the gaseous phase as compared to that in the liquid domains. This is exemplified by right cartoon in the inset in Fig. 3. As a particular consequence, for non-interconnected mesopores (e.g., in the form of isolated voids), no notable improvement of the transport due to the inclusion of the mesopores can be obtained. The thus emerging anti-correlations can only be broken if the mesopores are interconnected.
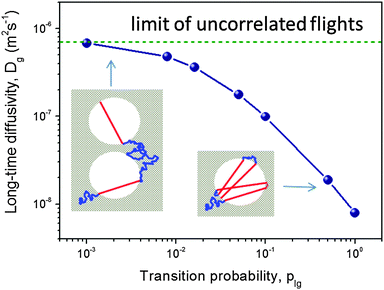 | ||
| Fig. 3 The diffusivity in the gas-filled mesoporous voids as a function of plg obtained using computer simulations for the model of isolated, spherical voids periodically imbedded in a microporous crystal.93 The insets demonstrate how, depending on the magnitude of the transition plg, anti-correlations in the subsequent Knudsen flights emerge (at high plg) and break down (at low plg). This image has been reproduced with permission from ref. 93, published by American Chemical Society. | ||
In the opposite case of low escape probability plg subsequent flights will be uncorrelated due to the fact that a molecule should travel sufficiently long distances before it may successfully perform a Knudsen flight (the left cartoon in the inset in Fig. 3). To this time instant the memory about the previous flight direction has been lost. The situation may therefore be referred to as the ‘uncorrelated Knudsen regime’. In this regime, the diffusivity Dmeso is easily obtained to be Dmeso = DKnudsen = Kd![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , where
, where ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is the molecular thermal velocity in the gas, d is the pore diameter, and K is a numerical constant determined by the mesopore space geometry (K = 1/8 for spherical, isolated mesopores,93K = 1/3 for cylindrical ones,86 and it assumes intermediate values for more complex pore geometries95). In this particular case, the geometry of the mesopore space plays a minor role (only via K) because the respective trajectories appear to be intrinsically stochastic. The overall pattern is exemplified in Fig. 3 showing a strong dependence of Dmeso on the transition probability plg.
is the molecular thermal velocity in the gas, d is the pore diameter, and K is a numerical constant determined by the mesopore space geometry (K = 1/8 for spherical, isolated mesopores,93K = 1/3 for cylindrical ones,86 and it assumes intermediate values for more complex pore geometries95). In this particular case, the geometry of the mesopore space plays a minor role (only via K) because the respective trajectories appear to be intrinsically stochastic. The overall pattern is exemplified in Fig. 3 showing a strong dependence of Dmeso on the transition probability plg.
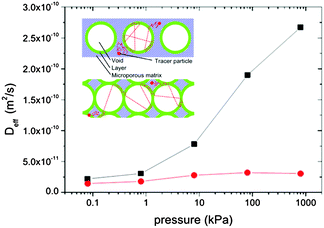
For microporous materials with intrinsically low diffusion rates, the incorporation of transport mesopores may yield much higher enhancement factors.96 This is provided by the second term on the right hand side of eqn (12), which can appreciably exceed the first one. Here, however, in full contrast to the case of uncorrelated Knudsen diffusion considered in the preceding paragraph, the geometry turns out to be vital in deciding on mass transfer acceleration. As exemplified by Fig. 3, the effect of the anti-correlations in the Knudsen flights in closed mesopores will render Dmeso very low, thus prohibiting any perceptible mass transfer acceleration. Only for mesopores traversing the whole microporous particle, the second term on the right hand side of eqn (12) may become sufficiently high. This is demonstrated in Fig. 4 showing simulation data for two model microporous materials, one with imbedded isolated and the other with interconnected spherical domains containing the gaseous phase. It is clearly seen that, with increasing gas pressure, the effective diffusivity notably increases for interconnected mesopores, as a consequence of the increase of Dmeso in eqn (12). That means that Dmeso is sufficiently high for warranting the condition pmesoDmeso ≪ pmicroDmicro ≈ Dmicro. Even though, in the second case considered (i.e. with isolated mesopores), pmeso is almost the same, the decrease of Dmeso with increasing pressure P gives rise to an only two-fold increase of Deff in comparison with Dmicro. This example demonstrates that, for parent materials possessing intrinsically low transport rates, special care about the geometry of the intentionally-added mesopore space has to be taken during material synthesis and all further steps of fabrication. Thus, only truly hierarchical materials become beneficial for transport improvement.
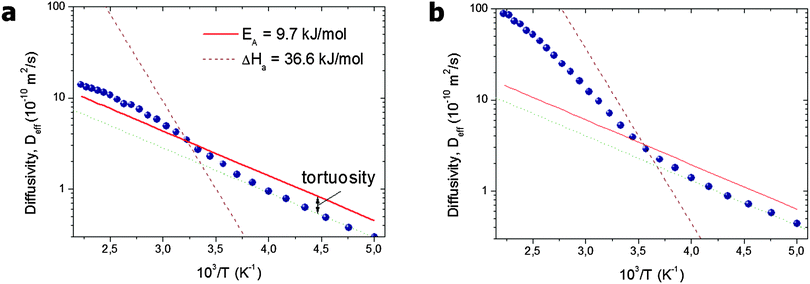 | ||
| Fig. 5 Arrhenius plot of the effective diffusivities found in the simulations for a system of (a) separated and (b) interconnected mesopores.96 The solid line shows the diffusivity D0,micro in the pure microporous host material without included mesoporosity. The slope of the broken line shows the heat of vaporization. This image has been reproduced with permission from ref. 96, published by Elsevier. | ||
With increasing temperature, increasing gas pressure gives rise to a respective increase of pmeso and, hence, of pmesoDmeso. This term may thus become comparable to pmicroDmicro and lead to the observed enhancement of Deff. The slope of the effective diffusivity in the Arrhenius plot may approach the heat of vaporization which controls the value of pmeso. With increasing pmeso, however, Dmeso in the material with the closed mesopores starts to decrease in parallel (the anti-correlated Knudsen regime). Thus, at high temperatures only a slight increase of Deff over D0,micro is observed. In contrast, in the material with the connected mesopores Deff grows substantially at high temperatures (the uncorrelated Knudsen regime), until the mean-free-path of the molecules decreases due to mutual molecular encounters, signifying transition from Knudsen diffusion to genuine gas-phase diffusion.
2.4 Non-equilibrium techniques of diffusion measurements
Despite the fact that numerous demonstrations of enhanced activities of hierarchical micro-mesoporous materials were interrelated with their improved transport properties,99,100 the latter have only rarely been in the focus of laboratory studies. Several works dealing with transport in hierarchical microporous materials have mostly been assessed using macroscopic techniques, which are based on the measurement of the equilibration kinetics of the intra-porous fluid concentration upon a stepwise change of the external conditions. For these studies different techniques, such as gravimetric sorption, zero-length column (ZLC) measurements, and NMR spectroscopy were utilized.As selected examples, the elution of iso-butane from conventional zeolite ZSM-5 and mesoporous zeolites obtained by carbon templating was followed.101 The experimental results revealed three-fold increase of the effective diffusivity in mesoporous zeolite over the conventional one. These data were further supported by assessing diffusive properties of reactants during catalytic conversion. Hierarchical SAPO-34, in which transport pores were added by templating using carbon nanotubes, has shown much more efficient uptake of n-butane over the parent zeolite.102 In a similar way, by measuring adsorption/desorption of neo-pentane,19 2,2-dimethylbutane,34 cumene,103 and iso-octane104 to/from mesoporous ZSM-5 obtained by controlled desilication and alkali-treatment, notable transport improvements of mesoporous zeolites over microporous ones were reported.
Analogous conclusions have been drawn for mesoporous LTA zeolites, generated by adding organosilane surfactants during zeolite synthesis, by measuring the uptake kinetics of 129Xe using NMR spectroscopy.105 It was found that the mesoporosity generated within the zeolite accelerated the uptake of xenon. Moreover, it was experimentally demonstrated that, with increasing of the amount of the surfactant added, i.e. by increasing mesoporosity, the uptake rate increased. Interestingly, the uptake rates, which in that work were associated with increased diffusion rates, were found to scale linearly with the mesopore surface area of the LTA zeolites. The uptake/release rates were analysed based on the solution of Fick's diffusion equation under the following assumptions: (i) mass distribution within the mesoporous zeolite crystal is described by a single, effective intra-particle diffusivity, (ii) the boundary conditions are fixed at the crystal outer edge and (iii) no additional transport resistances at the outer surface are assumed to be effective. Notably, the same type of analysis is typically used in the literature for the quantification of transport in hierarchical host systems, although the criteria of the applicability of these assumptions are loosely defined.
Among others, the ZLC technique106 was successfully applied to study molecular transport in several materials. Enhanced transport of n-heptane, toluene and o-xylene in bi-porous UL-silicalite, consisting of micro- and mesopores in which zeolite nanoparticles were inter-grown in one-dimensional mesoporous structure used as a matrix, was reported by Hoang et al.107 In this way, strong influence of the mesopores in facilitating mass transport through the complex micro-/mesopore structure was demonstrated. In a recent study, diffusion of cyclohexane in hierarchically-organized silicalite-1 materials with well-controlled mesoporosities was studied and order of magnitude enhancement over conventional silicalite-1 was reported.108
2.5 Equilibrium techniques of diffusion measurements
Acceleration of molecular exchange between the micropore spaces and the particle surroundings due to the introduced transport pores may clearly be revealed already by macroscopic diffusion studies as just described. In view of the complexity of the involved phenomena and processes, however, these techniques alone generally fail in providing that amount of information which is necessary for a comprehensive description of the transport mechanisms within such materials needed for knowledge-based process optimizations. This can be caused, e.g., by the occurrence of additional transport resistances between the micro- and mesopores, by heat dissipation during transient uptake, and by uncontrolled distribution of the particle sizes and shapes. Any purposeful exploration of the above-mentioned problems may require the respective experiments performed with a series of materials with well-controlled variations of their structural characteristics.In this respect, access to the internal microdynamics using analytical techniques with variable spatial or time scales is a very attractive, alternative route which is absolutely essential for giving a deeper insight into the transport properties of mesoporous solids. That is why the synergetic application of complementary techniques of microscopic measurement becomes increasingly vital for a better understanding of transport properties of hierarchical porous solids.109,110 This microscopic approach will be in the focus of this work.
Internal microdynamics can be accessed under both equilibrium and non-equilibrium situations. The latter option is provided, e.g., by the recently introduced microimaging technique.111–113 However, it is still in the initial stage of its development and application to micro-mesoporous materials remains an attractive field of future research with, so far, only a few reports demonstrating its potential concerning porous materials containing mesopores.114 Thus, techniques operating under equilibrium conditions remain the first choice to assess the internal dynamics in micro-mesoporous adsorbents. These methods, as applicable to porous media, include pulsed field gradient (PFG) NMR,115–119 neutron scattering,120–122 electron paramagnetic resonance,123,124 fluorescence correlation spectroscopy (FCS),125–128 dynamic light scattering (DLS),129,130 and single particle tracing techniques.131–137
Among them, PFG NMR proves to be especially suited for the exploration of internal microdynamics of hierarchical micro-mesoporous materials. It operates under equilibrium condition and, hence, corresponds with the situation illustrated in Fig. 1c. Its fundamentals and the wealth of information about mass transfer in mesoporous materials which, most recently, has been gained with this technique is in the focus of this contribution and shall be dealt with in more detail in Section 3.
3 Diffusion measurements using PFG NMR
It is the key quantity of diffusion, the mean square displacement 〈x2〉 of the probe molecules in the sample, which can be probed using PFG NMR in the most direct way.117,118 The phenomenon of NMR itself is based on the occurrence of a precessional motion of nuclear spins, like 1H or 13C, placed in an external magnetic field. The Larmor frequency ω of the precession is given as the product of the magnetic field strength B0 and the gyromagnetic ratio γ of the nuclei under study. Different nuclei possess different γ. This allows frequency-based signal separation and provides sensitivity to the chemistry of the molecular species. By bringing the spin system into coherence by a resonant radio-frequency (r.-f.) field in the form of a short pulse with a well-defined duration (the so-called 90°-pulse, see Fig. 6) and by letting the system evolve for a time period τ, the spins will acquire a phase γB0τ. The effect of a subsequently applied second r.-f. pulse (or a series of two 90°-pulses) is equivalent to inverting the precessional direction so that, at time τ after the inversion, the initial coherence will again be restored. The thus formed signal is called the spin-echo.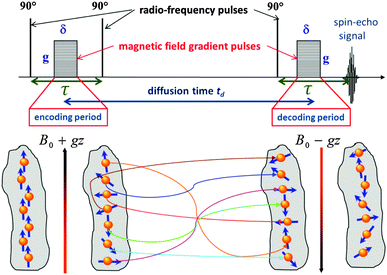 | ||
| Fig. 6 Schematic representations of the stimulated echo PFG NMR pulse sequence used for the diffusion measurements. The lower part of the figure shows how a helically-wounded spin coherence obtained during the encoding period is not rewound back during the decoding period due to diffusion occuring during the diffusion time t, resulting thus in lowering of the measured spin-echo signal in accordance with eqn (14). | ||
For the diffusion measurements, the series of r.-f. pulses are combined with those of the magnetic field gradients (the so-called ‘field gradient pulses’), i.e. the constant magnetic field is superimposed over two short time intervals of length δ by an inhomogeneous field. They are typically linear in space with the linearity constant 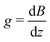 , where the z-axis§ is chosen to align in the direction of the external magnetic field B0. The effect of the two gradient pulses shown in Fig. 6 is to encode and to decode positionally the nuclear spins according to their Larmor frequencies, or, more precisely, by the phase differences γδgz acquired during δ. Thus, if the spins are hypothetically immobilized in space, the effects of the two pulses would compensate each other and the spin-echo signal intensity would remain unchanged in comparison with the situation without gradient pulses. If, however, the spins interchange their positions by Δz = z − z0, their contribution to the signal will be attenuated by the factor cos(γδgΔz). The overall signal S appears as the average over all spins
, where the z-axis§ is chosen to align in the direction of the external magnetic field B0. The effect of the two gradient pulses shown in Fig. 6 is to encode and to decode positionally the nuclear spins according to their Larmor frequencies, or, more precisely, by the phase differences γδgz acquired during δ. Thus, if the spins are hypothetically immobilized in space, the effects of the two pulses would compensate each other and the spin-echo signal intensity would remain unchanged in comparison with the situation without gradient pulses. If, however, the spins interchange their positions by Δz = z − z0, their contribution to the signal will be attenuated by the factor cos(γδgΔz). The overall signal S appears as the average over all spins
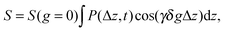 | (13) |
| S = S(q = 0)e−½q2〈z2〉 = S(q = 0)e−q2Defft, | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S vs. q2t. The possibility to vary the separation time between the magnetic field gradients in the pulse sequence in a range between a few milliseconds to a few seconds allows tracing the mean square displacements as a function of the observation time t in this time window. This time window, depending on the mobility of the species under consideration, may correspond to length scale probed by these species from about hundred nanometers to several micrometers. These potentials of PFG NMR are indeed unique, compared with the options of other techniques of diffusion measurement, making PFG NMR particularly powerful and informative under quite different circumstances.
S vs. q2t. The possibility to vary the separation time between the magnetic field gradients in the pulse sequence in a range between a few milliseconds to a few seconds allows tracing the mean square displacements as a function of the observation time t in this time window. This time window, depending on the mobility of the species under consideration, may correspond to length scale probed by these species from about hundred nanometers to several micrometers. These potentials of PFG NMR are indeed unique, compared with the options of other techniques of diffusion measurement, making PFG NMR particularly powerful and informative under quite different circumstances.
Due to its operating principle providing, among others, non-invasive and non-perturbative access to mean square displacements in broad time- and length-scales, the PFG NMR technique has become one of the most widely used methods for transport characterization in porous media.54,98,113,119,138–147 The experimental results presented in this work were obtained using exactly this method.
3.1 Diffusion in micro- and mesoporous solids
Before addressing transport properties of materials with multiple porosities, it is essential to recollect some basic information on mass transfer occurring in their different sub-spaces. In this contribution, we confine ourselves to porous materials containing only micro- and mesoporosities. In micropores, whose sizes are comparable to the molecular sizes of guest species, diffusion is predominantly determined by the guest–host interactions.5 Obviously, the tighter the confinement, the slower is the motion. At the same time, as exemplified by Fig. 7, the diffusivities may also be a function of the guest concentration in the pore spaces. Fig. 7 provides an overview of the different patterns of concentration dependence so far observed. Correlating these different patterns with the underlying molecular mechanisms is an attractive task of current MD simulations. For the purposes of this work, we have to emphasize the most remarkable feature of diffusion in zeolites, namely that depending on the guest concentration the diffusivities of the guest molecules may vary over orders of magnitude.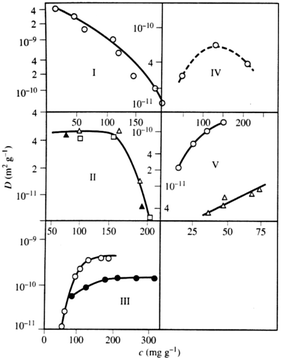 | ||
| Fig. 7 Different patterns of the concentration dependence of intracrystalline diffusivities: (I) n-hexane in NaX at 358 K; (II) ortho- (full triangle), meta- (square), and para-xylenes (triangle) in NaX at 393 K; (III) ammonia (circle) and water (full circle) in NaX at 298 K; (IV) acetonitrile in NaX at 393 K; (V) ethane (circle) at 173 K and propane (triangle) at 413 K in NaCaA.148,149 This image has been reproduced with permission from ref. 148, published by Elsevier. | ||
Concerning mass transfer in mesoporous materials, one must be aware of the fact that, in contrast to microporous materials, the guest molecules may occur in different phase states coexisting with each other within the mesopore spaces. Because molecular mobilities in gases and liquids dramatically differ from each other, this immediately leads to an interplay of these two mechanisms in mesoporous materials causing the effective diffusivity to be a function of the phase coexistence.94,150–156 In conjunction with alternating periods of migration in both phases in the molecular trajectories, severe modifications of the transport mechanisms may occur. The latter can result, in particular, due to the existence of interfaces between the domains of different phases.
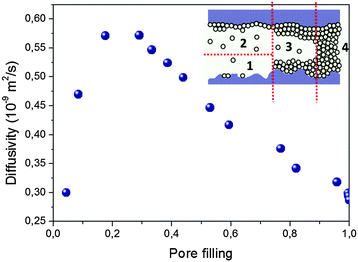
Quite generally, the trajectories may include periods of surface diffusion,157–159 diffusion in multilayers on the pore walls and diffusion through the pore space. A combination of these transport modes leads, typically, to a pattern as exemplified in Fig. 8. It shows quite a complex behavior which is, however, generic for mesoporous materials, irrespective of their fine structure. Starting from zero loading one observes, with increasing pore filling determined by the external gas pressure, (i) a strong increase in the diffusivities, (ii) the formation of a maximum at intermediate loadings and (iii), finally, after the capillary condensation is completed, an essentially constant value of the diffusivities. On decreasing pressure, over the range of capillary condensation, the diffusivities are typically found to notably deviate from those observed at the same external pressures during adsorption, exhibiting a pronounced hysteresis in the diffusivities.94,154
3.2 Selected examples of diffusion measurements in materials with hierarchical porosities
In materials with multiple porosities, the complexity of the pore structure translates into the respective complexity in the dynamics.160 Moreover, very rich phase behavior of fluids confined to mesopores,161–163 giving rise to inhomogeneous density distributions within the pore space, may significantly complicate molecular transport.154,164,165 Nevertheless, the theoretical approaches developed so far, including those discussed in Section 2, can successfully be used to predict general patterns. To demonstrate their validity, in this section we briefly discuss the results of a few case studies obtained using PFG NMR. In particular, we are going to demonstrate how the parameters of eqn (12) are determined by structural organization of real materials and by thermodynamical conditions under which the experiments have been performed.With the progress attained in synthesis of well-ordered porous materials, particularly convenient conditions for an in-depth study of structure-mobility correlations in such systems has become possible.167–169 As an example, which particularly suits these purposes, we may refer to studies performed using PIB-IL material.73,170 It consists of regularly arrayed spherical pores with diameters of about 16 nm connected by worm-like cylindrical micropores with diameters up to 2 nm. Because (i) the diffusivities of the molecules in the cylindrical micropores are sufficiently high (namely of the order of 10−10 m2 s−1) and (ii) the large mesopores are isolated from each other, this material may serve as an ideal system for verifying the transport mechanisms and the emergence of anti-correlations in the flight direction statistics.
The experimental data of the effective diffusivities of cyclohexane at room temperature obtained by PFG NMR are shown in Fig. 9 as a function of the external gas pressure.93 Notably, due to the requirement of equilibrium, the same gas pressure P is attained in the mesoporous voids for P < Pc, where Pc is the capillary condensation pressure.73,171 At the same time, the micropores contain already at this pressures a high-density condensed phase. The pressure dependence of the diffusivities resembles the typical pattern observed for mesoporous materials, with the formation of the maximum at intermediate pressures.54,94 This maximum unequivocally points out a notable contribution of gas phase diffusion to total mass transfer. The enhancement factor is found to be only of about 2, in full agreement with the theoretical prediction for the system containing isolated mesopores.
 | ||
| Fig. 9 Effective diffusivities of cyclohexane in PIB-IL material. PIB-IL is composed of spherical voids with a diameter of 16 nm interconnected by small micropores with about 2 nm pore diameter as a function of gas pressure.93 The inset shows cartoon-like structures of PIB-IL, with the left and the right panels showing, respectively, coexistence of the gas-filled and liquid-filled mesopores with the micropores containing condensed phase. This image has been reproduced with permission from ref. 93, published by American Chemical Society. | ||
If mass transfer in the mesopores occurs as uncorrelated Knudsen flights, due to the highly ordered structure of PIB-IL the experimental data can be readily compared also quantitatively with the theoretical predictions. Indeed, pmicro and pmeso in eqn (12) are known from the thermodynamical conditions and structural information, Dmicro can be measured independently, and Dmeso in this regime is, with a high accuracy, given by DKnudsen = d![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /8. The thus calculated data are shown in Fig. 9 together with the experimental data and are found to be in an almost perfect agreement, evidencing, thus, the validity of both the theoretical analysis performed and the establishment of the uncorrelated Knudsen regime. Additional diffusion studies using ordered multi-porous materials with different geometries of their sub-pore spaces is a challenging task for further experimental explorations with the aim to clarify finer details of the parameters in eqn (12).
/8. The thus calculated data are shown in Fig. 9 together with the experimental data and are found to be in an almost perfect agreement, evidencing, thus, the validity of both the theoretical analysis performed and the establishment of the uncorrelated Knudsen regime. Additional diffusion studies using ordered multi-porous materials with different geometries of their sub-pore spaces is a challenging task for further experimental explorations with the aim to clarify finer details of the parameters in eqn (12).
 | ||
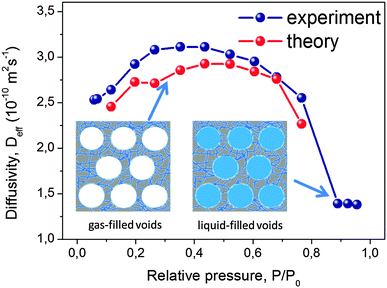
| Fig. 10 Diffusion in purely microporous zeolite NaX and in zeolite NaX containing a network of transport pores.172 (a) Shows the SEM image of the two materials with (b) the respective nitrogen sorption isotherms. (c) Shows the diffusion attenuation measured using PFG NMR with slopes being proportional to the effective diffusivity according to eqn (14). This image has been reproduced with permission from ref. 172, published by John Wiley and Sons. | ||
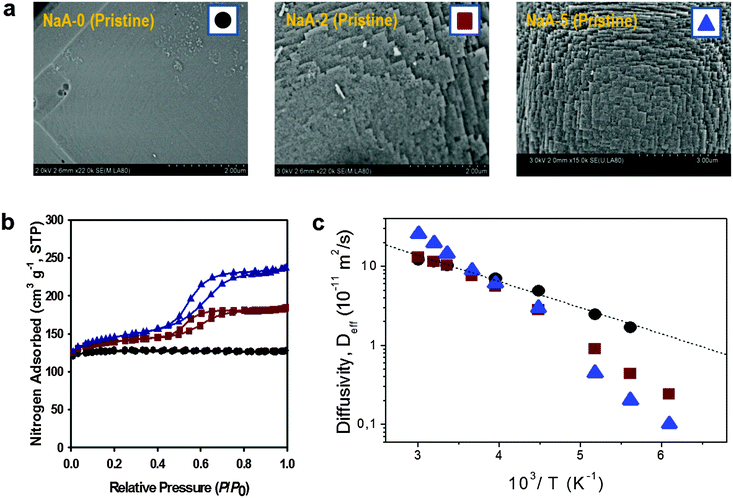 | ||
| Fig. 11 Diffusion in purely microporous zeolite NaCaA and in two specimens of zeolite NaCaA containing a mesopore network. (a) Shows the SEM images of the three materials, (b) presents the respective nitrogen sorption isotherms, (c) shows, in an Arrhenius plot, the diffusivities of ethane in the purely microporous NaCaA-0 (circles) and in the two mesoporous zeolites NaCaA-2 (squares) and NaCaA-5 (triangles). This image has been reproduced with permission from ref. 58, published by Elsevier. | ||
The diffusivities of ethane measured using PFG NMR at different temperatures are shown in Fig. 11 as an Arrhenius plot. The amount of ethane provided was equal to 3 molecules per super-cage of the zeolite. For the purely microporous material, both the diffusivities and the activation energy for diffusion were found to be in good agreement with the experimental data reported earlier.177 Most remarkably, for the mesoporous NaCaA materials the diffusivities can be either slower (at low temperatures) or faster (at high temperatures) than the diffusivities in the parent material! Thus, this experimental finding provides the most direct support for the theoretical foundation provided in the theoretical section. Indeed, the diffusion data of Fig. 11 reproduce qualitatively the behavior seen in Fig. 5.
With this perfect match between experiment and theory, it is now straightforward to associate the different patterns revealed by Fig. 11 with the corresponding transport regimes as discussed in the preceding sections. Thus, transport reduction at low temperatures reflects the occurrence of the regime of blocked mesopores with negligible mass transfer through the mesopores (see Section 2.3.4). In this case, the larger the amount of the mesopores, the lower should be the diffusivity through the space of micropores due to the higher tortuosity brought about by the presence of the (now essentially impermeable) mesopores. Exactly this behavior is seen in the experiment.
With increasing temperature, increasing density of ethane in the gaseous phase of the mesopores gives rise, via the term pmesoDmeso in eqn (12), to higher apparent activation energies. The latter is mainly determined by the heat of adsorption, controlling the increase of pmeso in pmesoDmeso, with increasing temperature. The diffusivity data observed with NaCaA-2 do not exceed the diffusivities in the purely microporous specimen which may, possibly, indicate onset of the regime of anti-correlated Knudsen flights (see Section 2.3.2). For NaCaA-5, however, with the higher amount of the mesopores, mass transfer through the mesopores is clearly seen to occur in the uncorrelated Knudsen regime (see Section 2.3.2), with effective diffusivities notably exceeding the diffusivities in the purely microporous samples.
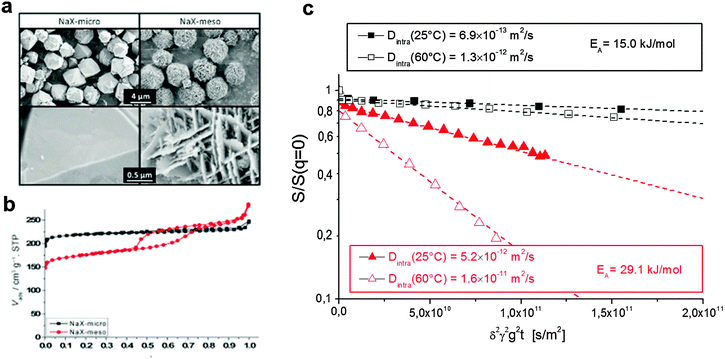
To provide an independent proof for the increasing tortuosity of the mesopore space with decreasing amount of the organosilane template added during synthesis, and to introduce an additional tool for the characterization of hierarchical pore systems, PFG NMR experiments using cyclohexane as a tracer molecule have been performed. The use of probe molecules with different size and functionality has already been proven to provide an exciting opportunity to probe different properties of interest.178 In our case, the kinetic diameter of cyclohexane is sufficiently large to exclude entering the micropore space in the NaCaA zeolite. Thus, cyclohexane can diffuse only in the mesopores. The data of Fig. 12 nicely illustrate that the diffusivity of cyclohexane indeed decreases (respectively, the tortuosity increases) with decreasing mesopore volume. It is also instructive to see the opposing tendencies of transport in exclusively the micropores (as recorded with ethane and blocked mesopores) and the mesopores (as recorded with cyclohexane), respectively.
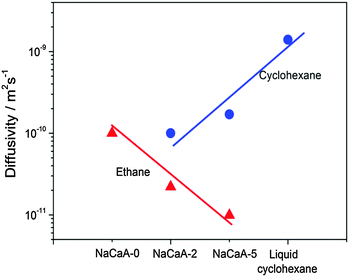 | ||
| Fig. 12 Diffusivities of ethane (diffusing in only micropores) and cyclohexane (diffusing in only mesopores) in the NaCaA zeolites under study.58 The amount of ethane was equal to 2 molecules per super-cage of the zeolite and the volume of added cyclohexane was equal to the mesopore volume. This image has been reproduced with permission from ref. 58, published by Elsevier. | ||
3.3 Tracer exchange and near-equilibrium sorption measurements
Besides direct measurements of the mean square displacements, NMR provides other means for assessing the rates of molecular propagations in porous solids. As an example, a large pool of NMR-based imaging approaches are proven to be a versatile tool to probe spatial distributions of fluids within porous materials and to follow their evolution with time.143,180 The application of these methods is however limited due to the spatial resolution exceeding tens of micrometers. Here, for instructive purposes, we shall briefly mention only two other approaches. Rationalizing their working principles of which may help to better understand the relationships between the equilibrium and non-equilibrium techniques of diffusion measurements.In the so-called NMR Tracer Desorption (‘Tracer-Exchange’) technique (see, e.g. Section 11.4.3 in ref. 5) the experiments are performed in the spirit of Fig. 1b. They are conducted under equilibrium conditions, but by creating a non-equilibrium apparent density profiles by labeling some part of the molecules and by following their equilibration. Note that labeling is done in a way to not perturb the thermodynamic equilibrium. In porous materials, such a labeling can naturally be done based on different diffusivities, smaller ones in the pore spaces of porous materials, and faster ones in the bulk phases surrounding the porous particles.154,181,182 The two pools of molecules with differing diffusivities can easily be distinguished in the NMR spin-echo diffusion attenuation functions. Indeed, different diffusivities give rise to different slopes in ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S vs. q2t plots with the weights determined by the populations of the molecules in the two pore spaces as demonstrated in Fig. 13a.154 The results show, essentially, the release of cyclohexane from porous silicon particles driven by simple diffusion in the absence of any gradients in concentration or chemical potential. The thus obtained data can be analyzed using equations analogous to eqn (5) and (6).
S vs. q2t plots with the weights determined by the populations of the molecules in the two pore spaces as demonstrated in Fig. 13a.154 The results show, essentially, the release of cyclohexane from porous silicon particles driven by simple diffusion in the absence of any gradients in concentration or chemical potential. The thus obtained data can be analyzed using equations analogous to eqn (5) and (6).
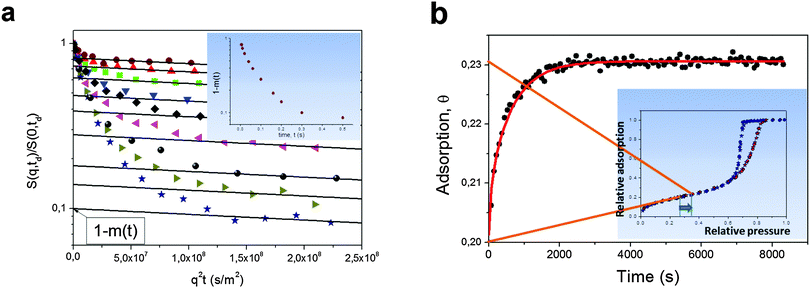 | ||
| Fig. 13 (a) Normalized spin-echo diffusion attenuations for cyclohexane in porous silicon powder for different diffusion times increasing from top to bottom.154 Cyclohexane was given in amount to fill both intra- and inter-particle pore spaces. The solid lines show eqn (14) approaching the intra-porous component with the intercept of the vertical axis being the relative fraction (1 − m(t)) of cyclohexane molecules which have never left the intra-particle space during the diffusion time. The inset shows (1 − m(t)) as a function of time. (b) Adsorption kinetics for cyclohexane in Vycor porous glass monolith upon small pressure step in the surrounding gas as indicated in the inset, which shows the respective sorption isotherm.179 The solid line is the solution of a Fick's diffusion equation (for the particular geometry of the monolith) with the independently measured diffusivity of cyclohexane within the porous glass. This image has been reproduced with permission from ref. 154 and 179, published by Royal Society of Chemistry and Nature Publishing Group, respectively. | ||
Another example refers to transient adsorption experiments in a Vycor porous glass monolith with well-defined shape.179 Here, the experiments are performed under the occurrence of a gradient in the chemical potential and refer, therefore, to the situations depicted by Fig. 1a. Because the pressure step used is, however, very small, the main component of that gradient is given by the difference in the excess molecular concentration. In this case, the effect of intermolecular interaction¶ may be neglected and the density equilibration will predominately be controlled by normal diffusion. This line of arguing is corroborated by the experimental data showing that, in this case, the uptake curves recorded under quasi-non-equilibrium conditions are seen to be in an excellent agreement with the prediction of Fick's diffusion equation with the diffusivity independently measured under equilibrium using PFG NMR.
4 Classification, simulation, and resulting diffusivities
In most practical cases, technological use of hierarchical porous solids occurs under non-equilibrium conditions either under the occurrence of concentration gradients or under transient conditions. In this respect, understanding the relationships between the messages obtained using equilibrium techniques of diffusion measurements discussed in the preceding section and their non-equilibrium counterpart is of vital importance. Any knowledge-driven optimization of technological processes involving porous solids requires understanding of the fundamentals of the diffusion processes in these complex objects and of the elementary processes occurring within the hierarchical porous solids. They thus become one of the key elements in overall process design. Last, but not least, assessment of the various transport mechanisms and a complete characterization of their interaction must be based on a combined application of different techniques which, once again, requires a solid understanding of their correlations.It is the goal of this section to introduce a lattice model allowing for a transport-based classification scheme for different bi-porous hierarchical materials. It will be used to cover different situations and to highlight correlations between diffusivity measurements performed along different routes using dynamic Monte Carlo simulations.183,184 These considerations may, ultimately, also aid as a tool for selecting the materials of choice for specific applications. Before we consider different types of materials, we summarize briefly some relevant details of the simulation procedure (for an extended description of the simulation details we refer to ESI‡).
In order to model the hierarchical porous materials a simple cubic lattice is employed.185 It is subdivided in mesoporous and microporous domains, which in what follows will be referred to by the subscripts ‘meso’ and ‘micro’, respectively. The distinct porous spaces in the material are modeled by attributing specific transport properties to guest particles corresponding to their host domain, such as local diffusivity and equilibrium concentration. Additionally, surface barriers between the two domains can be introduced.
Random movement of the individual particles is simulated to occur completely unaffected by the presence of other particles. The simulations do, therefore, strictly refer to the conditions of self-diffusion or tracer exchange. These, however, are exactly the conditions under which, in Section 3, PFG NMR has been shown to operate and to provide unique information about the propagation rates over quite different length scales. Even under non-equilibrium conditions, self- or tracer diffusivities may serve as an informative first-order estimate as it has been discussed in Section 3.3. This is in particular true at low concentrations when mutual molecular interaction becomes negligibly small so that the transport and self-diffusivities coincide. In the following we refer to this case and drop the distinction between equilibrium and non-equilibrium measurements in the sense that in all cases mass transfer of non-interacting molecules is considered. Depending on the procedure of measurement, pore space hierarchy shall be shown to give rise to different diffusivities. Establishing correlations between them will be one of the goals of our consideration.
4.1 Scenarios considered
In the simulations, diffusivities have been determined following three different procedures, with the resulting diffusivities correspondingly specified:• Microscopic diffusivity Dmsd.
The ‘microscopic diffusivity’ Dmsd has been calculated by considering the mean square displacements and by applying eqn (8). For this purpose, the trajectories of each individual particle have been followed in the simulations. By choosing periodic boundary conditions, any limitation of the trajectories to a finite simulation grid, was avoided. The thus determined diffusivity resembles that resulting from the PFG NMR diffusion measurements.
• Flux diffusion coefficient Dflux.
According to Fick's first law given by eqn (1), applying a concentration gradient dc/dx leads to the occurrence of a directed flux j of particles from the regions of higher concentration to lower ones. By quantizing this flux, i.e. by counting the number of particles N passing through surface area S per time lapsed t,
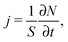 | (15) |
• Uptake diffusion coefficient Duptake.
As a measure of the time constant of molecular uptake or release, one may use the first statistical moment defined by the relation eqn (4). By recording the uptake curve during filling of the model system, the ‘uptake diffusion coefficient’ was calculated with eqn (6). This approach resembles the assessment of diffusivities in uptake/release experiments.
As a first result of our simulations, in all cases considered the microscopic diffusivity and flux diffusion coefficient were found to coincide. This result may be rationalized by simple effective medium arguments. Since the fluxes are a function of only the difference in concentration, rather than of the absolute concentrations, simulation grids of continuously decreasing population may be put together. Thus one is able to create the situation where, by means of the law of mass conversation, Fick's first law may be converted into Fick's second law (our eqn (1)–(3)). The probability distribution of molecular displacements, which results as a solution of Fick's second law for an initial particle distribution given by Dirac's delta function, is then known to be given by a Gaussian, with the mean square displacement following the Einstein relation, eqn (8), and with a diffusivity, appearing in this equation, being identical with the ‘flux diffusion coefficient’ appearing in Fick's first law. We took this coincidence in diffusivities Dmsd and Dflux attained along quite different routes of calculation as a proof of consistency of our simulations.
The simulations of the transport processes in materials with combined micro- and mesoporosities were considered for two representative situations:
• Fast-exchange regime.
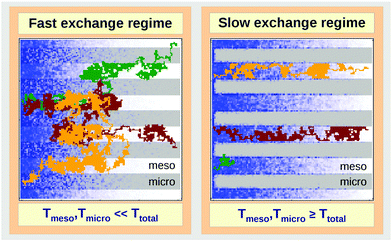
In micro-mesoporous materials the guest molecules diffuse in micro- and mesopores and alternate between them. Thus, three different time-scales naturally emerge. A first one is associated with time required for the diffusing species to traverse the entire particle with inner micro- and mesoporosity. It shall be denoted τ. The remaining ones, τi, where i = ‘micro’ or ‘meso’, are reflecting average lifetimes of the molecules in the micro- and mesopore spaces. In the fast-exchange regime it holds:
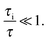 | (16) |
Concerning, e.g., uptake, under this condition the particles frequently alternate between different domains before global equilibration may occur, as exemplified in Fig. 14. The main peculiarity of this regime is that the system-averaged (effective) diffusivity can be described by eqn (12). In simulations, pmeso and pmicro denote the relative number of particles residing in the meso- and microporous domain, respectively, which are found as 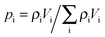 for domain i, where ρi denotes the fluid density and Vi the volume of the corresponding domain.
for domain i, where ρi denotes the fluid density and Vi the volume of the corresponding domain.
As representative estimates, τi can be designated as the uptake time constants in the respective domains. In the absence of surface barriers, in this case, by inserting eqn (6) into eqn (16), the fast-exchange regime is seen to be characterized by the following relation
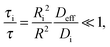 | (17) |
• Slow-exchange regime.
In the opposite limiting case of slow exchange, the average lifetimes τi of particles in one of the domains or in both domains can be of the order of τ or even larger. This may lead to situations where the particle density in mesopores may already approach equilibrium with the bulk phase, while density relaxation in the microporous domains will still be far from equilibrium. In this case, as shown in Fig. 14, the particles very infrequently change the domains. Such a condition is most frequently encountered if the diffusivities in micropores appear to be relatively slow. In this case and in the absence of surface barriers, the slow exchange regime can, in particular, be characterized by
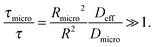 | (18) |
It has found growing evidence that, in addition to complex structure and to complex phase equilibria, the occurrence of surface barriers at the micropore/mesopore interfaces may strongly affect the transport.61,186–194 Thus, it may happen that sole the material structure and local diffusion rates in the domains would allow fast exchange, but the blockages on the interfaces between the pore spaces will prohibit it. Therefore, effects arising from these barriers were also covered.
In order to model these different scenarios, the particles residing in the domains with micro- and mesoporosities were allowed to diffuse with different local diffusivities. For the fast-exchange regime (as well as in the simulations with surface barriers), the diffusivities in the mesopores were assumed to exceed those in the micropores by a factor of 10. For approaching the slow-exchange regime, a factor of 104 was used. To model the surface barriers, the probability for particles to pass through any interface between the micro- and mesoporous regions was set to 10−4 (for both directions). The complete set of parameters used in the simulations may be found in the ESI.‡
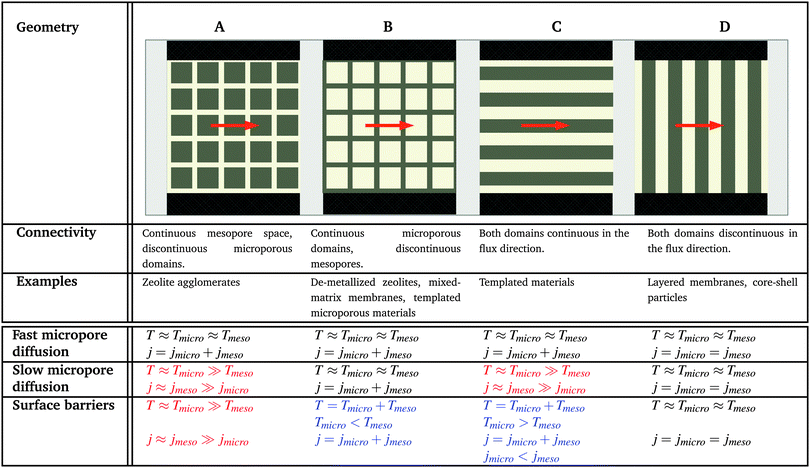
4.2 Topology classes of the host material
In order to relate the topology of the material to the measured diffusion coefficients, it is useful to identify generic classes which exhibit qualitatively similar transport patterns. The different approaches so far suggested for such classifications were, in general, chosen from the perspective of the given purpose.195 Thus, classification has e.g. been based on structural aspects,196,197 which are accessible by a variety of experimental techniques.33 Alternatively, structural characterization by the hierarchy factor has been proven to serve as a powerful key number for characterizing the efficiency of catalytic reactions.198 In what follows, we will base our consideration on a classification scheme shown in Table 1. For the purposes of our work, this subdivision is done based on the generic transport properties of the four classes of materials shown, which cover all different experimental situations.The four classes presented in Table 1 and which, in what follows, are referred to by the bold characters (A, B, C, D) were identified by considering the inter-connectivities of the two domains containing micro- and mesoporosities. In Section 2.3 this inter-connectivity has been identified as a crucial property deciding about the transport properties in materials with combined porosities and, thus, about their technological performance and application.199 Direct quantification of this influence is far from being trivial200–208 and remains a hot topic of current research. However, for the purposes of this work, it is sufficient to consider, quite generally, the ideal situations as shown in Table 1. In real materials, different inter-connectivities will give rise to different tortuosities of the respective subspaces. This may alter transport, but this effect will be of only quantitative, but not qualitative nature.
For simplicity, we are going to consider identical pore space volumes, namely containing 50% micropores and 50% mesopores. Moreover, only two cases of pore space equilibrium densities shall be considered, namely identical densities and a density ratio ρmicro/ρmeso = 5.
4.3 Identical fluid densities in micro- and mesopores
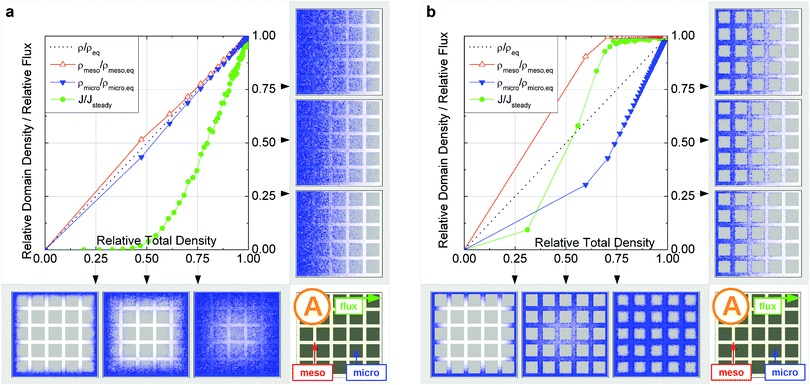
In this scenario, the equilibrium concentrations within the domains were considered to be identical. This may resemble situations of, e.g., liquid intrusion. Since the domain volumes in our models are as well identical, the relative number of particles in the domains under equilibrium are equal, so that pmicro = pmeso. In the absence of hierarchy, both domains would equally contribute to the macroscopic observables. This facilitates the investigation of the impact of the presented hierarchies on overall transport.Let us now consider which diffusivities will be delivered by the different techniques of diffusion measurements under these conditions. For this purpose, we will use the diffusivity–correlation plots as shown in Fig. 16. They demonstrate the correlations between the microscopic diffusivity Dmsd (recall that Dflux = Dmsd) and the macroscopic diffusivity Duptake. In this type of presentation, two coinciding diffusivities will appear as a symbol on the diagonal line. Exactly this behavior is found for all four geometries A–D in the regime of fast exchange regime. This finding is found to be in good agreement with the discussion in Section 2.
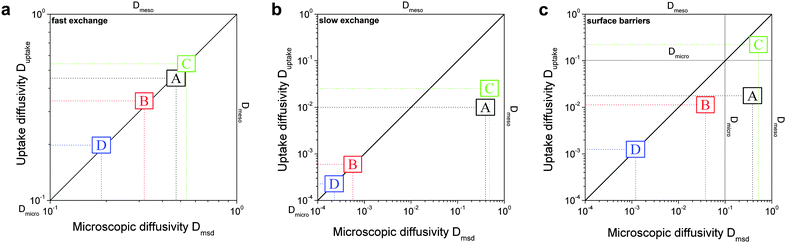 | ||
| Fig. 16 Correlation of the diffusivities (shown by the symbols A, B, C, and D) obtained in the four different pore space arrangements A–D in Table 1 by considering the mean square displacements and in uptake experiments for identical equilibrium fluid densities in the micro- and mesopores. The results were obtained under the following conditions: (a) relatively fast diffusion in the micropores (Dmicro/Dmeso = 0.1), (b) relatively slow diffusion in the micropores (Dmicro/Dmeso = 10−4), and (c) relatively fast diffusion (Dmicro/Dmeso = 0.1) with surface barriers corresponding to the transition probabilities pmeso→micro = pmicro→meso = 10−4 on the interface of the mesopores with the microporous space. | ||
In addition, the total flux is seen to attain its equilibrium magnitude simultaneously with equilibration of the mesopore densities. Thus, the mesopores act as highways for the particles moving through the material, while the contribution of the micropores is negligible (j ∼ jmeso). The relationship between the different diffusivities, as shown in Fig. 16b with the position of the label A, confirms these findings. The diffusivity based on the measurement of the mean square displacement (the ‘microscopic diffusivity’ Dmsd) is seen to notably exceed the ‘uptake diffusivity’. This is an immediate consequence of the fact that uptake is controlled by the small diffusivity in the micropores, while Dmsd is, essentially, controlled by the contribution of the ‘fast’ molecules in the mesopores to overall mass transfer. The latter is also true with the flux and, correspondingly, with the ‘flux diffusion coefficient’ (which we have already seen to coincide quite in general with the ‘microscopic diffusivity’).
It is important to emphasize that a reduction of Dmicro does not automatically lead to a transition to the limiting case of slow exchange. This is exemplified with Fig. 18 for geometry B. Here, the behavior appears to be totally different as compared to Fig. 15b. Thus, similar to the fast exchange case, the domains fill almost synchronously and both contribute to the total flux. The diffusivity–correlation plot Fig. 16b with the position of the label B, which is obtained on the diagonal, as well corroborates the occurrence of the fast molecular exchange between micro- and mesopores. Due to the particular geometry with isolated mesopores considered, irrespective of fast dynamics in the individual mesopores, the long-scale mean square displacements and the overall rate of uptake are controlled by the slow micropore dynamics. This situation corresponds to the ‘anti-correlated Knudsen’ regime discussed in Section 2.3.2.
Although this class B represents hierarchical materials in the structural sense, the arguments given above may be considered in favor of not classifying the material of class B as truly hierarchical ones on considering their transport properties. Indeed, consider a cartoon in Fig. 17 demonstrating two hierarchy levels in A and B. In the case of low micropore diffusivities, adding the second level of larger mesopores in geometry A leads to a notable transport improvement. In contrast, in geometry B the addition of the second level of larger mesopores leaves the overall transport almost unaffected.
 | ||
| Fig. 17 Two hierarchy levels for mesopores (in white) introduced into microporous material (in gray) for geometries A (a) and B (b). | ||
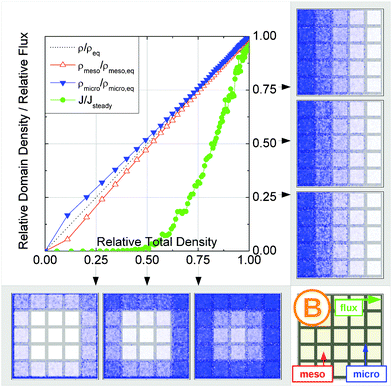 | ||
| Fig. 18 Uptake dynamics for geometry B in the regime of slow exchange for the case of identical equilibrium fluid densities in the micro- and mesopores. See the legend to Fig. 15 for further specification. | ||
Fig. 19a displays the dynamics for C. On considering the mesopore space, it resembles A. Hence, the results obtained appear to be similar. The fast equilibration of the mesopores is succeeded by a slow filling of the microporous space, which, thus, essentially determines the overall uptake time (T ∼ Tmicro). The flux is seen to be directly linked to the equilibration in the mesopores, which are acting as transport highways (j ∼ jmeso). Finally, the label C in the diffusivity–correlation plot, Fig. 16b, is found to be located near that for A, strengthening the similarity between the dynamics of the two topologies in the slow exchange case. In complete analogy, for D a close similarity with B is noted. This is demonstrated, in particular, by Fig. 19b. Here, the flux and the rate of long-range molecular propagation are found to be controlled by the slow dynamics in the micropores. The difference in the diffusivities with those of B is only quantitative, see Fig. 16b, related to the different tortuosities of the two sub-spaces.
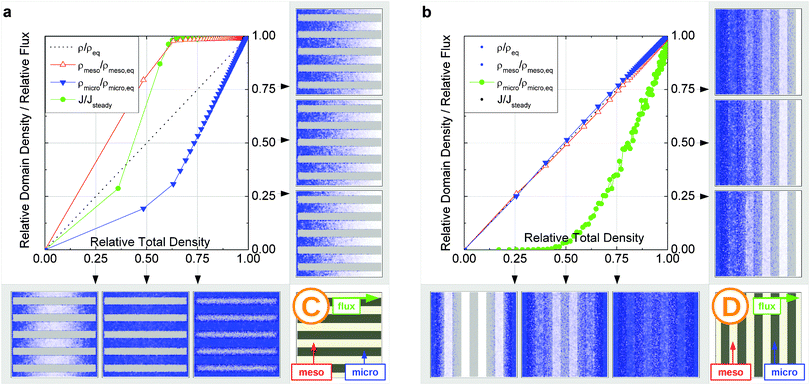 | ||
| Fig. 19 Uptake dynamics for geometries C and D in the regime of slow exchange for the case of identical equilibrium fluid densities in the micro- and mesopores. See the legend to Fig. 15 for further specification. | ||
For A, the overall behavior shown in Fig. 20a was found to reconcile the results obtained for the same topology for the slow exchange case (Fig. 15b). The only difference seen are the pathways of the density equilibration in the microporous domains. While in the slow exchange case the slow micropore diffusion prohibits fast density equilibration within these domains, fast density homogenization facilitated by fast diffusion is observed with surface barriers. In the latter case, however, a concentration step at the interface is formed.
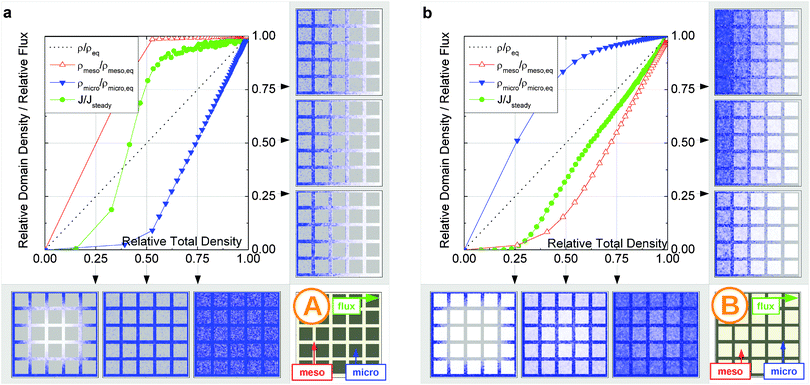 | ||
| Fig. 20 Uptake dynamics for geometries A and B in the presence of surface barriers for the case of identical equilibrium fluid densities in the micro- and mesopores. See the legend to Fig. 15 for further specification. | ||
For B, which could not be brought into the slow exchange regime by adjusting the local micropore diffusivity, this regime can now be attained. As demonstrated by Fig. 20b, the behavior becomes dramatically different as compared to that in Fig. 18. First, it is seen that uptake in the micropores proceeds notably faster than in the mesopores. Second, the onset of the flux build-up is shifted towards lower total densities. This is enforced by the occurrence of the surface barrier, which provide a more efficient build-up of the particle flux through the micropores as compared to the situation without surface barriers. At the later stages, the total flux behavior is determined by both domains with the weights given by the particular details of geometry and dynamics. Although the mesopores add significantly to the flux, their contribution is less pronounced than in the regime of fast exchange. This is evident in Fig. 16c, revealing that Duptake < Dmsd. It is worth noting that a further impairment of molecular exchange between the domains with higher surface barriers will asymptotically shift transport in B towards that observed for A in Fig. 20a, but with interchanged micro- and mesopores.
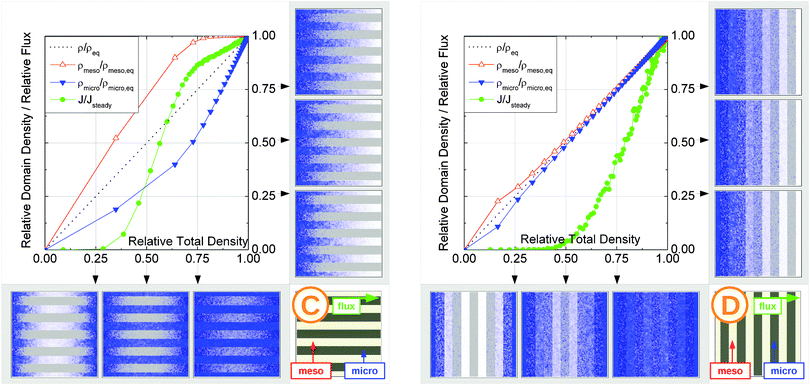 | ||
| Fig. 21 Uptake dynamics for geometries C and D in the presence of surface barriers for the case of identical equilibrium fluid densities in the micro- and mesopores. See the legend to Fig. 15 for further specification. | ||
On considering C and D it may be noted that their transport behaviors, as shown in Fig. 21, resemble those observed in Fig. 19 for the case of slow micropore diffusion. Here, and quite generally for the case of surface barriers, the latter affects overall transport less efficiently than slow diffusion in the micropores. Indeed, if the effective diffusion properties will scale with the volume of microporous domains, the effect of interface permeability scales only with its surface area.
4.4 Different fluid densities in micro- and mesopores
In many practical applications, fluid densities in regions containing pores with different pore sizes will be different. Also, the ratio of the diffusivities in the two domains may vary. Obviously, because overall transport is determined by the properties of all different sub-spaces, the ‘weights’ of their contributions to the total behavior may vary with changing density, porosity, or diffusivity. In order to highlight how this may affect the conclusions drawn so far, we have performed simulations by considering different fluid densities in the two domains, given by the concentration ratio ρmicro/ρmeso = 5. In this particular case, the ‘weight’ of the transport pores was decreased, while that of the micropores increased. Indeed, the simulation results confirm this prediction. As an example, by comparing Fig. 15b with Fig. 22 flux for the slow exchange case is now seen to be controlled by not only the mesopores, but also by the micropores. Nonetheless, for the concentration ratio studied the overall qualitative behavior remains unchanged, which is seen in the similar behavior of the diffusivity–correlation plot shown in Fig. 23. The two graphs, Fig. 16 and 23, can be used as a guide showing how the transport behavior may change upon variation of the system parameters.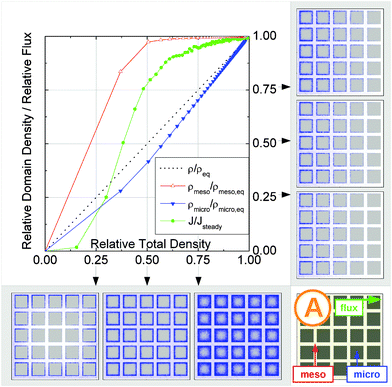 | ||
| Fig. 22 Uptake dynamics for geometry A in the regime of slow exchange for the case of low fluid density in mesopores. See the legend to Fig. 15 for further specification. | ||
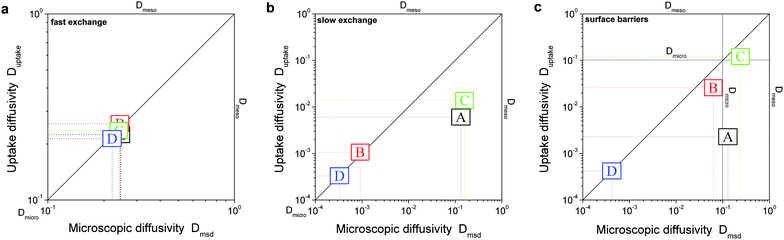 | ||
| Fig. 23 Correlation of the diffusivities (shown by the symbols A, B, C, and D) obtained in the four different pore space arrangements A–D in Table 1 by considering the mean square displacements and in uptake experiments for the ratio ρmicro/ρmeso = 5 of the fluid densities in the micro- and mesopores. All other parameters used in the simulations were the same as for Fig. 16. | ||
4.5 Case studies with the diffusivity correlation plots
The diffusivity–correlation plots, Fig. 16 and 23, have been introduced for a better visualization of the output of our simulations. Within these plots, the results attained with each individual system appear as a single point, with the abscissa and ordinate values given by the microscopic and uptake diffusivities. Fig. 24a summarizes the main features of such representations in a single map. We recollect, in particular:• The values of both the microscopic diffusivities Dmsd (abscissa) and the uptake diffusivities Duptake (ordinate) are in between the diffusivities in the micro- and mesopores.
• Data points appearing on the diagonal (Duptake = Dmsd) signal fast exchange. This means, in particular, that the micro- and mesoporous domains within the material are filled in parallel with each other, i.e. with similar time constants (Tmicro ∼ Tmeso) and fluxes (jmicro ∼ jmeso) (where, for simplicity, equal total amounts of guest molecules under equilibrium conditions has been implied).
• Data points shifted to the right lower corner refer to slow exchange conditions, with notably different time constants of pore space filling (Tmicro ≪ Tmeso) and fluxes (jmicro ≪ jmeso).
Rise in the tortuosity of the mesopore space (white arrow in the bottom) is able to shift the microscopic diffusivity (and with it the flux diffusivity) to lower values, corresponding with an enhanced hold-up time in the mesopores and, hence, access probability into the micropores. In addition to the absolute values of the diffusivities, the diffusivity correlation plots are thus seen to provide also information about the rate of interchange between the different domains of pore spaces. Two show cases may serve for illustrating the potential benefit of such possibilities.
This increase in the exchange rate corresponds, within the frame of the diffusivity–correlation map of Fig. 24a, with data points moving from the lower margin upwards to the Duptake = Dmsd diagonal. Fast exchange conditions are immediately seen to be crucial for high conversion rates since only in this case a sufficiently large amount of reactant molecules is able to penetrate into the space of micropores, i.e. into the reactive zone initiating their conversion. The reason for being under the slow exchange conditions may, e.g., be the occurrence of surface barriers or too slow micropore diffusion. Under these circumstances, moving the point upwards along the red line in Fig. 24a could be technologically demanding. We may note that, equivalently, enhanced reactivities could alternatively be obtained by enhancing the mesopore tortuosity, i.e. by following the direction of the blue arrow coinciding with the direction of increasing tortuosity shown in the bottom of the representation.
Fig. 24b does also include a representation of the fraction of the micropore space used by the educt molecules to react within the membrane, which can be associated with the effectiveness factor. This fraction is seen to drop, in the fast exchange limit, to essentially zero. This means that the rate of exchange is so high, that the major part of the guest molecules is converted in already the very first layer of the membrane. Under such conditions, obviously, reducing the membrane thickness would lead to significant flux (and, hence, conversion) enhancement, without any significant loss in the fraction of conversion.
5 Conclusions
The advent of a multitude of new porous materials, promoted by technological requirement, and the fascinating prospects of their exploitation as tailored host materials for fundamental research, is accompanied by a corresponding multitude of new questions concerning guest dynamics. With the ultimate goal being the establishment of structure–dynamics correlations for these materials, the task may most effectively be accomplished by identifying generic material classes sharing similar dynamics and by studying their various transport properties at different time- and length scales inherent in different experimental methods. The thus compiled information may be of direct relevance at different stages of technological process design. Primarily, the structure–dynamics relations may be used as a knowledge-based guide for material selection and design. It may be equally important on the material characterization stage, both concerning structure and transport. Indeed, the information obtained for different time and length scales and for different experimental conditions provides a means for establishing correlations between the experimental results delivered by different experimental techniques. This is often a crucial aspect due to various experimental limitations allowing to obtain only a very limited spectrum of information. From a more fundamental perspective, this information may help to select an appropriate experimental technique and to design an experimental procedure to address specific questions of interest. The present review may be considered as a first step in providing such a generalization.To approach the goal stated in the preceding paragraph, we have started with overviewing different experimental approaches, which are routinely applied for transport characterization of porous materials, with a special emphasize on their ‘pros’ and ‘cons’. Based on first experimental studies available in the literature, we have highlighted the potentials of microscopic equilibrium measurement techniques for the exploration of the most relevant questions in the context of in-depth transport characterization of hierarchical micro-mesoporous materials. In particular, we have shown that the pulsed field gradient NMR technique, which is proven to be a powerful and versatile technique of diffusion measurement in porous materials, has provided the first experimental evidence of enhanced transport in these materials by direct measurements and has delivered a set of experimental results, obtained with hierarchical materials with well-defined organization of their pore spaces for a broad range of thermodynamic conditions, which has stimulated the developments of theoretical approaches to tackle this complex problem.
In the second part of the review, we have demonstrated that already the earliest theoretical developments have notably contributed to a better understanding of mass transfer phenomena in complex micro-mesoporous materials. It turned out that considering diffusion from the microscopic perspective by analyzing the molecular trajectories, rather than the macroscopic fluxes, has provided an efficient way to rationalize the transport patterns resulting from specific structural hierarchy patterns. Thus, by a minute analysis of the correlations between subsequent displacements, this approach has been employed for demonstrating that in hierarchical materials with smaller and larger mesopores overall fluid diffusivities are promoted by the presence of the larger mesopores depending, essentially, on only their volume fraction rather than on their topology. In such cases, the gain in mobility by the presence of the larger mesopores, quite in general, remained rather limited.
The situation has been found to change notably when the diffusivity in the continuous micropore space was dramatically slowed down as, e.g., in the micropores of a zeolitic bulk phase. In this case, the incorporation of a network of mesopores has been shown to lead to an enhancement of intracrystalline diffusion over orders of magnitude while, for dispersed mesopores, separated from each other, again only a rather modest mobility increase was noted. These studies proved that transport enhancement through networks of mesopores is only possible if they are accessible for mass transfer. If this is not the case, the presence of the mesopores would even lead to a notable decrease in the intracrystalline diffusivities. Hence, with increasing time on stream, the technological benefit of nanoporous materials with hierarchical pore spaces in comparison with their purely microporous equivalent might even be worsened due to, e.g., coke deposition. The main conclusions following the theoretical analysis were shown to be nicely corroborated by the diffusion measurements in selected materials with hierarchical porosities, such as mesoporous zeolites.
Even the rather limited information available so far, including both experimental findings and theoretical predictions, has helped to make a transport classification of hierarchical porous materials. In complete analogy with the classification schemes based on structure hierarchies, as described e.g. in ref. 211, we have based our scheme on four classes of model micro-mesoporous materials which generalize all possible structure organizations. This dynamics-aided classification has naturally resulted by considering the inter-connectivities of the different sub-spaces of the entire pore network. As an important point, the uptake times relevant for different sub-spaces of the entire pore space have been identified to decide on the occurrence of three different transport regimes, in which the overall transport is controlled (i) by transport in both micro- and mesopore spaces, (ii) by transport in only one of the pore spaces, and (iii) by the occurrence of surface barriers at the interface between the micro- and mesopores. As one of the main conclusions of the work, the parameters controlling the overall uptake time and the overall flux has been established for each geometry class.
With the vast information obtained by the microscopic techniques of diffusion measurements, it remained very important to correlate their messages with those obtained using the techniques most frequently used in lab experiments. In first instance, the uptake measurements are most routinely performed. To provide this link, diffusivity–correlation maps for the diffusivities obtained using the uptake measurements and the diffusivities resulting from the assessment of the mean square displacements under equilibrium conditions were compiled. The maps have been obtained for different transport regimes, thus they may be used either to establish the transport-controlling parameters by means of diffusivity measurements or as a guide for structure design. The latter, however, proves to be an application-dependent problem. An exploration of the correlations between the transport maps and the application-relevant process efficiencies is a challenging task for future research.
Acknowledgements
The authors gratefully acknowledge funding from the German Science Foundation (DFG, project VA 463/6-1) and from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 608490 (project M4CO2).References
- J. Weitkamp and L. Puppe, Catalysis and Zeolites, Springer, Berlin Heidelberg, 1999 Search PubMed.
- O. Terasaki and T. Oshuna, in Zeolites and Mesoporous Materials at the Dawn of the 21th Century, ed. A. Galarneau, F. Di Renzo, F. Fajula and J. Vedrine, Elsevier, Amsterdam, 2001, pp. 61–72 Search PubMed.
- F. Schüth, K. S. W. Sing and J. Weitkamp, Handbook of Porous Solids, Wiley-VCH, 2002 Search PubMed.
- G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Handbook of Heterogeneous Catalysis, Wiley-VCH, Weinheim, 2nd edn, 2008 Search PubMed.
- J. Kärger, D. M. Ruthven and D. Theodorou, Diffusion in Nanoporous Materials, Wiley-VCH, Weinheim, 2012 Search PubMed.
- L. Tosheva and V. P. Valtchev, Chem. Mater., 2005, 17, 2494–2513 CrossRef CAS.
- J. X. Jiang, J. H. Yu and A. Corma, Angew. Chem., Int. Ed., 2010, 49, 3120–3145 CrossRef CAS PubMed.
- J. L. Paillaud, B. Harbuzaru, J. Patarin and N. Bats, Science, 2004, 304, 990–992 CrossRef CAS PubMed.
- J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459 RSC.
- S. T. Meek, J. A. Greathouse and M. D. Allendorf, Adv. Mater., 2011, 23, 249–267 CrossRef CAS PubMed.
- B. T. Holland, L. Abrams and A. Stein, J. Am. Chem. Soc., 1999, 121, 4308–4309 CrossRef CAS.
- C. J. H. Jacobsen, C. Madsen, J. Houzvicka, I. Schmidt and A. Carlsson, J. Am. Chem. Soc., 2000, 122, 7116–7117 CrossRef CAS.
- S. van Donk, A. H. Janssen, J. H. Bitter and K. P. de Jong, Catal. Rev.: Sci. Eng., 2003, 45, 297–319 CAS.
- M. Hartmann, Angew. Chem., Int. Ed., 2004, 43, 5880–5882 CrossRef CAS PubMed.
- M. Choi, H. S. Cho, R. Srivastava, C. Venkatesan, D. H. Choi and R. Ryoo, Nat. Mater., 2006, 5, 718–723 CrossRef CAS PubMed.
- Y. S. Tao, H. Kanoh, L. Abrams and K. Kaneko, Chem. Rev., 2006, 106, 896–910 CrossRef CAS PubMed.
- J. C. Groen, J. A. Moulijn and J. Perez-Ramirez, J. Mater. Chem., 2006, 16, 2121–2131 RSC.
- J. C. Groen, W. D. Zhu, S. Brouwer, S. J. Huynink, F. Kapteijn, J. A. Moulijn and J. Perez-Ramirez, J. Am. Chem. Soc., 2007, 129, 355–360 CrossRef CAS PubMed.
- W. Fan, M. A. Snyder, S. Kumar, P. S. Lee, W. C. Yoo, A. V. McCormick, R. L. Penn, A. Stein and M. Tsapatsis, Nat. Mater., 2008, 7, 984–991 CrossRef CAS PubMed.
- K. S. Xia, Q. M. Gao, J. H. Jiang and J. Hu, Carbon, 2008, 46, 1718–1726 CrossRef CAS.
- F. Thibault-Starzyk, I. Stan, S. Abello, A. Bonilla, K. Thomas, C. Fernandez, J. P. Gilson and J. Perez-Ramirez, J. Catal., 2009, 264, 11–14 CrossRef CAS.
- D. Verboekend and J. Perez-Ramirez, Chem. – Eur. J., 2011, 17, 1137–1147 CrossRef CAS PubMed.
- K. Na, C. Jo, J. Kim, K. Cho, J. Jung, Y. Seo, R. J. Messinger, B. F. Chmelka and R. Ryoo, Science, 2011, 333, 328–332 CrossRef CAS PubMed.
- G. J. D. Soler-illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093–4138 CrossRef PubMed.
- X. J. Meng, F. Nawaz and F. S. Xiao, Nano Today, 2009, 4, 292–301 CrossRef CAS.
- Z. L. Hua, J. Zhou and J. L. Shi, Chem. Commun., 2011, 47, 10536–10547 RSC.
- L.-H. Chen, X.-Y. Li, J. C. Rooke, Y.-H. Zhang, X.-Y. Yang, Y. Tang, F.-S. Xiao and B.-L. Su, J. Mater. Chem., 2012, 22, 17381–17403 RSC.
- K. Na, M. Choi and R. Ryoo, Microporous Mesoporous Mater., 2013, 166, 3–19 CrossRef CAS.
- D. P. Serrano, J. M. Escola and P. Pizarro, Chem. Soc. Rev., 2013, 42, 4004–4035 RSC.
- V. Valtchev, G. Majano, S. Mintova and J. Perez-Ramirez, Chem. Soc. Rev., 2013, 42, 263–290 RSC.
- J. Garcia-Martinez and K. Li, Mesoporous Zeolites: Preparation, Characterization and Applications, Wiley-VCH, 2015 Search PubMed.
- Y. Wei, T. E. Parmentier, K. P. de Jong and J. Zecevic, Chem. Soc. Rev., 2015, 44, 7234–7261 RSC.
- L. Gueudre, M. Milina, S. Mitchell and J. Perez-Ramirez, Adv. Funct. Mater., 2014, 24, 209–219 CrossRef CAS.
- A. Silvestre-Albero, A. Grau-Atienza, E. Serrano, J. García-Martínez and J. Silvestre-Albero, Catal. Commun., 2014, 44, 35–39 CrossRef CAS.
- S. Gheorghiu and M. O. Coppens, AIChE J., 2004, 50, 812–820 CrossRef CAS.
- G. Wang, E. Johannessen, C. R. Kleijn, S. W. de Leeuwa and M. O. Coppens, Chem. Eng. Sci., 2007, 62, 5110–5116 CrossRef CAS.
- G. Wang and M. O. Coppens, Chem. Eng. Sci., 2010, 65, 2344–2351 CrossRef CAS.
- M.-O. Coppens, Curr. Opin. Chem. Eng., 2012, 1, 281–289 CrossRef CAS.
- N. L. Michels, S. Mitchell, M. Milina, K. Kunze, F. Krumeich, F. Marone, M. Erdmann, N. Marti and J. Perez-Ramirez, Adv. Funct. Mater., 2012, 22, 2509–2518 CrossRef CAS.
- S. Mitchell, A. B. Pinar, J. Kenvin, P. Crivelli, J. Karger and J. Perez-Ramirez, Nat. Commun., 2015, 6, 8633 CrossRef CAS PubMed.
- F. J. Keil, Catal. Today, 1999, 53, 245–258 CrossRef CAS.
- F. J. Keil, R. Krishna and M. O. Coppens, Rev. Chem. Eng., 2000, 16, 71–197 CAS.
- R. Krishna, J. Phys. Chem. C, 2009, 113, 19756–19781 CAS.
- S. K. Bhatia, M. R. Bonilla and D. Nicholson, Phys. Chem. Chem. Phys., 2011, 13, 15350–15383 RSC.
- R. Krishna, Chem. Soc. Rev., 2012, 41, 3099–3118 RSC.
- F. J. Keil, Comput. Math. Appl., 2013, 65, 1674–1697 CrossRef.
- B. Coasne, A. Galarneau, C. Gerardin, F. Fajula and F. Villemot, Langmuir, 2013, 29, 7864–7875 CrossRef CAS PubMed.
- M. R. Bonilla, R. Valiullin, J. Kärger and S. K. Bhatia, J. Phys. Chem. C, 2014, 118, 14355–14370 CAS.
- E. Vargas L. and R. Q. Snurr, Langmuir, 2015, 31, 10056–10065 CrossRef CAS PubMed.
- N. Y. Chen, T. F. Degnan and C. M. Smith, Molecular Transport and Reaction in Zeolites, VCH, New York, 1994 Search PubMed.
- H. Marsh and F. Rodriguez-Reinoso, Activated Carbon, Elsevier, Amsterdam, 2006 Search PubMed.
- J. Kärger and R. Valiullin, Chem. Soc. Rev., 2013, 42, 4172–4197 RSC.
- R. Valiullin, Annu. Rep. NMR Spectrosc., 2013, 79, 23–72 CrossRef CAS.
- I. S. Park, D. D. Do and A. E. Rodrigues, Catal. Rev.: Sci. Eng., 1996, 38, 189–247 CAS.
- A. Herrmann, L. Schimmele, J. Mossinger, M. Hirscher and H. Kronmuller, Appl. Phys. A: Mater. Sci. Process., 2001, 72, 197–208 CrossRef CAS.
- R. Valiullin and J. Kärger, Chem. Ing. Tech., 2011, 83, 166–176 CrossRef CAS.
- D. Mehlhorn, R. Valiullin, J. Kärger, K. Cho and R. Ryoo, Microporous Mesoporous Mater., 2012, 164, 273–279 CrossRef CAS.
- J. Kärger, R. Valiullin, D. Enke and R. Gläser, in Measuring Mass Transport in Hierarchical Pore Systems, ed. J. Garcia-Martinez and K. Li, Wiley-VCH, Weinheim, 2015, pp. 385–424 Search PubMed.
- C. Chmelik and J. Kärger, Chem. Soc. Rev., 2010, 39, 4864–4884 RSC.
- J. Kärger, Microporous Mesoporous Mater., 2014, 189, 126–135 CrossRef.
- D. N. Theodorou, R. Q. Snurr and A. T. Bell, in Comprehensive Macromolecular Chemistry, ed. G. Alberti and T. Bein, Oxford, Oxford, 1996 Search PubMed.
- P. A. Monson, Microporous Mesoporous Mater., 2012, 160, 47–66 CrossRef CAS.
- Diffusion in nanoporous solids, http://www.iupac.org/, accessed September 2015.
- A. Taguchi, J. H. Smatt and M. Linden, Adv. Mater., 2003, 15, 1209–1211 CrossRef CAS.
- D. B. Kuang, T. Brezesinski and B. Smarsly, J. Am. Chem. Soc., 2004, 126, 10534–10535 CrossRef CAS PubMed.
- Z. Y. Yuan and B. L. Su, J. Mater. Chem., 2006, 16, 663–677 RSC.
- C. Song, J. P. Du, J. H. Zhao, S. A. Feng, G. X. Du and Z. P. Zhu, Chem. Mater., 2009, 21, 1524–1530 CrossRef CAS.
- Y. Ono, H. Mayama, I. Furo, A. I. Sagidullin, K. Matsushima, H. Ura, T. Uchiyama and K. Tsujii, J. Colloid Interface Sci., 2009, 336, 215–225 CrossRef CAS PubMed.
- J. Du, X. Y. Lai, N. L. Yang, J. Zhai, D. Kisailus, F. B. Su, D. Wang and L. Jiang, ACS Nano, 2011, 5, 590–596 CrossRef CAS PubMed.
- J. Xiao, D. H. Mei, X. L. Li, W. Xu, D. Y. Wang, G. L. Graff, W. D. Bennett, Z. M. Nie, L. V. Saraf, I. A. Aksay, J. Liu and J. G. Zhang, Nano Lett., 2011, 11, 5071–5078 CrossRef CAS PubMed.
- S. J. Yang, T. Kim, J. H. Im, Y. S. Kim, K. Lee, H. Jung and C. R. Park, Chem. Mater., 2012, 24, 464–470 CrossRef CAS.
- O. Sel, D. Kuang, M. Thommes and B. Smarsly, Langmuir, 2006, 22, 2311–2322 CrossRef CAS PubMed.
- Q. Zhang, I. Lee, J. B. Joo, F. Zaera and Y. D. Yin, Acc. Chem. Res., 2013, 46, 1816–1824 CrossRef CAS PubMed.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, Cambridge, 3rd edn, 2009 Search PubMed.
- D. Ruthven, S. Brandani and M. Eic, in Adsorption and Diffusion, ed. H. Karge and J. Weitkamp, Springer, Berlin, Heidelberg, 2008, vol. 7, pp. 45–84 Search PubMed.
- A. Fick, Ann. Phys. Chem., 1855, 94, 59–86 CrossRef.
- D. A. McQuarrie, Statistical Mechanics, University Science Books, Sausalito, California, 2000 Search PubMed.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 1975 Search PubMed.
- A. Yekta, J. Duhamel and M. A. Winnik, J. Chem. Phys., 1992, 97, 1554–1561 CrossRef CAS.
- A. Hadjitheodorou and G. Kalosakas, Mater. Sci. Eng., C, 2014, 42, 681–690 CrossRef CAS PubMed.
- A. Pochert, D. Schneider, J. Haase, M. Linden and R. Valiullin, Langmuir, 2015, 31, 10285–10295 CrossRef CAS PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- R. Klages, G. Radons and I. M. Sokolov, Anomalous Transport, Foundations and Applications, Wiley-VCH, Berlin, 2008 Search PubMed.
- D. T. Gillespie and E. Seitaridou, Simple Brownian Diffusion: An Introduction to the Standard Theoretical Models, Oxford University Press, Oxford, UK, 2012 Search PubMed.
- M. Knudsen, Ann. Phys., 1909, 28, 75 CrossRef CAS.
- W. G. Pollard and R. D. Present, Phys. Rev., 1948, 73, 762–774 CrossRef CAS.
- F. Rouquerol, J. Rouquerol and K. Sing, Adsorption by Powders and Porous Solids, Academic Press, San Diego, 1999 Search PubMed.
- D. H. Everett, in Adsorption hysteresis, ed. E. Alison Flood, Marcel Dekker, Inc., New York, 1967, pp. 1055–1113 Search PubMed.
- S. Gruener and P. Huber, Phys. Rev. Lett., 2008, 100, 064502 CrossRef PubMed.
- D. M. Ruthven, W. J. DeSisto and S. Higgins, Chem. Eng. Sci., 2009, 64, 3201–3203 CrossRef CAS.
- P. Levitz, J. Phys. Chem., 1993, 97, 3813–3818 CrossRef CAS.
- P. Zeigermann, S. Naumov, S. Mascotto, J. Kärger, B. M. Smarsly and R. Valiullin, Langmuir, 2012, 28, 3621–3632 CrossRef CAS PubMed.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, J. Chem. Phys., 2004, 120, 11804–11814 CrossRef CAS PubMed.
- P. Levitz, J. Phys.: Condens. Matter, 2005, 17, S4059–S4074 CrossRef CAS.
- P. Zeigermann, J. Kärger and R. Valiullin, Microporous Mesoporous Mater., 2013, 178, 84–89 CrossRef CAS.
- R. Valiullin and V. Skirda, J. Chem. Phys., 2001, 114, 452–458 CrossRef CAS.
- P. N. Sen, Concepts Magn. Reson., Part A, 2004, 23A, 1–21 CrossRef.
- L. P. Zhou, T. L. Lu, J. L. Xu, M. Z. Chen, C. F. Zhang, C. Chen, X. M. Yang and J. Xu, Microporous Mesoporous Mater., 2012, 161, 76–83 CrossRef CAS.
- J. Garcia-Martinez, M. Johnson, J. Valla, K. H. Li and J. Y. Ying, Catal. Sci. Technol., 2012, 2, 987–994 CAS.
- C. H. Christensen, K. Johannsen, E. Toernqvist, I. Schmidt and H. Topsoe, Catal. Today, 2007, 128, 117–122 CrossRef CAS.
- F. Schmidt, S. Paasch, E. Brunner and S. Kaskel, Microporous Mesoporous Mater., 2012, 164, 214–221 CrossRef CAS.
- L. Zhao, B. J. Shen, F. S. Gao and C. M. Xu, J. Catal., 2008, 258, 228–234 CrossRef CAS.
- F. C. Meunier, D. Verboekend, J. P. Gilson, J. C. Groen and J. Perez-Ramirez, Microporous Mesoporous Mater., 2012, 148, 115–121 CrossRef CAS.
- K. Cho, H. S. Cho, L. C. de Menorval and R. Ryoo, Chem. Mater., 2009, 21, 5664–5673 CrossRef CAS.
- D. M. Ruthven and M. Eic, ACS Symp. Ser., 1988, 368, 362–375 CrossRef CAS.
- V.-T. Hoang, Q. Huang, A. Malekian, M. Eic, T.-O. Do and S. Kaliaguine, Adsorption, 2005, 11, 421–426 CrossRef.
- C. C. Chang, A. R. Teixeira, C. Li, P. J. Dauenhauer and W. Fan, Langmuir, 2013, 29, 13943–13950 CrossRef CAS PubMed.
- H. Jobic, J. Kärger, C. Krause, S. Brandani, A. Gunadi, A. Methivier, G. Ehlers, B. Farago, W. Haeussler and D. M. Ruthven, Adsorption, 2005, 11, 403–407 CrossRef.
- C. Chmelik, D. Enke, P. Galvosas, O. Gobin, A. Jentys, H. Jobic, J. Kärger, C. B. Krause, J. Kullmann, J. Lercher, S. Naumov, D. M. Ruthven and T. Titze, ChemPhysChem, 2011, 12, 1130–1134 CrossRef CAS PubMed.
- C. Chmelik, L. Heinke, R. Valiullin and J. Kärger, Chem. Ing. Tech., 2010, 82, 779–804 CrossRef.
- J. Kärger, T. Binder, C. Chmelik, F. Hibbe, H. Krautscheid, R. Krishna and J. Weitkamp, Nat. Mater., 2014, 13, 333–343 CrossRef PubMed.
- J. Kärger, ChemPhysChem, 2015, 16, 24–51 CrossRef PubMed.
- A. Lauerer, P. Zeigermann, J. Lenzner, C. Chmelik, M. Thommes, R. Valiullin and J. Kärger, Microporous Mesoporous Mater., 2015, 214, 143–148 CrossRef CAS.
- P. P. Mitra, P. N. Sen, L. M. Schwartz and P. Ledoussal, Phys. Rev. Lett., 1992, 68, 3555–3558 CrossRef CAS PubMed.
- R. Kimmich, NMR: Tomography, Diffusometry, Relaxometry, Springer-Verlag, Berlin, Heidelberg, 1997 Search PubMed.
- W. S. Price, NMR Studies of Translational Motion, University Press, Cambridge, 2009 Search PubMed.
- P. T. Callaghan, Translational Dynamics & Magnetic Resonance, Oxford University Press, New York, 2011 Search PubMed.
- J. Kärger and R. Valiullin, in Encyclopedia of Magnetic Resonance, ed. R. K. Harris and R. E. Wasylishen, John Wiley, Chichester, 2011 Search PubMed.
- M. Bee, Quasielastic neutron scattering. Principles and applications in solid state chemistry, biology and materials science, Adam Higler, Briston, 1988 Search PubMed.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- H. Jobic, in Science and Technology - Molecular Sieves, ed. H. G. Karge and J. Weitkamp, Springer, Berlin, Heidelberg, 2008, vol. 7, pp. 207–233 Search PubMed.
- Y. Talmon, L. Shtirberg, W. Harneit, O. Y. Rogozhnikova, V. Tormyshev and A. Blank, Phys. Chem. Chem. Phys., 2010, 12, 5998–6007 RSC.
- M. Wessig, M. Spitzbarth, M. Drescher, R. Winter and S. Polarz, Phys. Chem. Chem. Phys., 2015, 17, 15976–15988 RSC.
- E. L. Elson and D. Magde, Biopolymers, 1974, 13, 1–27 CrossRef CAS.
- J. Ries and P. Schwille, BioEssays, 2012, 34, 361–368 CrossRef PubMed.
- S. M. Mahurin, S. Dai and M. D. Barnes, J. Phys. Chem. B, 2003, 107, 13336–13340 CrossRef CAS.
- T. Cherdhirankorn, M. Retsch, U. Jonas, H. J. Butt and K. Koynov, Langmuir, 2010, 26, 10141–10146 CrossRef CAS PubMed.
- I. Teraoka, K. H. Langley and F. E. Karasz, Macromolecules, 1993, 26, 287–297 CrossRef CAS.
- V. Beschieru, B. Rathke and S. Will, Microporous Mesoporous Mater., 2009, 125, 63–89 CrossRef CAS.
- A. Zürner, J. Kirstein, M. Doblinger, C. Bräuchle and T. Bein, Nature, 2007, 450, 705–708 CrossRef PubMed.
- J. Kirstein, B. Platschek, C. Jung, R. Brown, T. Bein and C. Brauchle, Nat. Mater., 2007, 6, 303–310 CrossRef CAS PubMed.
- C. Jung and C. Bräuchle, in Visualizing Single-Molecule Diffusion in Nanochannel Systems, ed. C. Bräuchle, D. C. Lamb and J. Michaelis, Wiley-VCH, Weinheim, 2010, pp. 309–333 Search PubMed.
- G. De Cremer, B. F. Sels, D. E. De Vos, J. Hofkens and M. B. J. Roeffaers, Chem. Soc. Rev., 2010, 39, 4703–4717 RSC.
- G. De Cremer, M. B. J. Roeffaers, E. Bartholomeeusen, K. F. Lin, P. Dedecker, P. P. Pescarmona, P. A. Jacobs, D. E. De Vos, J. Hofkens and B. F. Sels, Angew. Chem., Int. Ed., 2010, 49, 908–911 CrossRef CAS PubMed.
- F. Feil, S. Naumov, J. Michaelis, R. Valiullin, D. Enke, J. Kärger and C. Bräuchle, Angew. Chem., 2012, 124, 1178–1181 CrossRef.
- D. A. Higgins, S. C. Park, K. H. Tran-Ba and T. Ito, Annu. Rev. Anal. Chem., 2015, 8, 193–216 CrossRef CAS PubMed.
- M. P. Hollewand and L. F. Gladden, Chem. Eng. Sci., 1995, 50, 309–326 CrossRef CAS.
- A. T. Watson and C. T. P. Chang, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 343–386 CrossRef CAS.
- F. Stallmach and J. Kärger, Adsorption, 1999, 5, 117–133 CrossRef CAS.
- O. Geier, S. Vasenkov and J. Karger, J. Chem. Phys., 2002, 117, 1935–1938 CrossRef CAS.
- F. Rittig, T. S. Farris and J. M. Zielinski, AIChE J., 2004, 50, 589–595 CrossRef CAS.
- S. Stapf and S. Han, NMR Imaging in Chemical Engineering, Wiley-VCH, Weinheim, 2005 Search PubMed.
- N. Hedin, G. J. DeMartin, K. G. Strohmaier and S. C. Reyes, Microporous Mesoporous Mater., 2007, 98, 182–188 CrossRef CAS.
- Z. Adem, F. Guenneau, M. A. Springuel-Huet and A. Gedeon, Microporous Mesoporous Mater., 2008, 114, 337–342 CrossRef CAS.
- Q. Zhao and R. Q. Snurr, J. Phys. Chem. A, 2009, 113, 3904–3910 CrossRef CAS PubMed.
- L. F. Gladden and J. Mitchell, New J. Phys., 2011, 13, 035001 CrossRef.
- J. Kärger and H. Pfeifer, Zeolites, 1987, 7, 90–107 CrossRef.
- J. Kärger and D. Ruthven, Diffusion in Zeolites and Other Microporous Solids, Wiley & Sons, New York, 1992 Search PubMed.
- F. D'Orazio, S. Bhattacharja, W. P. Halperin and R. Gerhardt, Phys. Rev. Lett., 1989, 63, 43–46 CrossRef PubMed.
- F. D'Orazio, S. Bhattacharja, W. P. Halperin and R. Gerhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 6503–6508 CrossRef.
- I. Ardelean, C. Mattea, G. Farrher, S. Wonorahardjo and R. Kimmich, J. Chem. Phys., 2003, 119, 10358–10362 CrossRef CAS.
- H. Alsyouri and J. Lin, J. Phys. Chem. B, 2005, 109, 13623–13629 CrossRef CAS PubMed.
- R. Valiullin, J. Kärger and R. Gläser, Phys. Chem. Chem. Phys., 2009, 11, 2833–2853 RSC.
- C. Carrara, G. Pages, C. Delaurent, S. Viel and S. Caldarelli, J. Phys. Chem. C, 2011, 115, 18776–18781 CAS.
- W. P. Krekelberg, D. W. Siderius, V. K. Shen, T. M. Truskett and J. R. Errington, Langmuir, 2013, 29, 14527–14535 CrossRef CAS PubMed.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, J. Phys. Chem. B, 2005, 109, 5746–5752 CrossRef CAS PubMed.
- M. Dvoyashkin, A. Khokhlov, S. Naumov and R. Valiullin, Microporous Mesoporous Mater., 2009, 125, 58–62 CrossRef CAS.
- D. Weber, A. J. Sederman, M. D. Mantle, J. Mitchell and L. F. Gladden, Phys. Chem. Chem. Phys., 2010, 12, 2619–2624 RSC.
- D. ben Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, Cambridge, 2000 Search PubMed.
- L. D. Gelb, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573–1659 CrossRef CAS.
- B. Coasne, A. Galarneau, R. J. M. Pellenq and F. Di Renzo, Chem. Soc. Rev., 2013, 42, 4141–4171 RSC.
- M. Thommes and K. A. Cychosz, Adsorption, 2014, 20, 233–250 CrossRef CAS.
- R. Valiullin and I. Furo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031508 CrossRef PubMed.
- J. H. Nam and M. Kaviany, Int. J. Heat Mass Transfer, 2003, 46, 4595–4611 CrossRef CAS.
- P. Kortunov, S. Vasenkov, J. Kärger, R. Valiullin, P. Gottschalk, M. F. Elia, M. Perez, M. Stocker, B. Drescher, G. McElhiney, C. Berger, R. Gläser and J. Weitkamp, J. Am. Chem. Soc., 2005, 127, 13055–13059 CrossRef CAS PubMed.
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. Mccullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- U. Ciesla and F. Schüth, Microporous Mesoporous Mater., 1999, 27, 131–149 CrossRef CAS.
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS PubMed.
- K. Yu, B. Smarsly and C. J. Brinker, Adv. Funct. Mater., 2003, 13, 47–52 CrossRef CAS.
- M. Thommes, Chem. Ing. Tech., 2010, 82, 1059–1073 CrossRef CAS.
- D. Mehlhorn, A. Inayat, W. Schwieger, R. Valiullin and J. Kärger, ChemPhysChem, 2014, 15, 1681–1686 CrossRef CAS PubMed.
- R. Valiullin, M. Dvoyashkin, P. Kortunov, C. Krause and J. Kärger, J. Chem. Phys., 2007, 126, 054705 CrossRef PubMed.
- R. Valiullin, J. Kärger, K. Cho, M. Choi and R. Ryoo, Microporous Mesoporous Mater., 2011, 142, 236–244 CrossRef CAS.
- D. Mehlhorn, R. Valiullin, J. Kärger, K. Cho and R. Ryoo, ChemPhysChem, 2012, 13, 1495–1499 CrossRef CAS PubMed.
- K. Cho, R. Ryoo, S. Asahina, C. Xiao, M. Klingstedt, A. Umemura, M. W. Anderson and O. Terasaki, Solid State Sci., 2011, 13, 750–756 CrossRef CAS.
- W. Heink, J. Kärger, H. Pfeifer, K. P. Datema and A. K. Nowak, J. Chem. Soc., Faraday Trans., 1992, 88, 3505–3509 RSC.
- M. B. J. Roeffaers, B. F. Sels, H. Uji-i, F. C. De Schryver, P. A. Jacobs, D. E. De Vos and J. Hofkens, Nature, 2006, 439, 572–575 CrossRef CAS PubMed.
- R. Valiullin, S. Naumov, P. Galvosas, J. Kärger, H. J. Woo, F. Porcheron and P. A. Monson, Nature, 2006, 443, 965–968 CrossRef CAS PubMed.
- H. Van As and D. van Dusschoten, Geoderma, 1997, 80, 389–403 CrossRef CAS.
- R. Valiullin, V. D. Skirda, S. Stapf and R. Kimmich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 2664–2671 CrossRef CAS.
- O. Geier, R. Q. Snurr, F. Stallmach and J. Kärger, J. Chem. Phys., 2004, 120, 367–373 CrossRef CAS PubMed.
- K. A. Fichthorn and W. H. Weinberg, J. Chem. Phys., 1991, 95, 1090–1096 CrossRef CAS.
- K. Binder, Rep. Prog. Phys., 1997, 60, 487–559 CrossRef CAS.
- D. Schneider, D. Kondrashova, R. Valiullin, A. Bunde and J. Kärger, Chem. Ing. Tech., 2015, 1794–1809 CrossRef CAS.
- J. Kärger, W. Heink, H. Pfeifer, M. Rauscher and J. Hoffmann, Zeolites, 1982, 2, 275–278 CrossRef.
- L. Karwacki, M. H. F. Kox, D. A. M. de Winter, M. R. Drury, J. D. Meeldijk, E. Stavitski, W. Schmidt, M. Mertens, P. Cubillas, N. John, A. Chan, N. Kahn, S. R. Bare, M. Anderson, J. Kornatowski and B. M. Weckhuysen, Nat. Mater., 2009, 8, 959–965 CrossRef CAS PubMed.
- L. Karwacki, H. E. van der Bij, J. Kornatowski, P. Cubillas, M. R. Drury, D. A. M. de Winter, M. W. Anderson and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2010, 49, 6790–6794 CrossRef CAS PubMed.
- A. F. Combariza and G. Sastre, J. Phys. Chem. C, 2011, 115, 13751–13758 CAS.
- F. Hibbe, C. Chmelik, L. Heinke, S. Pramanik, J. Li, D. M. Ruthven, D. Tzoulaki and J. Kärger, J. Am. Chem. Soc., 2011, 133, 2804–2807 CrossRef CAS PubMed.
- L. Gueudre, N. Bats and E. Jolimaitre, Microporous Mesoporous Mater., 2012, 147, 310–317 CrossRef.
- N. E. R. Zimmermann, S. P. Balaji and F. J. Keil, J. Phys. Chem. C, 2012, 116, 3677–3683 CAS.
- A. R. Teixeira, C. C. Chang, T. Coogan, R. Kendall, W. Fan and P. J. Dauenhauer, J. Phys. Chem. C, 2013, 117, 25545–25555 CAS.
- A. R. Teixeira, X. D. Qi, W. C. Conner, T. J. Mountziaris, W. Fan and P. J. Dauenhauer, Chem. Mater., 2015, 27, 4650–4660 CrossRef CAS.
- B.-L. Su, C. Sanchez and X.-Y. Yang, in Insights into Hierarchically Structured Porous Materials: From Nanoscience to Catalysis, Separation, Optics, Energy, and Life Science, Wiley-VCH Verlag GmbH & Co. KGaA, 2011, pp. 1–27 Search PubMed.
- J. C. Groen and J. Pérez-Ramírez, in Hierarchical Porous Zeolites by Demetallation, Wiley-VCH Verlag GmbH & Co. KGaA, 2010, pp. 31–50 Search PubMed.
- S. Lopez-Orozco, A. Inayat, A. Schwab, T. Selvam and W. Schwieger, Adv. Mater., 2011, 23, 2602–2615 CrossRef CAS PubMed.
- J. Perez-Ramirez, D. Verboekend, A. Bonilla and S. Abello, Adv. Funct. Mater., 2009, 19, 3972–3979 CrossRef CAS.
- M. Milina, S. Mitchell, D. Cooke, P. Crivelli and J. Perez-Ramirez, Angew. Chem., Int. Ed., 2015, 54, 1591–1594 CrossRef CAS PubMed.
- G. Mason, J. Colloid Interface Sci., 1982, 88, 36–46 CrossRef CAS.
- N. A. Seaton, Chem. Eng. Sci., 1991, 46, 1895–1909 CrossRef CAS.
- Y. Sakamoto, M. Kaneda, O. Terasaki, D. Y. Zhao, J. M. Kim, G. Stucky, H. J. Shim and R. Ryoo, Nature, 2000, 408, 449–453 CrossRef CAS PubMed.
- E. L. Perkins, J. P. Lowe, K. J. Edler, N. Tanko and S. P. Rigby, Chem. Eng. Sci., 2008, 63, 1929–1940 CrossRef CAS.
- S. Naumov, R. Valiullin, J. Kärger, R. Pitchumani and M.-O. Coppens, Microporous Mesoporous Mater., 2008, 110, 37–40 CrossRef CAS.
- D. Kondrashova, C. Reichenbach and R. Valiullin, Langmuir, 2010, 26, 6380–6385 CrossRef CAS PubMed.
- M. Thommes, S. Mitchell and J. Perez-Ramirez, J. Phys. Chem. C, 2012, 116, 18816–18823 CAS.
- T. Kirchner, A. Shakhov, P. Zeigermann, R. Valiullin and J. Kärger, Carbon, 2012, 50, 4804–4808 CrossRef CAS.
- D. Stoeckel, C. Kubel, K. Hormann, A. Holtzel, B. M. Smarsly and U. Tallarek, Langmuir, 2014, 30, 9022–9027 CrossRef CAS PubMed.
- R. Mueller, S. H. Zhang, C. Zhang, R. Lively and S. Vasenkov, J. Membr. Sci., 2015, 477, 123–130 CrossRef CAS.
- B. Seoane, J. Coronas, I. Gascon, M. E. Benavides, O. Karvan, J. Caro, F. Kapteijn and J. Gascon, Chem. Soc. Rev., 2015, 44, 2421–2454 RSC.
- W. Schwieger, A. G. Machoke, T. Weissenberger, A. Inayat, T. Selvam, M. Klumpp and A. Inayat, Chem. Soc. Rev., 2016 10.1039/C5CS00599J.
Footnotes |
| † Part of ‘Hierarchically-structured porous materials: from basic understanding to applications’ themed issue. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cs00715a |
| § Here we use the convention for the axes assignment used in the NMR literature. In the context of this review, z is interchangable with x used in Section 2.1. |
| ¶ More precisely, here the variation of the intermolecular interaction with variation of concentration is assumed. Indeed, the intermolecular interaction are always present and they determine the absolute value of the molecular diffusivity. |
| This journal is © The Royal Society of Chemistry 2016 |