Dynamic evolution of specific catalytic sites on Pt nanoparticles
Hector
Barron
*a,
George
Opletal
a,
Richard D.
Tilley
b and
Amanda S.
Barnard
a
aCSIRO Virtual Nanoscience Laboratory, 343 Royal Parade, Parkville 3052, Victoria, Australia. E-mail: hector.barronescobar@csiro.au
bUNSW Mark Wainwright Analytical Centre, Division of Research, Sydney 2052, New South Wales, Australia
First published on 22nd September 2015
Abstract
Platinum nanoparticles are widely used catalysts in many important industrial applications, in the chemical, petrochemical, automotive and energy sectors. Due to the extremely high cost and the limited abundance of platinum, improving the efficiency of platinum-based nanocatalysts is key to the economic development of these materials, as well as being a challenge for basic research. Ultimately we seek to increase the active surfaces area, per unit volume, and to preserve the activity and selectivity over the functional lifetime of the product. In this work the formation of platinum nanoparticles is investigated by molecular dynamic simulations under different conditions of temperature and atomic deposition rates to identify the conditions that give rise to a greater density of different types of surface active sites. By tuning the growth conditions we obtained highly non-equilibrium morphologies with branches that expose larger surface areas that are consistent with experimental observations. The results are also used to clarify the relationship between growth conditions, surface structure and catalytic functionality based on a simple surface defect classification model, which differentiates between CO oxidation reactions, hydrogen evolution reactions (HER) and hydrogen oxidation reactions (HOR).
1 Introduction
In recent decades metallic nanoparticles have contributed to developments in numerous scientific fields, due to their superior properties and suitability for a range of high performance applications.1,2 Many of the interesting properties of metallic nanoparticles are related to the size, shape and surface structure, which influence their electronic and optical properties,3 and are critical to their catalytic activity.4,5 Since these features are often determined by the growth conditions6,7 considerable attention has been given to understanding the role of kinetics in engineering these materials.In particular, platinum (Pt) nanoparticles are exemplary; being stable and efficient in a range of important catalytic reactions, and with predictable performance that strongly depend on the surface structure.8 These nanoparticles have been produced via a variety of methods,9–12 that give rise to a diverse range of sizes and shapes. After the pioneering work of El-Sayed and co-workers,13,14 who successfully synthesized cubic and tetrahedral Pt nanoparticles through chemical reduction, various Pt nanocrystals with different shapes have been obtained by changing Pt precursors, reducing reagents, stabilizing reagents, and solvents.15,16
The purpose of targeting specific shapes is to enrich samples with the greater density of specific types of under-coordinated atoms at the surface, with preference given to those with as lower atomic coordination number as possible. Each crystallographic facet has a characteristic surface atomic arrangement and degree of “under-coordination”, and although this ultimately determines the concentration of active sites available for reactions, it is still challenging to predict the structure-dependent activity a priori. The structure-dependent activity can be inferred empirically (after samples are produced and tested), but correlating the microstructure and performance is nanocrystals hindered by the nature polydispersivity of samples. Alternatively, analytical models can be used to address the issue of sample diversity, but in most predicative models are usually idealized;17 the imperfections and surface defects omitted for the sake of simplicity. Defects, including stacking faults, kinks, steps, and terraces, routinely appear during crystal growth, and the inclusion of these features in predictive models can yield important insights.18
It has been shown that Pt nanoparticles (characterized by transmission electron microscopy, TEM) present as imperfect structures with “rougher” surfaces, the density of which correlates with the change in catalytic reactions in CO.19 The density of single crystal facets enriched with steps and kinks enhances the electrocatalytic reactivity.20 Defects sites with low coordinated numbers (or, conversely, a high degree of under-coordination) have also been shown to increase electro oxidation independently of the supporting electrolyte used;21–24 further highlighting the intrinsic relationship between surface imperfection (not just surface orientation) and catalytic performance.25 More recently, Tilley et al.26,27 developed a method for obtaining both isotropic and anisotropic particles, on demand. This involves the hydrogenation decomposition of organometallic precursors to form nanoparticles,28,29 and it is possible to selectively prepare Pt nanoparticles of a large variety of morphologies including platinum nanocubes, rectangular prisms, triangular prisms, nanorods, tripods, octapods, and polypods.30
A survey of the literature quickly reveals that most shape-controlled synthesis strategies are based upon manipulation of the growth processes, rather than nucleation, and these processes are also well described by computer simulations. Typically two types of molecular dynamics (MD) simulations are used to model this process: the single atom (or monomers) insertion to coalescence, under a specified set of conditions (often referred to as coarsening);31–33 and via the collision of two preexisting particles to form a single aggregate which then undergoes restructuring, again under specific conditions (often referred to as sintering).34 Typically the conditions used in these “virtual experiments” are either designed to reproduce conditions used in conventional experiments, or chosen to drive the system to the thermodynamic ground state. While valid strategies, neither are predisposed to the formation of highly non-equilibrium structures with significant surface roughening or branches.
In this study we have adopted the first computational approach described above (the single atom insertion), but with some important distinctions. Rather than employing or seeking the conditions conducive to the formation of isotropic and neatly facetted particles, we have begun to investigate the relationship between the formation temperature and the growth rate and the degree of disorder, and related this to some simple indicators of catalytic efficiency. By tracking the density of different types of under-coordinated surface atoms as a function of time, we are able to identify the stage in the growth process when the number of active sites will be maximized, and show how the relative activity may evolve with time.
2 Methods
The MD simulations were carried out using the LAMMPS code,35 under the embedded atom method (EAM), with a potential parameterized by Foiles et al. that proven to accurately describe the platinum atomic interactions.36 In this approach the total electronic density in the metal is well approximated by a linear superposition of contributions from individual atoms, so the electron density in the vicinity of each atom can be expressed as the sum of the contributions given by the atom in question, added to the electron density of all neighbouring atoms. For a system consisting of N atoms, the expression to calculate the energy could be written as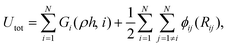 | (1) |
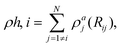 | (2) |
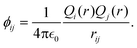 | (3) |
To provide insight on the nature of the nucleation that precedes the formation of Pt nanoparticles, we performed a set of MD simulations where single atoms were randomly inserted at temperatures of 30 °C, 100 °C and 200 °C, and with deposition rates (τ) of 1 atom each 5 simulation steps (τ = 2.5 × 10−5 atoms per ns), and 1 atom each 100 simulation steps (τ = 5 × 10−4 atoms per ns). The temperature values were chosen based on the experimental synthesis of Pt nanoparticles26 and the deposition rates in accordance with previous computational studies.37 All the atoms were deposited inside a large simulation box for 2 and 5 ns respectively, and began without the inclusion of an initial “seed”.
The trajectories generated by the simulations were analysed to track the evolution of different types of surface defects, by quantifying the coordination numbers of all surface atoms as a function of time. This analysis was performed using a program previously used to classify gold nanorod surface disorder.38 Identification of the atoms in the surface layer is achieved via a simple classification scheme using a radial shell of equidistance points near the bond cutoff distance, in 3D. Each point is systematically tested to see if it is occupied by another atom in the nanoparticle, and if no overlap is found the atom is classified as a surface atom. Once the surface layer is obtained, the surface coordination number (SCN) of each atom is simply the total number of atoms within the radial shell of that atom.
3 Results and discussion
3.1 Classification of surface defects
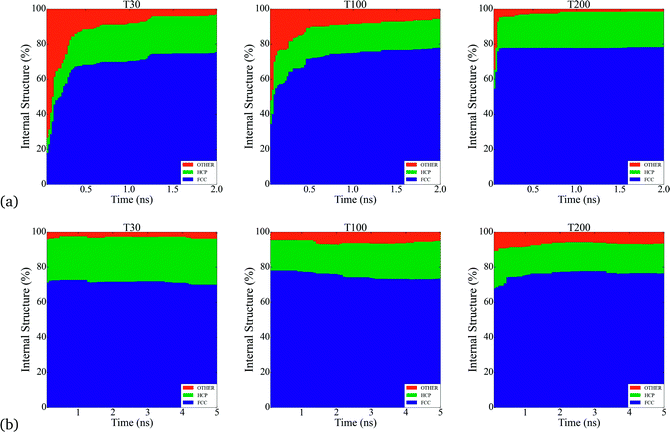
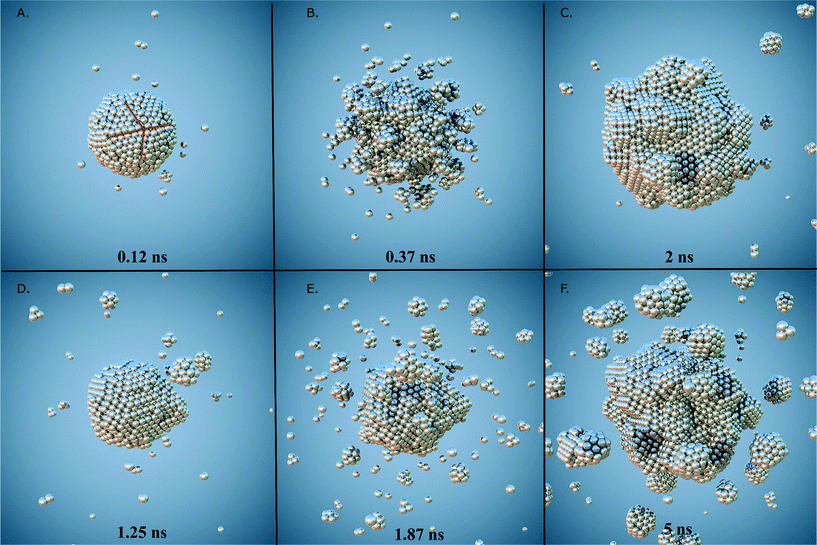
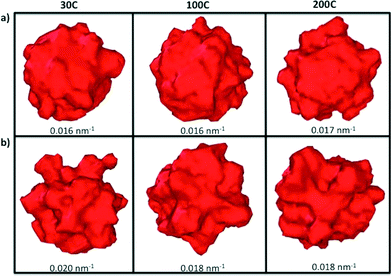
Throughout the simulations, we identified a number of key relationships between the insertion rates and temperatures, and the formation of different particle shapes and surface defects, which can be generally divided into two stages. The first stage involves the homogeneous nucleation and subsequent formation of small nuclei. In this stage, different types of nuclei can be created, including those with single-crystal, single-twinned and multiply-twinned cores. Each type of nucleus then evolves into nanocrystals with a unique shape, depending on the reaction conditions. For example, previous TEM studies39 have shown that metallic nanoparticles exhibit four basic shapes during their growth process: face-centred cubic (FCC) octahedron, icosahedral, decahedral, and single- and multiply-twinned nanoparticles. We have made a detailed analysis of all types of internal structure obtained in our simulations and conclude that the particles develop a FCC internal structure during the nucleation process (under our conditions). This is depicted in Fig. 1, where the particles are composed by approximately 70% to 80% of FCC morphology. These general trends are common to many FCC-bulk systems, as demonstrated by previously reported calculations40–43 and experiments.44,45 In Fig. 2, we can observe the formation of small nuclei in the initial nucleation stage exhibiting multiple twinning and stacking faults intersecting with the facets.The second stage involves the growth of the nuclei via constant deposition of the inserted metal atoms that coarsen and sintering as secondary particles collide. In this stage, the nucleus can be directed to evolve into a nanocrystal with a specific shape by controlling the reduction kinetics and surface diffusion. The competition between the energy barriers for atom diffusion on adjacent adsorption sites, and the energy barrier associated with the internal structuring that accompanies deposition and collisions determines the final shape. It is important to point out that each of these stages change the population of each type of surface site (characterized by the SCN). Once the atomic deposition wanes, there is an increase in the rate of surface diffusion as the newly deposited atoms move and adopt lower energy sites on (and in) the surface facets. This process is driven by the energy imparted as a result of the collisions, and as the size of the primary particle increases the probability of more significant restructuring decreases; limiting the restructuring to the atoms localised around the site of impact. The result is a gradual transformation of the nucleus into dendritic-like structures (see Fig. 2a) and c)), rather than the low energy perfect polyhedra typically observed in equilibrium studies. These structures have surfaces characterized by a high free energy and a much higher density of steps, kinks and terraces (composed of atoms with low SCN) than ideal polyhedra, making them highly desirable for use in various types of catalytic reactions.
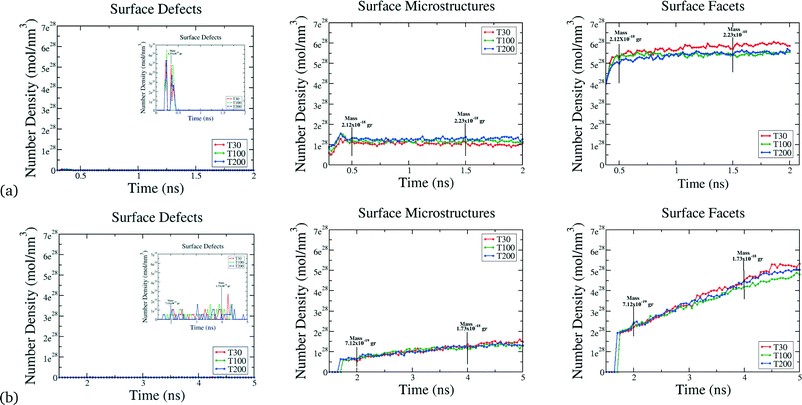
As we have previously established, the catalytic performance relies on the size, shape but also on the different surface defects of the material. In contrast with their bulk counterpart, the finite size of nanocrystals allows for the presence of multiple types of surface atoms each of which plays a different role in a catalytic reaction, such as (but not limited to) edges and corners. Previously we have established a simple classifications scheme relating SCN to functional similarities.17 Briefly, all Pt atoms with SCN of 1, 2 or 3 are classified as Surface Defects (where adatoms are placed on “top”, “bridge” and “hollow” sites); atoms with SCN of 4, 5, 6 or 7 are termed Surface Microstructures (corresponding to kinks/steps-like defects); and atoms with SCN of 8, 9, 10 or 11 are termed Surface Facets (corresponding to surface-like defects that includes any planar configuration). Each of these groups are linked to a specific catalytic reaction. For instance, it has been well established that CO oxidation is initiated on step sites on (111) terraces and diffuses rapidly to Surface Defect sites.25,46 Surface Microstructures are important in the first stage of CO reactions, and oxygen reduction reactions (ORR),25 since electrolyte anions adsorb more strongly on steps and kinks with coordination numbers of 4, 5 and 6, where oxygen–oxygen bonds can be readily broken. For the H oxidation (HOR) and evolution (HER) reactions,20 the desorption/adsorption of hydrogen increases with atoms in Surface Facets (with SCN of 7, 8 or 9).
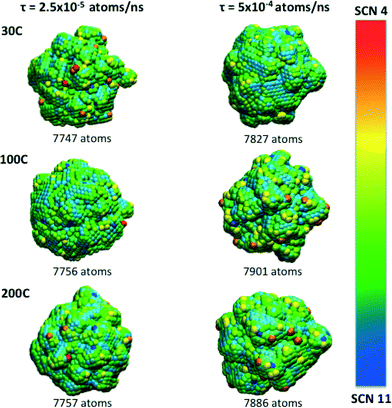
The manipulation of different experimental parameters such as the temperature and deposition rates, make it possible to attain a spectrum of morphological complexity, as is illustrated in Fig. 3. Atoms with SCN of 8, 9 and 10 (shown in green, cyan and blue, respectively) dominate the final particle structure, and are distributed along “planar” regions forming terraces and facets. Atoms with SCN of 4, 5 and 6 (shown in red, orange and yellow, respectively) are distributed over the branches and protuberances. Although low coordination sites are intrinsically related to the branches, they are not randomly distributed, even when the surface atoms do not reside on a lattice site.
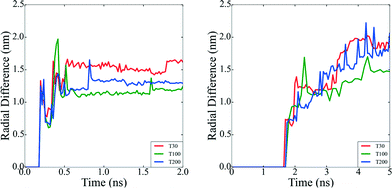
Beyond the availability of different types of active sites, the time evolution of these sites determines when the catalyst achieves maximum activity, and can provide guidance as to when to stop growing. For instance, particles formed at τ = 2.5 × 10−4 atoms per ns reach their maxima in only 0.5 ns, whereas the particles formed at higher rates at τ = 5 × 10−4 atoms per ns, require 5 ns to reach maximal performance (see Fig. 4). This is not a simple relationship that can be predicted based on the rates alone, since the time evolution of the surface defects depends on the atomic diffusion rate which increases at lower depositions. Looking to the different classes of defects we can see that Surface Facets and Surface Microstructure dominate, indicating that these conditions produce particles more suitable for CO first step reactions to break oxygen–oxygen bonds, HOR and HER reactions after the first 0.5 ns of the growth process in particles formed at τ = 2.5 × 10−5 atoms per ns, which will be smaller, and at the end for particles formed at τ = 5 × 10−4 atoms per ns, which will be larger (and therefore more expensive). The dependence of the SCN on the temperature does not contribute to the relative abundance of under-coordinated surface atoms; temperature curves exhibit similar values for the density of active sites in all the simulations; it is the atomic deposition rate determines that determines the surface. This is a useful finding, as the temperature can be selected to control the decomposition rate of the precursor without changing the relative abundance of under-coordinated active surface atoms.
3.2 Evolution of surface roughening
While the SCN provide specific details of the local disorder and microstructure, a more global measure of “roughness” provides valuable information regarding structural features of the particle as a whole. In order to characterize the roughness as the particles evolve, we have plotted the difference between the maximum and minimum distances between each surface atom and the centre of mass in all of the particles (Fig. 5). Particles with atomic deposition of τ = 2.5 × 10−5 atoms per ns exhibits small fluctuations after the first 0.5 ns, indicative of the formation of branches due to collisions with secondary nuclei, and the absorption of those branches shortly thereafter, due to restructuring. The faster the growth rate (in a highly supersaturated system, where collisions are more frequent), the more rounded the particle becomes. When particles are formed at τ = 5 × 10−4 atoms per ns, the growth is sufficiently slow, and the collisions sufficiently infrequently, that the branches persist. The collision and adsorption of secondary nuclei provides energy to the system, as well as mass, which activates the restructuring process. In short, faster atomic deposition creates “rounded” shapes and longer, slower deposition produce “rougher” particles with branches.To help illustrate how roughening impacts the total available area exposed to molecules during heterogenous catalysis, Fig. 6 depicts the surface mesh calculated for the final structures obtained at the end of the simulations and their corresponding surface-to-volume ratio. Particles with a higher degree of branches exhibit larger exposed surface areas as we obviously expected. All the surface analysis in the simulations were carried out using OVITO software.47
3.3 Experimental observations
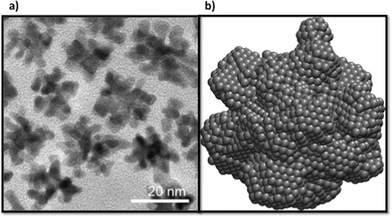
In recent years different synthesis conditions have been successful used to create Pt nanostructures including simple clusters,48,49 nanocrystals50,51 and nanowires52,53 and complex architectures.54–57 Among them, nano-branched structures with higher electrochemically active surface areas are usually characterised by open nanochannels and interconnected nanoarms, rich with catalytically active surface defects58–62 (as discussed above). In general branching follows the nucleation of well-defined geometries, and is supported in many cases by a seed.13,63 In Fig. 7 we can observe high-resolution transmission electron microscopy (HRTEM) images of various multi-branched structures obtained by the method of hydrogenation decomposition of organometallic precursors.26 Under this technique, the formation of particles occurs at a slow rate, leading the formation of multi-faceted shapes. In our simulations initial seeds were not used, but the internal structure of the particles were found to correspond to FCC (Fig. 1). This supports the hypothesis that branched Pt particles have cuboctahedral faceted cores from which branches growth due to the high activation energy for desorption or diffusion on the (111) and (100) facets that promotes the growth in these directions. This suggests that branches are more likely to grow from FCC regions than HCP regions.4 Conclusions
We have investigated the nucleation, growth and catalytic activity of Pt nanoparticles by analysing the surface atom coordination and final shapes generated via molecular dynamics simulations. A detailed study of the formation of these nanoparticles under different temperature and deposition conditions shows that the atomic deposition rates, rather than the temperature, leads to the coalescence and sintering conditions that act as an activation for the reorganization of the atomic surface structure and distribution of active sites. In this context, nanoparticles formed at slower atomic deposition rates (τ = 2.5 × 10−5 atoms per ns), have the tendency to exhibit “rougher” surfaces with a higher density of under-coordinated atoms and branches. This will directly impact the catalytic activity for many technologically important reactions, and we have shown that the particles obtained in the conditions considered herein are more suited to CO oxidation HER and HOR reactions. The branched particles are comparable with experimental evidence and we confirm that cuboctahedral nucleus or seeds are likely to be important in initiating branching. This significant result provides insights into how the degree of branching may be controlled, without the need for additional steps in the manufacturing process. Nanoparticles with a high density of surface defects and irregular shapes can still be tailored to specific applications, particularly given they are a more feasible option for the development of commercial nanocatalysts that require large scale mass production.Acknowledgements
We thank Dr. Soshan Cheong for obtaining the high-resolution TEM images of the Pt nanoparticles. Computational resources for this project were supplied by the National Computing Infrastructure national facility under Mass Allocation Scheme, Grant p00.References
- C. B. Murray, S. H. Sun, H. Doyle and T. Betley, MRS Bull., 2001, 26, 985–991 CrossRef CAS.
- S. O'Brien, L. Brus and C. B. Murray, J. Am. Chem. Soc., 2001, 123, 12085–12086 CrossRef.
- M. Law, J. M. Luther, Q. Song, B. K. Hughes, C. L. Perkins and A. Nozik, J. Am. Chem. Soc., 2008, 130, 5974–5985 CrossRef CAS PubMed.
- C. T. Campbell, S. C. Parker and D. E. Starr, Science, 2002, 298, 811–814 CrossRef CAS PubMed.
- M. A. Brown, E. Carrasco, M. Sterrer and H. J. Freund, J. Am. Chem. Soc., 2010, 132, 4064–4065 CrossRef CAS PubMed.
- S. Tsyganov, J. Keastner, B. Rellinghaus, T. Kauffeldt, F. Westerhoff and D. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045421 CrossRef.
- G. L. Bezemer, T. J. Remans, A. P. van Bavel and A. L. Dugulan, J. Am. Chem. Soc., 2010, 132, 8540–8541 CrossRef CAS PubMed.
- R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343–1348 CrossRef CAS.
- D. Duff, P. Edwards and B. Johnson, J. Phys. Chem., 1995, 99, 15934 CrossRef CAS.
- C. Chen and M. Akashi, Langmuir, 1997, 13, 6465 CrossRef CAS.
- T. Teraanishi, M. Hosoe, T. Tanaka and M. Miyake, J. Phys. Chem. B, 1999, 103, 3818 CrossRef.
- J. Yang, J. Lee, T. Deivaraj and H. Too, Langmuir, 2003, 19, 10361 CrossRef CAS.
- T. S. Ahmadi, Z. L. Wang, T. G. Green, A. Henglein and M. A. El-Sayed, Science, 1996, 272, 1924–1926 CAS.
- J. M. Petroski, Z. L. Wang, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 3316 CrossRef CAS.
- H. Song, F. Kim, S. Connor, G. A. Somorjai and P. D. Yang, J. Phys. Chem. B, 2005, 109, 188–193 CrossRef CAS PubMed.
- C. Wang, H. Daimon, Y. Lee, J. Kim and S. Sun, J. Am. Chem. Soc., 2007, 129, 6974–69745 CrossRef CAS PubMed.
- H. Barron and A. S. Barnard, Catal. Sci. Technol., 2015, 5, 2848–2855 CAS.
- A. S. Barnard and L. Y. Chang, ACS Catal., 2011, 1, 76–81 CrossRef CAS.
- K. J. J. Mayrhofer, M. Arenz, B. B. Blizanac, V. Stamenkovic, P. N. Ross and N. M. Markovic, Electrochim. Acta, 2005, 50, 5144–5154 CrossRef CAS.
- Q. S. Chen, F. J. Vidal-Iglesias, J. Solla-Gullon, S. G. Sun and J. M. Feliu, Chem. Sci., 2012, 3, 136–147 RSC.
- Q. S. Chen, J. Solla-Gullon, S. G. Sun and J. M. Feliu, Electrochim. Acta, 2010, 55, 7982 CrossRef CAS.
- N. P. Lebedeva, M. T. M. Koper, J. M. Feliu and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 12938 CrossRef CAS.
- G. Garcia and M. T. M. Koper, Phys. Chem. Chem. Phys., 2008, 10, 3802 RSC.
- G. Garcia and M. T. Koper, J. Am. Chem. Soc., 2009, 131, 5384 CrossRef CAS PubMed.
- N. Tian, Z. Y. Zhou and S. G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CAS.
- J. Ren and R. D. Tilley, Small, 2007, 3, 508–1512 CrossRef PubMed.
- J. T. Ren and R. D. Tilley, J. Am. Chem. Soc., 2007, 129, 3287–3291 CrossRef CAS PubMed.
- F. Dumestre, B. Chaudret, C. Amiens, M. Fromen, M. Casanove, P. Renaud and P. Zurcher, Angew. Chem., 2002, 114, 4462 CrossRef.
- F. Dumestre, B. Chaudret, C. Amiens, P. Renaud and P. Fejes, Science, 2004, 303, 821 CrossRef CAS PubMed.
- X. Teng, X. Liang, S. Maksimuk and H. Yang, Small, 2006, 2, 249 CrossRef CAS PubMed.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155420 CrossRef.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2003, 90, 135504 CrossRef CAS PubMed.
- T. J. Toai, G. Rossi and R. Ferrando, Faraday Discuss., 2008, 138, 49–58 RSC.
- M. M. Mariscal, S. A. Dassie and E. P. M. Leiva, J. Chem. Phys., 2005, 123, 184505 CrossRef PubMed.
- http://lammps.sandia.gov .
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 33, 7983–7991 CrossRef.
- F. Calvo, Nanoalloys from fundamentals to emergent applications, Elsevier Science, 2013, pp. 175–202 Search PubMed.
- G. Opletal, G. Grochola, Y. H. Chui, I. K. Snook and S. P. Russo, J. Phys. Chem. C, 2011, 115, 4375–4380 CAS.
- M. Jose-Yacaman, M. Marin-Almazo and J. A. Ascencio, J. Mol. Catal. A: Chem., 2001, 173, 61–74 CrossRef CAS.
- B. Raoult, J. Farges, M. F. De Feraudy and G. Torchet, Philos. Mag. B, 1989, 60, 881 CAS.
- C. L. Cleveland and U. Landman, J. Chem. Phys., 1991, 94, 7376 CrossRef CAS.
- J. Upperbrink and D. J. Wales, J. Chem. Phys., 1992, 96, 8520 CrossRef.
- J. P. K. Doye and D. J. Wales, J. Chem. Phys., 1999, 111, 11070–11079 CrossRef CAS.
- D. Reinhard, B. D. Hall, P. Berthoud, S. Valkealahti and R. Monot, Phys. Rev. Lett., 1997, 79, 1459 CrossRef CAS.
- J. Farges, M. F. De Feraudy, B. Raoult and G. Torchet, Surf. Sci., 1981, 106, 95 CrossRef CAS.
- J. S. Spendelow, X. Qinqin, J. D. Goodpaster, P. J. A. Kenis and A. Wieckowski, J. Electrochem. Soc., 2007, 154, F238 CrossRef CAS.
- A. Stukowski, JOM, 2013, 66, 399–407 CrossRef.
- P. Blonski, S. Dennler and J. Hafner, J. Chem. Phys., 2011, 134, 034107–034114 CrossRef PubMed.
- X. Wang, J. Lian and Y. Wang, Int. J. Hydrogen Energy, 2014, 39, 14288–14295 CrossRef CAS.
- B. W. Lim, X. M. Lu, M. J. Jiang, P. H. C. Camargo, E. C. Cho, E. P. Lee and Y. N. Xia, Nano Lett., 2008, 8, 4043–4047 CrossRef CAS PubMed.
- M. Chen, B. H. Wu, J. Yang and N. F. Zheng, Adv. Mater., 2012, 24, 862–879 CrossRef CAS PubMed.
- H. B. R. Lee, S. H. Baeck, T. F. Jaramillo and S. F. Bent, Nano Lett., 2013, 13, 457–463 CrossRef CAS PubMed.
- D. K. Lim, D. Lee, H. Lee, S. S. Bae, J. Choi, S. Kim, C. X. Ji, R. Ragan, D. A. A. Ohlberg, Y. A. Chang and R. S. Williams, Nanotechnology, 2007, 18, 095706–095710 CrossRef.
- L. X. Ding, A. L. Wang, G. R. Li, Z. Q. Liu, W. X. Zhao, C. Y. Su and Y. X. Tong, J. Am. Chem. Soc., 2012, 134, 5730–5735 CrossRef CAS PubMed.
- L. F. Liu, E. Pippel, R. Scholz and U. Gosele, Nano Lett., 2009, 9, 4352–4354 CrossRef CAS PubMed.
- P. Karthika, H. Ataee-Esfahani, H. J. Wang, M. A. Francis, H. Abe, N. Rajalakshmi, K. S. Dhathathreyan, D. Arivuoli and Y. Yamauchi, Chem. – Asian J., 2013, 8, 902–907 CrossRef CAS PubMed.
- L. Wang and Y. Yamauchi, Chem. Mater., 2011, 23, 2457–2465 CrossRef CAS.
- L. Wang, Y. Nemoto and Y. Yamauchi, J. Am. Chem. Soc., 2011, 133, 9674–9977 CrossRef CAS PubMed.
- X. Y. Han, D. W. Wang, D. Liu, J. S. Huang and T. Y. You, J. Colloid Interface Sci., 2012, 367, 342–347 CrossRef CAS PubMed.
- B. Lim, M. J. Jiang, P. H. C. Camargo, E. C. Cho, J. Tao, X. M. Lu, Y. M. Zhu and Y. N. Xia, Science, 2009, 324, 1302–1305 CrossRef CAS PubMed.
- W. Y. Wang, D. S. Wang, X. W. Liu, Q. Peng and Y. D. Li, Chem. Commun., 2013, 49, 2903–2906 RSC.
- Z. H. Lin, M. H. Lin and H. T. Chang, Chem. – Eur. J., 2009, 15, 4656–4662 CrossRef CAS PubMed.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |