Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic regimes in the tandem reactions of H-BEA catalyzed formation of p-xylene from dimethylfuran†
C. Luke
Williams‡
bd,
Katherine P.
Vinter‡
ad,
Chun-Chih
Chang
bd,
Ruichang
Xiong
 cd,
Sara K.
Green
bd,
Stanley I.
Sandler
cd,
Dionisios G.
Vlachos
cd,
Wei
Fan
bd and
Paul J.
Dauenhauer
*ad
cd,
Sara K.
Green
bd,
Stanley I.
Sandler
cd,
Dionisios G.
Vlachos
cd,
Wei
Fan
bd and
Paul J.
Dauenhauer
*ad
aUniversity of Minnesota, Department of Chemical Engineering Materials Science, 421 Washington Ave. SE, Minneapolis, MN, 55455 USA. E-mail: hauer@umn.edu
bUniversity of Massachusetts Amherst, Department of Chemical Engineering, 686 North Pleasant Street, Amherst, MA, 01003 USA
cUniversity of Delaware, Department of Chemical and Biomolecular Engineering, Colburn Laboratory, 150 Academy Street, Newark, DE, 19716 USA
dCatalysis Center for Energy Innovation, U.S. Department of Energy Frontier Research Center, USA Web: http://www.efrc.udel.edu
First published on 23rd October 2015
Abstract
Reaction kinetics and pathways of p-xylene formation from 2,5-dimethylfuran (DMF) and ethylene via cascade reactions of Diels–Alder cycloaddition and subsequent dehydration over H-BEA zeolite (Si/Al = 12.5) were characterized. Two distinct kinetic regimes were discovered corresponding to the rate limiting reaction, namely Diels–Alder cycloaddition and cycloadduct dehydration, as the concentration of Brønsted acid sites decreases. At catalyst loadings with effective acid site concentrations exceeding a critical value (~2.0 mM), the rate of formation of Diels–Alder products becomes constant. Under these conditions, the measured activation energy of 17.7 ± 1.4 kcal mol−1 and reaction orders correspond to the [4 + 2] Diels–Alder cycloaddition reaction of DMF and ethylene. Conversely, at catalyst loadings below the critical value, the formation rate of p-xylene becomes first order in catalyst loading, and the measured activation energy of 11.3 ± 3.5 kcal mol−1 is consistent with dehydration of the Diels–Alder cycloadduct to p-xylene. Experimental comparison between H-BEA and H-Y zeolite catalysts at identical conditions indicates that the micropore structure controls side reactions such as furan dimerization and hydrolysis; the latter is supported via molecular simulation revealing a substantially higher loading of DMF within H-Y than within H-BEA zeolites at reaction conditions.
1.0 Introduction
The production of renewable chemicals is currently of international interest due to increasing consumer demand for sustainable products combined with the need for national energy independence.1,2 Global energy demand for the chemical industry is 15 EJ per year, comprising 30% of the total industrial energy demand worldwide.3 Only five major products dominate chemical production in terms of volume and energy consumption: benzene/toluene/xylenes (BTX), methanol, ethylene, ammonia, and propylene.3 The North American shale gas revolution can significantly contribute to four of these products, with high production of low molecular weight chemicals (e.g. C2 and C3 compounds).4,5 However, production of larger molecules in the BTX family will not likely be replaced with shale gas derivatives and increased capacity will rely on larger chemicals, such as C6 sugars, being obtained from biomass.6,7One important BTX chemical requiring a low-cost, thermochemical process for renewable production is p-xylene.8p-Xylene is currently oxidized to terephthalic acid (PTA), the building block for polyethylene terephthalate (PET), which is used to manufacture plastic bottles, clothing, automobiles, and food packaging. Production of p-xylene or PTA directly from biomass has the benefit that it can be directly integrated into the existing chemical and product infrastructure.9,25 As such, there exist numerous ongoing research programs to produce renewable PET and its monomer precursors.10–12
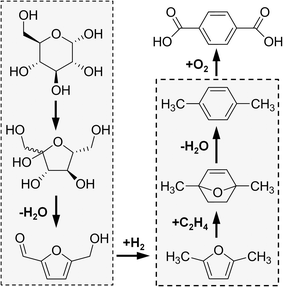
Diels–Alder reactions of biomass-derived furans have recently demonstrated potential for producing renewable six-carbon aromatic chemicals, including p-xylene and PTA. In the first step, a furan diene, 5-hydroxymethylfurfural (HMF), is produced by isomerization of glucose to fructose, performed using either base catalysts13,14 or heterogeneous Lewis acid catalysts, such as Sn-BEA.15 The subsequent dehydration of fructose produces HMF, with yields as high as 70%;16–18 HMF is currently manufactured at a scale of 20 tons per year.19 It has recently been proposed that oxidized variants of HMF can undergo Diels–Alder (DA) addition of ethylene, producing six-carbon ring aromatic chemicals with 1,4-substitution. For example, the oxidation of HMF to 2,5-furandicarboxylic acid (FDCA) and the subsequent DA addition of ethylene can produce PTA; however, this reaction has resulted in negligible yields of PTA.20–22 The DA reaction of ethylene with other oxidized variants has been reported but with only limited yields of six-carbon aromatic ring products.20
A more selective route to p-xylene and PTA first reduces HMF to 2,5-dimethylfuran (DMF).23,24 As shown in Fig. 1, the reaction of DMF and ethylene (itself produced from ethanol dehydration25–27) consists of the cascade reactions of Diels–Alder cycloaddition to 1,4-dimethyl-7-oxabicyclo[2.2.1]hept-2-ene (oxa-norbonene), followed by dehydration to p-xylene in a single reactor.28p-Xylene can then be integrated within the existing chemical process where it is oxidized to PTA.
Conversion of DMF and ethylene to p-xylene has been demonstrated using H-Y and H-BEA zeolites at yields of 75 and 90%, respectively, in the presence of n-heptane as a solvent.26,29 In competition with the pathway to p-xylene are three side reactions: (a) hydrolysis of dimethylfuran, (b) multiple additions of ethylene to form alkylated aromatic chemicals, and (c) dimerization of the furan feedstock and/or aromatic products.30,31 Density functional theory (DFT) studies have highlighted the benefit of strong acids for promotion of the main pathway and facilitating a high yield of p-xylene.30 Dehydration of the DA cycloadduct of DMF/C2H4 occurs in three steps, the first of which is prohibitive (Ea ~ 60 kcal mol−1) at moderate reaction conditions (T < 300 °C).26 Strong Brønsted acids have been predicted to dramatically lower the cycloadduct dehydration barrier (Ea ~ 10–20 kcal mol−1), providing a low-energy pathway to p-xylene.30 However, strong Brønsted acids have been predicted to have negligible impact on the rate of Diels–Alder cycloaddition of DMF and ethylene, while Lewis acids, such as lithium, can potentially lower the dimethylfuran DA energy barrier reaction from the value of ~25 kcal mol−1 to as low as ~15 kcal mol−1 when binding with ethylene.30
The reaction of DMF and ethylene on aluminum-substituted faujasite (H-Y) exhibits complex cascade kinetics of DA addition and dehydration. Initial studies of the DMF-ethylene reaction indicated a wide variation in the dependence of the reaction rate on acid concentration, such as zero-order rate dependence on the H-Y catalyst,26 while Dumesic and co-workers reported first-order dependence on the concentration of sites with tungstated zirconia.27 Using the strong acid sites in faujasite, it was recently shown that both interpretations of the dependence on catalyst concentration are possible, as the reaction can shift between overall rate limitation in either the Diels–Alder cycloaddition reaction or the subsequent multi-step dehydration.
In this work, we evaluate the kinetics of the reaction of dimethylfuran and ethylene with H-BEA zeolite and demonstrate a reaction pathway of tandem homogeneous Diels–Alder cycloaddition followed by Brønsted acid catalyzed dehydration to p-xylene, consistent with the overall mechanism occurring in H-Y zeolite. An improved catalytic selectivity towards p-xylene with H-BEA was evaluated by comparison with H-Y at identical experimental conditions and the results were interpreted via Grand Canonical Monte Carlo simulations, which revealed the distribution of reactants, intermediates and products within the different zeolite frameworks under the reaction conditions.
2.0 Research methods
Experiments consisted of reactions within a stirred-tank reactor with liquid sampling and ex situ characterization by gas chromatography-mass spectrometry. In addition, Grand Canonical Monte Carlo simulations were performed to evaluate the loading of organic species at reaction conditions over a range of dimethylfuran conversions.2.1 Batch reactions
Reactions were performed in Parr 4560 series reactors equipped with 4848 controllers and gas entrainment impellers. Chemicals were used without further purification and consisted of 2,5-dimethylfuran (Alfa Aesar 98+%), n-heptane (Alfa Aesar 99+%), ethylene gas (Airgas UHP), and n-tridecane (Sigma-Aldrich 98+%) as an internal standard.An ammonium-form BEA catalyst with a SiO2/Al2O3 ratio of 25 (Zeolyst CP814E) was calcined in flowing air at 550 °C for 12 hours to obtain an H-BEA zeolite with an acid site density of 0.64 mmol g−1, as measured by isopropylamine temperature programmed desorption. An H-Y zeolite catalyst (Zeolyst CBV600) with a SiO2/Al2O3 ratio of 5.2 exhibited an acid site density of 0.36 mmol g−1. The catalyst was stored in a desiccator and dried in a furnace at 200 °C prior to use in all reactions to minimize the amount of adsorbed water. In a typical reaction the Parr vessel was charged with DMF, heptane, tridecane, and catalyst prior to purging the reaction vessel with nitrogen. The reactor was then heated and the reaction was initiated by adding 13.6 atm (200 psi) of ethylene gas once the desired temperature was reached. Reaction pressures were held constant throughout the experiment through repressurization of the reaction vessel with ethylene after sampling.
2.2 Kinetic experiments
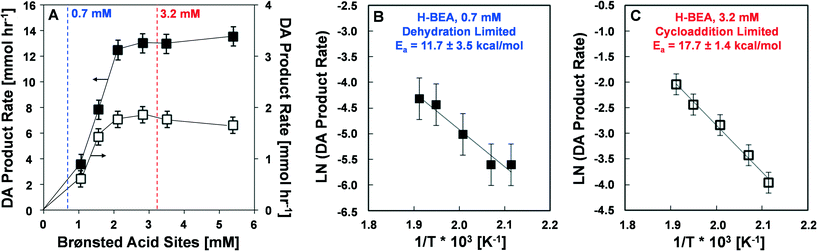
Reaction rates were measured at various conditions including different catalyst loading, DMF concentration, and ethylene partial pressure to determine the activation energies and reaction rate orders with respect to DMF and ethylene. Reactions investigating the rate of product formation (p-xylene, alkylated six-carbon ring aromatics, and dimers), shown in Fig. 2, utilized 1.4 M DMF in n-heptane with 0.082 M n-tridecane as an internal standard and 13.6 atm (200 psi) ethylene at either 200 or 250 °C. In these experiments, the mass of catalyst charged to the reactor varied from 0.15 to 0.75 g in 100 ml of reaction solution to yield effective Brønsted acid site concentrations between 0.96 mM and 4.8 mM. Experiments to determine the activation energy (Fig. 2B and C) were performed at both low (0.7 mM) and high (3.2 mM) catalyst loading over a temperature range of 200 to 250 °C. Experiments determining the reaction orders for DMF and ethylene (Fig. 3 and 4) were conducted at low (0.7 mM) and high (3.2 mM) catalyst loadings with DMF concentrations ranging from 0.46 M to 2.3 M and ethylene pressures ranging from 6.8 to 34 atm, respectively.2.3 Characterization of reaction products
Characterization of chemical components within the reaction mixture was performed with an Agilent 6890 gas chromatograph equipped with a G1513A autosampler, HP-Innowax column (to achieve the separation of o, m, and p-xylene isomers), and a flame ionization detector. Samples were collected under reaction conditions at high temperature and pressure utilizing a double block sampling system, which allows for samples to be taken at high pressure and temperature without opening the reaction vessel directly to the atmosphere. Major species were identified by matching retention times with pure standards and/or comparison with a library of MS spectra. The reported data have a carbon balance closure greater than or equal to 90%.2.4 Zeolite models
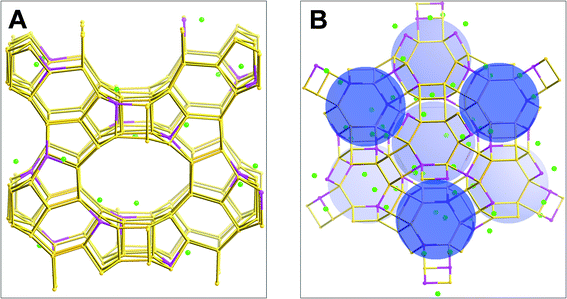
Adsorption simulations were performed for two zeolites, H-BEA (Si/Al = 15) and H-Y (Si/Al = 2.6). Zeolite beta is an intergrowth of two closely related polymorphs (polymorph A32 with a P4122 or P4322 space group and polymorph B33 with space group C2/c), both of which have a three-dimensional pore structure of 12-membered rings. Minor differences were found between the two polymorphs in simulating CO2 and N2 adsorption.34 Therefore, the model of H-BEA was constructed using the crystallographic atomic positions of all-silica polymorph A determined by Newsam et al.32 The simulation cell containing a 2 × 2 × 1 unit cell structure of all-silica polymorph A32 was composed of 256 Si and 512 O atoms with cell lattice parameters of 25.322 Å × 25.322 Å × 26.406 Å. After constructing the simulation cell composed of only silicon and oxygen atoms, 16 of the total of 256 Si atoms were randomly replaced with Al atoms to obtain a Si/Al ratio of 15. To make the entire H-BEA system neutral, 16 H atoms were added to the O atoms connected to the Al atoms to form hydroxyl groups, which leads to the chemical composition of the H-BEA simulation cell being Si240Al16O512H16. The H-Y (Si/Al = 2.6) zeolite was modeled as in our previous work35 and in a similar manner to the H-BEA zeolite. It was constructed based on the neutron diffraction data of Czjzek et al.36 characterized using the Fd3m space group with a cubic lattice parameter of 24.7665 Å. The simulation cell contains one unit cell of the structure37 with a chemical composition of Si139Al53O384H53.The active sites (Al atoms and protons) are distributed homogeneously in the H-BEA and H-Y zeolites, subject to the following constraints: the application of Lowenstein's rule37 (no Al–O–Al is allowed), no two hydroxyl groups can be linked to the same Si atom, and certain separation distance constraints between two protons and/or two Al atoms were applied depending on the Si/Al ratios. For example, no proton can be closer than 4.0 Å to another in H-Y (Si/Al = 2.6), and no Al atoms can be closer to each other than 7.0 Å and no protons can be closer than 5.0 Å in H-BEA (Si/Al = 15). The final configuration of the protons without any high-energy regions was obtained by performing an energy minimization of the fixed (except for the protons) zeolite structures using the conjugate gradient method.38 The final simulation cells for the two zeolites are shown in Fig. 5.
2.5 Simulation methods
The reaction of 2,5-dimethylfuran (DMF) and ethylene was carried out in a constant pressure reactor with the continuous addition of ethylene.26,29 Calculations were designed to mimic the experimental system.26,29 The side products are not considered here because of their relatively small fractions. Adsorption isotherms were calculated using configurational-bias Grand Canonical Monte Carlo (CB-GCMC)39,40 simulations, which were carried out in the above-created simulation cells for the H-BEA (Si/Al = 15) and H-Y (Si/Al = 2.6) zeolites with periodic boundary conditions applied in all three dimensions. At equilibrium, the chemical potential of each species in the zeolite is equal to that in the bulk phase. The chemical potential values required for the CB-GCMC simulations were calculated with the ASPEN Plus® commercial software package using the Soave–Redlich–Kwong–Kabadi–Danner (SRK–KD) equation of state (EOS), which is suitable for calculating the phase behavior of mixtures of hydrocarbons and water.41 The procedures to determine the bulk phase equilibria and the force fields used for the adsorption simulations are as in our previous work.36 We used the TraPPE-zeo force fields42,43 that have been shown to be transferrable among various zeolites including a faujasite-type zeolite44 and a beta zeolite.44 Literature force fields were used for the sorbates: p-xylene45–47 and DMF,46,48 ethylene,49 water50 and n-heptane.51 All sorbate–sorbate and sorbate–zeolite interactions were described using 12–6 Lennard-Jones (LJ) plus Coulombic point-charge potentials. The Lorentz–Berthelot combining rules were used to calculate the cross-term interaction parameters. The intermolecular interactions were truncated at a fixed cutoff distance of 12.0 Å with the long-range tail correction applied. The electrostatic interactions were computed using the Ewald summation method.52 Further simulation and force field details can be found in our previous work.353.0 Results and discussion
The kinetics of p-xylene production from DMF and ethylene with an H-BEA zeolite (Si/Al = 12.5) catalyst have been investigated using semi-batch Parr pressure vessels and analyzed with gas chromatography. Experimental data reveal the existence of two kinetic reaction regimes that coincide with the rate in each regime being controlled by a different reaction, either: (i) Diels–Alder cycloaddition or (ii) dehydration. Insight into both the cycloaddition-limited and dehydration-limited kinetic regimes has been obtained through the determination of activation energies and the reaction orders of DMF and ethylene in each regime. The enhanced catalytic performance of the H-BEA zeolite catalyst relative to the H-Y zeolites is further elucidated using molecular simulation.3.1 Characteristics of reactor transport
Ethylene gas–liquid mass transfer experiments were conducted to eliminate the potential for interphase mass transfer limitations. The experiments depicted in Fig. S1A† were performed by adding 60–100 mL of n-heptane to a reaction vessel and rapidly pressurizing to 54.4 atm (800 psi) with ethylene. Once pressurized, the gas dispersion impeller was turned on and operated at 1000 rpm; the system pressure was then monitored with 1/24th of a second precision. A least squares fit of the data provided a gas–liquid mass transfer coefficient of kLa = 0.066 s−1. The Damköhler number was calculated from Da = krxn/kLa, resulting in values of the order 10−4 to 10−3, providing quantitative support that no ethylene uptake limitation exists at any of the considered experimental conditions.Additional experiments were conducted to measure the rate of reaction of DMF and ethylene as a function of particle size of the H-BEA zeolite. As shown in Fig. S1B,† the overall reaction rate was determined at 1.38 M DMF in n-heptane, 250 °C, and 37.4 atm (550 psi) ethylene for four particle sizes of H-BEA: (i) 20 nm, (ii) 0.2 μm, (iii) 0.95 μm, and (iv) 4.5 μm. The synthesis of these particles is outlined in the ESI.† The two smallest particles achieved the same overall reaction rate, indicating that intraparticle diffusion limitations were not rate determining at the considered reaction conditions. All kinetic experiments used to determine reaction rates, activation energies, and reaction orders utilized a commercial H-BEA containing mesopores; this commercial catalyst exhibited an identical reaction rate to the smallest synthesized zeolites, indicating that no intraparticle diffusion limitations exist for the considered experimental conditions.
3.2 Reaction kinetics
The reaction of DMF and ethylene via the cascade reactions of Diels–Alder cycloaddition and dehydration exhibits two distinct kinetic regimes for the production of p-xylene and total Diels–Alder products (p-xylene, alkylated C6-aromatic chemicals, and dimers containing C6-aromatic chemicals). As shown in Fig. 2, the DA product rate as a function of total Brønsted acid sites per volume of reactor liquid exhibits first order behavior (linear). As the Brønsted acid concentration increases, the reaction rate eventually achieves a maximum rate. At 250 °C (solid black squares, left hand axis), the maximum rate of production of Diels–Alder compounds is about 13 mM h−1, while at 200 °C (open squares, right hand axis), the maximum reaction rate is 1.6 mM h−1. The transition between the two regimes occurs at a Brønsted acid site concentration between 2.0 and 2.5 mM, which corresponds to a catalyst loading of approximately 0.35 g H-BEA (Si/Al = 12.5) in 100 mL of reaction solution. The same trend is also observed at 200 °C, even though the overall reaction rate is lower by nearly an order of magnitude.Arrhenius plots were generated in each kinetic regime identified in Fig. 2A to evaluate the rate-limiting chemistry. Fig. 2B depicts an Arrhenius plot generated at the experimental conditions of Fig. 2A with an acid site concentration of 1.3 mM and variation in the temperature between 200 and 250 °C. The linear least squares fit reveals an activation energy of Ea = 11.7 ± 3.5 kcal mol−1 for the conditions exhibiting first order dependence on Brønsted acid concentration. Fig. 2C depicts an Arrhenius plot generated at the experimental conditions of Fig. 2A with an acid site concentration of 3.2 mM and variation in the temperature between 200 and 250 °C. The linear least squares fit indicates an activation energy of Ea = 17.7 ± 1.4 kcal mol−1 for the conditions exhibiting zero order dependence on Brønsted acid site concentration (the plateau regime of Fig. 2A).
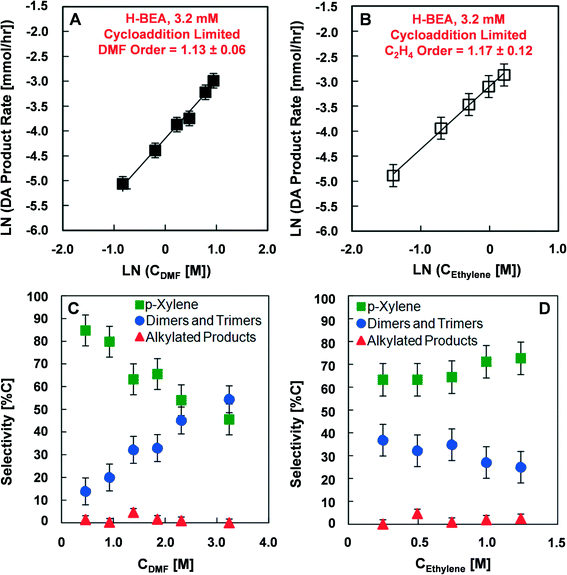
The high activation energy kinetic regime was further characterized to determine its dependence on the DMF and ethylene reactant concentrations. Fig. 3 depicts the reaction rate dependence for Diels–Alder products at a Brønsted acid site concentration of 3.2 mM and a temperature of 200 °C. As shown in Fig. 3A, variation of the initial concentration of DMF from 0.44 to 2.56 mM indicates a reaction dependence that is close to first order (1.13 ± 0.06). Similarly, Fig. 3B shows that the reaction rate dependence for ethylene is close to first order (1.17 ± 0.12) at a DMF concentration of 1.38 M (18 wt%) in n-heptane with the ethylene partial pressure varying from 6.8 to 34 atm. The ethylene concentration in Fig. 3B was determined from the data provided by Zhuze et al.53 The selectivity towards products in the high activation energy kinetic regime depends on the DMF and ethylene reactant concentrations, as shown in Fig. 3C. Increasing the initial DMF concentration decreases the selectivity towards p-xylene from 85% to 45% and increases the selectivity towards dimer products from 15% to 55%. A negligible change in selectivity towards alkylated species was detected. In contrast, as illustrated in Fig. 3D, variation in the initial ethylene pressure from 6.8 to 34 atm (100 to 500 psi) does not have a significant effect on selectivity towards p-xylene or other products.
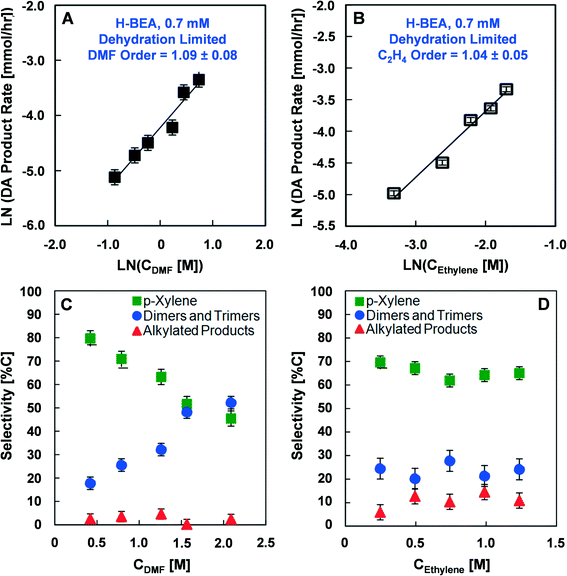
The reaction rate orders of DMF and ethylene with H-BEA (Si/Al = 12.5) were also determined in the low activation energy kinetic regime at a Brønsted acid concentration of 0.7 mM and 200 °C, as shown in Fig. 4A and B. With variation in the DMF concentration with a fixed ethylene concentration of 1.38 M (18 wt%), first order behavior is exhibited (1.09 ± 0.08), as shown in Fig. 4A. With variation of the initial concentration of ethylene from 0.44 to 2.56 mM in the dehydration limited regime, a reaction rate close to first order is indicated (1.04 ± 0.05), as shown in Fig. 4B.
The effect of variation in the initial DMF concentration or ethylene pressure on the selectivity towards Diels–Alder products in the low activation energy kinetic regime is illustrated in Fig. 4C. Increasing the initial DMF concentration decreases the selectivity towards p-xylene from 80% to 55% and increases the selectivity towards dimers and trimers from 18% to over 50%; no significant variation in the alkylated products was observed. Variation in the initial ethylene pressure from 6.8 to 34 atm (100 to 500 psi) shown in Fig. 4D resulted in no significant difference in selectivity towards any of the major products.
3.3 Simulation results
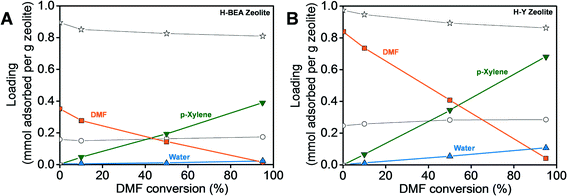
Simulations using the H-BEA and H-Y unit cells shown in Fig. 5 resulted in the adsorption isotherms for the reactants and products in the presence of the solvent n-heptane as a function of DMF conversion under the reaction conditions (250 °C and 56.1 atm), which are shown in Fig. 6. Four different extents of the reaction were studied, equivalent to 0, 10, 50 and 95% conversion of DMF. The adsorption trends of the reactants and products are similar in both the H-BEA and H-Y zeolites. As DMF is consumed and p-xylene is produced, the amount of adsorbed DMF is reduced and that of p-xylene increases.In our previous work,54 we have shown that the amount of water adsorbed in H-Y is significantly reduced in the presence of the solvent n-heptane. Since water causes DMF hydrolysis and the resulting 2,5-hexanedione can participate in side reactions, we have attributed the increased selectivity towards p-xylene in heptane to this effective enhanced hydrophobicity of the zeolite. The amount of water adsorbed decreases further in H-BEA (Si/Al = 15) to be about one-fifth of that in H-Y (Si/Al = 2.6) at 95% DMF conversion. The amount of DMF adsorbed in H-BEA also decreases from one-half to one-third compared to that in H-Y at all the DMF conversions studied. Since the heat of adsorption of DMF is higher in H-BEA than in H-Y, as shown in Table 1, the amount of DMF adsorbed is expected to be higher in H-BEA where the adsorption is dominated by the energetic interactions rather than the free pore volume. Therefore, we conclude that the decrease in the amount of DMF adsorbed is due to the smaller free pore volume in H-BEA than in H-Y. The decrease of DMF and water adsorption in H-BEA reduces the probability of the hydrolysis and dimerization side reactions. As a result, the selectivity towards p-xylene is increased in H-BEA, providing rationale for the experimental observations.2
| Species | Heats of adsorption at zero coverage (kcal mol−1) | |
|---|---|---|
| H-Y (Si/Al = 2.6) | H-BEA (Si/Al = 15) | |
| p-Xylene | 14.3 | 19.7 |
| Water | 8.5 | 7.2 |
| Ethylene | 4 | 5.4 |
| Heptane | 10.3 | 15.6 |
| DMF | 12.9 | 17 |
3.4 Comparison of faujasite and beta zeolites
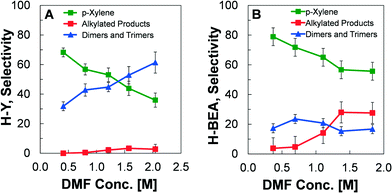
The H-BEA and H-Y zeolites were also compared experimentally to evaluate the differences in selectivity towards products under identical experimental conditions, as depicted in Fig. 7. Using a catalyst concentration at the transition between kinetic regimes ([H+] = 2.0 mM), the concentration of DMF was varied between about 0.25–2.0 M while fixing the temperature (200 °C), and ethylene pressure (19.7 atm). For these conditions, the selectivity towards products was measured at a conversion of DMF less than 10%. For the H-Y zeolite in Fig. 7A, it is clear that the maximum p-xylene yield occurs at lower concentrations of DMF. As the initial concentration of DMF increases, the production of p-xylene is reduced and the yield of dimers and trimers increases, while the production of alkylated species remains small (<5%). In comparison, the utilization of H-BEA zeolite results in higher p-xylene production than in H-Y for all initial DMF concentrations, as shown in Fig. 7B. The improved performance is due to the significantly reduced production of dimers and trimers.3.5 Interpretation of kinetics and reaction pathways
The catalytic conversion of DMF and ethylene in H-BEA zeolites is consistent with a recently published mechanism to describe the same reaction in H-Y.54 In that work, a microkinetic model considered the following reactions: (a) uncatalyzed Diels–Alder reaction of DMF and ethylene to form oxanorbornene, (b) uncatalyzed dehydration of oxanorbornene to p-xylene and water, (c) Brønsted acid catalyzed Diels–Alder reaction of DMF and ethylene to oxanorbornene, (d) Brønsted acid catalyzed dehydration of oxanorbornene to p-xylene and water, (e) catalytic hydrolysis of DMF to 2,5-hexanedione, and (f) all associated adsorption and desorption steps of the reactants, intermediates, and products. From insights obtained from a sensitivity analysis of the complete mechanism, it was determined that the Diels–Alder reaction of DMF and ethylene proceeds uncatalyzed, while dehydration of the Diels–Alder cycloadduct is catalyzed by the Brønsted acid sites. The resulting simplified mechanism was subsequently described by a rate expression using the liquid-phase concentration of dimethylfuran [DMF], liquid concentration of ethylene [C2H4], acid site concentration [H+], and water concentration [H2O]: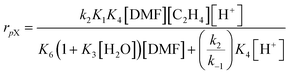 | (1) |
The simplified rate eqn (1) developed for the H-form faujasite is consistent with the kinetics of the reaction of DMF and ethylene with H-BEA, as depicted in Fig. 2A. At high Brønsted acid site concentrations ([H+] > 2.0 mM), the rate expression for the formation of p-xylene (rpX) reduces to rpX~[DMF][C2H4]. The reaction rate should be independent of acid site concentration with first order dependence on dimethylfuran and ethylene; this rate behavior is observed in the ‘plateau region’ of Fig. 2A and the first-order kinetics shown in Fig. 3A and B. Within this kinetic regime, the overall rate is limited by the rate of Diels–Alder cycloaddition of dimethylfuran and ethylene. In contrast, at low Brønsted acid site concentrations ([H+] < 2.0 mM), the rate expression for the formation of p-xylene (rpX) reduces to first order rate dependence on the acid site concentration and ethylene, rpX ~ [H+][C2H4], and variable order rate dependence on dimethylfuran (from zero to one). Consistent with this kinetic extreme, first order rate dependence on the acid site concentration is observed in the low catalyst loading conditions of Fig. 2A, and first order reaction rate dependence is observed for dimethylfuran and ethylene in Fig. 4A and B. Due to the similar behavior of the H-BEA and H-Y catalysts in the DMF and ethylene reaction, it can be concluded that the reaction proceeds by the same pathway; DMF and ethylene react in an uncatalyzed manner to form oxanorbornene, which adsorbs on acid sites and dehydrates to form water and p-xylene.
3.6 Interpretation of the differences between H-BEA and H-Y
While the reaction kinetics of DMF and ethylene indicate an identical reaction pathway to p-xylene and water regarding the main reaction paths for both H-BEA and H-Y, the difference in selectivity towards p-xylene and side products indicate the importance of pore properties and the micropore framework. As previously shown, the maximum demonstrated selectivity towards p-xylene at a high conversion of DMF was 90% with H-BEA29 and only 75%26 with H-Y. By comparing the two catalysts at identical conditions in Fig. 7, the difference in catalyst performance is clear; the H-Y catalyst promotes the formation of a significantly higher amount of dimer and trimer species of DMF than the H-BEA catalyst. The origin of this difference is seen in the distribution of molecules predicted by simulation to exist within the micropores during the reaction, as shown in Fig. 6. While the pores of MFI catalysts are too small to permit the formation of oxanorbornene and eventually p-xylene, the simulated quantities of DMF and p-xylene inside H-Y reveals that the supercages are too large. DMF and p-xylene are present within the faujasite pores at nearly twice the amount as within H-BEA, allowing for the increased formation of dimers and trimers. Moreover, H-Y contains more water and has a higher concentration of the ethylene reactant; higher ethylene concentration will promote alkylation, while water leads to the ring opening of DMF to form 2,5-hexanedione. The results of our simulations indicate that the zeolite exhibits a ‘Goldilocks effect’, whereby the most desirable pore for promotion of p-xylene formation is H-BEA, which is small enough to exclude the large oxanorbornene intermediate, but not too large to allow for significant formation of dimeric and trimeric side products.Despite small differences in product selectivity between the zeolite structures, it is worth speculating about the effect of the amount of DMF inside the zeolite on the overall reaction rate. In the dehydration limited regime (linear, [H+] < 2.0 mM in Fig. 2), the rate of p-xylene formation is determined by the concentration of cycloadduct inside the zeolite and its dehydration rate constant on the Brønsted acid sites. The former is determined from the equilibrium of the Diels–Alder reaction between DMF and ethylene in solution, since the volume of the zeolite is small in comparison to that of the solution. The latter is similar in value within H-Y and H-BEA. As a result, the reduction in the amount of DMF inside the zeolite should not affect the reaction rate in a significant way, which is what is observed. Additionally, in the Diels–Alder regime (plateau, [H+] > 2.0 mM), the rate-limiting Diels–Alder reaction occurs primarily in solution. The differences in the micropore framework should have no apparent effect on the overall reaction rate, which is what is observed under identical experimental conditions. Consequently, our molecular simulations support the view that both the presence of heptane and the different frameworks mainly affect the side reactions, and thus the yield, rather than the main reaction of DMF to p-xylene.
5.0 Conclusions
Experiments reveal the existence of two kinetic reaction regimes dependent on the loading of the H-BEA catalyst for the formation of p-xylene and water from 2,5-dimethylfuran (DMF) and ethylene. At low catalyst loading ([H+] < 2.0 mM), the overall reaction is limited by the rate of dehydration of the Diels–Alder cycloadduct of DMF and ethylene. As catalyst loading increases past an acid site concentration in solution of 2.0 mM, the formation of p-xylene becomes limited by the rate of the Diels–Alder cycloaddition of DMF and ethylene. It was also shown that lowering the initial concentration of DMF increases the selectivity towards p-xylene by decreasing the formation of dimer/trimer and alkylated products. Increasing the pressure of the reactant ethylene serves to increase the production rate of Diels–Alder compounds in both the cycloaddition and dehydration limited regimes without having a statistically significant effect on the selectivity towards products. Differences in the experimentally-observed selectivity towards products between BEA and FAU H-form zeolites was attributed to differences in the reactant DMF, product p-xylene and water concentrations within the pores, as determined from molecular simulation. Based on this study, maximum reaction rates with optimal selectivity to p-xylene occur at higher temperatures, lower DMF concentrations, higher ethylene pressures, and an effective Brønsted acid site concentration above 2.5 mM.Acknowledgements
This material is supported as part of the Catalysis Center for Energy Innovation, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award No. DE-SC0001004.References
- A. V. Bridgwater, Chem. Eng. J., 2003, 91, 87–102 CrossRef CAS.
- A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick, J. P. Hallett, D. J. Leak, C. L. Liotta, J. R. Mielenz, R. Murphy, R. Templer and T. Tschaplinski, Science, 2006, 311, 484–489 CrossRef CAS PubMed.
- Int. Energy Agency, Technology Roadmap Energy and GHG Reductions in the Chemical Industry via Catalytic Processes, 2013, pp. 1–60 Search PubMed.
- P. C. A. Bruijnincx and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2013, 52, 2–10 CrossRef PubMed.
- P. J. Dauenhauer and G. W. Huber, Green Chem., 2014, 16, 382–383 RSC.
- T. P. Vispute, H. Zhang, A. Sanna, R. Xiao and G. W. Huber, Science, 2010, 330, 1222–1227 CrossRef CAS PubMed.
- X. Tong, Y. Ma and Y. Li, Appl. Catal., A, 2010, 385, 1–13 CrossRef CAS.
- E. Sawicki, Ind. Biotechnol., 2014, 10, 69–72 CrossRef.
- R. J. Sheehan, Ulmann's Encyclopedia of Industrial Chemistry, 2011, pp. 17–28 Search PubMed.
- D. G. Vlachos, J. G. Chen, R. J. Gorte, G. W. Huber and M. Tsapatsis, Catal. Lett., 2010, 140, 77–84 CrossRef CAS.
- M. N. Masuno, P. B. Smith, D. A. Hucul, A. Dumitrascu, K. Brune, R. L. Smith, J. Bissell and M. Foster, US Pat., US20130245316, 2013 Search PubMed.
- B. Halford, Chem. Eng. News, 2012, 90(19), 28 Search PubMed.
- S. Lima, A. S. Dias, Z. Lin, P. Brandão, P. Ferreira, M. Pillinger, J. Rocha, V. Calvino-Casilda and A. A. Valente, Appl. Catal., A, 2008, 339, 21–27 CrossRef CAS.
- M. Watanabe, Y. Aizawa, T. Iida, T. M. Aida, C. Levy, K. Sue and H. Inomata, Carbohydr. Res., 2005, 340, 1925–1930 CrossRef CAS PubMed.
- M. Moliner, Y. Román-Leshkov and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6164–6168 CrossRef CAS PubMed.
- Y. Román-Leshkov, J. N. Chheda and J. A. Dumesic, Science, 2006, 312, 1933–1937 CrossRef PubMed.
- E. Nikolla, Y. Roman-Leshkov, M. Moliner and M. E. Davis, ACS Catal., 2011, 1, 408–410 CrossRef CAS.
- A. I. Torres, M. Tsapatsis and P. Daoutidis, Comput. Chem. Eng., 2012, 42, 130–137 CrossRef CAS.
- M. M. Bomgardner, Chem. Eng. News, 2014, 92, 10–14 Search PubMed.
- J. J. Pacheco and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8363–8367 CrossRef CAS PubMed.
- W. H. Gong, US Pat., US8299278B2, 2012 Search PubMed.
- B. Wang, G. J. Gruter, M. A. Dam and R. M. Kriegel, Int. Pat., WO2014/065647A1, 2014 Search PubMed.
- Y. Román-Leshkov, C. J. Barrett, Z. Y. Liu and J. A. Dumesic, Nature, 2007, 447, 982–985 CrossRef PubMed.
- J. Jae, W. Zheng, R. F. Lobo and D. G. Vlachos, ChemSusChem, 2013, 6, 1158–1162 CrossRef CAS PubMed.
- T. A. Brandvold, US Pat., US20100331568, 2010 Search PubMed.
- C. L. Williams, C.-C. Chang, P. Do, N. Nikbin, S. Caratzoulas, D. G. Vlachos, R. F. Lobo, W. Fan and P. J. Dauenhauer, ACS Catal., 2012, 2, 935–939 CrossRef CAS.
- D. Wang, C. M. Osmundsen, E. Taarning and J. A. Dumesic, ChemCatChem, 2013, 5, 2044–2050 CrossRef CAS.
- P. T. M. Do, J. R. McAtee, D. A. Watson and R. F. Lobo, ACS Catal., 2013, 3, 41–46 CrossRef CAS PubMed.
- C.-C. Chang, S. K. Green, C. L. Williams, P. J. Dauenhauer and W. Fan, Green Chem., 2014, 16, 585 RSC.
- N. Nikbin, P. T. Do, S. Caratzoulas, R. F. Lobo, P. J. Dauenhauer and D. G. Vlachos, J. Catal., 2013, 297, 35–43 CrossRef CAS.
- N. Nikbin, S. Caratzoulas and D. G. Vlachos, ChemSusChem, 2013, 6, 2066–2068 CrossRef CAS PubMed.
- J. M. Newsam, M. M. J. Treacy, W. T. Koetsier and C. B. Degruyter, Proc. R. Soc. London, Ser. A, 1988, 420, 375–405 CrossRef CAS.
- A. Corma, M. Moliner, A. Cantin, M. J. Diaz-Cabanas, J. L. Lorda, D. L. Zhang, J. L. Sun, K. Jansson, S. Hovmoller and X. D. Zou, Chem. Mater., 2008, 20, 3218–3223 CrossRef CAS.
- T. D. Pham, R. Xiong, S. I. Sandler and R. F. Lobo, Microporous Mesoporous Mater., 2014, 185, 157–166 CrossRef CAS.
- R. Xiong, S. I. Sandler, D. G. Vlachos and P. J. Dauenhauer, Green Chem., 2014, 16, 4086–4091 RSC.
- M. Czjzek, H. Jobic, A. N. Fitch and T. Vogt, J. Phys. Chem., 1992, 96, 1535–1540 CrossRef CAS.
- W. Loewenstein, Am. Mineral., 1954, 39, 92–96 CAS.
- R. Fletcher and C. M. Reeves, Comput. J., 1964, 7, 149–154 CrossRef.
- B. Smit and J. I. Siepmann, J. Phys. Chem., 1994, 98, 8442–8452 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, 1996 Search PubMed.
- K. S. Pedersen, P. L. Christensen and S. J. Azeem, Phase Behavior of Petroleum Reservoir Fluids, 2006 Search PubMed.
- P. Bai, M. Tsapatsis and J. I. Siepmann, J. Phys. Chem. C, 2013, 117, 24375–24387 CAS.
- P. Bai, P. Ghosh, J. C. Sung, D. Kohen, J. I. Siepmann and R. Q. Snurr, Fluid Phase Equilib., 2014, 366, 146–151 CrossRef CAS.
- P. Bai, J. I. Siepmann and M. W. Deem, AIChE J., 2013, 59, 3523–3529 CrossRef CAS.
- N. A. McDonald and W. L. Jorgensen, J. Phys. Chem. B, 1998, 102, 8049–8059 CrossRef CAS.
- W. L. Jorgensen, E. R. Laird, T. B. Nguyen and J. Tiradorives, J. Comput. Chem., 1993, 14, 206–215 CrossRef CAS.
- V. Lachet, A. Boutin, B. Tavitian and A. H. Fuchs, Faraday Discuss., 1997, 106, 307–323 RSC.
- W. L. Jorgensen, J. M. Briggs and M. L. Contreras, J. Phys. Chem., 1990, 94, 1683–1686 CrossRef CAS.
- S. L. Weitz and J. J. Potoff, Fluid Phase Equilib., 2005, 234, 144–150 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, 1987 Search PubMed.
- T. P. Zhuze and A. S. Zhurba, Bull. Acad. Sci. USSR, Div. Chem. Sci. (Engl. Transl.), 1960, 9, 335–337 CrossRef.
- R. E. Patet, N. Nikbin, C. L. Williams, S. K. Green, C. Chang, W. Fan, S. Caratzoulas, P. J. Dauenhauer and D. G. Vlachos, ACS Catal., 2015, 5(4), 2367–2375 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Catalyst and reactor information. See DOI: 10.1039/c5cy01320h |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |