Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In situ studies of materials for high temperature CO2 capture and storage
Matthew T.
Dunstan
a,
Serena A.
Maugeri
b,
Wen
Liu
c,
Matthew G.
Tucker
def,
Oluwadamilola O.
Taiwo
g,
Belen
Gonzalez
h,
Phoebe K.
Allan
a,
Michael W.
Gaultois
 a,
Paul R.
Shearing
g,
David A.
Keen
d,
Anthony E.
Phillips
b,
Martin T.
Dove
b,
Stuart A.
Scott
i,
John S.
Dennis
h and
Clare P.
Grey
*a
a,
Paul R.
Shearing
g,
David A.
Keen
d,
Anthony E.
Phillips
b,
Martin T.
Dove
b,
Stuart A.
Scott
i,
John S.
Dennis
h and
Clare P.
Grey
*a
aDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: cpg27@cam.ac.uk
bSchool of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK
cCambridge Centre for Advanced Research and Education in Singapore, Nanyang Technological University, 1 Create Way, Singapore 138602
dISIS Facility, Rutherford Appleton Laboratory, Harwell Campus, Didcot OX11 0QX, UK
eDiamond Light Source, Chilton, Oxfordshire OX11 0DE, UK
fSpallation Neutron Source, Oak Ridge National Laboratory, Oak Ridge, USA
gDepartment of Chemical Engineering, University College London, London WC1E 7JE, UK
hDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge, CB2 3RA, UK
iDepartment of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
First published on 12th April 2016
Abstract
Carbon capture and storage (CCS) offers a possible solution to curb the CO2 emissions from stationary sources in the coming decades, considering the delays in shifting energy generation to carbon neutral sources such as wind, solar and biomass. The most mature technology for post-combustion capture uses a liquid sorbent, amine scrubbing. However, with the existing technology, a large amount of heat is required for the regeneration of the liquid sorbent, which introduces a substantial energy penalty. The use of alternative sorbents for CO2 capture, such as the CaO–CaCO3 system, has been investigated extensively in recent years. However there are significant problems associated with the use of CaO based sorbents, the most challenging one being the deactivation of the sorbent material. When sorbents such as natural limestone are used, the capture capacity of the solid sorbent can fall by as much as 90 mol% after the first 20 carbonation–regeneration cycles. In this study a variety of techniques were employed to understand better the cause of this deterioration from both a structural and morphological standpoint. X-ray and neutron PDF studies were employed to understand better the local surface and interfacial structures formed upon reaction, finding that after carbonation the surface roughness is decreased for CaO. In situ synchrotron X-ray diffraction studies showed that carbonation with added steam leads to a faster and more complete conversion of CaO than under conditions without steam, as evidenced by the phases seen at different depths within the sample. Finally, in situ X-ray tomography experiments were employed to track the morphological changes in the sorbents during carbonation, observing directly the reduction in porosity and increase in tortuosity of the pore network over multiple calcination reactions.
Introduction
With the growing awareness of the effects of anthropogenic greenhouse gas emissions, especially CO2, comes the imperative to develop and implement new technologies that either reduce the production of CO2 or prevent its widespread release into the atmosphere. The latter is particularly important given the high likelihood that nations will continue to exploit their reserves of fossil fuels while is it economically feasible.1 Carbon capture and storage (CCS) has emerged as one of the most promising technologies to help achieve the ambitious emission targets set by these nations without needing massive reductions in CO2-emitting fuel use.2One of the most promising approaches to CCS is that of high-temperature absorption looping (processes which are variously referred to as calcium or carbonate looping), which involves the reversible reaction of a solid material (usually an alkaline earth oxide such as CaCO3) with gaseous CO2 to loop between the oxide and solid carbonate phase.3 The advantage of such processes is that they have very low theoretical energy penalties (∼6–8% with respect to reference power plants without CO2 capture), making them much more economically feasible for widespread use than the currently used amine scrubbing process.4
The crux of the development of these looping processes is finding a suitable material which is able to selectively react with CO2 in the flue gas with reasonable kinetics, and once carbonated is able to be regenerated (calcined) at higher temperatures to reform the original material. Crucially this cycled material should retain the properties of the original sorbent porosity, reactivity, capacity and kinetics, so that the material can be used in the process for thousands of cycles without degradation in its performance.
CaO is the standard material used in high-temperature carbonate looping, relying on the reversible reaction with CO2 to form CaCO3:
| CaO + CO2 → CaCO3, ΔHreaction = −179 kJ mol−1 | (1) |
Unfortunately the widespread use of CaO for CCS is problematic given its tendency to sinter upon cycling, leading to a loss of porosity and therefore carbonation capacity. Cycling studies of natural limestone show its capacity to reduce by as much as 90 mol% after only the first 20 cycles owing to sintering.5 While one focus of recent research has been to alter the properties of CaO through synthetic methods with different additives such as Al3O3, Ca12Al14O33, or SiO2,6–8 there is still a fundamental lack of understanding regarding how the carbonation reaction proceeds and what parameters control the function of absorbent materials.
Previously we have approached this lack of understanding in several different ways. Firstly, we developed a large scale screening methodology that combined theoretical and experimental techniques to screen and identify new candidate materials for high-temperature CCS efficiently.9 This screening identified 640 materials that could be potentially used in high-temperature CO2 looping, as well as elucidating several underlying trends that can be used to identify novel functional materials rationally, such as the generally improved performance of Mg-based materials over materials based on Ca, Li or Na.
Secondly we used a combination of diffraction and microscopy techniques to analyse a novel CCS material, Ba4Sb2O9, showing it to be the first perovskite type material that was able to be reversibly carbonated and regenerated.10 Furthermore, unlike CaO, Ba4Sb2O9 retained its capacity for over 100 carbonation cycles without any optimisation or addition of other phases. Tracking the microstructure of the material showed that this capacity retention was linked to the reformation of the material's original porosity upon regeneration, and that the existence of an inert chemical framework of Sb polyhedra most likely contributes to the retention of this porosity.
We have also investigated what role ionic transport plays in the carbonation process through the use of solid state nuclear magnetic resonance (NMR) spectroscopy. Experiments on Li2CO3 at temperatures up to 973 K showed coupling between the rate of Li ionic motion and that of carbonate ion rotation, and the presence of a faster regime with faster Li ionic motion that is only activated at high temperatures.11 This regime matches well with the second rapid regime of CO2 absorption seen in similar materials such as Li5AlO4 and Li2CuO2,12–14 and indicates that the rate of gas absorption may be linked to the rate of ionic transport in the bulk material.
Recent advances in diffraction and imaging techniques, especially those utilising intense X-ray or neutron sources, have allowed the development of in situ or in operando experiments where structural and morphological changes are able to be tracked in real time. Such approaches have been used to great success in their application to a diverse range of problems, including tracking microstructures and phase formation in lithium ion batteries, fuel cell cathode interfaces, and heterogeneous catalysts.15–17 In this work we have sought to apply these same techniques, including X-ray and neutron powder diffraction, pair distribution function (PDF) analysis, and X-ray tomography, to a number of outstanding questions regarding the carbonation of CaO in the hope of better understanding the fundamental behaviour of the material at an atomic level.
Our initial work involved the preparation of two different series of samples of CaO, one series originating from pure CaO nanoparticles (referred to hereafter as the CaO series), and the other from the calcination of limestone (the limestone series). Both sets of samples comprised samples that were carbonated for different lengths of time, with the aim of characterising changes in both the short and long range structure of the samples by utilising neutron scattering experiments that are sensitive to the different phase expected to be present. Additional analysis of small angle scattering (SAS) data allows determination of changes in surface roughness in the samples which may then be related to their performance.
Another element that we wished to investigate was the effect added steam has on the carbonation reaction, and how this influences the phases that are formed and the rate of reaction. To this end we performed a set of in situ synchrotron X-ray diffraction measurements on pelletised pure CaO under CO2 and under CO2 with added steam. These controlled experiments allowed the accurate determination of phase fractions both as a function of carbonation time and particle depth, an important insight into how CaO particles react as a whole.
Finally, we employed in situ X-ray tomography experiments as a way to directly image the morphology of CaO during both the carbonation and calcination reactions. Subsequent analysis of the data allows individual phases to be observed, giving information about their morphology and tortuosity. This data allows us for the first time to directly image CaO particles during reaction, with the hope of linking changes in phase composition and porosity throughout the particle with the known capacity loss seen in these materials.
Taken together, it is hoped that the combination of various scattering and imaging techniques can provide new insights into how CaO evolves during a CO2 looping process, and answer longstanding questions as to how changes on an atomic and particle scale lead to the observed capacity fading upon repeated cycling.
Methods and materials
Preparation of samples
For both the neutron and X-ray PDF experiments, the nominally CaO samples were prepared from (a) CaO nanopowders (98%, <160 nm, Sigma Aldrich), known as the CaO series, and (b) calcined Purbeck limestone, known as the limestone series. Scanning electron microscopy (SEM) images of the CaO nanopowder are shown in Fig. 1. The powder was pelletized to be able to react in a fluidized bed reactor (FBR), and was then carbonated in the FBR at 1023 K under 15% CO2 with and without the addition of ∼2% steam.18 The samples prepared were reacted for either 1, 2, 5, 10, 30, 60 or 120 minutes respectively. For the in situ X-ray diffraction experiments, the same CaO nanopowder was pelletized to ∼3 mm wide pellets using a specially made pellet press held under 0.1 GPa for 1 minute. For the tomography experiments Purbeck limestone was calcined at 1223 K to prepare samples that nominally contained CaO.Neutron total scattering experiment
Neutron total scattering experiments were performed on the NIMROD beamline at the ISIS neutron spallation source, Rutherford Appleton Laboratory, UK. The measurements on powder samples were performed at room temperature, using flat plate cans made of a TiZr alloy.The Near and InterMediate Range Order Diffractometer (NIMROD) is an instrument located in the second target station, optimised for the study of disordered materials, liquid and nanostructured materials.19 It bridges the gap between small angle and wide angle scattering, using a common calibration procedure for the whole length scale. For these reasons this instrument is particularly suitable for the study of nanoscale and mesoscale materials, as it allows analysis of the local atomic structure as well as the long range order and part of the small angle scattering (SAS), which provides information about the surfaces, shape and size of the particles.
Laboratory X-ray scattering and PDF
Room temperature X-ray total scattering data were collected using a PANalytical Ag-anode X-ray powder diffractometer (λ = 0.5609 Å).20 The samples were inserted inside polyimide capillaries (Cole–Parmer) of 1 mm diameter and the total scattering data were collected spanning scattering angles from 3° to 148° (Qmax = 21.9 Å−1), repeating the same run 5 times to improve the statistics on the collected data.Synchrotron X-ray diffraction
In situ X-ray diffraction were performed on the I15 beamline at the Diamond Light Source, Harwell Oxford, UK. A specially made gas flow capillary cell was constructed in order to be able to perform in situ measurements, which consisted of a 3 mm wide silica capillary mounted vertically in the beam, with gas delivered onto the sample from above, down through the capillary. The whole cell was mounted on a stage which allowed the cell to be moved between two positions: in the beam (during measurement), and in the hot zone of a hot air blower, out of the beam (during reaction). The pelletized sample was inserted in the middle of the capillary, with silica wool below the sample to prevent movement during the reaction. The pellet was made to fit exactly within the diameter of the capillary, with no gaps to either side.The measurements were performed at 76 keV, with a microfocused beam of size 70 μm. For each of the data collections, 5 dark images were measured for 1 minute each, followed by between 2 and 5 exposures of the sample for 1 minute each. The number of exposures was varied throughout the experiment to save time; the in situ measurements have 2 exposures per depth and reaction time. The pellet was moved in the beam in order to take measurements at different depths throughout the pellet. For these experiments, data were first collected at room-temperature and then the pellet was moved to the hot air blower operating at 973 K under the respective gas flow (CO2 with or without steam) and held to react for 1 minute. Steam was produced through flowing the CO2 gas through a water bubbler prior to the reaction cell. The sample was then moved out from the hot air blower and immediately into the beam, and data were collected at a number of depths (at room temperature). This process was then repeated, and data collected corresponding to a total carbonation reaction time of 2 minutes.
X-ray tomography
X-ray tomography (XRT) experiments were performed on the micro end-station of the TOMCAT beamline at the Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland.21 The radiographs were acquired with a magnification of ×20, pixel size of 0.33 μm, exposure time of 125 ms, rotation range of 0–180°, and at an energy of 20 keV. For each measurement, 1001 projections were collected. While this resolution means that only macro porosity can be measured, this is still a valuable source of information, especially given the reliance in the literature on nitrogen absorption surface area measurements which only measure micro and meso porosity.In situ variable temperature (VT) measurements were achieved through the use of a specially designed infrared furnace, comprising a 250 W infrared heater with elliptical reflector (Research Inc., MN, USA), with the sample enclosed in a water-cooled chamber.22 The heater provides a highly focussed heat spot of ∼5 mm, and a variable AC power source modulates the heater power and therefore the temperature of the sample. Additionally, the chamber has an inlet for gas flow, allowing a variable gas atmosphere to be exposed to the sample. In our experiments, the inlet was switched between continuous flows of pure N2 and CO2, moderated by flowmeters.
The samples were mounted on stainless steel pins, and placed within the furnace under an initial flow of N2. Tomographic measurements were taken at temperatures of 293 K, 473 K, 673 K, 823 K, 1023 K, and then 10 measurements at 1223 K with each measurement taking approximately 5 minutes. After the measurements at 1223 K, the sample was cooled to 923 K and the gas flow switched to CO2, with a further 10 measurements taken at this temperature. A further 10 measurements were then recorded at 1223 K under N2.
The experimental tomographs were reconstructed using the gridrec algorithm.23 Three dimensional datasets were constructed using the Avizo Fire software (Version 5, FEI Visualization Science Group, France), and subsequent visualisation and phase segmentation were carried out using the same software. The phases were segmented based on grayscale ranges, as the most dense phase is expected to attenuate the X-rays to the greatest extent and therefore will have the highest grayscale values. By visual inspection, the phases were binned according the following ranges: 0–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (pores), 10
000 (pores), 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (CaCO3) and 17
000 (CaCO3) and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–65
000–65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (CaO), with these ranges used for the entire analysis.
000 (CaO), with these ranges used for the entire analysis.
Results
Local structure of CaO during carbonation studied by neutron PDF
Room temperature neutron total scattering measurements were performed on two series of nominally CaO samples prepared from different precursors. The ‘CaO series’ was formed from CaO spherical nanoparticles (diameter < 160 nm) and the ‘limestone series’ from calcined limestone. Specifically, the CaO series consists of three samples of CaO nanoparticles which have undergone carbonation for different amounts of time: 0, 2 and 10 minutes (CaO 0 minutes, 2 minutes and 10 minutes). The limestone series of samples consists of a sample of the precursor limestone (limestone fresh), a sample that has only undergone calcination (limestone 0 minutes) and then a further two samples calcined and then carbonated for 2 and 5 minutes respectively (limestone 2 and 5 minutes). With these samples we can analyse how the structure of CaO evolves after different carbonation times, as well as the response to carbonation of samples that have already undergone calcination previously (limestone series), allowing observation of the effect of sintering on the structures formed upon carbonation.The experimental pair distribution functions (PDFs) D(r)24,25 were calculated by taking the sine Fourier transform of the neutron total scattering function i(Q):
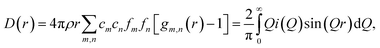 | (2) |
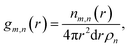 | (3) |
The background was subtracted, corrections for absorption and inelastic scattering and Fourier filters applied, and the Fourier transform finally taken using the software GudrunN.26 This calculation requires knowledge of the density, packing fraction and composition of the samples: the density was measured using a pycnometer, and the packing fraction was calculated from the ratio of the packing density to the true density. The composition of the samples was determined by X-ray fluorescence elemental analysis, but as the C content could not be determined by this method due to its low relative atomic mass, the composition used for the analysis was estimated partially by an iterative correction process.
The neutron total scattering experiment was followed by an X-ray total scattering experiment, performed on the same samples used for the neutron experiment (see the following section). X-ray and neutron measurements provide complementary information due to the differences in contrast between atomic scattering factors: neglecting the Q dependence of X-ray scattering factors, fC = 6 and fCa = 20, while the corresponding neutron scattering lengths are more comparable at bC = 6.6460 fm and bCa = 4.70 fm. Thus neutrons are more suitable for studying the C-containing components of these samples.
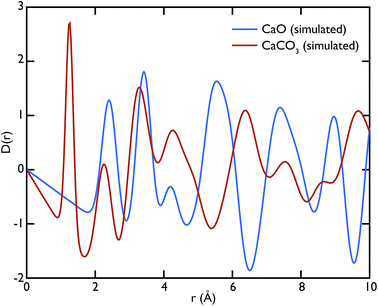
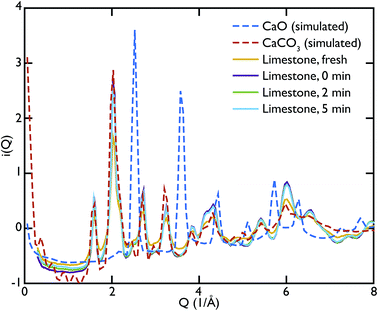
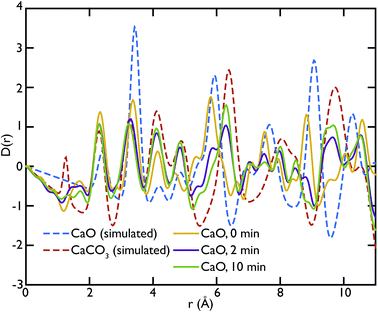
Theoretical neutron PDFs of bulk CaO and CaCO3 were calculated from structural models, simulated on the basis of previously reported potentials27 and phonon spectra, using the software GULP28 (Fig. 2). The experimental PDFs are broadened by experimental resolution and by the smoothing functions applied to remove truncation ripples; to improve the ability to reproduce these, the simulations were therefore performed at the artificially high temperature of 3000 K. Phonons were sampled on a 5 × 5 × 5 grid in reciprocal space for CaCO3 and a 10 × 10 × 10 grid in the case of CaO. The model PDFs provide a realistic and qualitative comparison for identifying the contribution that each of the two phases gives to the experimental PDFs calculated for our samples. While in most parts of the region shown the peaks are overlapping, there are a couple of isolated peaks; these are the C–O peak of the CaCO3, centred on 1.3 Å, and the Ca–O peak of the CaO at around 5.4 Å. These two peaks can be used to identify the increase or decrease of the two phases, since at the given positions only one of the two phases will contribute to the histogram of interatomic distances and hence to the total D(r).
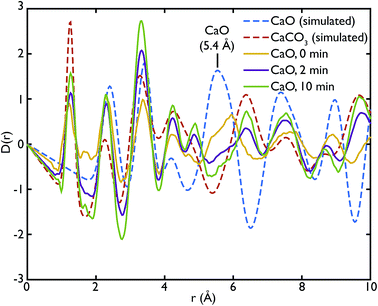
Fig. 3 shows the comparison between the PDFs of the CaO series and the calculated ones. We observe that the C–O peak at 1.3 Å increases in intensity with carbonation time, as expected as more CaCO3 forms. The presence of this peak in the fresh sample indicates that there is CaCO3 present in the sample even before carbonation, which may be due to slow carbonation in the atmosphere before the experiment. On the other hand, we can observe that the CaO content is reduced drastically even after only 2 minutes of carbonation, indicated by the loss of the Ca–O peak at 5.4 Å from the fresh sample (yellow line) to its complete absence after 10 minutes of carbonation (green line).
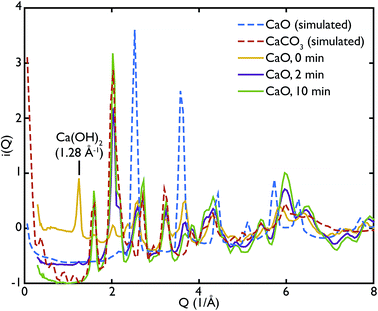
One of the advantages of performing a total scattering experiment is that the data can be analysed both in real space and reciprocal space. The total scattering functions, i(Q), were calculated from the PDF GULP models: the PDFs were first multiplied by a sine function (in order to reduce termination ripples) and then sine-Fourier transformed to calculate the total scattering functions (divided finally by Q to produce i(Q)). Fig. 4 shows the comparison between the data and the calculations for the CaO series. We can observe that the peak at ∼1.28 Å−1 in the non carbonated sample does not find any corresponding peak in the model i(Q) functions. This peak was identified as the (001) reflection of crystalline Ca(OH)2. Despite the fact that GULP calculations have not been performed for the Ca(OH)2, comparison with the crystalline model calculations is enough to confirm that non-carbonated sample contains this phase, while the other samples of the CaO series do not. Evidence of the presence of a Ca(OH)2 component is also given by the higher intensity of the total scattering function (compared to the other samples) and by the steep slope in the low-Q region of the total scattering, a signature of the recoil of the hydrogen atoms (Fig. 4). This would indicate that Ca(OH)2 may form initially prior to reaction on the CaO surface due to reaction with moisture in the atmosphere, but after carbonation does not form on the surface of the carbonated particles. Additionally, at low temperatures Ca(OH)2 would also carbonate to form additional CaCO3.
One can further observe that the CaCO3 component becomes predominant with increasing carbonation time (as highlighted by the reflections around at ∼1.6 Å−1 and ∼2.2 Å−1), while the CaO one is almost absent or minimal in the carbonated samples, confirming what was already observed in real space. This result is in agreement with the estimated phase fractions from the Rietveld refinements of the in situ XRD measurements on bulk samples (Fig. 10), presented in the next section.
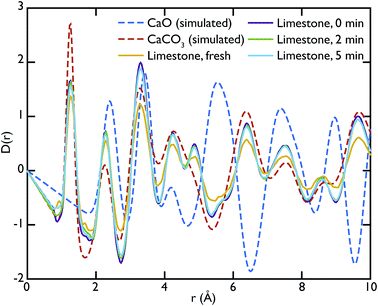
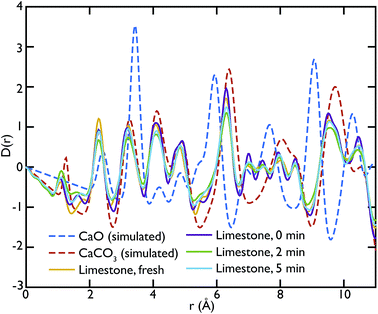
Fig. 5 shows the PDFs of the limestone series compared to the calculated PDFs. We can observe that the calcination process appears to be far from completion as the CaO content seems to be very low or even completely absent in the calcined sample that was not carbonated (limestone 0 min), as seen by the low intensity of the CaO reference peak at 5.4 Å. The effects of carbonation after 2 and 5 minutes are minimal, as the local structure as well as the intensity of the peaks is almost unaltered in the measured PDFs.
In the same fashion as CaO, the total scattering data of the limestone series were compared to the calculated PDFs. Fig. 6 shows this comparison and it is evident that in this case the calculated CaCO3 total scattering function matches the data quite well, confirming what was observed in the PDFs. Contrary to the CaO series there is no H content in the limestone series, since the starting compound in this case is mainly CaCO3.
This observation suggests that the CO2 absorption rate and capacity of the limestone series samples are very low compared to the CaO series of samples, where the starting material was CaO. This is probably a consequence of the initial incomplete calcination of the limestone samples leading to very little CaO being formed initially, and therefore there being little material to actually carbonate during the reaction.
Other more peculiar features appearing in the experimental PDFs will require further modelling to be interpreted and investigated. For example the peak at 4.9 Å, which is present in the carbonated samples of the two series, does not correspond to any feature of the calculated PDFs. This could possibly originate from different local structures at the phase boundary between CaO and CaCO3 that forms upon carbonation, or some other local atomic rearrangement.
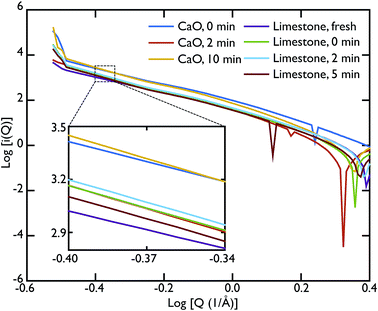
As mentioned previously, the ability of the instrument to measure scattering at Q values as low as 0.02 Å−1 allowed us to collect data also in the SAS region. In our case, we were able to access the Porod region. Fig. 7 shows the Porod plot, log[i(Q)] vs. log[Q]; the slope of the scattering functions yields information about the dimensions of the surface fractals of the scattering object. All the samples behave in a similar manner in this region with the slope of the curves is ∼−4. A value of ∼−4 is indicative of a 3D object with smooth surfaces, whereas a slope between −3 < n < −4 characterises rough interfaces of fractal dimension D with −n = 6 − D.
A linear fit to the SAS curves was performed in the region −0.48 < log[Q] < −0.25, corresponding to pores of sizes 11.2 Å < d < 17.7 Å. A closer look at the limestone series shows that the slope of the Porod plot of the initial sample is ∼−3.537 ± 0.001, while the calcined sample has a slope of −4.209 ± 0.004 (the carbonated samples have the same slope as the calcined sample within error), as shown in the inset of Fig. 7. This indicates that the initial sample has some surface roughness characterised by a surface fractal dimension of ∼2.6, which disappears after the calcination process. This relative lack of surface area further supports the idea that the samples were only partially calcined prior to carbonation, resulting in almost identical PDFs for the carbonated samples and the calcined, but non-carbonated sample (Fig. 5). The surface roughness (porosity) also decreases in the case of the CaO series, with the slope of the curves increasing with increasing carbonation time: −3.756 ± 0.003 for the non carbonated sample, increasing to −4.362 ± 0.008 and −4.346 ± 0.007 for the samples carbonated for 2 and 10 minutes respectively. Therefore the carbonation process causes a loss of porosity and surface roughness in both the limestone and CaO samples.
Local structure of CaO during carbonation studied by X-ray PDF
X-ray total scattering experiments were performed on the same samples analysed with neutrons, the CaO and limestone series. Theoretical X-ray PDFs for the CaO and CaCO3 phases were calculated from the partial radial distribution functions gm,n(r), generated from the GULP calculations performed at 1500 K for the same reasons explained in the neutron sections.Fig. 8 shows the X-ray experimental PDFs compared to the model PDFs. We can observe that while the CaO contributes to the PDFs of the non carbonated sample, as highlighted by the peak at ∼5.4 Å, the CaO component decreases gradually to almost disappear in the sample carbonated for 10 minutes. The peak starts shifting on the right and merging with the CaCO3 peak at ∼6.3 Å in the CaO 2 min sample; in the PDF of the CaO 10 min sample the 5.4 Å peak gives a minimal contribution, causing the overall peak shape to be slightly asymmetric. These observations are also confirmed by the CaO peak at ∼9 Å, which is present in the non-carbonated sample but not in the other two samples. This supports the neutron data and suggests that the carbonation process is almost completed in 2 minutes, with minimal changes after this time.
Fig. 9 shows the PDFs of the limestone series. In this series it is evident that the calcination and carbonation process did not particularly affect the composition of the samples, confirming what was previously observed by means of neutron diffraction. The local structure of the samples seems almost unaltered, as evidenced by the similarities of the PDFs. The characteristic peaks of CaO at 5.4 Å and 9 Å are absent or almost absent in the PDFs of the whole series, confirming that CaCO3 dominates the data. A sign of the presence of a small fraction of CaO could be observed in the two peaks between 7 and 8 Å, which have no corresponding components in the calculated CaCO3 data.
Influence of steam on carbonation observed by in situ XRD
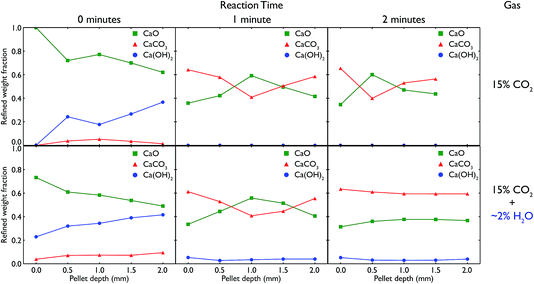
Recognising the difficulty posed by variations in sample preparation and composition as seen in the neutron diffraction experiments, as well as the apparent incomplete calcination of limestone leading to a lack of subsequent carbonation, it was desirable to try and explicitly control both the reaction conditions and sample composition, and if possible observe the samples during the reaction itself. Additionally, the presence of Ca(OH)2 in the previous samples encouraged further exploration of the specific role water had on the carbonation reaction. These aims led to the design of an in situ cell to be used with synchrotron X-ray radiation to try and more accurately characterise CaO at different stages of reaction, both in the presence and absence of water vapour (steam).Using the in situ setup on the I15 beamline, data were collected at room temperature at 0.5 mm intervals moving down a pelletised CaO sample, after different total amounts of elapsed time for the carbonation reaction. The Rietveld-refined relative phase fractions at the different depths, time steps and gas flow composition are shown in Fig. 10.
In both the carbonation experiments with and without steam, it is seen that as time elapses in the carbonation reaction, more and more CaO is converted to CaCO3 across the whole length of the pellet. However, there are significant differences between the different timesteps, gas compositions and depth of the pellet.
In regards to depth, after both 1 and 2 minutes of carbonation under both gas compositions, the ends of the pellet (at 0 and 2 mm respectively) react more quickly, leading to higher phase fractions of CaCO3. In fact, in all but the 2 minute measurement with steam, the majority of the centre of the pellet remains CaO, in a roughly inverse proportion to what is seen at the ends of the pellet. This shows the difference in the rate of surface reaction versus the slower mass transport of CO2 gas through the pellet, as the ends of the pellet have much more available surface area to react with the atmosphere. The ratio of surface to bulk is higher in both measurements at the ends which would also lead to an expected higher amount of CaCO3 observed.
However, there are also changes connected to the change in gas composition, from pure CO2 to CO2 with added steam. Under the influence of water vapour, we see the formation of a significant amount of Ca(OH)2, especially before the reaction begins (but the sample has been in contact with the reactive atmosphere for 20 minutes). In the pure CO2 experiment, the presence of Ca(OH)2 is due to remnant water present in the capillary after switching the gas composition from with to without steam, and this phase quickly disappears completely once the reaction begins and the gas stream is completely purged of any remnant water. In both cases, the gradual increase in Ca(OH)2 with depth may be due to the gas flow (which was down through the sample) pushing any water vapour present in the sample to lower depths. The temperature and partial pressure of steam were such that the formation of Ca(OH)2 was thermodynamically feasible, especially given the measurements were taken at room temperature after carbonating at 973 K. Further in situ experiments are planned to observe whether Ca(OH)2 is present at the actual carbonation temperature during reaction.
More important is the difference seen between the extent of the reaction after 2 minutes. In the pure CO2 case, the majority of the middle of the pellet is still CaO, whereas under CO2 with steam, the composition of the pellet is homogeneous along its entire length, with an equal amount of carbonation occurring. The fact that at the surface of the pellet (0 mm) there is little change in composition from 1 minute to 2 minutes indicates that ∼60% is approximately the full extent of the carbonation reaction (matching well with the ex situ samples that saw little change regardless of carbonation time), and that this extent of carbonation is achieved at all depths after 2 minutes with the addition of steam. This improved rate of reaction with the addition of steam appears to enable CO2 to penetrate further into the pellet, concurring with similar observations seen previously in the literature.29–31 However, it may also be an effect of changing porosity linked to the formation of Ca(OH)2 (especially additional porosity that is formed upon heating the hydroxide phase), especially considering the total extent of carbonation appears unchanged as compared to the pure CO2 experiments.
Morphological changes in CaO upon carbonation and calcination observed through X-ray tomography
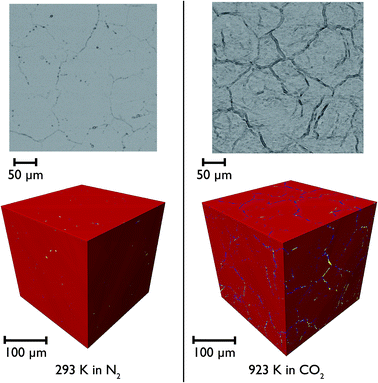
CaO particles of diameter ∼300 μm were mounted in the furnace and heated under N2 and then CO2 to simulate the carbonation reaction in situ. Representative individual tomographic slices and volume rendering of the reconstructed tomographic volume at various points in the experiment are shown in Fig. 11. The colouring in the images indicates the results of phase segregation of the images; materials with different X-ray attenuation will appear as having different grayscale contrast in the original images, and subsequent segregation of voxels into phases matching different grayscale ranges allows the different phases and their volumes to be distinguished from each other. In the first case it is significant that we are indeed able to distinguish the CaO and CaCO3 phases from each other, given their relatively small differences in X-ray attenuation, and this is the first time that such phase contrast has been imaged in such CCS systems in situ.It can be seen that there is little macro porosity present in the original sample, but upon heating the particles start to crack along grain boundaries, or between formerly agglomerated CaO particles. The CaO phase (artificially coloured in red) dominates throughout the reaction, showing that the reaction is far from completion (which is to be expected given the limitations of the in situ experimental setup). Additionally, CaCO3 is present in the sample under all temperatures and gas environments, even at 1223 K under N2, a temperature at which CaCO3 would be expected to decompose back to CaO. It may be there might be a higher PCO2 locally within the particles during calcination due to released CO2 being trapped within the particles, which may result in partial calcination and the persistence of CaCO3.
Closer observation of each of the two-dimensional reconstructed images (a representative image after carbonation is shown in Fig. 12) shows that CaCO3 fills all of the smaller macropores within the particle (<1–2 μm), but in the larger macropores the carbonate phase coats the surface, with some porosity remaining between these carbonate walls. This filling of smaller pores before larger pores are completely filled supports observations from many earlier studies that measured the changes in the pore size distribution upon carbonation.5,32 Their conclusions were that the carbonation reaction can be divided into two segments: the first, rapid segment consisting of the filling of smaller pores <100 nm, with the slower, diffusion limited segment beginning once these smaller pores were filled and layers of CaCO3 begin to be deposited on the surfaces of the larger pores. It appears that our results support these earlier measurements with direct evidence of more complete carbonation seen for smaller pores in CaO, with the smaller pores filling completely during the initial rapid segment of carbonation, before the onset of the slower diffusion controlled rate. The larger pores are not filled when this second stage begins, and therefore do not fill completely under the slower carbonation rate. Additionally we observe that the degree of carbonation appears uniform across the particle, meaning that there is no significant intra-particle concentration gradient, meaning the data obtained is particularly well suited to assist with reaction modelling.
 | ||
| Fig. 12 Reconstructed tomography slices of CaO after reacting under CO2 for 50 minutes. The colours show the phase segregation of the image into pores (yellow), CaCO3 (dark blue) and CaO (red). | ||
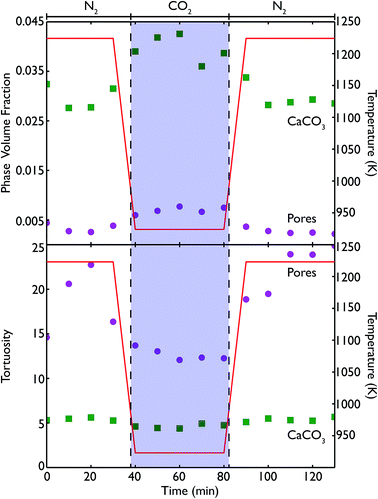
Phase volume fractions and centroid path tortuosities were obtained for the sample during the in situ carbonation reaction, using the Avizo Fire software, and the values for both the pores and CaCO3 phase are shown in Fig. 13. It should be noted that the absolute values of the phase fractions and tortuosities are not entirely accurate at very high temperatures, due to movement of the sample during data collection which leads to the introduction of severe image artifacts and blurring, thus making accurate quantification difficult. However, there are still a number of qualitative trends that can still be seen in the data.
The formation of more CaCO3 during reaction under flowing CO2 can be clearly seen, along with the subsequent reduction in phase fraction of CaCO3 upon calcination under N2 at 1223 K. This signifies that the furnace does enable the carbonation and calcination reactions to progress, and allows a true in situ observation of the overall process. The continuing presence of CaCO3 even after 40 minutes of calcination again indicates that the reaction does not go to completion, which may arise from the furnace design causing a distribution of temperatures in the sample. The pore volume is lower during both periods of calcination than during carbonation, and may be indicative of the sintering that occurs at higher temperatures or the lower molar volume of CaO, leading to a lower overall porosity in the sample. However, further cycling data is required to more fully quantify this phenomenon.
The tortuosity data (obtained by using the centroid path tortuosity module in Avizo Fire) indicates that the CaCO3 phase and pores evolve quite differently during the reaction. In the first instance, the tortuosity of the CaCO3 phase does not change much at all over the whole reaction, indicating that the degree of interconnection and permeation through the CaO is unaffected by cycles of carbonation and calcination. This would appear to indicate that during incomplete calcination, the microstructure of the carbonate phase remains intact, even if the overall amount of carbonate decreases. On the other hand, during calcination the tortuosity of the pores increases dramatically, indicating that sintering at higher temperatures is disrupting the pore network, making the network more tortuous and potentially reducing the available surface area for future carbonation (or generally making these pores less accessible to CO2). During carbonation the tortuosity of the pores fell to pre-calcination values, indicating that temperature may influence the tortuosity much more than the extent of carbonation. Finally, after a second cycle of recalcination the tortuosity is higher than the corresponding point after the first calcination cycle, indicating that successive periods at very high temperatures continually degrades the connectivity and ease of access through the pore network.
Because the resolution of the micro end-station is limited to measurement of macro porosity, there is an overestimation of the actual tortuosity and an underestimation of the CaCO3 phase fraction. However, the fact that we can make direct measurements of the tortuosity is significant improvement for classical reaction modelling, which typically approximated tortuosity by the inverse of porosity.33–35
There is also direct evidence for the loss of overall porosity in comparing the pore networks at 1223 K, both before the carbonation reaction, and after. Fig. 14 shows the segmented phase volume corresponding to the pores in the sample at these two stages, and clearly shows the reduction in porosity after the reaction.
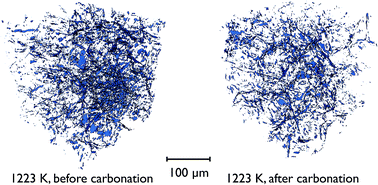 | ||
| Fig. 14 Volume renderings of the segmented tomographic volume corresponding to the pores in a portion of the CaO particle at 1223 K, both before and after the carbonation reaction. | ||
Discussion
In the first instance, the in situ XRD results indicate that with steam, CO2 can permeate much faster into CaO at ambient temperatures, leading to a shorter time needed to reach equilibrium with regards to carbonation. Furthermore, the depth analysis shows that the addition of steam also leads to a more uniform reaction, a model for which is shown in Fig. 15. In this model, at room temperature before reaction the composition of the pellet is mainly CaO, with a uniform dispersion of Ca(OH)2 throughout the pellet. Under reaction with CO2 without steam, with increasing reaction time there is a shrinking core of mostly pure CaO, with an increasing amount of CaCO3 forming from the surface inwards. However, limitations in the solid state transport of CO2 or access to porosity in the sample mean that pure CaO still persists in the centre. It should be noted that this model is for larger particles of diameter > 3 mm.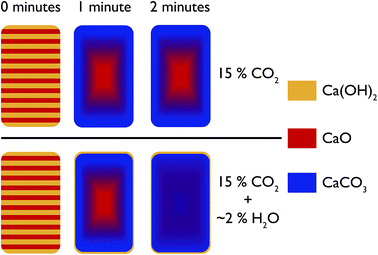 | ||
| Fig. 15 Schematic representation of the evolution of the phases present in the pelletised sample over time under pure CO2 and under CO2 with steam. | ||
With the addition of steam the CaO and CaCO3 are much better intermixed, with the steam aiding CO2 transport (via either maintaining porosity in the sample or aiding solid state transport) to the centre of the pellet. This model fits with an earlier hypothesis that steam changes the way CaCO3 nucleates on the surface, and enables the formation of significant mesoporosity.18
We hope to perform in operando XRD and X-PDF experiments in the future to further elucidate the role of steam in the carbonation process, and to see if Ca(OH)2 does indeed persist at higher temperatures during the carbonation reaction. Thermodynamics would suggest that Ca(OH)2 cannot form at the high temperatures at which the carbonation was performed, but we still observe the phase immediately after cooling the sample to measure it in the series with steam. Observing exactly the temperature range over which Ca(OH)2 is present in the reaction will hopefully aid in better understanding its role in the reaction. In addition, we will gain data on a greater number of samples to get a better idea of the variation amongst slightly different sample compositions and morphologies.
In any case, there is an open question as to how the formation of Ca(OH)2 influences the carbonation reaction, given that we have direct evidence of its persistence directly before the carbonation reaction, and how indeed this phase might react with CO2 and direct the morphological formation of carbonate on the surface. The role of porosity vs. solid state transport in improving the kinetics of the carbonation reaction also remains the subject of further experiments. Using a technique that is able to characterise ionic motion directly, such as NMR, could be employed to directly measure the rate of oxygen ionic motion in CaO, CaCO3 and Ca(OH)2, and therefore could help decide whether the formation of Ca(OH)2 assists the kinetics via improved ionic transport or improved porosity.
The neutron PDF data, especially the SAS, complements the results of the tomography in identifying the changes in porosity with increasing cycles of calcination. The reduction in surface roughness with calcination observed in SAS is mirrored by a similar increase in the tortuosity of the CaO seen in tomography, giving some indication of the link between the structure of the surface of the particles and their inherent porosity. The effect of temperature is also important, with the new porosity being observed to form in the in situ tomography during calcination could be due to thermal stress caused by the initial heating or volume contraction caused by phase change, as remnant CaCO3 is converted to CaO.36 The increase of tortuosity at high temperature and the fact that this increase can be reversed by lowering the temperature means that thermal expansion plays a very important role in the reaction, and its effect is to some degree reversible. This is an important discovery as previously it was generally believed that only phase and associated volume changes had an impact on the structure of the pore network.
Comparing the results obtained from the neutron and X-ray PDF data, they would seem to confirm that neutrons are more suitable to monitor the carbonation reaction given their apparent improved ability to better discern the various phases formed during the carbonation reaction of CaO. However, further experiments are planned to simultaneously measure thermogravimetric data with PDF measurements in order to quantify the extent of the carbonation to support the phases seen in the total scattering data. Due to the much longer acquisition times required for neutron scattering measurements, X-rays remain the only feasible way to achieve true in operando measurement of the reaction, and to be able to quantify the crystalline vs. amorphous content of the samples.
The tomography results show that larger pores, react to form CaCO3 at a similar time to smaller pores, questioning whether the rate at which pores of different sizes are carbonated is constant, or whether there is a preferentially fast reaction for smaller nanosized pores. In order to better elucidate this nanostructure we hope to prepare samples which can be measured on a nano endstation without the furnace, giving a much higher spatial resolution as well as removing entirely the difficulties of measuring in situ. These measurements would also allow more accurate values of tortuosity to be derived through measurement of meso and microporosity rather than just macroporosity as in the current work.
These preliminary results give us much hope as to the promise of such complementary scattering and imaging techniques to enable the investigation of the effect of additives on the performance of CaO, especially such as alumina and mayenite.7,35 In particular the phase contrast due to the additional Al atoms should be well suited to tomographic measurements that would enable direct observation of its location and evolution in the CaO particles during the carbonation process.
Conclusions
Through a combined X-ray scattering, neutron scattering and X-ray tomography study we have been able to directly observe the in situ structural and morphological evolution of CaO and limestone. Using these complementary techniques we have been able to observe several key insights, overcoming the inherent difficulties of such a multicomponent analysis. Firstly, the presence of steam during the carbonation reaction was directly seen to improve both the kinetics and overall homogeneity of the conversion to CaCO3, giving structural evidence to support many previous thermogravimetric studies that observed similar results.PDF measurements allowed the comparison of local structural changes to those on a bulk scale measured using X-ray diffraction, showing that carbonation reaches completion after 1 or 2 minutes of reaction. Neutron total scattering measurements are shown to be particularly useful to discern between the CaO CaCO3 phases, and to observe the presence or absence of Ca(OH)2 in the samples.
Finally, it was possible to image the evolution in the morphology and phase composition of CaO using in situ X-ray tomography. The different phases present were able to be tracked and in particular the reduction in volume of the pore network was able to be directly visualised, as well as quantified as an increase in the pore network's tortuosity.
This study shows the tremendous promise of using several complementary techniques to study carbonation and other reactions in real time, allowing the links between structural, chemical and morphological evolution to be better understood, as well as gaining a much more accurate picture of the impact that various changes in the reacting gas or composition have on the a material's overall performance.
Data
All supporting data for this work can be found on https://www.repository.cam.ac.uk.Acknowledgements
M. T. Dunstan acknowledges funding from the Cambridge Commonwealth Trusts and Trinity College, Cambridge. M. T. Dunstan, S. A. Scott, J. S. Dennis and C. P. Grey acknowledge funding from EPSRC Grant No. EP/K030132/1. W. Liu acknowledges funding from NRF, Singapore under its CREATE programme. The authors would like to thank the Science Facilities and Technologies Council, Diamond Light Source and Paul Scherrer Institut for the award of beamtime. The authors would especially like to thank Dr Julie Fife and Dr David Haberthür at TOMCAT, Dr Tristan Youngs and Dr Daniel Bowron at NIMROD, and Dr Philip Chater at I15 for their assistance in collecting and processing the data, and Simon Griggs for assistance with SEM. M. W. Gaultois is grateful for support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 659764.References
- Intergovernmental Panel on Climate Change, Climate Change 2013-The Physical Science Basis, Cambridge University Press, Cambridge, 2014 Search PubMed.
- S. Pacala, Science, 2004, 305, 968–972 CrossRef CAS PubMed.
- E. J. Anthony, Ind. Eng. Chem. Res., 2008, 47, 1747–1754 CrossRef CAS.
- M. E. Boot-Handford, et al. , Energy Environ. Sci., 2014, 7, 130 CAS.
- J. C. Abanades and D. Alvarez, Energy Fuels, 2003, 17, 308–315 CrossRef CAS.
- Z.-S. Li, N.-S. Cai and Y.-Y. Huang, Ind. Eng. Chem. Res., 2006, 45, 1911–1917 CrossRef CAS.
- J. S. Dennis and R. Pacciani, Chem. Eng. Sci., 2009, 64, 2147–2157 CrossRef CAS.
- A. M. Kierzkowska, R. Pacciani and C. R. Müller, ChemSusChem, 2013, 6, 1130–1148 CrossRef CAS PubMed.
- M. T. Dunstan, A. Jain, W. Liu, S. P. Ong, T. Liu, J. Lee, K. A. Persson, S. A. Scott, J. S. Dennis and C. P. Grey, Energy Environ. Sci., 2016, 9, 1346–1360 CAS.
- M. T. Dunstan, W. Liu, A. F. Pavan, J. A. Kimpton, C. D. Ling, S. A. Scott, J. S. Dennis and C. P. Grey, Chem. Mater., 2013, 25, 4881–4891 CrossRef CAS.
- M. T. Dunstan, J. M. Griffin, F. Blanc, M. Leskes and C. P. Grey, J. Phys. Chem. C, 2015, 119, 24255–24264 CAS.
- T. Avalos-Rendon, J. Casa-Madrid and H. Pfeiffer, J. Phys. Chem. A, 2009, 113, 6919–6923 CrossRef CAS PubMed.
- L. M. Palacios-Romero and H. Pfeiffer, Chem. Lett., 2008, 37, 862–863 CrossRef CAS.
- L. M. Palacios-Romero, E. Lima and H. Pfeiffer, J. Phys. Chem. A, 2009, 113, 193–198 CrossRef CAS PubMed.
- D. S. Eastwood, P. M. Bayley, H. J. Chang, O. O. Taiwo, J. Vila-Comamala, D. J. L. Brett, C. Rau, P. J. Withers, P. R. Shearing, C. P. Grey and P. D. Lee, Chem. Commun., 2015, 51, 266–268 RSC.
- P. Shearing, J. Gelb, J. Yi, W.-K. Lee, M. Drakopolous and N. Brandon, Electrochem. Commun., 2010, 12, 1021–1024 CrossRef CAS.
- K. T. Møller, B. R. S. Hansen, A.-C. Dippel, J.-E. Jørgensen and T. R. Jensen, Z. Anorg. Allg. Chem., 2014, 640, 3029–3043 CrossRef.
- B. González, W. Liu, D. Sultan and J. Dennis, Chem. Eng. J., 2016, 285, 378–383 CrossRef.
- D. T. Bowron, A. K. Soper, K. Jones, S. Ansell, S. Birch, J. Norris, L. Perrott, D. Riedel, N. J. Rhodes, S. R. Wakefield, A. Botti, M.-A. Ricci, F. Grazzi and M. Zoppi, Rev. Sci. Instrum., 2010, 81, 033905 CrossRef CAS PubMed.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714–726 CrossRef CAS.
- M. Stampanoni, A. Groso, A. Isenegger, G. Mikuljan, Q. Chen, A. Bertrand, S. Henein, R. Betemps, U. Frommherz, P. Böhler, D. Meister, M. Lange and R. Abela, Proc. SPIE, 2006, 6318, 63180M–14 CrossRef.
- P. R. Shearing, R. S. Bradley, J. Gelb, S. N. Lee, A. Atkinson, P. J. Withers and N. P. Brandon, Electrochem. Solid-State Lett., 2011, 14, B117–B120 CrossRef CAS.
- F. Marone and M. Stampanoni, J. Synchrotron Radiat., 2012, 19, 1029–1037 CrossRef CAS PubMed.
- M. T. Dove, Structure and Dynamics — An Atomic View of Materials, Oxford University Press, 2003 Search PubMed.
- D. A. Keen, J. Appl. Crystallogr., 2001, 34, 172–177 CrossRef CAS.
- A. K. Soper, GudrunN and GudrunX: programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, Science & Technology Facilities Council, 2011 Search PubMed.
- D. T. Archer, A. S. E. Birse, T. M. Dove, T. S. A. Redfern, D. J. Gale and T. R. Cygan, Phys. Chem. Miner., 2003, 30, 416–424 CrossRef.
- E. R. Cope and M. T. Dove, J. Appl. Crystallogr., 2007, 40, 589–594 CrossRef CAS.
- V. Nikulshina, M. Gálvez and A. Steinfeld, Chem. Eng. J., 2007, 129, 75–83 CrossRef CAS.
- V. Manovic and E. J. Anthony, Ind. Eng. Chem. Res., 2010, 49, 9105–9110 CrossRef CAS.
- I. Lindén, P. Backman, A. Brink and M. Hupa, Ind. Eng. Chem. Res., 2011, 50, 14115–14120 CrossRef.
- S. Bhatia and D. Perlmutter, AIChE J., 1983, 29, 79–86 CrossRef CAS.
- M. Matyka, A. Khalili and Z. Koza, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 026306 CrossRef PubMed.
- J. Y. Lim and J. S. Dennis, Ind. Eng. Chem. Res., 2012, 51, 15901–15911 CrossRef CAS.
- W. Liu, J. S. Dennis, D. S. Sultan, S. A. Redfern and S. A. Scott, Chem. Eng. Sci., 2012, 69, 644–658 CrossRef CAS.
- W. Liu, B. González, M. T. Dunstan, D. S. Sultan, A. Pavan, C. D. Ling, C. P. Grey and J. Dennis, Chem. Eng. Sci., 2016, 139, 15–26 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |