Microfluidic assessment of mechanical cell damage by extensional stress

Abstract

Mammalian cells have been widely used in bioreactors to produce biological products such as pharmaceutical materials. The productivity of such bioreactors is vastly affected by flow-induced cell damage in complicated flow environments, such as agitation-driven turbulence and oxygen bubble bursting at the interface between the culturing medium and air. However, there is no systematic approach to diagnose the cell damage caused by the hydrodynamic stress. In this work, we propose a novel microfluidic method to accurately assess the mechanical cell damage under a controlled extensional stress field, generated in a microfluidic cross-slot geometry. The cell damage in the extensional field is related to the oxygen bubble bursting process. We employed viscoelasticity-induced particle focusing to align the cells along the shear-free channel centerline, so that all the cells experience a similar extensional stress field, which also precludes the cell damage due to wall shear stress. We applied our novel microfluidic sensor to find the critical extensional stress to damage Chinese hamster ovary (CHO) cells; the critical stress is found to be ∼250 Pa. Our current results are relevant in the design of practical bioreactors, as our results clearly demonstrate that the control of the bubble bursting process is critical in minimizing cell damage in bioreactor applications. Further, our results will provide useful information on the biophysical cell properties under fluid flow environments.

---

Introduction

Mammalian cells get mechanically damaged under strong flow conditions such as turbulent flows.^1,2 The reduction of cell damage is essential in a wide range of bioreactor applications which produce biological products, such as viral vaccines, hormones, growth factors, enzymes, recombinant proteins, and monoclonal antibodies.^3,4 Conventional agitation-based bioreactors use a rotating impeller to homogenize the culturing medium, and spargers to provide oxygen to the cells⁵ [also refer to Fig. 1(a)]. The cells are exposed to hydrodynamic stresses by agitation or bubble bursting dynamics, which can cause damage to the mammalian cells.² Particularly, the oxygen bubbles, emanating from spargers at the bottom of the reactors, rise upwards, and eventually burst at the interface between the culturing medium and air, and generate very high stress fields.^2,6 During the rupture process, rapidly receding liquid films impact at the bottom of the cavity, forming upward and downward jets,^4,6 which generates strong extensional flows, as shown in Fig. 1(a).^7,8 The film rupture and accompanying extensional flow near the bottom of the cavity can cause significant damage to the cells.⁶ However, it is not yet well understood as to how the extensional field affects the cell damage in a quantitative manner. Efficient microfluidic methods to accurately assess the cell damage by the extensional stress involved in bubble bursting are essentially required for the optimal design and operation of such bioreactors.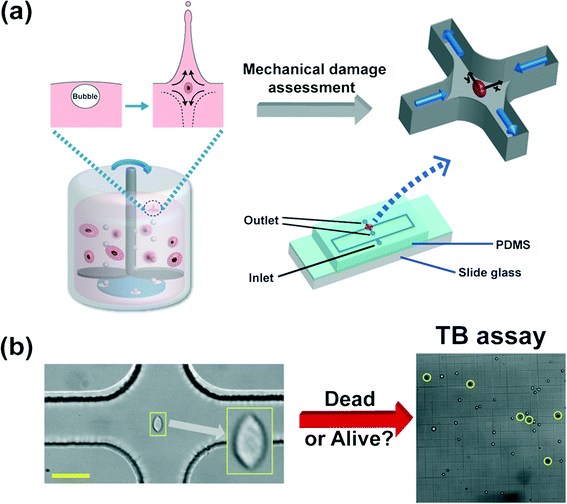

Fig. 1 (a) Schematic diagram of the microfluidic device to assess the mechanical damage of the Chinese hamster ovary (CHO) cells by the extensional stress field, which mimics the flow-induced cell damage during bubble bursting in stirred-based bioreactors. The bursting process of bubbles, emanating from the bottom spargers, is followed by both upward and downward jets at the liquid–air interface, which generates a strong extensional stress field as shown in the inset.⁶ The microfluidic device, which detects the critical extensional stress field to damage cells, has one inlet and two outlets. The cells are stretched along the y-direction (from the stagnation point to the outlet). The extensional stress field is generated in the red-circled region (cross-slot region) in the schematics of the microfluidic device. The cell-laden viscoelastic fluid is pumped through the inlet, and the cell suspension that experienced the extensional stress field is collected at the two outlets. The channel height is constant at 51.5 μm and the channel width in the straight region is 50 μm. The size of the rectangular area in the device schematics is 50 mm × 9 mm. The detailed information on the design of the current channel was presented in our previous work.⁹ (b) Sample image of a stretched CHO cell at the stagnant point where the extensional stress field is developed, when the flow rate is 1500 μL h⁻¹. The viability of the collected cells is analyzed by the trypan blue (TB) assay. A sample image of the TB assay is presented in Fig. 1(b). A dead cell appears as a dark cell outlined with a black circle in bright field microscopy (denoted as yellow circles) whereas a live cell appears as a bright cell. The scale bar denotes 50 μm.

In the current work, we employed the cross-slot geometry that generates controlled extensional flow fields, which mimic the extensional flow produced during the bubble bursting process consisting of film receding, film impact and upward/downward jet formation, and the cells are deformed close to the stagnation point (the center of the cross-slot channel)^9,10 [refer to Fig. 1(a) and (b)]. We investigated the viability of the collected cells, which were exposed to the extensional flow field, with a trypan blue assay [refer to Fig. 2(b)]. The highly deformed cells under the extensional flow field of the cross-slot channel are prone to mechanical damage, which mimics the cell damage by the strong extensional field of bubble bursting. The flow fields inside a bioreactor are very complicated, and include both shear and extensional flow components.⁸ The extensional flow field affects the cell more than the shear flow field, since the affine deformation under the extensional flow field increases exponentially, which is in contrast to the linear increase in the case of shear flow.¹¹ Further, the shear flow field includes a rotational component, and thus the steady state deformation under the shear flow field is significantly lower than that under the extensional flow field.¹²

Fig. 2 Rheological properties of the viscoelastic medium [PVP 6.8 wt% solution in the RPMI 1640 medium (HyClone, Logan, UT) including 0.5 wt% F-68 surfactant], which were measured at 20 °C with a rotational rheometer [cone and plate (60 mm); AR-G2, TA-instruments]. Each datum point was obtained by averaging three data points. (a) Steady shear viscosity of the viscoelastic solution. (b) Storage (G') and loss (G") moduli, and theoretical predictions using the Maxwell model.

On the other hand, in the current work, viscoelastic particle focusing was employed, so that most of the cells are aligned along the centerline, pass the stagnation point and consequently experience equal extensional stress. The cells in a Newtonian flow are randomly distributed under the channel flows, and thus only very small portions of the cells approach the stagnation point. In addition, the flow field inside the cross-slot channel is not homogeneous, and thus the cells experience different kinematic histories according to their trajectories.⁹ Therefore, aligning the cells along the channel centerline is a prerequisite to guarantee that most cells emanating from an inlet approach the stagnation point, and that the kinematic histories experienced by the cells are homogenized.^9,10 Recently, it was demonstrated that a rigid particle or a cell could be aligned along the channel centerline by viscoelasticity-induced migration in a non-Newtonian polymer solution, and that focusing is accomplished in a self-modulated manner, without any external forces such as an electric field.^13–17 The viscoelasticity-based particle focusing method was also employed so that a particle/cell is transported toward the stagnation point of a cross-slot channel to measure cell deformability.⁹

We have demonstrated in our study that the cross-slot microdevice, combined with the viscoelasticity-induced three-dimensional particle focusing,^9,13–17 can be harnessed as an efficient microfluidic method to accurately characterize mechanical cell damage by an extensional stress field. A three-dimensional numerical simulation was performed to investigate the stress field inside the microdevice in order to determine the critical stress to damage the cells. Finally, the origin of the cell damage occurring in practical bioreactor applications is discussed based on the current results.

Experimental

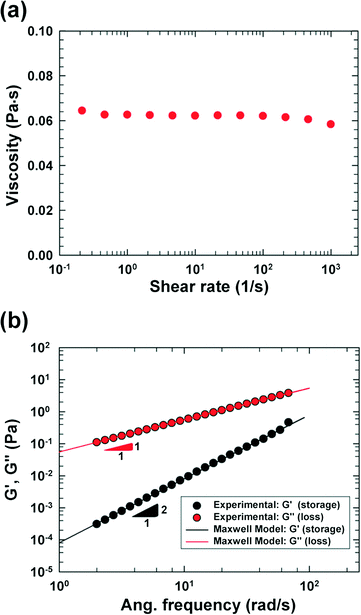
We fabricated a four-walled polydimethylsiloxane (PDMS) microfluidic channel with conventional soft lithography techniques¹⁸ following the procedures mentioned in our previous work;¹⁷ however, a PDMS-coated slide glass was used instead of a PDMS slab in this work. The specific design of the cross-slot channel was presented in our previous work focusing on cell deformability measurement.⁹ Briefly, the microchannel is of rectangular shaped area, and has one inlet and two outlets [refer to the schematic diagram in Fig. 1(a)]. The size of the rectangular area is 50 mm × 9 mm (width × height). The channel width (W) and height (H) are 50 μm and 51.5 μm, respectively, in the straight regions, and the side walls in the cross-slot region change as per a hyperbolic function (e.g., the side wall in the first quadrant is represented by y = 1875/x μm (x ∈ [W/2, 3W/2])).⁹

6.8 wt% polyvinylpyrrolidone (PVP) (Sigma-Aldrich, MW = 360 000 g mol⁻¹, molecular biology grade) solution in an RPMI 1640 medium (HyClone, Logan, UT) was used as a viscoelastic medium, and 0.5 wt% Pluronic F-68 surfactant (Sigma-Aldrich) was added to minimize cell aggregation. The PVP solution has been recently used in cell focusing and sorting experiments.^9,16,19 The rheological properties of the PVP/RPMI solution were measured at 20 °C with a rotational rheometer [cone and plate geometry (60 mm); AR-G2, TA Instruments], and the shear viscosity and small amplitude oscillatory shear (SAOS) test²⁰ results are presented in Fig. 2. The shear viscosity is nearly constant at 62 cP up to a shear rate of ∼1000 (1 s⁻¹), and the relaxation time is measured as 1.45 ms using the Maxwell model.²⁰

The Chinese hamster ovarian K1 cell lines (CHO-K1, KCLB 10061) were provided by the Korea Cell Line Bank (Seoul, Korea), and were cultured in the RPMI 1640 medium (HyClone, Logan, UT) containing fetal bovine serum (FBS, HyClone, Logan, UT) at a final concentration of 10% (vol/vol) and an antibiotic/antimycotic (100 Units per mL Penicillin G, 100 μg mL⁻¹ Streptomycin, and 0.25 μg mL⁻¹ Amphotericin B; HyClone, Logan, UT), and were incubated at 37 °C in a 5% humidified CO₂ atmosphere. For deformation measurements and viability tests, the CHO-K1 cells were detached with 0.25% trypsin and 0.1% EDTA (HyClone, Logan, UT) and the cells were washed twice with PBS, and re-suspended in the RPMI 1640 medium. The average concentration of the cells in the viscoelastic medium was estimated as ∼4 × 10⁵ cells mL⁻¹, and the average diameter was ∼13.4 μm; these were measured with a Coulter counter (Z2, Beckman).

The cell-laden viscoelastic fluid was pumped through an inlet with a syringe pump (Harvard apparatus), and the cell suspension (total volume of 250 μL), which was exposed to the extensional stress in the cross-slot, was collected in microtubes at the two outlets [Fig. 1(a)]. The cells were observed with an inverted microscope (IX71, Olympus). For the cell deformation measurement, the images were acquired with a high speed camera (MC2, Photron). The shutter speed was 1/5000 s, and the acquisition frame rate was 3000 fps for a flow rate ≤ 1000 μL h⁻¹, and 4000 fps for a flow rate >1000 μL h⁻¹. Image J software (NIH) was used to analyze the cell deformation.

The collected CHO-K1 cells, which passed the cross-slot channel, were re-suspended in a phosphate buffered solution (PBS) for cell viability analysis after centrifugation (3000 rpm for 5 min). We performed trypan blue (TB) assay²¹ to check the cell viability. The cell solution was prepared by 1 : 1 dilution of 0.4% trypan blue solution (Sigma-Aldrich), filtered with a membrane filter. The TB-stained cells were placed into a hemocytometer (Marienfeld-Superior) after an incubation period of 5 min and the images were viewed under a microscope (IX71, Olympus) with a CCD (charge-coupled device) camera (MC2, Photron); the dead/alive cells (total number ∼300 cells) were visually inspected and enumerated. A dead cell appears as a dark feature outlined with a circle in the bright field image, whereas a live cell appears as a bright feature with a circle [a representative example is presented in Fig. 1(b)]. Control experiments (cell viability test) were performed with the CHO-K1 cells, suspended in a viscoelastic medium, which were not exposed to the extensional stress field. The cells for the control experiments were stored in sterilized polyethylene conical tubes at room temperature, while the extensional stress-driven cell damaging experiments were performed. Then, viability tests were performed for both samples from the control and extensional stress-damaging experiments.

A three-dimensional numerical simulation based on a finite element method was performed with COMSOL Multiphysics^® to analyze the flow kinematics inside the cross-slot channel. We performed the numerical simulation assuming that the fluid flow is Newtonian, since there was no significant difference in the flow kinematics between Newtonian and viscoelastic fluid flows in our previous two-dimensional numerical simulations within the flow conditions considered.^9,22 The input data (channel dimensions and shear viscosity) for the numerical simulation were matched with the experimental conditions (refer to the ESI† Text 1 for the detailed information on the fluid properties, boundary conditions and finite element meshes). Numerical simulation based on accurate three-dimensional viscoelastic constitutive modelling could improve the accuracy in the prediction of fluid flows.

Results and discussion

In this work, we considered the CHO-K1 cell line as a model mammalian cell system to assess the mechanical cell damage by hydrodynamic stress, since the CHO cells have been widely utilized in various bioreactor applications.²³ The operation of the current microdevice to assess the mechanical cell damage under the extensional stress field is straightforward; it is performed by simply flowing the cell-suspended solution through the cross-slot microchannel [Fig. 1(a)]. The suspending medium is viscoelastic, which can be confirmed with a small amplitude oscillatory shear (SAOS) test [Fig. 2(b)]. The storage modulus (G') is non-zero for viscoelastic fluids such as the one used in the current work; it appears negligible for the Newtonian medium.²⁰ On the other hand, the slope in the graph of log(G') versus log(frequency) is 2, which follows the terminal zone of the Maxwell model.²⁰ The relaxation time is a representative material property to characterize the viscoelastic fluid; it can be obtained by fitting the Maxwell model with the experimental data [relaxation time (λ) = 1.45 ms in this work]. The viscoelasticity of a polymeric solution under flow is characterized by the Weissenberg number (Wi ≡ λ[small gamma, Greek, dot above]_c), where [small gamma, Greek, dot above]_c is the characteristic shear rate, and is defined by 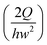,²⁴ where Q is the flow rate. The elastic property of the polymeric solution becomes more pronounced as Wi increases.

In viscoelastic fluid flows, the particles migrate laterally to the regions of low first or second normal stress difference (N₁ or N₂) under the viscoelastic medium,²⁵ and the second normal stress difference (N₂) is usually negligible;²⁰ here, N₁ is the difference between the normal stress in the streamwise direction and that in the velocity gradient direction and N₂ is the difference between the normal stress in the velocity gradient direction and that in the vorticity direction. The elastic force (F_e) exerted on a spherical particle is semi-empirically represented by the relationship F_e ∼ μλa³∇[small gamma, Greek, dot above]²,^{13,15–17,26} where μ is the shear viscosity and a is the particle radius. The relationship F_e ∼ μλa³∇[small gamma, Greek, dot above]², which indicates that the elastic force is directed to lower N₁ regions as N₁ roughly scales with [small gamma, Greek, dot above]², predicts that a particle migrates towards the channel centerline or the four corners under the rectangular channel flow, since these regions have the minimum strain rate in the cross-section of a rectangular channel.¹⁷ These multiple equilibrium positions can be altered by the inertial lift force under inertial flow or deformability-induced lift force for non-rigid cells.^16,17 The relative ratio between the elastic and inertial forces can be characterized by the elasticity number (El [triple bond, length half m-dash] 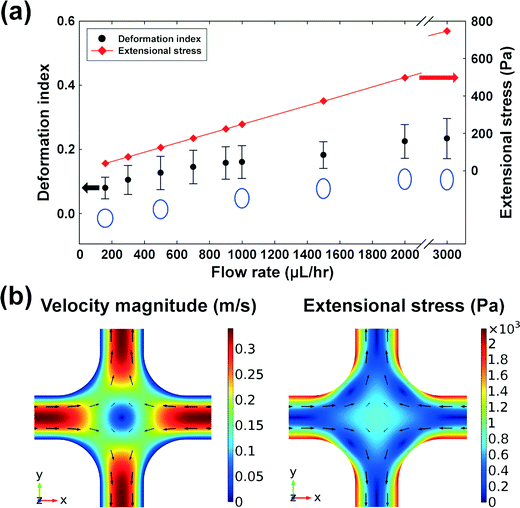Wi/Re), where Re is the Reynolds number defined by 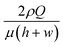²⁴ and ρ is the fluid density. In this work, the elasticity number is ∼70, and hence, the elastic force is dominant over the inertial force, and the order of magnitude of the maximum Reynolds number is ∼O(10⁻¹). However, an additional deformability-induced lift force pushes the cells away from the solid walls when the cells are deformable,^27,28 and the deformable cells form a single file along the channel centerline, while the rigid particles form multiple equilibrium positions at the channel centerline and the four corners.¹⁶ Hence, the multiplicity of the equilibrium positions depends upon the deformability of the CHO-K1 cells.

We investigated the trajectories of cells around the stagnation point (the center of the cross-slot in Fig. 3) to check whether the cells experience similar kinematic history. Most CHO cells pass through the dotted circle [in Fig. 3(a)], which corresponds to the area with a strain rate of at least 95% of the maximal strain rate at the stagnation point (the circle diameter is 25 μm).⁹ The probability with which the CHO cells touch the circle is ∼90% [Fig. 3(b)], which shows that the cells move along almost identical trajectories. Consequently, most cells experience similar extensional stress field (or kinematic history). In fact, the homogenization of the kinematic histories was a key step in the measurement of cell deformability^9,10 and it is also essentially required to accurately assess the effect of the extensional stress on the cell damage in the current work. On the other hand, we mention that the deformation-induced migration is relevant for the current CHO cell case^16,27,28 since most cells move along the channel centerline. In contrast, a significant number of rigid spherical particles or hardened cells move along the channel centerline and corners under the elasticity dominant flow in the previous work.¹⁶ The equilibrium positions of the cells are reduced to a single file along the channel centerline when the elasticity-driven and deformation-induced migration effects are synergistically combined.¹⁶ As a result, the deformation-induced cell migration contributes to the homogenization of cell kinematic histories.⁹

Fig. 3 (a) Trajectories of the CHO cells in the cross-slot region. The images were obtained by the Z-projection of 5000 frames with the standard deviation option in Image J software (NIH). (b) Focusing ratios of the CHO cells in the cross-slot channel according to the flow rates, where the focusing ratio is defined by the relative ratio of the cells, which touched the circled region shown in Fig. 3(a), to the total cells passing the cross-slot region [sample size (n) > 500]. The experiments were performed twice. The scale bar denotes 50 μm.

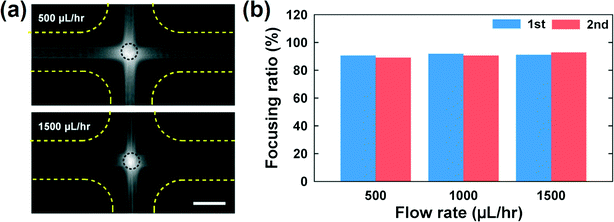
The CHO cells get significantly deformed as the flow rate increases, as shown in Fig. 4(a) (also see Movie S1†). In the figure, the deformation index (DI) is defined by (length of major axis – length of minor axis)/(length of major axis + length of minor axis), where the lengths of the major and minor axes are those of the ellipsoid matched with the outline of a deformed cell.⁹ Ellipsoidal shapes corresponding to the average DI value at each flow rate are presented in Fig. 4(a). The DI value gradually increases with increasing flow rate, but it gets saturated when the flow rate is more than 2000 μL h⁻¹. We also computed the extensional stress, which is obtained at the stagnation point with the velocity field based on the three-dimensional numerical simulation [Fig. 4(a) and (b)]. The extensional stress field increases monotonically as the flow rate increases [Fig. 4(a)]. In this work, the extensional stress is calculated considering the planar stress state due to the symmetry in the z-direction and the discrepancy in the extensional stress evaluation between using planar stress components and full stress ones is less than 0.3%. In Fig. 4(b), the magnitudes of the velocity and extensional stress (flow rate = 3000 μL h⁻¹) are presented. The velocity of the cells reduces as the cells approach the stagnation point from the left or right channel, and thus the cells are compressed at this stage. Then, the cells are stretched as they depart from the stagnation point. The stress field is high at the stagnation point or side walls. The latter is developed because of the high shear rate at the solid walls, which is relevant in pressure-driven flows. However, it is expected that the wall shear stress does not significantly affect the cell damage, since the cells migrate towards the centerline (or the shear free region) in the current microdevice.

Fig. 4 (a) Averaged deformation indices [DI ≡ (major axis – minor axis)/(major axis + minor axis)] of the CHO-K1 cells according to flow rates (flow rates = 160, 300, 500, 700, 900, 1000, 1500, 2000 and 3000 μL h⁻¹). The outline of the deformed cell in the cross-slot channel was matched with an ellipsoid, when a cell touches the circled area in Fig. 4(a). The DI values were obtained from the lengths of major and minor axes of the ellipsoid. The error bars denote standard deviations [sample size (n) = 50]. Additionally, the extensional stress at the stagnation point (predicted using numerical simulations) and the ellipsoidal shape corresponding to the averaged DI value are also shown. (b) Velocity magnitude (left) and extension stress (right) at the flow rate = 3000 μL h⁻¹ in the cross-slot region, which were computed using three-dimensional finite element numerical simulation.

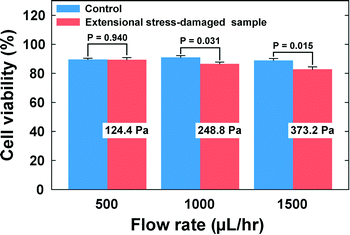
Finally, we investigated the viabilities of the cells which were exposed to the extensional stress field. The cells were collected at the outlets, and their viability was checked with a TB assay. The viability of the cells that experienced the extensional stress field at the stagnation point was directly compared with that of the control cell that was not exposed to the extensional stress field. As shown in Fig. 5 (also see Table S1†), the cell viability deteriorated significantly when the flow rate was more than 500 μL h⁻¹. Therefore, the current results indicate that cell damage occurs when the extensional stress is ∼250 Pa. On the other hand, additional tests were performed to exclude the possibilities that the cells can be damaged during any transportation steps from a syringe to the stagnation point. We directly punched a hole for the outlet at the location of the cross-slot, so that the cells bypass the extensional stress field. At a flow rate of 1500 μL h⁻¹, corresponding to the maximum flow rate (Fig. 5), there was no significant difference in the cell viabilities between this experiment (viability = 95.7%) and the control test (viability = 96.2%). We also tested flowing the cells through a straight channel of 50 μm × 50 μm dimensions (width × height) with 5 cm length (flow rate = 750 μL h⁻¹), which was designed to examine whether the cells can be damaged only with shear stress in the flow conditions similar to those in the case of the cross-slot channel [the flow rate (750 μL h⁻¹) corresponds to half of the maximum flow rate in the cell damage test using the cross-slot channel since the flow from an inlet is divided into two branch channels (Fig. 1(a))]. There was also no significant difference in the cell viabilities between the control (96.6%) and the straight channel (96.8%) experiments. Therefore, we can conclude that the cell damage originates from solely the extensional stress field excluding the wall shear stress effects. In fact, the viscoelasticity-induced particle migration minimizes the cell damage by shear stress, since this migration effect makes the cells align with the shear-free channel centerline, which protects the cells from damage by the wall shear stress. Additionally, we verified the critical extensional stress with a fluorescence-based LIVE/DEAD^® cell viability assay (Thermo Fisher, Cat. #: L3224). The viabilities of the extensional stress-damaged cells, measured with the LIVE/DEAD^® assay, deteriorated as compared to control samples when the flow rate was more than 500 μL h⁻¹, which is consistent with the results obtained with the TB assay.

Fig. 5 Trypan blue (TB) assay was performed to identify the effect of the extensional stress on cell viability. The cells collected at the outlets were stained with trypan blue following the standard staining protocol. The cell viability significantly decreases when the flow rate is greater than or equal to 1000 μL h⁻¹ (∼250 Pa). Student's t-tests were performed to check the statistical difference from the control in the cell viability and p < 0.05 is considered to be statistically significant. The error bars represent the standard errors (n = 6).

For agitation-based bioreactors, several researchers have reported on hydrodynamic forces in terms of turbulence intensity. Zhou and Kresta²⁹ measured the maximum local turbulent energy dissipation as ∼90 W kg⁻¹ (or the converted turbulent stress of 10.5 Pa acting on the cells of 12 μm in diameter) in the inertial subrange (derived from the Kolmogorov scale η = (v³/ε)^1/4 = 10.3 μm < cell diameter; τ ~ ρε^2/3D^2/3 ~ 10.5 Pa with ε, v, and D being the local energy dissipation rate, kinematic viscosity, and cell diameter, respectively) with laser Doppler velocimetry, while Wernersson and Trägårdh³⁰ used the constant temperature anemometry technique to measure the maximum local turbulent energy dissipation rate of 94 W kg⁻¹ (converted turbulent stress ~10.8 Pa) for four Rushton turbines rotating at 120 rpm in a 22 000 liter vessel. On the other hand, it was predicted using numerical simulation, that a bubble with a diameter of 1.7 mm in pure water amounts to a maximum energy of 1.66 × 10⁴–4 × 10⁵ W kg⁻¹ (converted stress 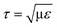of 128.9–632.8 Pa in the viscous subrange, with μ being the dynamic viscosity) during the bubble bursting process.^7,31 These numerical studies also demonstrated that the energy dissipation rate rapidly decreases with increasing bubble diameter. Meanwhile, there is no complete agreement regarding the critical stress that causes the cell damage. Orton and Wang³² suggested ∼100 Pa as the critical stress to damage animal cells, whereas Zhang et al.³³ proposed that hybridoma TB/C3 cells are damaged when the stress is more than 500 Pa.

The critical stress for the CHO cell damage reported in this work can be used as one of the important design parameters in an agitation-based bioreactor system, particularly for bubble generation systems. As was indicated in the above literature, the hydrodynamic forces due to the impeller rotation appear to be much smaller than the critical stress, observed in the current work, for the cell damage; however, the energy dissipation rate or the corresponding turbulent stress during the bubble bursting process near the free surface reaches a value of the same order as or much larger than the critical stress, depending on the bubble size and the interfacial tension (the amount of the Pluronic F68).³⁴ The importance of the bubble bursting process in cell damage has been recognized by bioreactor researchers^2,6 but the current work provides very quantitative information on the cell damage by the controlled extensional stress field, generated in a cross-slot microchannel. Therefore the critical stress of the CHO cell in this work will be of great importance in determining the bubble size, in designing the gas sparger, and in selecting the operating conditions for a given impeller speed and gas flow rate. One may reduce the cell damage by controlling the bubble size; a larger bubble induces lower stress during the bursting process.³⁵ The reduction in oxygen transfer can be compensated to some extent by operating at high speed agitation.

Conclusions

We developed a microfluidic sensor to assess the mechanical cell damage under an extensional stress field. Our novel microfluidic method has a microfluidic cross-slot channel to generate the extensional stress field, and a cell viability test procedure. The viscoelasticity-induced particle migration in the polymer solution plays a critical role in our novel microfluidic method. The cells are aligned along the channel centerline, so that the cells experience similar kinematic histories. In addition, the channel centerline is a shear-free region, and thus the cell damage by wall shear stress is minimized while the cells are transported to the cross-slot; this was confirmed by demonstrating that the cell damage is negligible when the cells bypass the cross-slot zone. We find that the CHO cells are mechanically damaged when the extensional stress is greater than ∼250 Pa. Our microfluidic method mimics the mechanical cell damage occurring in bioreactors, especially for the cell damage by the bubble bursting process. According to numerical simulations,^7,31 the maximum energy dissipation rate during the bursting process reaches up to 4 × 10⁵ W kg⁻¹ for a gas bubble of diameter 1.7 mm in water, which corresponds to 632.8 Pa. This suggests that the bubble bursting process, involving extensional stress, could be critical to the mechanical cell damage. Our microfluidic method provides very quantitative information on the cell damage under a controlled extensional stress field. Our novel microfluidic method is not limited to the assessment of mechanical damage of CHO cells; we expect that it can also be used for other cells such as red blood cells or white blood cells, which are essential for the design and operation of artificial organs such as artificial hearts.

Acknowledgements

This research was supported by the research program of the National Research Foundation of Korea (NRF), funded by the Ministry of Science, ICT and Future Planning (No. NRF-2013R1A1A1A05007406). W. R. H. acknowledges financial support from the National Research Foundation of Korea by the Ministry of Education (NRF-2013R1A1A2A100057693), and the Support Program for Commercialization of R&D Outcomes, Ministry of Science, ICT and Future Planning. We are thankful to Ms. Mi Ran Yu at Ajou University School of Medicine for cell culturing.

References

1. Y. Chisti, Crit. Rev. Biotechnol., 2001, 21, 67–110.
2. E. T. Papoutsakis, Trends Biotechnol., 1991, 9, 427–437.
3. M. Butler, Appl. Microbiol. Biotechnol., 2005, 68, 283–291.
4. R. Godoy-Silva, C. Berdugo and J. J. Chalmers, Aeration, Mixing and Hydrodynamics, Animal Cell Bioreactors, in Encyclopedia of Industrial Biotechnology: Bioprocess, Bioseparation, and Cell Technology, ed. M. C. Flickinger, John Wiley & Sons, Inc., 1st edn, 2009, pp. 1–27.
5. Y. Chisti and U. J. Jauregui-Haza, Biochem. Eng. J., 2002, 10, 143–153.
6. Y. Chisti, Trends Biotechnol., 2000, 18, 420–432.
7. M. A. Garcia-Briones, R. S. Brodkey and J. J. Chalmers, Chem. Eng. Sci., 1994, 49, 2301–2320.
8. M. A. Garcia-Briones and J. J. Chalmers, Biotechnol. Bioeng., 1994, 44, 1089–1098.
9. S. Cha, T. Shin, S. S. Lee, W. Shim, G. Lee, S. J. Lee, Y. Kim and J. M. Kim, Anal. Chem., 2012, 84, 10471–10477.
10. D. R. Gossett, H. T. Tse, S. A. Lee, Y. Ying, A. G. Lindgren, O. O. Yang, J. Rao, A. T. Clark and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7630–7635.
11. R. I. Tanner and R. R. Huilgol, Rheol. Acta, 1975, 14, 959–962.
12. D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727.
13. G. D'Avino, G. Romeo, M. M. Villone, F. Greco, P. A. Netti and P. L. Maffettone, Lab Chip, 2012, 12, 1638–1645.
14. K. Kang, S. S. Lee, K. Hyun, S. J. Lee and J. M. Kim, Nat. Commun., 2013, 4, 2567.
15. A. M. Leshansky, A. Bransky, N. Korin and U. Dinnar, Phys. Rev. Lett., 2007, 98, 234501.
16. S. Yang, S. S. Lee, S. W. Ahn, K. Kang, W. Shim, G. Lee, K. Hyun and J. M. Kim, Soft Matter, 2012, 8, 5011–5019.
17. S. Yang, J. Y. Kim, S. J. Lee, S. S. Lee and J. M. Kim, Lab Chip, 2011, 11, 266–273.
18. Y. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 550–575.
19. J. Nam, B. Namgung, C. T. Lim, J.-E. Bae, H. L. Leo, K. S. Cho and S. Kim, J. Chromatogr. A, 2015, 1406, 244–250.
20. R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Wiley Interscience, New York, 1987.
21. K. S. Louis and A. C. Siegel, in Mammalian Cell Viability: Methods and Protocols, ed. M. J. Stoddart, Humana press, 2011 edn, 2011, ch. 2, pp. 7–12.
22. J. M. Kim, Korean J. Chem. Eng., 2015 DOI:10.1007/s11814-015-0080-4.
23. Z. Xing, B. M. Kenty, Z. J. Li and S. S. Lee, Biotechnol. Bioeng., 2009, 103, 733–746.
24. L. E. Rodd, T. P. Scott, D. V. Boger, J. J. Cooper-White and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2005, 129, 1–22.
25. B. P. Ho and L. G. Leal, J. Fluid Mech., 1976, 76, 783–799.
26. M. A. Tehrani, J. Rheol., 1996, 40, 1057–1077.
27. M. Abkarian and A. Viallat, Soft Matter, 2008, 4, 653–657.
28. M. Abkarian and A. Viallat, Biophys. J., 2005, 89, 1055–1066.
29. G. Zhou and S. M. Kresta, AIChE J., 1996, 42, 2476–2490.
30. E. Ståhl Wernersson and C. Trägårdh, Chem. Eng. Sci., 1999, 54, 4245–4256.
31. J. M. Boulton-Stone and J. R. Blake, J. Fluid Mech., 1993, 254, 437–466.
32. D. R. Orton and D. I. C. Wang, AIChE Annual Meeting, Chicago, 1990.
33. Z. Zhang, M. A. Ferenczi, A. C. Lush and C. R. Thomas, Appl. Microbiol. Biotechnol., 1991, 36, 208–210.
34. A. W. Nienow, Cytotechnology, 2006, 50, 9–33.
35. J. Wu and M. F. A. Goosen, Enzyme Microb. Technol., 1995, 17, 241–247.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5lc01006c

---