Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Delivery of minimally dispersed liquid interfaces for sequential surface chemistry†
N.
Ostromohov
ab,
M.
Bercovici
*a and
G. V.
Kaigala
*b
aFaculty of Mechanical Engineering, Technion – Israel Institute of Technology, Haifa 3200003, Israel. E-mail: mberco@technion.ac.il
bIBM Research—Zurich, Saeumerstrasse 4, CH-8803 Rueschlikon, Switzerland. E-mail: gov@zurich.ibm.com
First published on 29th June 2016
Abstract
We present a method for sequential delivery of reagents to a reaction site with minimal dispersion of their interfaces. Using segmented flow to encapsulate the reagents as droplets, the dispersion between reagent plugs remains confined in a limited volume, while being transmitted to the reaction surface. In close proximity to the target surface, we use a passive array of microstructures for removal of the oil phase such that the original reagent sequence is reconstructed, and only the aqueous phase reaches the reaction surface. We provide a detailed analysis of the conditions under which the method can be applied and demonstrate maintaining a transition time of 560 ms between reagents transported to a reaction site over a distance of 60 cm. We implemented the method using a vertical microfluidic probe on an open surface, allowing contact-free interaction with biological samples, and demonstrated two examples of assays implemented using the method: measurements of receptor–ligand reaction kinetics and of the fluorescence response of immobilized GFP to local variations in pH. We believe that the method can be useful for studying the dynamic response of cells and proteins to various stimuli, as well as for highly automated multi-step assays.
Introduction
Delivery of multiple reagents in sequence is central in a large number of surface biochemical assays. For example, protein interactions and function analysis,1–3 cell stimulation response, signaling and chemical communication studies,4,5 and nucleic acid hybridization and immuno-assays6–8 all require delivery of multiple reagents to a reaction site in a fixed order. Manual sequential delivery of reagents for multi-step processes on conventional laboratory platforms, such as slides or 96-well plates, is a time-consuming and labor-intensive task. Automation (e.g. via pipetting robots) has enabled the wide-spread use of such assays, particularly in clinical laboratories, where high throughput is required.9 Increasingly, microfluidic platforms are used for such applications, as they enable the use of small sample volumes, allow individual addressing of a higher density of reaction sites, and provide relatively simple mechanisms for automation and control.10,11In microfluidic devices, the mechanical process of switching between one liquid and another can be performed either off- or on-chip. Off-chip switching can be performed using multiple-position selection valves,12 solenoid valves,13 electromagnetic valves,14 or pressure controllers,15 and benefits from the relatively high reliability of these instruments, while maintaining simple fabrication of the microfluidic layer as it does not need to include on-chip moving parts. However, a major practical limitation of such systems is that the physical distance between the switching element and the microfluidic device results in a significant dispersion of the interfaces between reagents, leading to the creation of mixed zones and thus very long transition times. In contrast, on-chip switching16–20 is able to eliminate much of the dispersion by acting on the liquid in close proximity to the reaction site, but requires complex and expensive fabrication of the microfluidic device, suffers from low reliability, and often limits the range of chemical solutions that can be processed. One strategy for on-chip liquid switching employs capillary pumps,21,22 which allow autonomous and passive delivery with accurate control of the sequence of the injected liquids and their flow rates, eliminating the need for actuators. However, capillary pumps require the design of a specific dedicated geometry for each assay, and cannot be programmed or adapted in real time. Another strategy for on-chip switching of liquids is integrating micro-mechanical elements such as membrane-valves actuated by pressure.23,24 These valves allow active and flexible switching of the flow, but require multilayer soft-lithography and the use of externally controlled pneumatic lines.
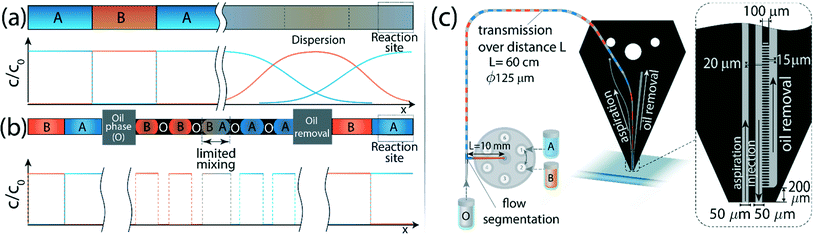
An elegant solution to this challenge is segmented flow, in which the homogeneous stream of reagent is converted into a series of discrete plugs carried by an immiscible fluid, thus confining the interface between liquids and preventing axial dispersion. This principle is most commonly used in segmented-flow analysis and droplet microfluidics for discretization of reactions, enabling multiple tests to be performed in parallel.25–30 Chin et al.31 used air segmentation to prevent dispersion between reagents delivered to a reaction site to perform sequential chemistry. This approach is useful for a wide range of assays; however it is not suitable for biological samples, such as live cells which must be kept in aqueous environments to maintain their native properties.32 This requirement was addressed by Chen et al.,33 who brought two inclined hydrophobic channels in contact with a hydrophilic surface and used water-in-oil droplets to deliver reagents to the surface. In this method, while the oil was not removed, the sample was still maintained in a purely aqueous environment by utilizing a wetting layer on the hydrophilic surface, which was continuously altered by the incoming droplets. This device allows very rapid sample switching, but operates only on a single reaction site, and requires a conformal physical contact with the substrate.
Here we present a method which allows contact-free sequential delivery of reagents to a reaction surface, with a characteristic switching time of less than 1 s. We use a standard off-chip selection valve to switch between reagents, which are immediately encapsulated as droplets in an immiscible liquid. The droplets confine the dispersion between reagent interfaces, and are delivered to a vertical microfluidic probe (vMFP)34 – a non-contact scanning device that hydrodynamically confines liquids to a nanoliter-scale volume between an injection and an aspiration channel at its apex. This confined flow can be brought into contact with any surface to drive a reaction. In close proximity to the apex, we implemented a passive phase-separation microstructure that allows complete removal of the oil phase, such that only the aqueous phase exits the chip and reaches the reaction surface. In contrast to previous solutions utilizing segmented flow to deliver processing liquids to a reaction site, implementing this strategy together with complete removal of the oil-phase enables operation without any physical contact between the delivery channels and the surface. The contact-free operation of the MFP prevents perturbation of the sample on the surface and allows addressing multiple reaction sites on the surface automatically. In the Theory section, we provide an analysis of the conditions under which the method can be applied as well as engineering guidelines for the design of such devices. In the Results and discussion section, we characterize the switching time between reagents, and demonstrate two examples of assays that can be implemented using the method: measurements of reaction kinetics and protein response to chemical stimuli. Although our focus here is on open-surface and contact-free analysis, we note that the method is equally applicable to reactions in more traditional closed microchannels.
Experimental
Microfluidic devices
We fabricated the two-layer silicon-glass MFP heads using standard photolithographic and dry-etching techniques, as described previously.34 The geometry of the MFP channels is provided in Fig. S1 in the ESI.† After fabrication, we coated the channels with a hydrophobic layer by first flowing through the channels piranha solution consisting of sulfuric acid (MicroChemicals GmbH, Ulm, Germany) and 30% hydrogen peroxide (MicroChemicals GmbH, Ulm, Germany), in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for 5 min, followed by rinsing with deionized (DI) water (Merck-Millipore, Darmstadt, Germany), and finally flushing the channels with a solution of 50 mM trichloro(octadecyl)silane (Sigma-Aldrich, St. Louis, MO) in hexadecane (Sigma-Aldrich, St. Louis, MO) for 1 min. The piranha solution activates the channel surfaces by introducing hydroxyl groups which covalently bind to the silane molecules, resulting in a hydrophobic surface.35 Following the hydrophobic treatment of the channels, we dipped the MFP apex in piranha solution for 2 min to ensure that the surface that is in contact with the aqueous immersion liquid is hydrophilic.
3 for 5 min, followed by rinsing with deionized (DI) water (Merck-Millipore, Darmstadt, Germany), and finally flushing the channels with a solution of 50 mM trichloro(octadecyl)silane (Sigma-Aldrich, St. Louis, MO) in hexadecane (Sigma-Aldrich, St. Louis, MO) for 1 min. The piranha solution activates the channel surfaces by introducing hydroxyl groups which covalently bind to the silane molecules, resulting in a hydrophobic surface.35 Following the hydrophobic treatment of the channels, we dipped the MFP apex in piranha solution for 2 min to ensure that the surface that is in contact with the aqueous immersion liquid is hydrophilic.
Experimental setup
We performed all experiments using an inverted microscope equipped with an automated XY stage (Ti-E, Nikon Instruments, Melville, NY) and an LED white light source (Sola, Lumencor, Beaverton, OR), using a pressure regulator (MFCS-EZ, Fluigent, Villejuif, France) connected to a selector valve (ESS M-switch, Fluigent, Villejuif, France). We used a PEEK T-junction (VICI, Schenkon, Switzerland) with a circular cross section, located at a distance of 1 cm from the selector valve for generation of segmented flow. The flow rates of the aqueous phase and the oil phase were 5 μL min−1 and 4 μL min−1, respectively. The length of the capillary between the selector valve and the MFP head was 60 cm, with a diameter of 125 μm (see Fig. S1 in the ESI† for detailed dimensions). We used a motorized Z-stage (T-LSM050, Zaber Technologies, Vancouver, Canada) to control the distance of the MFP device from the surface. We used MATLAB (R2013a, Mathworks, Natick, MA) to control the selector valve and synchronize it with the light source. For fluorescence experiments, we used a Zyla 5.5 sCMOS camera (Andor Technology, Belfast, NIR, UK), a FITC filter-cube (F36-525, AHF Analysetechnik, Tübingen, Germany) and a 20× water immersion objective (CFI Fluor, NA = 0.5, Nikon Instruments, Melville, NY). For experiments in bright field, we used a Nikon 1 camera (Nikon, Melville, NY) to capture the images. All images were processed and analyzed using MATLAB.Reagents
In all experiments, we used hexadecane (Sigma-Aldrich, St. Louis, MO) as the organic phase. In the fluorescence switching experiments, the aqueous plugs contained a concentration of 100 μM fluorescein (Sigma-Aldrich, St. Louis, MO) and DI water. To demonstrate switching between 4 different liquids, we used a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 dilution of Amaranth Red (E123), Brilliant Blue FCF (E133), and Dark Green (E104, E133) food dyes (Trawosa AG, St. Gallen, Switzerland) in DI water.
10 dilution of Amaranth Red (E123), Brilliant Blue FCF (E133), and Dark Green (E104, E133) food dyes (Trawosa AG, St. Gallen, Switzerland) in DI water.
GFP response to pH assay
We immobilized green fluorescent protein (GFP), (Abcam, Cambridge, UK) on an aldehyde-coated slide (SuperAldehyde 2, ArrayIt, Sunnyvale, CA), by depositing 1 μg μL−1 of GFP on the surface and incubating it overnight at 4 °C. We rinsed the area with phosphate-buffered saline (PBS) (Gibco pH 7.4, Thermo Fisher Scientific, Waltham, MA) to remove unbound protein molecules from the surface. We used PBS as the immersion liquid, and delivered to the surface a sequence of buffers having pH values between 4 and 9, for 5 s each, and recorded the fluorescence signal of the GFP (for details of the buffer solutions used, see Table S1 in the ESI†).Association kinetics measurement assay
We prepared a test surface by incubating an aldehyde-coated slide (SuperAldehyde 2, ArrayIt, Sunnyvale, CA) with 100 μg mL−1 of rabbit IgG solution (Sigma-Aldrich, St. Louis, MO) at room temperature for 30 min. We rinsed the surface three times using PBS for 2 min, then blocked the surface using 1% BSA in PBS for 30 min, and rinsed the surface again with PBS. We used PBS as the immersion liquid and alternately delivered rhodamine-conjugated anti-rabbit IgG produced in goat (Sigma-Aldrich, St. Louis, MO) and PBS to the surface for 5 s each. To prevent continuous photobleaching of the bound antibodies, we illuminated the surface for 1 s during the delivery of PBS and recorded the signal on the surface. We measured the signal for antibody concentrations of 200 nM, 330 nM and 670 nM.Theory and principle of the method
Limited switching rate in single phase flow
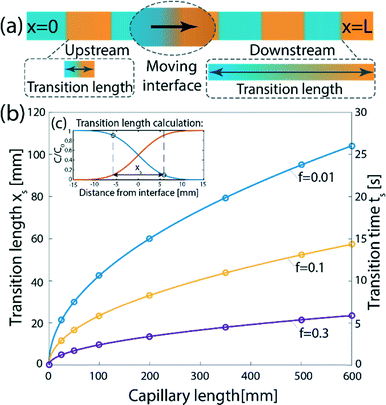
Consider a sequence of miscible liquid plugs consecutively injected under an external pressure gradient into a channel of length L and a characteristic cross-section length scale a, at a constant cross-section average velocity, U. We assume ideal switching, resulting in an initially sharp interface between each of the plugs. As illustrated in Fig. 1a, the width of this interface increases over time. For a plug containing species with a molecular diffusion coefficient D, the characteristic times of cross-channel diffusion and axial convection can be defined as td = h2/D and tc = L/U, respectively. For tc > td, the dispersion of the interface over time is a result of a combination of the axial convection and the transverse diffusion of the parabolic flow-profile, in accordance with the Taylor–Aris dispersion theory.36 The cross-sectional averaged concentration of species within a plug (in a coordinate system moving at the average flow velocity), c, is then given by37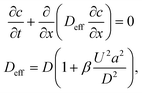 | (1) |
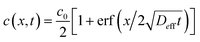 .36,37 As illustrated in Fig. 1c, to assess the extent of mixing between two adjacent plugs at the end of the channel, we define a factor f, which is a measure of dilution of the initial concentration (ranging between 0 and 1), and seek the distance xs over which the concentration varies from c = f·c0 to c = (1 − f)·c0 at t = L/U (e.g., for f = 0.1, this would indicate a variation in concentration between 10% and 90% of the injected concentration). Solving for x on both sides of the interface, with c = f·c0 and to c = (1 − f)·c0, and summing the results to obtain the total transition length, with an effective Péclet number defined as
.36,37 As illustrated in Fig. 1c, to assess the extent of mixing between two adjacent plugs at the end of the channel, we define a factor f, which is a measure of dilution of the initial concentration (ranging between 0 and 1), and seek the distance xs over which the concentration varies from c = f·c0 to c = (1 − f)·c0 at t = L/U (e.g., for f = 0.1, this would indicate a variation in concentration between 10% and 90% of the injected concentration). Solving for x on both sides of the interface, with c = f·c0 and to c = (1 − f)·c0, and summing the results to obtain the total transition length, with an effective Péclet number defined as 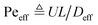 , we obtain
, we obtain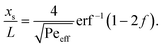 | (2) |
| ts = xs/U | (3) |
Principle of the method
To minimize dispersion, we encapsulate the aqueous solution into droplets (discrete phase) in an immiscible organic solvent (continuous phase) in close proximity to the outlet of the selector valve. Thus, mixing between sequentially injected plugs is confined to a single droplet containing the interface, as illustrated in Fig. 2b. We use a phase-separation device located at the end of the channel to remove the continuous phase and deliver only the aqueous plugs to the desired reaction site. The phase separator consists of an array of pillars forming N short capillaries, which are subjected to a negative pressure and, owing to differences in the hydrophobicity of each phase, allow removal of only the continuous phase (see Fig. 3a–c). We implement the method using the MFP to deliver sequences of processing liquids for reaction on the surface, as illustrated in Fig. 2c.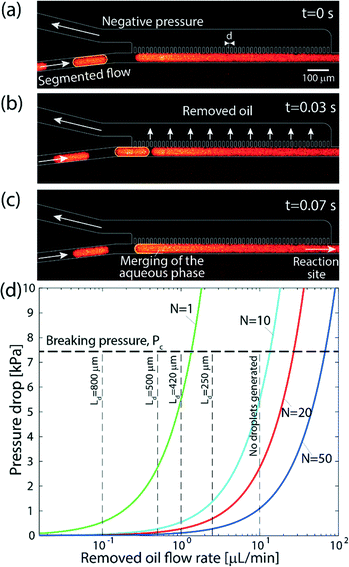 | ||
| Fig. 3 Operation of the on-chip continuous-phase removal module. (a–c) Sequence of raw fluorescence images showing the operation of the phase-separation structure. (a) The aqueous phase is delivered in individual droplets encapsulated in an organic solvent to an array of 20 μm wide and 100 μm long posts, located at a distance of 15 μm from one another. Across the array, we apply a negative pressure that is sufficiently high to remove the continuous phase, but lower than the capillary pressure of the interface between the phases such that the aqueous phase remains in the main channel. (b) As the oil phase is removed through the array of pillars, the distance between the approaching droplet and the continuous aqueous phase along the pillar array decreases. (c) The approaching aqueous droplet merges and continues through the main channel to the reaction site. (d) Theoretical results showing the maximum continuous phase flow rate that can be removed by the array as a function of the applied pressure drop, and for different numbers of capillaries. As the number of capillaries, N, increases, the device can be operated at higher flow rates and using a lower pressure. The horizontal dashed line represents the capillary pressure, above which the aqueous phase will begin to leak into the removal channel (eqn (6)) calculated for γ = 53.3 mN m−1. The vertical dashed lines correspond to different droplet lengths obtained experimentally at each of the oil flow rates, for a fixed aqueous phase flow rate of 3 μL min−1. As the mixing is limited to a single droplet, this length affects the transition length after the oil has been removed according to eqn (4). For organic-phase flow rates significantly higher than that of the aqueous phase, no segmented flow can be generated. | ||
Design considerations
Segmenting the fluid into individual droplets prevents dispersion on a scale larger than the droplet length Ld. However, within the droplet, one can assume near complete mixing.38,39 Thus, implementing sufficiently short droplets (shorter than the length of the intended transition length) is essential for minimizing the total dispersion. The remaining contributions to dispersion would be the channel segments connecting the valve and the droplet generator, along the phase separator itself, and from the phase separator to the desired delivery site. The total dispersion is thus on the order of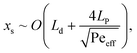 | (4) |
For a given aqueous flow rate, the size of the individual droplets can be reduced by increasing the flow rate of the organic phase. The maximum flow rate of the organic phase the separator is capable of removing is determined by the number of capillaries formed between the pillars, N, the hydrodynamic resistances of the separator geometry, Rh,sep, and the additional fluidic path after the separator, Rh,add. The hydrodynamic resistances can be calculated using the Hagen–Poiseuille equation,40 and the maximum removed flow rate is given by
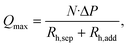 | (5) |
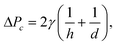 | (6) |
Fig. 3 demonstrates the operation of the phase separator and removal of the organic phase from the main channel. As long as the pressure drop across the capillary array is lower than the capillary pressure ΔPc, the capillary pressure counterbalances the applied pressure drop, preventing the aqueous phase from entering the removal channel, while the organic phase is removed through the array. The removal of the organic phase facilitates the merger of the aqueous droplets into a continuous flow in the main channel, which continues to the desired reaction site. A high frame rate video showing the operation of the phase separator is provided in the ESI† (SM-1).
Fig. 3d presents the maximum flow rate of the organic phase for different separator array sizes and pressure drops. The working point for the desired conditions (appropriate flow rates and minimal dispersion) can be chosen based on eqn (4) and Fig. 3d. For instance, using a geometry consisting of a single capillary, the contribution of the separator to the total dispersion in eqn (4) is negligible, and the mixing length is essentially the length of the droplet. However, oil flow rates higher than 1.3 μL min−1 cannot be achieved due to the pressure limitation of ΔPc, resulting in longer droplets. In contrast, using an array of 20 capillaries allows working at flow rates of up to 26 μL min−1, leading to shorter droplets, but requires a longer separator array, which results in dispersion along the separator.
Results and discussion
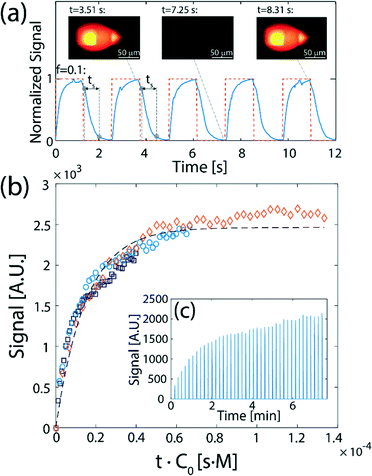
Fig. 4 presents a demonstration of flow-switching between two processing liquids delivered to a surface. Fig. 4a presents experimental results of alternately delivering a fluorescent dye (fluorescein) and DI water to the surface, using an oil-removal microstructure with N = 50. The signal was analyzed based on an average of a 30 × 30 μm2 area in the flow confinement between the channels. The signal on the surface (blue solid line) follows the rectangular input function (orange dashed line), with a switching time of ts = 0.56 s (based on an f = 0.1 criterion). The switching time that can be achieved is a function of the flow rate and the length of the segments in which the flow is subject to dispersion, as discussed in the Theory section. For a flow rate of 5 μL min−1 and an array of 50 capillaries as we used here, the obtained experimental switching time is comparable with the theoretical value of 0.49 s calculated for dispersion of an interface in the continuous flow sections, 11.7 mm in length. The continuous flow section before the flow segmentation junction, 10 mm in length, causes most of the dispersion, and is responsible for 0.44 s of the total transition time. A video showing the flow-switching between the two liquids is provided in the ESI† (SM-2). The ability to rapidly switch between two liquids, where each maintains a constant concentration in its turn, opens the door to measuring association kinetics using a fluorescently labeled reactant. In Fig. 4b we show the results of experiments in which we switch between an antibody solution containing rhodamine labeled anti-rabbit IgG and pure PBS buffer, delivered alternately (for a duration of Δt = 5 s) to a surface with immobilized rabbit IgG. This reaction can be described by Langmuir reaction kinetics,45,46cb = cs(1 + Kd/c0)−1(1 −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−(konc0 + koff)t) e−(konc0 + koff)t) | (7) |
The ability to switch between fluorescently labelled antibodies and non-fluorescent buffer enables the measurement of the fluorescence signal on the surface (indicative of the concentration of antibodies reacted with the IgG on the surface) during the buffer wash, as illustrated in Fig. 4c. Assuming Δt ≪ 1/koff (an assumption which holds well for the majority of antibodies), each data point corresponds to a reaction time which is the total time over which the surface was exposed to the antibody solution (since both the antibody and buffer are injected at equal intervals, Δt, this time is precisely half of the clock time). As shown in Fig. 4c, the measurements of the signal using three different concentrations of antibodies collapse to a single curve as a function of t·c0, fitting the Langmuir model with an association rate of kon = 6.7 × 104 [M−1 s−1]. This is consistent with the value of kon = 6.8 × 104 [M−1 s−1] measured by Sun et al.47 for binding of unlabeled Fab fragments of goat anti-rabbit IgG with rabbit IgG targets.
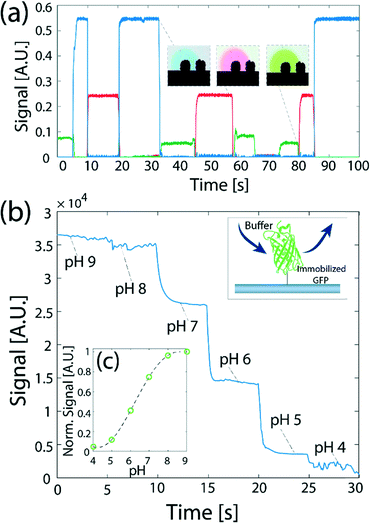
Fig. 5 presents experimental results of application of switching between multiple processing liquids to perform reactions on a surface. Fig. 5a presents a time-dependent plot of the signal on the surface obtained from switching four processing liquids: (a red dye, a green dye, a blue dye, and DI water), for varying time durations between 5 and 15 s, simulating a hypothetical multiple-step assay. We demonstrate the ability to switch and control the duration of each processing liquid injection on the surface, and show the signal stability over long injection times. This allows one to perform more complex chemical modifications to the surface using the method, such as delivery of longer chemical pulses and their temporal modulation, making the method useful for delivering reagents for multi-step reactions with varying time scales such as ELISA,48 or sandwich hybridization- and immuno-assays.10,11 A video showing the switching between the four processing liquids is provided in the ESI† (SM-3).
Fig. 5b presents the use of such switching to obtain, in under 30 s, the fluorescence response of GFP to pH, for six data points in the range 4 to 9. Here, we immobilized GFP on a glass surface, and delivered a set of solutions in a decreasing order of pH. As expected the signal on the surface exposed to the buffers decreases with the reduction in pH. The assay is capable of measuring the steady-state response of the GFP to the change in pH. However, because the time-scale of the dynamic response of a GFP molecule is on the order of 100 μs,49,50 and is shorter than the switching time between buffers using our device, the signal measured on the surface does not capture the dynamic response of the protein to the change in the environmental conditions.
Fig. 5c shows the steady-state signal dependence of the GFP on pH. Our measurements show similar values to previous results by Kneen et al.51 and Haupts et al.50 showing a gradual increase of signal with pH between pH of 5 and 8, with a saturation above a pH of 8 and below a pH of 5. At a pH of 6 the signal increases to 50% of its maximum value (recorded at pH 8–9), and the minimum signal is recorded in the range of pH 4–5 (below 20% of the maximum).
Conclusions
We presented a new method for sequential delivery of reagents to a surface-reaction site, with minimal dispersion of their interfaces. We minimize dispersion by segmenting the (aqueous) flow into individual water-in-oil droplets in close proximity to the switching valve, thus maintaining the dispersion between reagents within small confined volumes. The droplets can then be transported over long distances to the reaction site. Upstream of the reaction site, we use an array of micro-fabricated pillars, which act as capillaries for removal of the continuous oil phase, thus reassembling the content of the droplets, and allowing only the aqueous phase to come in contact with the reaction site. This makes the method particularly useful for interaction with biological samples, which must be maintained in a well-controlled aqueous environment at all times. We implemented the method on a microfluidic probe designed to deliver reagents to an open surface, and demonstrated two examples of assays which use the method: measurements of receptor–ligand reaction kinetics and measurement of the fluorescence response of immobilized GFP to local variations in pH.We have demonstrated the application of the method on an open surface using a microfluidic probe fabricated in silicon using standard photolithography and dry etching, but it is important to note that the necessary fabrication resolution would allow straightforward fabrication in other materials such as PDMS, epoxy, or plastic. In fact, the use of a naturally hydrophobic substrate would likely eliminate the need for surface coating which we have used to render the silicon and glass hydrophobic. The method is also equally applicable to sequential delivery of reagents to reaction sites in traditional closed channels.
In the experimental results presented in this work, we used an array of 50 capillaries to ensure that the oil is entirely removed. This resulted in a transition time of 560 ms between reagents (as compared to 15 s when flow segmentation is not used). While for many applications switching times on this order are sufficient, measurements of rapid cellular responses would require a sharper change of environmental conditions, on the order of hundreds of micro-seconds. The switching time in the current implementation of the method is mainly limited by the continuous flow segments between the selector valve and the encapsulation junction, and along the oil-removal micro-structure, where the reagents are subject to dispersion. This limitation may be overcome by replacing the commercially available T-junction and connectors we used here with a customized chip for generation of segmented flow in which the distance to the T-junction will be minimized, and by shortening the oil-removal microstructure (since for lower flow rates merger of the water droplets occurs early along the array). Assuming a negligible distance over which dispersion occurs in the first segment, the optimized switching time that can be achieved is a result of a trade-off between minimizing the length of the oil removal segment and maximizing the flow rates of the reagents. For example, using a flow-rate of 30 μL min−1 with 3 functioning capillaries in the array will lead to a switching time of 20 ms. However higher flow rates are not always practical for expensive reagents.
We believe that the method can be particularly useful for studying the dynamic response of biological samples (e.g., cells, proteins) to various stimuli, in which sharp transitions between reagents (i.e., clear initial conditions) are required, as well as for highly automated multi-step assays.
Acknowledgements
This work was supported by the ITN-EID grant, under the 7th Framework Program (Project No. 607322, Virtual Vials). We thank Dr. Ali Oskooei for valuable discussions and advice, and Ute Drechsler and Dr. Robert Lovchik for technical assistance. Dr. Bruno Michel and Dr. Walter Riess are acknowledged for their continuous support.References
- M. Pla-Roca, R. F. Leulmi, S. Tourekhanova, S. Bergeron, V. Laforte, E. Moreau, S. J. C. Gosline, N. Bertos, M. Hallett, M. Park and D. Juncker, Mol. Cell. Proteomics, 2012, 11, M111.011460 Search PubMed.
- S. Darmanis, R. Y. Nong, M. Hammond, J. Gu, A. Alderborn, J. Vänelid, A. Siegbahn, S. Gustafsdottir, O. Ericsson and U. Landegren, Mol. Cell. Proteomics, 2010, 9, 327–335 Search PubMed.
- G. MacBeath, Nat. Genet., 2002, 32, 526–532 CrossRef CAS PubMed.
- P. Ertl, D. Sticker, V. Charwat, C. Kasper and G. Lepperdinger, Trends Biotechnol., 2014, 32, 245–253 CrossRef CAS PubMed.
- M. Mrksich, Curr. Opin. Chem. Biol., 2002, 6, 794–797 CrossRef CAS PubMed.
- X. Pei, B. Zhang, J. Tang, B. Liu, W. Lai and D. Tang, Anal. Chim. Acta, 2013, 758, 1–18 CrossRef CAS PubMed.
- J. Shen, Y. Li, H. Gu, F. Xia and X. Zuo, Chem. Rev., 2014, 114, 7631–7677 CrossRef CAS PubMed.
- B. Krastins, A. Prakash, D. A. Sarracino, D. Nedelkov, E. E. Niederkofler, U. A. Kiernan, R. Nelson, M. S. Vogelsang, G. Vadali, A. Garces, J. N. Sutton, S. Peterman, G. Byram, B. Darbouret, J. R. Pérusse, N. G. Seidah, B. Coulombe, J. Gobom, E. Portelius, J. Pannee, K. Blennow, V. Kulasingam, L. Couchman, C. Moniz and M. F. Lopez, Clin. Biochem., 2013, 46, 399–410 CrossRef CAS PubMed.
- G. Wu and S. K. Doberstein, Drug Discovery Today, 2006, 11, 718–724 CrossRef CAS PubMed.
- A. H. C. Ng, U. Uddayasankar and A. R. Wheeler, Anal. Bioanal. Chem., 2010, 397, 991–1007 CrossRef CAS PubMed.
- L. Wang and P. C. H. Li, Anal. Chim. Acta, 2011, 687, 12–27 CrossRef CAS PubMed.
- J. Ruzicka and G. D. Marshall, Anal. Chim. Acta, 1990, 237, 329–343 CrossRef CAS.
- K. Ahn and S. Yokota, Mechatronics, 2005, 15, 683–702 CrossRef.
- X. Liu and S. Li, J. Lab. Autom., 2014, 19, 444–453 CrossRef PubMed.
- B. Kuczenski, P. R. LeDuc and W. C. Messner, Lab Chip, 2007, 7, 647 RSC.
- K. W. Oh and C. H. Ahn, J. Micromech. Microeng., 2006, 16, R13–R39 CrossRef.
- A. K. Au, H. Lai, B. R. Utela and A. Folch, Micromachines, 2011, 2, 179–220 CrossRef.
- K. Xu, M. R. Begley and J. P. Landers, Lab Chip, 2015, 15, 867–876 RSC.
- A. M. Leach, A. R. Wheeler and R. N. Zare, Anal. Chem., 2003, 75, 967–972 CrossRef CAS PubMed.
- J. Liu, C. Hansen and S. R. Quake, Anal. Chem., 2003, 75, 4718–4723 CrossRef CAS PubMed.
- P. Novo, V. Chu and J. P. Conde, Biosens. Bioelectron., 2014, 57, 284–291 CrossRef CAS PubMed.
- R. Safavieh and D. Juncker, Lab Chip, 2013, 13, 4180 RSC.
- F. Volpetti, J. Garcia-Cordero and S. J. Maerkl, PLoS One, 2015, 10, e0117744 CrossRef PubMed.
- M. A. Unger, H.-P. Chou, T. Thorsen, A. Scherer and S. R. Quake, Science, 2000, 288, 113–116 CrossRef CAS PubMed.
- K. Churski, P. Korczyk and P. Garstecki, Lab Chip, 2010, 10, 816–818 RSC.
- J. Q. Boedicker, L. Li, T. R. Kline and R. F. Ismagilov, Lab Chip, 2008, 8, 1265–1272 RSC.
- B. T. C. Lau, C. A. Baitz, X. P. Dong and C. L. Hansen, J. Am. Chem. Soc., 2007, 129, 454–455 CrossRef CAS PubMed.
- H. Lange, C. F. Carter, M. D. Hopkin, A. Burke, J. G. Goode, I. R. Baxendale and S. V. Ley, Chem. Sci., 2011, 2, 765–769 RSC.
- R. A. Kautz, W. K. Goetzinger and B. L. Karger, J. Comb. Chem., 2005, 7, 14–20 CrossRef CAS PubMed.
- Advances in flow analysis, ed. M. Trojanowicz, WILEY-VCH, Weinheim, 2008 Search PubMed.
- C. D. Chin, T. Laksanasopin, Y. K. Cheung, D. Steinmiller, V. Linder, H. Parsa, J. Wang, H. Moore, R. Rouse, G. Umviligihozo, E. Karita, L. Mwambarangwe, S. L. Braunstein, J. van de Wijgert, R. Sahabo, J. E. Justman, W. El-Sadr and S. K. Sia, Nat. Med., 2011, 17, 1015–1019 CrossRef CAS PubMed.
- H. Yin and D. Marshall, Curr. Opin. Biotechnol., 2012, 23, 110–119 CrossRef CAS PubMed.
- D. Chen, W. Du, Y. Liu, W. Liu, A. Kuznetsov, F. E. Mendez, L. H. Philipson and R. F. Ismagilov, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16843–16848 CrossRef CAS PubMed.
- G. V. Kaigala, R. D. Lovchik, U. Drechsler and E. Delamarche, Langmuir, 2011, 27, 5686–5693 CrossRef CAS PubMed.
- J. T. Schumacher, A. Grodrian, C. Kremin, M. Hoffmann, J. Metze and J. Micromechanics, Microengineering, 2008, 18, 55019 CrossRef.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1953, 219, 186–203 CrossRef CAS.
- R. Aris, Proc. R. Soc. London, Ser. A, 1956, 235, 67–77 CrossRef.
- J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127–9133 CrossRef CAS.
- J. D. Tice, A. D. Lyon and R. F. Ismagilov, Anal. Chim. Acta, 2004, 507, 73–77 CrossRef CAS.
- L. G. Leal, Advanced transport phenomena: fluid mechanics and convective transport processes, Cambridge University Press, 2007 Search PubMed.
- J. G. Kralj, H. R. Sahoo and K. F. Jensen, Lab Chip, 2007, 7, 256–263 RSC.
- A. Günther, M. Jhunjhunwala, M. Thalmann, M. A. Schmidt and K. F. Jensen, Langmuir, 2005, 21, 1547–1555 CrossRef PubMed.
- P.-G. De Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer Science & Business Media, 2013 Search PubMed.
- G. J. Hirasaki, J. Adhes. Sci. Technol., 1993, 7, 285–322 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- P. W. Atkins and J. de Paula, Atkins' physical chemistry, W. H. Freeman and Company, New York, 8th edn., 2006 Search PubMed.
- Y. S. Sun, J. P. Landry, Y. Y. Fei, X. D. Zhu, J. T. Luo, X. B. Wang and K. S. Lam, Langmuir, 2008, 24, 13399–13405 CrossRef CAS PubMed.
- J. E. Butler, J. Immunol., 2000, 21, 165–209 CAS.
- U. Kubitscheck, O. Kückmann, T. Kues and R. Peters, Biophys. J., 2000, 78, 2170–2179 CrossRef CAS PubMed.
- U. Haupts, S. Maiti, P. Schwille and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 13573–13578 CrossRef CAS.
- M. Kneen, J. Farinas, Y. Li and A. Verkman, Biophys. J., 1998, 74, 1591–1599 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6lc00473c |
| This journal is © The Royal Society of Chemistry 2016 |