To bend or not to bend – are heteroatom interactions within conjugated molecules effective in dictating conformation and planarity?

Abstract

We consider the roles of heteroatoms (mainly nitrogen, the halogens and the chalcogens) in dictating the conformation of linear conjugated molecules and polymers through non-covalent intramolecular interactions. Whilst hydrogen bonding is a competitive and sometimes more influential interaction, we provide unambiguous evidence that heteroatoms are able to determine the conformation of such materials with reasonable predictability.

---

Conceptual insights

The control of molecular architecture in organic semiconductors is a highly important aspect of organic electronics. This is particularly the case for planar conjugated structures to enhance charge transport and obtain low band gap materials. The goal of this paper is to present a solid argument, based on a combination of experimental data and modelling, for the importance of heteroatomic non-classical bonds in conjugated organic molecules and macromolecules and provides an insight to design rules for the manipulation of chemical structure towards targeted properties. Whilst potential non-covalent interactions can be easily identified in molecular structures determined by single crystal X-ray diffraction (XRD) studies, it is significantly more difficult to prove such interactions exist in polymers. A combination of XRD experiments on model structures, spectroscopy and computational studies can be a means to such an end, especially if the materials under study are members of a generic structure in which only the heteroatoms differ. The main question answered here is whether heteroatomic non-covalent interactions are coincidental or real, or if the sole driver for planar architectures in conjugated molecules is hydrogen bonding. The combined approach using experiment and theory clearly shows that heteroatom interactions are significantly influential.

In the design of new organic semiconductor materials, the ability to tune the electronic energy levels, the electronic and optical band gaps, and the charge-carrier transport properties of the organic semiconductor is essential in producing optimised or bespoke materials. In particular, the planarity (or indeed non-planarity) of a molecule has a dramatic influence on its behaviour, and hence on its potential application. In the context of light emission, for example, disorder can be beneficial in suppressing aggregation, but for photovoltaics and transistors where low energy absorption and/or effective charge transport are key issues, planar architectures are preferable for two reasons: (i) they increase the effective conjugation length of the chain with an associated narrowing of the energy gap between the highest-occupied and lowest-unoccupied molecular orbitals (HOMO and LUMO, respectively), and (ii) flat structures can foster long-range bulk intermolecular interactions among neighbouring, stacked π-conjugated backbones.

For the purpose of this article, non-covalent interactions can be viewed as supramolecular synthons that define the self-assembly between molecules in a crystal or co-crystal,¹ or those that have key importance within a single molecule or polymer chain. Here we focus mainly on the latter, in the context of conjugated organic semiconductors. There is a long-standing interest in the role that heteroatoms play in the conformation of organic conjugated molecules and polymers. Specifically, non-covalent interactions between heteroatoms are often observed to direct planarity or rigidity within a conjugated chain.² A non-covalent interaction between two heteroatoms is demonstrated by a contact distance which is shorter than the sum of the van der Waals radii of the two corresponding atoms.

Recently, Jackson et al. published an article that evaluated the role of intrachain hydrogen bonding vs. heteroatom interactions in planarising conjugated polymers and molecules, quoting that “nontraditional hydrogen-bonding interactions, oxygen–hydrogen (CH⋯O) and nitrogen–hydrogen (CH⋯N), are alone in inducing conformational control and enhanced planarity along a polymer or small molecule backbone at room temperature” and “We have [also] assessed the role of often-referenced oxygen–sulfur and nitrogen–sulfur nonbonding interactions and found weak, noninfluential binding tendencies.”³ These conclusions were established from a computational study of a selected series of conjugated materials that have the structural composition to feature either oxygen–sulfur and oxygen–hydrogen interactions, oxygen–nitrogen and nitrogen–hydrogen interactions, or fluorine–sulfur and fluorine–hydrogen interactions. Whilst these results indicate that non-traditional hydrogen bonding is more dominant than heteroatom interactions in the systems the authors chose to study, our work in fact demonstrates that binding between selected pnictogens, chalcogens and halogens in general are ‘influential’ in dictating conformation.

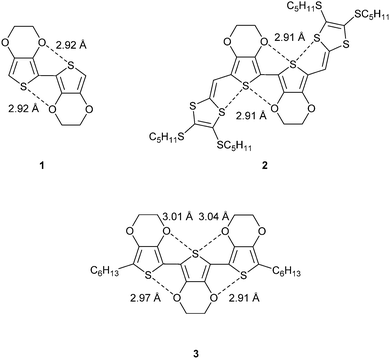
In choosing to study conjugated structures that are devoid of the possibility for hydrogen-bonding, but are rich in heteroatoms, one can begin to appreciate the significance of heteroatom non-covalent interactions in defining conformation. For example, dimers and trimers of the well-studied compound 3,4-ethylenedioxythiophene (EDOT) are planar molecules with short S⋯O contacts. Fig. 1 shows the molecular structures of three related compounds (1–3).^4–6 Short contacts between the marked S⋯O interactions are within the range of 2.9–3.1 Å, which is considerably less than the sum of the van der Waals radii for S (1.80 Å) and O (1.55 Å), at 3.35 Å. The molecules show a high degree of co-planarity between the thiophene units and this demonstrates the rigidification effect of the non-covalent interactions. Compound 2 shows a second association between sulfur atoms (3.10 Å), which creates a pseudo ribbon-type structure.

Fig. 1 Compounds 1–3 showing short contact distances between heteroatoms.

The well-known polymer PEDOT provides an excellent subject of study, since the oxygen atom can be replaced by other chalcogens and the properties of such a series of polymers scrutinised experimentally. To this end, we previously compared the optical gaps of this polymer, the all-sulfur analogue PEDTT and some hybrid copolymers (POSO and PSOS, Fig. 2).⁷ By inference from the structures of compounds 1–3 (and many other examples in the literature), one can assume a highly planar polymer structure for PEDOT. Likewise, from the molecular structures of EDTT derivatives determined by single crystal XRD, we know that a highly twisted conformation persists between the thiophene rings of this polymer (PEDTT). For instance, the dihedral angle in bis-EDTT (EDTT = 3,4-ethylenedithiothiophene) is 45°,⁸ compared to 0° in bis-EDOT.⁴ Comparing now the optical gaps of PEDOT and PEDTT, we see a large difference of ca. 0.5 eV. PEDOT has the narrower optical gap, yet if we expect simply a substituent effect to determine E_opt then we should see a lower value for the gap of PEDTT. Clearly, the experimental observations are due to a conformational effect. If, from the above, we conclude that the rigid and planar nature of PEDOT is due to S⋯O contacts, the structural nature of the polymer can be classed as a pseudo-ribbon type. The hybrid polymer POSO (Fig. 2) does not have the same number of S⋯O contacts as PEDOT, but a pseudo-ribbon motif can still be invoked. Note that the difference in the band gaps for PEDOT and POSO is negligible and well within experimental error. The hybrid copolymer PSOS has a greater weighting of EDTT units and the pseudo-ribbon structure is lost due to the greater abundance of S⋯S repulsive interactions, with co-planar units restricted to terthiophene segments. The optical gap of this polymer, compared to the hybrid POSO, is substantially wider and almost identical to that of PEDTT. The selenium analogue PEDST⁹ (Fig. 2), proves that the twisted nature of PEDTT is not due to the size of the chalcogen atoms. PEDST has an optical gap which is only ca. 0.15 eV wider than that of PEDOT and computational studies confirm a planar conformation. Finally here, it is worth noting that across the series of polymers presented in Fig. 2, there is no possibility of hydrogen-bonding and the conformation of the polymers can only be influenced by the identity of the chalcogen atoms in the backbone.

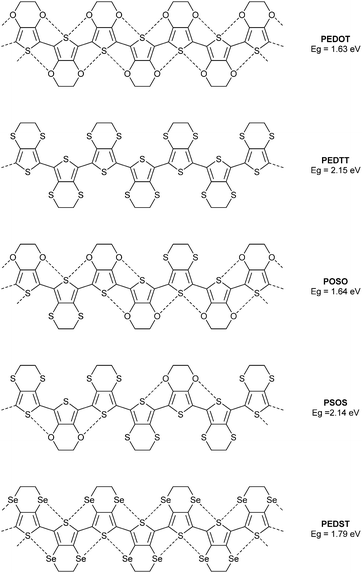Fig. 2 Chemical structure of the polymer PEDOT and its chalcogen variants, showing non-covalent interactions as dashed lines. The corresponding band gaps are given in eV.

The effect of such conformational control through heteroatom contacts on the HOMO/LUMO energy levels of polymers can be extremely large. We recently reported¹⁰ two closely related polymers containing bis-EDOT and bis-EDTT repeat units (polymers 4 and 5, respectively, Fig. 3). As stated above, the S⋯S interactions between repeat units in oligomers and polymers of EDTT derivatives are not co-operative and lead to non-planar conformations.⁷ This is in stark contrast to EDOT-containing systems and the difference is neatly demonstrated in polymers 4 and 5. The S⋯O contacts in polymer 4 create a pseudo-ribbon structure and the material has a low optical gap of 1.53 eV. In polymer 5 the disruptive nature of the S⋯S associations causes severe twisting in the polymer chain, resulting in a much wider band gap of 2.49 eV. It is quite remarkable that the extremely subtle change in heteroatoms between polymers 4 and 5 results in an energy gap variation of nearly 1 eV! Non-covalent intramolecular/intrapolymer interactions therefore demonstrate a powerful strategy for designing polymer structures with tailored conformations and targeted electronic properties. However, one should also be mindful of other factors that determine the optical band gaps of conjugated structures. For example, J-type and H-type aggregation in the solid state can lead to red/blue shifts of π–π* absorption maxima by a few 10s of nm, whereas in solution solvatochromism can lead to similar bathochromic or hypsochromic shifts.

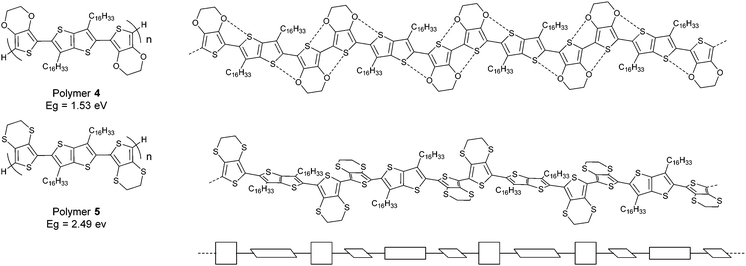Fig. 3 Structures of polymers 4 and 5 with the twisted conformation of 5 in schematic form shown on the bottom.

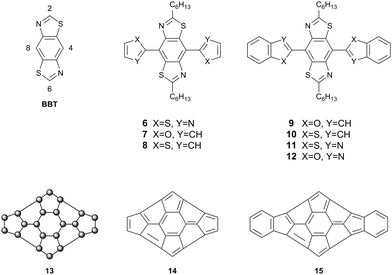
To probe heteroatom interactions in conjugated systems further and provide conclusive proof that such interactions are indeed influential on conformation, we embarked on a systematic approach to design and synthesise a novel conjugated molecule rich in heteroatoms. This unit can be used to construct conjugated polymers and features several possible heteroatomic interactions, including non-traditional hydrogen bonding. Using such a non-covalent approach to design novel planar, conjugated architectures, we synthesised a series of compounds based around benzo[1,2-d:4,5-d′]bis(thiazole) (BBT) as a core unit. Compounds 6–12 (Fig. 4) are π-extended derivatives of BBT with a range of heteroatoms that have been chosen as potential candidates for planarising non-covalent interactions. If close contacts can be established between the nitrogen and sulfur atoms of the BBT core and the heteroatoms at the X and Y positions of the peripheral heterocycles, then a highly π-delocalised molecule could be envisaged. Structure 13 represents such a hypothetical case, in which the skeleton of the molecule is constructed exclusively of sp² hybridised atoms. Such an organic system would be difficult, if not impossible, to obtain through covalent bonding. Applying carbon sp² atoms to the generic structure 13, for instance, would result in the nonsensical molecules 14 and 15, whereas the introduction of heteroatoms into 13 as a rigid heteroannulene would be synthetically challenging. These observations highlight another advantage of applying non-covalent interactions to attain delocalised, planar structures which are not accessible by orthodox structural design.

Fig. 4 Substitution pattern of BBT, target compounds 6–12 and hypothetical structures 13–15.

The BBT core was chosen due to its inherent rigidity and the presence of four heteroatoms. Non-covalent short contacts are typically observed between a wide variety of p-block elements, but very rarely between atoms if they are both from the first row of the p-block. The combination of sulfur and nitrogen atoms in the BBT unit can therefore support interactions with heteroatoms commonly found in aromatic heterocycles (e.g. O, N, S, Se). To this end, our first targets incorporated thiazole, furan and thiophene substituents on the BBT core. There are four possible connections one can make onto the unsubstituted BBT molecule, viz. the 2-, 4-, 6- and 8-positions (see BBT, Fig. 4). Extension of the conjugated unit through the 2,6-sites has been well studied, but the attachment of conjugated units at the 4,8-positions has been extremely limited.^11–14 The latter approach provides a better template for intramolecular non-covalent contacts, resulting in an extended π-system with a disc-like structure (see 13, Fig. 4) and this has been realised through compounds 6–12.

The synthesis of the target compounds (Scheme 1) began with the reaction of benzo[1,2-d:4,5-d′]bis(thiazole)-2,6-diamine¹⁵ (16) with KOH. The resulting yellow precipitate was filtered and treated with conc. HCl to give 2,5-diaminobenzene-1,4-dithiol dihydrochloride¹⁶ (17) as a white crystalline solid. This compound was then reacted almost immediately with heptanoyl chloride in the presence of trimethylsilyl polyphosphate to give the corresponding 2,6-dihexyl BBT derivative (18, 46% yield from 16). Bromination of compound 18 in dichloromethane solution was achieved in 45% yield by the addition of bromine at 0 °C. Compounds 6–8, 11, and 12 were obtained in 50–75% yield by the reaction of the dibromo derivative 19 with the corresponding aryl trialkyltin reagent under Stille coupling conditions. For compounds 9 and 10, the boronic esters of the corresponding aryl systems were reacted with 19 under Suzuki–Miyaura conditions to give the products in 65 and 43% yield, respectively. The full experimental data for all new compounds are given in the ESI.†

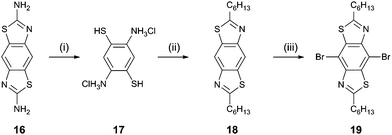Scheme 1 Reagents and conditions: (i) KOH reflux, then HCl; (ii) heptanoyl chloride, trimethylsilyl polyphosphate, 1,2-dichlorobenzene, reflux; (iii) bromine, dichloromethane, 0 °C.

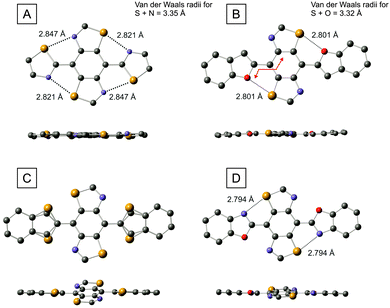
We were able to grow single crystals of the thiazole (6), benzofuran (9), benzothiophene (10) and benzoxazole (12) derivatives and the molecular structures of these compounds are shown in Fig. 5. Focussing on benzofuran 9 in the first instance, we observe a highly planar molecule with a maximum torsion angle of 4.1° between the furan ring and the benzene unit of the BBT molecule (measurement taken across the four connecting atoms shown by the red line in Fig. 5B). The planar architecture could be due to the interaction of the S⋯O atoms (2.801 Å), but there is an alternative possibility that planarisation arises from hydrogen bonding between the C–H group of the furan ring and the N atom of the BBT unit, which are positioned perfectly for such an interaction. However, in the thiazole analogue (compound 6, Fig. 5A), there is no opportunity for hydrogen bonding, yet the molecule is also highly planar with a maximum torsion angle of 5.1° between the thiazoles and the central benzene ring. In this case, there is only the possibility of S⋯N interactions and the corresponding non-covalent bond lengths are significantly shorter (0.5 Å) than the sum of the van der Waals radii for the corresponding atoms. Whilst this observation points strongly towards heteroatomic interactions dictating rigidification in the series of molecules under study, there is yet another possible reason for planarisation in these compounds – the molecules adopt a flat geometry simply due to extended conjugation and the structures observed in Fig. 5A and B merely represent lowest energy conformers as a function of efficient delocalisation of π-electrons. We expand on this notion in the following section through a computational study, but the structure of compound 10 (Fig. 5C), helps to clarify the situation from an experimental perspective. In contrast to benzofuran 9, the molecule is frustrated with respect to the positioning of the benzothiophene unit. There is a 72 : 28 probability of finding the sulfur atom of the thiophene ring adjacent to the sulfur or nitrogen atoms of the BBT unit. This is accompanied by a twisting between the benzothiophenes and the BBT benzene ring, with a maximum torsion angle of 19.7°. Considering that the only difference between compounds 9 and 10 is furan vs. thiophene, the variance in conformation is provided by the change in non-covalent interactions. We know from the comparison between PEDOT and PEDTT and other analogues that S⋯O interactions favour planarity whilst S⋯S can introduce highly twisted architectures. In compound 10, C–H⋯N hydrogen bonding is off-set by the unfavourable S⋯S interaction in one conformer, whereas the S⋯N close contact in the alternative geometry is presumably deterred by steric hindrance between the C–H and S species. It is relevant to point out here that sulfur is a significantly weaker proton acceptor than nitrogen,¹⁷ so the argument of steric repulsion is a feasible one. Compound 10 therefore provides some evidence that non-covalent interactions can disrupt planarity in certain circumstances, and that a flat geometry within this series is not simply a consequence of conjugation. In benzoxazole 12, a planar conformation is resumed to some degree. Of the two possible non-covalent interactions, S⋯N or S⋯O, the molecule exclusively prefers short contacts between the sulfur and nitrogen atoms. However, the maximum torsion angle between the benzene unit and the benzoxazole rings observed in this molecule is 11°, which is significantly larger than that of compounds 6 and 9. Having four intramolecular connections in these molecules (four S⋯N contacts in compound 6; two S⋯O contacts plus two C–H⋯N hydrogen bonds in 9), clearly provides a more planar molecule than two short contacts in 12 (recall that N⋯O interactions are assumed to be weak or negligible).

Fig. 5 Molecular structures of compounds 6 (A), 9 (B), 10 (C) and 12 (D), determined by single crystal X-ray diffractometry. The hexyl chains have been omitted for clarity. Close contacts between S–N and S–O are given as dashed lines.

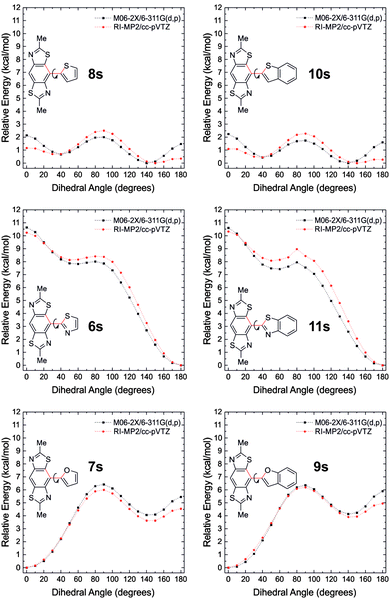
Computational studies have been performed to help rationalise the non-covalent interactions observed in the BBT derivatives and to determine the level of π-delocalisation present in the molecules in their neutral and doped states. The HOMO and LUMO wave functions of the BBT derivatives (the side-chains were replaced by methyl groups) calculated at the M06-2X/6-311G(d,p) level of theory using the Gaussian 09 package¹⁸ show a similar and complete delocalisation in all the molecules (Fig. S1, ESI†). This excludes the efficient delocalisation of π-electrons as the major and only reason for the degree of planarity observed experimentally by X-ray crystallography. To further investigate the reason that leads to the complete planar rigidification, fragments of the BBT derivatives 6s–11s (obtained by replacing one heterocyclic substituent of the BBT core with a hydrogen atom and limiting the side-chains to methyl groups), were used to calculate the torsional potentials between the BBT core and the heterocyclic substituents, in a similar approach to that used by Ratner et al.³ The dihedral angle between the BBT core and the heterocyclic substituent was fixed (from 0° to 180°, at 10° intervals) and a geometry optimisation on all remaining degrees of freedom was performed as above at the M06-2X/6-311G** level of theory. These geometries were then used as the inputs for single-point energy calculations at the RI-MP2/cc-pVTZ^19–21 level of theory using the QCHEM 4.1.2 package.²²

The potential energy surfaces (PESs) obtained are presented in Fig. 6, which suggest planar geometries for 6s, 7s, 9s, 11s, 12s (Fig. S2, ESI†) and twisted geometries for 8s and 10s. The latter two compounds show two energy minima that differ by only 0.4–0.7 kcal mol⁻¹ at the 150° (S⋯HC 2.62–2.44 Å, N⋯S 2.95–2.96 Å) and 40° (N⋯HC 2.58–2.59 Å, S⋯S 3.27 Å) twisted geometries. This energy, similar to kT at room temperature (∼0.6 kcal mol⁻¹), is fully consistent with the probability of finding the sulfur atom of the thiophene (and benzothiophene) ring adjacent to the nitrogen or sulfur atoms of the BBT unit, which is observed experimentally in the crystal structure of 10. Replacing the thiophenyl (benzothiophenyl) substituent with the furanyl (or benzofuranyl) unit in 7s (and 9s), the minimum in the PESs is at the 0° geometry where the S⋯O (2.78–2.80 Å) and N⋯HC (2.38–2.42 Å) interactions are stronger. In contrast to 8s and 10s, moving to the opposite geometry at an angle of 180° has a relatively large torsional barrier (5.5–6.0 kcal mol⁻¹) meaning that the N⋯O (2.66–2.68 Å) and S⋯HC (2.49–2.51 Å) interactions are highly unfavourable in this configuration. These interactions become less repulsive at the 140° geometry (second minimum) where the S⋯HC (2.92–2.93 Å) and N⋯O distances (2.88–2.89 Å) allow a positive attractive interaction. In compounds 6s and 11s the sum of the repulsive N⋯N (2.76–2.77 Å) and S⋯S (3.02–3.03 Å) interactions in the planar 0° configuration, leads to the largest torsional barriers in this series of molecules with maxima of 10.2 and 13.3 kcal mol⁻¹, respectively. On the other hand the absolute minimum is present in the PESs at the 180° geometry, showing that the S⋯N and N⋯S (2.83–2.88 Å) non-covalent interactions are important and that they force the molecule into this geometry. The activation energy necessary to bring the molecule into the other stable configuration (50° torsion angle) is 8.4–9.0 kcal mol⁻¹.

Fig. 6 Torsional potential surfaces for fragments of 6–11 calculated at the M06-2X/6-311G** (black) and RI-MP2/cc-pVTZ (red) levels of theory. Rotation occurs around the inter-ring C–C bond marked in red, starting from the conformation shown (0°).

For structure 12s, there is a lowest energy minimum when the planar molecule adopts a short contact between the sulfur of the BBT unit and the nitrogen atom of the benzoxazole ring (see Fig. S2, ESI†). The second energy minimum, where the BBT sulfur aligns with the oxygen of the benzoxazole, is 3.1–3.5 kcal mol⁻¹ higher in energy. The lowest energy conformation is in perfect agreement with the geometry observed in the molecular structure of 12 determined by single crystal X-ray diffraction studies.

In summary, the computational and experimental data corroborate each other well in the conclusion that planar rigidification is dictated by interactions between specific heteroatoms. Since the calculations were performed in the gas phase and the results correlate very closely with the crystal structures, one can assume that packing forces have little effect on the planarisation within the series of BBT molecules. Interpreting the role of H-bonding is still elusive, since such interactions can still have a role to play in compounds 7–10. However, the influential character of non-covalent heteroatom interactions on the conformations of the BBT series of compounds is unambiguous.

The nature of these interactions is not entirely clear, but one possible source of an attractive potential is a 3-centre-2-electron interaction between lone pairs and relatively low-lying antibonding orbitals.²³ From studies yet to be published, we have evidence that such interactions do not feature in analogous conjugated structures (see Fig. S3 and S4 and associated discussion in the ESI†). We therefore propose that the heteroatom interactions observed in this work are based on large electrostatic interactions between a negatively charged methoxy oxygen and a positively charged thiophene sulfur.³ To corroborate the assumption that electrostatic interactions are also dominant in the non-covalent contacts observed in the BBT series of compounds we carried out a natural bond orbital (NBO) population analysis calculated at the RI-MP2/cc-pVTZ level of theory (Fig. S5, ESI†). Population analysis is the study of charge distribution within molecules, which models partial charge magnitude and location within a molecule. From this study, we observed that in the lowest energy conformers (i.e. those presented in Fig. S5, ESI†), the sulfur atoms participating in non-covalent interactions are positively charged, and align with the negatively charged oxygen or nitrogen atoms, thereby confirming the electrostatic nature of the close contacts. Based on the population analysis we can conclude that: (a) the S⋯S interaction is repulsive while S⋯N and S⋯O are attractive, and (b) that S⋯O and S⋯N interactions are comparable.

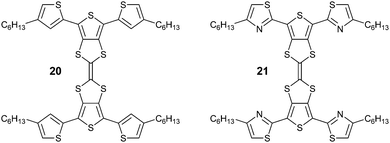
One plausible viewpoint is that the planarity observed in the structures presented in this paper could be attributed to conjugation, i.e. that breaking the extended π-conjugation of the molecules is more expensive in energetic terms than relaxing the S⋯O and S⋯N distances, assuming that such heteroatom interactions are repulsive. However, our hypothesis challenges this assumption, leading to the conclusion that the S⋯O and S⋯N interactions are not repulsive, or at least far less repulsive than previously thought. Hydrogen bonding undoubtedly features in the BBT structures, but we have proven that heteroatom interactions are certainly influential, on their own, in dictating the conformation of these systems. Care needs to be taken to take into account that these electrostatic interactions are in turn influenced by the local molecular environment, so that certain interactions between specific heteroatoms could be attractive in some structures and repulsive in others. This is particularly seen for S⋯S contacts, which we have shown in this and other work. In the case of attractive interactions the electronic structure of the compound might be affected not only by an improvement of the conjugation upon planarisation, but by the direct influence of the heteroatom on the electroactive unit it is interacting with in the planar molecular conformation. In a recent paper,²⁴ we have shown that substitution of peripheral thiophene units by more electron deficient thiazole moieties in an H-shaped hybrid TTF-terthiophene compound (20 and 21, respectively), in fact destabilises the HOMO, which is located on the central TTF unit. Such direct control over frontier orbital energy levels through non-covalent interactions opens up a new strategy of tailoring the electronic structure of organic semiconductors. In this case, as well as in the cases of compounds 6, 7, 9, 11, 12, described here, the “not to bend” scenario brings fascinating opportunities for molecular engineering.

Acknowledgements

P. J. S. thanks the Royal Society for a Wolfson Research Merit Award, E. A. and P. J. S. the European Commission (Marie Curie Action of FP7, Grant No: PIRSES-GA-2013-612670) and A. L. K. the EPSRC for funding (EP/I029141). J. L. B. and V. C. acknowledge generous support from King Abdullah University of Science and Technology. We thank Diamond Light Source for the allocation of beam time MT8521 on beamline I19 and acknowledge the EPSRC UK National Mass Spectrometry Facility (NMSF) at Swansea University for HRMS. All data supporting this research are openly available from http://dx.doi.org/10.15129/24e57291-5208-450f-87b8-ab1fc3143e85.

Notes and references

1. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952.
2. P. Frère and P. J. Skabara, Chem. Soc. Rev., 2005, 34, 69.
3. N. E. Jackson, B. M. Savoie, K. L. Kohlstedt, M. O. de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2013, 135, 10475.
4. J. M. Raimundo, P. Blanchard, P. Frere, N. Mercier, I. Ledoux-Rak, R. Hierle and J. Roncali, Tetrahedron Lett., 2001, 42, 1507.
5. P. Leriche, M. Turbiez, V. Monroche, P. Frère, P. Blanchard, P. J. Skabara and J. Roncali, Tetrahedron Lett., 2003, 44, 649.
6. M. Turbiez, P. Frere and J. Roncali, J. Org. Chem., 2003, 68, 5357.
7. H. J. Spencer, P. J. Skabara, M. Giles, L. McCulloch, S. J. Coles and M. B. Hursthouse, J. Mater. Chem., 2005, 15, 4783.
8. M. Turbiez, P. Frère, M. Allain, N. Gallego-Planas and J. Roncali, Macromolecules, 2005, 38, 6806.
9. H. Pang, P. J. Skabara, S. Gordeyev, J. J. W. McDouall, S. J. Coles and M. B. Hursthouse, Chem. Mater., 2007, 19, 301.
10. G. J. McEntee, P. J. Skabara, F. Vilela, S. Tierney, I. D. W. Samuel, S. Gambino, S. J. Coles, M. B. Hursthouse, R. W. Harrington and W. Clegg, Chem. Mater., 2010, 22, 3000.
11. S. W. Hwang, E. R. Park, Y. J. Chung, Y. J. Bae and I. T. Kim, Bull. Korean Chem. Soc., 2011, 32, 2446.
12. J.-G. Kang, H.-G. Cho, S. K. Kang, C. Park, S. W. Lee, G. B. Park, J. S. Lee and I. T. Kim, J. Photochem. Photobiol., A, 2006, 183, 212.
13. J.-G. Kang, H.-J. Kim, Y.-K. Jeong, M.-K. Nah, C. Park, Y. J. Bae, S. W. Lee and I. T. Kim, J. Phys. Chem. B, 2010, 114, 3791.
14. I. T. Kim, S. W. Lee, S. Y. Kim, G. B. Park, S. H. Lee, S. K. Kang, J. G. Kang, C. M. Park and S. H. Jin, Synth. Met., 2006, 156, 38.
15. J. K. Landquist, J. Chem. Soc. C, 1967, 2212.
16. J. F. Wolfe, B. H. Loo and F. E. Arnold, Macromolecules, 1981, 14, 915.
17. M. Domagała and S. J. Grabowski, J. Phys. Chem. A, 2005, 109, 5683.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
19. M. Katouda and S. Nagase, J. Chem. Phys., 2010, 133, 184103.
20. S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918.
21. J. S. Sears, R. R. Chance and J.-L. Bredas, J. Am. Chem. Soc., 2010, 132, 13313.
22. A. I. Krylov and P. M. W. Gill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 317.
23. A. F. Cozzolino, I. Vargas-Baca, S. Mansour and A. H. Mahmoudkhani, J. Am. Chem. Soc., 2005, 127, 3184.
24. R. G. D. Taylor, J. Cameron, I. A. Wright, N. Thomson, O. Avramchenko, A. L. Kanibolotsky, A. R. Inigo, T. Tuttle and P. J. Skabara, Beilstein J. Org. Chem., 2015, 11, 1148.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods, details of absorption, emission and diffusion coefficient measurements. CCDC 1440981–1440984. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6mh00051g

---