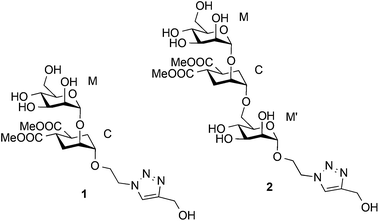
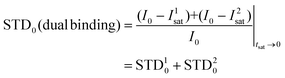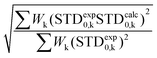Detection and quantitative analysis of two independent binding modes of a small ligand responsible for DC-SIGN clustering†
C.
Guzzi
ab,
P.
Alfarano
c,
I.
Sutkeviciute
def,
S.
Sattin
g,
R.
Ribeiro-Viana
a,
F.
Fieschi
def,
A.
Bernardi
g,
J.
Weiser
c,
J.
Rojo
a,
J.
Angulo
*ah and
P. M.
Nieto
*a
aGlycosystems Laboratory. Instituto de Investigaciones Químicas (IIQ)/cicCartuja. CSIC/US, Americo Vespucio, 49, 41092 Sevilla, Spain. E-mail: pedro.nieto@iiq.csic.es
bDept. of Biotechnology and Biosciences University of Millano-Bicocca Piazza della Scienza 2 20126, Milan, Italy
cAnterio Consult & Research GmbH, Augustaanlage 23 68165 Mannheim, Germany
dUniv. Grenoble Alpes, Institut de Biologie Structurale (IBS), F-38044 Grenoble, France
eCNRS, IBS, F-38044 Grenoble, France
fCEA, IBS, F-38044 Grenoble, France
gDipartimento di Chimica, Universita’ degli Studi di Milano, via Golgi 19, 20133 Milano, Italy
hSchool of Pharmacy, University of East Anglia, Norwich Research Park, Norwich, NR4 7TJ, UK. E-mail: j.angulo@uea.ac.uk
First published on 19th November 2015
Abstract
DC-SIGN (dendritic cell-specific ICAM-3 grabbing non-integrin) is a C-type lectin receptor (CLR) present, mainly in dendritic cells (DCs), as one of the major pattern recognition receptors (PRRs). This receptor has a relevant role in viral infection processes. Recent approaches aiming to block DC-SIGN have been presented as attractive anti-HIV strategies. DC-SIGN binds mannose or fucose-containing carbohydrates from viral proteins such as the HIV envelope glycoprotein gp120. We have previously demonstrated that multivalent dendrons bearing multiple copies of glycomimetic ligands were able to inhibit DC-SIGN-dependent HIV infection in cervical explant models. Optimization of glycomimetic ligands requires detailed characterization and analysis of their binding modes because they notably influence binding affinities. In a previous study we characterized the binding mode of DC-SIGN with ligand 1, which shows a single binding mode as demonstrated by NMR and X-ray crystallography. In this work we report the binding studies of DC-SIGN with pseudotrisaccharide 2, which has a larger affinity. Their binding was analysed by TR-NOESY and STD NMR experiments, combined with the CORCEMA-ST protocol and molecular modelling. These studies demonstrate that in solution the complex cannot be explained by a single binding mode. We describe the ensemble of ligand bound modes that best fit the experimental data and explain the higher inhibition values found for ligand 2.
Introduction
Protein–carbohydrate interactions are the key in many important biological processes, both physiological and pathological. In particular, these interactions play crucial roles in different aspects of the activation of the immune response, since they are involved in pathogen recognition and in the interactions with the cellular host that lead to pathogen neutralization or immune modulation. The key components of these interactions are the animal lectins.1–3 A large number of animal lectins are members of the C-type or the Ca2+-dependent lectin family.4 Dendritic cells (DCs) are antigen-presenting cells (APCs), operating at the interface of innate and acquired immunity as they recognize invading pathogens and thereupon activate the adaptive immune response.4 DCs express a range of Pathogen-Recognition Receptors (PRRs) including Toll-like receptors (TLRs), NOD-like receptors (NLRs), and C-type lectin receptors (CLRs). DC-SIGN (dendritic cell specific ICAM-3 (intercellular adhesion molecule-3) grabbing non-integrin) is a PRR present on the surface of the DCs that belong to the type II C-type lectin family.5DC-SIGN modulates the outcome of the immune response of DCs by recognition of a broad range of microorganisms, including viruses, bacteria, fungi and parasites.6–13 Therefore, it is considered a target for the development of new immunomodulatory and anti-infective therapies. Besides, many studies have revealed DC-SIGN as a promoter of both cis and trans infection, enabling the escape from host immune responses, such as in the case of HIV, Ebola or Hepatitis C virus.14–17 This highlights the remarkable therapeutic interest in developing DC-SIGN antagonists able to inhibit DC-SIGN–pathogen interactions. To improve the affinity and pharmacokinetic properties of natural ligands of DC-SIGN, glycomimetics based on different lead structures have been proposed.18–25
The carbohydrate-binding activity of lectins can be ascribed to a limited portion of the protein that is designated as the carbohydrate-recognition domain (CRD). The CRD of DC-SIGN has a globular structure consisting of five β-strands, two α-helices and four disulphide bridges. A loop protrudes from the protein surface and forms a part of two Ca2+-binding sites. One of these, known as the principal site, is essential for the direct coordination of the carbohydrate hydroxyl groups. Four amino acids (Glu347, Asn349, Glu354 and Asn365) interacting with the Ca2+ ion form the core of the ligand binding site and rule the specificity of the structures recognized.26–29 The CRD, together with the neck region that promotes the lectin's homotetramerization constitute the extracellular domain (ECD) of DC-SIGN.
DC-SIGN binds mannose or fucose epitopes present in the pathogen's envelope glycoproteins such as gp120 (Man9GlcNAc2) or blood group B antigens (Lewis-type). Both structures bind DC-SIGN CRD via Ca2+-mediated interactions in the same binding pocket, named the primary binding site, and with the same Ca2+ atom.26–29
We have investigated in detail the interactions of simple oligosaccharides and new glycomimetic ligands bearing mannose or fucose structures with DC-SIGN by NMR spectroscopy combined with computational methods to address the development of further generations of improved glycomimetic ligands.18,21,23,24,30–36 These studies have led us to propose that, in solution, mannose- and fucose-containing LewisX mimics interact within the same binding site with different but simultaneous modes in a multimodal fashion, according to NMR combined with molecular modeling and full matrix relaxation calculations.30,33,35–38 In a recent work by others this multimodal binding is described in another lectin (HML2 interacting with galactosides) demonstrating that it is not an exceptional feature.39 A recent analysis using high-resolution multinuclear NMR spectroscopy by Prestegard and coworkers provided the 3D structure of the complex of DC-SIGN with LewisX,40 in agreement with our studies on the fucose-containing ligands.21
Based on a similar concept, to mimic the natural Manα1-2Man and Manα1-2Manα1-6Man, a pseudo-mannobioside (1) and a pseudo-mannotrioside (2), were synthesized and tested.20,24,41 Recently we have fully characterized the binding mode of 1 within the DC-SIGN CRD by a combination of NMR analysis, X-ray crystallography, computational tools and other biophysical methods.24 We have demonstrated that it corresponds to a unique well-defined orientation, different from any of the two simultaneous binding modes described for the natural Manα1-2Man.31
The linear pseudo-mannotrioside 2 showed an inhibitory potency one order of magnitude higher than 1 (IC50 measured by SPR competition experiments).24 However, no explanation for the higher affinity and activity could be inferred from the solid-state structure as no additional contacts were observed in comparison with the pseudo-mannobioside 1.24 This affinity difference between 1 and 2 is lost when the compounds are tethered to multivalent scaffolds and both have similarly improved affinity.20 On the other hand, data from alternative biophysical techniques such as Isothermal Titration Calorimetry (ITC), Analytical Ultra Centrifugation (AUC), Static Light Scattering (SLS), and Dynamic Light Scattering (DLS), indicate the formation of a ternary complex, where 2 acts as a bridge capable of clustering two DC-SIGN ECD units (DC-SIGN tetramers) for low ligand-to-protein ratios (2/DC-SIGN ECD ratios between 0.5 and 5).25
Since for large ligand-to-protein ratios the binary ligand–protein complex is favoured, we decided to carry out STD NMR42 and transfer NOESY43 studies on the binding process of 2 with DC-SIGN ECD in the presence of a large excess of 2 (2/DC-SIGN ECD ratio 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Our aim was two-fold: (i) to compare the structural information with that obtained from X-ray crystallography in which a single binary protein–ligand complex was observed, and (ii) to characterize the binding under more relevant conditions to explain the absence of the multivalency effect.25
1). Our aim was two-fold: (i) to compare the structural information with that obtained from X-ray crystallography in which a single binary protein–ligand complex was observed, and (ii) to characterize the binding under more relevant conditions to explain the absence of the multivalency effect.25
Therefore, herein we provide an analysis of the molecular recognition of mimic 2 by DC-SIGN, using a large excess of the ligand (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in order to describe at the atomic level the binary complex 2/DC-SIGN (ECD) by a combination of NMR experiments in solution and computational techniques (molecular modelling and CORCEMA-ST44).
1) in order to describe at the atomic level the binary complex 2/DC-SIGN (ECD) by a combination of NMR experiments in solution and computational techniques (molecular modelling and CORCEMA-ST44).
Results and discussion
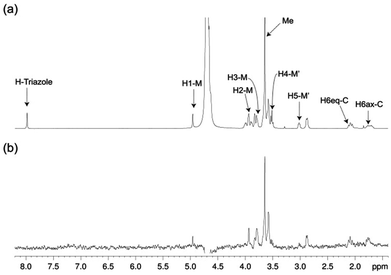
The structure of free pseudo-mannotrioside 2 was studied by NMR and it was fully consistent with the smaller homologous 1 (see details in the Experimental part).25 We have performed NMR studies on the interaction of the pseudo-mannotrioside with DC-SIGN ECD, using a ligand with an attached triazole moiety at the mannose reducing ring (M′, Scheme 1). The triazole moiety improves the spectral dispersion, while it does not affect the binding or the three-dimensional structure.24 The 3D structure of the Man-cyclohexyl moiety of 2 is consistent with the structure of the common part of 1, while the 1–6 linkage of the mannose at the reducing end has the expected structural features of a 1–6 linkage of a gluco configuration, in equilibrium between gg and gt conformers. The additional dispersion caused by the introduction of the triazole moiety in this case is less pronounced than for the analogous 1 and some overlap is observed (Fig. 1a). The chemical shifts of the mannose at the reducing end (M′) shift from the normal values towards the high field ones suggesting some shielding effect of the aromatic electronic cloud of the triazole moiety. The NOE values are consistent with an extended conformation with a similar structure for the Man-cyclohexyl pseudodisaccharide to 1.45 The rest of the molecule exhibits larger flexibility likely to be due to the 1–6 linkage, which has one additional rotatable bond.In a previous work by us, mimic 2 was co-crystallized with monomeric DC-SIGN CRD and the X-ray structure was solved (PDB 2xr6),25 providing a valuable structural insight aiding our parallel analysis. X-ray reported a single binding mode of 2, with identical orientation of the common part of the molecule as for 1, while the reducing mannose in the pseudo-mannotrioside appeared solvent exposed without new additional contacts observed compared with the pseudo-mannobioside 1.25 Thus, no explanation for the higher inhibition values of the pseudo-mannotrioside could be deduced from the solid-state structure. Data from other techniques under low ligand-to-protein ratios indicated that 2 could bridge two DC-SIGN ECD units.25 Therefore, we have performed STD NMR42 and transfer NOESY46 studies of the binding process of 2 with DC-SIGN ECD under conditions of a large excess of the ligand (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to favour a 1
1) to favour a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. The STD NMR experiments of 2 in the presence of DC-SIGN ECD clearly indicate binding in solution (Fig. 1 and 5). In spite of a significant signal overlap, some key intense STD signals could be accurately integrated, and their growth with saturation time is shown in Fig. 2a. Their intensities reflect short distances to the protein surface in the bound state, and their distribution in relative terms shows the main parts of the ligand contacting the protein, called the STD NMR binding epitope (Fig. 2a and c).47
1 complex. The STD NMR experiments of 2 in the presence of DC-SIGN ECD clearly indicate binding in solution (Fig. 1 and 5). In spite of a significant signal overlap, some key intense STD signals could be accurately integrated, and their growth with saturation time is shown in Fig. 2a. Their intensities reflect short distances to the protein surface in the bound state, and their distribution in relative terms shows the main parts of the ligand contacting the protein, called the STD NMR binding epitope (Fig. 2a and c).47
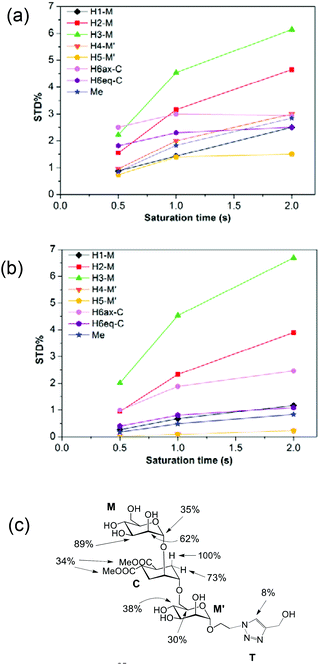 | ||
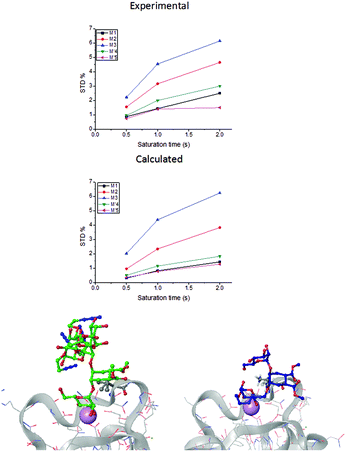
| Fig. 2 STD NMR curves and the ligand epitope map of 2. (a) Experimental STD build-up curves of the binding of 2 to DC-SIGN as a function of saturation time. (b) Theoretical STD intensities predicted by CORCEMA-ST using the Cartesian coordinates of the X-ray structure. (c) Ligand epitope map of 2 binding to DC-SIGN at 25 °C showing STD relative values at the shortest saturation time 0.5 s, for non-overlapped protons. (See the ESI†). | ||
The binding epitope indicates that the non-reducing mannose ring (M) makes additional contacts with the protein, and that the strongest saturation transfer occurs on proton H6ax-C on the cyclohexyl ring of the ligand (Fig. 2). This analysis also confirmed that the triazole moiety is not involved in significant protein contacts.
The STD results for the two first residues (non-reducing mannose, M, and cyclohexyl, C) are similar to those obtained for the pseudo-mannobioside 1 constituted by the same residues.24 They are compatible with the major bound conformation of pseudo-mannotrioside 2 in a binding mode equivalent to that of 1.
This is also in agreement with crystal data, as superimposition of both X-ray complexes25 shows identical bound orientation for the corresponding pseudo-disaccharide moiety, in which the H6ax-C proton is situated close to the methyl groups of Val351, explaining the large saturation received (100%). In addition to these favourable van der Waals interactions, the non-reducing mannose residue coordinates with the Ca2+ ion through its trans-diequatorial hydroxyl groups M-OH3 and M-OH4.24,25
However, and in contrast to the STD NMR results for 1 that were in complete agreement with the X-ray structure (PDB code 2it6), the observed distribution of saturation transferred to the protons of compound 2 did not accurately fit with the structure of the crystallographic complex (PDB code 2xr6).25
While in the X-ray structure the reducing mannose ring (M′) is solvent exposed, in solution we clearly detect the transfer of saturation to H4-M′ and H5-M′ (Fig. 2). This is incompatible with the geometry of the diffraction complex. Moreover, theoretical STD calculations performed with the program CORCEMA-ST44 using the X-ray coordinates of the complex did not reproduce the NMR observations. CORCEMA-ST predicts a lower intensity for H6ax and H6eq of the cyclohexyl ring (C) and, as expected, close to zero STD values for the reducing mannose residue H4-M′ and H5-M′ (Fig. 2b).
Compounds 1 and 2, in spite of their structural similarities, have a different outcome from STD-NMR experiments. We can discard a second low affinity binding site in the protein for 2 contributing to the STD effects, under the conditions for STD experiments (a large excess of the ligand). This circumstance was not detected in the case of 1,25 so we can exclude the participation of an extra binding site taking place only for ligand 2 and not for 1, as 2 corresponds to the structure of 1 with an additional mannose. Consequently, the most likely explanation for the discrepancy between 1 and 2 STD results is the existence of an additional minor mode of interaction for 2 in the same binding site in fast equilibrium with the major one observed in the X-ray complex (PDB code 2xr6) and in solution between DC-SIGN with 1.25 Based on earlier studies on mannose-based ligands,31 potential additional poses of 2 contributing to the STD signals via the interaction of reducing end mannose with the same binding site could be at the origin of this observation. This situation where the fast equilibrium between several binding modes at the same binding site is revealed by distortions of the binding epitope, as in this case, has been already described for this particular protein.21,23,31
Our first attempt to explain the NMR data in solution was to consider that the larger flexibility of the 1–6 linkage might be at the origin of the discrepancy, as several conformations could interact with DC-SIGN CRD. We built additional models based on a 1→6 torsional search. Starting from the X-ray structure, (PDB code 2xr6), the dihedral angles Ψ and ω were varied to generate an ensemble of all the potential conformers. Complexes with DC-SIGN were constructed and superimposed onto the positions of the common pseudodisaccharide (M and C residues, Scheme 1). They were further energy minimized and those with severe steric clashes in the complex were discarded.
The resulting initial models (A, B, C, and D see ESI Fig. S1–S4†) presented distances in agreement with NOE data. Nevertheless, the H4 and H5 protons of the reducing mannose (M′) remained solvent exposed and we did not appreciate any significant effect on their STD theoretical intensities upon changes in 1–6 torsion angles. In general, the theoretical STD build-up curves obtained from CORCEMA-ST calculations using the coordinates of these molecular models were practically equivalent to each other and very similar to those of the crystallographic complex (see the ESI†). Thus, all the attempts to explain the STD NMR results based on variations of the 1–6 linkage were unsuccessful.
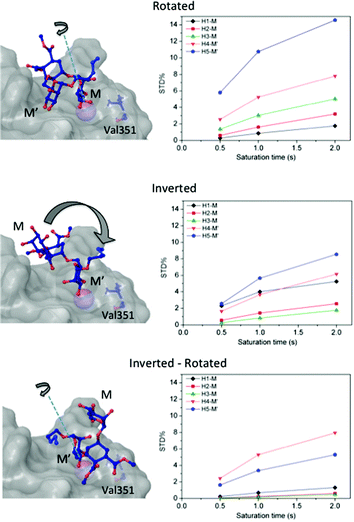
Then, we considered additional potential models of interaction based on the Ca2+ coordination of two hydroxyl groups of the ligand within the DC-SIGN binding site (Fig. 3). We applied rigid-body rotations and translations to the ligand starting from the crystallographic position, conserving the OH-3 and OH-4 Ca2+ coordinations.
Three operations were considered: swapping between OH-3 and OH-4 positions (rotations), changing the coordinating mannose residue (inversion), and the combination of both (inversion–rotation).21,31 The obtained structures were named according to an abbreviated nomenclature relative to the X-ray complex (Fig. 3 and the Experimental section). The CORCEMA-ST STD values for each individual mode of interaction were incompatible with the experimental STD NMR results, meaning that a single 3D molecular binding form was not able to fully explain the NMR data in solution.
Thus, we decided to carry out an analysis of the STD NMR observations assuming that two different binding modes, within the same site, contribute to the final intensities. In this way, the total saturation observed in the STD experiment would be the weighted average of the accumulated saturations corresponding to each binding mode. In this quantitative analysis, we only considered those signals that could be accurately integrated.33 We used the initial slope approach (STD0) to study this bimodal system in order to ensure that the individual STD values are not affected by cross-rebinding processes during the saturation time that would mix the STD information in a very complex way.37
| P + L ⇌ PL1 + PL2 |
Following the initial slope approach, the STD0 of the ensemble can be estimated by the addition of the STD0 contributions from the individual components.
For this multimodal binding analysis of the STD data only those protons that could be accurately integrated were considered avoiding uncertain contributions in the case of overlapped signals. Unfortunately, signal H6eq-C, which has the strongest STD effect, did not have enough dispersion to be quantified. The theoretical bimodal binding equilibrium was considered in all cases as pair-wise combinations of the initial structure, with the coordination to Ca2+ similar to the X-ray structure, with any of the other three molecular models of the complexes (Fig. 4 and Table 1). The NOE R-factor indicated the quality of the prediction. We found that a reasonable theoretical–experimental agreement (NOE R-factor = 0.2)48,49 could be reached by considering the equilibrium of the following two bound conformations in solution: the major one (∼80%) from the initial structure and a minor contribution (∼20%) from the complex as arranged in the “inverted–rotated” model (Table 1).
| Initial-calculated | Inverted–rotated | R-Factor |
|---|---|---|
| 100 | 0 | 0.46 |
| 80 | 20 | 0.22 |
| 60 | 40 | 0.26 |
| 40 | 60 | 0.51 |
| 20 | 80 | 0.79 |
| 0 | 100 | 1.08 |
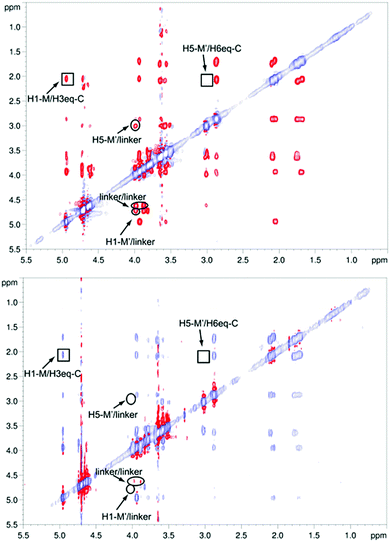
However, the major binding mode is still compatible with a mixture of different conformers (Fig. 4 bottom left, ESI Fig. S1–S4†). The absence of key NOE cross peaks (Fig. 5) did not allow the determination of the conformation around the cyclohexyl 1→6 mannose linkage, very likely due to an increased flexibility in that region of the molecule.50 We carried out NOESY experiments46,51 on pseudo-mannotrioside 2 both free and in the presence of DC-SIGN. Analysis of the spectra (Fig. 5) led us to the conclusion that there are no important conformational changes in the ligand upon binding to DC-SIGN. Only irrelevant differences in the NOE pattern are attributable to protein mediated spin diffusion.52,53
The conformation-defining key NOEs that could be unambiguously detected (highlighted by a square in Fig. 5) are either present (H1-M/H3eq-C) or absent (H5-M′/H6eq-C) equally in both spectra, indicating the same conformation in the free and bound states. As in the STD NMR study, the transfer NOESY data did not fully agree with the X-ray complex. In the crystal structure, the conformation around the 1,6 linkage between the cyclohexyl (C) and the reducing mannose ring (M′) should lead to a strong H5-M′/H6eq-C NOE, which was not observable in any of the spectra (Fig. 5). However, we observed a strong H1-M/H3eq-C NOE, characteristic of the extended conformation around the 1,2 linkage of the mannose-cyclohexyl moiety of the pseudo-trisaccharide, compatible with the X-ray structure,45 and similar to the previously studied pseudo-mannobioside 1.24
Experimental
Synthetic procedures
Thin layer chromatography (TLC) analyses were performed on silica gel 60 F254 precoated on aluminium plates (Merck) and the compounds were detected by staining with sulfuric acid/ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9), with cerium(IV) sulfate (10 g)/phosphomolybdic acid (13 g)/sulfuric acid (60 mL) solution in water (1 L), or with anisaldehyde solution [anisaldehyde (25 mL) with sulfuric acid (25 mL), ethanol (450 mL) and acetic acid (1 mL)], followed by heating at over 200 °C. Column chromatography was carried out on silica gel 60 (0.2–0.5 mm, 0.2–0.063 mm or 0.040–0.015 mm; Merck). 1H- and 13C-NMR spectra were acquired on Bruker DPX-300, Avance III-400 and DRX-500 spectrometers. Unit A refers to the reducing end monosaccharide in the NMR data. Electrospray mass spectra (ESI MS) were recorded with an Esquire 6000 ESI-Ion Trap from Bruker Daltonics.
9), with cerium(IV) sulfate (10 g)/phosphomolybdic acid (13 g)/sulfuric acid (60 mL) solution in water (1 L), or with anisaldehyde solution [anisaldehyde (25 mL) with sulfuric acid (25 mL), ethanol (450 mL) and acetic acid (1 mL)], followed by heating at over 200 °C. Column chromatography was carried out on silica gel 60 (0.2–0.5 mm, 0.2–0.063 mm or 0.040–0.015 mm; Merck). 1H- and 13C-NMR spectra were acquired on Bruker DPX-300, Avance III-400 and DRX-500 spectrometers. Unit A refers to the reducing end monosaccharide in the NMR data. Electrospray mass spectra (ESI MS) were recorded with an Esquire 6000 ESI-Ion Trap from Bruker Daltonics.
Synthesis of compound 2
Pseudo-mannotrioside 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (20 mg, 0.03 mmol), propargyl alcohol (10 μL, 0.02 mmol), CuSO4·5H2O (0.8 mg, 0.003 mmol), sodium ascorbate (1.3 mg, 0.006 mmol) and TBTA (3.4 mg, 0.006 mmol) were dissolved in 1 mL of THF/H2O (1
20 (20 mg, 0.03 mmol), propargyl alcohol (10 μL, 0.02 mmol), CuSO4·5H2O (0.8 mg, 0.003 mmol), sodium ascorbate (1.3 mg, 0.006 mmol) and TBTA (3.4 mg, 0.006 mmol) were dissolved in 1 mL of THF/H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). After 1.5 h, the solvent was evaporated and the resulting crude was purified by flash chromatography in silica (CH2Cl2/MeOH 9
1). After 1.5 h, the solvent was evaporated and the resulting crude was purified by flash chromatography in silica (CH2Cl2/MeOH 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5, 7
2.5, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), furnishing 17 mg (81% yield) of compound 2 as oil. 1H NMR (D2O, 500 MHz): δ 8.04 (s, 1H, Htriazol), 5.03 (bs, 1H, H-1mann′), 4.81 (bs, 1H, H-1mann), 4.73 (s, 2H, CtriazolCH2OH), 4.71–4.68 (m, 2H, CH2N), 4.10–4.05 (m, 1H, OCH2CH2N), 4.04–3.99 (m, 2H, H-2mann′, O6mannCHCHO), 3.98–3.94 (m, 1H, OCH2CH2N), 3.92–3.89 (m, 2H, H-2mann, H-6mann′), 3.88–3.83 (m, 1H, H-3mann′), 3.76–3.70 (m, 9H, H-6mann′, H-6mann, O6mannCHCHO, CH3), 3.69–3.63 (m, 4H, H-6mann, H-3mann, H-4mann′, H-5mann′), 3.58 (at J = 9.5 Hz, 1H, H-4mann), 3.12–3.07 (m, 1H, H-5mann), 2.97–2.93 (m, 2H, CHCOOCH3), 2.20–2.11 (m, 2H, OCHCHeqHax), 1.87–1.74 (m, 2H, OCHCHeqHax). 13C NMR (CDCl3, 100 MHz): δ 177.7, 177.4 (C
3), furnishing 17 mg (81% yield) of compound 2 as oil. 1H NMR (D2O, 500 MHz): δ 8.04 (s, 1H, Htriazol), 5.03 (bs, 1H, H-1mann′), 4.81 (bs, 1H, H-1mann), 4.73 (s, 2H, CtriazolCH2OH), 4.71–4.68 (m, 2H, CH2N), 4.10–4.05 (m, 1H, OCH2CH2N), 4.04–3.99 (m, 2H, H-2mann′, O6mannCHCHO), 3.98–3.94 (m, 1H, OCH2CH2N), 3.92–3.89 (m, 2H, H-2mann, H-6mann′), 3.88–3.83 (m, 1H, H-3mann′), 3.76–3.70 (m, 9H, H-6mann′, H-6mann, O6mannCHCHO, CH3), 3.69–3.63 (m, 4H, H-6mann, H-3mann, H-4mann′, H-5mann′), 3.58 (at J = 9.5 Hz, 1H, H-4mann), 3.12–3.07 (m, 1H, H-5mann), 2.97–2.93 (m, 2H, CHCOOCH3), 2.20–2.11 (m, 2H, OCHCHeqHax), 1.87–1.74 (m, 2H, OCHCHeqHax). 13C NMR (CDCl3, 100 MHz): δ 177.7, 177.4 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 146.9 (Ctriazol), 124.5 (CHtriazol), 99.6 (C-1mann), 98.4 (C-1mann′), 74.3 (C-1CH), 73.3 (C-4mann′), 71.7 (C-5mann), 70.8 (C-3mann), 70.4 (C-2mann′, C-2CH), 69.7 (C-2mann), 69.5 (C-3mann′), 66.7 (C-5mann′), 66.5 (C-4mann), 65.7 (OCH2CH2N), 60.9 (C-6), 54.5 (CtriazolCH2OH), 52.5 (CH3), 49.9 (OCH2CH2N), 38.9 (C-4CH, C-5CH), 26.8 (C-6CH), 26.5 (C-3CH) ESI-MS calc. for C27H43N3O17 (m/z): 681.3; found: 704.3 [M + Na].
O), 146.9 (Ctriazol), 124.5 (CHtriazol), 99.6 (C-1mann), 98.4 (C-1mann′), 74.3 (C-1CH), 73.3 (C-4mann′), 71.7 (C-5mann), 70.8 (C-3mann), 70.4 (C-2mann′, C-2CH), 69.7 (C-2mann), 69.5 (C-3mann′), 66.7 (C-5mann′), 66.5 (C-4mann), 65.7 (OCH2CH2N), 60.9 (C-6), 54.5 (CtriazolCH2OH), 52.5 (CH3), 49.9 (OCH2CH2N), 38.9 (C-4CH, C-5CH), 26.8 (C-6CH), 26.5 (C-3CH) ESI-MS calc. for C27H43N3O17 (m/z): 681.3; found: 704.3 [M + Na].
NMR spectroscopy experiments
NMR spectroscopy experiments were performed on a Bruker Avance DRX 500 MHz spectrometer equipped with a 5 mm inverse triple-resonance probe head, at 298 K. The samples were prepared at 2.3 mM in 550 μL of 99.9% D2O for complete assignment of the ligand signals and at 1 mM, in buffer D2O (150 mM NaCl, 4 mM CaCl2, 25 mM Tris-d11, pD 8) for the experiments in the presence of the receptor (DC-SIGN ECD 19 μM). The same sample was used for both, STD NMR and transfer NOESY experiments. NOESY experiments were carried out using a phase sensitive pulse program with gradient pulses in the mixing time and with presaturation.54 Mixing times of 150, 300, and 500 ms were used for TR-NOESY spectra and 500 ms for NOESY spectra.STD NMR experiments were registered with 3 K scans by using a train of Gaussian shaped pulses of 49 ms (field strength of ca. 80 Hz), an inter-pulse delay of 1 ms and 15 ms spin-lock pulse (field strength of 3.7 kHz) prior to acquisition. The on-resonance frequency was set to 0 ppm while the off-resonance frequency was 40 ppm. An appropriate blank experiment was performed to assure the lack of direct saturation of the ligand protons. Saturation times of 0.5, 1 and 2 s were used to obtain the STD build-up curves and, in each experiment, the recovery delay 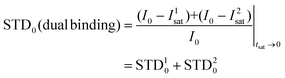
(d1) was inversely varied relative to the saturation time, in order to maintain constant the total time of the experiment.
The experimental STD growth curve (I0 – Isat/I0) of the H6ax proton of the cyclohexane ring could not be fitted to an exponential function (equation: STD (tsat) = STDmax(1 − e – ksat·tsat)), due to its fast relaxation. Therefore, instead of using the analysis of initial slopes of the STD intensities,55 the binding epitope was characterized by using the shortest saturation time (0.5 s) to avoid artefacts due to differential relaxation properties. The ligand epitope map was then obtained by normalization of the whole set of the STD intensities at 0.5 s against the highest STD value (proton H6ax of the cyclohexane ring as a reference), and the result was expressed in percentage.
CORCEMA-ST
The Cartesian co-ordinates of the crystal structure of the complex DC-SIGN CRD/pseudotrisaccharide 2 (pdb code 2xr6) were used for the full relaxation matrix calculations. In order to explain the NMR data in solution, starting from the X-ray complex, further models of the interaction were built (see above), and their Cartesian coordinates used for the full relaxation matrix calculations.As no chemical shift assignment of the protein protons was available, they were predicted by using the program ShiftX 1.1 (http://shiftx.wishartlab.com). Although the experimental irradiation frequency for selective saturation was established at 0 ppm, all the protein protons with chemical shifts predicted to be within the [0.7, −0.7] ppm range were included, as ShiftX56 does not consider the effects of line broadening under the experimental conditions. All exchangeable hydrogen atoms were excluded in the calculations, as the STD NMR experiments were performed in D2O. Identical PDB coordinates for the bound and free proteins were assumed and to reduce the dimensions of the matrices, a cut off of 8 Å from the ligand was used. Assuming a spherical shape for the protein tetramer, the correlation time of the bound ligand was set to 115 ns whereas 0.5 ns was used for the free ligand, and 10 ps for the internal correlation time of methyl groups.44 For this protein–ligand system, the classical assumption of an association step limited by diffusion (on-rate 108 M−1 s−1) was considered. An experimentally determined KD value of pseudo-trimannoside was used (5 μM) and the resulting off-rate was 500 Hz.
The theoretical STD intensities for each binding mode were calculated as percentage fractional intensity changes (Scalc,k = (([(I0k − I(t)k) × 100]/I0k), where k is a particular proton in the complex, and I0k its thermal equilibrium value from the intensity matrix I(t), and the calculation was carried out for the whole set of saturation times experimentally measured. From the resulting STD build-up curves, a mathematical fitting to a mono-exponential equation (STD(tsat) = STDmax (1 − exp(−ksat·tsat)) was performed, and the initial slope STD0,calc was obtained.
For the study of the bimodal system using the initial slope approach:
The STD0i contribution from each “i-th” binding mode will be proportional to the concentration of the complex in the sample ([PLi]; in this case, [PL1] or [PL2]), which will be determined by its corresponding affinity (KD1 or KD2). Nevertheless, for this protein–ligand system, the available data were the dissociation constant from ITC measurements (KD = 5 μM).25 In this measurement, the global affinity of the DC-SIGN lectin for 2 was obtained, so no information on the individual affinities of the potential different binding modes was available. We then considered the final dissociation constant from ITC as a weighted average of the different affinities of each binding mode, and, as an approximation, calculated each theoretical STD contribution using that value. By doing so, the weighting of each complex must be performed then by introducing a population factor for every contributing complex (f1 and f2, for PL1 and PL2, respectively, and f1 + f2 = 1):
| STDOBS0 = f1·STD10 + f2·STD20 |
For this multimodal binding analysis of the STD data only those protons that could be accurately integrated were used, avoiding uncertain contributions in the case of overlapped signals. The theoretical bimodal binding equilibrium was considered in all cases as pair-wise combinations of the X-ray structure with any one of the other three molecular models of the complexes (Fig. 5), and the goodness of the prediction was measured by the NOE R-factor.
The theoretical STD values were compared to the experimental ones using the NOE R-factor defined as:
Molecular modelling
Protein setup: by starting from the crystal structure (resolution = 1.55 Å) of human DC-SIGN in a complex with Man4 (PDB code 1sl4),29 a molecular model of the protein was constructed. By using the Protein Preparation Wizard within the Maestro graphical interface,57 the crystal structure was modified by deleting all crystal waters, assigning bond orders and adding hydrogen atoms. Protonation states of basic and acidic residues were assigned by optimization of the hydrogen-bonding network. A minimization was carried out on the final protein structure by using the OPLS2005 force field.58Ligand conformational search: models A, B, C, and D (based on 1→6 torsional search) were prepared by varying the dihedral angles Ψ and ω according to the most stable values (conformers gg gt and tg) followed by a minimization by using the OPLS2005 force field.
Conclusions
The analysis of the combined NMR data (STD-NMR and transfer NOESY) indicates that at a high ligand to protein ratio (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) the pseudo-mannotrioside ligand 2 binds to DC-SIGN in a binary but multimodal fashion involving both mannose ends, yielding two complexes with similar but asynchronous interactions with the same Ca2+ atom. The main binding mode is similar to that from the X-ray structure but with the participation of additional conformers originating from the flexible 1–6 linkage.
1) the pseudo-mannotrioside ligand 2 binds to DC-SIGN in a binary but multimodal fashion involving both mannose ends, yielding two complexes with similar but asynchronous interactions with the same Ca2+ atom. The main binding mode is similar to that from the X-ray structure but with the participation of additional conformers originating from the flexible 1–6 linkage.
The involvement of both mannose residues of 2 in the binding to DC-SIGN is compatible with the outcomes from other biophysical techniques (AUC, SLS and DLS).25 At a lower ligand to protein ratio (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the two mannose units of 2 cause clustering of DC-SIGN ECD by concurrent interactions of both residues with two protein tetramers explaining the stronger binding observed for 2 compared with the pseudo-disaccharide 1, as we previously reported.62 In addition, this model also explains the reduction of the affinity difference between the two ligands when they were tethered into multivalent systems attached from their reducing ends, because this prevents the second mannose unit of 2 from being involved in binding.25
1), the two mannose units of 2 cause clustering of DC-SIGN ECD by concurrent interactions of both residues with two protein tetramers explaining the stronger binding observed for 2 compared with the pseudo-disaccharide 1, as we previously reported.62 In addition, this model also explains the reduction of the affinity difference between the two ligands when they were tethered into multivalent systems attached from their reducing ends, because this prevents the second mannose unit of 2 from being involved in binding.25
In this work, as the NMR experiments have been registered with a very large excess of the ligand (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) we can ensure that no species other than 1
1 molar ratio) we can ensure that no species other than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are observed by STD-NMR nor transfer NOESY.25 Our results can be explained by the existence of multiple binding modes of carbohydrate-based ligands upon interactions with DC-SIGN as it has been previously reported.18–29 STD NMR has proven to be very sensitive to the existence of minor binding modes with alternative orientations of the ligand within the same binding site,18,21,23,30–39 and it avoids the possible loss of crucial structural information resulting from the individual detection of the major complex. We propose that this alternative mode should be present in the ternary complex between DC-SIGN tetramers and the glycomimetic 2 recently reported by some of us.25 Therefore we suggest that the STD NMR approach for the detection of bimodal binding involving other orientations of the ligand can predict dimerization of protein by ligand bridging interactions.
1 are observed by STD-NMR nor transfer NOESY.25 Our results can be explained by the existence of multiple binding modes of carbohydrate-based ligands upon interactions with DC-SIGN as it has been previously reported.18–29 STD NMR has proven to be very sensitive to the existence of minor binding modes with alternative orientations of the ligand within the same binding site,18,21,23,30–39 and it avoids the possible loss of crucial structural information resulting from the individual detection of the major complex. We propose that this alternative mode should be present in the ternary complex between DC-SIGN tetramers and the glycomimetic 2 recently reported by some of us.25 Therefore we suggest that the STD NMR approach for the detection of bimodal binding involving other orientations of the ligand can predict dimerization of protein by ligand bridging interactions.
Herein, we provide not only a complete description of the DC-SIGN recognition process of glycomimetic 2, but we propose that the STD NMR observation of bimodal binding involving inverted orientations of the ligand can be used as a predictor of protein dimer formation by ligand bridging interactions. In this way, STD NMR studies can avoid misinterpretation of affinity data under low ligand/protein ratio conditions in these particular systems. In addition, this work highlights how a multidisciplinary approach combining different experimental methods with the theoretical ones, is a highly appropriate strategy for the deeper structural characterization of weak protein–carbohydrate interactions.63
Author contributions
CG and JA performed NMR experiments and CORCEMA-ST calculations; CG, PA and JW designed and performed modelling; IS, SS, RR-V contributed with new compounds; CG, JA and PMN analysed the data, FF, AB, JW, JR, JA and PMN designed the research; JA and PMN supervised the project; CG, IS, S, FF, AB, JR, JA and PMN wrote the paper.Acknowledgements
This work was supported by the Spanish Ministry of Science and Innovation (CTQ2009-07168, CTQ2011-23410, CTQ2012-32605; and RYC-2007-01791 to J.A.), and the EU, FEDER. We thank the EU ITN Marie-Curie –program (CARMUSYS – Grant Number 213592) for funding C. G., P. A., I. S. and R. R. F. F. thanks the financial support by the Institut Universitaire de France.Notes and references
- D. C. Kilpatrick, Biochim. Biophys. Acta, 2002, 1572, 187–197 CrossRef CAS
.
- H. J. Gabius, H. C. Siebert, S. Andre, J. Jimenez-Barbero and H. Rudiger, ChemBioChem, 2004, 5, 740–764 CrossRef CAS PubMed
.
- G. R. Vasta, Nat. Rev. Microbiol., 2009, 7, 424–438 CrossRef CAS PubMed
.
- J. Banchereau and R. M. Steinman, Nature, 1998, 392, 245–252 CrossRef CAS PubMed
.
- Y. Van Kooyk and T. B. H. Geijtenbeek, Nat. Rev. Immunol., 2003, 3, 697–709 CrossRef CAS PubMed
.
- F. Baribaud, S. Pohlmann and R. W. Doms, Virology, 2001, 286, 1–6 CrossRef CAS PubMed
.
- F. Halary, A. Amara, H. Lortat-Jacob, M. Messerle, T. Delaunay, C. Houles, F. Fieschi, F. Arenzana-Seisdedos, J. F. Moreau and J. Dechanet-Merville, Immunity, 2002, 17, 653–664 CrossRef CAS PubMed
.
- C. P. Alvarez, F. Lasala, J. Carrillo, O. Muñiz, A. L. Corbí and R. Delgado, J. Virol., 2002, 76, 6841–6844 CrossRef CAS PubMed
.
- E. Navarro-Sanchez, R. Altmeyer, A. Amara, O. Schwartz, F. Fieschi, J. L. Virelizier, F. Arenzana-Seisdedos and P. Desprès, EMBO Rep., 2003, 4, 723–728 CrossRef CAS PubMed
.
- A. Cambi, K. Gijzen, I. J. M. de Vries, R. Torensma, B. Joosten, G. J. Adema, M. G. Netea, B. J. Kullberg, L. Romani and C. G. Figdor, Eur. J. Immunol., 2003, 33, 532–538 CrossRef CAS PubMed
.
- I. van Die, S. J. van Vliet, A. K. Nyame, R. D. Cummings, C. M. C. Bank, B. Appelmelk, T. B. H. Geijtenbeek and Y. van Kooyk, Glycobiology, 2003, 13, 471–478 CrossRef CAS PubMed
.
- A. Marzi, T. Gramberg, G. Simmons, P. Moller, A. J. Rennekamp, M. Krumbiegel, M. Geier, J. Eisemann, N. Turza, B. Saunier, A. Steinkasserer, S. Becker, P. Bates, H. Hofmann and S. Pohlmann, J. Virol., 2004, 78, 12090–12095 CrossRef CAS PubMed
.
- W. E. Paul, Cell, 2011, 147, 1212–1215 CrossRef CAS PubMed
.
- S. Pohlmann, F. Baribaud and R. W. Doms, Trends Immunol., 2001, 22, 643–646 CrossRef CAS PubMed
.
- Y. van Kooyk, B. Appelmelk and T. B. Geijtenbeek, Trends Mol. Med., 2003, 9, 153–159 CrossRef CAS PubMed
.
- P. Y. Lozach, H. Lortat-Jacob, A. De Lacroix de Lavalette, I. Staropoli, S. Foung, A. Amara, C. Houlès, F. Fieschi, O. Schwartz, J. L. Virelizier, F. Arenzana-Seisdedos and R. Altmeyer, J. Biol. Chem., 2003, 278, 20358–20366 CrossRef CAS PubMed
.
- P.-Y. Lozach, A. Amara, B. Bartosch, J.-L. Virelizier, F. Arenzana-Seisdedos, F.-L. Cosset and R. Altmeyer, J. Biol. Chem., 2004, 279, 32035–32045 CrossRef CAS PubMed
.
- J. J. Reina, S. Sattin, D. Invernizzi, S. Mari, L. Martinez-Prats, G. Tabarani, F. Fieschi, R. Delgado, P. M. Nieto, J. Rojo and A. Bernardi, ChemMedChem, 2007, 2, 1030–1036 CrossRef CAS PubMed
.
- M. J. Borrok and L. L. Kiessling, J. Am. Chem. Soc., 2007, 129, 12780–12785 CrossRef CAS PubMed
.
- S. Sattin, A. Daghetti, M. Thepaut, A. Berzi, M. Sanchez-Navarro, G. Tabarani, J. Rojo, F. Fieschi, M. Clerici and A. Bernardi, ACS Chem. Biol., 2010, 5, 301–312 CrossRef CAS PubMed
.
- C. Guzzi, J. Angulo, F. Doro, J. J. Reina, M. Thepaut, F. Fieschi, A. Bernardi, J. Rojo and P. M. Nieto, Org. Biomol. Chem., 2011, 9, 7705–7712 CAS
.
- N. Obermajer, S. Sattin, C. Colombo, M. Bruno, U. Svajger, M. Anderluh and A. Bernardi, Mol. Diversity, 2011, 15, 347–360 CrossRef CAS PubMed
.
- N. Varga, I. Sutkeviciute, C. Guzzi, J. McGeagh, I. Petit-Haertlein, S. Gugliotta, J. Weiser, J. Angulo, F. Fieschi and A. Bernardi, Chem. – Eur. J., 2013, 19, 4786–4797 CrossRef CAS PubMed
.
- M. Thepaut, C. Guzzi, I. Sutkeviciute, S. Sattin, R. Ribeiro-Viana, N. Varga, E. Chabrol, J. Rojo, A. Bernardi, J. Angulo, P. M. Nieto and F. Fieschi, J. Am. Chem. Soc., 2013, 135, 2518–2529 CrossRef CAS PubMed
.
- I. Sutkeviciute, M. Thépaut, S. Sattin, A. Berzi, J. McGeagh, S. Grudinin, J. Weiser, A. Le Roy, J. J. Reina, J. Rojo, M. Clerici, A. Bernardi, C. Ebel and F. Fieschi, ACS Chem. Biol., 2014, 9, 1377–1385 CrossRef CAS PubMed
.
- H. Feinberg, D. A. Mitchell, K. Drickamer and W. I. Weis, Science, 2001, 294, 2163–2166 CrossRef CAS PubMed
.
- Y. Guo, H. Feinberg, E. Conroy, D. A. Mitchell, R. Alvarez, O. Blixt, M. E. Taylor, W. I. Weis and K. Drickamer, Nat. Struct. Mol. Biol., 2004, 11, 591–598 CAS
.
- H. Feinberg, Y. Guo, E. Conroy, D. Mitchell, R. Alvarez, O. Blixt, M. Taylor, K. Drickamer and W. Weis, Glycobiology, 2005, 15, 1195–1195 Search PubMed
.
- H. Feinberg, R. Castelli, K. Drickamer, P. H. Seeberger and W. I. Weis, J. Biol. Chem., 2007, 282, 4202–4209 CrossRef CAS PubMed
.
- J. J. Reina, I. Diaz, P. M. Nieto, N. E. Campillo, J. A. Paez, G. Tabarani, F. Fieschi and J. Rojo, Org. Biomol. Chem., 2008, 6, 2743–2754 CAS
.
- J. Angulo, I. Diaz, J. J. Reina, G. Tabarani, F. Fieschi, J. Rojo and P. M. Nieto, ChemBioChem, 2008, 9, 2225–2227 CrossRef CAS PubMed
.
- G. Timpano, G. Tabarani, M. Anderluh, D. Invernizzi, F. Vasile, D. Potenza, P. M. Nieto, J. Rojo, F. Fieschi and A. Bernardi, ChemBioChem, 2008, 9, 1921–1930 CrossRef CAS PubMed
.
- J. Angulo and P.
M. Nieto, Eur. Biophys. J., 2011, 40, 1357–1369 CrossRef CAS PubMed
.
- D. Doknic, M. Abramo, I. Sutkeviciute, A. Reinhardt, C. Guzzi, M. K. Schlegel, D. Potenza, P. M. Nieto, F. Fieschi, P. H. Seeberger and A. Bernardi, Eur. J. Org. Chem., 2013, 5303–5314 CrossRef CAS
.
- C. Guzzi, J. C. Muñoz-García, P. M. Enriquez-Navas, J. Rojo, J. Angulo and P. M. Nieto, Pure Appl. Chem., 2013, 85(9), 1771–1787 CrossRef CAS
.
-
P. M. Enríquez-Navas, C. Guzzi, J. C. Muñoz-García, P. M. Nieto and J. Angulo, in Methods Mol. Biol, 2015, vol. 1273, pp. 475–487 Search PubMed
.
- J. Angulo, P. M. Enriquez-Navas and P. M. Nieto, Chem. – Eur. J., 2010, 16, 7803–7812 CrossRef CAS PubMed
.
-
P. M. Enriquez-Navas, C. Guzzi, J. C. Muñoz-Garcia, P. M. Nieto and J. Angulo, in Glycoinformatics, ed. T. Lütteke and M. Franck, Humana Press, 2015 Search PubMed
.
- F. Marcelo, F. Garcia-Martin, T. Matsushita, J. Sardinha, H. Coelho, A. Oude-Vrielink, C. Koller, S. André, E. J. Cabrita, H.-J. Gabius, S.-I. Nishimura, J. Jiménez-Barbero and F. J. Cañada, Chem. – Eur. J., 2014, 20, 16147–16155 CrossRef CAS PubMed
.
- K. Pederson, D. A. Mitchell and J. H. Prestegard, Biochemistry, 2014, 53, 5700–5709 CrossRef CAS PubMed
.
- J. J. Reina, O. S. Maldonado, G. Tabarani, F. Fieschi and J. Rojo, Bioconjugate Chem., 2007, 18, 963–969 CrossRef CAS PubMed
.
- M. Mayer and B. Meyer, Angew. Chem., Int. Ed., 1999, 38, 1784–1788 CrossRef CAS
.
- J. Jeener, B. H. Meier, P. Bachmann and R. R. Ernst, J. Chem. Phys., 1979, 71, 4546–4553 CrossRef CAS
.
- V. Jayalakshmi and N. R. Krishna, J. Magn. Reson., 2002, 155, 106–118 CrossRef CAS PubMed
.
- S. Mari, I. Sanchez-Medina, P. Mereghetti, L. Belvisi, J. Jimenez-Barbero and A. Bernardi, Carbohydr. Res., 2007, 342, 1859–1868 CrossRef CAS PubMed
.
- J. Jeener, B. H. Meier, P. Bachmann and R. R. Ernst, J. Chem. Phys., 1979, 71, 4546–4553 CrossRef CAS
.
- M. Mayer and B. Meyer, J. Am. Chem. Soc., 2001, 123, 6108–6117 CrossRef CAS PubMed
.
- N. R. Krishna, D. G. Agresti, J. D. Glickson and R. Walter, Biophys. J., 1978, 24, 791–814 CrossRef CAS PubMed
.
- Y. Xu, I. P. Sugar and N. R. Krishna, J. Biomol. NMR, 1995, 5, 37–48 CrossRef CAS PubMed
.
- The transfer NOE relies on the difference between the correlation times of the free ligand and the ligand when bound to a receptor. Ideally the small and faster moving free ligand shows a weak, slow growing positive NOE, while the complexed ligand should obtain the motional properties from the large and slow receptor leading to a strong, negative and fast growing NOE. As in transfer NOE the averaged NOE is observed, the predominant NOE should correspond to the large molecule, and is observed via the averaged signals of the ligand. Flexible molecules can be described using the Lipari–Szabo formalism where the order parameter and internal motions modify the influence of the global correlation time on relaxation properties. Consequently, regions of a molecule with larger flexibility show smaller relaxation parameters than those inferred by the global correlation time for the rigid zones and therefore show smaller relaxation rates and NOE. Thus, as the 1–6 linkages have larger flexibility, faster internal motions and smaller order parameters, and hence reduced NOE values, the observed averaged transfer NOE peaks might be underestimated.
- A. Kumar, R. R. Ernst and K. Wüthrich, Biochem. Biophys. Res. Commun., 1980, 95, 1–6 CrossRef CAS PubMed
.
- F. Ni, Prog. Nucl. Magn. Reson. Spectrosc., 1994, 26, 517–606 CrossRef CAS
.
- Spin diffusion was previously observed for the binding of the pseudomannobioside to DC-SIGN. In the present work, a sign of the presence of spin diffusion is the observation of the intra-residual cross peak H3-M/H1-M, corresponding to a fixed intra-ring distance, in the trNOESY spectrum, which is not observed in the free state (NOESY). Besides, other inter-residual NOEs (H3-M/H6eq-C) visible only in the presence of DC-SIGN (ECD) also involve the proton H3 of the non-reducing mannose. Significantly, this proton is very close to the protein surface as shown in the X-ray structure and observed in solution by its strong STD signal. This supports the protein-mediated spin diffusion pathway through this proton as the origin of these cross peaks.
- R. Wagner and S. Berger, J. Magn. Reson., Ser. A, 1996, 123, 119–121 CrossRef CAS PubMed
.
- M. Mayer and T. L. James, J. Am. Chem. Soc., 2004, 126, 4453–4460 CrossRef CAS PubMed
.
- S. Neal, A. M. Nip, H. Zhang and D. S. Wishart, J. Biomol. NMR, 2003, 26, 215–240 CrossRef CAS PubMed
.
-
Schrödinger Release 2013-2: Maestro version 9.5, Schrödinger, LLC, New York, NY, 2013 Search PubMed
.
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed
.
- W. C. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129 CrossRef CAS
.
- J. Weiser, P. S. Shenkin and W. C. Still, J. Comput. Chem., 1999, 20, 217–230 CrossRef CAS
.
- I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011–5019 CrossRef
.
- J. Luczkowiak, S. Sattin, I. Sutkeviciute, J. Juan Reina, M. Sanchez-Navarro, M. Thepaut, L. Martinez-Prats, A. Daghetti, F. Fieschi, R. Delgado, A. Bernardi and J. Rojo, Bioconjugate Chem., 2011, 22, 1354–1365 CrossRef CAS PubMed
.
- T. K. Dam and C. F. Brewer, Glycobiology, 2010, 20, 270–279 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Conformational analysis, models, calculated STD relative to ω orientation with STD values and NMR spectra. See DOI: 10.1039/c5ob02025e |
| This journal is © The Royal Society of Chemistry 2016 |