Mechanism, chemoselectivity and enantioselectivity for the rhodium-catalyzed desymmetric synthesis of hydrobenzofurans: a theoretical study

Abstract

Rhodium-catalyzed desymmetrization of cyclohexadienones is an efficient method for the asymmetric synthesis of hydrobenzofurans. The newly reported density functional theory (DFT) method MN12-L is used to investigate the mechanism, chemoselectivity and enantioselectivity for this type of reaction. Computational results indicate that the preferred pathway involves transmetallation to form an aryl–rhodium compound, alkyne insertion, intramolecular olefin insertion, and protonation to generate the hydrobenzofuran product. The enantioselectivity is controlled by the intramolecular olefin insertion step, which is ascribed to the steric repulsions between the ligand and substrate. In addition, the generation of a side product via a second intermolecular alkyne insertion has also been considered in calculations.

---

Introduction

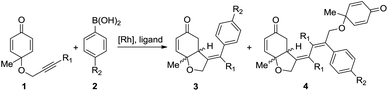
As the structural core in numerous biologically important natural products, chiral cis-hydrobenzofurans are considered to be attractive targets for synthetic chemists.¹ Chiral organocatalyst catalyzed intramolecular desymmetrization of cyclohexadienones² has been proven to be a useful approach for the synthesis of cis-hydrobenzofuran derivatives, such as Rauhut–Currier reaction³ and Stetter reaction.⁴ Besides, transition-metal catalysis has also emerged as a versatile and powerful tool among various synthetic methods.^5,6 In the presence of transition-metals, new carbon–carbon bonds can be formed easily via the unsaturated bond insertion into metal–carbon bonds.⁷ However, how to control the regio- and enantioselectivity in this type of insertion still remains a big challenge. More experimental⁸ and theoretical investigations⁹ need to be done to reveal the origin of selectivity.

Recently, rhodium-catalyzed asymmetric desymmetrization¹⁰ of cyclohexadienones was reported by the Lautens¹¹ group and the Lin group,¹² which provided a useful methodology for the synthesis of functionalized hydrobenzofurans. As shown in Scheme 1, the reaction between cyclohexadienone-tethered alkyne 1 and arylboronic acid 2 using a rhodium(I)-catalyst can afford cis-hydrobenzofuran 3 in yields up to 76%.¹¹ When a 3,4-dimethoxy-phenyl derivative diene ligand is added, an enantioselective product can be formed with up to 88% enantiometric excess (ee). In some cases, a side product 4 is also observed with about 19% yield. Almost at the same time, Lin reported a similar process for the rhodium-catalyzed synthesis of hydrobenzofurans.¹² The chiral bisphosphine ligand (R)-BINAP has numerous unique features, and exhibits extremely high chiral recognition ability in catalytic reactions.¹³ When the (R)-BINAP was employed, an enantioselective product, hydrobenzofurans, was obtained in 99% yield and 99% ee.

Scheme 1 The rhodium-catalyzed symmetric desymmetrization of cyclohexadienones.

Plausible mechanisms for this rhodium-catalyzed synthesis of hydrobenzofurans were individually proposed by Lautens and Lin; however, the generation of chemoselectivity and enantioselectivity is still unclear. Density functional theory (DFT) calculations were therefore performed to reveal the mechanism, chemoselectivity, enantioselectivity, and the ligand effect of this type of reaction.

Computational methods

All the DFT calculations were carried out with the GAUSSIAN 09 series of programs.¹⁴ The B3LYP¹⁵ functional with the standard 6-31G(d) basis set¹⁶ (LanL2DZ basis set¹⁷ for rhodium atoms) was used for geometry optimizations. Harmonic frequency calculations were performed for all stationary points to confirm whether they were local minima or transition states and to derive the thermochemical corrections for the enthalpies and free energies. The MN12-L functional,¹⁸ recently proposed by the Truhlar group, which could give more accurate energy information, was used to calculate the single-point energies. The solvent effects were determined by single-point calculations of the gas-phase stationary points with the SMD solvation model.¹⁹ The larger basis set 6-311+G(d,p)²⁰ (LANL08 basis set²¹ for rhodium atoms) was used in solvation single-point calculations. The energies given in this paper are the MN12-L calculated Gibbs free energies in methanol solvent.

Results and discussion

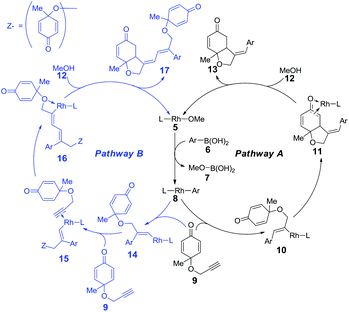
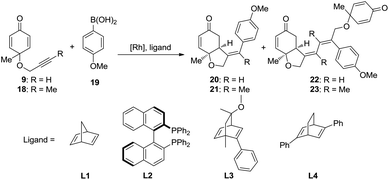
As shown in the mechanistic map²² (Scheme 2), two possible pathways were taken into account. Both of the pathways begin with the transmetallation between methoxyrhodium complex 5 and aryl boronic acid 6, which generates the aryl–rhodium intermediate 8. In pathway A, the cis-alkyne insertion of reactant 9 into the rhodium–carbon bond affords intermediate 10, in which the aryl group is linked with the terminal carbon of the alkene group. Subsequent intramolecular alkene insertion results in complex 11, followed by metholysis that leads to the release of product 13, as well as the regeneration of active catalyst 5. The enantioselectivity is thought to be controlled by the intramolecular alkene insertion step. In pathway B, after the intramolecular alkyne insertion, rhodium is linked with the terminal alkynyl carbon. Following the intermolecular alkyne insertion of another molecular reactant 9, complex 15 forms. Finally, the corresponding metholysis might give side product 17 and active catalyst 5.

Scheme 2 Proposed catalytic cycle for the rhodium-catalyzed synthesis of hydrobenzofurans.

The rhodium-catalyzed coupling reaction of cyclohexadienone-tethered alkyne with boronic acid 19 was chosen as the model reaction, and norbornadiene L1 was chosen as the model ligand to theoretically study the mechanism of this type of reaction (Scheme 3). Furthermore, (R)-BINAP L2 and chiral bicyclo[2.2.2]octane type ligands L3 and L4 were employed to study the enantioselectivity of the asymmetric desymmetrization step.

Scheme 3 Model reactions for the mechanistic investigation.

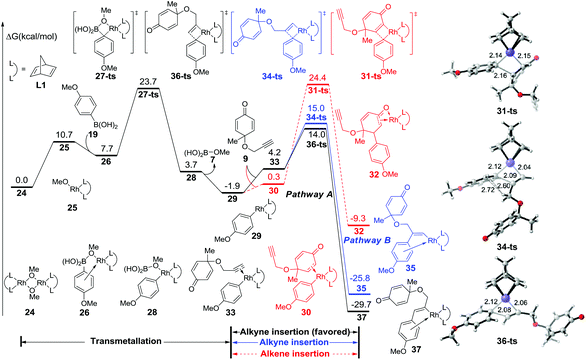
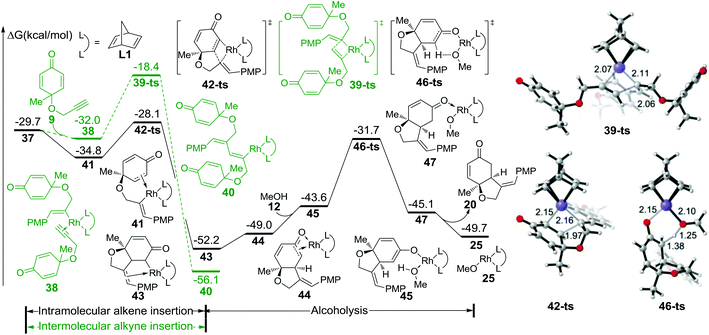
The free energy profile for the initial step is summarized in Fig. 1. After the dissociation of dimeric rhodium complex 24, the monomeric rhodium complex 25 undergoes transmetallation with reactant 19via a four-membered-ring transition state 27-ts with a barrier of 16.0 kcal mol⁻¹. The aryl–rhodium complex 29 is then generated with the release of methylborate. There are two reaction modes for the subsequent insertion of complex 9 into intermediate 29. The reaction free energy of alkyne insertion from intermediate 29 to 37via transition state 36-ts is 15.9 kcal mol⁻¹. Following this pathway, the major product 20 would be generated. In the other case, the insertion via transition state 34-ts would irreversibly generate intermediate 35, which is the precursor of side product 22. The relative free energy of the transition state 34-ts is 1.0 kcal mol⁻¹ higher than that of 36-ts because of the steric repulsion between the substituted groups of the alkyne and aryl groups (Fig. 1). Therefore, pathway A is favourable compared with pathway B, which leads to the formation of the major product 20. This result is consistent with experimental observations. Besides, the alkene group insertion into aryl–rhodium via transition state 31-ts was also calculated. The activation free energy is 26.3 kcal mol⁻¹, which is much higher than those of triple bond insertion transition states 34-ts and 36-ts.

Fig. 1 Free energy profile for the initial step and geometries of 31-ts, 34-ts, and 36-ts. The values given in kcal mol⁻¹ are the MN12-L calculated relative free energies in methanol solvent. The values of bond lengths are given in angstroms.

As shown in Fig. 2, intermediate 37 could isomerize into 41 through the coordination of intramolecular alkene to rhodium; this process is exothermic by 5.1 kcal mol⁻¹. Subsequently, intramolecular alkene insertion takes place via transition state 42-ts (the geometry is shown in Fig. 2) with only a barrier of 6.7 kcal mol⁻¹, and irreversibly generates intermediate 43. When intermediate 45 is formed with the coordination of methanol, the protonation of the carbon atom occurs via transition state 46-ts with a 20.5 kcal mol⁻¹ energy barrier. After releasing product 20, the active catalyst species 25 is regenerated to accomplish the catalytic cycle. The competition of intermolecular alkyne insertion has also been considered. When another molecular substrate 9 coordinates to intermediate 37, the relative free energy decreases by 2.3 kcal mol⁻¹. The following alkyne insertion would occur via transition state 39-ts, but the relative free energy for that transition state is 9.7 kcal mol⁻¹ higher than that of transition state 42-ts. Therefore, the insertion of another molecular alkyne is unfavorable.

Fig. 2 Free energy profile for the formation of the major product and geometries of transition states 39-ts, 42-ts, and 46-ts. The values given in kcal mol⁻¹ are the MN12-L calculated relative free energies in methanol solvent. The values of bond lengths are given in angstroms. PMP = p-methoxy phenyl.

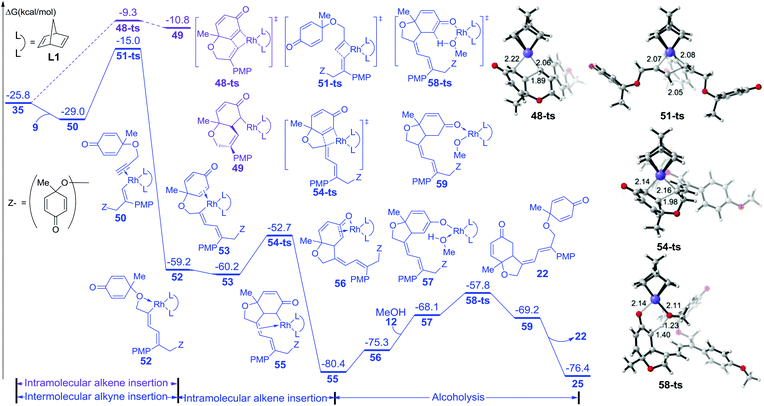
On the other hand, the free energy profile for the generation of side product 22 is summarized in Fig. 3. When intermediate 35 is formed, intramolecular alkene insertion via transition state 48-ts is inhibited because there is a (Z)-double bond in the six-membered-ring of insertion product 49. Another molecular alkyne insertion could take place through transition state 51-ts, generating the intermediate 52 irreversibly. The isomerization from 52 to 53 is exothermic by 1.0 kcal mol⁻¹ due to the coordination of the alkene group. The subsequent alkene insertion via transition state 54-ts forms intermediate 55. The coordination of methanol forms intermediate 57. Then the rhodium–carbon bond in intermediate 57 could be protonated by methanol via transition state 58-ts with an overall activation free energy of 22.6 kcal mol⁻¹. After releasing one side product 22, the active catalyst species 25 is regenerated.

Fig. 3 Free energy profile for the formation of side products and geometries of transition states 48-ts, 51-ts, 54-ts, and 58-ts. The values of bond lengths are given in angstroms. The values given in kcal mol⁻¹ are the MN12-L calculated relative free energies in methanol solvent. PMP = p-methoxy phenyl.

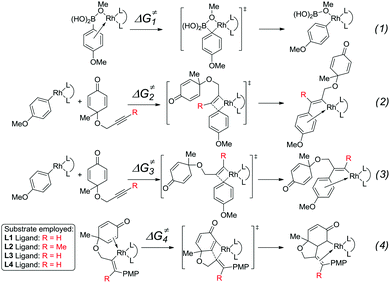
The mechanism and reactivity for the rhodium-catalyzed synthesis of hydrobenzofurans with ligand L2 were also studied. The activation free energies for the key steps are listed in Table 1 (the full potential energy surface for this reaction with ligand L2 is given in Fig. S1 of the ESI†). When the (R)-BINAP L2 is used as ligand, the activation free energy (ΔG^≠₂) of the insertion step (eqn (2)) is 13.5 kcal mol⁻¹. The activation energy (ΔG^≠₃) with ligand L2 of the insertion (eqn (3)) leading to the side product is 18.3 kcal mol⁻¹, which is 4.8 kcal mol⁻¹ higher than that of the insertion (eqn (2)) leading to the major product. Theoretical results indicate that compared to ligand L1, a lower amount of side products would be obtained when ligand L2 is used. The activation free energy (ΔG^≠₄) for intramolecular alkene insertion (eqn (4)) with ligand L2 is 5.5 kcal mol⁻¹, which is 1.2 kcal mol⁻¹ lower than that with ligand L1. The reactivities of these key steps with ligands L3 and L4 are also listed in Table 1.²³

Table 1 Free energies of 27-ts, 34-ts, 36-ts and 42-ts with L1–L4

Entry	Ligand	ΔG^≠1	ΔG^≠2	ΔG^≠3	ΔG^≠4
The values of this table are given in kcal mol^−1.
1	L1	16.0	15.9	16.9	6.7
2	L2	14.8	13.5	18.3	5.5
3	L3	14.5	12.8	14.8	5.7
4	L4	15.1	9.0	12.6	5.6

---

The experimental results indicate that when ligand L1, L2, or L3 is used, a high yield of the major product is obtained. However, a very low yield of the product is obtained when ligand L4 is used. This result is in conflict with the calculated energy profiles (Table 1 and Fig. S1, S3, and S5†). Therefore, the binding energies of ligands L1–L4 were calculated to understand the different reactivities. As shown in Fig. 4, intermediate 26 was chosen as the model to study the binding energy of ligands. The binding energy of the (R)-BINAP ligand L2 is 7.5 kcal mol⁻¹ higher than that of ligand L1, when intermediate 26-L2 is formed. The ligand exchange energy with ligand L3 is 0.8 kcal mol⁻¹, which indicates that the binding of ligand L3 is weaker than that of ligand L2. The ligand exchange energies with ligand L4 are 2.3 kcal mol⁻¹. Therefore, the lower binding energies of ligands L4 result in a lower yield of the major product.

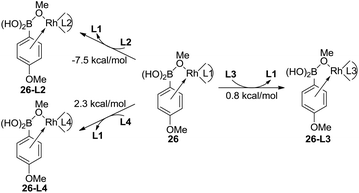Fig. 4 Ligand exchange energies of intermediate 26 for ligands L2–L4. The values are Gibbs free energies.

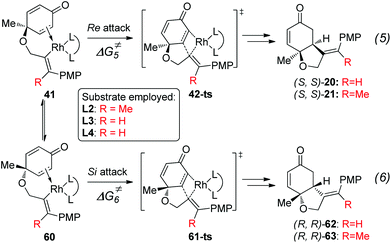
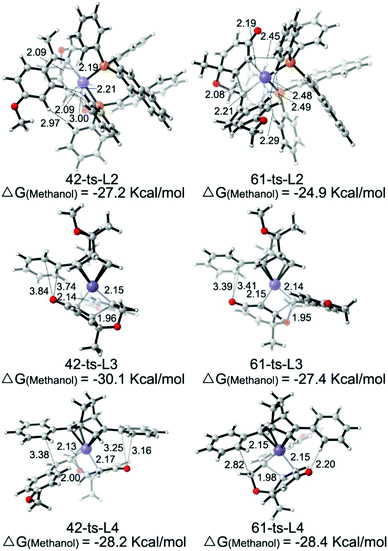
As shown in Fig. 5, the enantioselectivity for the desymmetrization of cyclohexadienone is controlled by the free energy difference between the irreversible intramolecular alkene insertion steps via the four-membered-ring transition state 42-ts or 61-ts. The Re-face attack (via transition state 42-ts) would lead to the (4S,5S)-cyclohexanone product, while the (4R,5R)-cyclohexanone product would be generated by Si-face attack via transition state 61-ts.

Fig. 5 Enantioselectivity determining step for the desymmetrization of cyclohexadienone.

Based on these results, the ee values were predicted from the Eyring equation (eqn (7)), where R is the gas constant, T is the absolute temperature, and k is the reaction rate constant. The calculated ee value is derived from this equation at 300 K in methanol.

ee = (k_S/k_R − 1)/(k_S/k_R + 1) = (e^ΔΔG≠/RT − 1)/(e^ΔΔG≠/RT + 1) (7)

The theoretically calculated and experimentally observed ee values^11,12 with ligands L2–L4 are shown in Table 2.²⁴ When ligand L2 is used, the calculated ee is 96%, which is consistent with experimental observations. The enantioselectivity is determined by using the energy difference between transition states 42-ts-L2 and 61-ts-L2 (Fig. 6). The closest H⋯H distance is 2.29 Å in transition state 61-ts-L2. This result indicates that due to the steric repulsion between the aryl moiety of the substrate and the phenyl group of the ligand, the relative free energy of 61-ts-L2 is 2.3 kcal mol⁻¹ higher than that of 42-ts-L2. When ligand L3 is used, the calculated ee value is 22% higher than the experimentally observed value. In the geometry of 61-ts-L3, the closest distance between the oxygen atom in the carbonyl group of the substrate and a carbon atom in the phenyl group of the ligand is 3.39 Å. Thus, the higher relative free energy of 61-ts-L3 can be attributed to the steric repulsion between the carbonyl group of the substrate and the phenyl group of the ligand. When ligand L4 is used, the calculated ee value is −17%, which is close to experimental observations. In the geometry of 42-ts-L4, the C⋯O distances between the oxygen atom in the carbonyl group of the substrate and carbon atoms in the phenyl group of the ligand are 3.16 Å and 3.25 Å, but the distance between the phenyl group of the ligand and the 4-methoxyphenyl group of the substrate is 3.38 Å. Therefore, the low enantioselectivity can be attributed to an attractive, non-covalent interaction between the phenyl group of the ligand and the p-methoxy phenyl group of the substrate.

Fig. 6 Geometries of transition states 42-ts and 61-ts with ligands L2, L3 and L4. The values of bond lengths are given in angstroms. The values given in kcal mol⁻¹ are the MN12-L calculated relative free energies.

Table 2 Calculated ee values at 300 K and experimentally observed ee values with ligands L2–L4

Entry	Ligand	ΔΔG^≠ = (ΔG^≠6–ΔG^≠5)	ee (calc.)	ee (exp.)
1	L2	2.3	96%	96%
2	L3	2.7	98%	76%
3	L4	−0.2	−17%	−6%

---

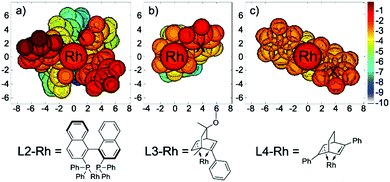
To better illustrate the steric repulsions at different regions of the ligand, 2D contour maps along the z-axis of the van der Waals surface²⁵ of L2-Rh, L3-Rh and L4-Rh are plotted in Fig. 7. The geometries of L2-Rh, L3-Rh and L4-Rh are respectively derived from the transition state structure of 61-ts-L2, 61-ts-L3 and 42-ts-L4 by omitting the substrates.

Fig. 7 2D contour maps of the van der Waals surface of ligands L2, L3 and L4 with rhodium. Distances are given in Å. Rh is located at the origin of the coordinate system in the contour maps. The contour line of zero is defined as in the same plane of the Rh atom. Negative distance (blue) indicates that the atoms on the ligand are farther away from the substrate; positive distance (red) indicates that the atoms on the ligand are closer to the substrate.

When ligand L2 is used, the atoms closest to the substrates, which result in the most steric repulsion, are two of the standing phenyl groups (labeled in red). This highly hindered region is very close to the phenyl group on the substrate of 61-ts-L2 (labeled “X” in Fig. 7a). Similarly, the strong stereogenic control by ligands L3 and L4 can be attributed to the repulsion between the phenyl group on the ligand and the substrate (labeled “X” in Fig. 7b and c). These figures provide a straightforward explanation for the enantioselectivities observed in the asymmetric synthesis of hydrobenzofurans by a rhodium-catalyzed cyclohexadienone reaction.

Conclusions

The newly reported density functional theory method MN12-L was employed to clarify the mechanism, reactivity, and enantioselectivity for the asymmetric synthesis of hydrobenzofurans through rhodium-catalyzed desymmetrization of cyclohexadienone reaction. The reaction pathway involves the transmetallation of aryl boronic acid to form an aryl–rhodium compound, intermolecular alkyne insertion, intramolecular olefin insertion, and protonation to generate the hydrobenzofuran product. Another type of intermolecular alkyne insertion would lead to the generation of a side product, which is in competition with the major pathway. The addition of biphosphine- and diene-type ligands results in a similar reactivity as the corresponding activation energies of the key steps are close. However, the bulky diene-type ligands give very low yield and enantioselectivity, which can be attributed to the low binding energies. Moreover, the calculated enantioselectivity, which corresponds well with the experimental observations, can be explained by the steric repulsion between the substrate and ligand.

Acknowledgements

We thank Professor Stephen G. Newman of University of Ottawa, and Professor Mark Lautens and Doctor Juliane Keilitz of University of Toronto for helpful discussions. This work was supported by the National Natural Science Foundation of China (grants 51302327 and 21372266) and the Foundation of 100 Young Chongqing University (project 0903005203191). We are also thankful for the project (no. 106112015CDJZR228806) supported by the Fundamental Research Funds for the Central Universities (Chongqing University). This work was supported by the China Scholarship Council.

Notes and references

1. (a) Y.-Q. Chen, Y.-H. Shen, Y.-Q. Su, L.-Y. Kong and W.-D. Zhang, Chem. Biodiversity, 2009, 6, 779–783; (b) P. D. Brown, A. C. Willis, M. S. Sherburn and A. L. Lawrence, Org. Lett., 2012, 14, 4537–4539; (c) K. Zhao, G.-J. Cheng, H. Yang, H. Shang, X. Zhang, Y.-D. Wu and Y. Tang, Org. Lett., 2012, 14, 4878–4881; (d) J. Tian, Q.-S. Zhao, H.-J. Zhang, Z.-W. Lin and H.-D. Sun, J. Nat. Prod., 1997, 60, 766–769; (e) Y.-P. Gao, Y.-H. Shen, S.-D. Zhang, J.-M. Tian, H.-W. Zeng, J. Ye, H.-L. Li, L. Shan and W.-D. Zhang, Org. Lett., 2012, 14, 1954–1957; (f) J. K. Hexum, R. Tello-Aburto, N. B. Struntz, A. M. Harned and D. A. Harki, ACS Med. Chem. Lett., 2012, 3, 459–464.
2. (a) X. Yang, J. Wang and P. Li, Org. Biomol. Chem., 2014, 12, 2499–2513; (b) N. Miyamae, N. Watanabe, M. Moritaka, K. Nakano, Y. Ichikawa and H. Kotsuki, Org. Biomol. Chem., 2014, 12, 5847–5855; (c) Q. Gu and S.-L. You, Org. Lett., 2011, 13, 5192–5195; (d) H. U. Vora and T. Rovis, Aldrichimica Acta, 2011, 44, 3–11; (e) Q. Gu and S.-L. You, Chem. Sci., 2011, 2, 1519–1522.
3. (a) X. Su, W. Zhou, Y. Li and J. Zhang, Angew. Chem., Int. Ed., 2015, 54, 6874–6877; (b) S. Takizawa, T. M.-N. Nguyen, A. Grossmann, D. Enders and H. Sasai, Angew. Chem., Int. Ed., 2012, 51, 5423–5426.
4. (a) R. Kuniyil and R. B. Sunoj, Org. Lett., 2013, 15, 5040–5043; (b) M.-Q. Jia, C. Liu and S.-L. You, J. Org. Chem., 2012, 77, 10996–11001; (c) N. E. Wurz, C. G. Daniliuc and F. Glorius, Chem. – Eur. J., 2012, 18, 16297–16301; (d) A. Bhunia, S. R. Yetra, S. S. Bhojgude and A. T. Biju, Org. Lett., 2012, 14, 2830–2833; (e) M.-Q. Jia and S.-L. You, Chem. Commun., 2012, 48, 6363–6365; (f) Q. Liu and T. Rovis, J. Am. Chem. Soc., 2006, 128, 2552–2553; (g) Q. Liu and T. Rovis, Org. Process Res. Dev., 2007, 11, 598–604.
5. For reviews, see: (a) X.-F. Wu, H. Neumann and M. Beller, Chem. Soc. Rev., 2011, 40, 4986–5009; (b) E.-i. Negishi, C. Copéret, S. Ma, S.-Y. Liou and F. Liu, Chem. Rev., 1996, 96, 365–393; (c) B. E. Rossiter and N. M. Swingle, Chem. Rev., 1992, 92, 771–806; (d) K. A. Kalstabakken and A. M. Harned, Tetrahedron, 2014, 70, 9571–9585; (e) A. Marinetti, H. Jullien and A. Voituriez, Chem. Soc. Rev., 2012, 41, 4884–4908; (f) L. F. Tietze, Chem. Rev., 1996, 96, 115–136.
6. As recent examples of transition-metal catalyzed desymmetrization of cyclohexadienones reactions, see: (a) P. Liu, Y. Fukui, P. Tian, Z.-T. He, C.-Y. Sun, N.-Y. Wu and G.-Q. Lin, J. Am. Chem. Soc., 2013, 135, 11700–11703; (b) R. Tello-Aburto and A. M. Harned, Org. Lett., 2009, 11, 3998–4000; (c) S. Cai, Z. Liu, W. Zhang, X. Zhao and D. Z. Wang, Angew. Chem., Int. Ed., 2011, 50, 11133–11137; (d) R. Imbos, M. H. G. Brilman, M. Pineschi and B. L. Feringa, Org. Lett., 1999, 1, 623–625; (e) K. Takenaka, S. C. Mohanta and H. Sasai, Angew. Chem., Int. Ed., 2014, 53, 4675–4679.
7. (a) T. Hayashi and K. Yamasaki, Chem. Rev., 2003, 103, 2829–2844; (b) H. J. Edwards, J. D. Hargrave, S. D. Penrose and C. G. Frost, Chem. Soc. Rev., 2010, 39, 2093–2105; (c) G. P. Howell, Org. Process Res. Dev., 2012, 16, 1258–1272; (d) Z.-Q. Wang, C.-G. Feng, M.-H. Xu and G.-Q. Lin, J. Am. Chem. Soc., 2007, 129, 5336–5337; (e) E. Okazaki, R. Okamoto, Y. Shibata, K. Noguchi and K. Tanaka, Angew. Chem., Int. Ed., 2012, 51, 6722–6727; (f) T. A. Davis, T. K. Hyster and T. Rovis, Angew. Chem., Int. Ed., 2013, 52, 14181–14185; (g) R. Shintani, W.-L. Duan and T. Hayashi, J. Am. Chem. Soc., 2006, 128, 5628–5629; (h) T. Seiser and N. Cramer, Chem. – Eur. J., 2010, 16, 3383–3391; (i) Y. Takaya, M. Ogasawara and T. Hayashi, J. Am. Chem. Soc., 1998, 120, 5579–5580.
8. (a) S. Gosiewska, J. A. Raskatov, R. Shintani, T. Hayashi and J. M. Brown, Chem. – Eur. J., 2012, 18, 80–84; (b) D. A. DiRocco, E. L. Noey, K. N. Houk and T. Rovis, Angew. Chem., Int. Ed., 2012, 51, 2391–2394; (c) C. Shao, H.-J. Yu, N.-Y. Wu, C.-G. Feng and G.-Q. Lin, Org. Lett., 2010, 12, 3820–3823; (d) R. Tello-Aburto, K. A. Kalstabakken, K. A. Volp and A. M. Harned, Org. Biomol. Chem., 2011, 9, 7849–7859; (e) Y. Li and M.-H. Xu, Org. Lett., 2014, 16, 2712–2715.
9. (a) H.-L. Qin, J.-B. Han, J.-H. Hao and E. A. B. Kantchev, Green Chem., 2014, 16, 3224–3229; (b) L. R. Domingo, R. J. Zaragozá, J. A. Saéz and M. Arnó, Molecules, 2012, 17, 1335–1353; (c) E. A. B. Kantchev, S. R. Pangestu, F. Zhou, M. B. Sullivan and H.-B. Su, Chem. – Eur. J., 2014, 20, 15625–15634; (d) K. Sasaki, T. Nishimura, R. Shintani, E. A. B. Kantchev and T. Hayashi, Chem. Sci., 2012, 3, 1278–1283; (e) E. A. B. Kantchev, Chem. Sci., 2013, 4, 1864–1875; (f) E. A. B. Kantchev, Chem. Commun., 2011, 47, 10969–10971; (g) S. Liu, H. Shen, Z. Yu, L. Shi, Z. Yang and Y. Lan, Organometallics, 2014, 33, 6282–6285.
10. (a) P. Tian, H.-Q. Dong and G.-Q. Lin, ACS Catal., 2012, 2, 95–119; (b) Y. Fukui, P. Liu, Q. Liu, Z.-T. He, N.-Y. Wu, P. Tian and G.-Q. Lin, J. Am. Chem. Soc., 2014, 136, 15607–15614.
11. J. Keilitz, S. G. Newman and M. Lautens, Org. Lett., 2013, 15, 1148–1151.
12. Z.-T. He, B. Tian, Y. Fukui, X. Tong, P. Tian and G.-Q. Lin, Angew. Chem., Int. Ed., 2013, 52, 5314–5318.
13. (a) R. Noyori, Acc. Chem. Res., 1990, 23, 345–350; (b) M. Kitamura, M. Tsukamoto, Y. Bessho, M. Yoshimura, U. Kobs, M. Widhalm and R. Noyori, J. Am. Chem. Soc., 2002, 124, 6649–6667; (c) C. A. Sandoval, T. Ohkuma, K. Muñiz and R. Noyori, J. Am. Chem. Soc., 2003, 125, 13490–13503; (d) R. Kramer and R. Brückner, Angew. Chem., Int. Ed., 2007, 46, 6537–6541; (e) T. Hayashi, M. Takahashi, Y. Takaya and M. Ogasawara, J. Am. Chem. Soc., 2002, 124, 5052–5058; (f) S.-Y. Wang, S.-J. Ji and T.-P. Loh, J. Am. Chem. Soc., 2007, 129, 276–277; (g) D. A. Evans and R. J. Thomson, J. Am. Chem. Soc., 2005, 127, 10506–10507; (h) S. Ge and J. F. Hartwig, J. Am. Chem. Soc., 2011, 133, 16330–16333.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D. 01, 2013, Gaussian, Inc., Wallingford, CT.
15. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frish, J. Phys. Chem., 1994, 98, 11623–11627.
16. (a) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222; (b) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (c) J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923; (d) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
17. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283; (b) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
18. (a) R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 13171–13174; (b) M. Hölscher and W. Leitner, Eur. J. Inorg. Chem., 2014, 6126–6133.
19. (a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396; (b) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543; (c) X. Xu, P. Liu, X.-Z. Shu, W. Tang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 9271–9274.
20. (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654; (b) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
21. L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031.
22. (a) K. Fagnou and M. Lautens, Chem. Rev., 2003, 103, 169–196; (b) Z. Yu and Y. Lan, J. Org. Chem., 2013, 78, 11501–11507.
23. The full potential energy surfaces for this reaction with ligands L2, L3, and L4 are given in Fig. S1, S3, and S5, respectively, in the ESI.†.
24. The B97D3 functional, M06-L functional and M11-L functional calculated ee values are given in Table S1 of the ESI.†.
25. (a) S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885; (b) P. Liu, J. Montgomery and K. N. Houk, J. Am. Chem. Soc., 2011, 133, 6956–6959; (c) A. Poater, F. Ragone, R. Mariz, R. Dorta and L. Cavallo, Chem. – Eur. J., 2010, 16, 14348–14353; (d) F. Ragone, A. Poater and L. Cavallo, J. Am. Chem. Soc., 2010, 132, 4249–4258; (e) X. Hong, P. Liu and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 1456–1462; (f) H. Wang, P. Kohler, L. E. Overman and K. N. Houk, J. Am. Chem. Soc., 2012, 134, 16054–16058.

---

Footnote

† Electronic supplementary information (ESI) available: The calculated Cartesian coordinates and energies of all the reported structures. See DOI: 10.1039/c5qo00334b

---