DFT perspective toward [3 + 2] annulation reaction of enals with α-ketoamides through NHC and Brønsted acid cooperative catalysis: mechanism, stereoselectivity, and role of NHC†
Yang
Wang
,
Bohua
Wu
,
Linjie
Zheng
,
Donghui
Wei
* and
Mingsheng
Tang
*
The College of Chemistry and Molecular Engineering, Center of Computational Chemistry, Zhengzhou University, Zhengzhou, Henan Province 450001, P.R. China. E-mail: donghuiwei@zzu.edu.cn; mstang@zzu.edu.cn
First published on 27th November 2015
Abstract
A systematic theoretical study has been carried out to understand the possible mechanisms and stereoselectivity of the N-heterocyclic carbene (NHC)-catalyzed [3 + 2] annulation reaction of enals with α-ketoamides using density functional theory (DFT) calculations. The calculated results reveal that the favorable pathway comprises of seven steps, i.e., addition of the catalyst, formation of the Breslow intermediate, formation of the enolate intermediate, the C–C bond formation step, the proton transfer process, the ring-closure process and the regeneration of the catalyst. For the proton transfer process, apart from the direct proton transfer mechanism, the base TMEDA and the in situ generated Brønsted acid TMEDA·H+ mediated proton transfer mechanisms are also investigated; the free energy for the crucial proton transfer steps is found to be significantly lowered by explicit inclusion of the Brønsted acid TMEDA·H+. The computational results show that the C–C bond formation step is the stereoselectivity-determining step, in which two chirality centers assigned to the coupling carbon atoms are formed, and the RR-configured diastereomer is the predominant product, which is in good agreement with the experimental observations. Global reaction index (GRI) analysis has been performed to confirm that NHC mainly plays a role of a Lewis base catalyst. In addition, the distortion/interaction, NCI, and NBO analyses show that the strong interaction and electron delocalization of the reaction active site determine the stereoselectivity, with the RR-configured product being generated preferentially. The mechanistic insights obtained in the present study should be valuable for the rational design of an effective organocatalyst for this kind of reaction with high stereoselectivity.
1. Introduction
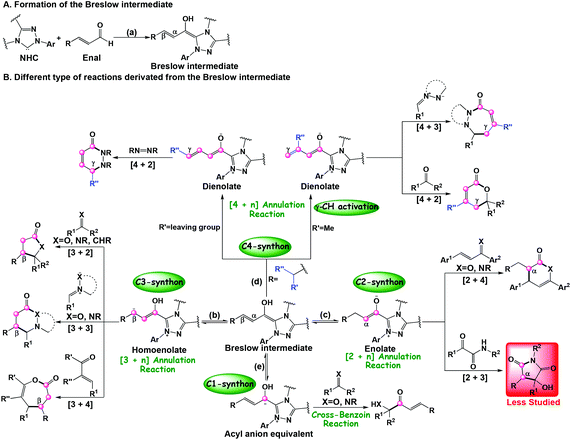
During the past few decades, N-heterocyclic carbenes (NHC) have been widely applied in organic chemistry.1 As important organocatalysts, NHCs have been successfully used in carbon–carbon and carbon–heteroatom bond formation reactions including cross-benzoin, Stetter, homoenolate, cycloaddition, annulation reactions, and so on.2 Specially, NHC catalysis has emerged as a powerful tool for the development of new transformations to construct heterocycles with high stereoselectivity and regioselectivity. Owing to the unique properties of NHC catalysts, many advances continue to be made. For example, various types of ketene cycloaddition reactions, including the [2 + 2],2c,j,3 [2 + 2 + 2],3c,4 and [4 + 2]5 cycloaddition reactions with high stereoselectivity, have been reported by Ye's group for the construction of N/O-containing heterocycles.Recently, several types of the NHC catalyzed annulation reactions between enals and different electrophilic coupling partners, such as alkenes, imines, and ketones have attracted more and more attention. Interestingly, addition of the NHC catalyst to the enals can allow the inversion of the normal reactivity (i.e. umpolung) through the formation of Breslow intermediates (Scheme 1a) and serve as the prenucleophiles, which then will lead to different reactive intermediates bearing more than one reactive carbon center of the enals, such as the β-carbon (homoenolate intermediate, Scheme 1b),2k,6 α-carbon (enolate intermediate, Scheme 1c),7 γ-carbon (dienolate intermediate, Scheme 1d),2b,8 and carbonyl carbon (acyl anion equivalent intermediate, Scheme 1e).9 As shown in Scheme 1, the Breslow intermediates can be employed as the one-, two-, three-, and four-carbon synthons in different annulation reactions. For example, the cross-benzoin reaction takes place when the Breslow intermediate works as the C1-synthon (Scheme 1e).9 When they function as two-, three-, and four-carbon synthons, various types of annulation reactions including [2 + 4],2i,10 [3 + n] (n = 2, 3, 4),2d,e,g,h,6e,11 and [4 + n] (n = 2, 3)6d,12 then occur under the NHC catalysis. Most of the reported NHC-catalyzed [3 + 2] annulation reactions of enals between enals and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X bonds (X = O, NR, and CHR) involve a homoenolate intermediate (Scheme 1b), while the NHC-catalyzed [3 + 2] annulation via azolium enolate intermediates (Scheme 1c) has been less studied. Recently, an outstanding work on the first example of the NHC-catalyzed [3 + 2] annulation reaction of α,β-unsaturated aldehydes (enals) with α-ketoamides (Scheme 2) was reported by Enders and co-authors.13 It should be noted that no other group has focused on applying the azolium enolate strategy in order to synthesize useful heterocycles by the NHC-catalyzed [3 + 2] annulation reactions, indicating a unique propensity in azolium enolate chemistry to give useful heterocycles or natural products.
X bonds (X = O, NR, and CHR) involve a homoenolate intermediate (Scheme 1b), while the NHC-catalyzed [3 + 2] annulation via azolium enolate intermediates (Scheme 1c) has been less studied. Recently, an outstanding work on the first example of the NHC-catalyzed [3 + 2] annulation reaction of α,β-unsaturated aldehydes (enals) with α-ketoamides (Scheme 2) was reported by Enders and co-authors.13 It should be noted that no other group has focused on applying the azolium enolate strategy in order to synthesize useful heterocycles by the NHC-catalyzed [3 + 2] annulation reactions, indicating a unique propensity in azolium enolate chemistry to give useful heterocycles or natural products.
Accompanied by the great development of NHC-catalyzed annulation reactions of enals in experiment, the theoretical investigations on the detailed mechanisms have also been reported in the literature. For example, Bode and co-workers computationally studied the NHC-catalyzed [4 + 2] annulation reaction of α,β-unsaturated aldehydes with enones via the enolate intermediate, they identified that the oxyanion-steering mechanism and CH–π interaction are the two crucial interactions for high selectivity.14 Our group has performed theoretical investigation on the mechanism of the NHC-catalyzed [4 + 2] annulation reaction of enals via enolate or dienolate intermediates, and the computational results show that the acetic acid or the in situ formed acid can assist the proton transfer process.15 Sunoj et al. performed a series of theoretical investigations on the mechanism and enantioselectivity of NHC-catalyzed Stetter reaction and annulation reactions of enals via the homoenolate intermediate.16 More recently, we have also studied the annulation reaction of allenals with chalcones catalyzed by NHC, in which the origin of the unexpected chemoselectivity has been disclosed.17 Moreover, the mechanisms and stereoselectivities of the NHC-catalyzed ketene cycloaddition reactions (including [2 + 2],18 [2 + 2 + 2],19 and [4 + 2] cycloaddition reactions20) have also been investigated by our group. These theoretical studies have greatly enhanced our understanding of the mechanistic insights into the NHC catalysis. Noteworthily, the reaction mechanism might be diverse for different NHC catalytic annulation reactions of enals, because the catalysts, reactants, and additives will influence the proton transfer process involved in these kinds of reactions. Thus, a theoretical investigation is necessary for these special organocatalytic reactions.
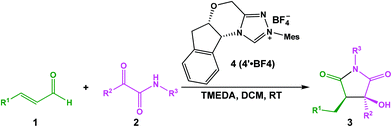
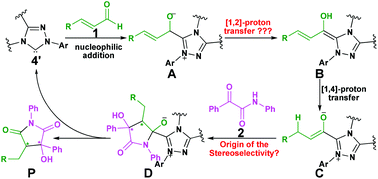
As mentioned above, Scheme 2 illustrates the experimental details of the NHC-catalyzed [3 + 2] annulation reaction of enals with α-ketoamides: enal 1 reacts with α-ketoamide 2 to give the desired five-membered heterocyclic compound 3 catalyzed by NHC 4′ in the presence of TMEDA using DCM as the solvent, which is generated from the triazolium salt 4 at room temperature. As shown in Scheme 3, Enders and co-workers have made some efforts to propose the possible reaction mechanism taking place during experiment, their exploration of this novel reaction is quite instructive, but there still are some key issues that need to be settled: (1) In the second step, the direct [1,2]-proton transfer process for the formation of the Breslow intermediate has quite a high energy barrier due to the large strain in the three-membered ring transition state. Moreover, the reaction proceeds without a protic additive in the reaction system, so how does the [1,2]-proton transfer process happen? (2) What are the roles of the NHC catalyst and the base TMEDA? (3) As the design of a new organocatalyst relies on a detailed understanding of the underlying factors that govern the stereoselectivity of these kinds of reactions, what are the key factors controlling the stereoselectivity of this reaction? To the best of our knowledge, the computational investigation on the detailed mechanism and stereoselectivity of NHC-catalyzed [3 + 2] annulation reaction of enals with α-ketoamides remains unexplored to date. Our interests in the NHC catalysis promotes us to pursue a theoretical investigation on the title reaction to not only obtain a preliminary picture from the α,β-unsaturated aldehyde [3 + 2] annulation reaction, but also explore the factors that govern the stereochemistry of this reaction. We believe that the mechanistic information should be important for understanding the NHC-catalyzed [3 + 2] annulation reactions and providing novel insights into recognizing this kind of reaction in detail.
As depicted in Scheme 2, the [3 + 2] annulation reaction between the enal with R1 = Ph (denoted as R1) and α-ketoamide with R2 = R3 = Ph (denoted as R2) catalyzed by the active NHC catalyst 4′ (denoted as Cat) for the formation of a N-heterocyclic product, in which high yields (83%) with excellent enantioselectivities (99%) and very good diastereoselectivities (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are obtained, has been chosen as the model reaction to investigate the detailed mechanism and stereoselectivity for this kind of reaction using density functional theory.
1) are obtained, has been chosen as the model reaction to investigate the detailed mechanism and stereoselectivity for this kind of reaction using density functional theory.
2. Computational details
Quantum mechanical calculations reported herein were carried out with the Gaussian 09 suite of programs21 by using density functional theory, which has been revealed to be a powerful tool for clarifying the detailed reaction mechanisms and predicting the stereoselectivity as well as chemoselectivity in both organic and biological reactions, and so on.22 The solution-phase geometry optimization of all species is performed with the recently developed M06-2X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 density functional along with the 6-31G(d,p) basis set in DCM solvent using the integral equation formalism polarizable continuum model (IEF-PCM).24 The harmonic vibrational frequency calculations were performed at the same level of theory as that used for geometry optimizations to provide thermal corrections of Gibbs free energies and make sure that the local minima had no imaginary frequencies, while the saddle points had only one imaginary frequency. Intrinsic reaction coordinates (IRCs)25 were calculated to confirm that the transition state structure connected the correct reactant and product on the potential energy surface. The natural bond orbital (NBO)26 analysis was employed to assign the atomic charges. Non-covalent interaction (NCI) analysis was plotted using Multiwfn (version 3.3.8).27 The computed structures were rendered using the CYLView software.28 We choose to discuss the calculated results based on the solution-phase Gibbs free energies obtained at the M06-2X/6-31G(d,p)/IEF-PCM(DCM) level.
23 density functional along with the 6-31G(d,p) basis set in DCM solvent using the integral equation formalism polarizable continuum model (IEF-PCM).24 The harmonic vibrational frequency calculations were performed at the same level of theory as that used for geometry optimizations to provide thermal corrections of Gibbs free energies and make sure that the local minima had no imaginary frequencies, while the saddle points had only one imaginary frequency. Intrinsic reaction coordinates (IRCs)25 were calculated to confirm that the transition state structure connected the correct reactant and product on the potential energy surface. The natural bond orbital (NBO)26 analysis was employed to assign the atomic charges. Non-covalent interaction (NCI) analysis was plotted using Multiwfn (version 3.3.8).27 The computed structures were rendered using the CYLView software.28 We choose to discuss the calculated results based on the solution-phase Gibbs free energies obtained at the M06-2X/6-31G(d,p)/IEF-PCM(DCM) level.
To test the accuracy of the M06-2X/6-31G(d,p)//IEF-PCMDCM level, we have performed the single-point energy calculations for the key transition states by using the higher basis sets, i.e. M06-2X/6-311++G(2df, 2pd)//IEF-PCMDCM, M06-2X/6-311++G(2df, 2pd)//SMDDCM, ωB97X-D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29/6-311++G(2df, 2pd)//IEF-PCMDCM, and ωB97X-D/6-311++G(2df, 2pd)//SMDDCM, and the computed single-point energies with the zero-point and thermal corrections calculated at the M06-2X/6-31G(d,p)//IEF-PCMDCM level are summarized in Table S1 of the ESI.† Further, we have additionally optimized the geometries and calculated the free energies of the reactants, catalysts, and the stationary points involved in the stereoselectivity-determining step at the M06-2X/6-31G(d,p)//SMDDCM, ωB97X-D/6-31G(d,p)//IEFPCMDCM, and ωB97X-D/6-31G(d,p)//SMDDCM levels, which are summarized in Table S2 of the ESI.† The computational outcomes show that the free energies calculated at the M06-2X/6-31G(d,p)//IEF-PCMDCM level has the same trend and small differences with those calculated at the different levels mentioned above, indicating that the selected M06-2X functional, 6-31G(d,p) basis set, and IEF-PCM solvation model are suitable and reliable for studying the NHC-catalyzed [3 + 2] annulation reaction.
29/6-311++G(2df, 2pd)//IEF-PCMDCM, and ωB97X-D/6-311++G(2df, 2pd)//SMDDCM, and the computed single-point energies with the zero-point and thermal corrections calculated at the M06-2X/6-31G(d,p)//IEF-PCMDCM level are summarized in Table S1 of the ESI.† Further, we have additionally optimized the geometries and calculated the free energies of the reactants, catalysts, and the stationary points involved in the stereoselectivity-determining step at the M06-2X/6-31G(d,p)//SMDDCM, ωB97X-D/6-31G(d,p)//IEFPCMDCM, and ωB97X-D/6-31G(d,p)//SMDDCM levels, which are summarized in Table S2 of the ESI.† The computational outcomes show that the free energies calculated at the M06-2X/6-31G(d,p)//IEF-PCMDCM level has the same trend and small differences with those calculated at the different levels mentioned above, indicating that the selected M06-2X functional, 6-31G(d,p) basis set, and IEF-PCM solvation model are suitable and reliable for studying the NHC-catalyzed [3 + 2] annulation reaction.
3. Results and discussion
3.1. Reaction mechanisms
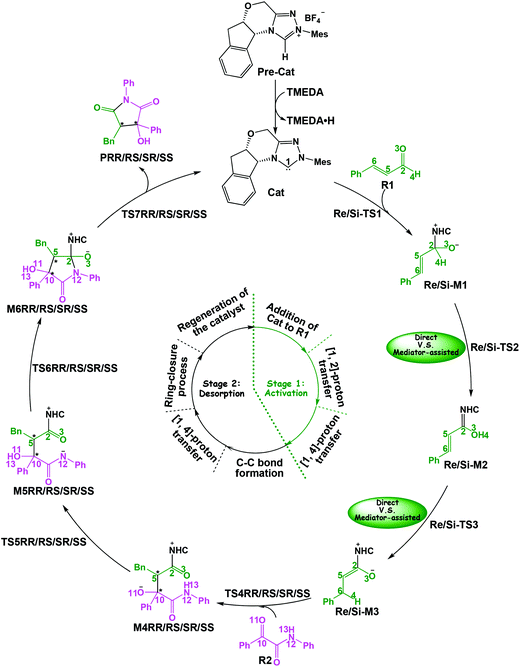
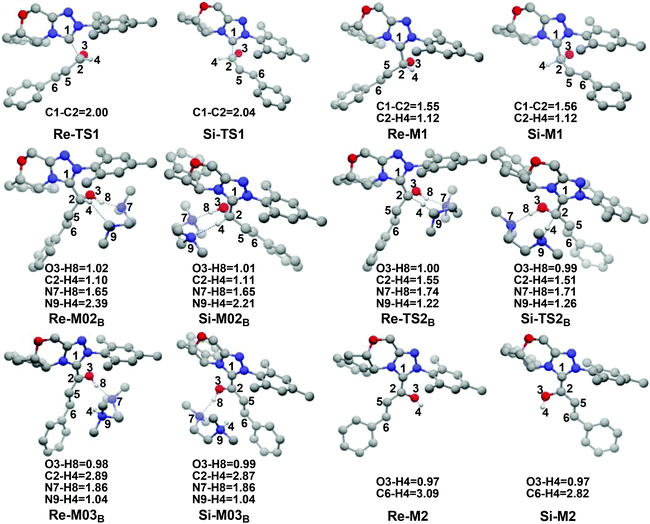
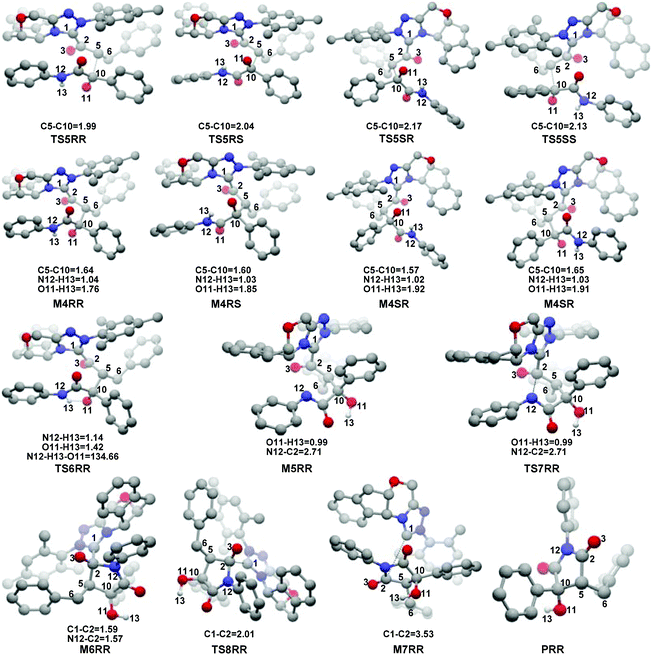
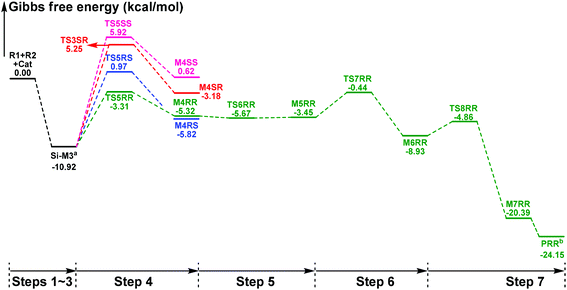
In this part, the detailed mechanisms of enals (R1) with α-ketoamides (R2) catalyzed by NHC have been studied and discussed intensively. As shown in Scheme 4, we suggested the possible catalytic cycle which comprises of seven reaction steps, i.e. the addition of the catalyst Cat to the Re/Si-face of R1 for the formation of the zwitterionic intermediate Re/Si-M1via the transition state Re/Si-TS1, the [1,2]-proton transfer process to generate the Breslow intermediate Re/Si-M2via the transition state Re/Si-TS2, the [1,4]-proton transfer process for the formation of the azolium enolate intermediate Re/Si-M3via the transition state Re/Si-TS3, addition of another reaction pattern R2 to give the zwitterionic intermediate M4RR/RS/SR/SSvia the transition state TS4RR/RS/SR/SS, the [1,4]-proton transfer process to afford the zwitterionic intermediate M5RR/RS/SR/SSvia the transition state TS5RR/RS/SR/SS, the ring-closure process to form the five-membered heterocycle M6RR/RS/SR/SSvia the transition state TS6RR/RS/SR/SS, and the disassociation of the catalyst from the desired product PRR/RS/SR/SSvia the transition state TS7RR/RS/SR/SS. As presented in Fig. 1 and 2, we have divided the free energy profiles into two parts including the free energy profiles of Stages 1 (steps 1–3) and 2 (steps 4–7). In Stage 1 (i.e. the activation stage, Scheme 4), the reaction proceeds under the NHC and Brønsted acid TMEDA·H+ cooperative catalysis, and a TMEDA·H+ molecule is included in the reaction models associated with the structural transformation from the intermediate M02B to the intermediate M06B, while the TMEDA·H+ molecule is removed in the reaction models of Stage 2 (i.e. the desorption stage). Because of the significant difference between the models in the two stages, and the energy of the stationary point with TMEDA·H+ (such as Si-M06B) is much lower than that without TMEDA·H+ (such as Si-M3), we think it is not reasonable to connect the two energy profiles to each other directly. It should be noted that the subscript “D”, “B”, and “T” of the intermediates and transition states in Stage 1 represent the direct proton transfer pathway, the TMEDA·H+-assisted proton transfer pathway, and the TMEDA-assisted proton transfer pathway, respectively.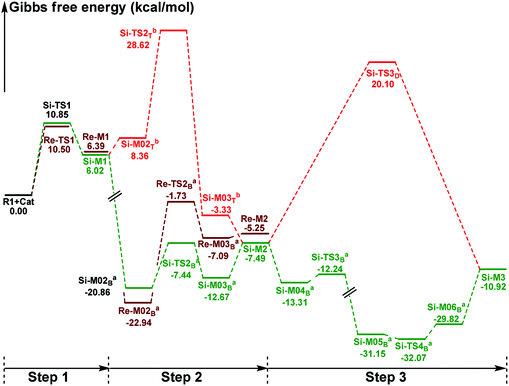 | ||
| Fig. 1 The Gibbs free energy profiles of Stage 1 of the title reaction (a subtracting the free energy of TMEDA·H+, b subtracting the free energy of TMEDA). | ||
 | ||
| Fig. 2 The Gibbs free energy profiles of Stage 2 involved in the title reaction (a adding the free energy of R2, b adding the free energy of Cat). | ||
It has been reported that the generation of the Breslow intermediate could be assisted by a base or protic media. In view of this, the previously formed Brønsted acid TMEDA·H+ assisted proton transfer process has been taken into consideration. As depicted in Scheme 5A, the cleavage of the C2–H bond and formation of the hydroxyl O3–H bond are supposed to occur simultaneously in the eight-membered ring transition state, however, the computational outcomes show that the elongated C2–H bond always reformed, the O3–H bond generated automatically, and the transition state turned into Re/Si-M02B after optimization, which is due to the strong acidity of the Brønsted acid and basicity of the O3 atom. In other words, the O3 atom of Re/Si-M1 is first protonated by Brønsted acid TMEDA·H+ directly to give the intermediate Re/Si-M02B. The O–H⋯N hydrogen bonds in intermediates Re-M02B and Si-M02B make them very stable with a free energy of −22.94/−20.86 kcal mol−1 (Fig. 1). The calculated results indicate that this step is a barrierless, highly exergonic, and irreversible process. Then the proton H4 located on the C2 atom transfers to the N9 atom of TMEDA via the transition state Re/Si-TS2B for the formation of the intermediate Re/Si-M03B. The distances of C2–H4 and N9–H4 are changed from 1.55/1.51 Å and 1.22/1.26 Å in the transition state Re/Si-TS2B to 2.89/1.04 Å and 2.87/1.04 Å in the intermediate Re/Si-M03B respectively, revealing the accomplishment of the proton transfer process and regeneration of the Brønsted acid TMEDA·H+. After passing through a barrier of 21.21/13.42 kcal mol−1 (Re/Si-TS2B, Fig. 1) and disassociation of Brønsted acid, the Breslow intermediate Re/Si-M2 is formed completely. The calculated outcomes indicate that the reaction pathway for the formation of Re-M2 (ΔG≠ = 21.21 kcal mol−1) is much less favorable than that leading to Si-M2 (ΔG≠ = 13.42 kcal mol−1), therefore, we believe it is reasonable to omit the reaction pathway associated with the Re face attack on R1 in the following parts.
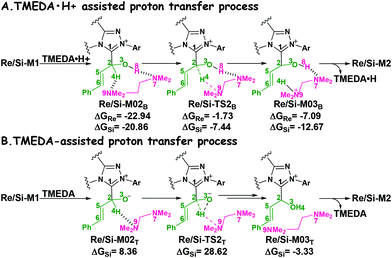 | ||
| Scheme 5 The TMEDA·H+- and TMEDA-assisted proton transfer pathways for the formation of Breslow intermediate (energies in kcal mol−1). | ||
In addition, we have also considered the base TMEDA-assisted proton transfer mechanism. As shown in Scheme 5B, the reaction precursor Si-M02T is first formed (we only calculated the Si addition pathway for the sake of convenience), and then the N9 atom in TMEDA abstracts the proton H4 in the C2 atom via the transition state Si-TS2T. The intermediate Si-M03T is then formed by abstracting the H4 atom from the N9 atom and this process is barrierless due to the strong basicity of the O3 atom. The energy barrier of this process is 28.62 kcal mol−1, which is much higher than the TMEDA·H+-assisted proton transfer process via the transition state Si-TS2B (13.42 kcal mol−1, Fig. 1). Thus the TMEDA-assisted proton transfer mechanism is not favorable to occur under the experimental conditions.
Taken together, two possible pathways for the proton transfer process to afford Si-M2 have been suggested and studied. In this step, apart from the direct proton transfer mechanism, the in situ generated Brønsted acid TMEDA·H+ mediated proton transfer mechanism for the formation of the Breslow intermediate Si-M2via the transition state Si-TS2B is more energetically feasible than the other proton transfer processes.
(1) Direct proton transfer process. For the direct proton transfer process, the H4 atom directly transfers from the O3 atom to C6 atom for the formation of Si-M3via a five-membered transition state Si-TS3D. The optimized structures and geometrical parameters depicted in Fig. 4 show that the distance of O3–H4 is increased from 0.97 Å in the intermediate Si-M2 to 1.25 Å in the transition state TS3D, and finally to 2.54 Å in the intermediate Si-M3, while that of C6–H4 is shortened from 1.44 Å in the transition state Si-TS3D to 1.10 Å in the intermediate Si-M3, indicating that the proton transfer process is completed. Interestingly, the free energy barrier of this step is 27.59 kcal mol−1 with respect to Si-M2 (Fig. 1), which is a little high for the formation of the enolate intermediate Si-M3 under the experimental conditions.
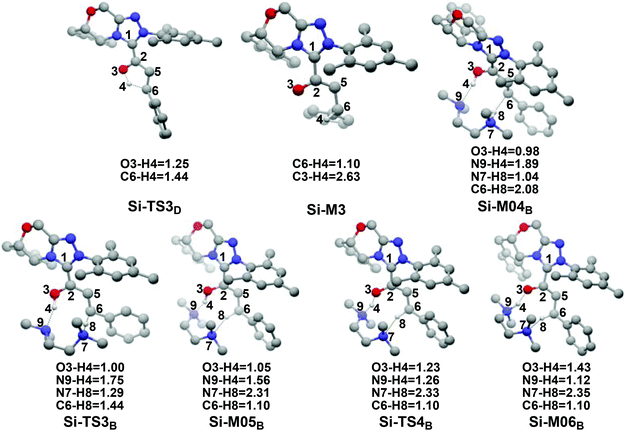 | ||
| Fig. 4 The optimized structures and geometrical parameters involved in the third step (distance in Å and only the hydrogen involved in the reaction are shown for the sake of clarity). | ||
(2) Brønsted acid-assisted proton transfer process. As discussed above, the newly generated Brønsted acid can promote the proton transfer process in the second step. Thus, we also suggested and investigated the Brønsted acid-assisted proton transfer process in this step. It should be noted that we can only obtain the structures of the stepwise transition state when we tried to locate the concerted TMEDA·H+ assisted [1,4]-proton transfer transition state. As mapped in Scheme 6, the intermediate Si-M2 and Brønsted acid TMEDA·H+ first form a more stable complex Si-M04B (ΔG≠ = −13.31 kcal mol−1, Fig. 1) through electrostatic attraction between the two components and the formation of the O–H⋯N (the distance of H4–N9 is 1.89 Å, Fig. 4) and N–H⋯C hydrogen bonds (the distance of C6–H8 is 2.04 Å, Fig. 4). The TMEDA·H+-assisted proton transfer process is calculated to be in a stepwise manner. Initially, the proton H8 transfers from N7 to C6 atoms via the transition state Si-TS3B to form the intermediate Si-M05B (ΔG≠ = −31.15 kcal mol−1). Subsequently, the proton H4 smoothly transfers from the O2 to N9 atom via the transition state Si-TS4B to give the enolate intermediate Si-M3B.
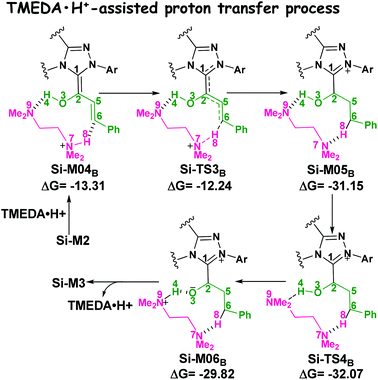 | ||
| Scheme 6 The TMEDA·H+-assisted proton transfer mechanism for the formation of enolate intermediate (energies in kcal mol−1). | ||
The free energy barrier calculated for the first process of the TMEDA·H+-assisted proton transfer pathway is very low (1.07 kcal mol−1viaSi-TS3B, Fig. 1), which indicates that it occurs easily under the experimental conditions. The second process has a free energy barrier of 0.92 kcal mol−1 based on the total energy (E, for details see the ESI†), but it is a barrierless process based on the free energy (G) profile depicted in Fig. 1. Overall, the free energy barrier of the TMEDA·H+-assisted proton transfer mechanism is only 1.07 kcal mol−1, and it is remarkably lower than that of the direct proton transfer pathway (Si-TS3D).
In addition, as shown in Scheme 4, the enolate intermediate is necessary for the [2 + 3] cycloaddition, and we have further considered two other possible reaction pathways, i.e. the direct proton transfer from the C2 to C6 atom and the TMEDA·H+-assisted direct proton transfer from the C2 to C6 atom, respectively. The calculated results show that the direct proton transfer pathway has an extremely high energy barrier (42.70 kcal mol−1, Scheme S1†), which is mainly due to the large strain of the four-membered ring in the transition state. It should be noted that only the structure of the intermediate Re/Si-M02B can be obtained when we put the structures of Re/Si-M1 and TMEDA·H+ together, that is to say, the proton can be transferred to the O3 atom automatically, so we do not think that the TMEDA·H+-assisted direct proton transfer from the C2 to C6 atom can occur.
| Addition face of Si-M3 | Addition face of R2 | Chirality of the C5 atom | Chirality of the C10 atom | Configuration of M4 |
|---|---|---|---|---|
| Si | Si | R | R | RR |
| Si | Re | R | S | RS |
| Re | Si | S | R | SR |
| Re | Re | S | S | SS |
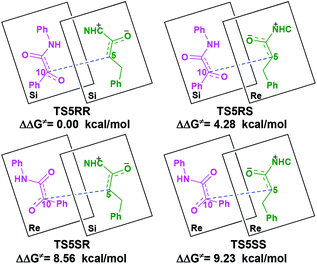
With the approach of R2 to Si-M3, the distance between C5 and C10 atoms changed from 1.99/2.04/2.08/2.03 Å in the transition state TS5RR/RS/SR/SS to 1.64/1.60/1.57/1.65 Å in the intermediate M4RR/RS/SR/SS, which implies that the complete formation of the C5–C10 bond takes place during the fourth step (Fig. 7). The free energy barriers of this step shown in Fig. 2 are 7.61, 11.87, 16.17, and 16.84 kcal mol−1 with respect to Si-M3, respectively. Obviously, the formation of the intermediate M4RR has the lowest energy barrier and the energy barrier viaTS5RR is 4.28–9.23 kcal mol−1 lower than those viaTS5RS/SR/SS, which demonstrates that the formation M4RR is more energy favorable and supports the reported preference to form the product with RR-configuration. Thus, we think it is reasonable to only discuss the RR-configuration pathway as reference in the following parts. Furthermore, the energy barriers of this step in the NHC-catalyzed annulations with different substrates in DCM solvent have also been calculated, and the results summarized in Table S3 of the ESI† show that the RR-configured product is the main product, which are aligned well with the experimental observations and thus demonstrates that our calculated results are reliable.
3.2 Origin of the stereoselectivity
For the organocatalytic reaction, it is important to figure out the factors governing the stereoselectivities within the established mechanism. As discussed above, the entire reaction mechanisms contain more than one step, and the most energy favorable reaction mechanism for the entire energy profile of the NHC-catalyzed [3 + 2] annulation reaction is the Si face addition of R1 to Cat, and the Brønsted acid-assisted proton transfer mechanism is the most favorable pathway. Starting from the intermediate Si-M3, the two chirality centers (C5 and C10 atoms) emerged in the C–C bond formation step, so we think that the transition states TS5RR/RS/SR/SS involved in this step is crucial for the stereoselectivity. As shown in Fig. 2 and Scheme 7, the computed energy difference between the transition states TS5RR and TS5SS is 9.23 kcal mol−1, and the energy difference between the diastereomeric TS5RR and TS5RS is 4.28 kcal mol−1, which corresponds to an enantiomeric excess of >99% in favor of the RR diastereomer. These predictions are in good accordance with the experimentally observed ee of 99%. To obtain deep insights into the origins of the stereoselectivity for the NHC-catalyzed [3 + 2] annulation reaction, we then performed the distortion/interaction analysis of the transition state TS5. The distortion/interaction analysis30 is a fragment approach to understand organic reactions, in which the height of the energetic barrier is described in terms of the original reactants. As depicted in Fig. 6, the activation energy of the transition state is decomposed into to two main components: the distortion (ΔE≠dist) and the interaction (ΔE≠int) energy. The distortion energy involves geometric and electronic changes to deform the reactants into their transition state geometry, which involves bond stretching, angle decrease or increase, dihedral changes and so on. The interaction energy contains repulsive exchange-repulsive and stabilizing electrostatic, polarization, and orbital effects in the transition state structure. The interaction energy is recovered by the relationship: ΔE≠int = ΔE≠ − ΔE≠dist.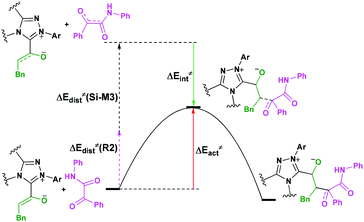 | ||
| Fig. 6 The relationship between the activation energy, distortion and interaction energies of reaction patterns. | ||
The calculated distortion and interaction energies of the reactants in transition state geometries are listed in Table 2. Comparing with the distortion/interaction energies of these four transition states, the distortion energy of TS5RR (28.32 kcal mol−1, Table 2) is larger than that of TS5RS and TS5SR (23.11 and 22.32 kcal mol−1, Table 2), but the larger distortion energy of TS5RR is offset by the largest interaction energy discrepancy (−39.80 kcal mol−1, Table 2), and this is the dominant factor determining the RR-configuration product generated preferentially.
| ΔΔG≠ | ΔE≠dist | ΔE≠act | ΔE≠int | ||
|---|---|---|---|---|---|
| ΔE≠dist (Si-M5) | ΔE≠dist (R2) | ||||
| Note: (a) The ΔE≠ value is the calculated total energy (E) of each transition state relative to the sum of the total energies of the two separate reactants. | |||||
| TS5RR | 0 | 11.36 | 14.96 | −13.48 | −39.80 |
| TS5RS | 4.28 | 8.64 | 14.47 | −9.68 | −32.79 |
| TS5SR | 8.56 | 8.90 | 13.42 | −1.64 | −23.96 |
| TS5SS | 9.23 | 11.99 | 16.73 | −3.73 | −32.45 |
As discussed above, the distortion/interaction analysis reveals the existence of interactions between enolate (Si-M3) and α-ketoamide (R2) moieties. To further identify the type of these interactions, we then performed the non-covalent interaction (NCI) analysis, which is demonstrated to be capable of distinguishing strong interaction, van der Waals interactions and repulsive steric interactions. Fig. 7 and S4† show the NCI results for the transition states TS5RR, TS5RS, TS5SR, and TS5SS. In TS5RR, there are three CH⋯π interactions, one π⋯π interaction, and one LP–π interaction. Specifically, the distances between the inner hydrogen and phenyl group are 2.39 Å (CH–π interaction a, Fig. 7), 2.62 Å (CH–π interaction b, Fig. 7), and 2.87 Å (CH–π interaction c, Fig. 7) separately, well within the combined van der Waals distance of 2.90 Å. As can be seen from Fig. S4 of the ESI,† the CH–π and π–π interactions can also be observed in the other transition states between the π-system of enolate and R2 moieties. Noteworthily, the noncovalent interactions indeed seem to be not significantly different among the four NCIs.
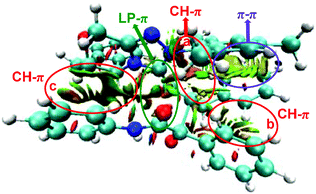 | ||
| Fig. 7 The interaction analysis of the transition state TS5RR (blue, green, and red represent the strong interaction, weak interaction, and steric effect, respectively). | ||
Furthermore, the natural bond orbital (NBO) analysis of the reaction active site is performed to explain the origin of the stereoselectivity. As shown in Fig. S5 of the ESI,† the net NBO charge values on the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C5 π system are 0.060e (TS5RR), 0.049e (TS5RS), 0.028e (TS5SR), and 0.015e (TS5SS), respectively. Obviously, the NBO charge populated on the C2
C5 π system are 0.060e (TS5RR), 0.049e (TS5RS), 0.028e (TS5SR), and 0.015e (TS5SS), respectively. Obviously, the NBO charge populated on the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C5 π system is more positive in TS5RR than that in the other three transition states, this phenomenon indicates that the more electron delocalization in TS5RR stabilizes the transition state and makes the RR-configuration isomer prominent. Then, we have performed frontier molecular orbital analysis for the stereoselectivity-determining step, which mainly involves the orbital interaction between HOMOSi-M3 and LUMOR2. As shown in Fig. 8, the energy gaps between HOMOM3-part and LUMOR2-part are 3.68, 3.79, 3.93, and 4.02 eV in the four key transition states TS5RR, TS5RS, TS5SR, and TS5SS respectively, indicating that the energy gap in the transition state TS5RR is narrowest, thus, the reaction pathway associated with the transition state TS5RR should have the lowest energy barrier and be the most favorable pathway, which is in agreement with the above energy profiles and experimental results.
C5 π system is more positive in TS5RR than that in the other three transition states, this phenomenon indicates that the more electron delocalization in TS5RR stabilizes the transition state and makes the RR-configuration isomer prominent. Then, we have performed frontier molecular orbital analysis for the stereoselectivity-determining step, which mainly involves the orbital interaction between HOMOSi-M3 and LUMOR2. As shown in Fig. 8, the energy gaps between HOMOM3-part and LUMOR2-part are 3.68, 3.79, 3.93, and 4.02 eV in the four key transition states TS5RR, TS5RS, TS5SR, and TS5SS respectively, indicating that the energy gap in the transition state TS5RR is narrowest, thus, the reaction pathway associated with the transition state TS5RR should have the lowest energy barrier and be the most favorable pathway, which is in agreement with the above energy profiles and experimental results.
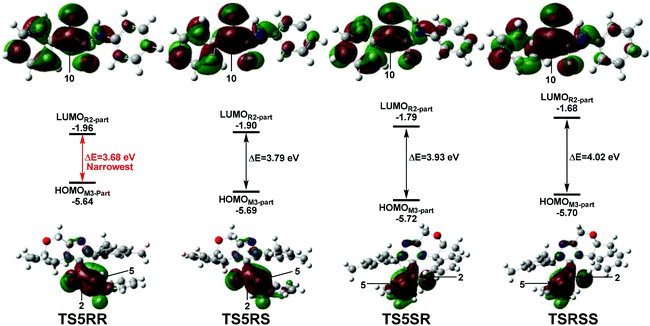 | ||
| Fig. 8 The energy gaps between HOMOM3-part and LUMOR2-part parts in the four transition states TS5RR, TS5RS, TS5SR, and TS5SS. | ||
3.3 Role of the NHC catalyst
Having established the most favorable reaction pathway and the origin of the stereoselectivity, we now explore the special role of the NHC catalyst in this [3 + 2] annulation reaction. The natural bond orbital (NBO) charge value of the H4 atom is slightly increased from 0.168 e in the enal (R1) to 0.178 e in the intermediate Si-M1, which indicates that the NHC strengthens the acidity of the H4 atom, this would make the breaking of the C–H bond more easy. This phenomenon shows that the NHC catalyst can activate the carbonyl C–H bonds of enals by strengthening the acidity of the H4 atom.In addition, our previous work18 has proved that the NHC catalyst plays the role of the Lewis base by global reactivity index (GRI) analysis in NHC catalyzed ketene cycloadditions. Thus, we also wanted to know if the NHC plays the same role in this reaction system. With this question in mind, GRI analysis was performed in this work. As summarized in Table 3, the molecule's global electrophilicity character is measured by the electrophilicity index, ω, which is obtained from the following expression, ω = (μ2/2η),31 where μ is the electronic chemical potential and η is the chemical hardness. Both quantities may be determined in terms of their one-electron energies of the frontier molecular orbital HOMO and LUMO, EH and EL, as μ ≈ (EH + EL)/2 and η ≈ (EL − EH). Moreover, according to the HOMO energies obtained within the Kohn–Sham scheme,32 Domingo and co-workers gave the nucleophilicity index N to determine a nucleophilicity scale.33 The nucleophilicity index is defined as N = EH(SR) − EH(TCE). This nucleophilicity scale is determined with tetracyanoethylene (TCE) taken as the reference. After the coordination with the NHC catalyst, the electrophilicity of enal is dramatically decreased, but its nucleophilicity is increased greatly from 2.504 to 3.498/3.514 eV (Re/Si-M1), and finally to 4.302 eV (Si-M3). Thus, the GRI analysis demonstrates that the NHC catalyst mainly works as the Lewis base catalyst to strengthen the nucleophilicity of the reactant enal.
| SR | E H (a.u.) | E L (a.u.) | μ (a.u.) | η (a.u.) | ω (eV) | N (eV) |
|---|---|---|---|---|---|---|
| a E H(TCE) = −0.37826 a.u. (calculated at the M06-2X/6-31G**/IEF-PCMDCM level). | ||||||
| R1 | −0.28623 | −0.04411 | −0.16517 | 0.24212 | 1.533 | 2.504 |
| Re-M1 | −0.24973 | 0.00474 | −0.122495 | 0.25447 | 1.605 | 3.498 |
| Si-M1 | −0.24912 | −0.00203 | −0.125575 | 0.24709 | 1.737 | 3.514 |
| Si-M3 | −0.22018 | −0.00374 | −0.11196 | 0.21644 | 1.576 | 4.302 |
In summary, the results of NBO and GRI analysis reveal that the NHC plays a bifunctional organocatalyst role in this novel [3 + 2] annulation reaction of enals. That is to say, the NHC catalyst not only works as the Lewis base catalyst to strengthen the nucleophilicity of the enals, but also activates the carbonyl C–H bonds in the subsequent proton transfer processes.
4. Conclusion
In this article, the comprehensive DFT calculations on the NHC-catalyzed intermolecular [3 + 2] annulation reaction of enals with α-ketoamides have been performed to pursue deep understanding of the detailed mechanisms and stereoselectivity. On the basis of our calculations, the most energy favorable reaction mechanism is demonstrated to occur through seven elementary steps, i.e., addition of the catalyst, formation of the Breslow intermediate, formation of the enolate intermediate, the C–C bond formation step, the proton transfer process, the ring-closure process and the regeneration of the catalyst. The calculated results reveal that the in situ generated Brønsted acid TMEDA·H+ plays an important role in the [1,2]- and [1,4]-proton transfer processes associated with the formation of the Breslow intermediate and the enolate intermediate, respectively. The C–C bond formation step is verified to be the stereoselectivity-determining step, and the two chiral centers (C5 and C10 atoms) are determined by the Re or Si face addition of R2 to the Re or Si face of Si-M3. The strong interaction and electron delocalization of the reaction active site were demonstrated to be responsible for the favorability of RR-configured product by the distortion/interaction, NCI, and NBO analyses. All the calculated results are in good agreement with the experimental observations.Furthermore, NBO and GRI analyses were carried out to explore the role of the NHC catalyst in this kind of reaction. The computational outcomes reveal that the NHC catalyst works as a bifunctional organocatalyst, i.e. Lewis base and the carbonyl C–H activation. The new insights gained from this work might help to refine the stereochemistry model of NHC-catalyzed [3 + 2] cycloaddition reactions and would be beneficial for the future development of this field as well as design of novel efficient catalysts.
Acknowledgements
The work described in this paper was supported by the National Natural Science Foundation of China (no. 21303167), China Postdoctoral Science Foundation (no. 2013M530340 and 2015T80776) and Excellent Doctoral Dissertation Engagement Fund of Zhengzhou University in 2014.References
- (a) D. M. Flanigan, F. Romanov-Michailidis, N. A. White and T. Rovis, Chem. Rev., 2015, 115, 9307 CrossRef CAS PubMed; (b) D. Enders, O. Niemeier and A. Henseler, Chem. Rev., 2007, 107, 5606 CrossRef CAS PubMed; (c) F. Glorius and K. Hirano, Nucleophilic Carbenes as Organocatalysts, Springer-Verlag, Berlin, Heidelberg, 2008, vol. 2, p. 159 Search PubMed; (d) J. L. Moore and T. Rovis, Top. Curr. Chem., 2010, 291, 77 CrossRef CAS PubMed; (e) D. Enders and T. Balensiefer, Acc. Chem. Res., 2004, 37, 534 CrossRef CAS PubMed; (f) V. Nair, S. Vellalath and B. P. Babu, Chem. Soc. Rev., 2008, 37, 2691 RSC; (g) M. Fèvre, J. Pinaud, Y. Gnanou, J. Vignolle and D. Taton, Chem. Soc. Rev., 2013, 42, 2142 RSC.
- (a) J. Xu, C. Mou, T. Zhu, B. A. Song and Y. R. Chi, Org. Lett., 2014, 16, 3272 CrossRef CAS PubMed; (b) M. Wang, Z. J. Huang, J. F. Xu and Y. R. Chi, J. Am. Chem. Soc., 2014, 136, 1214 CrossRef CAS PubMed; (c) H. M. Zhang, Z. H. Gao and S. Ye, Org. Lett., 2014, 16, 3079 CrossRef CAS PubMed; (d) Y. Zhang, Y. Y. Lu, W. F. Tang, T. Lu and D. Du, Org. Biomol. Chem., 2014, 12, 3009 RSC; (e) S. H. Hu, B. Y. Wang, Y. Zhang, W. F. Tang, M. Y. Fang, T. Lu and D. Du, Org. Biomol. Chem., 2015, 13, 4661 RSC; (f) A. Lee and K. A. Scheidt, Chem. Commun., 2015, 51, 3407 RSC; (g) Z. Q. Liang, Z. H. Guo, W. Q. Jia and S. Ye, Chem. – Eur. J., 2015, 21, 1868 CrossRef CAS PubMed; (h) H. Lu, J. Y. Liu, C. G. Li, J. B. Lin, Y. M. Liang and P. F. Xu, Chem. Commun., 2015, 51, 4473 RSC; (i) X. Q. Fang, X. K. Chen and Y. R. Chi, Org. Lett., 2011, 13, 4708 CrossRef CAS PubMed; (j) T. Wang, X. L. Huang and S. Ye, Org. Biomol. Chem., 2010, 8, 5007 RSC; (k) D. E. A. Raup, B. Cardinal-David, D. Holte and K. A. Scheidt, Nat. Chem., 2010, 2, 766 CrossRef CAS PubMed; (l) J. Kaeobamrung, M. C. Kozlowski and J. W. Bode, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20661 CrossRef CAS PubMed; (m) X. K. Chen, X. Q. Fang and Y. R. Chi, Chem. Sci., 2013, 4, 2613 RSC; (n) L.-H. Sun, Z.-Q. Liang, W.-Q. Jia and S. Ye, Angew. Chem., Int. Ed., 2013, 52, 5803 CrossRef CAS PubMed.
- (a) X. L. Huang, X. Y. Chen and S. Ye, J. Org. Chem., 2009, 74, 7585 CrossRef CAS PubMed; (b) X. N. Wang, P. L. Shao, H. Lv and S. Ye, Org. Lett., 2009, 11, 4029 CrossRef CAS PubMed; (c) X. N. Wang, L. T. Shen and S. Ye, Org. Lett., 2011, 13, 6382 CrossRef CAS PubMed.
- X. N. Wang, L. T. Shen and S. Ye, Chem. Commun., 2011, 47, 8388 RSC.
- (a) T. Y. Jian, X. Y. Chen, L. H. Sun and S. Ye, Org. Biomol. Chem., 2013, 11, 158 RSC; (b) T. Y. Jian, P. L. Shao and S. Ye, Chem. Commun., 2011, 47, 2381 RSC.
- (a) C. Burstein and F. Glorius, Angew. Chem., Int. Ed., 2004, 43, 6205 CrossRef CAS PubMed; (b) S. S. Sohn, E. L. Rosen and J. W. Bode, J. Am. Chem. Soc., 2004, 126, 14370 CrossRef CAS PubMed; (c) H. Lv, B. Tiwari, J. M. Mo, C. Xing and Y. R. Chi, Org. Lett., 2012, 14, 5412 CrossRef CAS PubMed; (d) H. Lv, W. Q. Jia, L. H. Sun and S. Ye, Angew. Chem., Int. Ed., 2013, 125, 8769 CrossRef; (e) C. Guo, M. Schedler, C. G. Daniliuc and F. Glorius, Angew. Chem., Int. Ed., 2014, 53, 10232 CrossRef CAS PubMed; (f) A. Chan and K. A. Scheidt, J. Am. Chem. Soc., 2007, 129, 5334 CrossRef CAS PubMed; (g) E. M. Phillips, T. E. Reynolds and K. A. Scheidt, J. Am. Chem. Soc., 2008, 130, 2416 CrossRef CAS PubMed; (h) T. Zhu, P. Zheng, C. Mou, S. Yang, B. A. Song and Y. R. Chi, Nat. Commun., 2014, 5, 5027 CrossRef CAS PubMed; (i) Z. Q. Liang, Z. H. Gao, W. Q. Jia and S. Ye, Chem. – Eur. J., 2015, 21, 1868 CrossRef CAS PubMed; (j) M. Wang, Z. Q. Rong and Y. Zhao, Chem. Commun., 2014, 50, 15309 RSC.
- (a) Y. Q. Lin, L. M. Yang, Y. Deng and G. F. Zhong, Chem. Commun., 2015, 51, 8330 RSC; (b) Z. Q. Fu, H. Sun, S. J. Chen, B. Tiwari, G. H. Li and Y. R. Chi, Chem. Commun., 2013, 49, 261 RSC.
- (a) X. Y. Chen, F. Xia, J. T. Cheng and S. Ye, Angew. Chem., Int. Ed., 2013, 52, 10644 CrossRef CAS PubMed; (b) J. M. Mo, X. K. Chen and Y. R. Chi, J. Am. Chem. Soc., 2012, 134, 8810 CrossRef CAS PubMed; (c) R. Liu, C. X. Yu, Z. X. Xiao, T. J. Li, X. S. Wang, Y. W. Xie and C. S. Yao, Org. Biomol. Chem., 2014, 12, 1885 RSC.
- (a) L. H. Sun, Z. Q. Liang, W. Q. Jia and S. Ye, Angew. Chem., Int. Ed., 2013, 52, 5803 CrossRef CAS PubMed; (b) X. Fang, X. Chen, H. Lv and Y. R. Chi, Angew. Chem., Int. Ed., 2011, 50, 11782 CrossRef CAS PubMed; (c) D. A. DiRocco and T. Rovis, J. Am. Chem. Soc., 2011, 133, 10402 CrossRef CAS PubMed.
- L. M. Fang, F. Wang, P. J. Chua, Y. B. Lv, L. J. Zhong and G. F. Zhong, Org. Lett., 2012, 14, 2894 CrossRef PubMed.
- (a) S. R. Yetra, S. Mondal, E. Suresh and A. T. Biju, Org. Lett., 2015, 17, 1417 CrossRef CAS PubMed; (b) J. D. Tessier, E. A. O'Bryan, T. B. H. Schroeder, D. T. Cohen and K. A. Scheidt, Angew. Chem., Int. Ed., 2012, 124, 5047 CrossRef; (c) A. G. Kravina, J. Mahatthananchai and J. W. Bode, Angew. Chem., Int. Ed., 2012, 51, 9433 CrossRef CAS PubMed.
- (a) J. Izquierdo, A. Orue and K. A. Scheidt, J. Am. Chem. Soc., 2013, 135, 10634 CrossRef CAS PubMed; (b) Y. W. Xie, Y. L. Que, T. J. Li, L. Zhu, C. X. Yu and C. S. Yao, Org. Biomol. Chem., 2015, 13, 1829 RSC.
- L. Wang, Q. Ni, M. Blumel, T. Shu, G. Raabe and D. Enders, Chem. – Eur. J., 2015, 21, 8033 CrossRef CAS PubMed.
- S. E. Allen, J. Mahatthananachai, J. W. Bode and M. C. Kozlowski, J. Am. Chem. Soc., 2012, 134, 12098 CrossRef CAS PubMed.
- (a) Z. Y. Li, D. H. Wei, Y. Wang, Y. Y. Zhu and M. S. Tang, J. Org. Chem., 2014, 79, 3069 CrossRef CAS PubMed; (b) Y. Wang, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2015, 2, 874 RSC.
- (a) P. Verma, P. A. Patni and R. B. Sunoj, J. Org. Chem., 2011, 76, 5606 CrossRef CAS PubMed; (b) Y. Reddi and R. B. Sunoj, Org. Lett., 2012, 14, 2810 CrossRef CAS PubMed; (c) R. Kuniyil and R. B. Sunoj, Org. Lett., 2013, 15, 5040 CrossRef CAS PubMed.
- Y. Qiao, D. Wei and J. Chang, J. Org. Chem., 2015, 80, 8619 CrossRef CAS PubMed.
- (a) M. M. Zhang, D. H. Wei, Y. Wang, S. J. Li, J. F. Liu, Y. Y. Zhu and M. S. Tang, Org. Biomol. Chem., 2014, 12, 6374 RSC; (b) D. H. Wei, Y. Y. Zhu, C. Zhang, D. Z. Sun, W. J. Zhang and M. S. Tang, J. Mol. Catal. A: Chem., 2011, 334, 108 CrossRef CAS.
- W. J. Zhang, D. H. Wei and M. S. Tang, J. Org. Chem., 2013, 78, 11849 CrossRef CAS PubMed.
- W. J. Zhang, Y. Y. Zhu, D. H. Wei, Y. X. Li and M. S. Tang, J. Org. Chem., 2012, 77, 10729 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, M. I. J. Hasegawa, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision C.01), Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- (a) Y. Qiao and K. L. Han, Org. Biomol. Chem., 2012, 10, 7689 RSC; (b) D. H. Wei, B. L. Lei, M. S. Tang and C. G. Zhan, J. Am. Chem. Soc., 2012, 134, 10436 CrossRef CAS PubMed; (c) L. Zhang and D. C. Fang, J. Org. Chem., 2013, 78, 2405 CrossRef CAS PubMed; (d) Y. M. Chen, G. A. Chass and D. C. Fang, Phys. Chem. Chem. Phys., 2014, 16, 1078 RSC; (e) Y. Li and D. C. Fang, Phys. Chem. Chem. Phys., 2014, 16, 15224 RSC; (f) Y. Li and Z. Y. Lin, Org. Chem. Front., 2014, 1, 1188 RSC; (g) Y. Wang, D. H. Wei, Z. Y. Li, Y. Y. Zhu and M. S. Tang, J. Phys. Chem. A, 2014, 118, 4288 CrossRef CAS PubMed; (h) A. N. Hancock, Y. Kavanagh and C. H. Schiesser, Org. Chem. Front., 2014, 1, 645 RSC; (i) Y. Wang, D. H. Wei, W. J. Zhang, Y. Y. Wang, Y. Y. Zhu, Y. Jia and M. S. Tang, Org. Biomol. Chem., 2014, 12, 7503 RSC; (j) D. Leboeuf, M. Gaydou, Y. H. Wang and A. M. Echavarren, Org. Chem. Front., 2014, 1, 759 RSC; (k) M. Quan, G. Q. Yang, F. Xie, L. Gridney and W. Zhang, Org. Chem. Front., 2015, 2, 398 RSC; (l) Q. Zhang, H. Z. Yu and Y. Fu, Org. Chem. Front., 2014, 1, 614 RSC; (m) D. M. Li, Y. Wang and K. L. Han, Coord. Chem. Rev., 2012, 256, 1137 CrossRef CAS; (n) Y. Wang, X. Guo, M. Tang and D. Wei, J. Phys. Chem. A, 2015, 119, 8422 CrossRef CAS PubMed; (o) S. S. Chen, Y. Su, K. L. Han and X. W. Li, Org. Chem. Front., 2015, 2, 783–791 RSC; (p) X. K. Guo, L. B. Zhang, D. H. Wei and J. L. Niu, Chem. Sci., 2015, 6, 7059–7071 RSC.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- (a) B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151 CrossRef CAS; (b) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- (a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- (a) J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211 CrossRef CAS; (b) A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066 CrossRef CAS; (c) E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, 2009 (http://www.cylview.org) Search PubMed.
- J. D. Chai and M. H. Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- (a) R. Gordillo and K. N. Houk, J. Am. Chem. Soc., 2006, 128, 3543 CrossRef CAS PubMed; (b) C. D. Anderson, T. Dudding, R. Gordillo and K. N. Houk, Org. Lett., 2008, 10, 2749 CrossRef CAS PubMed; (c) O. Gutierrez, R. G. Iafe and K. N. Houk, Org. Lett., 2009, 11, 4298 CrossRef CAS PubMed; (d) M. A. M. Capozzi, C. Centrone, G. Fracchiolla, F. Naso and C. Cardellicchio, Eur. J. Org. Chem., 2011, 4327 CrossRef CAS.
- (a) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef CAS; (b) L. R. Domingo, M. T. Picher and J. A. Saez, J. Org. Chem., 2009, 74, 2726 CrossRef CAS PubMed.
- (a) L. J. Sham and W. Kohn, Phys. Rev., 1966, 145, 561 CrossRef CAS; (b) W. Kohn and L. J. Sham, Phys. Rev., 1965, 137, 1697 CrossRef CAS.
- (a) L. R. Domingo, E. Chamorro and P. Perez, J. Phys. Chem. A, 2008, 112, 4046 CrossRef CAS PubMed; (b) L. R. Domingo, E. Chamorro and P. Perez, J. Org. Chem., 2009, 2009, 3036 Search PubMed; (c) L. R. Domingo, P. Perez and J. A. Saez, RSC Adv., 2013, 3, 1486 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5qo00338e |
| This journal is © the Partner Organisations 2016 |