Mechanism, catalysis and predictions of 1,3,2-diazaphospholenes: theoretical insight into highly polarized P–X bonds

Abstract

Density functional theory (DFT) calculations were carried out to investigate the hydridic character of several main group hydrides. A P-hydrido-1,3,2-diazaphospholene 1f with two π-electron donor amino groups on the heterocyclic skeleton framework performs as a strong hydride donor owing to the significant n(N)–σ*(P–H) hyperconjugation. The natural bond orbital analysis reveals that high π-electron delocalization exists in both 1f and the corresponding stable phosphenium E_f⁺. In addition, 1f is calculated to have a similar catalytic ability for the hydroboration of acetone with pinacolborane, compared to 1e. Thus, a variety of organic substrates activated by 1f are explored, including ketone, imine, isocyanate, CO₂, diazene, alkene, alkyne and epoxide. The results show that the highly polarized and electron-deficient bonds such as C=O π bonds are readily activated, whereas 1f seems difficult to react with electron-rich unsaturated bonds of propene and propyne. More importantly, 1,3,2-diazaphospholene-based compounds, featuring an extremely polarized P–X bond (X = C≡CMe, NMe₂, PMe₂ and SMe), are predicted to have a useful catalytic ability. The preliminary computational results suggest that these P–X compounds could catalyze the silylamination, silylphosphination and silylsulfenylation of acetone with TMSNMe₂, TMSPMe₂ and TMSSMe, respectively. The products are silylethers, which are equivalent to the corresponding alcohols since they easily undergo hydrolysis. Our computational study opens a new avenue to the design of novel main group organocatalysts.

---

Introduction

The last three decades have witnessed spectacular development of the chemistry of heavier main-group elements.¹ Syntheses and isolations of heavier homologues of ethylene,² acetylene,² carbene,³ ketone,⁴ and benzene⁵ have been successfully achieved by various research groups. Not only do the compounds of heavier main group elements have different electronic properties or molecular structures from their lighter congeners, but also the chemical behavior of these compounds resembles that of transition-metal complexes. For example, some of these heavier compounds showed intriguing reactivity for activation of small molecules, including carbon monoxide,⁶ carbon dioxide,⁷ dihydrogen,⁸ ammonia^7a,8c,9 and molecules featuring C=C,^10,11 C≡C,^7a N=N¹¹ and C–H^7a,12 bonds, which provides a desirable alternative to transition-metal catalysis.¹³ Particularly, recent progress in reducing organic substrates into valuable products by main group element mimicking of typical transition metal catalysts has attracted increasing attention due to its reduced environmental impact and lower cost.^13c For instance, Hill and co-workers developed a Mg-catalyzed hydroboration of carbonyl compounds^14a and imines^14b with pinacolborane.

Since the observation of strong n(N)–σ*(P–Cl) hyperconjugation in P-chloro-1,3,2-diazaphospholenes by Gudat and co-workers,¹⁵ both experimental and theoretical studies have revealed that the corresponding P-hydrido-1,3,2-diazaphospholenes 1 contain an umpolung P–H bond (Fig. 1), which showed a hydridic character.¹⁶ Gudat demonstrated that the reaction of 1 with stoichiometric amounts of benzaldehyde gave benzyloxyphosphine.^16a,b,17 Following this, Kinjo, Hirao and co-workers showed that benzyloxyphosphine can further react with pinacolborane to afford PhCH₂OBpin and regenerate 1,^18a which posed an interesting question as to whether 1 can be possibly used as an organocatalyst. Indeed, very recently, 1-catalyzed hydroboration^18a of carbonyl compounds, as well as the hydrogenation^18b of the N=N bond with NH₃BH₃ and N-formylation^18c of amines, have been reported.

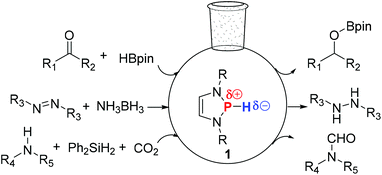Fig. 1 P-Hydrido-1,3,2-diazaphospholenes 1 catalyzed hydroboration of carbonyl compounds, hydrogenation of the N=N bond and N-formylation of amines.

Inspired by the interesting results, we performed DFT calculations to investigate the hydridic character of several E–H bonds (E = Mg, Al, Ge and P). We found that the amino groups bonded to the unsaturated carbons of 1f (Table 1) can further stabilize the corresponding phosphenium cation by means of hyperconjugative delocalization and thus 1f is a better hydride donor. Furthermore, our calculations revealed that 1f has a similar catalytic ability for the hydroboration of acetone compared to 1e. Activation of a small molecule is one of the crucial reactions of transition-metal compounds, which usually acts as an essential step of a catalytic cycle. Therefore, a computational prediction was carried out to probe the small molecule (ketone, imine, isocyanate, CO₂, diazene, alkene, alkyne and epoxide) activation ability of 1f. More importantly, the catalytic ability of a series of P–X (X = C≡CMe, NMe₂, PMe₂ and SMe) compounds for the functionalization of acetone was investigated, which provides hints for further development of 1,3,2-diazaphospholene-based organocatalysis.

Table 1 Hydridic characters of various E–H Bonds (E = Mg, Al, Ge and P)

Entry	EH 1	NBO charges^a of EH	ΔH^b
a NBO charges are given in atomic units. b Energies are given in kcal mol^−1.
1		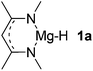Mg (1.56) H (−0.69)	125.3
2		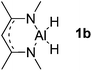Al (1.32) H (−0.40)	113.4
3		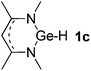Ge (0.76) H (−0.28)	100.1
4		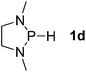P (0.93) H (−0.15)	117.8
5		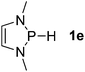P (0.93) H (−0.16)	102.5
6		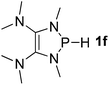P (0.94) H (−0.16)	93.3
7		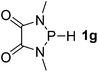P (0.96) H (−0.08)	160.3
8		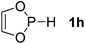P (1.13) H (−0.14)	156.9

---

Results and discussion

Exploration of hydridic character

Main group hydridic compounds have emerged in the past decade as organocatalysts.^13c,19 The strong hydridic character of the well-defined β-diketiminato magnesium 1a,^14,19a,20 aluminium 1b ^19b and germanium 1c ^19c (Table 1, entries 1–3) was demonstrated experimentally by various research groups. In this work, we first probed the hydridic character of various E–H bonds (E = Mg, Al, Ge and P) by means of the relative heterolytic bond dissociation (HBD) energies and natural bond orbital (NBO) analysis at the M06-2X/TZVP level of theory. The relative HBD energies were calculated from the reactions between BEt₃ and E–H compounds (Table 1).²¹ The NBO charges of 1 show that the E–H bonds are polarized at E^δ+–H^δ−. For main group metal hydrides (entries 1–3), the Mg atom of 1a is the most positively charged owing to its considerably lower electronegativity (1.31) compared to those of Al (1.61) and Ge (2.01).²² However, the E–H HBD energy of 1a (125.3 kcal mol⁻¹) is higher than those of 1b (113.4 kcal mol⁻¹) and 1c (100.1 kcal mol⁻¹).

Next, a P-hydrido-1,3,2-diazaphospholidine 1d (entry 4), several P-hydrido-1,3,2-diazaphospholenes with different substituents (1e–1g, entries 5–7), and a 1,3,2-dioxaphosphole 1h (entry 8) were explored. The lone pair of electrons of P-bonded amino or alkoxyl groups could donate into the P–H σ* orbital with concurrent increasing charge density at the hydrogen atom, which can enhance the hydridic character of the P–H bond.¹⁶ However, the higher electronegativity²² of an oxygen atom (3.44) relative to a nitrogen atom (3.04) prevents the above interaction and results in a higher P–H HBD energy (156.9 kcal mol⁻¹) of 1h than that (102.5 kcal mol⁻¹) of 1e (entries 5 and 8).

Although the NBO charges of 1d and 1e are similar (entries 4 and 5), the P–H HBD energy of 1e is lower than that (117.8 kcal mol⁻¹) of 1d. We reason that the saturated carbons of the heterocyclic skeleton in 1d undoubtedly prevent the residual π-electron delocalization of the C₂N₂ fragment (σ* aromaticity)^15,16 and thus strengthen the P–H bond.

It is important to note that Lewis acidic²³ phospheniums E⁺ are formed with heterolytic cleavage of the P–H bond. The stability of E⁺ plays a crucial role in the dissociation process. We assumed that incorporation of functional groups on the heterocyclic skeleton would constitute a rational strategy to stabilize or destabilize E⁺. Indeed, modification of the electronic donor properties by two dimethylamino groups of 1f on the skeleton leads to a weakening of the P–H bond (93.3 kcal mol⁻¹, entry 6) relative to 1e, whereas two strong electron-withdrawing carbonyl groups of 1g strengthen the P–H bond (160.3 kcal mol⁻¹, entry 7). In brief summary, 1f is evaluated to be the best hydride donor, even better than main group metal hydrides.

To gain more insight into the strong hydridic character of 1f, NBO analysis was employed for both 1f and the corresponding E_f⁺. Fig. 2 depicts the 3D structures and selected Wiberg bond index (WBIs) of 1f (a) and E_f⁺ (b). As expected, 1f has a distorted ring (sum of the N1 angles: 341.1°) with a pyramidal geometry around the phosphorus center, and E_f⁺ contains a planar ring (sum of the N1 angles: 359.8°). In E_f⁺, the computed nucleus independent chemical shift NICS(0)_zz and NICS(1)_zz values are −2.9 and −21.8 ppm, respectively.²⁴ These data are a clear indication that the five-membered ring of E_f⁺ is 6π-electron aromatic. The π electron delocalization over the ring of E_f⁺ results in the shortening of the P–N and C–N bonds and lengthening of the C1–C2 bond compared to those of 1f. In addition, WBIs show that the bond orders of C1–N1 and C1–C2 in 1f are 1.01 and 1.68, indicating single and double bond characters, respectively, while they are averaged to be 1.19 and 1.34 in E_f⁺. Note that the geometry of the ring in 1f has transformed from distorted to planar during the process of heterolytic cleavage of the P–H bond. In the meanwhile, the aromaticity of the ring was gained, which could facilitate the process.

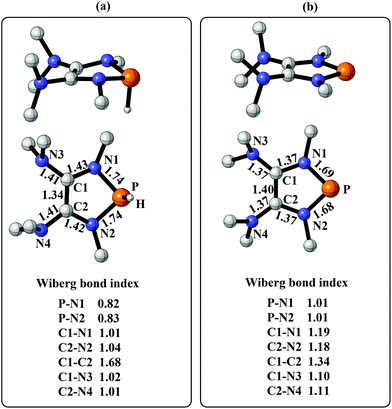Fig. 2 (a) The 3D structure and selected WBIs of 1f. (b) The 3D structure and selected WBIs of E_f⁺. The bond lengths are given in angstroms.

We next turned our attention to finding out how the amino groups promote the heterolytic P–H bond dissociation of 1f. The selected natural localized molecular orbitals (NLMOs) of 1f are illustrated in Fig. 3, displaying the highly delocalized π bond contributions from the lone pairs of electrons of the nitrogen atoms in 1f. As shown in Fig. 3a, two dimethyl amino groups push their electrons into the C–C π* orbital of 1f, which makes the two P-bonded amino groups stronger electron donors by means of lone pair repulsion. The lone pairs of the P-bonded nitrogen atoms are significantly delocalized over the CNP fragments. Direct consequences of this delocalization in 1f are an increase of the charge density at the hydrogen atom of the P–H bond. Indeed, the second-order perturbation theory of the NBO method manifests two hyperconjugative delocalizations from the p-type N lone pairs to the P–H σ* antibonding orbital with donor–acceptor stabilization energies of 8.0 and 8.3 kcal mol⁻¹ (Fig. 3b).

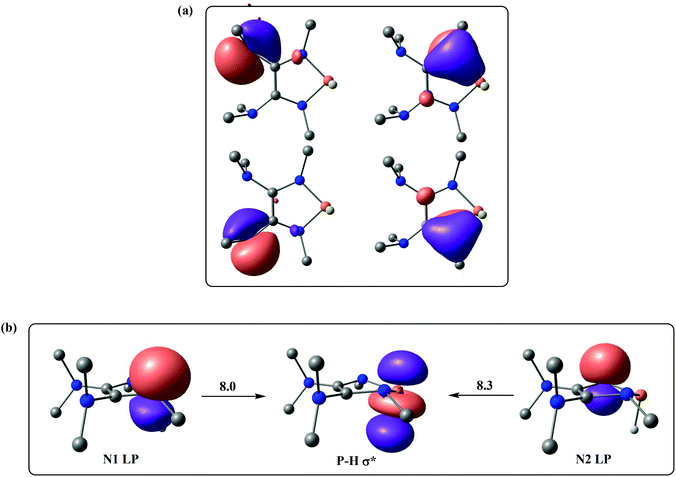Fig. 3 (a) Selected NLMOs of 1f. (b) Selected NBOs of 1f for the second-order perturbation theory analysis (energies are given in kcal mol⁻¹).

Also, high π-electron delocalization is found in E_f⁺ (Fig. 4). The selected NLMOs of E_f⁺ reveal that the lone pairs of the P-bonded amino groups not only delocalize onto the phosphorus, but also onto the unsaturated carbons (Fig. 4a). Interestingly, the second-order perturbation theory analysis suggests strong hyperconjugative delocalizations from the p-type N lone pairs of the dimethyl amino groups to the C–N π* orbitals (Fig. 4b). The strong donor–acceptor interactions between the lone pair of phosphorus and the C–N π* orbitals are also suggested by the stabilization energy of approximately 58.0 kcal mol⁻¹. This high π-electron delocalization in E_f⁺, coupled with the aromaticity, results in stabilizing the electron-deficient phosphorus center and promoting the heterolytic P–H bond cleavage.

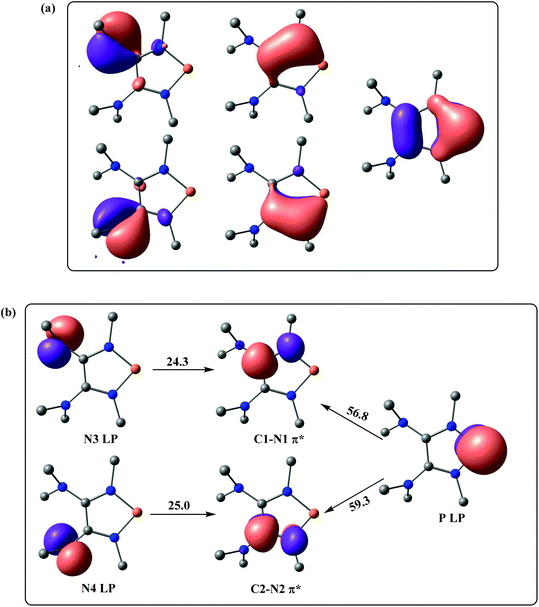Fig. 4 (a) Selected NLMOs of E_f⁺. (b) Selected NBOs of E_f⁺ for the second-order perturbation theory analysis (energies are given in kcal mol⁻¹).

Investigation of the catalytic ability

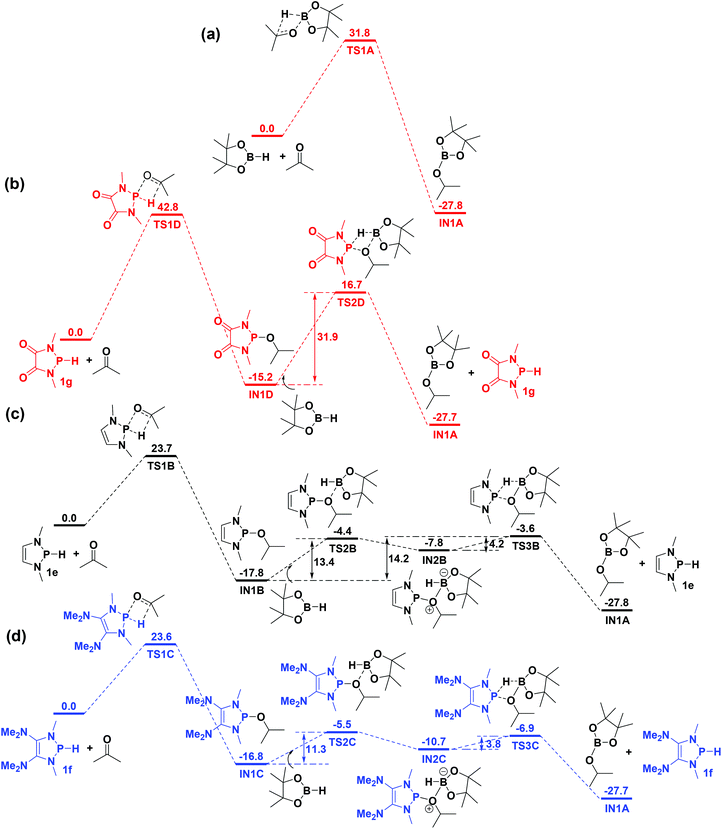
Kinjo, Hirao and co-workers reported the 1-catalyzed hydroboration of carbonyl compounds (Fig. 1), and the mechanism study revealed that the process involved a stepwise σ-bond metathesis, including P–H cleavage/P–O formation, B–O formation, and B–H cleavage/P–H formation.^18a Our calculation results are consistent with their findings (Fig. 5c). For comparison, the catalyst-free hydroboration of acetone was also researched and it revealed a relatively high energy barrier of 31.8 kcal mol⁻¹ (Fig. 5a). Expectedly, the less hydridic character of the P–H bond in 1g leads to a significantly high barrier (42.8 kcal mol⁻¹) in the P–H cleavage/P–O formation step (Fig. 5b). To our delight, 1f is predicted to have a similar catalytic ability for the hydroboration of acetone relative to 1e (Fig. 5c and d). For instance, the energy barriers of 1e (23.7 kcal mol⁻¹) and 1f (23.6 kcal mol⁻¹) are similar in the P–H cleavage/P–O formation step (rate-determining step). Further, in the B–O formation and B–H cleavage/P–H formation steps, the energy barrier of 1f is 11.3 kcal mol⁻¹, which is 2.9 and 20.6 kcal mol⁻¹ lower than those of 1e (14.2 kcal mol⁻¹) and 1h (31.9 kcal mol⁻¹), respectively.

Fig. 5 (a) Catalyst-free hydroboration of acetone. (b) Hydroboration of acetone catalyzed by 1g. (c) Hydroboration of acetone catalyzed by 1e. (d) Hydroboration of acetone catalyzed by 1f. Free energies are given in kcal mol⁻¹.

Activation of organic substrates

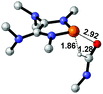
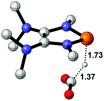
Functionalization of unsaturated bonds has been a continuous research interest of chemists. Experimentally, 1,3,2-diazaphospholenes 1 have been reported to activate some unsaturated organic substrates such as benzaldehyde^16,18a and CO₂.^18c Encouraged by our achievements in theoretical predictions,²⁵ activation of several organic substrates by 1f is evaluated computationally, involving ketone, imine, isocyanate, CO₂, diazene, alkene, alkyne and epoxide (Table 2). We find that the substrates S, featuring a highly polarized bond, are readily activated by 1f. For example, the NBO atomic-charge distributions (C = 0.57 a.u. and O = −0.52 a.u.) on the C–O bond in acetone are much more polarized than those (C = 0.29 a.u. and N = −0.42 a.u.) on the C–N bond in N-methylpropan-2-imine, resulting in a lower energy barrier (23.6 kcal mol⁻¹) of acetone activation (entries 1 and 2). The more polarized C–O bonds in isocyanatomethane and CO₂ lead to much lower activation energies (relative to acetone, entries 1, 3 and 4).

Table 2 Activation of organic substrates by 1f

Entry	S^a	3D structure^b of TS	ΔGTS^c	P^a	ΔGp^c
a NBO charges are given in atomic units at the M06-2X/TZVP//B3LYP/6-31G(d) level of theory. b Bond lengths are given in angstroms. c Energies are given in kcal mol^−1.
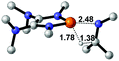
1		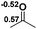	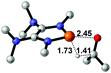23.6		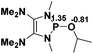−16.8
2		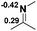	32.1		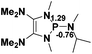−19.3
3		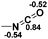	8.5		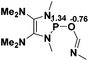−12.3
4		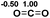	9.4		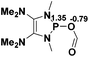−7.6
5		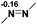	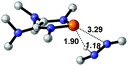29.7		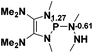−20.0
6		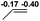	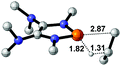38.3		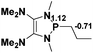−23.7
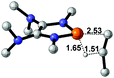
7		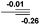	36.5		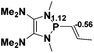−29.1
8		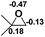	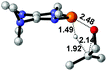49.5		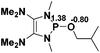−45.2

---

NBO analysis suggests that dimethyldiazene, propene, and propyne are electron-rich unsaturated substrates (entries 5–7), which appear to be less susceptible to 1f with activation energies of 29.7, 38.3 and 36.5 kcal mol⁻¹, respectively. Lastly, we investigated the ring opening of 2,2-dimethyloxirane mediated by 1f (entry 8). The high activation barrier (49.5 kcal mol⁻¹) indicates that the process is impossible to take place.

It is interesting to note that the NBO charges of the products P in Table 2 show that the phosphorus atoms are highly positively charged, whereas the P-bonded atoms (O, N and C) carry more negative charges compared to the corresponding starting materials (i.e. acetone and CO₂), which could be mainly attributed to the significant hyperconjugation of the five-membered ring as discussed above. Further, Gudat and co-workers showed that P-phosphino-1,3,2-diazaphospholene, which contains a polarized P–P bond, could stoichiometrically react with electron-poor alkenes and alkynes, affording the corresponding phosphinyl-phosphination products.^17,26 We were wondering whether these 1,3,2-diazaphospholene-based compounds, featuring extremely polarized P–X bonds (X = O, N or C), can be used as organocatalysts.

Catalytic ability of P–X compounds

The model P–X compounds (X = C≡CMe, NMe₂, PMe₂ and SMe) 2 were chosen to explore the catalytic ability (Fig. 6). As expected, all of the P–X bonds of 2 are found to be highly polarized and weak with partial single bond character (WBIs of P–X bonds are less than 1.0). We therefore assumed that the polarization would bring the desired reactivity.

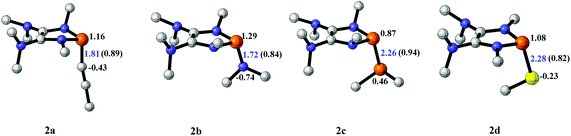Fig. 6 3D structures of P–X (X = C≡CMe, NMe₂, PMe₂ and SMe) compounds. NBO charges are given in atomic units in black. Bond lengths are given in angstroms in blue. WBIs are given in parentheses.

Catalytic functionalization of carbonyl compounds is a fundamental research topic for chemists. Gratifyingly, the energies of the transition states TS4 involving C=O bond activation of acetone by 2a, 2b, 2c, and 2d are computed to be 30.4, 19.2, 23.7, and 25.2 kcal mol⁻¹ (Fig. 7), respectively, which are much lower than those of the direct addition of the corresponding HX [X = C≡CMe (65.5 kcal mol⁻¹), NMe₂ (39.7 kcal mol⁻¹), PMe₂ (49.4 kcal mol⁻¹) and SMe (43.2 kcal mol⁻¹)] to acetone. However, the reversible processes are identified for 2b and 2d as the reverse barrier being equal or less compared to the forward barrier (Fig. 7b and d).

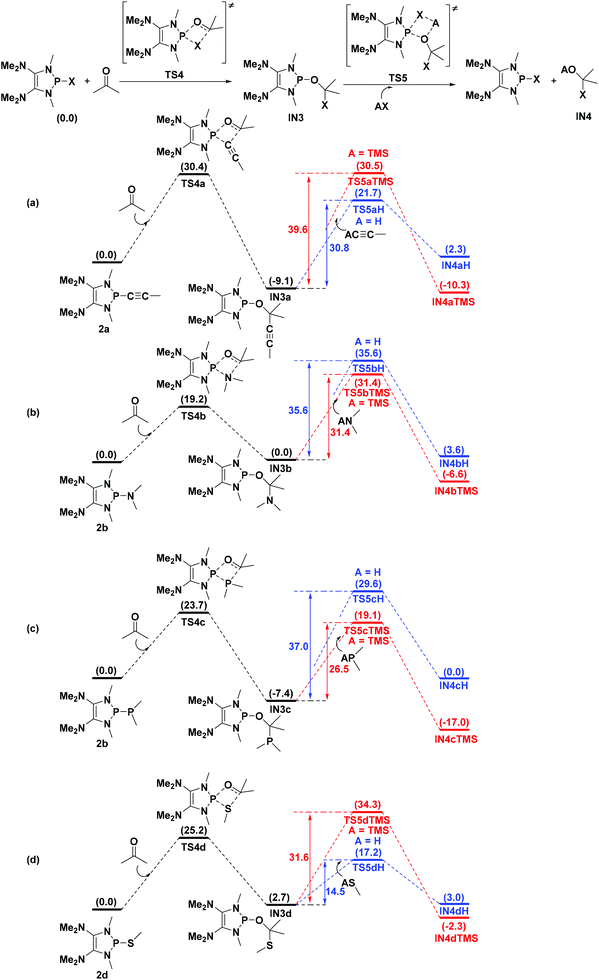Fig. 7 Theoretical predictions of the catalysis ability of P–X [X = C≡CMe (a), NMe₂ (b), PMe₂ (c) and SMe (d)] compounds. Energies are given in kcal mol⁻¹.

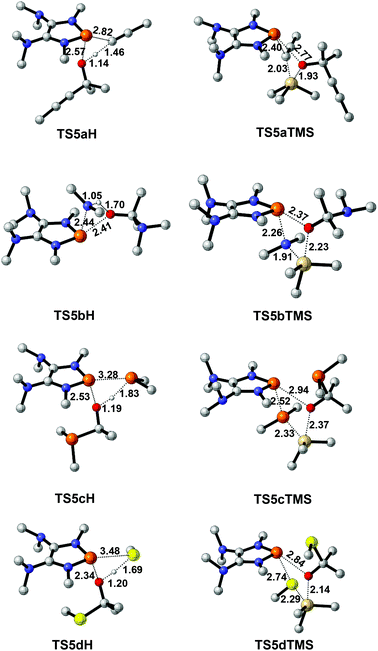
To design a catalytic cycle, we need to regenerate catalysts from IN3 (Fig. 7). Several AX (A = H or TMS, TMS = trimethylsilyl, X = C≡CMe, NMe₂, PMe₂ or SMe) compounds are tested to react with IN3, which would lead to the P–O cleavage/P–X formation via four-membered ring transition states TS5 (Fig. 8).

Fig. 8 3D structures of TS5. Bond lengths are given in angstroms.

For 2a (Fig. 7a), the result shows that while the activation energy (30.8 kcal mol⁻¹) of HC≡CMe with IN3a is much lower than that (39.6 kcal mol⁻¹) of TMSC≡CMe, the formation of IN4aH is endergonic by 2.3 kcal mol⁻¹. These data suggest that 2a might be reluctant to catalyze the hydroalkynation of acetone.

For 2b and 2c (Fig. 7b and c), the relatively high barriers of hydroamination (35.6 kcal mol⁻¹) and hydrophosphination (37.0 kcal mol⁻¹) indicate that IN3c and IN3d might be inert to HNMe₂ and HPMe₂. However, the silylamination and silylphosphination (rate-determining steps) of acetone with TMSNMe₂ or TMSPMe₂ seem facile to take place since the processes are not energy demanding (31.4 kcal mol⁻¹ for TMSNMe₂ and 26.5 kcal mol⁻¹ for TMSPMe₂) and exergonic, especially at elevated temperatures.²⁷

Lastly (Fig. 7d), although the reaction of IN3d with HSMe (14.5 kcal mol⁻¹) seems much easier than that (31.6 kcal mol⁻¹) of IN3d with TMSSMe, the energy of the product IN4dH is 3.0 kcal mol⁻¹, which is higher than that (2.7 kcal mol⁻¹) of IN3d, indicating that the hydrosulfenylation is endothermic. However, the silylsulfenylation (rate-determining step, 31.6 kcal mol⁻¹) of acetone with TMSSMe appears to be possible at elevated temperatures.

Conclusions

The hydridic characters of eight main group hydrides have been investigated computationally. Among them, 1f is the best hydride donor with the aid of two π-electron donor amino groups. NLMOs and the second-order perturbation theory of the NBO method performed on 1f and the corresponding stable phosphenium E_f⁺ show strong π-electron delocalization. The lone pairs of electrons of the P-bonded amino groups donate into the P–H σ* orbital in 1f. This significant hyperconjugation could increase the electron density at the H atom of the P–H bond, enhancing the hydridic character. The mechanism study of the hydroboration of acetone confirms the high catalytic ability of 1f compared to 1e and 1h. Moreover, several organic substrates activated by 1f were explored. The highly polarized and electron-deficient bonds such as C=O π bonds in CO₂ are readily activated, whereas it seems difficult to react with electron-rich unsaturated bonds of propene and propyne by 1f. Finally, the catalytic ability of the P–X (X = C≡CMe, NMe₂, PMe₂ and SMe) compounds 2 has been probed. To our delight, the silylamination, silylphosphination and silylsulfenylation of acetone with TMSNMe₂, TMSPMe₂ and TMSSMe, respectively, seem highly possible to take place because the processes are not energy demanding with activation energies of 31.4 kcal mol⁻¹ (TMSNMe₂), 26.5 kcal mol⁻¹ (TMSPMe₂), and 31.6 kcal mol⁻¹ (TMSSMe). The products are silylethers, which are equivalent to the corresponding alcohols since they easily undergo hydrolysis. Our findings provide hints for further development of main group organocatalysts.

Computational details

Calculations were performed with the Gaussian 09 package.²⁸ Natural bond orbital (NBO) calculations were carried out using the NBO 5.9 program.²⁹ The M06-2X³⁰ functional with the TZVP³¹ basis set was used for the study of hydridic characters of various E–H bonds (Table 1) and NBO analysis of 1f and E_f⁺ (Fig. 2–4). The nucleus independent chemical shift (NICS)³² of E⁺ was computed at the M06-2X/6-311++G(2d,p)//M06-2X/TZVP level of theory in the gas-phase. When the environments at points 1 angstrom above and below the ring centers are not equivalent, the averaged values are used for NICS(1)_zz.

For the mechanistic studies (Fig. 5–8 and Table 2), geometry optimizations were carried out with the B3LYP functional³³ and the 6-31G(d)³⁴ basis set was used for all the atoms. Frequency calculations at the same level of theory were performed to identify the number of imaginary frequencies (zero for local minimum and one for transition states) and provide the thermal corrections of the Gibbs free energy. Dispersion correction calculations using the corresponding B3LYP-D functional were performed with the DFT-D3 program of Grimme.³⁵ The transition states were subjected to intrinsic reaction coordinate (IRC)³⁶ calculations to determine two corresponding minima.

The M06-2X functional was used for the solution-phase, single-point energy calculations (Fig. 5–8 and Table 2), because this method was recently established as an excellent functional for describing reaction energetics of main group systems.³⁷ The gas-phase geometry was used for all the solution phase calculations. A similar treatment was also used in many recent computational studies.³⁸ A larger basis set, that is, 6-311++G(2d,p)³⁹ was used. The default self-consistent reaction field (SCRF) polarizable continuum model (PCM) was used with acetonitrile,⁴⁰ while Bondi radii⁴¹ were chosen as the atomic radii to define the molecular cavity. The Gibbs energy corrections from the frequency calculations and dispersion corrections were added to the single-point energies to obtain the Gibbs free energies in solution. All the solution-phase free energies reported in this paper correspond to the reference state of 1 mol L⁻¹, 298 K. The optimized structures were visualized by the CYLview program⁴² or Chemcraft.⁴³

Acknowledgements

We acknowledge financial support from the Chinese National Natural Science Foundation (Grants 21375113, 21232005, 21103142, 21573179, and 21133007), the National Basic Research Program of China (Grants 2012CB821600, 2013CB910700 and 2011CB808504), the Program for New Century Excellent Talents in University (NCET-13-0511), the Fundamental Research Funds for the Central Universities (Grant 2012121021), and the Program for Changjiang Scholars and Innovative Research Team in University (Grant IRT1263). Thanks are also given to Dr D. A. Ruiz from UCSD for the valuable discussion.

Notes and references

1. For reviews, see: (a) P. P. Power, Nature, 2010, 463, 171–177; (b) R. Gleiter and D. B. Werz, Chem. Rev., 2010, 110, 4447–4488; (c) M. A. Malik, M. Afzaal and P. O'Brien, Chem. Rev., 2010, 110, 4417–4446.
2. For a review, see: R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877–3923.
3. For a review, see: Y. Mizuhata, T. Sasamori and N. Tokitoh, Chem. Rev., 2009, 109, 3479–3511.
4. L. Li, T. Fukawa, T. Matsuo, D. Hashizume, H. Fueno, K. Tanaka and K. Tamao, Nat. Chem., 2012, 4, 361–365.
5. (a) K. Wakita, N. Tokitoh, R. Okazaki and S. Nagase, Angew. Chem., Int. Ed., 2000, 39, 634–636; (b) N. Nakata, N. Takeda and N. Tokitoh, J. Am. Chem. Soc., 2002, 124, 6914–6920.
6. X. Wang, Z. Zhu, Y. Peng, H. Lei, J. C. Fettinger and P. P. Power, J. Am. Chem. Soc., 2009, 131, 6912–6913.
7. (a) S. Yao, Y. Xiong and M. Driess, Organometallics, 2011, 30, 1748–1767; (b) J. Li, M. Hermann, G. Frenking and C. Jones, Angew. Chem., Int. Ed., 2012, 51, 8611–8614.
8. (a) G. H. Spikes, J. C. Fettinger and P. P. Power, J. Am. Chem. Soc., 2005, 127, 12232–12233; (b) Y. Peng, M. Brynda, B. D. Ellis, J. C. Fettinger, E. Rivard and P. P. Power, Chem. Commun., 2008, 6042–6044; (c) Y. Peng, J.-D. Guo, B. D. Ellis, Z. Zhu, J. C. Fettinger, S. Nagase and P. P. Power, J. Am. Chem. Soc., 2009, 131, 16272–16282; (d) J. Li, C. Schenk, C. Goedecke, G. Frenking and C. Jones, J. Am. Chem. Soc., 2011, 133, 18622–18625.
9. (a) S. M. McCarthy, Y.-C. Lin, D. Devarajan, J. W. Chang, H. P. Yennawar, R. M. Rioux, D. H. Ess and A. T. Radosevich, J. Am. Chem. Soc., 2014, 136, 4640–4650; (b) J. Cui, Y. Li, R. Ganguly, A. Inthirarajah, H. Hirao and R. Kinjo, J. Am. Chem. Soc., 2014, 136, 16764–16767.
10. (a) R. Kinjo, M. Ichinohe, A. Sekiguchi, N. Takagi, M. Sumimoto and S. Nagase, J. Am. Chem. Soc., 2007, 129, 7766–7767; (b) Y. Peng, B. D. Ellis, X. Wang, J. C. Fettinger and P. P. Power, Science, 2009, 325, 1668–1670.
11. C. Cui, M. M. Olmstead, J. C. Fettinger, G. H. Spikes and P. P. Power, J. Am. Chem. Soc., 2005, 127, 17530–17541.
12. (a) O. T. Summerscales, J. C. Fettinger and P. P. Power, J. Am. Chem. Soc., 2011, 133, 11960–11963; (b) O. T. Summerscales, C. A. Caputo, C. E. Knapp, J. C. Fettinger and P. P. Power, J. Am. Chem. Soc., 2012, 134, 14595–14603; (c) Z. D. Brown, P. Vasko, J. C. Fettinger, H. M. Tuononen and P. P. Power, J. Am. Chem. Soc., 2012, 134, 4045–4048.
13. For reviews, see: (a) R. L. Melen, Chem. Soc. Rev. 10.1039/C5CS00521C; (b) E. M. Leitao, T. Jurca and I. Manners, Nat. Chem., 2013, 5, 817–829; (c) K. Revunova and G. I. Nikonov, Dalton Trans., 2015, 44, 840–866; (d) C. C. Chong and R. Kinjo, ACS Catal., 2015, 5, 3238–3259.
14. (a) M. Arrowsmith, T. J. Hadlington, M. S. Hill and G. Kociok-Kohn, Chem. Commun., 2012, 48, 4567–4569; (b) M. Arrowsmith, M. S. Hill and G. Kociok-Köhn, Chem. – Eur. J., 2013, 19, 2776–2783.
15. D. Gudat, A. Haghverdi, H. Hupfer and M. Nieger, Chem. – Eur. J., 2000, 6, 3414–3425.
16. (a) D. Gudat, A. Haghverdi and M. Nieger, Angew. Chem., Int. Ed., 2000, 39, 3084–3086; (b) S. Burck, D. Gudat, M. Nieger and W.-W. Du Mont, J. Am. Chem. Soc., 2006, 128, 3946–3955.
17. D. Gudat, Acc. Chem. Res., 2010, 43, 1307–1316.
18. (a) C. C. Chong, H. Hirao and R. Kinjo, Angew. Chem., Int. Ed., 2015, 54, 190–194; (b) C. C. Chong, H. Hirao and R. Kinjo, Angew. Chem., Int. Ed., 2014, 53, 3342–3346; (c) C. C. Chong and R. Kinjo, Angew. Chem., Int. Ed., 2015, 54, 12116–12120.
19. For selected recent publications, see: (a) D. J. Liptrot, M. S. Hill, M. F. Mahon and A. S. S. Wilson, Angew. Chem., Int. Ed., 2015, 54, 13362–13365; (b) Z. Yang, M. Zhong, X. Ma, S. De, C. Anusha, P. Parameswaran and H. W. Roesky, Angew. Chem., Int. Ed., 2015, 54, 10225–10229; (c) T. J. Hadlington, M. Hermann, G. Frenking and C. Jones, J. Am. Chem. Soc., 2014, 136, 3028–3031.
20. For selected recent publications, see: (a) C. Weetman, M. S. Hill and M. F. Mahon, Chem. Commun., 2015, 51, 14477–14480; (b) D. J. Liptrot, M. Arrowsmith, A. L. Colebatch, T. J. Hadlington, M. S. Hill, G. Kociok-Köhn and M. F. Mahon, Angew. Chem., Int. Ed., 2015, 54, 15280–15283.
21. M. T. Mock, R. G. Potter, D. M. Camaioni, J. Li, W. G. Dougherty, W. S. Kassel, B. Twamley and D. L. DuBois, J. Am. Chem. Soc., 2009, 131, 14454–14465.
22. A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221.
23. (a) J. M. Slattery and S. Hussein, Dalton Trans., 2012, 41, 1808–1815; (b) L. Liu, D. A. Ruiz, F. Dahcheh and G. Bertrand, Chem. Commun., 2015, 51, 12732–12735.
24. The NICS values of the E⁺ derivatives listed in Table 1 are shown in Table S1 in the ESI.†.
25. (a) L. Liu, H. Yuan, T. Fu, T. Wang, X. Gao, Z. Zeng, J. Zhu and Y. Zhao, J. Org. Chem., 2014, 79, 80–87; (b) T. Wang, S. Sang, L. Liu, H. Qiao, Y. Gao and Y. Zhao, J. Org. Chem., 2014, 79, 608–617; (c) L. Liu, Y. Wu, Z. Wang, J. Zhu and Y. Zhao, J. Org. Chem., 2014, 79, 6816–6822; (d) L. Liu, C. Chan, J. Zhu, C.-H. Cheng and Y. Zhao, J. Org. Chem., 2015, 80, 8790–8795; For experimental realization of ref. 25d, see: (e) D. Wu, R. Ganguly, Y. Li, S. N. Hoo, H. Hirao and R. Kinjo, Chem. Sci., 2015, 6, 7150–7155; (f) K. An and J. Zhu, Organometallics, 2014, 33, 7141–7146; (g) Y. Huang and J. Zhu, Chem. Asian J., 2015, 10, 405–410.
26. (a) S. Burck, D. Gudat and M. Nieger, Angew. Chem., Int. Ed., 2004, 43, 4801–4804; (b) I. Hajdók, F. Lissner, M. Nieger, S. Strobel and D. Gudat, Organometallics, 2009, 28, 1644–1651.
27. We estimate the barrier value from the Eyring equation, i.e., k = (k_BT/h) exp(−ΔG^‡/RT), where k is the rate constant, k_B is the Boltzmann's constant, h is the Planck's constant, ΔG^‡ is the activation free energy, R is the gas constant, and T is the temperature. Assuming that the concentration of each reactant is 1 mol L⁻¹ and the second-order rate constant k of a reaction whose half-life is 24 h is 1.2 × 10⁻⁵ L mol⁻¹ s⁻¹, we obtain ΔG^‡ as 31.4 kcal mol⁻¹ at 110 °C.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010.
29. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2009; http://www.chem.wisc.edu/~nbo5.
30. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
31. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
32. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. V. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
33. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
34. (a) R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728; (b) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (c) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222; (d) J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923; (e) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
35. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799; (c) S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
36. (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
37. (a) Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241; (b) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868; (c) Y. Wu, L. Liu, J. Su, K. Yan, J. Zhu and Y. Zhao, Chem. Commun., 2016, 52, 1582–1585.
38. For selected recent publications, see: (a) L. Liu, J. Zhu and Y. Zhao, Chem. Commun., 2014, 50, 11347–11349; (b) M. N. Grayson, M. J. Krische and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 8838–8850; (c) G. Lu, C. Fang, T. Xu, G. Dong and P. Liu, J. Am. Chem. Soc., 2015, 137, 8274–8283; (d) Y. Yang and P. Liu, ACS Catal., 2015, 5, 2944–2951; (e) L. Liu, Y. Wu, T. Wang, X. Gao, J. Zhu and Y. Zhao, J. Org. Chem., 2014, 79, 5074–5081.
39. (a) R. Krishan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654; (b) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648; (c) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
40. Experimentally, all of the 1,3,2-diazaphospholene-catalyzed reactions were performed in acetonitrile. See ref. 18 for details.
41. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
42. C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, Sherbrooke, Québec, Canada, 2009; http://www.cylview.org.
43. G. A. Andrienko, ChemCraft, http://www.chemcraftprog.com.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6qo00002a

---