Controlling dielectrical properties of polymer blends through defined PEDOT nanostructures

Abstract

The paper reports the crucial role of the morphology of poly(3,4-ethylenedioxythiophene) (PEDOT) nanostructures on the thermal and dielectric properties of polymer blends prepared thereof. PEDOT nanostructures with two different morphologies (nanoparticles and nanowires) were synthesized. The size for the nanoparticles was in the range 10–40 nm and the diameter of the nanowires was of ca. 200 nm. These nanostructures were blended with an insulating polymer matrix, poly(methyl methacrylate) (PMMA), to evaluate the dielectrical properties of the materials. The results of broadband dielectric spectroscopy showed a strong correlation between the morphology of the nanostructure and the improvement of the electrical properties of the material.

---

1. Introduction

Most polymers exhibit high electrical resistance and their conductivity probably results from the presence of ionic impurities.^1–3 To improve the conductivity while maintaining the desired properties attributed to the polymer, the formation of composites or blends has become a common strategy during the last two decades.^4–7 The combination of the physical and chemical properties of each component provides a new material, whose properties are determined by the amount, type and shape of the conductive one.⁸ Accordingly, the control of morphology, which includes both dispersion and alignment, plays a crucial role in the final properties of the material.^9,10 Although most of the investigations about composites and blends are focused on reinforcement aspects, many other parameters and property enhancements are being actively studied. Generally, the optimum properties for composites will usually require excellent dispersion of the second component. Nevertheless, it has been observed that the enhancement of the electrical conductivity is achieved by formation of a continuous network of the additive through the polymer matrix. In this case, a hierarchical structure can be desired because it may be responsible of the percolation pathway needed for an improvement of electrical conductivity.¹¹

Furthermore, it has been found that conductive properties can be achieved with very low content of a second component added to the matrix in the nanometric range.^12,13 The reason for the significant improvement of the macroscopic properties at very low additive contents is the very high surface-to-volume ratio of nanoparticles. With this premise, several matrix/nanostructure combinations have been studied. In many of them, poly(methyl methacrylate) (PMMA) is the used matrix.^14,15 Indeed, PMMA has been applied as a matrix not only in the context of conductivity, but also for a wide range of uses, including optical applications,¹⁶ gas sensing,^17,18 and coatings.^19,20 Although several PMMA-based systems have been extensively studied, the influence of the load on the dynamics and flexibility of PMMA remains unclear. In some systems, the addition of additive nanoparticles produces an increase of the glass transition temperature, T_g, due to the restriction of chain mobility caused by the interactions between additive and matrix.²¹ In contrast, a decrease in the T_g has also been observed in other systems.²² The “nano-effect”²³ of the additive is related to the local properties of the matrix, caused, as above mentioned, by the extremely high surface area of the nanostructure and the small distances between nanoparticles, even at low loadings. The increase or decrease in the T_g depends on the specific interactions between both phases. The effect of the additive is different, depending on the type of polymer matrix and nanometric additive and/or due to different preparation/processing conditions.^24,25

Diverse nanofillers, such as silica, expanded graphite, carbon nanotubes, nanoclays, titania and metal nanoparticles, have been employed to achieve an improvement in the conductive properties.^26–34 However, considering the different results obtained for several nanocomposite systems, a high number of challenging questions remain unsolved.

Conducting polymeric materials, along with their plastic properties, possess electrical, magnetic and optical properties that can be similar to metals. In recent years, the poly(3,4-ethylenedioxythiophene) (PEDOT) has attracted much attention in many applications due to their high electrical properties and electrochemical stability.^11,35,36 The use of PEDOT as a second component has many advantages, including transparency and low cost. By varying the synthesis method and processing conditions, it is possible to control the conductive properties of the material.³⁷ Due to its properties, PEDOT is an interesting material to change the electrical properties of composites for electronic and optoelectronic applications. In this work, cast films were prepared by blending PEDOT with PMMA to observe how the properties of the blends are affected by the morphology of PEDOT. Two defined PEDOT nanostructures were used: nanoparticles (NP) and nanowires (NW). We studied the effect of morphological changes on the conductivity of the polymer films, finding an interrelationship between morphology, thermal stability and conductivity.

2. Experimental section

Chemicals

3,4-Ethylenedioxythiophene (EDOT, 97%), p-dodecylbenzenesulfonic acid (DBSA, 95%), iron(III) p-toluenesulfonate hexahydrate (FeTos), hydrogen peroxide (33 wt% aqueous solution), lithium perchlorate (LiClO₄, 98%), ethanol and sodium hydroxide were purchased from Sigma Aldrich and used as received without further purification. Poly(methyl methacrylate) (PMMA) was purchased commercially (ICI DIAKON 102) with number average molar mass M_n = 28 270, polydispersity index PI = 1.98, and glass transition temperature of approximately 112 °C.

Synthesis of defined PEDOT nanostructures

Miniemulsion polymerization³⁸ was used to synthetize PEDOT nanoparticles. 0.2 g of EDOT was added to 40 mL of a water solution containing 0.5 g of DBSA. The EDOT emulsion was created by ultrasonic treatment for 10 min (1/2-inch tip, 70% of amplitude, Branson Sonifier 450). Then, a first oxidant, 0.25 g of iron(III) p-toluenesulfonate hexahydrate (FeTos), was added to the emulsion. This reaction was carried out at 45 °C for one hour. After that, H₂O₂ (0.5 mL, 33 wt% aqueous solution) was added as a second oxidizer and the reaction was kept at 45 °C for 24 hours. The dark suspension obtained was filtered several times by using dialysis centrifuge tubes (Amicon Ultra, 3000 MWCO, Millipore) to remove the residual free surfactant. Finally, a black powder was obtained after freeze-drying. The synthesis process is schematically summarized in Fig. 1a.

Fig. 1 Schematic representation of the synthesis of (a) PEDOT nanoparticles (PEDOT-NP) and (b) PEDOT nanowires (PEDOT-NW).

PEDOT-NW were synthesized by an electrochemical polymerization method in porous alumina templates (Whatman anodisc 13) previously covered on one side with a gold layer (thickness of 20 nm) (see Fig. 1b). A solution with 0.01 M of EDOT and 0.1 M of LiClO₄ was prepared in acetonitrile. The electropolymerization was carried out in an IVIUM n-stat multi potentiostat at 3 mA. The alumina template was used as the working electrode, a platinum grid was used as a counter electrode and an Ag/AgCl electrode was used as the reference one. After the reaction, the alumina template was removed by using a 6 M NaOH aqueous solution. Finally, the PEDOT nanowires were dispersed in ethanol by ultrasonic treatment in an ultrasound bath and the solvent was evaporated in vacuum conditions at room temperature.

Preparation of polymer films

The nanocomposite films were prepared by solution casting of CH₂Cl₂ solutions containing the synthesized PEDOT nanoparticles (NP) and nanowires (NW). An amount of 5 mg of PEDOT was added to 50 g of a solution of 1 wt% of PMMA in CH₂Cl₂. The solution was sonicated in an ultrasonic bath for 20 min at room temperature and then subjected to mechanical stirring for 2 h. The homogeneous solution was dropped on a circular aluminum mold over a glass substrate and the solvent was evaporated at room temperature for 48 h. Transparent homogeneous films were obtained of PMMA/PEDOT with 1 wt% of PEDOT nanoparticles and nanowires.

Characterization techniques

Scanning electron microscopy (SEM) was carried on a Hitachi 4800 S microscope at an acceleration voltage of 20 kV and at a working distance of 14 mm. The samples, placed in the sample holder (ca. 5 cm diameter), were coated with a thin Au–Pd layer before testing. Transmission electron microscopy (TEM) was performed on a JEM-1010 microscope equipped with a digital camera MegaView III, operating at an acceleration voltage of 100 kV. Samples were prepared by drop casting on copper grids.

Thermogravimetric analysis (TGA) was performed by using a Setaram Setsys 16/18 TGA-ATD thermobalance. The samples were heated in alumina pan from 30 to 1000 °C at a heating rate of 10 °C min⁻¹ under oxygen atmosphere. Sample masses ranged from 7 to 10 mg.

Differential scanning calorimetry (DSC) was performed in a TA Instrument Q20 equipped with a refrigerated cooling system and nitrogen purge. Calibration was performed with indium according with manufacturer recommended procedures. About 5–7 mg of sample was sealed in an aluminum pan for every test. Thermal behavior was investigated by scanning the samples from −90 to 230 °C at a heating rate of 20 °C min⁻¹. A second run (to delete the thermal history) was used for the thermal characterization of the films. The midpoint of the heat capacity change has been chosen to represent the glass transition temperature, T_g.

The analysis of the electrical behavior of PMMA/PEDOT samples was carried out by using broadband dielectric relaxation spectroscopy (DRS). Isothermal relaxation spectra of PMMA/PEDOT samples were collected by using a Novocontrol Broadband Dielectric Spectrometer (Hundsagen, Germany) consisting of an Alpha analyzer to carry out measurements from 5 × 10⁻² to 3 × 10⁶ Hz. Inert N₂ atmosphere in a range of temperatures from −20 °C to 170 °C was used in all experiments. The temperature was controlled by a nitrogen jet (QUATRO from Novocontrol) with a temperature error of 0.1 °C during every single sweep in frequency. Molded disc shaped samples of about 0.20 mm thickness and 20 mm diameter was used. The experimental uncertainty was better than 5% in all cases.

One of the best potential of the linear dielectric analysis is that impedance data allow the analysis of different processes related to: (a) dipoles motions associated with local and cooperative micro-Brownian motions of molecular chains, (b) charge transport across the samples and (c) the separation of charges at the interface lead to an additional polarization. The latter can take place at inner dielectric boundary layers (Maxwell–Wagner–Sillars polarization, MWS) and/or at the external electrodes contacting the sample (electrode polarization, EP).^39–41

By employing an alternating voltage

V(ω) = V₀Im[exp(jωt)] (1)

where ω (=2πf) is the angular frequency of the electric field, the current crossing a sample sandwiched between two parallel plane electrodes can be expressed as

i = dq/dt = V(ω)/Z*(ω) (2)

where q is the charge of the capacitor and Z*(ω) is the complex impedance. The complex dielectric permittivity is expressed in terms of the impedance as

ε*(ω) = (l/A)(1/iωe₀Z*) (3)

where A and l are, respectively, the area and thickness of the sample between electrodes and e₀ (=8.854 pF m⁻¹) is the dielectric permittivity of the empty space.

Alternative representations of the dielectric properties of the material are: (i) the conductivity which is expressed in terms of dielectric permittivity as

σ*(ω) = iωe₀ε*(ω) (4)

and (ii) the complex electric modulus

M*(ω) = 1/ε*(ω) (5)

The use of the last representations is very interesting because allow us to emphasize different aspects of polarization and charge transport in the tested material.⁴⁰

3. Results and discussion

The analysis of the synthesized PEDOT nanostructures was carried out by SEM and TEM. Micrographs of the prepared PEDOT nanoparticles (PEDOT-NP) and PEDOT nanowires (PEDOT-NW) are presented in Fig. 2. The size of the nanoparticles is in the range 10–40 nm (Fig. 2a), while the diameter of the nanowires was 200 ± 1 nm, given by the pore diameter of the alumina template (Fig. 2b). The length of the nanowires was 32 ± 2 μm before template removal. Fig. 2b shows the wide length distribution (4–20 μm) due to the breaks produced by the ultrasonic treatment after template removal.

Fig. 2 TEM micrograph of the PEDOT nanoparticles (a) and SEM micrograph of the PEDOT nanowires (b) used in this work.

TGA results displayed the effect of the morphology of the PEDOT nanostructures on the thermal stability of the blends. The weight loss curve and its first derivative for pure PMMA, PMMA/PEDOT-NP and PMMA/PEDOT-NW samples are displayed in Fig. 3. For the three samples, a small loss of mass at low temperatures (T < 150 °C) is assigned to elimination of water or residual solvent. The degradation of the polymer takes place in on step, with an increase of the thermal stability upon addition of PEDOT. The mid-point temperature (temperature at 50% mass loss) increases when compared to PMMA matrix by 31 °C for the PMMA/PEDOT-NP sample and 51 °C for the PMMA/PEDOT-NW one (Table 1), which is in agreement with previous observations for other PMMA nanocomposites.⁴²

Fig. 3 TGA thermograms of PMMA, PEDOT and of the two analyzed PMMA/PEDOT-NP and PMMA/PEDOT-NW blends. Inset: first derivative weight loss thermal curves.

Table 1 Glass transition temperature (T_g), mid-point temperature (T_50%), resistivity values at 100 °C (ρ_dc) and activation energy of the conductivity process (E_a^σ) of PMMA and PMMA/PEDOT-y (y = NW and NP) samples

	PMMA	PMMA/PEDOT-NP	PMMA/PEDOT-NW
Tg (°C)	113	115	108
T50% (°C)	318	349	369
Ea^σ (kJ mol^−1)	145.5 ± 1.4	128.3 ± 1.8	123.4 ± 1.1
ρdc (Ω m) at 100 °C	3.18 × 10^10	5.78 × 10^9	1.64 × 10^6

---

Fig. 4 exhibits the second run DSC thermograms of the pure PMMA matrix and of the two nanocomposites (PMMA/PEDOT-NP, PMMA/PEDOT-NW). According to the results, the PEDOT morphology in PMMA/PEDOT blends affects the glass transition temperature value of the samples (Table 1). A T_g of 113 °C was observed for the PMMA matrix. The addition of 1 wt% of PEDOT-NP to the PMMA caused only a very small increase in the T_g (∼2 °C). In contrast, an opposite effect (decrease of 5 °C) was observed upon addition of 1 wt% of PEDOT-NW to PMMA. The decrease suggests that the NW morphology produces a slight plasticizing effect.

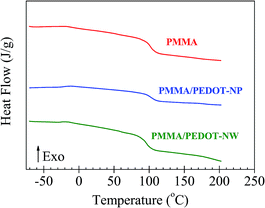Fig. 4 Differential scanning calorimetry (DSC) curves of the PMMA and the two PMMA/PEDOT-y polymer blends (y = NP and NW) analyzed. Data are vertically shifted for a better visualization.

In order to study how the PEDOT morphology affects the conductive properties of the PMMA/PEDOT blends an analysis of the dielectric response of the pure and blend samples was carried out. One attractive feature of dielectric spectroscopy lies in the direct correlation between the response of a real system and an idealized model circuit composed of discrete electrical components (resistors and capacitors). In this sense, the equivalent circuit modeling the complex impedance in the frequency domain is made up of a constant phase element (CPE) of admittance Y*(ω) = Y₀(jω)^a (0 < a ≤ 1), in parallel with a polarization resistance R_p. Phenomenologically, a resistance R_p is taken to represent the dissipative component of the dielectric response, while the CPE describe the storage component.⁴³

The Cole–Cole impedance plots at several temperatures for the PMMA and the two PMMA/PEDOT blends are presented in Fig. 5. The plots are arcs, nearly semicircles, that intersect the abscissa axis at the extreme frequencies in such a way that Z′(∞) = 0 and Z′(0) = R_p, being R_p the polarization resistance. A strong decrease of the last parameter with increasing temperature is observed for the three samples. Additionally, we also observe a significant decrease of the polarization resistance to conduction charges transport across the sample with the addition of a 1 wt% of PEDOT-NW.

Fig. 5 Cole–Cole impedance plots, at several temperatures for (a) PMMA, (b) PMMA/PEDOT-NP and (c) PMMA/PEDOT-NW.

Fig. 6 presents the real (ε′) and the imaginary (ε′′) parts of the complex dielectric permittivity, at room temperature and at 100 °C, recorded for PMMA and for the polymer blends. The results demonstrate a clear influence of the morphology of the PEDOT in the values of the complex dielectric permittivity. Fig. 6a gives an increase in the dielectric constant ε′ at all the studied frequencies when PEDOT is added to the PMMA matrix, being this increase significantly higher with the addition of nanowires when comparing to nanoparticles. In all cases a decrease of ε′ with the frequency, attributed to the electrical relaxation processes and a nearly frequency independent behavior above 10 kHz are observed. Besides that, at low frequencies, a significant increase of ε′ takes place in the PMMA/PEDOT-NW sample. This upturn can be attributed to the charge accumulation at the interface between electrode and the PMMA/PEDOT-NW blend (material-electrode polarization mechanism, EP).

Fig. 6 Frequency dependence of the real and imaginary part of the dielectric permittivity at 25 °C (open symbols) and at 100 °C (full symbols) for PMMA (circle), PMMA/PEDOT-NP (square) and PMMA/PEDOT-NW (triangle).

Fig. 6b plots the dielectric loss factor (ε′′) recorded as a function of frequency for pure PMMA and blends. The low frequency dielectric dispersion occurs due to the electrode polarization and ionic conduction phenomena. However, the high frequency dielectric dispersion corresponds to the molecular reorientation dynamics and to intramolecular group rotations. At 100 °C, the definition of the peak related to the last dipolar process corresponding to the PMMA and PMMA/PEDOT-NP samples is nearly the same. A slight shift to higher frequencies in the last case indicates a decrease of the characteristic relaxation time. For PMMA/PEDOT-NW sample it is interesting to note that the dipolar relaxation cannot be easily observed due to the significant increase of the loss permittivity when frequency decreases. This increase indicates that the conductivity contributions (combination of the bulk conduction and interfacial polarizations effects) are dominant in the dielectric response.

To evaluate the bulk conductive process, the experimental data were plotted in terms of σ*(ω). The ac (alternating current) conductivity isotherms corresponding to high temperatures exhibit a plateau in the low frequency region, reflecting a frequency independent conductivity, i.e., dc conductivity, as Fig. 7 shows. The frequency range covered by the plateau increases with temperature. On the other hand, the isotherms exhibit dispersion in the high frequency region. Thus, the behavior of σ_ac follows the Jonscher power law,^44,45

σ(ω) = σ_dc + Aωⁿ (6)

where σ_dc is the dc conductivity (frequency independent plateau in the low frequency region), A is the pre-exponential factor and n is the fractional exponent between 0 and 1. The effect of electrode polarization (EP) is evidenced in the low frequency region by a small deviation of σ_dc (plateau region) value in the conductivity spectrum and by the increase in the imaginary conductivity (inset Fig. 7). As the temperature increases, EP phenomena become more prominent and thus the plateau region shifts to high frequency values. The last phenomenon is specially defined for the PMMA/PEDOT-NW sample.

Fig. 7 Frequency dependence of the real part of the conductivity at room temperature (open symbols) and at 100 °C (full symbols) for PMMA and PMMA/PEDOT-NP PMMA/PEDOT-NW blends. Inset: frequency dependence of the imaginary part of the conductivity at 100 °C.

These data were converted into complex electric modulus M* to study the conduction process in more detail.⁴⁶ For the PMMA and PMMA/PEDOT-NP systems two well-defined processes are observed in the frequency dependence of M′′ = ε′′/(ε′² + ε′′²) (see Fig. 8). They are separated in the frequency range through almost three decades. However, both processes become closely overlapped for the PMMA/PEDOT-NW blend. The low frequency peak is associated to the conductivity process, whereas the high frequency one is associated to dipolar processes. The conductivity process appears at higher frequencies (lower times) for the two composites tested. However, the displacement for the PEDOT-NW is considerably higher. In the latter case, both dipolar and conductive processes appear closely overlapping.

Fig. 8 Frequency dependence of the M′ (open symbols) and M′′ (full symbols) for PMMA (circle), PMMA/PEDOT-NP (square) and PMMA/PEDOT-NW (triangle) at 100 °C.

The resistivity values ρ_dc (Ω m) = 1/σ_dc obtained at 100 °C from the plateau at low frequencies in the σ′ vs. f plot were: 3.18 ×p10¹⁰ (PMMA), 5.78 × 10⁹ (PMMA-PEDOT-NP) and 1.64 × 10⁶ (PMMA-PEDOT-NW). These values show a significant reduction of the resistivity for the polymer blend with a 1 wt% of PEDOT-NW, as was also clearly reflected in the Cole–Cole plot (Fig. 5).

The temperature dependence of dc conductivity follows an Arrhenius-type behavior, as shown in Fig. 9. These values were estimated from: (i) the plateau at low frequencies of the σ′ plots and (ii) the R_p values by means of the relationship σ_dc = l/R_pA. In both cases, the obtained σ_dc values are in a reasonable good agreement.

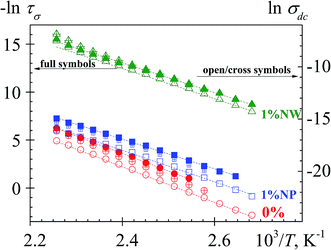Fig. 9 Temperature dependence of the τ_σ (s) (full symbols) and of the σ_dc (S m) evaluated from low frequency plateau (open symbols) and using the relationship σ_dc = l/AR_p (cross symbols).

M′′ spectra were used to evaluate the conductivity relaxation time. The value of τ_σ, for several experimental isotherms, was evaluated from the maximum frequency of the low frequency peak: τ_σ = 1/2πf_max. The temperature dependence of τ_σ and σ_dc is similar, as seen in Fig. 9. The evaluated activation energies associated with the conductivity process are listed in Table 1. At low temperatures, more data points are available for σ_dc than for τ_σ because the modulus peaks start to shift out of the available frequency window (Fig. 8) and the peak frequency cannot be unequivocally determined. According to these results, the presence of PEDOT produces a reduction of the activation energy of the conductivity process. This reduction is slightly higher in the case of the nanowire morphology.

4. Conclusions

PEDOT nanoparticles and nanowires with well-defined structure were synthesized by miniemulsion and electrochemical polymerization, respectively. PMMA polymer blends containing small concentrations (1% wt) of these defined PEDOT nanostructures were prepared via the solution-casting method. We demonstrate that the morphology of the PEDOT nanostructures influences the properties of the corresponding PMMA/PEDOT blends.

An improving of the thermal stability is produced upon addition of the PEDOT nanostructures in the PMMA matrix, being higher for the case of the nanowires, as demonstrated by TGA. The glass transition temperature, determined by DSC, exhibited a slight increase with the incorporation PEDOT nanoparticles and a decrease of 5 °C with the incorporation of the nanowires.

Broadband DRS was used as a tool to study the full range of molecular motions of the PMMA in the presence of the PEDOT. The incorporation of the PEDOT nanostructures in the PMMA matrix resulted in a significant increase in the dielectric permittivity and conductivity. These results indicate that PEDOT nanostructures are potentially interesting materials for the enhancement of conductive polymer properties, especially in the case of the nanowire morphology.

Acknowledgements

The authors acknowledge the financial support of the DGCYT through Grant MAT2015-63955-R. R. M. E. also acknowledges the financial support from the Spanish Ministry of Economy and Competitiveness through a Ramón y Cajal grant (grant No. RYC-2013-13451) and M. C. acknowledges the FPU program of the Spanish Ministry of Culture, Education and Sports.

Notes and references

1. M. Latour, J. Appl. Phys., 1975, 46, 42.
2. Y. C. Anada, Adv. Mater. Res., 2013, 740, 630–635.
3. Y. Anada, Energy Procedia, 2013, 34, 17–25.
4. J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Carbon, 2006, 44(9), 1624–1652.
5. R. Rohini, P. Katti and S. Bose, Polymer, 2015, 70, A17–A34.
6. V. Dhand, G. Mittal, K. Y. Rhee, S. J. Park and D. Hui, Composites, Part B, 2015, 73, 166–180.
7. S. Sen, S. Patil and D. S. Argyropoulos, Thermal properties of lignin in copolymers, blends, and composites: a review, Green Chem, 2015, 17, 4862–4887.
8. S. Devasahayam and S. Bandyopadhyay, Evolution of novel size-dependent properties in polymer–matrix composites due to polymer filler interactions. New developments in polymer composites research, NOVA Science Publishers, USA, 1st edn, 2014, pp. 1–32.
9. D. W. Schaefer and R. S. Justice, Macromolecules, 2007, 40(24), 8501–8517.
10. R. A. Vaia and J. F. Maguire, Chem. Mater., 2007, 19(11), 2736–2751.
11. A. Efteknari, Nanostructured Conductive Polymers, John Wiley and Sons, Inc., Publication, United Kingdom, 2010.
12. P. J. Brigandi, J. M. Cogen and R. A. Pearson, Polym. Eng. Sci., 2014, 54(1), 1–16.
13. H. Deng, L. Lin, M. Ji, S. Zhang, M. Yang and Q. Fu, Prog. Polym. Sci., 2014, 39(4), 627–655.
14. A. Kaur, I. Singh, J. Kumar, C. Bhatnagar, S. K. Dixit, P. K. Bhatnagar and M. da Conceicao Paiva, Mater. Sci. Semicond. Process., 2015, 31, 166–174.
15. H. Muto, N. Hakiri, N. H. Phuc, G. Kawamura and A. Matsuda, ECS Trans., 2013, 50(6), 165–169.
16. M. M. Demir and G. Wegner, Macromol. Mater. Eng., 2012, 297, 838–863.
17. B. Philip, J. K. Abraham, A. Chandrasekhar and V. K. Varadan, Smart Mater. Struct., 2003, 12, 935–939.
18. P. Molla-Abbasi, S. R. Ghaffarian and E. Danesh, Smart Mater. Struct., 2011, 20(10), 105012.
19. A. Schoth, E. S. Adurahim, M. A. Bahattab, K. Landfester and R. Muñoz-Espí, Macromol. React. Eng., 2016, 10, 47–54.
20. G. Babu and L. M. R. Arava, RSC Adv., 2015, 5(59), 47621–47627.
21. K. Parker, R. T. Schneider, R. W. Siegel, R. Osizik, J. C. Cabanelas, B. Serrano, C. Antonelli and J. Baselga, Polymer, 2010, 51(21), 4891–4898.
22. C. K. Chan, S. L. Peng, I. M. Chu and S. C. Ni, Polymer, 2001, 42(9), 4189–4196.
23. D. R. Raul and L. M. Robeson, Polymer, 2008, 49(15), 3187–3204.
24. R. Kumar, Polymer–Matrix Composites. Types, Applications and Performance, Nova Science Publishers, New York, 2014.
25. Applied Research on Polymer Composites, ed. Pooria Pasbakhsh, A. K. Haghi and Gennady E. Zaikov, Apple Academic Press (Taylor Francis Group), 2015.
26. K. Kyriakos, K. N. Raftopoulos, P. Pissis, A. Kyritsis, F. Näther, L. Häußler, D. Fischer, A. Vyalikh, U. Scheler, U. Reuter and D. Pospiech, J. Appl. Polym. Sci., 2013, 128(6), 3771–3781.
27. M. Singhi and M. Fahim, Polym. Compos., 2012, 33(5), 675–682.
28. W. Zheng and S. C. Wong, Compos. Sci. Technol., 2013, 63, 225–235.
29. B. Redondo-Foj, P. Ortiz-Serna, M. Carsí, M. J. Sanchis, M. Culebras, C. M. Gómez and A. Cantarero, Polym. Int., 2015, 64, 284–292.
30. F. Bussolotti, V. Grossi, S. Santucci, L. Lozzi and M. Passacantando, J. Phys.: Conf. Ser., 2008, 100, 012012.
31. C. K. Kum, Y. T. Sung, M. S. Han, W. N. Kim, H. S. Lee, S. J. Lee and J. Joo, Macromol. Res., 2006, 14(4), 456–460.
32. A. Basavaraja Sannakki, Phys. Procedia, 2013, 49, 15–26.
33. A. Chandra and W. H. Meyer, J. Appl. Polym. Sci., 2013, 128(5), 2857–2864.
34. S. A. Acharya and K. Singh, Adv. Mater. Lett., 2014, 5(2), 61–66.
35. Handbook of Conducting Polymers, Conjugated Polymers. Theory, Synthesis, Properties and Characterization, ed. A. Terje, Skotheim and John R. Reynolds, CRC Press Taylor & Francis Group, New York, 3rd edn, 2007.
36. Polymers for Electricity and electronics. Materials, Properties and Applications, ed. J. G. Drobny, John Wiley and Sons, Inc., Publication, New Jersey, 2012.
37. A. Elschner, S. Kirchmeyer, W. Lövenich, U. Merker and K. Reuter, PEDOT. Principles and Applications of an Intrisically Conductive Polymer, CRC Press Taylor & Francis Group, 2011.
38. C.-H. Wu, T.-M. Don and W.-Y. Chiu, Polymer, 2011, 52, 1375–1384.
39. N. G. McCrum, B. E. Read and G. Williams, Anelastic and Dielectric Effects in Polymeric Solids, Wiley, London, 1967.
40. F. Kremer and A. Schönhals, in Broadband Dielectric Spectroscopy, Springer, Berlin, 2003.
41. E. Riande and R. Díaz-Calleja, Electrical Properties of Polymers, Dekker, New York, 2004.
42. S. Su and C. A. Wilkie, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 1124–1135.
43. E. Barsoukov and J. R. Macdonals, Impedance Spectroscopy. Theory, Experiment, and Applications, Wiley Interscience, 2005.
44. A. K. Jonscher, Dielectric Relaxation in Solids, Chelsea Dielectric Press, London, 1983.
45. A. K. Jonscher, Nature, 1977, 267, 673–679.
46. I. M. Hodge, K. L. Ngai and C. T. Moynihan, J. Non-Cryst. Solids, 2005, 351, 104–115.

---