DFT study of ethanol dehydration catalysed by hematite†
Juliana F. Lopesa,
Juliana C. M. Silvab,
Maurício T. M. Cruzc,
José Walkimar de M. Carneirod and
Wagner B. De Almeida*d
aLaboratório de Química Computacional (LaQC), Instituto de Física e Química, Universidade Federal de Itajubá (UNIFEI), Av. BPS, 1303 Pinheirinho, Itajubá, MG 37500-903, Brazil
bDepartamento de Química, ICEx, Universidade Federal de Minas Gerais (UFMG), Campus Pampulha, Belo Horizonte, MG 31270-901, Brazil
cInstituto de Química, Universidade do Estado do Rio de Janeiro (UERJ), Rua São Francisco Xavier, 524, Pavilhão Haroldo Lisboa da Cunha, Maracanã, Rio de Janeiro, RJ 20550-900, Brazil
dLaboratório de Química Computacional (LQC), Departamento de Química Inorgânica, Instituto de Química, Universidade Federal Fluminense (UFF), Campus do Valonguinho, Centro, Niterói, RJ CEP: 24020-141, Brazil. E-mail: wbdealmeida@gmail.com
First published on 12th April 2016
Abstract
Hematite (α-Fe2O3) has been used as an ethanol gas sensor and as a catalyst for nanomaterial synthesis, motivating the investigation of ethanol dehydration over a hematite surface using computational chemistry methods. Using a molecular approach and a simple model for α-Fe2O3 to mimic the catalyst effect on the thermodynamics and kinetics of the reaction and quantum chemical Density Functional Theory (DFT) calculations, we showed that the energy barrier for the formation of ethylene plus water is around 70% lower than the corresponding gas phase value and that the products are thermodynamically stable with respect to the ethanol reactant in the presence of a non-planar model catalyst (Fe10O15). This stimulating result supports a mechanism proposed for ethylene formation at mild temperatures using hematite as a catalyst. We also showed that the effect of a catalyst on a chemical process can be very satisfactorily simulated as a local effect through first principles quantum chemical calculations, being of practical use, and so, large cluster calculations with many atomic layers or the use of large periodic super cells are not strictly required to reach reasonable estimates of temperature dependent rate constants and products stabilization. Our results strongly support a proposal that the main intermolecular interactions between the species present in a chemical process and the catalyst, leading to stabilization of transition state structure and consequent reduction of energy barrier can be fairly described by the DFT level of theory using small molecular models based on sound chemical ground.
Introduction
In nanomaterial studies, the deposition of carbon as graphite, amorphous carbon, nanotubes, and nanofibers over red mud waste (rich in hematite) has been observed experimentally using ethanol as a carbon source at high temperatures in a chemical vapour deposition (CVD) reaction.1 One possible step in this complex composite synthesis is the dehydration of ethanol catalysed by hematite. This reaction is represented in eqn (1). Other experimental works involving hematite and alcohols have investigated the production of hematite nanoparticles applied as gaseous ethanol sensors,2 in the dissociative adsorption of methanol3 and polyvinyl-alcohol on hematite surfaces,4 and in the reactivity of alcohols in powder hematite.5 In the last study, Fourier-transform infrared spectroscopy (FTIR) was used to detect the absorption of methanol into powder hematite in a molecular and dissociative manner.| CH3CH2OH → C2H4 + H2O | (1) |
Nanostructured materials are considered large systems from a molecular perspective, despite being very small for the macroscopic world. As experimental researchers try to synthesize new nanomaterials, theoreticians may help understand the behaviour of these materials at a molecular level and suggest synthesis mechanisms. The more is known about nanomaterial synthesis, the better the process can be tuned to yield materials with the desired properties.
The non-catalysed decomposition of ethanol has been studied experimentally and theoretically.6–8 Although this decomposition may proceed by numerous mechanisms, leading to different products, the main products observed are ethylene and water, which indicates that the dehydration reaction of ethanol is dominant at temperatures up to 2500 K.6 Most studies related to ethanol dehydration catalysed by oxides refer to reactions using alumina as a support. Dabrowski et al.9 performed a classic Monte Carlo (MC) simulation and experiments investigating the ethanol reaction on an alumina surface, varying the hydration degree of both the surface and the reagent mixture. The MC simulation revealed that the ethylene production was greater than the ether production in both cases and that an increase in surface hydration improves the yields of both reactions.
Other mechanisms may be found in the literature related to this reaction, including the production of ether by the interaction of ethoxide neighbour groups,10 the production of olefin by intermolecular degradation (hydrogen abstraction by the catalyst),11 the production of ether via a Rideal-type mechanism (an adsorbed molecule reacts with a molecule in the gas phase) involving an ethoxide and an ethanol,12 the formation of ether by the reaction of an ethoxide group on the surface with molecularly adsorbed alcohol,13 and the formation of ethylene in a concerted mechanism by paired acid-base sites.14
The main aim of this work is a theoretical quantum chemical investigation of the effect of the presence of a hematite surface on the ethanol dehydration process using a molecular approach. We used well established first-principles quantum chemical methods to calculate the energy barrier for a proposed mechanism for alcohol dehydration and the stability of the products. Theoretical ab initio temperature-dependent gas-phase results are also reported and used to assess the role played by the catalyst in the reaction mechanism of ethylene and water formation from ethanol. No ab initio study of the adsorption or reaction of ethanol on hematite has been reported in the literature, to the best of our knowledge. Using a molecular approach to model the catalyst effect on the ethanol dehydration process, the efficaciousness of the hematite catalyst can be assessed, confirming quantitatively that the production of ethylene from ethanol is considerably enhanced through a catalysed process.
Methodology
The molecular structures of the species (see Scheme 1) participating in the main channel for the gas phase decomposition of ethanol into ethylene plus water (eqn (1)) were fully optimized without any geometrical restraints at the Density Functional Theory (DFT) level15 using the B3LYP functional16,17 and employing the post-Hartree–Fock Møller–Plesset second-order perturbation theory (MP2)18 method using the Pople's 6-31G(d,p) basis set.19 Harmonic frequency calculations were performed to characterize the gas-phase stationary points as true minima (no imaginary frequency found) or first-order transition state (TS) structures (occurrence of only one imaginary frequency) at the B3LYP/6-31G(d,p) and MP2/6-31G(d,p) levels of calculation. The intrinsic reaction coordinate (IRC) method20 was used to confirm the connection of the TS structure with the reactants (ethanol) and products (ethylene plus water). In addition, Møller–Plesset fourth-order perturbation theory with single, double, triple, and quadruple excitations (MP4(SDTQ))18 and coupled cluster with single, doubles and perturbative triple excitations (CCSD(T))21 single-point calculations using the MP2/6-31G(d,p)-optimized geometries were performed to assess electron correlation effects. The 6-31++G(d,p)19 and 6-311++G(2d,2p)19 triple-zeta quality larger basis sets were also used for a better description of the energetic of the ethanol dehydration process. The temperature-dependent thermodynamic properties (enthalpy (ΔH), entropy (ΔS), and Gibbs free energy (ΔG)) for the gas-phase process were evaluated using the MP2/6-31G(d,p) and B3LYP/6-31G(d,p) fully optimized geometrical parameters and harmonic frequencies using the standard statistical thermodynamics formulae.22 The reaction kinetic depends on the temperature at which the reaction proceeds, as shown by the variation of the rate constant calculated using eqn (2):
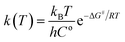 | (2) |
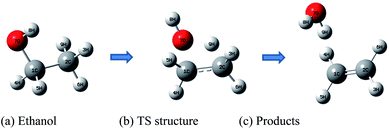 | ||
| Scheme 1 Relevant species for the ethanol dehydration process. (a) Reactant: ethanol (b) transition state structure (c) products: ethylene + water. | ||
In a second stage, we modelled the effect of the hematite catalyst on the energy barrier and the stabilization of the reaction products. The catalyst surface was represented by a simple model structure containing a total of 25 to 30 atoms (Fe10O15 and Fe12O18), which we believe would give an adequate description of the catalyst–ethanol intermolecular interactions. We also try to improve the description of the catalyst using a two layer model (Fe24O36), which seems more realistic than the one-layer model (Fe12O18). A three layer system (Fe36O54) was not attempted to save computer time. A snapshot of the B3LYP/6-31G(d,p)-optimized structures of the model catalyst structures (Fe10O15, Fe12O18 and Fe24O36) are shown in Fig. 1, with the X-ray distances23 given (see the caption of Fig. 1) for comparison. The effective core potential (ECP) of Hay and Wadt's LANL2DZ24 was used for the Fe atoms in the quantum chemical calculations.
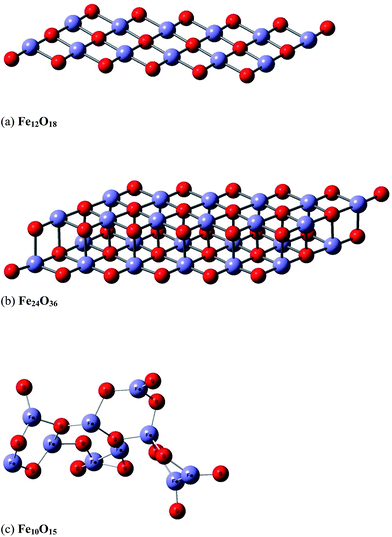 | ||
| Fig. 1 B3LYP/6-31G(d,p)-optimized structure of model hematite catalyst: Fe12O18 (a), Fe24O36 (b) and Fe10O15 (c). The theoretical average interatomic distances are: (a and b) Fe–O = 1.79 Å, 1.91 Å; Fe–Fe = 2.61 Å; O–O = 2.61 Å and (c) Fe–O ∼ 1.53–1.84 Å and Fe–Fe ∼ 2.31–2.99 Å. The corresponding experimental values are Fe–O ∼ 1.94–2.12 Å and Fe–Fe ∼ 2.90–3.98 Å.27 (a) Model hematite Fe12O18 catalyst (planar one-layer system). (b) Model hematite Fe24O36 catalyst (planar two-layer system). (c) Model hematite Fe10O15 catalyst (non-planar system). | ||
All calculations were carried out using the Gaussian03-09 suite of program.25
Results and discussion
Gas phase results
MP2/6-31G(d,p) calculations were carried out for the species shown in Scheme 1 for the gas-phase process (without the catalyst). Table S1 (ESI†) provides the relevant intra- and intermolecular geometrical parameters, which can be compared to data already reported in the literature, confirming that the minima and TS structure located on the potential energy surface (PES) are well characterized. The MP2/6-31G(d,p) imaginary frequency value is 2080i cm−1, in agreement with other reported gas phase values. B3LYP/6-31G(d,p) geometrical parameters are also quoted in Table S1† in parenthesis, for reason of comparison, showing a very good agreement with the MP2 values (the corresponding DFT-B3LYP imaginary frequency is 1972i cm−1). The IRC curve is shown in Fig. S1 (ESI†), along with the animation of the imaginary frequency mode, revealing that the calculated first-order TS structure correctly connects the reactants (ethanol) and products (ethylene plus water).To assess the effect of the level of theory on the calculated energy values, a higher correlated level of theory, MP4(SDTQ)18 and the state of the art CCSD(T)21 methods, were also used. B3LYP, MP2, MP4(SDTQ) and CCSD(T) gas-phase results obtained with three basis sets of increasing size (6-31G(d,p), 6-31++G(d,p), and 6-311++G(2d,2p)), along with B3LYP results with the 6-311++G(3df,3pd)19 and aug-cc-pVTZ26 larger basis sets, are reported in Table S2 (see ESI†). These results show the near-insensitivity of the DFT level (using four distinct functional) with the basis set in the determination of the energy barrier. In addition, the use of the B3LYP-optimized geometry in single-point MP2 energy calculations (MP2/6-31G(d,p)//B3LYP/6-31G(d,p)) yields relative energy values quite similar to those obtained with the MP2-optimized geometry. Thus, the B3LYP-optimized geometries seem very reasonable and computationally viable for large molecular systems. Table S2 (ESI†) also includes the DFT energy values calculated with three other well known functionals: PBE1PBE,27,28 M062x29–31 and CAM-B3LYP.32 It can be observed from Table S1† that the energy values are not significantly altered by changing the DFT functional, retaining almost the same profile and also a very close agreement between M062x and MP2 results. It can be observed from Table S2 (ESI†) that the electron correlation effect has moderate influence on gas phase energy values with a good agreement between B3LYP and CCSD(T) results, thus validating the use of B3LYP/6-31G(d,p) DFT level of calculation for the investigation of large molecular systems. In addition, it can be also noted that the small 6-31G(d,p) basis set tend to produce energy barriers slightly overestimated and may be considered as an upper limit value.
MP2/6-311++G(2d,2p)//B3LYP/6-31G(d,p) gas-phase Gibbs free energy results for the product formation (ΔG) and activation (ΔG#) are given in Table S3† for a range of temperatures from 300 to 1200 K (the double slash means that single-point energy calculations were performed with the 6-311++G(2d,dp) basis set using the geometry optimized with the 6-31G(d,p) basis set), along with thermodynamic properties and rate constants, as evaluated using eqn (2).
It can be observed that the gas-phase activation barrier for the ethanol dehydration process is essentially independent of the temperature, with a high, almost constant value of approximately 65 kcal mol−1. The products can be considered stabilized with respect to ethanol at approximately 550 K. As expected, the enthalpy has a slight dependence on the temperature and can be estimated at room temperature by the energy difference (ΔE) calculated for the molecular species in vacuum (no harmonic frequency calculations are needed). The calculated rate constants as a function of temperature reported in Table S3† show that substantial amounts of products would be obtained only at very high temperatures for a non-catalysed process.
Model α-Fe2O3 catalyst results
As a first approach we considered the reaction of ethanol with the catalyst surface as a local effect. The spin multiplicity for these molecular systems containing Fe3+ atoms with an open shell electronic configuration ([Ar]3d5) deserve our attention. A recent theoretical study33 on structure and magnetic properties of (Fe2O3)n neutral clusters (n = 1, 2, 3, 4 and 5), using genetic algorithm for extensive search through configuration space and DFT calculations, reported various spin multiplicities, characterized as antiferromagnetic (AF) and ferromagnetic (FM) ground states. For the Fe2O3 monomer the lowest energy structure is a singlet state having a angular optimized structure, followed by a triplet and undecet angular structures. For the largest cluster corresponding to n = 5 (Fe10O15) there are two distinct stable structures: singlet and undecet states. It is opportune to mention that the existence of chemical compounds with very large spin multiplicity value is not so uncommon. Some years ago the design, preparation and electron spin resonance detection of aromatic hydrocarbon synthetic organomagnetic material having a ground-state undecet with ten parallel spins was reported by Fujita et al.34 We have performed UB3LYP/6-31G(d,p) and UMP2/6-31G(d,p) geometry optimizations for a linear neutral structure of the Fe2O3 monomer for spin multiplicities running from 1 to 17. We found that the global minimum ground state linear structure is a undecet state, with the singlet state being less favourable for a linear Fe2O3 neutral monomer. This is confirmed by UMP4/6-311++G(2d,2p)/UMP2/6-31G(d,p) and UCCSD(T)/6-311++G(2d,2p)/UMP2/6-31G(d,p) single point calculations (see Table S4, ESI†). According to these results the two spin state of interest here are singlet and undecet. It was found in ref. 33 that the influence of magnetic states on the structure and also relative energies of larger (Fe2O3)n cluster is small. Therefore, following these results the DFT calculations carried out in this work were first performed for singlet spin state.The effect of the catalyst on the energy barrier and product stabilization was determined using the B3LYP-optimized molecular structures shown in Fig. 2 and 3 for planar (Fe12O18 and Fe24O36) and non-planar (Fe10O15) hematite models singlet state. The main geometrical parameters for the TS singlet state structures are given in Table 1, together with the TS imaginary frequency values. No TS frequency is quoted for Fe12O18 and Fe24O36 structures, since the geometry was constrained to be planar (not fully optimized). The HO⋯Fe distances for the TS structures are 1.94 Å for Fe10O15 and 1.91–1.92 Å for Fe12O18 and Fe24O36 model catalysts. IRC calculation in the presence of a model catalyst has not been attempted due to the computational difficulties, but the correct TS structure may be assigned based on structural comparison with the gas-phase TS geometry. Corresponding geometrical parameters for undecet state structures, shown as ESI (Fig. S2†), are given in parenthesis showing similarity with singlet state.
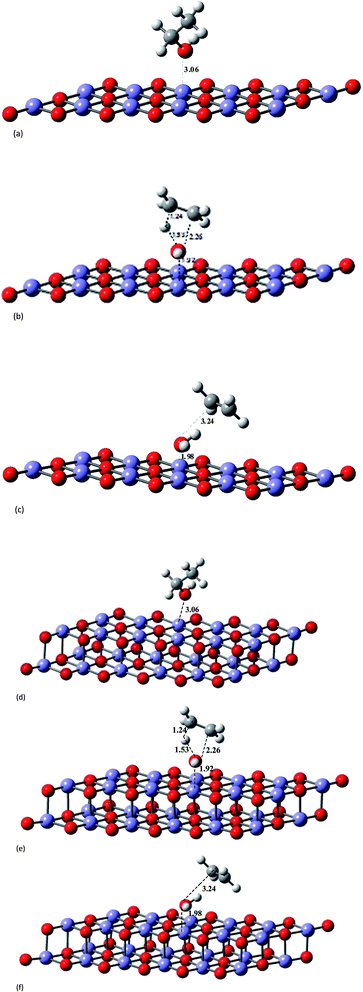 | ||
| Fig. 2 B3LYP/6-31G(d,p)-LANL2DZ-optimized singlet state structures for the ethanol dehydration process shown in Scheme 1, including the presence of a planar hematite model catalyst (Fe12O18 and Fe24O36). Average distances: dFe–O = 1.83 Å; dFe–Fe = 2.59 Å; dO–O = 2.59 Å. (a) Ethanol–hematite (Fe12O18). (b) TS–hematite (Fe12O18). (c) Ethylene plus water products–hematite (Fe12O18). (d) Ethanol–hematite (Fe24O36). (e) TS–hematite (Fe24O36). (f) Ethylene plus water products–hematite (Fe24O36). | ||
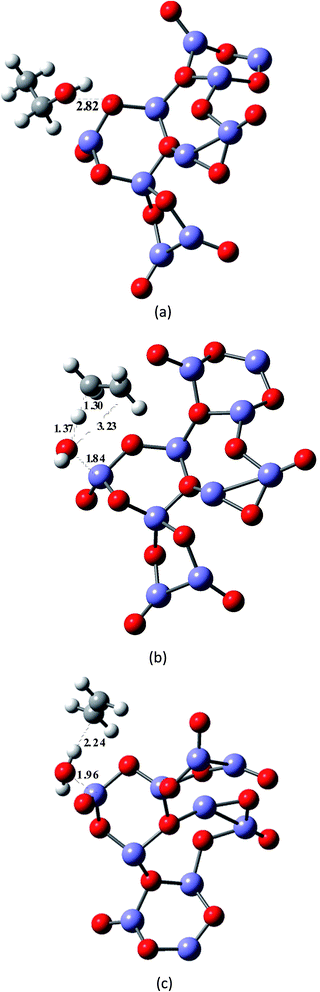 | ||
| Fig. 3 B3LYP/6-31G(d,p)-LANL2DZ-optimized singlet state structures for the ethanol dehydration process shown in Scheme 1, including the presence of a non-planar hematite model catalyst (Fe10O15). (a) Ethanol–hematite model (Fe10O15). (b) TS–hematite model (Fe10O15). (c) Ethylene plus water products–hematite model (Fe10O15). | ||
| TS structure | |||
|---|---|---|---|
| Gas phase | Hematite model catalyst | ||
| Fe12O18 and Fe24O36 | Fe10O15 | ||
| (a) Scheme 1b | (b) Planar (Fig. 2b and e) | (c) Non-planar (Fig. 3b) | |
| a Value for undecet spin state structure.b The O–Fe distance for the neighbour Fe atom is 1.98 Å which is closer to the singlet state value.c No full geometry optimization was performed (planar constraint) so frequency calculations were not done. | |||
| Dist: O⋯Fe | — | 1.92 (3.25)a,b | 1.84 (1.83)a |
| Dist: O⋯C1 | 1.86 | 2.27 (2.27)a | 3.23 (3.21)a |
| Dist: O⋯H9 | 1.24 | 1.53 (1.54)a | 1.37 (1.28)a |
| Dist: O–H8 | 0.97 | 0.97 (0.97)a | 0.97 (0.97)a |
| Angle: O⋯C1–C2 | 94.0 | 87.0 (93.0)a | 53.1 (50.7)a |
| Angle: H9⋯O⋯C1 | 63.8 | 50.2 (43.1)a | 23.6 (19.8)a |
| Angle: H9⋯O–H8 | 111.3 | 112.7 (132.2)a | 112.6 (108.1)a |
| Dihedral: O⋯C1–C2–H3 | 108.1 | 105.3 (104.7)a | 129.6 (124.7)a |
| Dihedral: H9⋯O⋯C1–C2 | −1.6 | 0.1 (−5.5)a | −18.9 (−9.2)a |
| Dihedral: H8–O⋯C1–C2 | −105.6 | −100.8 (−117.8)a | −134.6 (−136.2)a |
| Imaginary frequency (cm−1) | 1972i | —c | 1103i (403i)a |
From the data reported in Table 1 for FenO3/2n species, it can be observed that the TS structure deviates from the corresponding gas-phase structure due to the presence of the catalyst, but retains a spatial configuration, similar to the optimized gas-phase geometry, with small variations in the bond and dihedral angles, except for the non-planar Fe10O15 model catalyst structure. The O⋯C1 distance increases from 1.86 to 2.21–3.23 Å. According to the results reported in Table 1, for the non-planar Fe10O15 model catalyst, the deviation from the gas-phase TS structure is quite significant, with the O⋯C1 distance reaching 3.23 Å and some dihedral angles changing by more than 90°. These results show how the chemical molecular environment around the catalyst active site can affect the geometry of the TS structure, which in turn significantly affects the calculated energy barrier for the process. Therefore, modelling a catalysed process theoretically using ab initio methods aimed at producing accurate structural and energy results is a hard computational task.
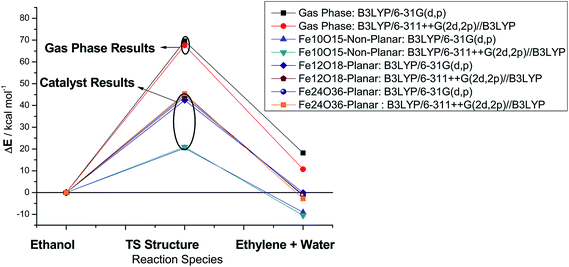
B3LYP energy results for gas phase and catalyzed processes are reported in Fig. 4 (highlighted to ease visualization) for singlet structures, employing the 6-31G(d,p) and 6-311++G(2d,2p) basis sets. It can be seen that the size of the basis set has a small effect on the energy barrier and only a moderate influence on the product stabilization energy. Therefore, the small 6-31G(d,p) basis set can be considered enough to provide reasonable estimate of the energy barrier at an affordable computational cost. The planar catalyst leads to a good reduction in the energy barrier, showing a decrease of approx. 35%, with respect to the B3LYP/6-311++G(2d,2p)/B3LYP/6-31G(d,p) gas-phase energy barrier, for both one-layer (Fe12O18) and two-layers (Fe24O36) catalyst models. An outstanding result is obtained with the non-planar catalyst model (Fe10O15) with an approx. 70% reduction in the energy barrier and consequent substantial increase in the room temperature rate constant value. These results just confirm how choices of a molecular structure for representation of a model catalyst can considerably influence the calculated relative energy data.
B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) Gibbs free energy (ΔG) profiles as a function of the temperature for the ethanol dehydration using the non-planar Fe10O15 catalyst (singlet state) is shown in Fig. 5. Contrary to the results presented in Table S3 (ESI†) for the gas-phase non-catalysed dehydration process, where the activation barrier was practically independent of the temperature, having a high constant value of approximately 65 kcal mol−1, in the presence of a catalyst, the ΔG# value increases smoothly with the temperature from 20 kcal mol−1 (T = 300 K) to 25 kcal mol−1 (T = 1200 K), with prediction of a much smaller barriers than for the non-catalysed process. The ΔG values follow the same pattern observed in the gas-phase reaction. The catalytic process is spontaneous at room temperature, and the corresponding rate constant (k in s−1) evaluated with eqn (2) is quoted, which is enormously smaller than the corresponding gas phase value. The Fe10O15 model catalyst exhibited higher efficiency to convert ethanol into water plus ethylene at mild temperature conditions, compared to the other planar catalyst models.
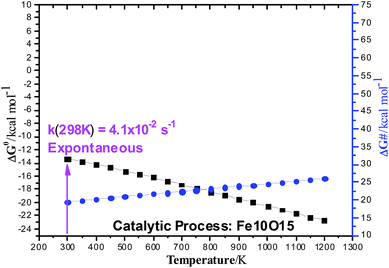 | ||
| Fig. 5 B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) Gibbs free energy (ΔG) profiles (in units of kcal mol−1) for the ethanol dehydration Fe10O15 catalyzed process (singlet state). The reactant, transition state (TS), and products are shown in Fig. 2. Black square: ΔG0; Blue circle: ΔG#. | ||
The B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) rate constants for gas phase and model catalysts ethanol dehydration process as a function of the temperature are reported in Fig. 6 (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(T) is shown to ease visualization). The larger the k(T) is, less negative (or slightly positive) the ln(k) value. ΔE# replaces ΔG# value in eqn (2) for the evaluation of k(T). However, it can be seen that the temperature dependent rate constants calculated with eqn (2) using ΔE#, ΔH# and ΔG# values exhibited a very similar profile (see Fig. S3, ESI†), thus validating the results shown in Fig. 6. The effect of choice of specific molecular structure to model the catalyst can be clearly seen from analysis of Fig. 6, by comparison with the gas phase B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) profile. It can be seen that the non-planar Fe10O15 catalyst and also the planar Fe12O18 and Fe24O36 catalysts are able to improve the efficiency of the ethanol dehydration process. The room temperature k value for the gas-phase reaction is 2.3 × 10−35 s−1, the corresponding k value at 298.15 K in the presence of the model Fe10O15 catalyst is k = 4.1 × 10−2 s−1. So, the effect of the catalyst is quite drastic, enhancing remarkably the production of ethylene through ethanol dehydration process.
k(T) is shown to ease visualization). The larger the k(T) is, less negative (or slightly positive) the ln(k) value. ΔE# replaces ΔG# value in eqn (2) for the evaluation of k(T). However, it can be seen that the temperature dependent rate constants calculated with eqn (2) using ΔE#, ΔH# and ΔG# values exhibited a very similar profile (see Fig. S3, ESI†), thus validating the results shown in Fig. 6. The effect of choice of specific molecular structure to model the catalyst can be clearly seen from analysis of Fig. 6, by comparison with the gas phase B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) profile. It can be seen that the non-planar Fe10O15 catalyst and also the planar Fe12O18 and Fe24O36 catalysts are able to improve the efficiency of the ethanol dehydration process. The room temperature k value for the gas-phase reaction is 2.3 × 10−35 s−1, the corresponding k value at 298.15 K in the presence of the model Fe10O15 catalyst is k = 4.1 × 10−2 s−1. So, the effect of the catalyst is quite drastic, enhancing remarkably the production of ethylene through ethanol dehydration process.
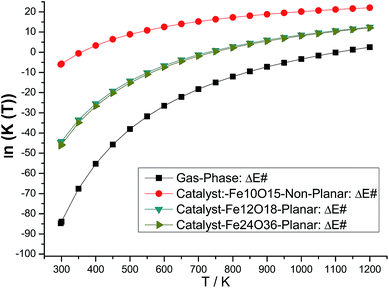 | ||
Fig. 6 B3LYP/6-311++G(2d,2p)//B3LYP/6-31G(d,p) rate constants (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(T)) profiles for the ethanol dehydration process. The reactant, transition state (TS), and products are shown in Scheme 1. The optimized structures using the hematite model catalyst (Fe10O15, Fe12O18 and Fe24O36 singlet state) are shown in Fig. 1 and 2. The geometrical parameters are given in Table 1. ΔE# replaces ΔG# value in eqn (2) for the evaluation of k(T). k(T)) profiles for the ethanol dehydration process. The reactant, transition state (TS), and products are shown in Scheme 1. The optimized structures using the hematite model catalyst (Fe10O15, Fe12O18 and Fe24O36 singlet state) are shown in Fig. 1 and 2. The geometrical parameters are given in Table 1. ΔE# replaces ΔG# value in eqn (2) for the evaluation of k(T). | ||
It is worth saying that the main focus here is on the energy barrier, used for the evaluation of temperature dependent rate constant, and product stabilization for the ethanol dehydration process, not specifically the adsorption on the catalyst surface. As it will be shown later ethanol adsorption is significantly affected by the entropy contribution, however, there is a minor influence on the calculation of energy barrier (and so rate constant) and product (ethylene plus water) stabilization, as already reported in Fig. S3 (ESI†).
Table 2 reports B3LYP/6-31G(d,p) relative energies (ΔE) for the species involved in the catalyzed ethanol dehydration process (Scheme 1) for singlet and undecet spin states. It can be seen from Table 2 that the non-planar Fe10O15 singlet state structure exhibit a considerable lower energy barrier than the undecet spin state and also slightly more stabilized products. For the planar Fe12O18 model catalyst the situation is similar regarding the TS structure but the undecet state structure leads to a much higher stabilization of the products. Independent of the spin state both model catalysts lower significantly the energy barrier and stabilize the products (ethylene plus water), to a distinct degree, for the ethanol dehydration process with respect to the gas phase procedure. Also reported in Table 2 are ΔG# and ΔG values (Fe10O15) and BSSE results to be discussed later. Comparing ΔE and ΔG (bracket results) results it can be seen that the entropy has a minor effect on the evaluation of energy barrier, and so rate constant, and product (ethylene plus water) stabilization. The optimized undecet molecular TS structures are similar to the ones for the singlet state and are given as ESI (Fig. S2†).
| ΔE/kcal mol−1 | Hematite model catalyst | ||||
|---|---|---|---|---|---|
| Fe10O15: non-planar str. | Fe12O18: planar str. | Fe24O36: planar str. | |||
| Singlet | Undecet | Singlet | Undecet | Singlet | |
| a BSSE corrected value.b Room temperature ΔG value. | |||||
| Reactant | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| TS struct. | 20.4 | 48.9 | 42.4 | 49.3 | 43.5 |
| (28.8)a | (58.1)b | ||||
| [18.7]b | |||||
| Product | −9.1 | −8.9 | −0.1 | −16.4 | −2.7 |
| (−4.5)a | (10.5)a | ||||
| [−11.9]b | |||||
Table 3 reported adsorption energy values (ΔEads) between distinct FenO3/2n model catalysts (singlet and undecet states) and ethanol (reactant, TS and product). The Fe10O15 singlet state show a much favourable adsorption capacity than the undecet state, with the opposite behaviour found for the Fe12O18 planar undecet structures. This confirms the spin state preference for planar and non-planar catalyst model structures. The effect of the entropy on the adsorption process can be clearly seen from the ΔG values given in bracket. There is a regular decrease in the adsorption energy of approx. 14, 16 and 18 kcal mol−1 respectively for reactant, TS and product optimized structures, which is quite sizeable values, showing the importance of the entropy contribution for the calculation of adsorption energies.
| ΔE/kcal mol−1 | Hematite model catalyst | ||||
|---|---|---|---|---|---|
| Fe10O15: non-planar str. | Fe12O18: planar str. | Fe24O36: planar str. | |||
| Singletb | Undecet | Singlet | Undecet | Singlet | |
| a BSSE value.b The ΔGads values for the Fe10O15 singlet state structure for reactant, TS and product are respectively: 3.9, −42.1 and −18.7/kcal mol−1. | |||||
| Reactant | −9.5 | 37.2 | −10.9 | −31.5 | 33.3 |
| (5.5)a | (4.2)a | ||||
| [3.9]b | |||||
| TS struct. | −58.8 | 16.5 | −38.0 | −51.9 | 7.2 |
| (14.0)a | (29.2)a | ||||
| [−42.1]b | |||||
| Product | −36.9 | 10.0 | −29.2 | −66.1 | 12.3 |
| (10.1)a | (19.2)a | ||||
| [−18.7]b | |||||
The basis set superposition error (BSSE),35 which should be taken into account when interaction energy between two molecular subunits is calculated, was evaluated at the B3LYP/6-31G(d,p) level for the ethanol–Fe10O15 adsorption and quoted in Table 3 (the BSSE corrected energy is given by: ΔEBSSEc = ΔE + BSSE). The BSSE correction is larger than the B3LYP/6-31G(d,p) values of 2 kcal mol−1 evaluated for the cisplatin@nanohorn complexes reported in ref. 36 and also DFT results for cisplatin–water complexes (around 2–3 kcal mol−1) from ref. 37. It was shown in ref. 37 that the triple-zeta quality basis set 6-311++G(2df,2p) yielded BSSE values around 1 kcal mol−1 and less negative interaction energies (the 6-31G(d,p) produces overestimated stabilization energies). Therefore the BSSE corrected interaction energies for cisplatin–water complexes with 6-31G(d,p) and 6-311++G(2df,2p) basis sets are very similar and so, from a computational point of view, the 6-31G(d,p) basis can be used for larger molecular systems without a considerable loss of accuracy compared to larger basis set calculations. We expected a similar behaviour for large scale basis set calculations for the ethanol interaction with model hematite catalysts.
One point that may be questioned is the B3LYP/6-31G(d,p) level of calculation utilized in this work. Other DFT functional (for example including dispersion correction) and maybe Pos-HF MP2 level of theory could have been used, as done for the gas phase ethanol dehydration process (see Table S2, ESI†). We have tried to perform single point MP2, PBE1PBE, M06-2x and CAM-B3LYP/6-31G(d,p) relative energy calculations using the B3LYP/6-31G(d,p) ethanol–catalyst singlet and undecet optimized structures. However, different from the gas phase case where single point calculations worked very well (see Table S2, ESI†) for the catalysed process the results make no sense at all. It can be due to the fact that the optimized ethanol–catalyst structures are substantially different for distinct DFT functional, and so in this case single point calculations, such as CAM-B3LYP/6-31G(d,p)//B3LYP/6-31G(d,p), lead to the prediction of unreal energy results. To make use of other improved DFT functional, for example having dispersion correction, or MP2 level of theory, all catalyzed structure must be fully re-optimized at the respective level of calculation. This is computationally unviable being totally out of question in the context of the present work. In this way we have to rely on the B3LYP ability to predict structural and relative energy data and so, our theoretical results should be seen as good estimates of energy barrier and product stabilization energy rather than accurate results. Nevertheless, we can be sure that the B3LYP/6-31G(d,p) results reflects fairly well the correct energetic balance due to the effect of the hematite model catalyst on the ethanol dehydration process. Unless we have experimental data for the rate constant for a given catalyzed process there is no way to foreseen with certainty which DFT level of calculation would be the most adequate for the evaluation of energy barriers. There are many DFT functional available at the present time that can be tested to reach the best reasonable choice. And this is indeed a long and time consuming computation work.
Conclusions
Modelling the effect of a catalyst on a chemical process at a molecular level using high-level ab initio quantum chemical methods is indeed a formidable theoretical challenge. When a model catalyst is chosen, a compromise between the accuracy of the theoretical approach and the trueness of the model catalyst is implicitly assumed. Hybrid methods (classical-quantum), which can be applied to larger catalyst models, are certainly appealing because they closely resemble the real macroscopic solid-state catalyst structure. However, high-level ab initio quantum chemical methods, which are certainly more accurate than hybrid approaches, require the use of simple structural models to describe the catalyst. Other theoretical approaches, which are based on solid-state theory formalism and may describe the real catalyst structure more realistically, can be used for the determination of the energy profile for a catalysis process, such as ethanol dehydration. However, this is not the purpose of this work, which is restricted to the description of the substrate–catalyst interaction at a molecular level using ab initio quantum chemical methods. In this work, three model hematite catalysts, Fe10O15 (non-planar), Fe12O18 (planar) and Fe24O36 (planar), were used for B3LYP calculations of the ethanol dehydration process. The catalyst models predicted a considerable lowering of the energy barrier and stabilization of the products with respect to the corresponding gas-phase results. Using the Fe10O15 non-planar hematite catalyst model, a reduction in the activation energy of around 70% and significant stabilization of the products relative to the ethanol reactant was obtained, making the process feasible under mild temperature conditions. The calculated rate constant (k) is decreased by a factor of approximately 1036 at room temperature relative to the non-catalysed dehydration process. Our results also strongly suggested that the use of DFT quantum chemical methods, such as B3LYP functional, with moderate size basis sets can be used for a reasonable estimate of the energetic of the process. The limitation of the methodology used here is that it must be applied to small structure model systems due to the computational demand of first principles ab initio calculations. On the other hand, using even simple models, if they produce reasonably accurate results, the chemistry governing the catalyst process can be very well understood on solid theoretical basis. In our view an attempt to use small molecular models may be considered attractive keeping in mind the computational efforts required to perform high quality ab initio calculations. And that is precisely what we would like to show in this work. Our results corroborate the idea that the relevant intermolecular interactions between reactants, transition state and products with the catalyst, lowering the energy barrier and increasing the rate constant of a chemical process, can be accounted for by the DFT level of theory using an adequate molecular approach.Acknowledgements
J. C. M. Silva thanks the CNPq for a M.Sc Scholarship. We thank the Brazilian Agencies CNPq, CAPES, FAPEMIG and FAPERJ for their continuing support of our laboratories.References
- A. A. S. Oliveira, I. F. Teixeira, L. P. Ribeiro, J. C. Tristão, A. Dias and R. M. Lago, Magnetic amphiphilic composites based on carbon nanotubes and nanofibers grown on an inorganic matrix: effect on water–oil interfaces, J. Braz. Chem. Soc., 2010, 21, 2184–2188 CrossRef CAS.
- Y. Wang, J. Cao, S. Wang, X. Guo, J. Zhang, H. Xia, S. Zhang and S. Wu, Facile Synthesis of Porous alpha-Fe2O3 Nanorods and Their Application in Ethanol Sensors, J. Phys. Chem. C, 2008, 112(46), 17804–17808 CAS.
- M. A. Henderson, Surface stabilization of organics on hematite by conversion from terminal to bridging adsorption structures, Geochim. Cosmochim. Acta, 2003, 67(5), 1055–1063 CrossRef CAS.
- S. Chibowski, Study on adsorption properties of polyvinyl-alcohol on hematite surface, Pol. J. Chem., 1985, 59(10–12), 1193–1199 Search PubMed.
- A. Glisenti, G. Favero and G. Granozzi, Reactivity of simple alcohols on Fe2O3 powders An XPS and FTIR study, J. Chem. Soc., Faraday Trans., 1998, 94(1), 173–182 RSC.
- J. Park, R. S. Zhu and M. C. Lin, Thermal decomposition of ethanol. I. Ab Initio molecular orbital/Rice–Ramsperger–Kassel–Marcus prediction of rate constant and product branching ratios, J. Chem. Phys., 2002, 117(7), 3224–3231 CrossRef CAS.
- J. Li, A. Kazakov and F. L. Dryer, Experimental and Numerical Studies of Ethanol Decomposition Reactions, J. Phys. Chem. A, 2004, 108(38), 7671–7680 CrossRef CAS.
- W. Tsang, Energy transfer effects during the multichannel decomposition of ethanol, Int. J. Chem. Kinet., 2004, 36(8), 456–465 CrossRef CAS.
- J. E. Dabrowski, J. B. Butt and H. Bliss, Monte carlo simulation of a catalytic surface: Activity and selectivity of γ-alumina for dehydration, J. Catal., 1970, 18(3), 297–313 CrossRef CAS.
- W. H. Wade, S. Teranishi and J. L. Durham, The Dehydration of Ethanol on Aluminas of Various Specific Surface Areas, J. Phys. Chem., 1965, 69(2), 590–595 CrossRef CAS.
- H. Arai, Y. Saito and Y. Yoneda, Ethanol dehydration on alumina catalysts: II. The infrared study on adsorption of diethyl ether over alumina, J. Catal., 1968, 10(2), 128–133 CrossRef CAS.
- H. J. Solomon, H. Bliss and J. B. Butt, Catalysis of Alcohol and Ether Dehydration on Gamma-Alumina, Ind. Eng. Chem. Fundam., 1967, 6(3), 325–333 CAS.
- H. Knoezinger, A. Scheglila and A. M. Watson, Dehydration of alcohols over alumina. VIII. Ether formation from the deuterated methanols CH3OH, CD3OH, CH3OD, and CD3OD, J. Phys. Chem., 1968, 72(8), 2770–2774 CrossRef CAS.
- H. Knözinger, H. Bühl and E. Ress, The dehydration of alcohols over alumina : VII. The dependence of reaction direction on the substrate structure, J. Catal., 1968, 12(2), 121–128 CrossRef.
- See for example: R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5662 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789 CrossRef CAS.
- See for example: A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, Introduction to Advanced Electronic Structure Theory, Dover Plublications, Inc., New York, 1996 Search PubMed.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- C. Gonzalez and H. B. Schlegel, An improved algorithm for reaction path following, J. Phys. Chem., 1989, 90, 2154–2161 CrossRef CAS.
- R. J. Bartlett and J. F. Stanton, in Reviews In Computational Chemistry, Aplications of Post–Hartree–Fock Methods, ed. K. B. Lipkowitz and D. B. Boyd, VCH Publishers, Inc., New York, 1994, ch. 3, vol. 5 Search PubMed.
- See for example: D. A. McQuarrie, Statistical Thermodynamics, University Science Books, Mill Valle, 1973 Search PubMed.
- N. Pailhé, A. Wattiaux, M. Gaudon and A. Demourgues, Impact of structural features on pigment properties of [alpha]-Fe2O3 haematite, J. Solid State Chem., 2008, 181, 2697–2704 CrossRef.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. S. Schlegel, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
- T. H. Jr Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023 CrossRef.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions, J. Chem. Phys., 2005, 123(16), 161103 CrossRef PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2006, 2(2), 364–382 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functional, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. Erlebach, C. Huhn, R. M. Jana and M. Sierka, Structure and magnetic properties of (Fe2O3)n clusters (n = 1–5), Phys. Chem. Chem. Phys., 2014, 16, 26421–26426 RSC.
- I. Fujita, Y. Teki, T. Takui, T. Kinoshita and K. Itoh, Design, preparation, and electron spin resonance detection of a ground-state undecet (S = 5) hydrocarbon, J. Am. Chem. Soc., 1990, 112, 4074–4075 CrossRef CAS.
- For a review on BSSE see: F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, State of the Art in Counterpoise Theory, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS.
- J. F. Lopes, W. R. Rocha, H. F. dos Santos and W. B. de Almeida, An Investigation of the BSSE Effect on the Evaluation of Ab Initio Interactions Energies for Cisplatin-Water Complexes, J. Braz. Chem. Soc., 2010, 21, 887–896 CrossRef CAS.
- L. A. De Souza, C. A. S. Nogueira, J. F. Lopes, H. F. Dos Santos and W. B. De Almeida, DFT Study of Cisplatin@Carbon Nanohorns Complexes, J. Inorg. Biochem., 2013, 129, 71–83 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra08509a |
| This journal is © The Royal Society of Chemistry 2016 |