Drug resistance mechanisms of three mutations V32I, I47V and V82I in HIV-1 protease toward inhibitors probed by molecular dynamics simulations and binding free energy predictions†
Jianzhong Chen
School of Science, Shandong Jiaotong University, Jinan 250357, China. E-mail: jzchen1970@126.com; chenjianzhong1970@163.com
First published on 25th May 2016
Abstract
Drug resistance of mutations in HIV-1 protease (PR) badly reduce the efficiency of the current inhibitors in clinical treatments of AIDS. In this work, molecular dynamics (MD) simulations coupled with binding free energy predictions were performed to study drug-resistant mechanisms of three mutations V32I, I47V and V82I on inhibitors saquinavir (SQV), amprenavir (APV) and darunavir (DRV). The results from dynamics analyses suggest that the side-chain alternations of three mutated residues produce important effects on distances between the flaps and catalytic sites of HIV-1 protease and the dihedral angle Chi1 of the mutated residues and I50/I50′. These conformational changes induce significant decreases in the occupancy of most hydrogen bonds and the interaction enthalpy of key residues with inhibitors in the mutated complexes, especially for the flap residues I50/I50′, which provide the main contributions to drug resistance of mutations toward these inhibitors. The results of binding free energy calculations show that the decrease in van der Waals interaction of inhibitors with the mutated PR relative to the wild-type (WT) PR mostly drive drug resistance of mutations toward inhibitors. We expect that this study can theoretically contribute significant guidance to designs of potent inhibitors targeting HIV-1 protease.
1. Introduction
Acquired immunodeficiency syndrome (AIDS) is a worldwide disease that badly threatens human health. A major challenge has been put in front of clinical treatment of anti-AIDS and many researchers have paid attention to how to efficiently combat AIDS. Numerous studies demonstrated that HIV-1 protease (PR) plays a significant role in the life cycle of the AIDS virus.1–3 PR can cleave the gag-pol poly-protein into small protein particles and assemble these particles into mature and infective HIV virus.4,5 Structurally, PR is a C2-symmetric homo-dimer structure with two identical 99 amino acid monomers6 (Fig. 1A). The conserved catalytic strands (D25/D25′-T26/T26′-G27/G27′) are located between interfaces of two monomers, which plays a functional role in catalytic cleavage of large poly-protein precursors gag.7 A small molecule inhibitors similar to structure of substrates, located at the catalytic site, can prevent substrate from going into the binding pocket, which will efficiently inhibit catalytic function of active PR.8–11 Thus, designs of small potent compounds targeting PR currently become an efficient approach of anti-HIV therapeutics.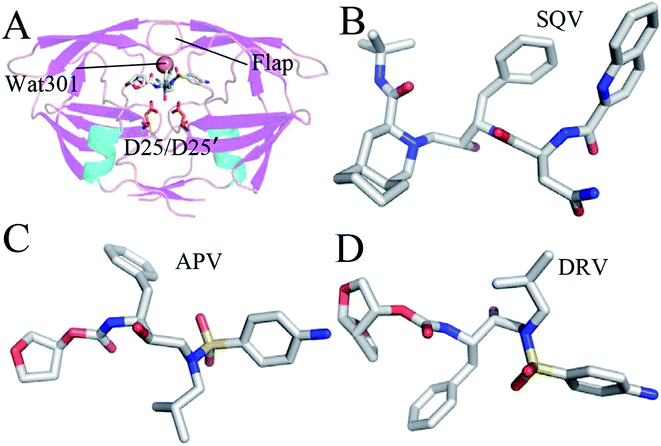 | ||
| Fig. 1 Molecular structures: (A) the inhibitor-WT PR, (B) SQV, (C) APV and (D) DRV. The WT PR is displayed in cartoon mode, and three inhibitors and D25/D25′ are shown in stick mode. | ||
Ten HIV-1 PR inhibitors (PIs) approved by the U.S. food and drug administration (FDA)12,13 have obtained great success in the starting phase of anti-HIV clinical treatment. However, residue mutations induce drug adaptability of HIV-1 PR toward the current inhibitors, which heavily weakens the ability of these inhibitors inhibiting function of the active PR.14–17 Single mutations of several conserved residues such as V32I, D30N, G48V, I50V, V82A, I54M, A71V and I84V show strong drug resistance toward inhibitors.14,18–22 Certainly, most of double mutations and multiple mutations also obviously reduced efficiency of inhibitors toward PR.6,23–27 Thus, presence of mutant drug resistance makes development of potent anti-HIV inhibitors face a big challenge.
The previous studies suggested that mutations in HIV-1 PR not only produce important effects on its catalytic activity, but also change its binding ability and stability.28,29 Work from Tie et al. gave an evidence that three mutations V32I, I47V and V82I obviously weaken inhibiting efficiency of several inhibitors on PR.30 Kovalevsky et al. also proved that these three mutants in HIV-2 protease caused weaker binding affinity of inhibitors to HIV-2 PR relative to HIV-1 PR,12 which is supported by the calculated studies of ours and Kar et al.31,32 Structurally, the positions of these three mutations are different. The mutation I47V is located at the flaps of PR, while the mutations V32I and V82I are far away from the flaps. From the view of size, I47V shortens the length of side chain for residue 47, but V32I and V82I increase the size of mutated side chains. Commonly, the three mutations heavily affects flexibility of the flaps. More importantly, these three residues in the WT PR do not produce strong interactions with PIs, but their mutations generate obvious drug resistance on inhibitors. Therefore, it is of importance to elucidate potential mechanism of drug resistance of three mutations V32I, I47V, and V82I toward inhibitors and understand the conformational changes induced by mutations at an atomic level for development of potent inhibitors targeting PR.
All-atom MD simulations not only provide dynamical details of atom fluctuations, but also contribute important information on interactions of ligands with proteins by using post-process analysis based on MD trajectories.33–43 The calculated simulations have also got success in investigating drug resistance of mutations toward PIs.18,44–51 To obtain deeper insight into drug-resistant mechanism of three mutations V32I, I47V and V82I toward PIs, three PIs saquinavir (SQV), amprenavir (APV) and darunavir (DRV) were selected and their structures were shown in Fig. 1B–D. SQV is the first-generation PI approved by FDA with a Ki value of 0.11 nM (Fig. 1B).52 Compared with SQV, the structure of APV contains a sulfonamide and a hydroxyethylamine, and it produces potent inhibition ability on PR with a Ki value of 0.15 nM (Fig. 1C).53 DRV is a new-generation potent PI and its Ki value reaches 0.04 nM (Fig. 1D).13 Three mutations V32I, I47V and V82I generate different-level drug resistance on the three current selected inhibitors.30 In this work, MD simulations, binding free energy calculations and dynamical analyses were combined to probe drug-resistant mechanism of three mutations toward inhibitors. We expect that this work can contribute a significant theoretical guidance to development of potent inhibitors targeting HIV-1 PR.
2. Materials and methods
2.1. System preparation
The initial conformations used in our simulations were taken from the crystal structures of protein data bank (PDB): 3OXC for the SQV-wild type (WT) PR,54 3S56 for the SQV-mutated PR,30 3NU3 for the APV-WT PR,55 3S43 for the APV-mutated PR,30 4LL3 for the DRV-WT PR56 and 3S53 for the DRV-mutated PR complex.30 Five mutations Q7K, L33I, L63I, C67A, S95A in wild-type structures used in our current studies were only used to construct structures of HIV-1 protease, they do not change the specificity and kinetic properties of the wild-type enzyme.57–61 Thus, we neglected these mutations during initialization of systems. Due to importance of D25/D25′ protonated states,62,63 the program PROPKA64,65 was applied to check the protonated states of these two residues and assign a monoprotonated state to D25′. All crystal water molecules were kept in the initial model. According to chemical bond information, the missing hydrogen atoms were connected to the corresponding heavy atoms by using the Leap module in Amber 12 program.66 The Amber ff14SB force field67 was assigned to PR and water molecules. The structures of three inhibitors SQV, APV and DRV were minimized at the semiempirical AM1 level and then the AM1-BCC charges were added to three PIs by using the AM1-BCC program68,69 and the general Amber force field (GAFF) was applied to generate the force field parameters of three inhibitors.70 Each complex was solvated in a truncated octahedral box of TIP3P water molecules with a 12.0 Å buffer along each dimension.71 Cl- counterions were placed around solute to neutralize the system.2.2. MD simulations in water
To relieve any bad inter-atoms contacts generated by initialization of systems, each initialized system was relaxed in 5000 steps with constraint on the complex, followed by full minimization of 5000 steps without any restriction. Then, each system was gently heated from 0 to 300 K in 1000 ps at constant volume and equilibrated at 300 K for another 1000 ps. Finally, six 120 ns MD simulations without any constraints were carried out at a constant pressure and the conformation was recorded every 8 ps. All simulations were run by using the Sander module in Amber 12. During MD simulations, the SHAKE method was employed to restrict the chemical bonds between hydrogen atoms and any heavy atoms.72 The Langevin thermostat73 with a collision frequency of 2.0 ps−1 was applied to control temperature of systems. Electrostatic interactions were computed by using the particle mesh Ewald (PME) method.74,75 A distance cutoff of 12.0 Å was set to treat non-bond interactions.2.3. MM-PBSA method
Molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) method was applied to compute binding free energies of three inhibitors to the WT and mutated PRs.76,77 For each binding complex, 500 snapshots were taken from the last 80 ns of MD trajectory with an interval of 160 ps for calculations. The binding free energies (ΔG) can be determined using the following equation:| ΔG = ΔEele + ΔEvdW + ΔGpol + ΔGnonpol − TΔS | (1) |
2.4. Solvated interaction energy method
Solvated interaction energy (SIE) is an end point method that calculates free energy differences between two states (free and bound states).80 This method has been successfully applied to predict the binding modes of inhibitors to proteins involving several life system.81,82 For the current work, 500 snapshots extracted from the last 80 ns of MD trajectory at an interval of 160 ps were used for the binding free energy analyses. The following SIE function was adopted to calculate inhibitor-PR binding free energies| ΔGbind(ρ, Din, α, γ, C) = α × [ΔEc(Din) + ΔGR + ΔEvdW + ΔGcav(ρ)] + C | (2) |
The first two terms ΔEc and ΔEvdW embody the intermolecular Coulomb and van der Waals interaction energies induced by inhibitor bindings, respectively. These two terms were evaluated using the Amber molecular mechanics force field ff14SB. The third term ΔGR describes the difference in the reaction field energy upon inhibitor bindings, which can be derived by solving the Poisson equation with the boundary element method BRI BEM83,84 and a variable-radius solvent probe.85 The fourth term ΔGcav reflects a change in the molecular surface area upon bindings, which can be calculated by using the following empirical equation:
| ΔGcav = γ × ΔSASA | (3) |
2.5. Cross-correlation analysis
To probe the effect of residue mutations on the internal dynamics changes of PR, the cross-correlation matrix Cij was constructed by using the coordinates of Cα atoms from the last 80 ns of MD trajectories. This matrix reflects the fluctuations of the Cα atoms relative to its average positions and can be determined by:
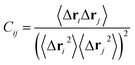 | (4) |
The angle bracket describes a time average over the equilibrated time of MD simulations, Δri represents the displacement vector from the mean position of Cα atom in the ith residue.87,88 The calculated values of matrix elements Cij fluctuates from −1 to 1. A correlated motion of Cα atoms of the ith residue relative to the jth residue is depicted by the positive Cij value, while an anticorrelated motion is described by the negative Cij value.
3. Results and discussion
3.1. Drug resistance of mutations revealed by MM-PBSA calculation
To obtain the detailed energy information involving drug resistance of mutations in PR toward inhibitors, six 120 ns MD simulations followed by MM-PBSA calculations were carried out. Root-mean-square deviations (RMSD) of backbone heavy atoms in six systems demonstrated that the simulations reach the equilibrium after ∼30 ns (Fig. S1†), thus yielding stable trajectories for post process analysis. Binding free energies of SQV, APV and DRV to the WT PR and mutated PRs and the corresponding separate free energy components were computed by the MM-PBSA method using 500 conformations taken from the last 80 ns of MD trajectories at intervals of 160 ps (Table 1).| Energy | SQV-WT | SQV-mutant | APV-WT | APV-mutant | DRV-WT | DRV-mutant |
|---|---|---|---|---|---|---|
a Errors labeled by the signs ± represent standard errors.b ΔGele+pol = ΔEele + ΔGpol.c ΔGbind = ΔEele + ΔEvdw + ΔGpol + ΔGnopol − TΔS.d The experimental values were derived from the experimental ki values in ref. 30 using the equation ΔGexp = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ki. ki. |
||||||
| ΔEele | −26.29 ± 5.37a | −38.78 ± 6.32 | −41.90 ± 5.14 | −44.55 ± 4.45 | −43.12 ± 5.16 | −46.22 ± 5.46 |
| ΔEvdW | −70.11 ± 3.16 | −68.37 ± 4.60 | −61.89 ± 3.42 | −58.25 ± 3.06 | −65.59 ± 3.28 | −62.67 ± 3.01 |
| ΔGpol | 64.86 ± 4.55 | 77.32 ± 5.02 | 70.39 ± 4.47 | 73.34 ± 4.21 | 72.61 ± 3.66 | 75.94 ± 3.64 |
| ΔGnopol | −7.97 ± 0.15 | −8.17 ± 0.24 | −7.02 ± 0.14 | −6.90 ± 0.11 | −6.86 ± 0.10 | −6.93 ± 0.09 |
| ΔGele+polb | 38.57 ± 4.62 | 38.54 ± 5.12 | 28.49 ± 4.30 | 28.79 ± 0.32 | 29.49 ± 4.39 | 29.72 ± 4.39 |
| −TΔS | 25.10 ± 1.01 | 25.73 ± 0.17 | 27.11 ± 0.17 | 26.74 ± 0.20 | 26.68 ± 0.15 | 27.13 ± 0.21 |
| ΔGbindc | −14.41 | −12.27 | −13.31 | −9.62 | −16.28 | −12.75 |
| ΔGexpd | −13.61 | −13.22 | −13.45 | −11.83 | −14.24 | −13.22 |
According to Table 1, the binding free energies of SQV, APV and DRV to the mutated PRs with three mutants V32I, I47V and V82I are decreased by 2.14, 3.69 and 3.53 kcal mol−1 relative to the WT PR, respectively. This result suggests that three mutations induce strong drug resistances toward PIs SQV, APV and DRV.
Comparisons of the separate free energy components between the mutated and WT PR can reveal origin of drug resistance induced by mutations. As shown in Table 1, van der Waals interactions (ΔEvdW) of SQV, APV and DRV with the mutated PR are reduced by 1.74, 3.64 and 2.92 kcal mol−1 relative to the WT PR, respectively, which indicates that the decrease in the van der Waals interactions plays an important role in drug resistance of mutations toward these three inhibitors. The polar interactions of APV and DRV with the mutated PR (ΔGele+pol), composing of the electrostatic interactions (ΔEele) and polar solvation energies (ΔGpol), are increased by 0.3 and 0.23 kcal mol−1, respectively, which provides a weak contribution to drug resistance, while the polar interaction of SQV with the mutant does not contribute to drug resistance. The non-polar interactions (ΔGnopol) of SQV and DRV with the mutated PR are strengthened slightly, while the one of APV with the mutated PR hardly changes. This result proves that the non-polar interactions do not produce obvious drug resistance on these three inhibitors. For the mutated systems complexed SQV and DRV, three mutations lead to the increase of 0.63 and 0.45 kcal mol−1 in the entropy term (−TΔS) relative to the WT system, respectively, which displays a weak contribution to drug resistance. However, the entropy term in the APV-mutated PR is decreased by 0.37 kcal mol−1, suggesting that the entropy change are not main causes of drug resistance induced by mutations. Totally, the decrease in the van der Waals interactions of SQV, APV and DRV with the mutated PR relative to the WT PR is a main force driving drug resistance of three mutants toward inhibitors. This result also basically agrees with the previous experimental studies of Tie et al.30
3.2. Drug resistance revealed by solvated interaction energy method
To further reveal the effect of three mutations V32I, I47V and V82I on inhibitor bindings, the SIE method was adopted to compute the binding free energies of SQV, APV and DRV to the WT and mutated PRs. The same conformations as the MM-PBSA calculation was used to perform the SIE calculations and the corresponding results were given in Table 2.| Component | SQV-WT | SQV-mutant | APV-WT | APV-mutant | DRV-WT | DRV-mutant |
|---|---|---|---|---|---|---|
a All energy are in kcal mol−1.b ΔGpol = ΔEc + ΔGR.c ΔGR were derived from the experimental values30 in using the equation ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ki. ki. |
||||||
| ΔEvdW | −67.07 ± 3.34 | −63.04 ± 4.53 | −65.13 ± 3.45 | −60.29 ± 3.14 | −69.49 ± 3.53 | −64.61 ± 3.09 |
| ΔEc | −18.08 ± 2.56 | −22.34 ± 3.48 | −18.32 ± 2.30 | −19.43 ± 2.26 | −19.23 ± 2.33 | −20.26 ± 2.37 |
| ΔGcav | −13.16 ± 0.41 | −13.44 ± 0.46 | −11.27 ± 0.38 | −11.10 ± 0.37 | −11.15 ± 0.28 | −11.12 ± 0.26 |
| ΔGR | 22.02 ± 1.89 | 26.42 ± 1.74 | 22.30 ± 1.72 | 23.02 ± 1.93 | 23.07 ± 1.81 | 23.93 ± 1.50 |
| ΔGpolb | 3.94 ± 0.41 | 4.08 ± 0.61 | 3.98 ± 0.50 | 3.59 ± 0.42 | 3.84 ± 0.58 | 3.67 ± 0.38 |
| ΔGbind | −10.89 ± 0.38 | −10.48 ± 0.56 | −10.48 ± 0.36 | −9.99 ± 0.34 | −10.94 ± 0.36 | −10.44 ± 0.33 |
| ΔGexpc | −13.61 | −13.22 | −13.45 | −11.83 | −14.24 | −13.22 |
One can observe from Table 2 that the binding affinities of SQV, APV and DRV to the mutated PRs are decreased by 0.41, 0.49 and 0.5 kcal mol−1 relative to the WT PR, respectively. This result shows that three mutations induce obvious drug resistance toward SQV, APV and DRV. Compared to the WT PR, the van der Waals interactions (ΔEvdW) of SQV, APV and DRV with the mutated PR are weakened by 4.03, 4.84 and 4.88 kcal mol−1, respectively, which indicates that the decrease in the van der Waals interactions provides an important contributions to drug resistance. Table 2 demonstrates that the nonpolar interactions (ΔGcav) of APV and DRV with the mutated PR do not provide contributions to drug resistance, only the one of SQV with the mutated PR is slightly weaken and offers a weak contribution to drug resistance. The polar interactions (ΔGpol) of inhibitors with the mutated PR, including the intermolecular Coulomb interaction energies (ΔEc) and the reaction force field energies (ΔGR), do not obviously change relative to the WT PR. Thus, the changes in the polar interactions hardly provide contributions to drug resistance. The above analyses suggest that the decrease in the van der Waals interaction of inhibitors with the mutated PR relative to the WT PR play a key role in drug resistance of mutations toward SQV, APV and DRV, which agrees well with the previous results from the MM-PBSA calculations.
3.3. Internal dynamics changes induced by mutations
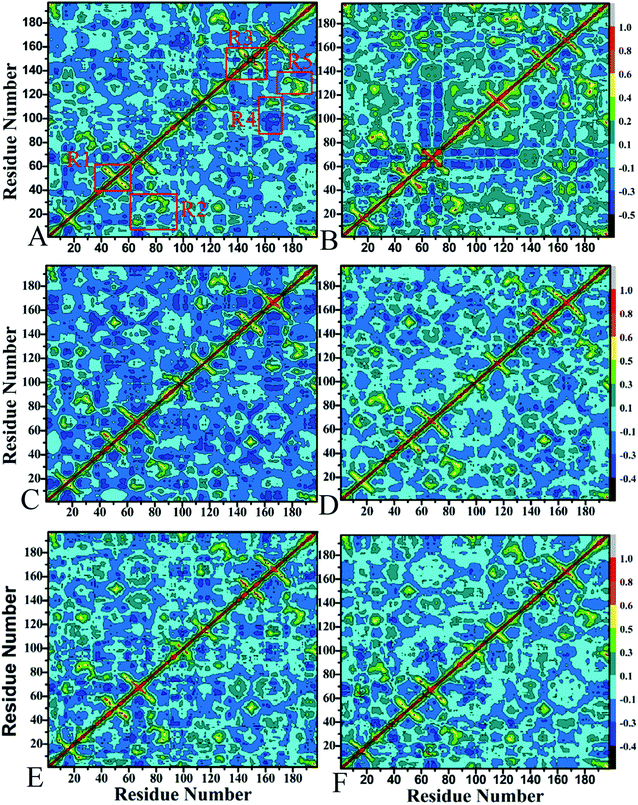
To probe the effect of mutations on internal dynamics of PR, the cross-correlation matrices were calculated using the Cpptraj program89 in Amber based on the equilibrated MD trajectories, and the results are depicted in Fig. 2. Strongly correlated and anticorrelated motions are highlighted by the highly positive regions (red and yellow) and negative ones (blue), respectively. Overall, apart from the diagonal regions depicting the correlated motion of a specific residue relative to itself, few highly correlated motions are watched. However, the difference in anti-correlated movements induced by mutations are still obvious, especially for the APV-mutated PR.Compared to the SQV-WT PR (Fig. 2A and B), three mutations not only induce the increase in the correlated motions of two flaps labeled by regions R1 and R3 (Fig. 2A and B), but also strengthen the correlated motions of regions R2 and R5 (red). The anticorrelated motion of region R4 is heavily weakened by mutations. In addition, the mutations also strengthen the anticorrelated motion of two terminates (residues 80–120) relative to residues 60–80 in chain A. For the APV-WT/mutated PR, the anticorrelated movements are obviously decreased by three mutations, which includes two flap regions. Additionally, the correlated motions of the flap in chain B is gently strengthened (Fig. 2C and D). In the case of DRV-WT/mutated PR, the correlated motion in the flap of chain A is slightly decreased by mutations, while the correlated movement in the flap of chain B is obviously increased (Fig. 2E and F). The above difference in internal dynamics of PR should reflect the changes in relative positions of residues induced by mutations.
To further reveal the changes in flexibility of PR due to mutations, the differences (ΔRMSF) in root-mean-square fluctuation (RMSF) of Cα atoms between the WT and mutated PR are calculated (Fig. 3). The results display that three mutations result in an obvious increase of RMSF near residues 50 and 50′ (flaps), which demonstrate that the flexibility of two flaps change highly. The RMSFs of regions near residues 82 and 82′ also produce a slight increase. This result proves that V82I mutation induce the change in flexibility of its nearby residues. However, the RMSFs of regions near mutation V32I do not change obviously.
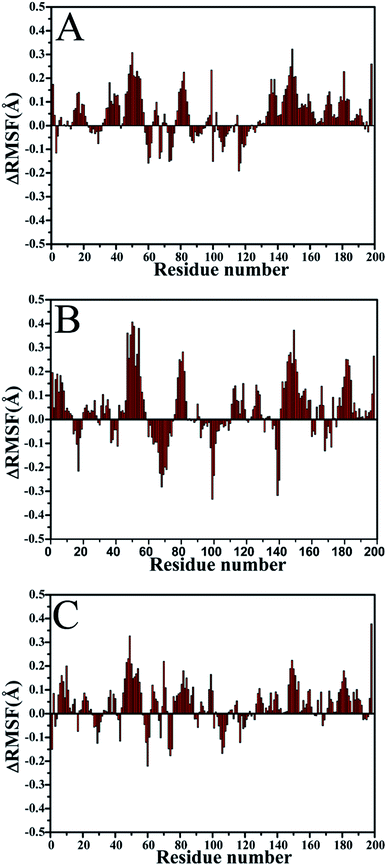 | ||
| Fig. 3 Changes in RMSF values of Cα atoms induced by three mutations: (A) the changes in the SQV-WT/mutated PR, (B) the changes in the APV-WT/mutated PR and (C) the changes in the DRV-WT/mutated PR. | ||
The effects of three mutations on conformational changes of PR can be further explored using free energy landscape constructed by backbone angles ψ and φ of residues 32, 47, I50 and 82 in chain A. The results were depicted in Fig. S2–S4.† For the SQV-WT/mutated PR, three mutation do not generate obvious change of the backbone angles ψ and φ of residues 32, 47 and I50, only the ones of residue 82 are changed by about 10° (Fig. S2†). According to Fig. S3,† the changes of the backbone angle ψ and φ of residues 32, 47 and 50 in the APV-WT/mutated PR is similar to the SQV-WT/mutated PR, but the angle φ of residue 82 has a change of ∼25°. In the case of the DRV-WT/mutated PR, the changes of the backbone angle ψ and φ of residues 32, 47 and 82 caused by three mutations are small, but the backbone angle φ of residue I50 produces an obvious change of about 83° (Fig. S4†). Overall, the changes of the backbone angle ψ and φ for residues 32, 47, 50 and 82 caused by mutations are not large, except for the residue I50 in the DRV-WT/mutated PR. According to the C2 symmetry of PR, the changes in the backbone angle ψ and φ of those corresponding residues in chain B should have similar results to chain A.
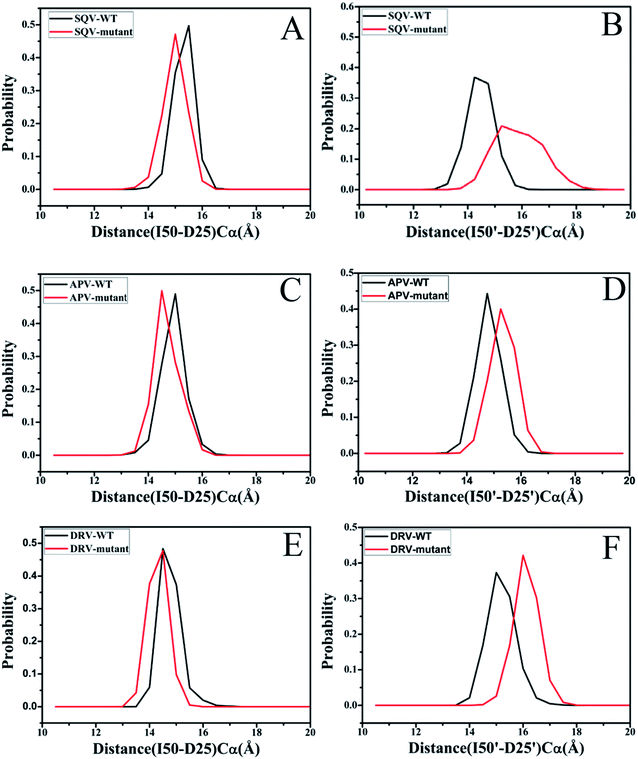
The previous studies suggested that mutations generate a significant effect on the distances between the flaps (I50/I50′) and the catalytic site (D25/D25′) of PR.18,31 Fig. 4 gives the probability distribution of these distances. The results indicate that the distances of the flaps away from the catalytic site change obviously, apart from the distance between I50 and D25 in the DRV-WT/mutated PR (Fig. 4E). As shown in Fig. 4A and C, because of three mutations, the distances between I50 and D25 in the SQV- and APV-mutated PR are decreased by ∼0.5 Å relative to the WT-PR. However, the distances between I50′ and D25′ in three mutated systems are enlarged by about 0.5 Å compared to the WT-PR. Thus, the changes of the distance between the flaps and the catalytic site must produce certain effect on inhibitor bindings to PR.
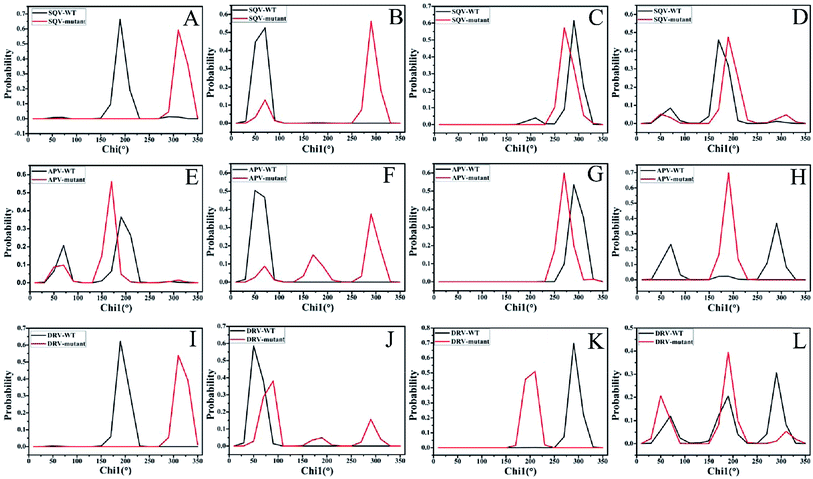
The analyses of dihedral angles Chi1 for side chains of mutated residues and I50 were performed on six systems to evaluate the effect of mutations on the binding pocket of PR. Fig. 5 depicts the frequency distribution of dihedral angle Chi1 of residues 32, 47, I50 and 82 in chain A. Due to mutation V32I, the dihedral angles Chi1 of residue 32 in the SQV- and DRV-mutated PR are increased by 120° relative to the WT-PR, while the one in the APV-mutated PR is decreased by 20° (Fig. 5A, E and I). In the case of I47V (Fig. 5B, F and J), the dihedral angles Chi1 of residue 47 in the SQV-, APV- and DRV-mutated PR are raised by 220°, 240° and 40° relative to the corresponding WT PR, respectively. Fig. 5C, G and K show that three mutations generate significant effect on the dihedral angle Chi1 of residue I50, and this angle in the SQV-, APV- and DRV-PR is reduced by 20°, 20°, and 80° compared to the WT PR, respectively. According to Fig. 5H and L, the dihedral angles Chi1 of residue 82 corresponding to the higher peak value in the APV- and DRV-mutated PR are diminished by 100° relative to the WT PR, while this angle in the SQV-mutated PR is increased by 20°. According to the C2 symmetry of PR structure, the dihedral angles Chi1 of residues 32′, 47′, I50′ and 82′ in the chain B should have similar results to the chain A. The above analyses suggest that three mutations bring obvious changes in the dihedral angles Chi1 of residues 32/32′, 47/47′, 50/50′and 82/82′, and these changes should change the shape and size of the binding pocket. Thus, three mutations are supposed to heavily affect the stability of hydrogen bonds and the inhibitor–residue interactions.
3.4. Effect of mutations on stability of hydrogen bonds
To estimate effect of three mutations on stability of hydrogen bonds between inhibitors and residues, the Cpptraj tool in Amber is applied to perform statistical analyses on hydrogen bonds in six systems (Table 3). The geometry information forming hydrogen bonds is depicted in Fig. S5.† One can observe from Table 3 that multiple hydrogen bonding interactions stabilize the inhibitor-PR structures in both the WT and mutated states. In particular, all three inhibitors are involved in several important hydrogen bonds with the catalytic sites of PR, mostly with residues D25/D25′, D29 and D30/D30′. Hydrogen bonding interactions between the side chain of D25/D25′, as well as between D30 and the inhibitors, are seen in every system. The backbones of D29′ and D30′ are also involved in two significant hydrogen bonds with all inhibitors except for SQV. However, the backbone of D29 only interacts with the inhibitor DRV. Another hydrogen bonding interaction with the backbone G27′ is found in all complexes. By comparison with the WT PR, three mutations produce obvious decrease in occupancy of all hydrogen bonds between inhibitors and residues, except for the hydrogen bond of the side chain of D25 with three inhibitors.| Hydrogen bondsa | Occupancyb | |||||
|---|---|---|---|---|---|---|
| SQV-PR | APV-PR | DRV-PR | ||||
| WT | Mutated | WT | Mutated | WT | Mutated | |
| a The hydrogen bonds are determined by the acceptor⋯donor distance of <3.5 Å and acceptor⋯H-donor angle of >120°.b Occupancy is defined as the percentage of simulation time that a specific hydrogen bond exists. | ||||||
| OD2@D25 | 51.8 | 97.6 | 70.1 | 81.7 | 32.3 | 69.5 |
| OD2@D25′ | 68.1 | 59.6 | 72.4 | 33.4 | 56.5 | 35.4 |
| OD1@D25′ | 87.2 | 21.5 | 20.2 | 5.4 | 26.3 | 13.7 |
| OD2@D30 | 38.2 | 12.9 | 73.6 | 36.7 | 61.4 | 28.2 |
| N–H@D30 | 13.5 | 1.6 | 82.2 | 70.3 | 78.8 | 59.2 |
| N–H@D29 | 25.4 | 11.3 | 76.3 | 45.6 | ||
| O@G27′ | 14.2 | 2.4 | 11.8 | 5.4 | 11.5 | 3.3 |
| N–H@D29′ | 40.2 | 11.6 | 69.5 | 51.4 | ||
| N–H@D30′ | 13.5 | 19.3 | 82.4 | 39.9 | ||
| OD2–HD2@D25′ | 15.3 | 9.6 | 46.4 | 20.5 | 43.5 | 17.3 |
| Lig⋯O–H1@Wat | 97.8 | 84.2 | 89.8 | 82.1 | 86.3 | 64.7 |
| Lig⋯O–H2@Wat | 98.2 | 81.9 | 91.8 | 74.8 | 94.5 | 70.3 |
| O@Wat⋯N–H@I50 | 86.5 | 94.3 | 87.1 | 92.3 | 91.2 | 43.5 |
| O@Wat⋯N–H@I50′ | 45.8 | 40.4 | 97.6 | 90.2 | 57.8 | 66.2 |
Table 3 also suggests that a water-bridged interaction occurs between the two flaps of PR and the current three inhibitors (Fig. S5†). The occupancy of all hydrogen bonds involving the water molecule is more than 40%, which shows that these water-mediated hydrogen bonds are stable during MD simulations. Thus, this water molecule (Wat301) contributes significantly toward efficient binding of drugs to PR. Because of mutations, the occupancy of the hydrogen bonds between Wat301 and inhibitors in the mutated systems are obviously reduced relative to the WT system. Only the hydrogen bonds of wat301 with I50 in APV- and SQV-mutated system, as well as with I50′ in the DRV-mutated PR are slightly increased. The above analyses prove that three mutations produce significant effect on stability of hydrogen bonding interactions and induce the decrease in the occupancy of most hydrogen bonds, which provides certain contributions to drug resistance of three mutations toward inhibitors.
3.5. Changes of inhibitor–residue interactions induced by three mutations
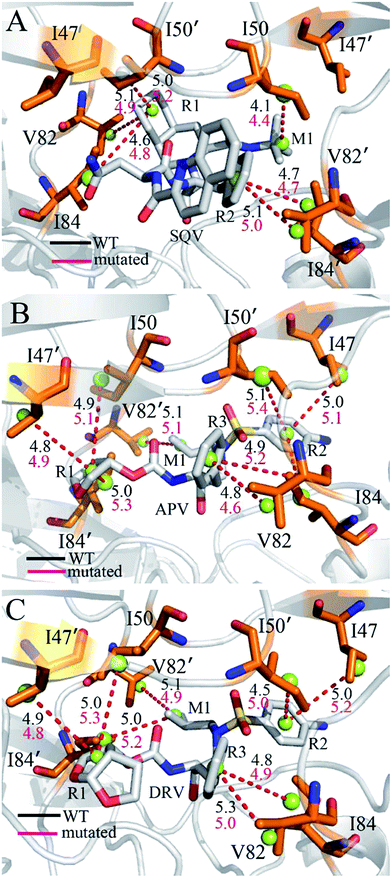
To further reveal origin of drug resistance caused by three mutations, the differences between the interaction enthalpy of inhibitors with individual residues in the WT and mutated PR were calculated (Fig. 6). The positions of residues involving significant change of the interaction enthalpy relative to inhibitors were displayed in Fig. 7 by using the averaged structure calculated from the last 20 ns MD trajectories. The averaged distances between mass centers of atoms involving significant hydrophobic interactions were also computed and labeled in Fig. 7.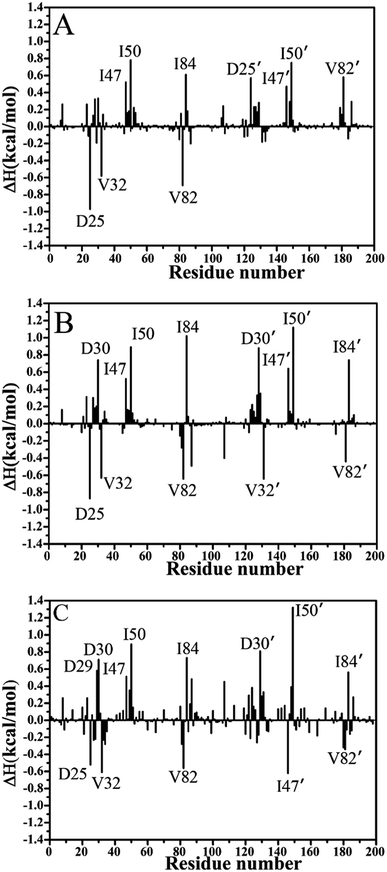 | ||
| Fig. 6 The difference between the interaction enthalpy of inhibitors with the mutated PR and the WT PR: (A) SQV, (B) APV and (C) DRV. | ||
Compared to the SQV-WT PR, the interactions of seven residues D25′, 47/47′, I50/I50′, I84 and 82′ with SQV in the mutated PR complex are weakened, while the ones of D25, 32 and 82 in the mutated PR with SQV are strengthened (Fig. 6A). The interactions of SQV with residues 32 and 82 in the mutated PR are 0.58 and 0.67 kcal mol−1 stronger than in the WT PR, respectively. This result should be reasonable, because the mutations V32I and V82I increase the size of the hydrophobic side chain of V32 and V82, which in turn increase the number of van der Waals contacts of residues I32 and I82 with SQV. However, the interaction of residue I82′ in the mutated PR with SQV is reduced by 0.56 kcal mol−1 relative to the WT PR. This result may arise from the adjustment of the dihedral angle Chi1 in I82′ (Fig. 5A). The interaction of D25 with SQV is strengthened by 0.97 kcal mol−1 in the mutated PR, which agrees well with the decrease of I50-D25 distance induced by mutations (Fig. 4A), but because of the increase of I50′-D25′ distance in the mutated system, the interaction of D25′ with SQV is weakened by 0.56 kcal mol−1 (Fig. 6A and 4B). Although residues I47/I47′ do not generate strong interactions with SQV, the interactions V47/V47′ with SQV in the mutated PR are diminished by 0.50 and 0.43 kcal mol−1 compared to the WT PR. Fig. 6A suggests that three mutations produce the most significant effect on the interactions of I50/I50′ with SQV. According to Fig. 7A, the interaction of I50 with SQV mainly origins from the CH–CH interaction between the alkyl of I50 and the one (M1) of SQV, while the interaction of I50′ with SQV is mostly contributed by the CH–π interaction between the alkyl of I50′ and the hydrophobic ring R1 of SQV. One can observe that the distances of I50 and I50′ away from the groups M1 and R1 of SQV in the mutated PR are increased by 0.3 and 0.2 Å relative to the WT PR, respectively, which in turn respectively induce the decreases of 0.77 and 0.75 kcal mol−1 in the interaction enthalpy of I50/I50′ with SQV in the mutated PR and thus provide key contributions to drug resistances of mutations toward SQV. Although residues I50/I50′ do not involve mutations, three mutants significantly affect the dihedral angles Chi1 of side chains in residues I50/I50′ and correspondingly change their orientation, which is a main reason for the reduction of the interactions between I50/I50′ and SQV in the mutant of PR. As shown in Fig. 6A, the binding ability of I84 to SQV in the PR mutant is reduced by 0.6 kcal mol−1 compared to the WT PR, which agrees well with the increase of distance between the alkyl of I84 and the hydrophobic ring R1 of SQV in the PR mutant. Although residue I84 does not also take part in mutation, the increase in the backbone angle ψ and the side-chain dihedral angle Chi1 of residue I82 in the PR mutant induces the change of side-chain orientation of I84 (Fig. 6A and S3†), which correspondingly weakens the interaction of I84 with SQV in the PR mutant.
In the case of the APV-WT/mutated PR, the reason why the interactions of D25, V32 and V82 with APV are strengthened in the APV-mutated PR is similar to the SQV-WT/mutated PR, moreover the cause of the decrease in the interaction of I47/I47′, I50/I50′ and I84 with APV in the PR mutant is also similar to the SQV-PR complex (Fig. 6B and 7B). Fig. 6B suggests that the binding abilities of I32′ and I82′ to APV in the APV-PR mutant are strengthened by 0.64 and 0.44 kcal mol−1 relative to the APV-WT PR, respectively, which should owe to the increase of the side-chain size caused by mutations V32I and V82I. According to Fig. 6B, three mutations induce the reduction of 0.72/0.81 kcal mol−1 in the interactions of D30/D30′ with APV in the mutated complex relative to the WT complex, which is in coincidence with the decrease in the occupancy of hydrogen bonds between these two residue and APV in the mutated complex (Table 3). The mutation V82I extends the size of side chain of residues 82′ in the mutated complex and changes its dihedral angle Chi1 (Fig. S3†), which induces the conformational changes of its nearby residues. As a result, the distance between the alkyl of I84′ and the hydrophobic ring R3 of APV in the mutated complex is increased by 0.3 Å compared to the WT complex, which thus reasonably explain a decrease of 0.72 kcal mol−1 in the interaction of I84′ with APV induced by three mutations.
For the DRV-WT/mutated PR, the interactions of residues D25, V32 and V82/V82′ with DRV in the DRV-mutated PR are raised by 0.51, 0.60, 0.56 and 0.40 kcal mol−1 compared to the WT complex (Fig. 6C and 7C), respectively, and the reason for this result is similar to the above four system. It is also observed from Fig. 6C that the interaction of I47′ with DRV in the mutated complex is strengthened by 0.62 kcal mol−1 relative to the WT complex, which agrees well with the decrease of the distance between the alkyl of I47′ and the hydrophobic ring R1 of DRV in the mutated system (Fig. 7C). As shown in Fig. 6C, the interactions of D29 and D30/D30′ with DRV in the DRV-mutated PR are weakened by 0.57, 0.70 and 0.81 kcal mol−1 relative to the WT complex, respectively. This result is in coincidence with the decrease in the occupancy of hydrogen bonds of these three residues in the PR mutant with DRV relative to the WT PR (Table 3). Compared to the DRV-WT PR, the binding abilities of residues 47, I50/I50′ and I84/I84′ to DRV are reduced by 0.49, 0.88/1.30 and 0.72/0.56 kcal mol−1 in the mutated complex, respectively, and the reasons for these results should owe to the decrease in the distance between the alkyls of these five residues and the corresponding hydrophobic groups of DRV. It is worthy to note that I50/I50′ produces very strong decrease of 0.88/1.30 kcal mol−1 in all residues and provides the most significant contributions to drug resistance of mutations toward DRV. This result should have close relation with the big changes in the backbone angles and the dihedral angle Chi1 of these two residues in the mutated complex (Fig. S4† and 5C). The above results basically agree with those of previous computational and experimental studies.30–32
Based on the above analysis of interaction enthalpy changes of inhibitors with the WT/mutated PR, although the residues I50/I50′ and I84/I84′ do not involve the mutations, the interaction enthalpy of these four residues with inhibitors in the mutated complex obviously decreased by mutations relative to the WT one, except for residue I84′ of the SQV-WT/mutated PR. These changes provide key contributions to drug resistance of three mutations toward inhibitors. The previous dynamics analyses suggest that three mutations induce significant changes in the I50/I50′-D25/D25′ distances and the side-chain dihedral angle Chi1 of the residues I50/I50′ and I84/I84′, which changes the interactions of these residues with inhibitors in the mutated states. Thus, the conformational changes of key residues induced by mutations are responsible for drug resistances of three mutants on inhibitors SQV, APV and DRV.
4. Conclusions
120 ns MD simulations were performed on the inhibitor-WT/mutated PR complexes to probe the drug resistance mechanisms of three mutations V32I, I47V and V82I toward inhibitors SQV, APV and DRV. The results indicate that three mutations not only produce important effects on the correlated motions and flexibility of HIV-1 PR, but also change the distances of I50/I50′ away from D25/D25′ and the dihedral angle Chi1 of mutated residues and I50/I50′. These changes induce the decrease in the occupancy of hydrogen bonds and the interaction enthalpy of key residues in the mutated PR with inhibitors compared to the WT PR, especially for the flap residues I50/I50′, which are mainly responsible for the drug resistance of mutations toward inhibitors. MM-PBSA and SIE methods were combined to comparatively reveal the origin of drug resistance of mutations in HIV-1 PR. The results suggest that the decrease in the van der Waals interactions of inhibitors with the mutated PR are a main force driving drug resistance of three mutations. This study is expected to provide significant theoretical contributions to development of potent inhibitor targeting HIV-1 protease.Acknowledgements
This work is supported by the National Natural Science Foundation of China (11504206 and 11274206), Shandong province university science and technology project (J14LJ07), and major development projects of Shandong Jiaotong University.References
- A. S. Perelson, A. U. Neumann, M. Markowitz, J. M. Leonard and D. D. Ho, Science, 1996, 271, 1582–1586 CrossRef CAS PubMed.
- B. Poon, K. Grovit-Ferbas, S. A. Stewart and I. S. Chen, Science, 1998, 281, 266–269 CrossRef CAS PubMed.
- E. O. Freed, Virology, 1998, 251, 1–15 CrossRef CAS PubMed.
- M. A. Navia, P. M. Fitzgerald, B. M. McKeever, C.-T. Leu, J. C. Heimbach, W. K. Herber, I. S. Sigal, P. L. Darke and J. P. Springer, Nature, 1989, 337, 615–620 CrossRef CAS PubMed.
- R. Lapatto, T. Blundell, A. Hemmings, J. Overington, A. Wilderspin, S. Wood, J. R. Merson, P. J. Whittle, D. E. Danley and K. F. Geoghegan, Nature, 1989, 342, 299–302 CrossRef CAS PubMed.
- A. L. Perryman, J. H. Lin and J. A. McCammon, Protein Sci., 2009, 13, 1108–1123 CrossRef PubMed.
- R. Ishima, D. I. Freedberg, Y.-X. Wang, J. M. Louis and D. A. Torchia, Structure, 1999, 7, 1047–1055 CrossRef CAS PubMed.
- A. M. Silva, R. E. Cachau, H. L. Sham and J. W. Erickson, J. Mol. Biol., 1996, 255, 321–340 CrossRef CAS PubMed.
- W. R. Scott and C. A. Schiffer, Structure, 2000, 8, 1259–1265 CrossRef CAS PubMed.
- D. A. Judd, J. H. Nettles, N. Nevins, J. P. Snyder, D. C. Liotta, J. Tang, J. Ermolieff, R. F. Schinazi and C. L. Hill, J. Am. Chem. Soc., 2001, 123, 886–897 CrossRef CAS PubMed.
- Y.-X. Wang, D. I. Freedberg, T. Yamazaki, P. T. Wingfield, S. J. Stahl, J. D. Kaufman, Y. Kiso and D. A. Torchia, Biochemistry, 1996, 35, 9945–9950 CrossRef CAS PubMed.
- A. Y. Kovalevsky, J. M. Louis, A. Aniana, A. K. Ghosh and I. T. Weber, J. Mol. Biol., 2008, 384, 178–192 CrossRef CAS PubMed.
- A. K. Ghosh, Z. L. Dawson and H. Mitsuya, Bioorg. Med. Chem., 2007, 15, 7576–7580 CrossRef CAS PubMed.
- V. A. Johnson, F. Brun-Vézinet, B. Clotet, H. Gunthard, D. R. Kuritzkes, D. Pillay, J. M. Schapiro and D. D. Richman, Top. HIV. Med., 2009, 17, 138–145 Search PubMed.
- S. De Meyer, H. Azijn, D. Surleraux, D. Jochmans, A. Tahri, R. Pauwels, P. Wigerinck and M.-P. de Béthune, Antimicrob. Agents Chemother., 2005, 49, 2314–2321 CrossRef CAS PubMed.
- K. G. Šašková, M. Kožíšek, K. Stray, D. de Jong, P. Řezáčová, J. Brynda, N. M. van Maarseveen, M. Nijhuis, T. Cihlář and J. Konvalinka, J. Virol., 2014, 88, 3586–3590 CrossRef PubMed.
- C. Wang, Y. Mitsuya, B. Gharizadeh, M. Ronaghi and R. W. Shafer, Genome Res., 2007, 17, 1195–1201 CrossRef CAS PubMed.
- B. R. Meher and Y. Wang, J. Phys. Chem. B, 2012, 116, 1884–1900 CrossRef CAS PubMed.
- A. Y. Kovalevsky, Y. Tie, F. Liu, P. I. Boross, Y. F. Wang, S. Leshchenko, A. K. Ghosh, R. W. Harrison and I. T. Weber, J. Med. Chem., 2006, 49, 1379–1387 CrossRef CAS PubMed.
- K. Wittayanarakul, O. Aruksakunwong, S. Saen-oon, W. Chantratita, V. Parasuk, P. Sompornpisut and S. Hannongbua, Biophys. J., 2005, 88, 867–879 CrossRef CAS PubMed.
- E. T. Baldwin, T. N. Bhat, B. Liu, N. Pattabiraman and J. W. Erickson, Nat. Struct. Mol. Biol., 1995, 2, 244–249 Search PubMed.
- J. E. Foulkes-Murzycki, C. Rosi, N. Kurt Yilmaz, R. W. Shafer and C. A. Schiffer, ACS Chem. Biol., 2012, 8, 513–518 CrossRef PubMed.
- M. J. Todd, I. Luque, A. Velázquez-Campoy and E. Freire, Biochemistry, 2000, 39, 11876–11883 CrossRef CAS PubMed.
- Z. Chen, Y. Li, H. B. Schock, D. Hall, E. Chen and L. C. Kuo, J. Biol. Chem., 1995, 270, 21433–21436 CrossRef CAS PubMed.
- J. Deval, K. L. White, M. D. Miller, N. T. Parkin, J. Courcambeck, P. Halfon, B. Selmi, J. Boretto and B. Canard, J. Biol. Chem., 2004, 279, 509–516 CrossRef CAS PubMed.
- J. M. Louis, L. Deshmukh, J. M. Sayer, A. Aniana and G. M. Clore, Biochemistry, 2015, 54, 5414–5424 CrossRef CAS PubMed.
- N. M. King, M. Prabu-Jeyabalan, R. M. Bandaranayake, M. N. Nalam, E. A. Nalivaika, A. e. l. Özen, T. r. Haliloğlu, N. e. K. Yılmaz and C. A. Schiffer, ACS Chem. Biol., 2012, 7, 1536–1546 CrossRef CAS PubMed.
- T. W. Ridky, A. Kikonyogo, J. Leis, S. Gulnik, T. Copeland, J. Erickson, A. Wlodawer, I. Kurinov, R. W. Harrison and I. T. Weber, Biochemistry, 1998, 37, 13835–13845 CrossRef CAS PubMed.
- S. Mittal, R. M. Bandaranayake, N. M. King, M. Prabu-Jeyabalan, M. N. Nalam, E. A. Nalivaika, N. K. Yilmaz and C. A. Schiffer, J. Virol., 2013, 87, 4176–4184 CrossRef CAS PubMed.
- Y. Tie, Y. F. Wang, P. I. Boross, T. Y. Chiu, A. K. Ghosh, J. Tozser, J. M. Louis, R. W. Harrison and I. T. Weber, Protein Sci., 2012, 21, 339–350 CrossRef CAS PubMed.
- J. Chen, Z. Liang, W. Wang, C. Yi, S. Zhang and Q. Zhang, Sci. Rep., 2014, 4, 6872 CrossRef CAS PubMed.
- P. Kar and V. Knecht, J. Phys. Chem. B, 2012, 116, 2605–2614 CrossRef CAS PubMed.
- G. Hu, Z. Cao, S. Xu, W. Wang and J. Wang, Sci. Rep., 2015, 5, 16481 CrossRef CAS PubMed.
- E. L. Wu, K. L. Han and J. Z. H. Zhang, Chem.–Eur. J., 2008, 14, 8704–8714 CrossRef CAS PubMed.
- P. Pan, S. Tian, H. Sun, X. Kong, W. Zhou, D. Li, Y. Li and T. Hou, J. Chem. Inf. Model., 2015, 55, 2693–2704 CrossRef CAS PubMed.
- J. Chen, J. Wang, Q. Zhang, K. Chen and W. Zhu, Sci. Rep., 2015, 5, 17421 CrossRef CAS PubMed.
- B. E. Olausson, A. Grossfield, M. C. Pitman, M. F. Brown, S. E. Feller and A. Vogel, J. Am. Chem. Soc., 2012, 134, 4324–4331 CrossRef CAS PubMed.
- C. Yi and T. O. Wambo, Phys. Chem. Chem. Phys., 2015, 17, 23074–23080 RSC.
- J. Wang, Q. Shao, Z. Xu, Y. Liu, Z. Yang, B. P. Cossins, H. Jiang, K. Chen, J. Shi and W. Zhu, J. Phys. Chem. B, 2013, 118, 134–143 CrossRef PubMed.
- Y. Gao, X. Lu, L. L. Duan, J. Z. Zhang and Y. Mei, J. Phys. Chem. B, 2011, 116, 549–554 CrossRef PubMed.
- T. Zhu, J. Z. Zhang and X. He, J. Chem. Theory Comput., 2013, 9, 2104–2114 CrossRef CAS PubMed.
- D. Li, L. Chen, Y. Li, S. Tian, H. Sun and T. Hou, Mol. Pharm., 2014, 11, 716–726 CrossRef CAS PubMed.
- T. S. Banipal, A. Kaur, I. A. Khan and P. K. Banipal, RSC Adv., 2016, 6, 34754–34769 RSC.
- P. Kar and V. Knecht, J. Comput.-Aided Mol. Des., 2012, 1–18 CAS.
- G. Leonis, T. Steinbrecher and M. G. Papadopoulos, J. Chem. Inf. Model., 2013, 53, 2141–2153 CrossRef CAS PubMed.
- H. Tzoupis, G. Leonis, T. Mavromoustakos and M. G. Papadopoulos, J. Chem. Theory Comput., 2013, 9, 1754–1764 CrossRef CAS PubMed.
- G.-D. Hu, T. Zhu, S.-L. Zhang, D. Wang and Q.-G. Zhang, Eur. J. Med. Chem., 2010, 45, 227–235 CrossRef CAS PubMed.
- J. Chen, X. Wang, T. Zhu, Q. Zhang and J. Z. Zhang, J. Chem. Inf. Model., 2015, 55, 1903–1913 CrossRef CAS PubMed.
- D. Li, J. G. Han, H. Chen, L. Li, R. N. Zhao, G. Liu and Y. Duan, J. Mol. Model., 2012, 18, 1841–1854 CrossRef CAS PubMed.
- R. Duan, R. Lazim and D. Zhang, J. Comput. Chem., 2015, 36, 1885–1892 CrossRef CAS PubMed.
- Y. Yu, J. Wang, Q. Shao, J. Shi and W. Zhu, Sci. Rep., 2015, 5, 10517 CrossRef PubMed.
- A. E. Kim, J. M. Dintaman, D. S. Waddell and J. A. Silverman, J. Pharmacol. Exp. Ther., 1998, 286, 1439–1445 CAS.
- G. C. Williams and P. J. Sinko, Adv. Drug Delivery Rev., 1999, 39, 211–238 CrossRef CAS PubMed.
- Y. Tie, A. Y. Kovalevsky, P. Boross, Y. F. Wang, A. K. Ghosh, J. Tozser, R. W. Harrison and I. T. Weber, Proteins, 2007, 67, 232–242 CrossRef CAS PubMed.
- C. H. Shen, Y. F. Wang, A. Y. Kovalevsky, R. W. Harrison and I. T. Weber, FEBS J., 2010, 277, 3699–3714 CrossRef CAS PubMed.
- M. Kožíšek, M. Lepšík, K. Grantz Šašková, J. Brynda, J. Konvalinka and P. Řezáčová, FEBS J., 2014, 281, 1834–1847 CrossRef PubMed.
- J. M. Louis, R. Ishima, I. Nesheiwat, L. K. Pannell, S. M. Lynch, D. A. Torchia and A. M. Gronenborn, J. Biol. Chem., 2003, 278, 6085–6092 CrossRef CAS PubMed.
- A. M. Mildner, D. J. Rothrock, J. W. Leone, C. A. Bannow, J. M. Lull, I. M. Reardon, J. L. Sarcich, W. J. Howe and C.-S. C. Tomich, Biochemistry, 1994, 33, 9405–9413 CrossRef CAS PubMed.
- J. M. Louis, G. M. Clore and A. M. Gronenborn, Nat. Struct. Mol. Biol., 1999, 6, 868–875 Search PubMed.
- R. Ishima, R. Ghirlando, J. Tözsér, A. M. Gronenborn, D. A. Torchia and J. M. Louis, J. Biol. Chem., 2001, 276, 49110–49116 CrossRef CAS PubMed.
- S. Thaisrivongs, H. I. Skulnick, S. R. Turner, J. W. Strohbach, R. A. Tommasi, P. D. Johnson, P. A. Aristoff, T. M. Judge, R. B. Gammill and J. K. Morris, J. Med. Chem., 1996, 39, 4349–4353 CrossRef CAS PubMed.
- J. Chen, M. Yang, G. Hu, S. Shi, C. Yi and Q. Zhang, J. Mol. Model., 2009, 15, 1245–1252 CrossRef CAS PubMed.
- J. Chen, S. Zhang, X. Liu and Q. Zhang, J. Mol. Model., 2010, 16, 459–468 CrossRef PubMed.
- D. C. Bas, D. M. Rogers and J. H. Jensen, Proteins: Struct., Funct., Genet., 2008, 73, 765–783 CrossRef CAS PubMed.
- H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Genet., 2005, 61, 704–721 CrossRef CAS PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, et al., Amber 12, University of California, San Francisco, 2012 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- J. A. Izaguirre, D. P. Catarello, J. M. Wozniak and R. D. Skeel, J. Chem. Phys., 2001, 114, 2090–2098 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- W. Wang and P. A. Kollman, J. Mol. Biol., 2000, 303, 567–582 CrossRef CAS PubMed.
- J. Wang, P. Morin, W. Wang and P. A. Kollman, J. Am. Chem. Soc., 2001, 123, 5221–5230 CrossRef CAS PubMed.
- H. Gohlke, C. Kiel and D. A. Case, J. Mol. Biol., 2003, 330, 891–913 CrossRef CAS PubMed.
- B. Xu, H. Shen, X. Zhu and G. Li, J. Comput. Chem., 2011, 32, 3188–3193 CrossRef CAS PubMed.
- M. Naïm, S. Bhat, K. N. Rankin, S. Dennis, S. F. Chowdhury, I. Siddiqi, P. Drabik, T. Sulea, C. I. Bayly and A. Jakalian, J. Chem. Inf. Model., 2007, 47, 122–133 CrossRef PubMed.
- J. Chen, J. Wang and W. Zhu, PLoS One, 2014, 9, e99862 CrossRef PubMed.
- Q. Cui, T. Sulea, J. D. Schrag, C. Munger, M.-N. Hung, M. Naïm, M. Cygler and E. O. Purisima, J. Mol. Biol., 2008, 379, 787–802 CrossRef CAS PubMed.
- E. O. Purisima, J. Comput. Chem., 1998, 19, 1494–1504 CrossRef CAS.
- E. O. Purisima and S. H. Nilar, J. Comput. Chem., 1995, 16, 681–689 CrossRef CAS.
- S. Bhat and E. O. Purisima, Proteins, 2006, 62, 244–261 CrossRef CAS PubMed.
- A. Perdih, U. Bren and T. Solmajer, J. Mol. Model., 2009, 15, 983–996 CrossRef CAS PubMed.
- T. Ichiye and M. Karplus, Proteins, 1991, 11, 205–217 CrossRef CAS PubMed.
- C. G. Ji and J. Z. H. Zhang, J. Am. Chem. Soc., 2011, 17727–17737 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham III, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra09201b |
| This journal is © The Royal Society of Chemistry 2016 |