Rational computing of energy levels for organic electronics: the case of 2-benzylidene-1,3-indandiones

Abstract

Device engineering in organic electronics, an active area of research, requires knowledge of the energy levels of organic materials (traditionally but ambiguously denoted as HOMO and LUMO). These can be effectively determined by electrochemical investigation, but yet more effective would be quantum chemical (QC) computation of these quantities. However, there is no consensus on the computational method in the research community. Ongoing discussions often focus on choosing the right density functional method, but neglect other model parameters, in particular, the basis set. This study considers comparison of various methodologies and parameters for predicting ionization energy I and electron affinity A. Our aim was to outline a QC ‘recipe’ used in the search of new structures with desired energy levels for application in the field of organic electronics. Validation of calculated results to electrochemically determined values through linear regression and effect decomposition were used for compiling the recipe, ensuring trend-descriptive and resource–effective combination of QC model parameters. In particular, accounting for solvation by the medium is found to be essential and hardly consuming any additional CPU time. Basis set extension with extra valence functions is found to be much more effective than by adding diffuse functions. Among explored methods, B3LYP/6-311G(d) + CPCM is the recommended one for ionization energy, providing experimental quality results suitable for screening purposes. CAM-B3LYP is deemed more efficient for electron affinity, though by far not achieving the desired quality. Correction by computed reference redox pair potential is also found to be overall advantageous.

---

Introduction

The interest in organic solid thin films, especially during the last decades, has produced noticeable achievements in developing effective organic-based transistors, light-emitting diodes, solar cells and other devices.^1–12 It is well-known that the efficacious search for new materials starts with narrowing the range of possible candidates based on some relevant properties of them; in the case of organic thin-film materials, their charge-carrier transport properties are very important. As these are, in molecular (e.g., organic) materials, intimately coupled with molecule's ability either to acquire or to lose an electron,^9,10 usual estimate for the properties mentioned are ionization energy (or ionization potential) I and electron affinity A.^3,8,13 However, these are intrinsically theoretical quantities expressed through placing the electron infinitely far from the molecule in vacuum – therefore, some practical (computable or experimentally measurable) estimates of I and A ought to be used.

Choice of appropriate estimate depends on several criteria. The characterizing property should be as easy as possible to evaluate; it should also be familiar to or easy-to-introduce for the most of research community. The ground requirement is, nevertheless, the confidence that the criterion holds justified at least in most (preferably in all) cases of study. Trade-off between the ready obtaining of criterion value and its accuracy suggests that the appraisal of certain criteria will shift in time along with the advancing technology. For long time, in partial due to unworkability of high-level quantum chemical computations, approaches based on Koopmans' theorem or on corresponding theorems in DFT world – Janak's theorem¹⁴ (JT) and ‘IP theorem’^15–18 (IPT) – were, and still are used, despite their often-questioned reliability.^1,19,20 In these I and A were approximated as orbital energies (eigenvalues), HOMO and LUMO, from Hartree–Fock (HF) or Kohn–Sham (KS) equations, respectively, taken with the opposite sign. Nowadays, explicit calculation of energy difference in the neutral and the ionized state of molecule (sometimes abbreviated as ΔSCF^20–23 or, more generally, simply Δ²⁴ or ΔE (ref. 25)) is used for molecular screening by many authors.^{11,23,26–29} This way requires more computation time, but is that increase significant for contemporary computers? Besides, computational path is to be selected among other options: which functional and basis set (largest available?)^{23,24,30–32} to choose, whether to use solvent modelling (sometimes^2,33,34 still not included), whether to make thermochemical and reference redox pair^35,36 corrections, is there point in modelling H bonding if it is intuitively predicted to be weak, etc.

On the other hand, in the experimental domain, cyclic voltammetry (CV) has been used widely for the same purposes.^13,37–39 Here the similarity in the nature between oxidation potential and I, as well as between reduction potential and A, is exploited, indicating at the same time chemical reactivity as another field that demands correct values of I and A.^{21,26,29,40,41} Both evaluation methods mentioned, however, reflect behavior of a molecule (real or modelled) either in gas phase or in a solution, and with either relaxed or non-relaxed geometry. Much more close to describing the desired properties are I and A measured by, respectively, ultraviolet photoelectron spectroscopy (UPS)^{11,13,19,26,37,38} and inverse photoelectron spectroscopy (IPES)^{3,11,13,19,37} (as well as some other methods, particularly in gas phase)^37,42,43 of thin organic solid films. Yet well appropriate, these techniques are very elaborate, costly and specimen-dependent, therefore not appropriate for preliminary screening of candidate molecules, but rather for high-level research. As CV is still an experimental method and therefore tedious, one might opt for using some computational methodology.

The focus of this article is to identify optimal computational scheme for I and A estimation. Such scheme used at early design stage of novel compounds for molecular electronics allows selecting promising structures for further synthesis. For judging the reliability of proposed computational schemes we have used CV experimental data as a reference. Specifically, we tried to find out which computational aspects are and which are not important. This could be useful for synthetic chemists who generally are not acquainted with computational chemistry as a recipe for estimation of I and A on an ordinary lab computer equipped with some well-known computational suite. The only aspect we do not consider in detail is the choice of density functional, as there is already ample literature covering this topic. Choice of benzylidene-1,3-indandione series stemmed in the long research experience our groups have with these molecules, particularly with their application in organic electronics.^89–92 These molecules are of classical D–π–A structure, featuring many classical electron donors and acceptors as well as somewhat extended aromatic system.

Experimental and QC calculation details

The molecules under study are various derivatives of 2-benzylidene-1,3-indandione, with position 4′ of benzylidene ring functionalized. We have chosen to focus on a row of compounds similar in structure to minimize number of factors affecting their electrochemical description and also because straight the derivatization is the main route of computational screening. Chart 1 below list the codes and substituents of molecules studied.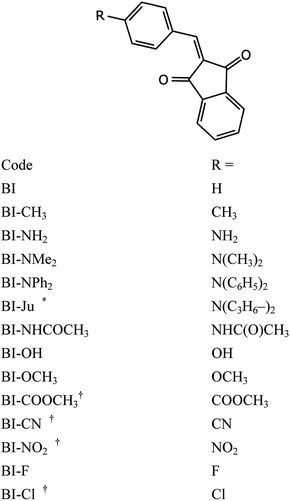

Chart 1 Structure of compounds under investigation. * Together with the benzene ring of benzylidene constitutes julolidine system. ^† Ionization energy was not measured (see text above).

The cyclic voltammograms were recorded using a computer-controlled electrochemical system PARSAT 2273 using glassy carbon disk (Ø 0.5 cm) as a working electrode. The measurements were carried out using a three-electrode cell configuration. Saturated calomel electrode (SCE) served as a reference electrode and Pt wire – as an auxiliary electrode. The potential scan rate was 100 mV s⁻¹. Electrochemical redox reactions were studied in deaerated 0.1 M tetrabutylammonium tetrafluorophosphate (TBAPF₆) solution in acetonitrile (ACN). ACN (Merck, puriss. grade) was distilled over phosphorus pentoxide, then redistilled over potassium carbonate and stored over 0.4 nm molecular sieves. Unfortunately, it was impossible to determine oxidation potentials of four compounds (BI–Cl, BI–COOCH₃, BI–CN and BI–NO₂) in acetonitrile, as it lies above that of solvent.

All quantum chemical calculations were performed using Gaussian 09, rev. D.01 program,⁴⁴ using GaussView 5,⁴⁵ Avogadro,⁴⁶ Gabedit⁴⁷ and OpenBabel⁴⁸ for auxiliary tasks. Both vertical (I_v and A_v) and adiabatic (I_a and A_a) energy differences were considered, the last ones including not only relaxation of electron system during the ionization, but also that of geometry after the electron transfer has occurred. In electrochemistry, one deals with adiabatic transitions, according to modern electron transfer theory.^49–54 Among functionals, ubiquitous (see our mini-comparison in ESI 3†) B3LYP^55,56 and its close analogue, range-separated hybrid CAM-B3LYP,⁵⁷ were chosen for energy calculations and geometry optimizations. We have seen no point in carrying out another plenty-of-functionals study as there are plenty already available in scientific literature (see, e.g., ref. 5, 8, 19, 21, 25, 73 and 83–85). These studies also suggest that range-separated hybrids are suitable for ionization calculations with either methodology. We did not consider other QC methods in this study, too. Hartree–Fock (HF), though showing appreciable performance when using Koopmans' theorem for ionization potential,^{5,20,24,37,72,87,88} provides completely senseless results for electron affinity when using the same orbital energy methodology;^5,88 while most experimentalists would probably prefer to use one single method throughout the study. HF results for ΔSCF are also found to be rather unsatisfactory.^86,87 Again, HF performance for correlation figures-of-merit is found not very honourable.^25,83 Correlated methods like MPn or Coupled Cluster are, in turn, too costly for computational screening for ordinary users, so also not covered in this study.

On the other hand, there are not many studies considering basis set impact systematically. Classical work by Stowasser and Hoffmann,⁵⁸ as well some other systematic study,⁸⁷ both on small molecules, discovered that polarization functions on heavy atoms are important for double-zeta BS but there is no considerable impact of them for triple-zeta BS, at least for orbital energies. Polarization functions on H atoms are found to be not important,^27,58,87 though increasing computational cost. Much less attention is paid to whether diffuse or extra valence functions are to be used; it is often just stated that these are essential, especially in A calculations.^{23,28,72,79,80} Most of these studies were, in addition, focused on prediction of absolute values, not trends, and considered small molecules. Therefore, we chose systematic performance comparison of various BS for regression figures-of-merit as the main part of this study. For computing I and A, we employed various Pople basis sets, double and triple valence, with or without diffuse functions, with and without polarization functions on hydrogen atoms. Basis set 6-31G(d,p) was employed in geometry optimizations and frequency/zero-point energy correction calculations (no frequency scaling was applied). Frequently used^{20,22,24,30,40,41,43} zero-point energy correction is thermochemical correction that accounts for vibrational energy difference in neutral and ionized molecule, which is persistent also at zero temperature. The correction is important because simple energy calculation considers only electronic energy. We also attempted to compute thermal correction (to compare not for 0  K, but for 298  K); however, the default results in Gaussian are unsatisfactory and the possible correction is too complicated for non-professionals. We would also like to note that it is worth performing additional geometry optimization with correct force constants at the end of standard geometry optimization (in Gaussian, Opt=CalcAll), because when it was employed our results became somewhat more consistent. Usually this does not take too much computation time, but in difficult cases can be valuable.

All energy difference calculations were done not as frequently used^20,40,41,59 RKS–UKS, but as UKS–UKS differences, i.e., paired electrons restriction was lifted also for neutral molecules. This was achieved by breaking the spin symmetry in initial guess through Guess=Mix keyword. Spin contamination levels were low – almost usually ≤ 10% (acceptable),^60,61 higher for cations. Ferrocene⁶² and ferricenium⁶³ cation were considered to be in the low-spin state. Use of orbitals energies from unrestricted wave functions is legitimate,⁶⁴ so we did not recompute these data. All energy calculations were checked for wave function stability. No symmetry constraints were applied (except in geometry optimization of ferrocene species), as compounds in series studied have different symmetry while one of the key characteristics we study is computational time, which is normally reduced by imposing particular symmetry on the wave function. All other computational parameters were mostly Gaussian 09 defaults (for some difficult cases SCF with steepest descent initial steps with optional quadratic steps at the end was carried out – YQC option; sometimes also Fermi broadening).

Solvent (ACN) was modelled with SCRF=CPCM keyword, using all default parameters (UFF atomic radii system with scaling factor 1.1, etc.). Non-equilibrium solvation was forced in vertical ΔSCF jobs. We did not focus on how different solvent models impact the results computed, rather to check (or show) the importance of using them in common.

Our study utilized 12-core CPU and 64 GB RAM nodes of Latvian Super Cluster (LaSC; GNU/Linux-based). In our methodology, we chose not to concentrate on searching for the best empirical correlations suited for the particular case of our molecules (and therefore not very valuable for much of the readers).³⁷ Rather, we tried to assess the overall quality of such predictions by determining the most important parameters of calculation (i.e., factors) that affect figures of merit for prediction quality, while removing unimportant ones. In traditional statistics, these insignificant ‘factors’ are told to emerge from random perturbations and to have nothing to do with real quantities they correspond to. In our case, we deem it justifiably to treat these ‘noises’ as consequences of confined dataset, i.e., of using derivative series of single basic structure. We hope therefore that removing these insignificant ‘effects’ strengthens reliability of our study, as well as its transferability to other compounds.

As figures of merit mentioned we chose traditional quality descriptors for linear regression, namely slope and intercept of correlation equation, expected to be as close as possible to 1 and 0, respectively; the square of correlation coefficient, R², is also of importance. The intercept characterizes the overall absolute deviation of calculated values from experimental ones, but is not quite reliable figure of merit as CV experimental values can³⁶ shift to some extent that is not expected to be very prominent, but rather unpredictable. The slope is characteristic of systematic shift in I or A due to structure of compounds and R² describes unsystematic shift. In particular, we sought to minimize deviations of these parameters from their ideal case. In addition, we made shorter computation time as one of our goals, because for screening it matters not less than precision. Therefore, all calculations were performed on identical cluster nodes. To implement the discrimination of factors, we used well-known effect significance test introduced by Daniel in 1959.⁶⁵ Details of corresponding analysis can be found in the ESI 1C.† All figures of merit defined previously were then recalculated from effect, omitting insignificant ones. Effect calculation was carried out according to ref. 66, using R statistical language (version 3.1.1). ANOVA was also performed and showed similar results while not allowing excluding numerical noise from the results. Time for ΔSCF includes those of both energy calculations; it is to be noted that Gaussian 09 on GNU/Linux outputs calculation times converted as per single CPU core, and these were timings we used.

Results and discussion

General considerations

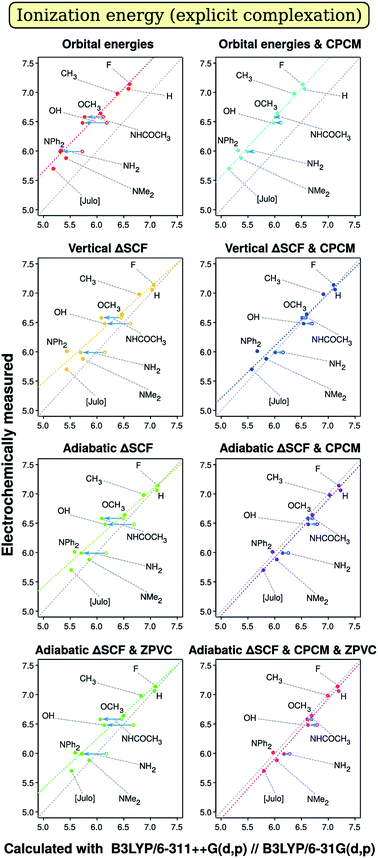
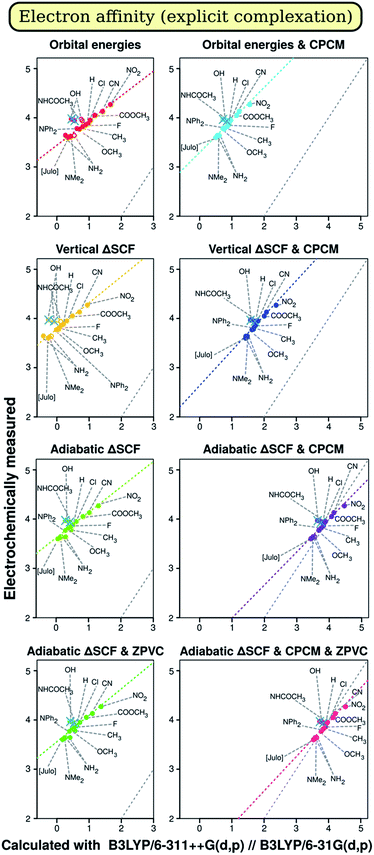
Analysis of results should probably start with evaluation of the primary results, of those we obtain from quantum chemical calculation. We start with discussion of correlation graphs themselves. Some characteristic examples are shown on Fig. 1 and 2. We would not consider slope, intercept or R² here, as these are subject to further discussion of factor analysis results. Rather, we will focus on specific characteristics seen only on the plots themselves. Points corresponding to different compounds are marked with the short formula of their p-substituent R in Chart 1.

Fig. 1 A representative sample of correlation between electrochemically measured peak potentials and calculated ionization energy when including and when not including explicit complexation into the model. Points without considering explicit complexation are shown without fill and with arrows pointing to the ‘corrected’ point. Black dotted line is the diagonal, which represents exact correspondence between the experiment and the calculation. Similar plots for different functional/basis set combinations are available from authors upon request.

Fig. 2 A representative sample of correlation of electrochemically measured peak potentials and calculated electron affinity when including and not including explicit complexation into the model. Points without considering explicit complexation are shown without fill. Points not used in further analysis are crossed out. Black dotted line is the diagonal, which represents exact correspondence between the experiment and the calculation. Similar plots for different functional/basis set combinations are available from authors upon request. Notice the gradual approach of points towards the diagonal when changing computation methodology.

On both Fig. 1 and 2, we see some points that can be described as outliers (hollow circles), not really from statistical point of view, but rather due to their nature. Most noticeable is that the phenolic compound (denoted by OH) is outlier on both plots. Fig. 1 tells us that OH- and NH₂-substituted compounds have too small measured ionization energy to match the regression-predicted values. Fig. 2 boasts that phenolic and acetanilidic (R = NHCOCH₃) species have too large apparent reduction potential. As all these compounds contain hydrogen atoms bound to significantly more electronegative atoms, it would be straightforward to explain these deviations by different electrochemical properties of H-bonded complexes of these compounds either with each other or with a molecule, or molecules, of weakly protophilic solvent acetonitrile (pK^⊕_BH = −10.1 in water⁶⁷). Small concentration of species (of order 10⁻⁴ M) and rather high polarity of the solvent presumably favors the interaction with solvent molecules over their mutual interaction, so it is not considered, though can in principle be stronger. Obviously, in the case of H bonding we should observe smaller ionization energies, as when hydrogen atom (the ‘proton’) transfers towards the solvent molecule it leaves its ‘parent’ one with surplus partial negative charge, which facilitates ionization process.

On the other hand, it also should hamper electron capture (decreasing A) – what we are not recognizing on Fig. 2. It is quite peculiar therefore why compounds with R = OH and R = NHCOCH₃ have higher A relative to what is expected by calculation. Moreover, BI-NHCOCH₃ point is not seen to be shifted from the ‘right’ regression place on Fig. 1, what should take place if our explanation is right. Then it should even do so more than the point of R = NH₂, because amidic proton is by far more acidic than aminic one. So, there is noticeable evidence that the effect of ‘outliers’ can be of random origin.

To affirm this assumption, we tried to model complexation explicitly by optimizing structures that include one acetonitrile molecule oriented with its N atom towards the acidic proton of three compounds mentioned. The results improved notably for modeling oxidation of BI–OH and BI–NH₂ derivatives in vacuo, what can be seen on Fig. 1; in solution, there is no notable change in results. This suggests that the weak hydrogen bon ding in our case is almost completely electrostatic and therefore can be described by the continuum solvation model. On the other hand, introducing just a single solvent molecule [presumably] in the right place heals most of error from not taking the solvent into account. However, for description of reduction (Fig. 2), such improvement (being very marginal) is discovered only for aniline derivative and only when solvent is included in the model. Even more, there is also worsening of description of phenol and acetanilide, albeit to hardly noticeable amount, so that these points remain distinct outliers. Presumably, the reduction is coupled with deprotonation of molecule with reduction of the proton to hydrogen atom, probably accompanied by formation of covalent bond with electrode surface or by reduction of surface carbonyl oxygen to hydroxyl one. As these processes might have considerable activation energy, it may produce additional overpotential, so the reduction peak will shift more away from equilibrium one than for other compounds. Unfortunately, treating these interactions, although possible, is not straightforward enough to be included in our study. Also, there was no positive changes when introducing Counterpoise correction^68,69 for complexes. Thus we simply omit data points for compounds with R = OH, NHCOCH₃ and NH₂ from correlation data on electron affinity.

We have also checked whether it is important to force non-equilibrium solvation for vertical energy difference calculations. Z test was applied for this purpose, and almost for all data sets difference in coefficients of regression line was deemed insignificant. The only exception is intercept for modeling electron affinity, being large in absolute size. Therefore, solvent orientational relaxation as modeled by CPCM is mainly governed by the change of species charge in the series of structurally similar compounds. This is similar to the classical Born model. Notice that despite apparent differences between coefficients obtained when using and when not using non-equilibrium solvation, these differences appear to be smaller than RMSDs of corresponding coefficients. Hence, there should be no much harm if one does not account for these non-equilibrium processes in their calculation. Contrarily, for absolute values, significant difference was noted by other researchers.⁴

Ionization energy

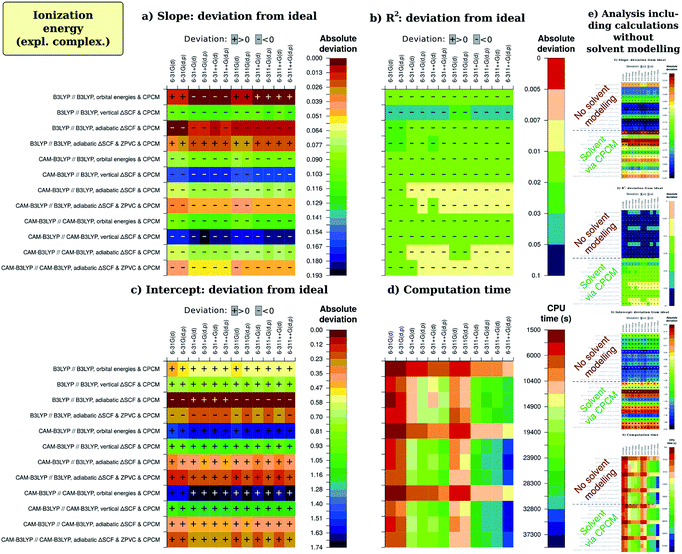
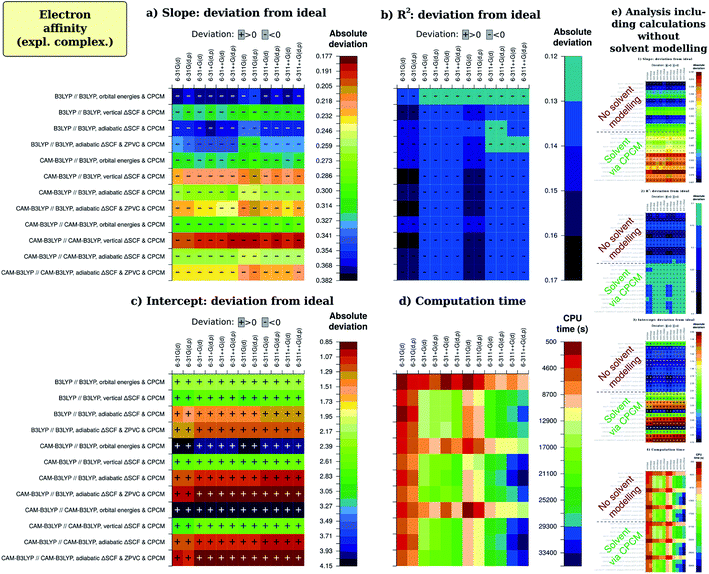
Now, we continue with description of the results from factor analysis. To not make our discussion too entangled with statistics, we will not discuss Daniel's normal distribution plots but rather present regression and calculation time results in an easily perceptible form. All figures of merit that were recalculated with omission of unimportant (presumably random) effects of various factors were then arranged in tables. Next, each cell was given a color depending on their vicinity to the ideal value, which is unity for slope and R², zero for intercept and calculation time. The sign of deviation from this ideal is also written to cells. The coloring was chosen as on physiogeographical maps, with reddish brown for the mountain ridges (small deviation) and dark blue for the depths of the ocean (large deviation). The color stepping was selected to be by the standard deviation for regression coefficients (slope and intercept), which was also recalculated after removal of insignificant effects; for R², we used non-uniformly dropping quality scale, adjusted for each particular case to facilitate descriptivity. For calculation time, the split was done arbitrarily. Numerical values that resulted in the analysis are available in ESI 2.†

The picture for ionization energy is available in the form of colored tables on Fig. 3. The most obvious result is that accounting for general solvent effects in the calculation model is essential to obtain qualitative result, and this holds for all combinations of other parameters for all regression-related figures of merit. At the same time, solvent modelling with CPCM is computationally so cheap that almost no difference is noticeable between average computation time with and without using this model. Therefore, one should always use solvent modelling in their calculations. This was not a surprise, as many previous studies^1,3,4,41,42 confirmed significance of accounting for the solvent; however, possibly due to fears of computational costs, some^2,33,34 still avoid solvent modelling. Our main goal to include this factor in present study was to simultaneously confirm both essentiality and resource-effectivity of including the solvent in computational model.

Fig. 3 Results of factor analysis for ionization energy (including explicit complexation). Sign of deviation is indicated in each cell of the tables. Cell coloring represents the quality of results, with reddish brown corresponding to high precision mountains and dark blue – to deep discord seas. On slices (a) to (d) all studied factors are displayed but the most significant one (the inclusion of solvent in the computational model), effect of which can be overviewed on slice (e) as designed for better comprehension.

In fact, as the impact of solvent factor is by much the greatest, it can unreasonably distract reader's attention from the remaining factors. To ensure better comprehension, we have excluded the factor of solvent from the main part of Fig. 3 and provided an inset-like slice (e) for overview, as well as in ESI 1D.† The data on main slices (a)–(d) was then recalculated without the definitely erroneous data obtained without solvent modelling, but virtually no difference in results was observed. This assures us of robustness of the chosen factorial analysis methodology which compensates the possible bias in main factor by recognizing significant interactions (see ESI 1†).

There are, however, other factors of noticeable importance, as determined by factor analysis (and also supported by ANOVA). The next most striking result is that the best predictions of regression slope are by KS HOMO orbital energy for B3LYP calculations on B3LYP-optimized geometry. This seemingly underlines the practical applicability of Janak's and IP theorems. The second best result for slope and the best result all in all is from adiabatic ΔSCF predicted by the same theory level, and this approach is also the best for CAM-B3LYP calculations with different geometries. Success of the adiabatic ΔSCF approach conforms to predictions of electrochemical Marcus–Hush–Chidsey theory^49–53,70 This theory states that the electron transfer at the electrode takes place after the reagent specie assumes geometry of the corresponding electrode reaction product during the thermal motion. The thermal energy acquired from the bath is called reorganization energy λ and corresponds to difference between I_a and I_v, so that only adiabatic ionization potential includes λ and therefore corresponds to the results of electrochemical study.

Interestingly though, both JT and IPT speak about correspondence between the vertical ionization energies and KS orbital levels but we have evidence in this study that orbital energies approach can work as well for describing adiabatic ionization energies from CV experiment. For absolute values, such a good correspondence could be only due to some cancellation of errors due to aforementioned geometry reorganization. The λ can vary strongly from electron-rich to electron-poor compounds, as we found for our molecules, as well as for some other series studied by Vannucci et al.³⁹ Therefore, the slope a of I_a = aI_v + b dependence should be less than unity. This is shown on Fig. 4 as the green line below the blue diagonal (the I_v = f (I_v) case). If we subsequently approximate I_v with minus the energy of Kohn–Sham HOMO, −ε_KS–HOMO, the values decrease because so-called electron-self-interaction error (SIE) increase the energy of neutral species more than that of cations. The error should also be greater in the case of more compact orbitals,^19,12 as in electron-poor molecules. This shifts especially the top part of the regression line to left from the “ideal” case (blue line on Fig. 4) along the axis of calculated values, increasing the slope c of correlation −ε_KS–HOMO = cI_v + d over unity (line 3 on Fig. 4). Such a slope is quite common, both for correlations of (minus) the KS HOMO energy with I_v computed with^1,25,71 and with experimental I_v.^5,25,72 Then the slope s of the actual relation studied, −ε_KS–HOMO = sI_a + i, which is the combination of both previously mentioned dependencies, is restored to be close to unity (line 1 on Fig. 4), just what is observed on Fig. 3(a). So, the apparent success of orbital energies approach in our case seems to be explained. Of course, this restoration of unity slope does not^2,51 appear for any series of molecules, because the ‘remedy’ is in fact fortuitous error cancellation. Therefore, it would be injudicious to recommend for screening purposes orbital energy approach with B3LYP//B3LYP & CPCM model, despite its apparent success. Presumably, this is due to different pattern in reorganization energies. For CAM-B3LYP, the unity-slope-restoring error cancellation does not occur as completely as for B3LYP. The reason is that CAM-B3LYP suffers less from self-interaction error, what results in smaller −ε shift (in terms of Fig. 4) because compact orbitals in electron-poor molecules are more prone to SIE.^19,12 Hence, the slope of −ε_KS–HOMO = sI_a + i dependence becomes less positive, so further from unity.

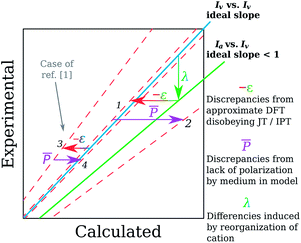Fig. 4 Qualitative reasoning to explain apparent quality of results obtained as minus the orbital energies. Blue diagonal represents ideal case of predicting vertical ionization energies, while the green line is common dependence of adiabatic I on vertical ones. This is the case when CV measurement results are correlated with vertical IP calculations (λ shift). Orbital energies approximation introduces a bias (−ε shift) almost recovering the one-to-one correspondence (line 1). However, if solvent effects are not accounted for (P̄ shift), regression line drops to position 2. If experimental values are from vertical ionization (as in ref. 1), P̄ effect acts favorably instead, restoring regression line from position 3 to 4.

As one can see from Fig. 3(a), for B3LYP//B3LYP in vacuo the orbital energy approach also performs quite acceptably. Previously, Schwenn et al.¹ observed even more prominent effect for correlations of −ε_KS–HOMO with vertical ionization energy from thin films into the vacuum. In their case, self-interaction error approximately counterbalanced that due to not including polarizing effect of the medium into the model. The polarization effect is usually higher for electron-deficient compounds,⁷³ what is observed also in the present study. Therefore, slope of experimental I_v vs. −ε_KS–HOMO regression line will go down, resulting sometimes¹ in error cancellation (P̄ vector pointing towards the line 4 on Fig. 4). In our case of modeling adiabatic transitions, this is only disturbing (line 2 on Fig. 4), as the error cancellation is reached by other means.

The next interesting issue is better performance of adiabatic energy difference method for B3LYP than for CAM-B3LYP, even for the same geometry. This is evident mostly for the slope, less notably for intercept and not observed in the case of R². The last one describes unsystematic deviations from the experiment, indirectly – from the absolute value. The slope characterizes systematic deviations, while the intercept has well-defined meaning only in the case of good slope – then it indicates the ability to predict absolute values. Hence, CAM-B3LYP can be good at predicting absolute values (as also found in other studies)²¹ while experiencing some systematic bias. Possibly this is the intrinsic size inconsistency of both global and range-separated hybrid functionals due to their approximate nature. It was in fact observed previously that for systems with relatively more extended delocalization there is need for slower decay of DFT-like exchange contribution with inter-electron distance.^8,71 Other groups also report that CAM-B3LYP has non-optimal range-separation parameters for ionization description.²⁵ There are multiple reparametrizations of this functional,^74,75 and possibly our next studies will consider them.

Another factor to discuss is the zero-point vibrational energy correction (ZPVC). It has the effect of making not-so-good results better but somewhat decreasing quality of the ‘best’ results (especially results of B3LYP//B3LYP with adiabatic ΔSCF & CPCM). In our opinion, the most reliable conclusion is that usage of this correction is fully justified, but the model chemistry we selected for optimizing the geometries (B3LYP/6-31G(d,p)) is too simplified to correctly describe thermochemistry, in particular the ZPVC.

Next, we should consider the basis-set-induced variations in figures of merit. The most noticeable and systematic effect is that by adding the diffuse functions (+ and ++). Obviously, it strengthens quality of the best slopes and weakens that of worse ones, ‘emphasizing’ the methodology differences. In the case of intercept, the effect of BS extension is not so uniform, but the best results are generally improved upon the extension. The square of correlation coefficient is most frequently improved upon extending the basis set, especially if the quality was already praiseworthy. It should also be mentioned that the overall quality of results is also raised upon adding extra valence functions to the basis set, albeit to notably smaller extent. The last observation is notable because computational cost of adding valence functions is significantly less than that required by introducing diffuse functions; however, we will look at the computation time in separate paragraph below.

The ‘emphasizing’ effect on slope from adding diffuse functions stems from the fact that ‘the best’ slopes are the only ones which exhibit a slight positive deviation from unity, whereas in the other cases this deviation is negative. The effect of adding diffuse functions is, therefore, always to lower slope of regression line. Adding diffuse functions to hydrogen atoms does not change slope quality significantly; more interestingly, polarization functions on hydrogen atoms tend also to lower the slope to greater or smaller extent, and the same is true for extra valence functions (triple-zeta instead of double-zeta). Thus we can generalize our observation: extending basis set generally lowers the slope, but the only noteworthy effect is from adding diffuse functions to heavy (non-hydrogen) atoms. As the basis sets we studied are too far from complete basis set limit, we would not like to ascribe some effects to over-extended basis set. So, this effect can be caused either by too low ionization energy for electron-poor molecules or by too high ionization energy for electron-rich molecules when the basis is tight. The second alternative seems to be more plausible and especially complies with the effect of diffuse functions: when the basis set is too tight, the electron density is too confined and its decay – too fast, causing too high ionization energies especially for electron-rich structures which in reality have comparatively more diffuse electron density distribution.

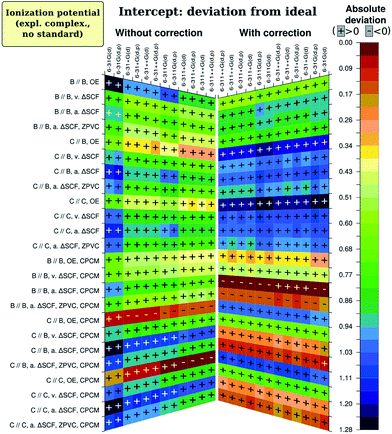
There is one specific factor for the intercept, namely correction of calculated absolute I and A by the I calculated for the standard redox couple with the same method (abbreviated here as CCRRCC – correspondingly-computed reference redox pair correction). To illustrate the significance of this correction, we present on Fig. 5 results for just the intercept obtained with correction just to the literature value of Fc/Fc⁺ pair potential of 5.24 eV in ACN.⁷⁶ As is evident, the results quality then becomes leveled among different combinations of parameters (and therefore worse for most reasonable cases). Moreover, consistency of impact by different factors is now lost among different figures of merit. This is in complete accord with studies by Roy et al.³⁵ and Konezny et al.³⁶ on transition metal complexes. Interestingly, without CCRRCC orbital energy approach again appears to perform well. Probably the explanation here is also similar to what was discussed for slope, and parallels can be drawn with the case of Schwenn et al.,¹ too.

Fig. 5 Results of factor analysis for ionization energy. Deviation of regression intercept from the ideal value of zero, with and without correction to calculated I of Fc/Fc⁺ standard redox couple. B and C stand for B3LYP and CAM-B3LYP, OE for orbital energies methodology, v. and a. for vertical and adiabatic, respectively.

Very important from the viewpoint of experimentalist as an end-user is how different parameters affect average computational time. Especially this is important if one needs to find a reasonable compound in a haystack of different structures, the usual task for experimentalists working in engineering. Therefore, not high-precision calculations are needed for screening purposes but those trustable enough to enable selection of structures for the following, more precise study. Preferably, such calculations should not involve much user action. However, to facilitate such a ‘black-box-performance’ the methodology should also be robust enough to not require frequent user intervention. This is the reason why at the beginning of this section we chose to discuss rather the precision of different computational methods and not the swiftness of them.

The time is, nevertheless, greatly important, so we should now discuss how different computational parameters affect computation time (Fig. 3(d)). The most obvious effect is from extending the basis set, though mostly this does not lead to any significant improvement in the slope, intercept or R². Overall, the least expensive extension of basis set is that by adding valence functions. Then, it is quite significant that adding CPCM to the model, which results in very prominent increase of quality, does not lead to any significant increase in computation time. What relates to functional effect, B3LYP is found to be a bit less CPU-time-demanding than CAM-B3LYP both for ΔSCF computations and for single-point energy calculations leading to orbital energies. From didactic point of view, it is interesting to note that after removing insignificant effects computation times with and without ZPVC are slightly different. The reason is similarity in computation time for both vertical and adiabatic energy difference computations, with and without ZPVC. This causes some counter-intuitive perturbations in factor analysis which are explained in ESI 1C.† The same is observed for combination of tight basis set, CAM-B3LYP functional and CPCM, where adding polarization functions on hydrogen atoms apparently promotes faster convergence, what is not observed in uncorrected results. Hence, small differences are still disputable even after removing insignificant effects.

To make conclusions for calculations of electrochemical ionization energy, we should define priorities. For computational screening purposes, correct trend has more importance than accurate prediction of specific values; therefore slightly better regression slope is preferred over slightly higher R². Hence, we suggest to use adiabatic energy difference (ΔSCF) method together with CPCM, reference redox pair correction and B3LYP/6-311G(d) functional and basis set combination, using neutral and ionic form geometries optimized with B3LYP/6-31G(d,p). Usage of basis set 6-31+G(d) instead of 6-311G(d) can lead to a further improvement in predicted values, but notably increases demands for CPU time. Without ZPVC which is apparently spoiling results if calculated at B3LYP/6-31G(d,p), intercept deviation from zero, as well as mean absolute deviation (not shown on graphs), is of the same order as the uncertainty of experimental results.^36,77 As the slope is well-predicted, we assume good prediction of absolute values of I_a.

Electron affinity

The analysis for electron affinity is available on Fig. 6. Just like in the case of ionization energy, most influential factor is the presence of solvent in computational model, having by no doubts largest positive effect on results. The best results for electron affinity (A) are almost unequivocally provided by the CAM-B3LYP functional, consistently with the improved long-range exchange character of this functional. As the ‘extra’ electron lies in the very outer region of negatively charged molecule, there should be more need for correct description of long-range electron interactions in the molecule. This was one of main goals when range-separated hybrids as CAM-B3LYP were developed,^57,78 and therefore description of the reality should in total be better for CAM-B3LYP than for B3LYP. We do observe this for both regression coefficients – slope and intercept –, while for R² CAM-B3LYP results are not much lower than that of B3LYP. Only for the intercept the best methodology is adiabatic ΔSCF with CPCM, what is suggested by the Marcus–Hush–Chidsey theory.^49–54 In conformity, adiabatic ΔSCF shows good results also for the slope and results for R² are not much worse with this methodology than with orbital energy approach. Notably, for all figures of merit results are not very impressive, and, analogically as with I, ZPVC is propitious in these cases. Optimizing the geometry with the same CAM-B3LYP rather than with B3LYP shows slightly better quality of slope, but slightly worse quality of R², not affecting intercept at all. Just as for ionization energy, when applying CCRRCC the best results for intercept become better while the worst – even worse; therefore, the correction is again advantageous. The trends in results persist, however. Only results by orbital energy approach worsen greatly when the correction is applied, probably due to the same reasons as for ionization energy.

Fig. 6 Results of factor analysis for electron affinity. Sign of deviation is indicated in each cell of the tables. Cell coloring represents the quality of results, with reddish brown corresponding to high precision mountains and dark blue – to deep discord seas. On slices (a) to (d) all studied factors are displayed but the most significant one (the inclusion of solvent in the computational model), effect of which can be overviewed on slice (e) as designed for better comprehension.

In the case of electron affinity, sleazy nature of intercept as a figure of merit is very obvious, because – as can be seen on Fig. 2 and from data in ESI 2A† – mean absolute deviation (MAD) of results is quite low, in best cases even lower than that in the case of ionization energy. The data are not shown in article itself, because for screening means good prediction of trends has much more sense than good prediction of absolute values.

The extension of basis set brings notable advance in the quality of results; however, despite the common^{23,28,72,79,80} belief, addition of diffuse functions is not more essential than addition of extra valence ones. This is very prominent conclusion, as calculations with diffuse functions require much more CPU time than with triple-zeta basis sets, as seen also on Fig. 6(d). Redundancy of diffuse functions for cases when electron affinity A > 0 was already reported,⁷ as well as importance of additional valence functions;^6,58,72,87 another study (but for narrow class of oligothiophenes) reveal small difference between the impact of the two.⁸ In our case, augmenting the basis set with diffuse functions usually has positive effect for intercept and R², but also worsens the quality of slope. We would also like to note here that diffuse functions for some cases caused instability of wave function, as well as that non-normal distribution of model residuals was also observed only for calculations with diffuse functions in use. It is noteworthy that for mean absolute deviation diffuse functions seem to be essential to get it less than typical experimental error; thus diffuse functions can be fitted for particular compounds but do not allow modelling trends well. The only difference between diffuse and valence functions is that the first ones have especially low exponents, thus dying off much slower than the latter ones. It follows that these default exponents are the origin of the deteriorating effect. These exponents were once optimized for atoms and small molecules;^81,82 we, however, use them for medium-sized molecules with highly delocalized electron system. Especially supportive for this assumption is the fact that the lowest MAD was for less polar compounds located in the middle of series and in the group having two moderate acceptor groups. Hence, this is likely the reason of the amusing result that diffuse functions can in some senses worsen the quality of predicted trends of I and A. Polarization functions on hydrogen atoms, in their turn, have effect similar to that of diffuse functions, but very marginal in absolute value.

Considering time consumption, CAM-B3LYP calculations are somewhat slower than B3LYP-driven ones, but this difference is not significant. Except for naturally more pronounced resource consumption by the ΔSCF procedure, there are no other important effects on computation time.

Quite amusing are results for slope in the case of A: undoubtedly, results for vertical ΔSCF ‘in solution’ are better than for adiabatic one. This can be explained by – again – some fortuitous error annihilation. To not involve in details once more, we rather summarize our analysis. Not accounting for reorganization energy should increase the slope, while SIE differences for different compounds in the series will probably decrease it (many DFT studies^1,6,7,33,34 report slopes less than one). Therefore, partial cancellation occurs only for vertical energy difference and not for physically expected adiabatic one, confusingly leading to better performance of the first.

To sum up for electron affinity, the overall best method is adiabatic ΔSCF + CPCM, zero-point energy and reference redox pair corrections with CAM-B3LYP/6-311G(d) energy calculation model, with little difference between CAM-B3LYP/6-31G(d,p) and B3LYP/6-31G(d,p)-optimized geometries.

Conclusions

Our study considered various methodologies and parameters for predicting ionization energy I and electron affinity A of compounds that could find application in the field of organic electronics. Comparison of calculated results to electrochemically determined values through linear regression and factor analysis were used for this purpose. We have found that rather reliable estimate of I can be obtained from adiabatic energy difference (ΔSCF) calculation with B3LYP functional and 6-311G(d) basis set, necessarily accounting for the solvent effects by using CPCM model. The conclusions about A estimation are the same, except for that CAM-B3LYP functional is found to be more appropriate. The success of adiabatic ΔSCF is consistent with the Marcus–Hush–Chidsey model for electron transfer mechanism. Orbital energy approach is found to be fairly acceptable for calculating ionization energies, just like vertical ΔSCF for electron affinities, but these are probably series-specific effects. Making initial exponents of basis functions more diffuse brings in some improvement in calculations of ionization energy only, but also significantly increases computation time; thus we suggest using 6-31+G(d) basis set instead of 6-311G(d) only if there are enough computational resources available. Contrary to popular belief, but in accord with some literature, adding diffuse functions does not improve the overall quality of predicted electron affinity. There was no significant effect from polarization functions on hydrogen atoms in basis set. We have also found that results for geometries optimized either with CAM-B3LYP/6-31G(d,p) or with B3LYP/6-31G(d,p) are only marginally different. Considering weak protophilicity of acetonitrile and explicitly including a molecule of it in calculations, as well as Counterpoise correction, appears to be redundant for ionization energy prediction. For calculations of electron affinity, such direct modelling of H bonding is found to disastrously increase errors. The possible reason is specific features in experimental data, caused by coupling of the reduction to hydrogen atom transfer to some surface oxygen groups of glassy carbon electrode. Reference redox pair correction is important for both I and A, whereas zero-point energy correction improves only results for A. Finally, the best methods described are able to produce absolute values of both I_a and A_a reasonably enough for structure screening purpose. This basically allows substituting the practical investigation with a less tedious and costly quantum chemical computation.

Acknowledgements

This contribution is devoted to now deceased Dr habil. phys. Inta Muzikante who worked in the field of organic electronics since its very infancy and inspired our work in present direction. We express our gratitude to Pauls Janis Pastors for synthesis of the compounds studied. Also, we are very thankful to the National Research Program of Latvia in Materials Science ‘MultIfunctional Materials and composItes, photonicS and nanotechnology (IMIS2)’ for financial support.

Notes and references

1. P. E. Schwenn, P. L. Burn and B. J. Powell, Org. Electron., 2011, 12, 394–403.
2. A. V. Subhas, J. Whealdon and J. Schrier, Comput. Theor. Chem., 2011, 966, 70–74.
3. P. K. Nayak and N. Periasamy, Org. Electron., 2009, 10, 1396–1400.
4. T. B. de Queiroz and S. Kümmel, J. Chem. Phys., 2015, 143, 034101.
5. G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561.
6. L. Longo, C. Carbonera, A. Pellegrino, N. Perin, G. Schimperna, A. Tacca and R. Po, Sol. Energy Mater. Sol. Cells, 2012, 97, 139–149.
7. M. Meunier, N. Quirke and D. Binesti, Mol. Simul., 1999, 23, 109–125.
8. H. Sun and J. Autschbach, J. Chem. Theory Comput., 2014, 10, 1035–1047.
9. S. Köber, M. Salvador and K. Meerholz, Adv. Mater., 2011, 23, 4725–4763.
10. M. Kuik, G. A. H. Wetzelaer, H. T. Nicolai, N. I. Craciun, D. M. De Leeuw and P. W. M. Blom, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 26, 512–531.
11. Z. Gong and J. B. Lagowski, Mol. Simul., 2009, 35, 737–747.
12. N. Dori, M. Menon, L. Kilian, M. Sokolowski, L. Kronik and E. Umbach, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–6.
13. S. U. Lee and Y.-K. Han, J. Mol. Struct.: THEOCHEM, 2004, 672, 231–234.
14. J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168.
15. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694.
16. M. Levy, J. P. Perdew and V. Sahni, Phys. Rev. A, 1984, 30, 2745–2748.
17. C. O. Almbladh and U. Von Barth, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3231–3244.
18. J. P. Perdew and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16021–16028.
19. L. Kronik and S. Kümmel, in Topics in Current Chemistry, ed. C. Di Valentin, S. Botti and M. Cococcioni, Springer, Heidelberg, 2014, vol. 347, pp. 137–191.
20. D. Bégué, J. Sotiropoulos, C. Pouchan and D. Y. Zhang, Can. J. Chem., 2006, 84, 5–9.
21. A. Alparone, Monatshefte für Chemie - Chemical Monthly, 2012, 143, 513–517.
22. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2005, 122, 1–8.
23. H. Chermette, S. Joantéguy and G. Pfister-Guillouzo, in Recent Advances in Density Functional Methods, eds. V. Barone, A. Bencini and P. Fantucci, World Scientific, Singapore, 2002, pp. 91–105.
24. B. Hajgató, D. Szieberth, P. Geerlings, F. De Proft and M. S. Deleuze, J. Chem. Phys., 2009, 131, 084308.
25. S. McKechnie, G. H. Booth, A. J. Cohen and J. M. Cole, J. Chem. Phys., 2015, 142, 194114.
26. L. Zhang, Y. Pan and F. Qi, J. Theor. Comput. Chem., 2009, 8, 1103–1115.
27. S. A. Betterton, A. S. Berka and P. E. Fleming, J. Theor. Comput. Chem., 2010, 9, 189–200.
28. J. Garza, C. A. Fahlstrom, R. Vargas, J. A. Nichols and D. A. Dixon, in Reviews of Modern Quantum Chemistry, World Scientific, Singapore, 2002, pp. 1508–1536.
29. B. Kovač, I. Novak, O. S. Abdel-Rahman and R. F. Winter, J. Organomet. Chem., 2013, 727, 64–67.
30. K. Tang, H.-T. Sun, Z.-Y. Zhou and Z.-Z. Wang, J. Theor. Comput. Chem., 2009, 8, 187–201.
31. N. M. Boffi, M. Jain and A. Natan, J. Chem. Phys., 2016, 144, 084104.
32. G. I. Csonka, A. Ruzsinszky and J. P. Perdew, J. Phys. Chem. A, 2005, 109, 6779–6789.
33. Z.-M. Xue and C.-H. Chen, Int. J. Quantum Chem., 2007, 107, 637–646.
34. T. J. Muller, J. Conradie and E. Erasmus, Polyhedron, 2012, 33, 257–266.
35. L. E. Roy, E. Jakubikova, M. G. Guthrie and E. R. Batista, J. Phys. Chem. A, 2009, 113, 6745–6750.
36. S. J. Konezny, M. D. Doherty, O. R. Luca, R. H. Crabtree, G. L. Soloveichik and V. S. Batista, J. Phys. Chem. C, 2012, 116, 6349–6356.
37. J.-L. Bredas, Mater. Horiz., 2014, 1, 17–19.
38. B. W. D'Andrade, S. Datta, S. R. Forrest, P. I. Djurovich, E. Polikarpov and M. E. Thompson, Org. Electron., 2005, 6, 11–20.
39. A. K. Vannucci, R. A. Snyder, N. E. Gruhn, D. L. Lichtenberger and J. H. Enemark, Inorg. Chem., 2009, 48, 8856–8862.
40. J. Lameira, I. G. Medeiros, M. Reis, A. S. Santos and C. N. Alves, Bioorg. Med. Chem., 2006, 14, 7105–7112.
41. L. Lu, M. Qiang, F. Li, H. Zhang and S. Zhang, Dyes Pigm., 2014, 103, 175–182.
42. E. A. Siliņš, Organic Molecular Crystals. Their Electronic States, Springer-Verlag, 1980.
43. M. Huzak, B. Hajgató and M. S. Deleuze, Chem. Phys., 2012, 406, 55–64.
44. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09 (Rev. D.01), Gaussian, Inc., Wallingford, CT, 2009.
45. R. Dennington, T. Keith and J. Millam, Gaussview 5, Semichem, Inc., Shawnee Mission, KS, 2009.
46. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
47. A. R. Allouche, J. Comput. Chem., 2011, 32, 174–182.
48. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
49. R. A. Marcus, J. Chem. Phys., 1956, 24, 966.
50. N. S. Hush, J. Chem. Phys., 1958, 28, 962.
51. N. S. Hush, Trans. Faraday Soc., 1961, 57, 557–580.
52. V. G. Levich and R. R. Dogonadze, Dokl. Akad. Nauk SSSR, 1959, 124, 123–126.
53. C. E. D. Chidsey, Science, 1991, 251, 919–922.
54. M. C. Henstridge, N. V. Rees and R. G. Compton, J. Electroanal. Chem., 2012, 687, 79–83.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
56. P. Stephens, F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
57. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
58. R. Stowasser and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 3414–3420.
59. M. Hutter and T. Clark, J. Am. Chem. Soc., 1996, 118, 7574–7577.
60. D. C. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real World Problems, Wiley-VCH, 2001.
61. J. Cioslowski, Quantum-Mechanical Prediction of Thermochemical Data, Kluwer Academic Publishers, Hingham, MA, 2001.
62. M. Swart, Inorg. Chim. Acta, 2007, 360, 179–189.
63. R. Prins, Mol. Phys., 1970, 19, 603–620.
64. O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2004, 120, 8364–8372.
65. C. Daniel, Technometrics, 1959, 1, 311–341.
66. R. Mead, S. G. Gilmour and A. Mead, Statistical Principles for the Design of Experiments: Applications to Real Experiments, Cambridge University Press, New York, 2012.
67. H. Maskill, The physical basis of organic chemistry, Oxford University Press, Oxford, 1985.
68. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
69. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024.
70. M. C. Henstridge, N. V. Rees and R. G. Compton, J. Electroanal. Chem., 2012, 687, 79–83.
71. T. Stein, J. Autschbach, N. Govind, L. Kronik and R. Baer, J. Phys. Chem. Lett., 2012, 3, 3740–3744.
72. C. G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195.
73. L. O. Van Dorn, S. C. Borowski and D. L. Lichtenberger, Inorg. Chim. Acta, 2015, 424, 316–321.
74. M. Seth and T. Ziegler, J. Chem. Theory Comput., 2012, 8, 901–907.
75. K. Okuno, Y. Shigeta, R. Kishi, H. Miyasaka and M. Nakano, J. Photochem. Photobiol., A, 2012, 235, 29–34.
76. S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966.
77. N. G. Tsierkezos and U. Ritter, J. Appl. Electrochem., 2010, 40, 409–417.
78. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433.
79. A. Canal Neto, E. P. Muniz, R. Centoducatte and F. E. Jorge, J. Mol. Struct. THEOCHEM, 2005, 718, 219–224.
80. G. W. Spitznagel, T. Clark, J. Chandrasekhar and P. V. R. Schleyer, J. Comput. Chem., 1982, 3, 363–371.
81. L. A. Curtiss, M. P. McGrath, J.-P. Blaudeau, N. E. Davis, R. C. Binning and L. Radom, J. Chem. Phys., 1995, 103, 6104.
82. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229.
83. R. Kar, J. W. Song and K. Hirao, J. Comput. Chem., 2013, 34, 958–964.
84. T. B. de Queiroz and S. Kümmel, J. Chem. Phys., 2014, 141, 084303.
85. T. Tsuneda, J.-W. Song, S. Suzuki and K. Hirao, J. Chem. Phys., 2010, 133, 174101.
86. M. M. Heaton and M. R. El-Talbi, J. Chem. Phys., 1986, 85, 7198.
87. J. Zevallos and A. Toro-Labbé, J. Chil. Chem. Soc., 2003, 48, 1–18.
88. J. Z. H. Zhang, in Theory and Application of Quantum Molecular Dynamics, World Scientific, Singapore, 1998, pp. 13–25.
89. K. Traskovskis, V. Kokars, A. Tokmakovs, I. Mihailovs, E. Nitiss, M. Petrova, S. Belyakov and M. Rutkis, J. Mater. Chem. C, 2016, 4, 5019–5030.
90. I. Muzikante, M. Rutkis, E. Fonavs, B. Stiller, D. Neher, V. Kampars and P. Pastors, Proc. SPIE, 2007, 6470, 647010.
91. M. Rutkis, E. Wistus and S. E. Lindquist, Proc. SPIE, 1997, 2968, 34–39.
92. K. Pudzs, A. Vembris, R. Grzibovskis, J. Latvels and E. Zarins, Mater. Chem. Phys., 2016, 173, 117–125.

---

Footnote

† Electronic supplementary information (ESI) available: Details of factor analysis, computational figures of merit and experimental data, as well as results of database search studies. See DOI: 10.1039/c6ra16456k

---