A PGSE NMR approach to the characterization of single and multi-site halogen-bonded adducts in solution†
Gianluca Ciancaleoni *a,
Alceo Macchionib,
Luca Rocchigianibc and
Cristiano Zuccacciab
*a,
Alceo Macchionib,
Luca Rocchigianibc and
Cristiano Zuccacciab
aDepartamento de Química, Universidade Federal de Santa Catarina, 88040-900 Florianópolis, SC, Brazil. E-mail: g.ciancaleoni@ufsc.br
bDipartimento di Chimica, Biologia e Biotecnologie, Universitá degli Studi di Perugia, Via Elce di Sotto 8, I-06123, Perugia, Italy
cSchool of Chemistry, University of East Anglia, Norwich, NR4 7TJ, UK
First published on 18th August 2016
Abstract
We demonstrate here that the Pulsed field Gradient Spin Echo (PGSE) NMR diffusion technique can be effectively used as a complementary tool for the characterization of mono- and multi-site intermolecular halogen bonding (XB) in solution. The main advantage of this technique is that it provides the possibility of unambiguously determining the stoichiometry of the supramolecular adduct, information that is particularly important when multi-site molecular systems are studied. As an example, PGSE NMR measurements in chloroform indicate that hexamethylenetetramine (HMTA), a potentially four-site XB acceptor, actually exploits only two sites for the interaction with the XB donor N-bromosuccinimide (NBS), leaving the other two nitrogen sites unoccupied. Charge displacement calculations suggest that this is due also to the anti-cooperativity of the XB interaction between HMTA and NBS.
Introduction
Halogen bonding (XB),1 i.e. the non-covalent interaction between a halogen atom (XB donor) and a Lewis base (XB acceptor), mostly reveals its potential in solid state chemistry, being nowadays a powerful tool for the engineering of advanced materials2–4 and a relevant motif in the structure of biomolecules.5 XB has emerged also as an interesting topic for theoretical chemistry, which has tried to determine, not without controversy, the relative weights of charge transfer, electrostatic, dispersion, and polarization effects on XB.6 In the past few years, XB has started to find intriguing applications even in solution, mainly in catalysis7 and anion recognition.8 As a consequence, the characterization of the supramolecular structure of XB adducts in solution and the determination of the formation equilibrium constants have assumed a higher importance, also because the pattern of intermolecular interactions in solution could differ from that found in the solid state.Recently, it has been suggested9 that halogen bonding is not the only interaction that XB donors and acceptors can establish in solution, even when no other obvious interactions are possible, leading to adducts with different geometries but same stoichiometry. We recently demonstrated that 19F, 1H HOESY NMR, previously exploited with success to investigate ion pairing10 and frustrated Lewis pairs,11 can be also exploited to disclose the intermolecular structure of XB adducts.12 Furthermore, in combination with theoretical studies, it can be used to estimate the relative weights of XB and non-XB interactions.12
Concerning the equilibrium constants involved in the XB interactions, many useful titration techniques have been applied13,14 and the choice of the best one (UV-Vis, IR, NMR…) depends on the nature of the system under investigation. In all cases, the presence of more interactions is a potential complication, because the effect of each interaction on the experimental observable is, in principle, of a different magnitude, and their disentanglement is not easy. An additional layer of complexity arises when multi-site acceptors and donors are taken into account. In this case, the exact nuclearity of the adduct should be known a priori, since the fitting equation depends on the stoichiometry of the adduct (except when the different aggregation steps are clearly consecutive and with very different affinities14). Information about the latter can be derived from the Job's plot, but the general applicability of this technique is limited15 and its coupling with other methodologies is always desirable.
Here, we propose the diffusion Pulsed field Gradient Spin Echo (PGSE)16,17 NMR technique as a tool for the characterization of mono- and multi-site intermolecular halogen bonding systems, with the only requirement that NMR-active nuclei (preferably 1H, 19F or 31P) are present on at least one, but preferably both, of the components. To the best of our knowledge, such a technique has been applied only in a few recent cases, to support the formation of strong halogen-bonded adducts and to study the counterion influence on the same adduct.18,19
PGSE NMR allows information about the hydrodynamic volume (VH) of molecular species in solution to be determined.17 In the case of an aggregation process, the measured VH increases, allowing the estimation of the equilibrium constants (Ka) involved in the process.20 Remarkably, in the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts, the Ka can be evaluated by one single experiment,21 making it a useful tool for preliminary measurements.
1 adducts, the Ka can be evaluated by one single experiment,21 making it a useful tool for preliminary measurements.
Furthermore, since PGSE NMR is based exclusively on the VH, it takes into account all the possible aggregation processes, irrespectively from the supramolecular structure of the adduct. This offers the possibility to validate the data coming from titration techniques, where the effect of various interactions could be different on the chosen observable, with the general rule that Ka (PGSE) ≥ Ka (titration). In addition, PGSE NMR is very useful when investigating symmetric multi-site XB donors or acceptors, since it gives directly the average size of the adducts and allows the determination of the average number of units that are interacting.
To illustrate the potential of the PGSE approach, we considered here Lewis acids and bases shown in Scheme 1, which already proved to be XB acceptors/donors,22 having different XB strength and number of sites. In particular, 1,4-diazabicyclo[2.2.2]octane (DABCO) and hexamethylenetetramine (HMTA) are commonly used in the fabrication of crystalline materials assembled by XB.23
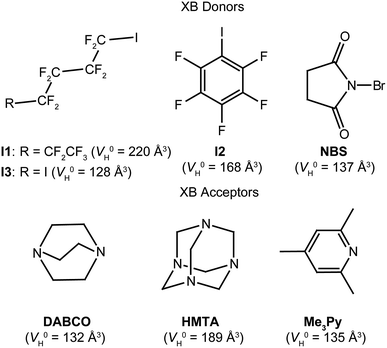 | ||
| Scheme 1 XB donors and acceptors considered in this work. In parenthesis, the respective values for the hydrodynamic volume of the single molecule (V0H) are reported. | ||
In both cases, the number of nitrogen atoms involved in XB interactions depends on the XB donor and the crystallization conditions. 2,4,6-Trimethylpyridine (Me3Py) is rarely used because the resulting XB adduct is very weak, so weak that other minor interactions, as lone pair/π, cannot be neglected.12 On the other hand, perfluorinated alkanes and benzenes (as perfluorohexyl-1-iodide, I1, pentafluoroiodobenzene, I2 and 2,4-diiodooctafluorobutane, I3) have always been used in XB studies,24 whereas N-bromosuccinimide (NBS) only recently revealed its potential as XB donor.22c
Results and discussion
The quantification of the hetero intermolecular aggregation by PGSE NMR asks for the preliminary evaluation of the hydrodynamic volume of the single molecule (V0H) and their tendency to undergo self-aggregation.For this reason, we initially performed PGSE NMR experiments on solutions of increasing concentration of the single components in toluene-d8 or chloroform-d, obtaining concentration-independent (within the experimental error of ±10%) values of V0H equal to 220, 168, 128, 137, 135, 132 and 189 Å3 for I1, I2, I3, NBS, Me3Py, DABCO and HMTA, respectively (Table 1 and Scheme 1).
| C | Dt | rH | VH |
|---|---|---|---|
| Me3Py | |||
| 3.1 | 16.1 | 3.18 | 135 |
| 38.0 | 15.9 | 3.20 | 137 |
| 175 | 16.2 | 3.18 | 135 |
| 385 | 16.1 | 3.18 | 135 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| DABCO | |||
| 46.0 | 16.9 | 3.17 | 133 |
| 262 | 17.2 | 3.14 | 130 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| I1 | |||
| 11.0 | 12.8 | 3.78 | 226 |
| 123 | 12.9 | 3.70 | 212 |
| 181 | 12.8 | 3.75 | 221 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| I2 | |||
| 17.4 | 15.3 | 3.37 | 160 |
| 471 | 14.5 | 3.47 | 175 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| I3 | |||
| 19.0 | 14.1 | 3.11 | 126 |
| 210.0 | 14.2 | 3.14 | 130 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| HMTA | |||
| 19.0 | 12.0 | 3.54 | 187 |
| 110 | 12.2 | 3.58 | 192 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| NBS | |||
| 5.4 | 14.3 | 3.20 | 137 |
| 61.0 | 14.3 | 3.20 | 137 |
The hydrodynamic volume of any adduct can be calculated by the sum of the V0H values of the constituents (eqn (1)), always under the spherical approximation.17
| VaggH(nD, mA) = n × V0H(D) + m × V0H(A) | (1) |
Me3Py/I1
As stated in the Introduction, substituted pyridines usually afford quite weak XB interactions. As a confirmation, for an equimolar mixture of Me3Py and I1, the experimental hydrodynamic volumes of the two components [VH(Me3Py) and VH(I1)] are practically identical to the corresponding values of V0H (Table 2). For this reason, only when a large excess of one of the components is used the measured VH of the other component is significantly altered (Table 2). In particular, I1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Me3Py molar ratios 1
Me3Py molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 or 1
3 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 are still not enough to have VH(I1) markedly different from its V0H, but using a molar ratio around to 1
14 are still not enough to have VH(I1) markedly different from its V0H, but using a molar ratio around to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 leads to an increase of VH(I1) from 220 to 340 Å3 [VaggH(Me3Py, I1) = 355 Å3]. Being Me3Py in large excess, VH(Me3Py) is clearly close to its V0H, since most of the molecules are not involved in the formation of aggregates. By applying eqn (S1) and (S2) (ESI†) to the experimental data with the lowest I1
200 leads to an increase of VH(I1) from 220 to 340 Å3 [VaggH(Me3Py, I1) = 355 Å3]. Being Me3Py in large excess, VH(Me3Py) is clearly close to its V0H, since most of the molecules are not involved in the formation of aggregates. By applying eqn (S1) and (S2) (ESI†) to the experimental data with the lowest I1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Me3Py molar ratio (Table 2), a value of Ka = 1.6 ± 0.5 M−1 is obtained.
Me3Py molar ratio (Table 2), a value of Ka = 1.6 ± 0.5 M−1 is obtained.
| C(Me3Py) | Dt(Me3Py) | Dt(I1) | VH(Me3Py) | VH(I1) |
|---|---|---|---|---|
| 24.9 | 16.1 | 12.9 | 146 | 219 |
| 64.1 | 16.1 | 12.8 | 144 | 221 |
| 346 | 16.1 | 12.4 | 146 | 232 |
| 4910 | 15.7 | 10.3 | 152 | 340 |
On the other hand, the 19F NMR titration method gives a value of Ka = 0.85 ± 0.01 M−1 (Fig. S1, ESI†).25 The titration allows to rapidly collect a large number of data, minimizing the experimental error. By the way, the formation constant obtained by diffusion measurements is double with respect to that obtained by the titration method, and this can be explained with the presence of two different 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts, as already evidenced by HOESY results:12 the observable of the titration (δF of the α fluorine atoms, –CF2I) is mainly influenced by the XB interaction established between the nitrogen of Me3Py and the iodine of I1, whereas the observable of the PGSE (VH) is influenced by all the possible interactions, including electrostatic H⋯F ones.12 Since the Ka estimated by the PGSE measurement is the sum of all the equilibrium constants active in solution, by coupling the two techniques we can conclude that the formation constant of non-XB adducts is approximately 0.75 M−1.
1 adducts, as already evidenced by HOESY results:12 the observable of the titration (δF of the α fluorine atoms, –CF2I) is mainly influenced by the XB interaction established between the nitrogen of Me3Py and the iodine of I1, whereas the observable of the PGSE (VH) is influenced by all the possible interactions, including electrostatic H⋯F ones.12 Since the Ka estimated by the PGSE measurement is the sum of all the equilibrium constants active in solution, by coupling the two techniques we can conclude that the formation constant of non-XB adducts is approximately 0.75 M−1.
Remarkably, also combining 19F, 1H HOESY results with DFT calculations, the XB adducts resulted to be predominant over the non-XB ones (XB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) non-XB = 78
non-XB = 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22);12 considering the approximations used in that paper, a reasonably good agreement is obtained.
22);12 considering the approximations used in that paper, a reasonably good agreement is obtained.
Interestingly, in the solid state only the XB can be detected,26 demonstrating that the supramolecular behavior of a pair in solution can differ from the structure of the same pair in the crystal.
DABCO/I1
In the case of multi-site XB acceptor, as DABCO is, the possibility of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adduct must be taken into account. The symmetry of DABCO and the kinetic lability of XB in solution hinder the possibility to use Overhauser-based experiments to determine how many nitrogen atoms are interacting with the Lewis acid. Also in this case, the investigation of non-stoichiometric mixtures is very informative. In fact, studying the pair DABCO/I1 in the presence of an excess of DABCO makes the concentration of the 1
2 adduct must be taken into account. The symmetry of DABCO and the kinetic lability of XB in solution hinder the possibility to use Overhauser-based experiments to determine how many nitrogen atoms are interacting with the Lewis acid. Also in this case, the investigation of non-stoichiometric mixtures is very informative. In fact, studying the pair DABCO/I1 in the presence of an excess of DABCO makes the concentration of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adduct negligible and the analysis of VH(I1) trends is related only to the formation of the 1
2 adduct negligible and the analysis of VH(I1) trends is related only to the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct (Ka1). On the other side, information about Ka2 can be derived using an excess of I1.
1 adduct (Ka1). On the other side, information about Ka2 can be derived using an excess of I1.
Maintaining C(I1) constant at 20 mM (solvent: toluene-d8) and increasing C(DABCO) from 3.6 to 108 mM, VH(I1) increases from 239 to 338 Å3, whereas VH(DABCO) decreases from 221 to 162 Å3. As stated before, the effect of aggregation is more visible on the least abundant species, consequently when C(DABCO) < C(I1), VH(I1) is just slightly larger than V0H(I1) and VH(DABCO) is markedly larger than V0H(DABCO). On the contrary, when C(DABCO) > C(I1), the situation is the opposite, with VH(DABCO) similar to V0H(DABCO) and VH(I1) markedly higher than V0H(I1). Indeed, when the concentration ratio I1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DABCO is 20
DABCO is 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108, V0H(I1) approaches VaggH(DABCO, I1), which is 352 Å3, evidencing an almost complete association of I1 under these conditions.
108, V0H(I1) approaches VaggH(DABCO, I1), which is 352 Å3, evidencing an almost complete association of I1 under these conditions.
Applying eqn (S1) and (S2) (ESI†) to this single data, Ka1 was estimated to be 34 ± 10 M−1, which corresponds to a free energy of association (ΔGa1) of −2.1 kcal mol−1. The 19F NMR titration gives Ka1 = 37.2 ± 0.4 M−1 (Fig. S2, ESI†), in agreement within the experimental errors.27 In line with these findings, 19F, 1H HOESY NMR data demonstrated that non-XB interactions can be neglected for this particular pair.12 Obviously, this does not mean that non-XB interactions are absent, but simply that their effects are completely hidden by the much more intense XB interaction, as in the PGSE as in the HOESY NMR experiments.
Successively, maintaining C(DABCO) at 7 mM and increasing C(I1) from 37 to 343 mM, VH(DABCO) increases from 250 to 517 Å3 (Table 3). In the last case, the hydrodynamic volume is much higher than V0H(DABCO), even higher than the volume of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct (352 Å3) and close to that of the 1
1 adduct (352 Å3) and close to that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adduct [VaggH(DABCO, 2I1) = 572 Å3].
2 adduct [VaggH(DABCO, 2I1) = 572 Å3].
| C(DABCO) | C(I1) | Dt(DABCO) | Dt(I1) | VH(DABCO) | VH(I1) |
|---|---|---|---|---|---|
| 3.6 | 20.0 | 12.8 | 12.3 | 221 | 239 |
| 17.6 | 20.0 | 13.7 | 11.9 | 194 | 250 |
| 108 | 20.0 | 15.1 | 10.3 | 162 | 328 |
| 7.0 | 37.0 | 12.0 | — | 250 | — |
| 7.0 | 85.0 | 10.5 | — | 326 | — |
| 7.0 | 216 | 9.2 | — | 426 | — |
| 7.0 | 343 | 8.5 | — | 517 | — |
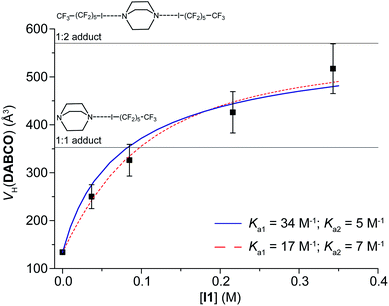
The data of VH(DABCO) as a function of C(I1) can be fitted considering two equilibria (Fig. 1 and eqn (S3) and (S4), ESI†),15 either imposing Ka1 = 34 M−1, as determined previously, to find the best value of Ka2 or optimizing both Ka1 and Ka2. In the former case, Ka2 = 5 ± 1 M−1 (ΔGa2 = −0.9 kcal mol−1); in the latter case, Ka1 = 17 ± 6 M−1 and Ka2 = 7 ± 2 M−1. The results of the two methodologies are qualitatively similar, even if the second one, having more degrees of freedom, better fits the experimental data (Fig. 1). In any case, Ka2 is lower than Ka1. This is likely due to the low entropy of the adduct formed by three molecules.
More importantly, the PGSE results offer an immediate and intuitive insight into the nuclearity of the adducts, at each concentration ratio (Fig. 1).
DABCO/I2
Three solutions of DABCO (8.8 mM) in toluene-d8 with increasing concentrations of I2 (44, 177 and 403 mM) have been studied (Table 4). Under these experimental conditions, VH(DABCO) spans from 194 to 352 Å3, reaching a value that is in between VaggH(DABCO, I2) and VaggH(DABCO, 2I2). The fitting of the data, using VaggH(DABCO, I2) = 303 Å3 and VaggH(DABCO, 2I2) = 471 Å3, leads to the values of 11.0 ± 0.2 and 2.1 ± 0.1 M−1 for Ka1 and Ka2, respectively (ΔGa1 = −1.5 kcal mol−1; ΔGa2 = −0.4 kcal mol−1, Fig. S3, ESI†).| C(DABCO) | C(I2) | Dt(DABCO) | VH(DABCO) |
|---|---|---|---|
| 8.8 | 44.0 | 13.6 | 194 |
| 8.8 | 177 | 11.2 | 286 |
| 8.8 | 403 | 10.1 | 352 |
HMTA/NBS
Crystallographic studies on the pairs HMTA/NIS (NIS = N-iodo-succinimide) and HMTA/NBS revealed many interesting properties of such systems.22c For example, in the former case all the four basic sites of HMTA interact with a molecule of NIS, while in the latter case only two nitrogen atoms interact with a molecule of NBS. Unfortunately, the solubility of the pair HMTA/NIS is not enough to allow a PGSE NMR study, but the pair HMTA/NBS is soluble enough in chloroform-d, even if very large excesses of one component cannot be explored.For HMTA/NBS, the calculated hydrodynamic volumes for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 adducts are 323, 457, 591 and 729 Å3, respectively.
4 adducts are 323, 457, 591 and 729 Å3, respectively.
Using chloroform-d as solvent and keeping C(NBS) fixed at 3.9 mM, three solutions with C(HMTA) = 12.1, 50 and 179 mM have been analyzed. VH(NBS) increases as C(HMTA) increases, going from 254 to 317 Å3 (Table 5), which is very close to VaggH(HMTA, NBS). Fitting the data, Ka1 results to be 161 ± 27 M−1 (ESI†).
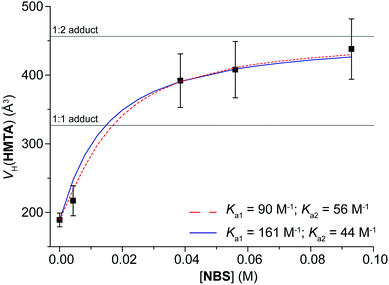
In a second set of experiments, to a solution of HMTA (C = 2.1 mM) in chloroform-d, NBS was added to reach C(NBS) = 4.3, 38.5, 56 and 93 mM (Table 5). As before, the hydrodynamic volume of the component in excess decreases as its concentration increases [VH(NBS) goes from 150 to 131 Å3], whereas the hydrodynamic volume of the other component (VH(HMTA)) increases from 217 to 438 Å3. Noteworthy, passing from C(NBS) = 56 to 93 mM, VH(HMTA) increases of only 30 Å3, which is within the experimental error of 10%. Unfortunately, a higher concentration of NBS is not possible because of the solubility limit of the mixture, but the final value of VH(HMTA) is very close to VaggH(HMTA, 2NBS). Such a value is the average of all the volumes of the species present in solution, but considering also that the trend of VH(HMTA) vs. C(NBS) shows a plateau in the correspondence of VaggH(HMTA, 2NBS) (Fig. 2), we can deduce that Ka3 and Ka4 are likely too small to be determined. Consequently, the experimental data can be fitted with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model, in agreement with the crystal structure of this pair.22c The absence of a plateau in this range of VHs (400–500 Å3) would have been an indication for the existence of larger adducts, as 1
2 model, in agreement with the crystal structure of this pair.22c The absence of a plateau in this range of VHs (400–500 Å3) would have been an indication for the existence of larger adducts, as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.
4.
This reveals another great advantage of the diffusion NMR technique: for multi-site systems, the maximum stoichiometry is not a hypothesis, but can be derived from the trend of VH with the concentration.
Fitting the experimental data with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model and fixing Ka1 = 161, the best value of Ka2 is 44 ± 12 M−1 (ΔGa2 = −2.2 kcal mol−1), whereas optimizing both the values the results are 90 ± 20 and 56 ± 8 M−1 for Ka1 and Ka2, respectively (ΔGa1 = −2.6 kcal mol−1; ΔGa2 = −2.4 kcal mol−1). Also in this case, both methodologies give similar results and, again, Ka1 is larger than Ka2.
2 model and fixing Ka1 = 161, the best value of Ka2 is 44 ± 12 M−1 (ΔGa2 = −2.2 kcal mol−1), whereas optimizing both the values the results are 90 ± 20 and 56 ± 8 M−1 for Ka1 and Ka2, respectively (ΔGa1 = −2.6 kcal mol−1; ΔGa2 = −2.4 kcal mol−1). Also in this case, both methodologies give similar results and, again, Ka1 is larger than Ka2.
In order to understand better why the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 adducts are not easily accessible in solution, DFT calculations have been performed on this system. Optimizing the structure of the 1
3 adducts are not easily accessible in solution, DFT calculations have been performed on this system. Optimizing the structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 adducts (level of theory M06-2X/def2-TZVP, as suggested by a recent, dedicated benchmark,28 see details in the Computational details), the N⋯Br distances results to be 2.533, 2.585 and 2.628 Å, respectively. The progressive lengthening of the N⋯Br distance already indicates that the interaction is weaker as the number of NBS molecules around the central HMTA increases.
3 adducts (level of theory M06-2X/def2-TZVP, as suggested by a recent, dedicated benchmark,28 see details in the Computational details), the N⋯Br distances results to be 2.533, 2.585 and 2.628 Å, respectively. The progressive lengthening of the N⋯Br distance already indicates that the interaction is weaker as the number of NBS molecules around the central HMTA increases.
Other information can be obtained with the Charge Displacement (CD) method,29 which already proved to be useful for the characterization of coordinative30 and non-covalent bonds,11,31 including halogen bonding.32 In particular, CD results demonstrated to be correlated linearly to the formation constants of chalcogen-bonded adducts.33
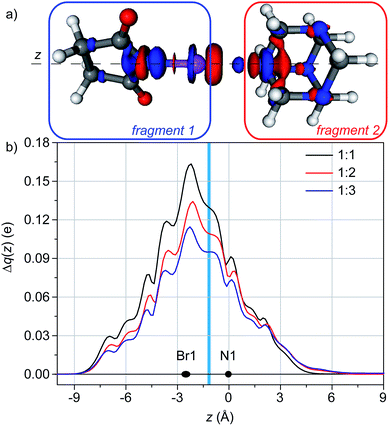
In the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts, the difference of electron density (Δρ) between the adduct and the separate fragments (HMTA and NBS) is shown in Fig. 3a. It clearly shows that the nitrogen of HMTA is in a region of electron depletion, whereas a region of electron accumulation is present between the nitrogen and the bromine. As expected, a charge transfer between the two molecules exists, going from the nitrogen to the bromine. The latter shows a polarization pattern (depletion in the direction of HMTA, accumulation on the other side) and a remarkable region of electron accumulation is on the nitrogen of the NBS. The backbone of the NBS show a small charge accumulation, whereas the nitrogen atoms of the HMTA not involved in the XB show a small charge depletion, indication that the charge flux involve the entire system.
1 adducts, the difference of electron density (Δρ) between the adduct and the separate fragments (HMTA and NBS) is shown in Fig. 3a. It clearly shows that the nitrogen of HMTA is in a region of electron depletion, whereas a region of electron accumulation is present between the nitrogen and the bromine. As expected, a charge transfer between the two molecules exists, going from the nitrogen to the bromine. The latter shows a polarization pattern (depletion in the direction of HMTA, accumulation on the other side) and a remarkable region of electron accumulation is on the nitrogen of the NBS. The backbone of the NBS show a small charge accumulation, whereas the nitrogen atoms of the HMTA not involved in the XB show a small charge depletion, indication that the charge flux involve the entire system.
Integrating Δρ along the axis containing the nitrogen of HMTA and the bromine of NBS (z), the charge transfer (CT) can be quantified as 0.130 e (Fig. 3b).
Applying the same method to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 adducts, the corresponding Δρ maps reveal a qualitative similarity with the one calculated for the 1
3 adducts, the corresponding Δρ maps reveal a qualitative similarity with the one calculated for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct (Fig. 4a and S5, ESI†). This is reasonable, since in all the cases the interaction is similar. From the quantitative point of view, the integration of the Δρ functions leads to CT values of 0.110 and 0.095 for the 1
1 adduct (Fig. 4a and S5, ESI†). This is reasonable, since in all the cases the interaction is similar. From the quantitative point of view, the integration of the Δρ functions leads to CT values of 0.110 and 0.095 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 adduct, respectively. The attenuation of the CT as the number of NBS molecules around the central HMTA increases gives a framework to explain the attenuation of the formation constants: the four nitrogen atoms on the HMTA are not mutually independent, and the donation of electronic density from one nitrogen atom to a Lewis acid makes the donation properties of the non-involved nitrogen atoms lower.
3 adduct, respectively. The attenuation of the CT as the number of NBS molecules around the central HMTA increases gives a framework to explain the attenuation of the formation constants: the four nitrogen atoms on the HMTA are not mutually independent, and the donation of electronic density from one nitrogen atom to a Lewis acid makes the donation properties of the non-involved nitrogen atoms lower.
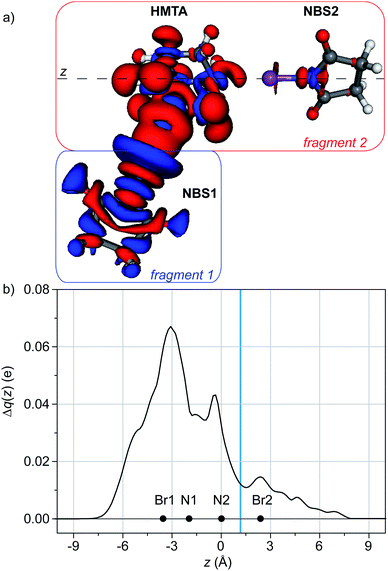
This effect can be quantified applying the CD on a different axis.34 If we consider the adduct between HMTA and two NBS moieties, we obviously have two interactions between two different nitrogen atoms of the HMTA and the two molecules of NBS. They can be labeled N1⋯NBS1 and N2⋯NBS2. Taking as fragments NBS1 and HMTA/NBS2 and integrating Δρ along the axis containing N2 and the bromine of NBS2 (Fig. 4), the effect of the establishment of N1⋯NBS1 on N2⋯NBS2 can be evaluated. In this case, the analysis of the Δρ shows that, upon the formation of N1⋯NBS1, the nitrogen of NBS2 is located in a region of electron density depletion. This indicates a charge transfer from NBS2 to HMTA, leading to a XB weakening. The integration along the axis containing N2 and Br2 confirms the direction of the flux and leads to a weakening of 0.011 e (Fig. 4b).
The electronic energies ΔE of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 adducts are −11.6, −20.5 and −28.0 kcal mol−1 (ESI†) with respect to the isolated components (see Table S1, ESI†). If we calculate ΔE/n, where n is the number of NBS involved in the adduct, it results −11.6, −10.2 and −9.3 kcal mol−1, respectively, again indicating that the interactions become weaker for larger aggregates (anti-cooperativity), in agreement with CD results. Therefore, the formation of adducts with higher stoichiometric ratios, as 1
3 adducts are −11.6, −20.5 and −28.0 kcal mol−1 (ESI†) with respect to the isolated components (see Table S1, ESI†). If we calculate ΔE/n, where n is the number of NBS involved in the adduct, it results −11.6, −10.2 and −9.3 kcal mol−1, respectively, again indicating that the interactions become weaker for larger aggregates (anti-cooperativity), in agreement with CD results. Therefore, the formation of adducts with higher stoichiometric ratios, as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, is made difficult not only for obvious entropic reasons (each additional moiety loses its translational degree of freedom, making the ΔG more positive), but also for enthalpic ones (the charge transfer becomes weaker as the number of units increases). Interestingly, in other cases the XB resulted to be cooperative in nature.35
4, is made difficult not only for obvious entropic reasons (each additional moiety loses its translational degree of freedom, making the ΔG more positive), but also for enthalpic ones (the charge transfer becomes weaker as the number of units increases). Interestingly, in other cases the XB resulted to be cooperative in nature.35
DABCO/I3
A very intriguing combination is when both the acceptor and the donor are multi-site, and, in principle, any n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m adduct can exist. The pair DABCO/I3, for example, is able to form infinite chains in the solid state.36 Also in this case the pair presents a low solubility, limiting the possibility to use non-stoichiometric solutions. Anyway, at least three different situations can be explored: an excess of DABCO, an excess of I3 and a substantial equivalence between the concentrations of the two components. In all the cases the solution is saturated, but both VH(DABCO) and VH(I3) are always much lower than 260 Å3, which is the value of VaggH(DABCO, I3) (Table 6). Consequently, even if the presence of higher adducts cannot be excluded, their concentration should be very low in all cases.
m adduct can exist. The pair DABCO/I3, for example, is able to form infinite chains in the solid state.36 Also in this case the pair presents a low solubility, limiting the possibility to use non-stoichiometric solutions. Anyway, at least three different situations can be explored: an excess of DABCO, an excess of I3 and a substantial equivalence between the concentrations of the two components. In all the cases the solution is saturated, but both VH(DABCO) and VH(I3) are always much lower than 260 Å3, which is the value of VaggH(DABCO, I3) (Table 6). Consequently, even if the presence of higher adducts cannot be excluded, their concentration should be very low in all cases.
Applying eqn (S1) and (S2) (ESI†) to the experiments where one component is in excess [C(DABCO) = 85.8 and C(I3) = 58 mM, Table 6], Ka1 results to be 6 ± 2 and 10 ± 3 M−1, respectively (ΔGa1 = −1.2 kcal mol−1).
Conclusions
Diffusion NMR demonstrated to afford valuable information on the stoichiometry and the strength of the interactions of halogen-bonded adducts.In particular, for the pair Me3Py/I1 the complementarity of the NMR titration and the PGSE method allowed the estimation of the formation constant of the adducts held together by interactions different from the XB (non-XB).
In the case of the ditopic halogen acceptor DABCO, both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adducts have been directly detected, either using aliphatic and aromatic perfluorinated XB donors (I1 and I2). The corresponding formation constants have been evaluated and the formation of the 1
2 adducts have been directly detected, either using aliphatic and aromatic perfluorinated XB donors (I1 and I2). The corresponding formation constants have been evaluated and the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adduct showed an equilibrium constant considerably lower than that of the 1
2 adduct showed an equilibrium constant considerably lower than that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct. For this system, the formation constant of the 1
1 adduct. For this system, the formation constant of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct evaluated by NMR titration is in agreement with that measured by PGSE, indication that non-XB adducts are negligible.
1 adduct evaluated by NMR titration is in agreement with that measured by PGSE, indication that non-XB adducts are negligible.
The case of HMTA is even more interesting, since it bears four symmetric nitrogen atoms and all of them potentially could establish an interaction with NBS. PGSE NMR data unequivocally demonstrate that only two nitrogen atoms are involved in the interaction with NBS and, again, the formation constant of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adduct resulted lower than that of the 1
2 adduct resulted lower than that of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct. DFT and charge displacement investigations demonstrated that each molecule of NBS that binds on a nitrogen atom of the HMTA reduces the electron-donating properties of the other nitrogen atoms (anti-cooperativity).
1 adduct. DFT and charge displacement investigations demonstrated that each molecule of NBS that binds on a nitrogen atom of the HMTA reduces the electron-donating properties of the other nitrogen atoms (anti-cooperativity).
Finally, PGSE NMR data demonstrated also that the interaction between DABCO and I3 is too weak in chloroform-d to produce aggregates larger than the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct, despite both the XB acceptor and donor possess two binding sites and despite the existence in the solid state of infinite chains.
1 adduct, despite both the XB acceptor and donor possess two binding sites and despite the existence in the solid state of infinite chains.
In conclusion, PGSE NMR can be surely considered a powerful technique, which gives information that could be a complement for the titration methods routinely used up to now. For this reason, an integrated multi-technique approach, which include titrations, diffusion and Overhauser NMR techniques (but also DFT calculations, when needed) is highly desirable, for a complete characterization of XB systems in solution.
Experimental section
All solvents and chemicals were purchased from Sigma-Aldrich and Cortecnet at the highest purity available and used as received. 1D and 2D NMR spectra were measured at 298 K on a Bruker DRX Avance 400 spectrometer equipped with a BBFO probe, on a Bruker Avance III HD 400 spectrometer equipped with a smartprobe. Referencing is relative to residual of undeuterated solvents (1H) and CCl3F (19F).PGSE NMR measurements
1H and 19F PGSE NMR measurements were performed by using the double-stimulated echo sequence with longitudinal eddy current delay37 at 298 K without spinning. The dependence of the resonance intensity (I) on a constant waiting time and on a varied gradient strength G is described by the following equation:
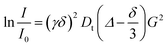 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (19F) and processed with a line broadening of 1.0. The semi-logarithmic plots of ln
000 (19F) and processed with a line broadening of 1.0. The semi-logarithmic plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (I/I0) versus G2 were fitted by using a standard linear regression algorithm, and a correlation factor better than 0.99 was always obtained. Different values of Δ, G, and number of transients were used for different samples.
(I/I0) versus G2 were fitted by using a standard linear regression algorithm, and a correlation factor better than 0.99 was always obtained. Different values of Δ, G, and number of transients were used for different samples.
The self-diffusion coefficient Dt, which is directly proportional to the slope m of the regression line obtained by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (I/I0) versus G2, was estimated by evaluating the proportionality constant for a sample of HDO (5%) in D2O [known diffusion coefficients in the range 274–318 K (ref. 38)] under the exact same conditions as the sample of interest. The solvent or TMS was taken as internal standard.
(I/I0) versus G2, was estimated by evaluating the proportionality constant for a sample of HDO (5%) in D2O [known diffusion coefficients in the range 274–318 K (ref. 38)] under the exact same conditions as the sample of interest. The solvent or TMS was taken as internal standard.
Computational details
All the optimizations and thermodynamic calculations were performed using the Gaussian 09 program,39 using density functional theory employing hybrid meta-generalized gradient approximation functional M06-2X40 and the triple-ζ def2-TZVP basis set. The solvent and its polarity has been modeled through the PCM procedure (chloroform).41 All the optimized adducts show only positive vibrations, except HMTA–3NBS, which showed three small uneliminable negative frequencies that could not be avoided during optimization. The negative vibrational modes were checked to make sure that they did not correspond to any motion along the halogen bond axes (bond formation or breaking). Rather, they refer to the rotation/vibration of the NBSs around the halogen bond axis.All the charge displacement29 calculations were carried out using density functional theory employing the same level of calculation used for optimizations. Such an approach relies on the integration along a given direction z (eqn (3)) of the difference of electronic density [Δρ(x, y, z)] between the adduct and its non-interacting fragments, frozen in the same positions they occupy in the adduct.
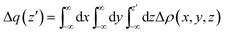 | (3) |
The value of Δq(z′) defines the amount of the electronic charge that, upon formation of the adduct, has moved across a plane perpendicular to the axis through the coordinate z′. At the boundary between the fragments (the point on the z axis at which equal-valued isodensity surfaces of the isolated fragments are tangent) the value of Δq is represented by CT.
The electronic density matrices have been manipulated through the suite of tools “Cubes”.42
Acknowledgements
Instituto de Física da Universidade Federal da Bahia is acknowledged for computational resources. C. Z. thanks the University of Perugia (Fondo Ricerca di Base 2014 D. D. n. 170, 23/12/2014) for financial support.References
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711 CrossRef CAS.
- (a) G. Berger, J. Soubhyea and F. Meyer, Polym. Chem., 2015, 6, 3559–3580 RSC; (b) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118 CrossRef CAS PubMed; (c) P. A. Gale and J. W. Steed, Supramolecular Chemistry: from molecules to nanomaterials, John Wiley & Sons Ltd, New York, 1st edn, 2012 Search PubMed; (d) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478 CrossRef CAS PubMed.
- (a) E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2000, 39, 1782 CrossRef CAS; (b) P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386 CrossRef CAS PubMed; (c) P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114 CrossRef CAS PubMed; (d) P. Metrangolo, Y. Carcenac, M. Lahtinen, T. Pilati, K. Rissanen, A. Vij and G. Resnati, Science, 2009, 323, 1461 CrossRef CAS PubMed.
- (a) F. Wang, N. Ma, Q. Chen, W. Wang and L. Wang, Langmuir, 2007, 23, 9540 CrossRef CAS PubMed; (b) H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, J. Am. Chem. Soc., 2004, 126, 16 CrossRef CAS PubMed; (c) O. Bolton, D. Lee, J. Jung and J. Kim, Chem. Mater., 2014, 26, 6644 CrossRef CAS; (d) S.-Q. Zang, Y.-J. Fan, J.-B. Li, H.-W. Hou and T. C. W. Mak, Cryst. Growth Des., 2011, 11, 3395 CrossRef CAS.
- (a) M. Carter, A. R. Voth, M. R. Scholfield, B. Rummel, L. C. Sowers and P. S. Ho, Biochemistry, 2013, 52, 4891 CrossRef CAS PubMed; (b) M. R. Scholfield, C. M. V. Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139 CrossRef CAS PubMed; (c) P. Zhou, F. Tian, J. Zou and Z. Shang, Mini-Rev. Med. Chem., 2010, 10, 309 CrossRef CAS PubMed.
- (a) L. P. Wolters, P. Schyman, M. J. Pavan, W. L. Jorgensen, F. M. Bickelhaupt and S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 523 CrossRef CAS; (b) S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918 CrossRef CAS PubMed; (c) T. Clark, M. Hennemann, J. Murray and P. J. Politzer, J. Mol. Model., 2007, 13, 291 CrossRef CAS PubMed; (d) P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748 RSC; (e) T. Clark, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 13–20 CrossRef CAS; (f) S. M. Huber, E. Jimenez-Izal, J. M. Ugaldeb and I. Infante, Chem. Commun., 2012, 48, 7708 RSC; (g) C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726 CrossRef CAS PubMed.
- (a) A. Bruckmann, M. Pena and C. Bolm, Synlett, 2008, 2008, 900 CrossRef; (b) S. M. Walter, F. Kniep, E. Herdtweck and S. M. Huber, Angew. Chem., Int. Ed., 2011, 50, 7187 CrossRef CAS PubMed; (c) S. Dordonne, B. Crousse, D. Bonnet-Delpon and J. Legros, Chem. Commun., 2011, 47, 5855 RSC; (d) G. Lefèvre, G. Franc, C. Adamo, A. Jutand and I. Ciofini, Organometallics, 2012, 31, 914 CrossRef; (e) S. H. Jungbauer, S. M. Walter, S. Schindler, L. Rout, F. Kniepa and S. M. Huber, Chem. Commun., 2014, 50, 6281 RSC; (f) D. P. de Sousa, C. Wegeberg, M. S. Vad, S. Mørup, C. Frandsen, W. A. Donald and C. J. McKenzie, Chem.–Eur. J., 2016, 22, 3810 CrossRef CAS PubMed; (g) V. P. N. Nziko and S. Scheiner, J. Org. Chem., 2016, 81, 2589 CrossRef CAS PubMed.
- (a) M. J. Langton, I. Marques, S. W. Robinson, V. Félix and P. D. Beer, Chem.–Eur. J., 2016, 22, 185 CrossRef CAS PubMed; (b) S. W. Robinson, C. L. Mustoe, N. G. White, A. Brown, A. L. Thompson, P. Kennepohl and P. D. Beer, J. Am. Chem. Soc., 2015, 137, 499 CrossRef CAS PubMed; (c) M. G. Sarwar, B. Dragisic, S. Sagoo and M. S. Taylor, Angew. Chem., Int. Ed., 2010, 49, 1674 CrossRef CAS PubMed.
- (a) K. Gao and N. S. Goroff, J. Am. Chem. Soc., 2000, 122, 9320 CrossRef CAS; (b) P. D. Rege, O. L. Malkina and N. S. Goroff, J. Am. Chem. Soc., 2002, 124, 370 CrossRef CAS PubMed; (c) N. Ma, Y. Zhang, B. Ji, A. Tian and W. Wang, ChemPhysChem, 2012, 13, 1411 CrossRef CAS PubMed.
- (a) G. Bellachioma, B. Binotti, G. Cardaci, C. Carfagna, A. Macchioni, S. Sabatini and C. Zuccaccia, Inorg. Chim. Acta, 2002, 330, 44 CrossRef CAS; (b) G. Ciancaleoni, L. Belpassi, F. Tarantelli, D. Zuccaccia and A. Macchioni, Dalton Trans., 2013, 42, 4122 RSC.
- L. Rocchigiani, G. Ciancaleoni, C. Zuccaccia and A. Macchioni, J. Am. Chem. Soc., 2014, 136, 112 CrossRef CAS PubMed.
- G. Ciancaleoni, R. Bertani, L. Rocchigiani, P. Sgarbossa, C. Zuccaccia and A. Macchioni, Chem.–Eur. J., 2015, 21, 440 CrossRef CAS PubMed.
- M. Erdély, Chem. Soc. Rev., 2012, 41, 3547 RSC , and references within.
- S. H. Jungbauer, S. Schindler, E. Herdtweck, S. Keller and S. M. Huber, Chem.–Eur. J., 2015, 21, 13625 CrossRef CAS PubMed.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305 RSC.
- (a) G. Bellachioma, G. Ciancaleoni, C. Zuccaccia, D. Zuccaccia and A. Macchioni, Coord. Chem. Rev., 2008, 252, 2224 CrossRef CAS; (b) P. S. Pregosin, Spectroscopic Properties of Inorganic and Organometallic Compounds: Techniques, Materials and Applications, 2011, vol. 42, p. 248 Search PubMed; (c) L. Avram and Y. Cohen, Chem. Soc. Rev., 2015, 44, 586 RSC; (d) L. Rocchigiani and A. Macchioni, Dalton Trans., 2016, 45, 2785 RSC; (e) P. S. Pregosin, Magn. Reson. Chem., DOI:10.1002/mrc.4394.
- A. Macchioni, G. Ciancaleoni, C. Zuccaccia and D. Zuccaccia, Chem. Soc. Rev., 2008, 37, 479 RSC.
- (a) A.-C. C. Carlsson, J. Gräfenstein, A. Budnjo, J. L. Laurila, J. Bergquist, A. Karim, R. Kleinmaier, U. Brath and M. Erdélyi, J. Am. Chem. Soc., 2012, 134, 5706 CrossRef CAS PubMed; (b) M. Bedin, A. Karim, M. Reitti, A.-C. C. Carlsson, F. Topić, M. Cetina, F. Pan, V. Havel, F. Al-Ameri, V. Sindelar, K. Rissanen, J. Gräfenstein and M. Erdély, Chem. Sci., 2015, 6, 3746 RSC.
- During the evaluation process of the present paper, other two articles that use diffusional NMR techniques on XB systems have been published: (a) L. Maugeri, J. Asencio-Hernandez, T. Lébl, D. B. Cordes, A. M. Z. Slawin, M.-A. Delsuc and D. Philp, Chem. Sci., 10.1039/c6sc01974a; (b) C. J. Massena, N. B. Wageling, D. A. Decato, E. M. Rodriguez, A. M. Rose and O. B. Berryman, Angew. Chem., Int. Ed., DOI:10.1002/anie.201605440.
- (a) L. Rocchigiani, G. Bellachioma, G. Ciancaleoni, S. Crocchianti, A. Laganá, C. Zuccaccia, D. Zuccaccia and A. Macchioni, ChemPhysChem, 2010, 11, 3243 CrossRef CAS PubMed; (b) G. Ciancaleoni, I. Di Maio, D. Zuccaccia and A. Macchioni, Organometallics, 2007, 26, 489 CrossRef CAS.
- L. Fielding, Tetrahedron, 2000, 56, 6151 CrossRef CAS.
- For I1 and DABCO, see: (a) R. Cabot and C. A. Hunter, Chem. Commun., 2009, 2005 RSC; for I2, see: (b) M. G. Sarwar, B. Dragisic, L. J. Salsberg, C. Gouliaras and M. S. Taylor, J. Am. Chem. Soc., 2010, 132, 1646 CrossRef CAS PubMed; for I3, see ref. 3d; for NBS and HMTA, see: (c) K. Raatikainen and K. Rissanen, CrystEngComm, 2011, 13, 6972 RSC; for Me3Py, see: (d) C. Laurence, J. Graton, M. Berthelot and M. J. El Ghomari, Chem.–Eur. J., 2011, 17, 10431 CrossRef CAS PubMed.
- (a) R. B. Walsh, C. W. Padgett, P. Metrangolo, G. Resnati, T. W. Hanks and W. T. Pennington, Cryst. Growth Des., 2001, 1, 165 CrossRef CAS; (b) C. Perkins, S. Libri, H. Adams and L. Brammer, CrystEngComm, 2012, 14, 3033 RSC; (c) L. Catalano, S. Perez-Estrada, G. Terraneo, T. Pilati, G. Resnati, P. Metrangolo and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2015, 137, 15386 CrossRef CAS PubMed.
- E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2000, 39, 1782 CrossRef CAS.
- Ka for the pair Py/I1 in benzene results to be 1.0, see ref. 22a.
- A. Wasilewska, M. Gdaniec and T. Połoński, CrystEngComm, 2007, 9, 203 RSC.
- Ka for the pair DABCO/I1 in benzene results to be 32, see ref. 22a.
- S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918 CrossRef CAS PubMed.
- L. Belpassi, I. Infante, F. Tarantelli and L. Visscher, J. Am. Chem. Soc., 2008, 130, 1048 CrossRef CAS PubMed.
- (a) G. Ciancaleoni, L. Biasiolo, G. Bistoni, A. Macchioni, F. Tarantelli, D. Zuccaccia and L. Belpassi, Chem.–Eur. J., 2015, 21, 2467 CrossRef CAS PubMed; (b) G. Ciancaleoni, N. Scafuri, G. Bistoni, A. Macchioni, F. Tarantelli, D. Zuccaccia and L. Belpassi, Inorg. Chem., 2014, 53, 9907 CrossRef CAS PubMed; (c) G. Bistoni, S. Rampino, N. Scafuri, G. Ciancaleoni, D. Zuccaccia, L. Belpassi and F. Tarantelli, Chem. Sci., 2016, 7, 1144 RSC.
- D. Cappelletti, E. Ronca, L. Belpassi, F. Tarantelli and F. Pirani, Acc. Chem. Res., 2012, 45, 1571 CrossRef CAS PubMed.
- (a) D. Cappelletti, A. Bartocci, F. Grandinetti, S. Falcinelli, L. Belpassi, F. Tarantelli and F. Pirani, Chem.–Eur. J., 2015, 21, 6234 CrossRef CAS PubMed; (b) A. Bartocci, L. Belpassi, D. Cappelletti, S. Falcinelli, F. Grandinetti, F. Tarantelli and F. Pirani, J. Chem. Phys., 2015, 142, 184304 CrossRef PubMed; (c) G. Ciancaleoni, M. Arca, G. F. Caramori, G. Frenking, F. S. S. Schneider and V. Lippolis, Eur. J. Inorg. Chem., 2016, 23, 3804 CrossRef.
- G. Ciancaleoni, C. Santi, M. Ragni and A. L. Braga, Dalton Trans., 2015, 44, 20168 RSC.
- K. M. Lemishko, G. Bistoni, L. Belpassi, F. Tarantelli, M. M. Montero-Campillo and M. Yáñez, Charge Transfer in Beryllium Bonds and Cooperativity of Beryllium and Halogen Bonds. A New Perspective, in Applications of Topological Methods in Molecular Chemistry, ed. R. Chauvin et al., Springer Ed., Switzerland, 2016, pp. 461–489 Search PubMed.
- J. George, V. L. Deringer and R. Dronskowski, J. Phys. Chem. A, 2014, 118, 3193 CrossRef CAS PubMed.
- P. Cardillo, E. Corradi, A. Lunghi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Tetrahedron, 2000, 56, 5535 CrossRef CAS.
- A. Jerschow and N. Müller, J. Magn. Reson., 1997, 125, 372 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685 CrossRef CAS.
- M. J. Frisch, G. W. Trunks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- S. Rampino, VIRT&L-COMM, 2015, vol. 7, p. 6 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra17455h |
| This journal is © The Royal Society of Chemistry 2016 |