Catalytic mechanism of acetolactate decarboxylase from Brevibacillus brevis towards both enantiomers of α-acetolactate

Abstract

Acetolactate decarboxylase catalyzes both enantiomers of α-acetolactate to give a single product, (R)-acetoin, however, the reaction details are still ambiguous. In this paper, the catalytic mechanism of ALDC using both enantiomers of α-acetolactate as substrates has been investigated by means of the combined quantum mechanical/molecular mechanical (QM/MM) approach based on the recently obtained crystal structures of ALDC in complex with the designed transition state mimics. The conversion of (S)-α-acetolactate only contains two elementary steps: the direct decarboxylation of the substrate to form an enolate intermediate, and the protonation of the intermediate to generate the final product. The decarboxylation corresponds to an energy barrier of 13.5 kcal mol⁻¹. In the protonation process, E253 is suggested to be the more likely proton donor, and the overall energy barrier of the catalytic reaction is 23.1 kcal mol⁻¹. The direct conversion of the non-natural substrate (R)-α-acetolactate is calculated to be difficult. It should be firstly rearranged to the natural substrate (S)-α-acetolactate by a carboxylate migration, then the converted substrate undergoes a rotation to enter the decarboxylation manifold of (S)-α-acetolactate. Since the energy barrier of carboxylate migration of (R)-AL is calculated to be only 11.2 kcal mol⁻¹, considering the fact that the conversion of (R)-α-acetolactate to (R)-acetoin by ALDC is at a lower rate, the weak binding of (R)-α-acetolactate in the active site is thus suggested to be the main factor to lower its conversion rate.

---

1. Introduction

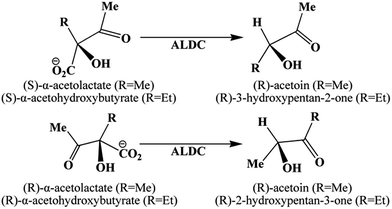
Acetolactate decarboxylase (ALDC) is an interesting enzyme that catalyzes the decarboxylation of both enantiomers of (S)-α-acetolactate and (R)-α-acetolactate (AL) to the single product, (R)-acetoin.^1–4 ALDC also catalyzes the conversion of (S)-α-acetohydroxybutyrate to (R)-3-hydroxypentan-2-one and (R)-α-acetohydroxybutyrate to (R)-2-hydroxypentan-3-one, as shown in Scheme 1.^1,3,4 The (S)-α-acetolactate is the natural substrate, whereas the (R)-enantiomer is a non-natural substrate, which corresponds to a lower conversion rate.^1–4

Scheme 1 Decarboxylation reaction catalyzed by ALDC.

Acetolactate decarboxylase (ALDC) has important application in the process of beer production. In the traditional brewing process, the diacetyl is an unavoidable substance in the beer,^5–10 which can cause undesirable buttery off-flavor when its concentration is over the flavor threshold of 0.02–0.1 mg L⁻¹.^5,11,12 In the presence of oxygen, AL can spontaneously convert to diacetyl, which is then reduced to acetoin.¹¹ Traditionally, the beer brewing would take 2 to 12 weeks.^6,11 However, at the catalysis of ALDC, AL can directly convert to acetoin and thus the use of ALDC can significantly increase the production rate of beer and decrease the adverse flavor caused by diacetyl.^6,7,11–14 In addition, ALDC has also been used for the production of enantiomerically pure diols.^15–17

Acetoin exists widely in wine, cocoa, butter, honey, coffee and strawberries, etc.,^18–20 and it is also defined by the U.S. Department of Energy as one of the potential top 30 sugar-derived chemical building blocks,²¹ which has a great value in the food, flavor, cosmetics, pharmaceutical and chemical industries. As is well known, the biosynthesis is usually environmentally friendlier than the conventional chemical synthesis,²² and ALDC may be used for the industrial production of acetoin. In fact, the pure (R)-acetoin has been biosynthesized by using acetolactate synthase (ALS) and ALDC,^23–26 despite the yield of (R)-acetoin is very low. In addition, the ALDC activity has been found to be rate-limiting for the acetoin biosynthesis,²⁵ it is thus important to understand the reaction detail of ALDC, which may provide useful guide for promoting its catalytic activity.

As early as 1951,² Juni had described the ALDC, and indicated that the product (acetoin) formed from the decarboxylation of racemic α-acetolactate catalyzed by ALDC is levorotatory, and the levorotatory α-acetolactate is a non-natural substrate of ALDC enzyme. Structurally, ALDC is a two domain α/β tertiary structure, and its N-terminal domain includes a 7-stranded mixed β-sheet, which extends into the equivalent β-sheet of the 2-fold symmetry-relaxed molecule generating a 14-stranded β-sheet.³ In the past decades, the structures of ALDC from different species, such as Bacillus subtilis, Bacillus brevis, Lactococcus lactis subsp. lactis, have been solved.^3,5,11,27,28 In 2003, the crystal structure of ALDC from Bacillus brevis was published by Fülöp group.²⁸ Recently, they further reported the structures of ALDC in complex with a range of designed transition state analogues.³ In these crystal structures, a divalent cation Zn²⁺ is observed, which is coordinated by residues H207, H196, H194 and transition state analogue. In the structure of ALDC in complex with (2R,3R)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT3), the Zn²⁺ ion is hexacoordinated, and the ligand mimics the binding mode of (S)-AL. However, in the structures of ALDC in complex with (2S,3S)-2,3-dihydroxy-2-methylbutanoic acid and (2S,3R)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT4, 4BT5), the Zn²⁺ is pentacoordinated and the two ligands mimic the binding of (R)-AL.

Above structures provided significant information about the structure of active site and the binding modes of substrates. According to these crystallographic and mutagenesis studies, a rough reaction mechanism of ALDC has been obtained.^3,4 However, a detailed description still lacks. Here, we employed the combined quantum-mechanics/molecular-mechanics (QM/MM) method to explore the catalytic mechanism of ALDC. On the basis of our calculations, the reaction details, including the energetics of the conversions of (S)-α-acetolactate to (R)-acetoin and (R)-α-acetolactate to (S)-α-acetolactate, the role of Zn-binding site, as well as the electrostatic contribution of some surrounding residues to the calculated energy barrier are all presented.

2. Computational methods

2.1 Preparation of reactant models

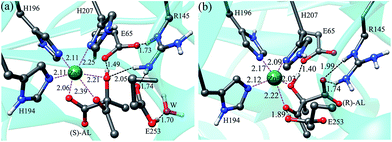
The computational models used in this work were constructed on the basis of the crystal structures of ALDC in complex with transition state analogues (2R,3R)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT3) and (2S,3S)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT4). The active pockets derived from the two crystal structures are shown in Fig. 1, which shows that the transition state analogues (2R,3R)-2,3-dihydroxy-2-methylbutanoic acid and (2S,3S)-2,3-dihydroxy-2-methylbutanoic acid occupy the corresponding positions of (S)-α-acetolactate (S-AL) and (R)-α-acetolactate (R-AL) in the active site of ALDC. The carboxylate groups of transition state analogues mimic the positions of the ketone groups of two substrates, and the hydroxyl groups mimic the substrate carboxylic acid.³ To construct the enzyme-substrate models, the (2R,3R)-2,3-dihydroxy-2-methylbutanoic acid was manually converted to (S)-AL, and (2S,3S)-2,3-dihydroxy-2-methylbutanoic acid to (R)-AL. The protonation states of all titratable residues were determined according to the pK_a values predicted by the PROPKA²⁹ and the experimental condition. Three Zn-coordinated histidine residues (H207, H196 and H194) were determined as singly protonated with H196 and H194 at δ sites and H207 at ε site. A glutamate residue (E253) was set to its protonated state, which is supposed to be necessary for the protonation of enolate intermediate. All other titratable residues adopt their normal protonation states. The final structures were checked carefully by the VMD program, and all the missing hydrogen atoms were added to the crystal structures by using the HBUILD program in the CHARMM program package.³⁰ Subsequently, the obtained enzyme-substrate complexes were hydrated using a droplet model with a 32 Å sphere of equilibrated TIP3 water molecules, while the crystallographic water molecules were kept in their original positions. And then 5 sodium ions were added at random positions to neutralize the solvated system. Finally, a neutral system was formed. The ALDC–(S)-AL complex contains 14 030 atoms, and the ALDC–(R)-AL complex contains 14 663 atoms, because the numbers of water molecules are different in these two systems. To pre-equilibrate the resulted system, after a succession of energy minimizations, 7 ns molecular dynamics (MD) simulations were performed with the CHARMM22 (ref. 30 and 31) all-atom force field for both systems. As it is difficult to properly describe the zinc coordination shell by MM force field,^32,33 in the molecular dynamics (MD) simulations, the Zn²⁺ and Zn-coordinated residues (H194, H196, H207) were kept frozen. The root-mean-squared deviations (RMSD) for the backbone atoms relative to the crystal structures during the MD simulations are displayed in Fig. S1 of ESI,† which show that the whole systems have been equilibrated after MD simulations.

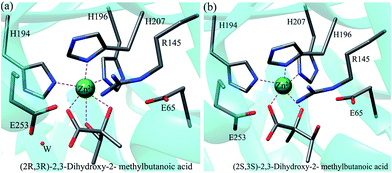Fig. 1 Active site structures of ALDC in complex with (2R,3R)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT3) (a) and (2S,3S)-2,3-dihydroxy-2-methylbutanoic acid (PDB code: 4BT4) (b).

2.2 QM/MM calculations

The reaction mechanism of ALDC was explored by using QM/MM calculations, in which the ChemShell package³⁴ was used to combine the Turbomole program for the QM region³⁵ and the DL-POLY program for the MM region.³⁶ In our computational models, the QM regions contain 84 atom, including residues H207, H196, H194, E65, R145, the protonated E253, one water molecule, Zn²⁺ ion, and substrate (S)-AL or (R)-AL. The remaining atoms were assigned to the MM regions. The total charge of each QM part is +1. During the QM/MM calculations, the QM and the MM atoms within a distance of 16 Å from the C_A2 or C_B2 atom of substrate (labeled in Fig. 3) were kept free, whereas the rest MM atoms were kept frozen. MM regions were treated with the CHARMM22 force field,³¹ and QM regions were treated with DFT at B3LYP functional.³⁷ The electronic embedding scheme was used to describe the electrostatic interaction between the QM and MM part.³⁸ The hybrid delocalized internal coordinate (HDLC) optimizer was used for geometry optimizations and transition state searches.³⁹ A quasi-Newton limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS)⁴⁰ method was employed to search for minima on potential energy surfaces and the partitioned rational function optimization (P-RFO) algorithm⁴¹ was used to search transition state. To recognize the transition states, we firstly scanned the potential energy profile along the reaction coordinate, then the highest point on the energy curve was chosen to optimize the transition state. The last structure from the PES scan was optimized to find the intermediate, which was employed to start another scan to find the consecutive transition state and intermediate on the reaction path. Thus, we can confirm that each transition state is connected by the corresponding minima. For geometry optimization, except Zn²⁺, all atoms of QM regions were treated by 6-31G (d, p) basis set. For Zn²⁺, the Stuttgart ECP/basis set (SDD)⁴² was used. After the geometry optimization, the single-point calculations were performed using the Stuttgart ECP and 6-311++G (2d, 2p) basis sets combination. Since B3LYP functional lacks a proper description of the attractive long-range dispersion interaction, to obtain more accurate energies, the DFT-D3 program has been used to correct the B3LYP energies. Thus, all the reported energies in this work have included the dispersion corrections.⁴³

3. Results and discussion

3.1 Structures of ALDC–substrate complexes

As described above, the initial reactant models of ALDC–(S)-AL and ALDC–(R)-AL, which are named as R_A and R_B, respectively, were prepared on the basis of crystal structures of ALDC in complex two transition state analogues. The QM/MM optimized structures are displayed in Fig. 2.

Fig. 2 QM/MM optimized active site structures of ALDC in complex with the (S)-AL and (R)-AL denoted as R_A and R_B, respectively. The atoms in QM regions are displayed in ball and stick models. Some key distances are shown in angstroms. Hydrogen bonds are shown in black dash lines and coordination bonds are shown in purple dash lines.

In R_A, the Zn²⁺ ion forms a hexacoordinated structure with H207, H196, H194 and the substrate. The distances between the Zn²⁺ ion and the binding atoms are 2.25, 2.11, 2.11, 2.06, 2.39 and 2.21 Å respectively, indicating a strong coordination interaction of Zn²⁺ ion with the three histidine residues and the substrate. The deprotonated residue E65 forms a strong hydrogen bond to the substrate hydroxyl group with a distance of 1.49 Å. R145 makes three hydrogen bonds to the carboxyl groups of E65 and E253 as well as the hydroxyl group of (S)-AL, implying the important role of R145. In addition, E253 forms a hydrogen bond with the water molecule in the active site.

R_B shows a slightly different binding mode of (S)-AL. As shown in Fig. 2b, the carboxyl group of (R)-AL is closer to R145, forming two hydrogen bonds with the amino group of R145. Thus, the Zn²⁺ ion only forms a pentacoordinated structure with H207, H196, H194 and the substrate, with binding distances of 2.09, 2.17, 2.12, 2.22 and 2.03 Å, respectively. The carboxyl group of E65 makes a strong hydrogen bond to the hydroxyl group of (R)-AL with a distance of 1.40 Å, and the carboxyl group of E253 forms a hydrogen bond with the carbonyl group of (R)-AL. These hydrogen bonds stabilize the substrate in the active site of the enzyme.

3.2 Reaction paths

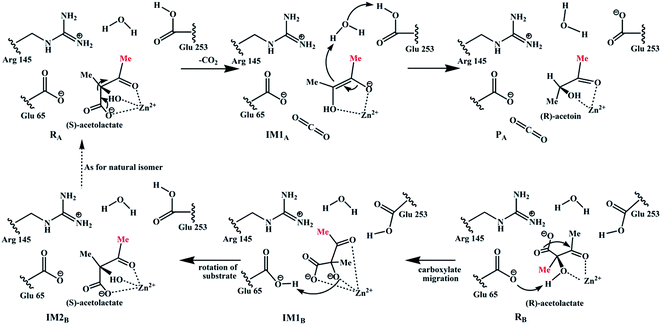
Based on the previously proposed mechanism³ and our calculations, the conversion of (S)-α-acetolactate (R_A) to the final product (R)-acetoin (P_A) only contains two elementary steps. However, for the conversion of (R)-α-acetolactate (R_B), it should be firstly converted to the (S)-α-acetolactate (IM1_B) by a carboxyl migration, which then undergoes a self-rotation (IM1_B → IM2_B) to generate a favorable conformation for the subsequent decarboxylation, as shown in Scheme 2. To clearly elucidate the catalytic mechanism, the reactions of (S)-AL and (R)-AL are respectively discussed in the following subsections.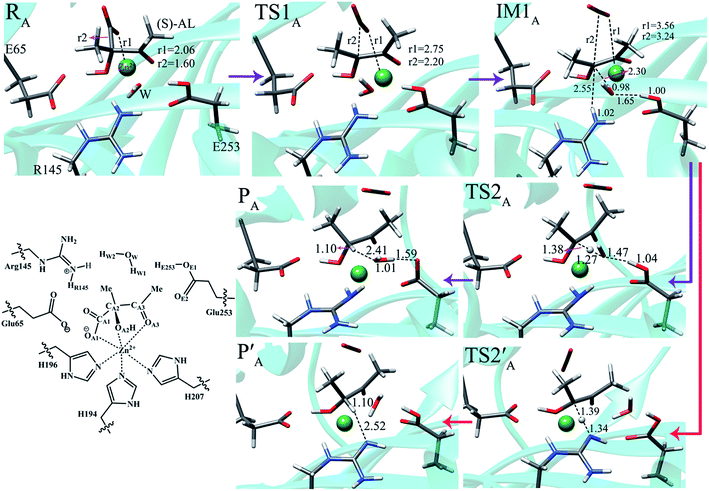

Scheme 2 Proposed catalytic mechanisms of ALDC for (S)- and (R)-α-acetolactate.

3.2.1 Conversion of (S)-α-acetolactate to (R)-acetoin. As shown in Scheme 2, the conversion of (S)-α-acetolactate to (R)-acetoin contains two chemical steps: the direct decarboxylation of substrate to generate an intermediate enolate (IM1_A), and a water-mediated proton transfer from E253 to the C_A2 of the substrate, producing the final (R)-acetoin (P_A). For comparison, another possibility that R145 acts as the proton acceptor was also considered. The optimized structures of reactant (R_A), transition states (TS1_A, TS2_A and TS2′_A), intermediate (IM1_A) and products (P_A, P′_A) are shown in Fig. 3, and the corresponding energy profiles are displayed in Fig. 4.

Fig. 3 Optimized structures of the involved species in the conversion of (S)-AL to (R)-acetoin. Distances are given in angstroms.

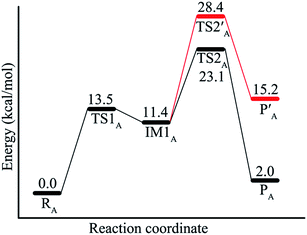Fig. 4 Energy profiles of the ALDC-catalyzed reaction of (S)-AL. During the proton transfer process, either E253 (black line) or R145 (red line) acts as the proton donor.

The first step is the decarboxylation of substrate. As shown in Fig. 3, from reactant R_A to intermediate IM1_A, the C_A1–C_A2 bond (r2) of substrate is gradually weakened with its length changes from 1.60 in R_A to 3.24 Å in IM1_A via 2.20 Å in TS1_A, which means in IM1_A the C_A1–C_A2 bond has been completely broken and the enolate intermediate (IM1_A) has been formed. The decarboxylation process corresponds to an energy barrier of 13.5 kcal mol⁻¹. It is also calculated to be endothermic by 11.4 kcal mol⁻¹, which is similar to most of the decarboxylation process owing to the accumulation of negative charge on the α-carbon. Thus, IM1_A can either return back to R_A or abstract a proton from the nearby residue to form the final product. The coordination between Zn²⁺ ion and the substrate is supposed to play an important role in stabilizing this intermediate (IM1_A). During the decarboxylation process, the coordination of Zn²⁺ with the carboxyl and carbonyl groups of substrate exhibits obvious change. For instance, from R_A to IM1_A, the distance (r1) between Zn²⁺ and the carboxyl oxygen (O_A1) changes from 2.06 to 3.56 Å, leading to the coordination of Zn²⁺ changed from hexacoordination to pentacoordination. Besides, the length of d_Zn–OA3 decreases from 2.39 to 1.92 Å, showing the enhancement of the interaction between Zn²⁺ ion and the carbonyl oxygen (O_A3) during this process. However, the distances between Zn²⁺ and other ligated atoms are almost unchanged. The detailed bond lengths between Zn²⁺ and the binding atoms are listed in Table S1 of ESI.† We also note that the length of d_CA2–CA3 bond decreases from 1.52 to 1.37 Å, which means the C_A2–C_A3 bond has partial double bonding characteristic. Therefore, accompanying the decarboxylation of the substrate, the coordination between Zn²⁺ and substrate serves to stabilize the transition state (TS1_A) and intermediate (IM1_A).

After the decarboxylation of the substrate, E253 donates a proton to the enolate intermediate (IM1_A) via a mediated water molecule to complete the catalytic reaction. As shown in Fig. 3, the bond length of C_A2–H_W1 decreases from 2.30 Å in IM1_A to 1.38 Å in TS2_A. Downhill from TS2_A, the final product P_A is generated, and simultaneously the deprotonated water molecule (OH⁻) accepts a proton from E253. The energy barrier of this process is only 11.7 kcal mol⁻¹, but TS2_A corresponds to the highest point along the reaction path, and therefore the overall energy barrier is suggested to be 23.1 kcal mol⁻¹. It can be seen that the conversion of (S)-α-acetolactate to (R)-acetoin is endothermic by 2.0 kcal mol⁻¹.

In addition, we also explored another proton transfer pathway in which residue R145 acts as the proton donor. The calculated energy barrier of the proton transfer process is 17 kcal mol⁻¹ and the overall energy barrier increases to 28.4 kcal mol⁻¹, which is too high for an enzymatic reaction. Thus, R145 is unlikely to serves as the proton donor. The optimized structures of the involved intermediate, transition state (TS2′_A) and product (P′_A) are also displayed in Fig. 3.

3.2.2 Rearrangement of (R)-α-acetolactate to (S)-α-acetolactate. The conversion of (R)-α-acetolactate to (S)-α-acetolactate involves a migration of carboxylate ion, by which the carboxyl group of (R)-AL migrates from C_B2 to C_B3 and the (R)-AL transforms to its (S)-enantiomer. The optimized structures of reactant (R_B), transition state (TS1_B) and intermediate (IM1_B) are shown in Fig. 5. From R_B to TS1_B, the bond length of C_B1–C_B2 changes from 1.66 Å to 2.29 Å and the distance of d(C_B1–C_B3) from 2.38 Å to 1.74 Å. In IM1_B, the newly formed C_B1–C_B3 bond further shortens to 1.57 Å. Accompanying this carboxylate migration, the deprotonated E65 spontaneously abstracts a proton from the hydroxyl group of substrate, and simultaneously the hybridization of C_B2 atom changes from sp³ to sp², by which the hydroxyl group at C_B2 is oxidized to carbonyl group. The energy barrier of this migration process is calculated to be 11.2 kcal mol⁻¹ (Fig. 6), and the formed intermediate IM1_B, which is now the (S)-α-acetolactate, is lower than R_B by 8.4 kcal mol⁻¹, indicating the (S)-α-acetolactate is stably bound in the active site. It should be noted that the original carbonyl oxygen (O_B3) in (R)-AL has been changed to hydroxyl ion owing to the changes of hybridization of C_B3. From R_B to IM1_B, the distance (r6) between Zn²⁺ and the carboxyl oxygen of substrate shortens from 3.31 Å to 2.23 Å, which indicates the variation of the Zn²⁺ from pentacoordination to hexacoordination.

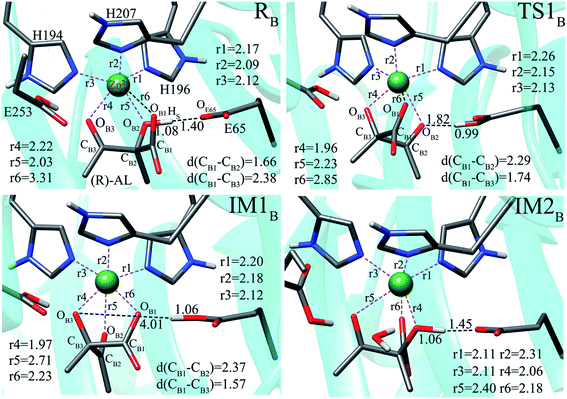Fig. 5 Optimized structures of species involved in the conversion of (R)-α-acetolactate to (S)-α-acetolactate. All distances are shown in angstroms.

Fig. 6 Energy profile of the conversion of (R)-α-acetolactate to (S)-α-acetolactate catalyzed by ALDC.

3.2.3 Conversion of (R)-α-acetolactate to acetoin starting from IM1_B or R_B. From IM1_B, after migration of carboxylate ion, the decarboxylation of IM1_B was also explored by our QM/MM calculations. However, the results reveal that the decarboxylation of IM1_B corresponds to a high energy barrier of 33.1 kcal mol⁻¹ (Fig. 7). It may be caused by the two strong hydrogen bonds formed by the –COO⁻ group to residues E65 and R145. Therefore, the (R)-α-acetolactate in the bound state of IM1_B is difficult to undergo a direct decarboxylation. It should firstly adjust its bound conformation as shown in R_A, then follows the decarboxylation manifold of (S)-α-acetolactate. Since it is difficulty to simulation rotation process of the substrate, we manually changes the binding mode of (S)-α-acetolactate in IM1_B and create the new computational model (named as IM2_B), which is 5.4 kcal mol⁻¹ higher than IM1_B. According to the experimental observation,^1,2,4 the conversion rate of (R)-α-acetolactate to (R)-acetoin is lower than that of (S)-α-acetolactate to (R)-acetoin. Therefore, we deduce that it is the weak binding of (R)-α-acetolactate that lowers its conversion rate.

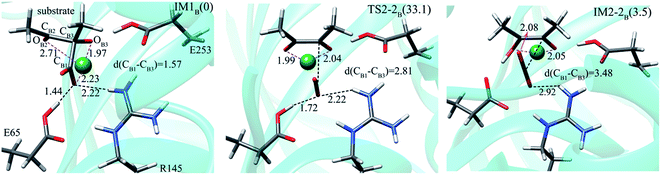Fig. 7 Optimized structures for the decarboxylation of IM1_B. Relative energies (kcal mol⁻¹) are given in parentheses. All distances are shown in angstroms.

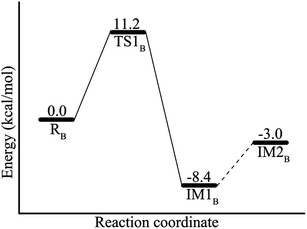
For comparison, starting from R_B, we also explored the conversion of (R)-AL to acetoin, i.e., the (R)-AL firstly undergoes direct decarboxylation rather than carboxylate migration. The related reaction pathways are shown in Scheme S1.† Our calculations reveal that the direct decarboxylation of (R)-AL is quite easy, corresponding to an energy barrier of 5.1 kcal mol⁻¹, which is much lower than the decarboxylation of (S)-AL (13.5 kcal mol⁻¹). We attribute it to the different coordination of the substrates with the Zn²⁺. In the enzyme-substrate complexes, the carboxyl group of (R)-AL does not coordinate with Zn²⁺, causing Zn²⁺ to be a more strong Lewis acid than the case in (S)-AL in which the –COO⁻ group to be dissociated coordinates with the Zn²⁺ and the negative charge in the transition state of decarboxylation is not well stabilized by Zn²⁺. In the second step, the O_B3⁻ abstracts a proton from E253, forming the symmetrical enediol (IM2′_B) with an energy barrier of 7 kcal mol⁻¹. The final step is the conversion of enediol to the (S)- and (R)-acetoins. Inspection of the active site reveals that the most possible proton donor should be R145, because the protonated R145 situates in a favorable position to donate its proton to C_B3 or C_B2. However, our calculations reveal that the proton transfers from R145 to both C_B3 and C_B2 correspond to high energy barriers of 46.4 kcal mol⁻¹ and 33.6 kcal mol⁻¹, respectively (Fig. S2 and S3†). Besides, E253 was also calculated to be an unfavorable proton donor. In summary, in the active site of ALDC, the direct conversion (R)-AL to both (R)- and (S)-acetoin was calculated to be unlikely, and the carboxylate migration pathway for the conversion of (R)-AL is the most possible one.

3.3 Influence of protein environment and the Zn-coordination

The distant residues may also have significant influence on the catalytic reaction. Therefore, we estimated the electrostatic effect of fourteen residues around the QM region on the conversion of (S)-AL to (R)-acetoin. The variation of activation energy barrier ΔEⁱ⁻⁰ caused by the change of charge on residue i can be determined as:

ΔEⁱ⁻⁰ = ΔEⁱ − ΔE⁰

ΔEⁱ is the energy barrier with charge on residue i set to 0, and ΔE⁰ is the original energy barrier. During our calculations, the geometrical structures of related species were kept unchanged.^44,45 The ΔEⁱ⁻⁰ values associated with fourteen residues were listed in Table 1. One can see that all the values of ΔEⁱ fall in the range from −1.39 to 0.5 kcal mol⁻¹. Since all these residues are neutral, the electrostatic influence of these residues is suggested to be very weak. Relatively, G57 and T58 are two residues that have stronger influence on the reaction.

Table 1 ΔEⁱ⁻⁰ values of fourteen residues toward the whole reaction of (S)-AL catalyzed by ALDC

Residue	Charge	ΔE^i−0
		RA → IM1A	IM1A → PA
I31	0	0.13	0.08
L34	0	0.06	−0.16
M35	0	−0.57	0.03
G57	0	−1.39	−1.25
T58	0	−0.42	−1.17
L62	0	−0.16	0.00
G64	0	−0.11	−0.24
F93	0	−0.51	−0.33
V147	0	0.17	0.27
L157	0	0.04	0.25
T161	0	0.40	0.07
V190	0	0.01	−0.24
V249	0	0.20	0.44
A252	0	0.50	0.44

---

During the catalytic reaction, besides fixing the substrate, Zn²⁺ also plays an important role in stabilizing the transition state and intermediate by forming coordinate bonds with the nearby residues. The distances between Zn²⁺ and its ligated atoms are shown in Table S1† and Fig. 5. In the conversion of (S)-α-acetolactate to (R)-acetoin, at the reactant state (R_A), the carboxyl oxygen (S)-AL (O_A1) coordinates with Zn²⁺ with bond length of 2.06 Å, whereas in IM1_A, after the decarboxylation of the substrate, the distance of d_Zn–OA1 increases to 3.56 Å. In addition, the distance between Zn²⁺ and carbonyl oxygen atom of substrate (O_A3) also shows a clear fluctuation. From R_A to IM1_A, the distance of d_Zn–OA3 decreases from 2.39 Å to 1.92 Å. Besides, during the migration of carboxylate (Fig. 5), the coordination structure of Zn²⁺ also undergoes obvious changes. Thus, besides fixing the substrate, Zn²⁺ also plays an important role in stabilizing the intermediates and transition state.

4. Conclusions

In this paper, the conversion of (S)-α-acetolactate to (R)-acetoin and (R)-α-acetolactate to (S)-α-acetolactate catalyzed by ALDC have been investigated by using the QM/MM method. The conversion of (S)-α-acetolactate to (R)-acetoin contains two steps: decarboxylation of substrate to form enolate intermediate and protonation of enolate intermediate to form the final product (R)-acetoin. The decarboxylation process corresponds to an energy barrier 13.5 kcal mol⁻¹. Subsequently, the enolate intermediate is protonated by E253 via a mediate water molecule. The protonation of enolate intermediate corresponds to an energy barrier of 11.7 kcal mol⁻¹, and the overall energy barrier is 23.1 kcal mol⁻¹. For the non-natural substrate (R)-α-acetolactate, it should be firstly rearranged to (S)-enantiomer by a carboxylate migration, then the converted substrate undergoes a rotation to enter the decarboxylation manifold of (S)-α-acetolactate. The energy barrier of carboxylate migration of (R)-AL is 11.2 kcal mol⁻¹, which is lower than both the energy barriers of decarboxylation and overall reaction of (S)-α-acetolactate. As is known, ALDC catalyzes (R)-α-acetolactate at a lower rate. Therefore, we deduce the weak binding of (R)-α-acetolactate may be the main factor to lower its conversion rate. These results may provide useful information for the enzyme redesign of biocatalytic application in brewing, biosynthesis of pure diols, acetoin and so on.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21573127, 21373125).

References

1. D. H. G. Crout and D. L. Rathbone, Biotransformations with acetolactate decarboxylase: unusual conversions of both substrate enantiomers into products of high optical purity, J. Chem. Soc., Chem. Commun., 1988, 98–99.
2. E. Juni, Mechanisms of formation of acetion by bacteria, J. Biol. Chem., 1951, 195, 715–726.
3. V. A. Marlow, D. Rea, S. Najmudin, M. Wills and V. Fülöp, Structure and mechanism of acetolactate decarboxylase, ACS Chem. Biol., 2013, 8, 2339–2344.
4. V. A. Marlow, Mechanistic studies of acetolactate decarboxylase, Doctoral dissertation, University of Warwick, 2013.
5. X. Zhang, Z. Rao, J. Li, J. Zhou, T. Yang, M. Xu, T. Bao and X. Zhao, Improving the acidic stability of Staphylococcus aureus α-acetolactate decarboxylase in Bacillus subtilis by changing basic residues to acidic residues, Amino acids, 2015, 47, 707–717.
6. E. J. C. Choi, H. W. Ahn and W. J. Kim, Effect of α-acetolactate decarboxylase on diacetyl content of beer, Food Sci. Biotechnol., 2015, 24, 1373–1380.
7. S. E. Godtfredsen, A. M. Rasmussen, M. Ottesen, P. Rafn and N. Peitersen, Occurrence of α-acetolactate decarboxylases among lactic acid bacteria and their utilization for maturation of beer, Appl. Microbiol. Biotechnol., 1984, 20, 23–28.
8. S. D. Aunsbjerg, A. H. Honoré, J. Marcussen, P. Ebrahimi, F. K. Vogensen, C. Benfeldt, T. Skov and S. Knøchel, Contribution of volatiles to antifungal effect of Lactobacillus paracasei in defined medium and yogurt, Int. J. Food Microbiol., 2015, 194, 46–53.
9. T. Wainwright, Diacetyl-a review: Part I-analytical and biochemical considerations: Part II-brewing experience, J. Inst. Brew., 1973, 79, 451–470.
10. K. Krogerus and B. R. Gibson, 125th Anniversary Review: Diacetyl and its control during brewery fermentation, J. Inst. Brew., 2013, 119, 86–97.
11. B. Diderichsen, U. Wedsted, L. Hedegaard, B. R. Jensen and C. Sjøholm, Cloning of aldB, which encodes alpha-acetolactate decarboxylase, an exoenzyme from Bacillus brevis, J. Bacteriol., 1990, 172, 4315–4321.
12. K. Blomqvist, M. L. Suihko, J. Knowles and M. Penttilä, Chromosomal integration and expression of two bacterial α-acetolactate decarboxylase genes in brewer's yeast, Appl. Environ. Microbiol., 1991, 57, 2796–2803.
13. C. Dulieu, M. Moll, J. Boudrant and D. Poncelet, Improved performances and control of beer fermentation using encapsulated α-acetolactate decarboxylase and modeling, Biotechnol. Prog., 2000, 16, 958–965.
14. S. E. Godtfredsen and M. Ottesen, Maturation of beer with α-acetolactate decarboxylase, Carlsberg Res. Commun., 1982, 47, 93–102.
15. X. J. Ji, L. G. Liu, M. Q. Shen, Z. K. Nie, Y. J. Tong and H. Huang, Constructing a synthetic metabolic pathway in Escherichia coli to produce the enantiomerically pure (R,R)-2,3-butanediol, Biotechnol. Bioeng., 2015, 112, 1056–1059.
16. Y. Yan, C. C. Lee and J. C. Liao, Enantioselective synthesis of pure (R,R)-2,3-butanediol in Escherichia coli with stereospecific secondary alcohol dehydrogenases, Org. Biomol. Chem., 2009, 7, 3914–3917.
17. J. W. Oliver, I. M. Machado, H. Yoneda and S. Atsumi, Cyanobacterial conversion of carbon dioxide to 2,3-butanediol, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1249–1254.
18. S. Li, L. Liu and J. Chen, Compartmentalizing metabolic pathway in Candida glabrata for acetoin production, Metab. Eng., 2015, 28, 1–7.
19. S. Gao, W. Guo, L. Shi, Y. Yu, C. Zhang and H. Yang, Characterization of acetoin production in a budC gene disrupted mutant of Serratia marcescens G12, J. Ind. Microbiol. Biotechnol., 2014, 41, 1267–1274.
20. Z. Xiao and J. R. Lu, Generation of acetoin and its derivatives in foods, J. Agric. Food Chem., 2014, 62, 6487–6497.
21. T. Werpy, G. Petersen, A. Aden, J. Bozell, J. Holladay, J. White, A. Manheim, D. Elliot, L. Lasure, S. Jones, M. Gerber, K. Ibsen, L. Lumberg and S. Kelley, Top value added chemicals from biomass, Volume 1, Results of screening for potential candidates from sugars and synthesis gas, report DOE/GO-102004–1992, Office of Scientific and Technical Information, U.S. Department of Energy, Oak Ridge, TN, 2004, http://www.eere.energy.gov/biomass/pdfs/35523.pdf.
22. L. Zhang, S. Chen, H. Xie, Y. Tian and K. Hu, Efficient acetoin production by optimization of medium components and oxygen supply control using a newly isolated Paenibacillus polymyxa CS107, J. Chem. Technol. Biotechnol., 2012, 87, 1551–1557.
23. Q. Xu, L. Xie, Y. Li, H. Lin, S. Sun, X. Guan, K. Hu, Y. Shen and L. Zhang, Metabolic engineering of Escherichia coli for efficient production of (3R)-acetoin, J. Chem. Technol. Biotechnol., 2015, 90, 93–100.
24. C. Frädrich, A. March, K. Fiege, A. Hartmann, D. Jahn and E. Härtig, The transcription factor AlsR binds and regulates the promoter of the alsSD operon responsible for acetoin formation in Bacillus subtilis, J. Bacteriol., 2012, 194, 1100–1112.
25. S. Li, X. Gao, N. Xu, L. Liu and J. Chen, Enhancement of acetoin production in Candida glabrata by in silico-aided metabolic engineering, Microb. Cell Fact., 2014, 13, 55.
26. S. Ui, A. Mimura, M. Okuma and T. Kudo, The production of D-acetoin by a transgenic Escherichia coli, Lett. Appl. Microbiol., 1998, 26, 275–278.
27. V. Phalip, C. Monnet, P. Schmitt, P. Renault, J. J. Godon and C. Diviès, Purification and properties of the α-acetolactate decarboxylase from Lactococcus lactis subsp. lactis NCDO 2118, FEBS Lett., 1994, 351, 95–99.
28. S. Najmudin, J. T. Andersen, S. A. Patkar, T. V. Borchert, D. H. Crout and V. FüLöP, Purification, crystallization and preliminary X-ray crystallographic studies on acetolactate decarboxylase, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 1073–1075.
29. C. R. Søndergaard, M. H. Olsson, M. Rostkowski and J. H. Jensen, Improved treatment of ligands and coupling effects in empirical calculation and rationalization of pKa values, J. Chem. Theory Comput., 2011, 7, 2284–2295.
30. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, CHARMM: a program for macromolecular energy, minimization, and dynamics calculations, J. Comput. Chem., 1983, 4, 187–217.
31. J. Chen, W. Im and C. L. Brooks, Balancing solvation and intramolecular interactions: toward a consistent generalized Born force field, J. Am. Chem. Soc., 2006, 128, 3728–3736.
32. Y. P. Pang, Successful molecular dynamics simulation of two zinc complexes bridged by a hydroxide in phosphotriesterase using the cationic dummy atom method, Proteins, 2001, 45, 183–189.
33. R. A. Karjiban, M. B. A. Rahman, M. Basri, A. B. Salleh, D. Jacobs and H. A. Wahab, Molecular dynamics study of the structure, flexibility and dynamics of thermostable L1 lipase at high temperatures, Protein J., 2009, 28, 14–23.
34. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, QUASI: a general purpose implementation of the QM/MM approach and its application to problems in catalysis, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28.
35. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: The program system turbomole, Chem. Phys. Lett., 1989, 162, 165–169.
36. W. Smith and T. R. Forester, DL_POLY_2.0: a general-purpose parallel molecular dynamics simulation package, J. Mol. Graphics, 1996, 14, 136–141.
37. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
38. D. Bakowies and W. Thiel, Hybrid models for combined quantum mechanical and molecular mechanical approaches, J. Phys. Chem., 1996, 100, 10580–10594.
39. S. R. Billeter, A. J. Turner and W. Thiel, Linear scaling geometry optimisation and transition state search in hybrid delocalised internal coordinates, Phys. Chem. Chem. Phys., 2000, 2, 2177–2186.
40. J. Nocedal, Updating quasi-Newton matrices with limited storage, Math. Comput., 1980, 35, 773–782.
41. A. Banerjee, N. Adams, J. Simons and R. Shepard, Search for stationary points on surfaces, J. Phys. Chem., 1985, 89, 52–57.
42. M. Dolg, U. Wedig, H. Stoll and H. Preuss, Energy-adjusted abinitio pseudopotentials for the first row transition elements, J. Chem. Phys., 1987, 86, 866–872.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104–154123.
44. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97, 10269–10280.
45. A. Barrozo, F. Duarte, P. Bauer, A. T. Carvalho and S. C. Kamerlin, Cooperative Electrostatic Interactions Drive Functional Evolution in the Alkaline Phosphatase Superfamily, J. Am. Chem. Soc., 2015, 137, 9061–9076.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18264j

---