Dielectric and ferroelectric behavior of an incipient ferroelectric Sr(1−3x/2)CexTiO3 novel solid solution†
Burhan Ullahab,
Wen Lei*ab,
Xiao-Hong Wangab,
Gui-Fen Fanab,
Xiao-Chuan Wangab and
Wen-Zhong Lu*ab
aSchool of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, P. R. China. E-mail: lwz@mail.hust.edu.cn; wenlei@mail.hust.edu.cn; Fax: +86 27 8754 3134; Tel: +86 27 8755 6493
bKey Lab of Functional Materials for Electronic Information (B), Ministry of Education, Wuhan 430074, P. R. China
First published on 20th September 2016
Abstract
Phase formation, chemical structure, microwave (MW) dielectric properties, and relaxor-to-ferroelectric phase transition behavior of a novel solid solution with Ce-doped, A-site SrTiO3 (Sr(1−3x/2)CexTiO3) ceramic sintered in nitrogen have been investigated. X-ray diffraction (XRD) showed that the samples with x ≤ 0.3 appeared cubic but exhibited splitting and superstructure reflections consistent with tetragonal (0.4 ≤ x ≤ 0.45) and orthorhombic (0.5 ≤ x ≤ 0.6) structures. Chemical structure analysis revealed that the addition of small amounts of ceria (x ≤ 0.3) promoted Ti3+ cation and oxygen vacancy 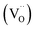 . By contrast, the addition of large amounts of ceria (x ≥ 0.4) inhibited this process. Sr(1−3x/2)CexTiO3 ceramics displayed frequency-dependent relaxor dielectric anomalies and frequency-independent normal ferroelectric behaviors. The relaxor/dielectric properties were strongly dependent on structure-chemical factors. The value of εr decreased several times when Sr was subsequently substituted with Ce, and induced a relaxor-to-ferroelectric phase transition. A good combination of the following microwave dielectric properties was obtained for the Sr0.1Ce0.6TiO3 orthorhombic solid solution at an optimum temperature of 1300 °C for 3 h: εr = 50, Q × f = 11
. By contrast, the addition of large amounts of ceria (x ≥ 0.4) inhibited this process. Sr(1−3x/2)CexTiO3 ceramics displayed frequency-dependent relaxor dielectric anomalies and frequency-independent normal ferroelectric behaviors. The relaxor/dielectric properties were strongly dependent on structure-chemical factors. The value of εr decreased several times when Sr was subsequently substituted with Ce, and induced a relaxor-to-ferroelectric phase transition. A good combination of the following microwave dielectric properties was obtained for the Sr0.1Ce0.6TiO3 orthorhombic solid solution at an optimum temperature of 1300 °C for 3 h: εr = 50, Q × f = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 GHz, and τf = +3 ppm per °C.
311 GHz, and τf = +3 ppm per °C.
1. Introduction
In recent years, the low solubility of rare earth (RE) ions in ABO3 perovskites has been a challenging topic and remains an open and engaging question. Among ABO3 perovskites, those in a RE-doped SrTiO3 (ST) ceramic system have been widely explored because of their unique behaviors and properties. Such properties of RE-doped ST ceramics are likely associated with the influence of processing conditions, firing atmospheres, and oxygen deficiencies.1–6 Other effects on local structure, giant permittivity (εr),1 room temperature ferroelectricity,2 quantum paraelectricity,3 and more recently an interesting thermoelectric response fired in air and N2/H2 atmospheres have also been reported.4 However, little attention and effort has been paid to the dielectric and ferroelectric properties of doped ST based ceramics because of their incipient ferroelectric nature. The challenge is to find ways of tuning the temperature coefficient of the resonant frequency (τf) while maintaining values of the dielectric constant (εr), and Q × f suitable for use in microwave components. Therefore, it is an important issue to further understand the structure–property relationship and the physical nature of RE ion doped ST ceramic systems.In highly A-site Ce-doped ST ceramics, Ce ions can be incorporated in both existing ion valance states. In trivalent state Ce3+, it enters the ST lattice at the A-site, whereas in tetravalent state Ce4+ it is mainly incorporated at the B-site. For Sr-site, Ce ions act as a donor, as such, their incorporation requires the formation of negatively charge compensating lattice defects. At evaluate sintering temperature, Ce is incorporated as Ce3+ at Sr sites; donor charge is compensated by Ti3+ cations [Sr(1−x)Cex3+Ti1−x4+Tix3+O3, electronic compensation] and ionized vacancies [Sr(1−3x/2)Cex3+(VSr)0.5xTiO3, 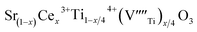 , vacancy compensation]. The cation vacancies, namely,
, vacancy compensation]. The cation vacancies, namely, 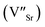 and
and 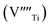 , are favorable vacancy defects in a ST lattice.6,7 The dynamics feature of these vacancy defects, including their mobility and aggregation related with other defects, has an apparent impacts on the ferroelectric and dielectric properties of doped ST ceramics.
, are favorable vacancy defects in a ST lattice.6,7 The dynamics feature of these vacancy defects, including their mobility and aggregation related with other defects, has an apparent impacts on the ferroelectric and dielectric properties of doped ST ceramics.
The only known work related with Ce doped ST system was reported by Subodh et al. investigated the structure and MW dielectric properties of Sr(2+n)Ce2Ti(5+n)O16+3n (n ≤ 10) homologous series.8 X-ray photoelectron spectroscopy (XPS) studies have revealed that the ion valance state of cerium in such ceramics is primarily trivalent (Ce3+ ≥ 90%) rather than tetravalent (Ce4+ ≤ 10%); which leads to the correct molecular formula Sr(2+n)Ce2Ti(5+n)O15+3n (n ≤ 10).8 The Sr(2+n)Ce2Ti(5+n)O15+3n (n ≤ 10) solid solution could be alternative described by Sr(1−3x/2)CexTiO3 (x ≤ 0.4) ceramic systems. In sintering atmosphere air at 1300 °C/2 h, this ceramic system yields a dielectric constant (εr) ranging from 113 to 185, an intermediate Q × f between 6000 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz at 2 GHz, and a high temperature coefficient of the resonant frequency of +306 ppm per °C. Moreira et al. investigated the optical phonon spectra of Sr(1−3x/2)CexTiO3 (x ≤ 0.4) solid solution through Raman and infrared (IR) spectroscopy and revealed that εr is completely influenced by polar optical phonons due to its incipient ferroelectricity.9,10 Subodh and Moreira et al. observed the cubic symmetry of the Sr(1−3x/2)CexTiO3 (x ≤ 0.4) system through vibrational spectroscopy and XRD.8,9 Conversely, Ubic et al. performed X-ray, electron, and neutron diffraction analyses on Sr0.4Ce0.4TiO3 and revealed trigonal symmetry in R
000 GHz at 2 GHz, and a high temperature coefficient of the resonant frequency of +306 ppm per °C. Moreira et al. investigated the optical phonon spectra of Sr(1−3x/2)CexTiO3 (x ≤ 0.4) solid solution through Raman and infrared (IR) spectroscopy and revealed that εr is completely influenced by polar optical phonons due to its incipient ferroelectricity.9,10 Subodh and Moreira et al. observed the cubic symmetry of the Sr(1−3x/2)CexTiO3 (x ≤ 0.4) system through vibrational spectroscopy and XRD.8,9 Conversely, Ubic et al. performed X-ray, electron, and neutron diffraction analyses on Sr0.4Ce0.4TiO3 and revealed trigonal symmetry in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group because of octahedral tilting.11 Further, it was explored that the MW dielectric properties of the Sr(1−3x/2)CexTiO3 ceramic system with an increasing x are directly related to their solid solubility and crystal symmetry partly because of the sensitivity of Sr(1−3x/2)CexTiO3 ceramics to processing variables, such as sintering temperature, atmosphere, and time.7–10 Considering the potential value of these ceramic systems in various microwave applications, it is necessary and meaningful to carry out some initial study to modify its ferroelectric and MW dielectric properties.
c space group because of octahedral tilting.11 Further, it was explored that the MW dielectric properties of the Sr(1−3x/2)CexTiO3 ceramic system with an increasing x are directly related to their solid solubility and crystal symmetry partly because of the sensitivity of Sr(1−3x/2)CexTiO3 ceramics to processing variables, such as sintering temperature, atmosphere, and time.7–10 Considering the potential value of these ceramic systems in various microwave applications, it is necessary and meaningful to carry out some initial study to modify its ferroelectric and MW dielectric properties.
In this study, the solid solution of Sr(1−3x/2)CexTiO3 (x = 0.1–0.6) ceramic system was reported in detail. Ce doping can be applied to enhance the dielectric and ferroelectric responses of ST ceramics. Regarding the Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) solid solution system, in contrast to what is written by Subodh and Moreira et al.8,9 in their abstract, no ferroelectric behavior was observed and, hence, reported incipient ferroelectric nature for SrTiO3 substituted with Ce on the A-sites. However, for the orthorhombic (Sr0.25Ce0.5TiO3, sintered in nitrogen) solid solution, we find the novel dielectric behavior along with the formation of superstructure reflections. Finally, apart from novel dielectric behavior there are other evidences of the relaxor as well as ferroelectric nature for the orthorhombic Sr0.25Ce0.5TiO3 solid solution. Understanding the origin and fundamental mechanism of the reported enhancement in this work should be elucidated to improve further the dielectric and ferroelectric properties of SrTiO3-based ceramics.
2. Experimental section
2.1 Synthesis
A conventional solid-state reaction was used to prepare Sr(1−3x/2)CexTiO3 (x = 0.1–0.6) solid solution using SrCO3 (≥99.98% purity), CeO2 (≥99.99% purity) and TiO2 (≥99.98% purity). Stoichiometric amount of raw powders were weighted and mixed using moderate ball-mill for 24 h with yttria-stabilized zirconia (YSZ) media in ethanol. The mixture powders were calcined at 1200 °C for 10 h in air after being dried at 80 °C. The powders were pressed into samples with average diameter of 12 mm and about 6 mm in height under a pressure of 200 MPa. The pellets were embedded in the same calcined powder to minimize loss. These pallets were then preheated at 650 °C, for 2 h, to burn the binder before sintering in nitrogen at temperatures ranging from 1300 to 1400 °C for 3 h with heating rate of 600 °C h−1. Before the pellets were characterized, the surfaces of all sintered ceramics had been wiped off carefully to minimize the effects of oxide loss caused by evaporation. The lattice parameters were calculated using a least square refinement method. The bulk densities of the sintered ceramics were measured with Archimedes method. The relative densities were obtained on the basis of bulk and theoretical densities. The theoretical densities of the solid solution samples were calculated using eqn (1):
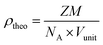 | (1) |
2.2 Structure/chemical analysis
The structure and morphology of the samples were studied using X-ray diffractometer (XRD-7000, Shimadzu, Kyoto, Japan) with Cu Kα radiation, transmission electron microscopy (TEM, Tecnai G2 20, FEI, Oregon, USA), and scanning electron microscope (FSEM, Sirion 200, FEI, Eindhoven, the Netherlands). For TEM analysis, the ceramic samples were disposed by the conventional method of mechanical thinning, dimpling, and ion beam milling. The chemical structure was analyzed through X-ray photoelectron spectroscopy (AXIS-ULTRA DLD-600W, Shimadzu, Kyoto, Japan).2.3 Dielectric properties analysis
The permittivity (εr) and the unloaded Q × f value were measured in the TE011 mode by Hakki and Coleman method using a microwave network analyzer (Agilent E8362B Agilent Technologies, Santa Clara, USA) and a waveguide of parallel silver boards.12 The temperature coefficient of resonant frequency (τf) in the temperature range of 25 °C to 80 °C was calculated with the following equation:
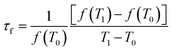 | (2) |
3. Results and discussion
3.1 Phase-chemical structure of SCT ceramics
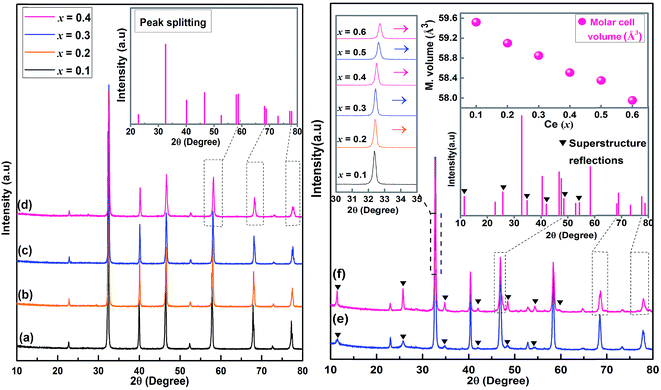
Sr(1−3x/2)CexTiO3 ceramics sintered in nitrogen exhibited peaks associated with the solid solution of perovskite phase (Fig. 1a–f). Samples with x ≤ 0.3 appeared cubic by XRD (ST-like structure, space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, JCPDS # 86-0176), but for x = 0.4, the splitting of the major perovskite peaks at higher 2θ angles (46.81° and 77.78°) indicated tetragonal structure (ST-like structure, PDF # 46-1235). Upon examination of the major perovskite peaks, splitting or broadening was not observed with x ≤ 0.3; thus, for x ≤ 0.3, there is no tetragonal distortion, and this phenomenon is consistent with that of Subodh and Moreira et al.8,9 On the basis of electron and neutron diffraction analyses, Ubic et al. revealed trigonal symmetry in R
m, JCPDS # 86-0176), but for x = 0.4, the splitting of the major perovskite peaks at higher 2θ angles (46.81° and 77.78°) indicated tetragonal structure (ST-like structure, PDF # 46-1235). Upon examination of the major perovskite peaks, splitting or broadening was not observed with x ≤ 0.3; thus, for x ≤ 0.3, there is no tetragonal distortion, and this phenomenon is consistent with that of Subodh and Moreira et al.8,9 On the basis of electron and neutron diffraction analyses, Ubic et al. revealed trigonal symmetry in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group for Sr0.4Ce0.4TiO3, because of octahedral tilting.11 By contrast, the samples with 0.5 ≤ x ≤ 0.6 exhibited only peaks associated with the orthorhombic structure (space group Pmmm (47), JCPDS # 70-3939). At 0.5 ≤ x ≤ 0.6, the splitting of major perovskite peaks, along with the appearance of superstructure reflections, indicated an orthorhombic structure, which was similarly observed in the Sr(1−3x/2)LaxTiO3 (SLT) ceramic system.4 The intensity of these superstructure reflections increased with Ce addition (Fig. 1e and f). The presence of superstructure reflections implies compositional ordering in the A-sites. The existence and the nature of these superlattice reflections were further confirmed through TEM analysis (Fig. 2a–d). Based on the inspection of TEM patterns, Sr(1−3x/2)CexTiO3 (x ≥ 0.5) exhibits planar defects and superlattice reflections consistent with a structure tilted in antiphase reflection (“α”) and antiparallel displacement of the A-site cation (“β”), which was in accordance with the work of Reaney,4 and Ubic et al.7,13
c space group for Sr0.4Ce0.4TiO3, because of octahedral tilting.11 By contrast, the samples with 0.5 ≤ x ≤ 0.6 exhibited only peaks associated with the orthorhombic structure (space group Pmmm (47), JCPDS # 70-3939). At 0.5 ≤ x ≤ 0.6, the splitting of major perovskite peaks, along with the appearance of superstructure reflections, indicated an orthorhombic structure, which was similarly observed in the Sr(1−3x/2)LaxTiO3 (SLT) ceramic system.4 The intensity of these superstructure reflections increased with Ce addition (Fig. 1e and f). The presence of superstructure reflections implies compositional ordering in the A-sites. The existence and the nature of these superlattice reflections were further confirmed through TEM analysis (Fig. 2a–d). Based on the inspection of TEM patterns, Sr(1−3x/2)CexTiO3 (x ≥ 0.5) exhibits planar defects and superlattice reflections consistent with a structure tilted in antiphase reflection (“α”) and antiparallel displacement of the A-site cation (“β”), which was in accordance with the work of Reaney,4 and Ubic et al.7,13
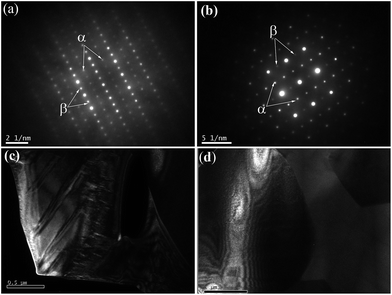 | ||
| Fig. 2 〈111〉 zone axis diffraction patterns from Sr(1−3x/2)CexTiO3 (x = 0.5 and 0.6) ceramics: (a) x = 0.5 and (b) x = 0.6. Superstructure reflections are indicated as follows: α = antiphase tilt reflection and β = antiparallel displacement of the A-site cation. The dark TEM images [(c) and (d), x = 0.5] reveals the presence of planar like defects similar to those reported as long range ferroelectric domains in Ba-based compositions by Stennett et al.14,15 | ||
These superstructure reflections possibly originated and/or resulted from the ordering of oxygen vacancies together with octahedral tilting. This ordered structure and/or ordering of oxygen vacancies was a probable associated with sintering and/or doping process. Furthermore, the tilting of the oxygen octahedra is a well-known phenomenon observed in SrTiO3 perovskite.4,11 Therefore, the splitting of the Bragg reflection of the simple cubic structures at higher 2θ angle, and the corresponding appearance of superstructure, may result from cell doubling induced by octahedral tilting.13 The dark and bright TEM images (Fig. 2c and d, x = 0.5) reveal the presence of planar-like defects, which are similar to those reported by Stennett et al. as long range ferroelectric domains in Ba-based compositions.14,15
A shift to higher angles was observed in the main SCT peaks, which indicates the shrinkage of the lattice due to the substitution by Ce3+ (rCe,XII3+ = 1.34 Å) of Sr2+ (rSr,XII2+ = 1.44 Å). The unit cell volume exhibited this shrinkage at x ≤ 0.4,9 before it sharply increased at x ≥ 0.5 with a positive slope, which was associated with the onset of a transition to an orthorhombic structure (Table 1). In general, the variation of lattice parameters and/or unit cell volume for ST-based solid solution with cerium addition is very small, and is likely determined by the complex defect formation and charge compensation mechanisms. In principle, cation and isolated oxygen vacancies were expected to have opposite effects on the dimensional changes of the crystal lattice, while consistently inducing cell expansion and contraction, whereas other effects caused by defect clusters should also not be neglected. Furthermore, other studies reported that the solubility of ceria in SrTiO3 (Sr(1−3x/2)CexTiO3, x ≤ 0.4) ceramics sintered in air was quite small (∼40%),8,9 which was primarily caused by the significant difference between the ionic sizes of Sr2+ (rSr2+ = 1.44 Å) and Ce4+ (rCe4+ = 0.87 Å), and/or the formation of core–shell-structured fine grains or layered intergrowth compounds. In contrast to this phenomenon, increasing the Ce(x) content, obviously and independently decreased the lattice parameters under the sintering atmosphere. This result indicated that the lower solubility of ceria in SrTiO3 is not due to the formation of core–shell-structured fine grains and/or layered intergrowth compounds. The phenomenon could be attributed to the absence of extra strontium vacancies in a sintering atmosphere air compared with that composed of sintering atmosphere nitrogen, which caused the partial dissolution of CeO2 in SrTiO3 ceramics. Therefore, the increase in the solubility of cerium in SrTiO3 ceramics (≥90%) indicates that nitrogen atmosphere is more beneficial than air in the formation of more vacancy defect.1,4
| Sr(1−3x/2)CexTiO3 | Structure parameters | Microwave dielectric parameters | |||||
|---|---|---|---|---|---|---|---|
| 0.1 ≤ x ≤ 0.6 | a (Å) | b (Å) | c (Å) | V (Å3) | εr | Q × f (GHz) | τf (ppm per °C) |
| Sr0.85Ce0.1TiO3 | 3.9044 | 3.9044 | 3.9044 | 59.52 | No resonant peak | — | — |
| Sr0.7Ce0.2TiO3 | 3.8952 | 3.8952 | 3.8952 | 59.14 | No peak | — | — |
| Sr0.55Ce0.3TiO3 | 3.8898 | 3.8898 | 3.8898 | 58.85 | 131 | 496 | 420 |
| Sr0.4Ce0.4TiO3 | 3.8856 | 3.8856 | 3.8773 | 58.69 | 113 | 8012 | 280 |
| Sr0.25Ce0.5TiO3 | 3.8852 | 3.8576 | 7.7514 | 116.17 | 82 | 8504 | 212 |
| Sr0.1Ce0.6TiO3 | 3.8680 | 3.8646 | 7.7083 | 115.22 | 50 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
3 |
Fig. 3a–d display the dense and nearly free porous microstructures of sintered ceramics except at x = 0.6. The variation tendency in the observed microstructure was consistent with the XRD results. Both patterns did not show any secondary phases (Fig. 1). For x ≤ 0.4, the stripes seen on the grains appeared to grow striations, which indicate that Ce ions acted as modifiers, and increased the ceramic grain size. However, the grain size obviously decreased at x ≥ 0.5, indicating the non-uniform distribution of grains, which were approximately 2–10 μm in size.
 | ||
| Fig. 3 Scanning electron microscope images of the sintered unpolished samples surfaces of Sr(1−3x/2)CexTiO3 ceramics: (a) x = 0.3, (b) x = 0.4, (c) x = 0.5 and (d) x = 0.6. | ||
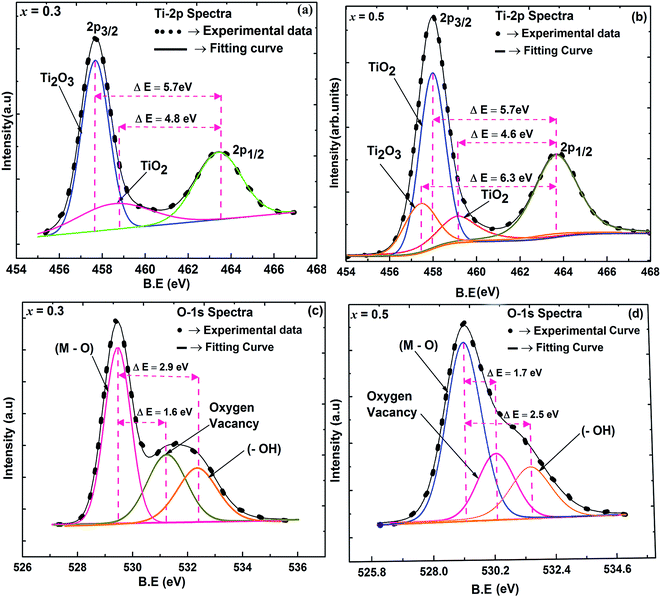
X-ray photoelectron spectra (XPS) was performed to confirm the chemical structure evolution of the Sr(1−3x/2)CexTiO3 ceramic system (Fig. 4a–f and Table 2). The Ti-2p and O-1s region in SCT (x = 0.3 and 0.5) samples fitted well into the Gaussian sub peaks (Fig. 4a–f). The binding energies of the peaks (Fig. 4a–f) were found to be within the reported values as illustrated in Table 2. The peak at around 532.1 eV was attributed to the oxide in hydroxide (–OH), which included the absorption of oxygen on the surface of the Sr(1−3x/2)CexTiO3 ceramics in the form H2O and/or O2.17,18 Adding small amounts of ceria (x ≤ 0.3) enhanced the peaks area ratio of Ti3+/Ti(total) and O2/O(total), whereas addition of large amounts of ceria (x ≥ 0.4) inhibited this process (Fig. 4 and Table 2). This result implies that cerium ion acts as a donor (Sr-site), and thus, its incorporation requires the formation of effectively negative charge compensating lattice defects (electrons, ionized cation vacancies). On the basis of XPS studies, Subodh et al.8 revealed that Ti3+ ions were not detected in Sr(1−3x/2)CexTiO3 (x ≤ 0.4) solid solution sintered in air at 1300 °C for 2 h.8 The reduction of Ti4+ cations can be described principally in terms of either the formation of oxygen vacancies (reaction (3)) or oxygen vacancies, and Ti3+ cations (reaction (4)), which are computed as follows:
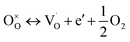 | (3) |
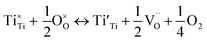 | (4) |
| Binding energy (eV) | Relative peak area ratio | Reference | ||||||
|---|---|---|---|---|---|---|---|---|
| Sr(1−3x/2)CexTiO3 | Ti-2p3/2, 2p1/2 | (O-1s) | –OH | |||||
| x = 0.3, 0.5 | Ti(IV) | Ti(III) | O1 (atom) | O2 (vacancy) | (–OH) | ATi3+/ATi(total) | AO2/AO(T) | Ti, O2, OH |
| Sr0.55Ce0.3TiO3 | 458.6 | 457.7 | 529.4 | 531.0 | 532.3 | 48% | 51% | 1, 17 and 18 |
| 463.4 | ||||||||
| Sr0.25Ce0.5TiO3 | 458.0 | 457.6 | 529.1 | 530.8 | 531.6 | 18% | 21% | 16–18 |
| 458.8 | ||||||||
| 463.5 | ||||||||
For composition x ≤ 0.2, the oxygen vacancies may be doubly ionized due their giant dielectric (εr) behavior. The Ti3+ cation can be viewed as a Ti4+·e, which caused the formation of defect dipoles, 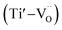 and
and 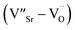 .1 Further, for the samples x ≥ 0.4, the decrease in the peak area ratios of [Ti3+/Titotal] and [O2/Ototal] was in accordance with the chemical composition (Table 2). This decrease implies that the substitution by ceria on the Sr-site generated electrons and A-site cation vacancies (Sr-vacancies), which combined with and led to the degradation in the amount of oxygen vacancies described as follows:
.1 Further, for the samples x ≥ 0.4, the decrease in the peak area ratios of [Ti3+/Titotal] and [O2/Ototal] was in accordance with the chemical composition (Table 2). This decrease implies that the substitution by ceria on the Sr-site generated electrons and A-site cation vacancies (Sr-vacancies), which combined with and led to the degradation in the amount of oxygen vacancies described as follows:
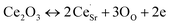 | (5) |
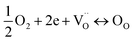 | (6) |
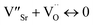 | (7) |
The decrease in the relative amount of oxygen vacancies and Ti3+ cation with ceria content, which was expected to significantly promote the microwave dielectric properties of SCT ceramics, was in good agreement with the present study.
3.2 Dielectric properties of SCT ceramics
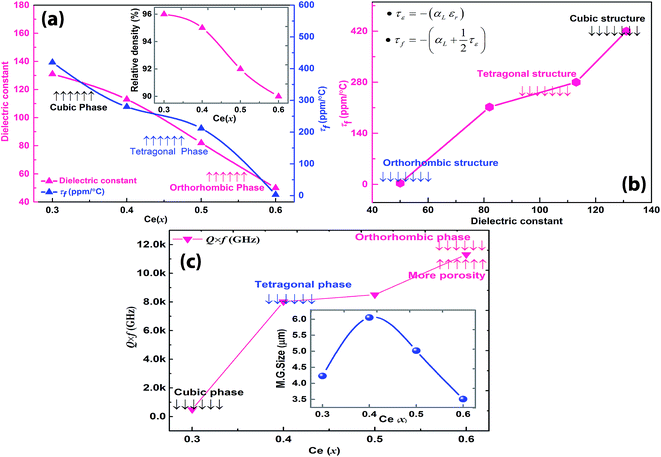
The variations of the microwave dielectric properties as functions of cerium content of the solid solution Sr(1−3x/2)CexTiO3 (x = 0.1–0.6) are illustrated in Fig. 5. In the Sr(1−3x/2)CexTiO3 ceramic system, the dielectric constant (εr), quality factor (Q × f), and percentage density reached their maximum values at 1300 °C/3 h, whereas further increase in the sintering temperature caused the degradation of the microwave dielectric properties. The composition dependence behavior of εr and τf showed similar variation trends, whereas the Q × f value exhibited the opposite behavior, that is, the values of εr and τf decreased, and the Q × f values increased non-monotonically with increasing cerium content. εr and τf were affected by a number of factors, such as volume of TiO6 octahedra, tilting of the octahedra, and polarizability of the ions.19,20 Vacancies produced by the substitution of cations with different ion valence states, such as substitution of Sr2+ with cerium in large cation sites, play an important role in obtaining good quality dielectric properties.20 Due to the substitution of larger Sr2+ ions with smaller Ce3+ ions, the octahedral B-site containing Ti ions shrunk, producing smaller εr, τf, and comparatively large Q × f values.21 No previous data could be found for the orthorhombic Sr0.1Ce0.6TiO3 solid solution; however, in this work, εr was set to 50, Q × f = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 GHz, and τf = +3 ppm per °C at 4 GHz (Fig. 5a–c).
311 GHz, and τf = +3 ppm per °C at 4 GHz (Fig. 5a–c).
The interpretations of εr and τf showed that the properties displayed strong dependence on composition (Fig. 5a; Table 1). For samples with x ≤ 0.2, microwave dielectric properties cannot be obtained because of their conductive characteristic and no resonant peak during measurement, which was primarily caused by the presence of oxygen vacancies 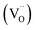 and defect dipoles, such as
and defect dipoles, such as 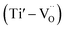 and
and 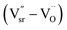 (see ESI† for x ≤ 0.2, Fig. 6).1 For the solid solution with x ≥ 0.3, a second phase was not detected; conversely, εr and τf decreased monotonically, which can be attributed to the decrease in relative density (Fig. 5a), structure transition (XRD, Fig. 1a–f), and change in crystal symmetry induced by the coexistence of in-phase and antiphase tilting (TEM, Fig. 2a and b). At x ≥ 0.3, the large decrease in εr of SrTiO3 (εr = 300, Q × f = 3000 GHz, τf = +1650 ppm per °C)8,9 was unexpected because Ce3+ yields an ionic polarizability [αD (Ce3+) = 6.15 Å3] larger than Sr2+ [αD (Sr2+) = 4.24 Å3] ion.22 This decrease can be attributed to the change in TiO6 octahedra and to the vibration between the TiO6 octahedron and the A-site cation, which directly influences the effective ionic polarizabilities.10,19–21 A similar phenomenon was observed by Subodh and Moreira et al.8,9 in Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) solid solution, which exhibits a drastic decrease in dielectric constant.
(see ESI† for x ≤ 0.2, Fig. 6).1 For the solid solution with x ≥ 0.3, a second phase was not detected; conversely, εr and τf decreased monotonically, which can be attributed to the decrease in relative density (Fig. 5a), structure transition (XRD, Fig. 1a–f), and change in crystal symmetry induced by the coexistence of in-phase and antiphase tilting (TEM, Fig. 2a and b). At x ≥ 0.3, the large decrease in εr of SrTiO3 (εr = 300, Q × f = 3000 GHz, τf = +1650 ppm per °C)8,9 was unexpected because Ce3+ yields an ionic polarizability [αD (Ce3+) = 6.15 Å3] larger than Sr2+ [αD (Sr2+) = 4.24 Å3] ion.22 This decrease can be attributed to the change in TiO6 octahedra and to the vibration between the TiO6 octahedron and the A-site cation, which directly influences the effective ionic polarizabilities.10,19–21 A similar phenomenon was observed by Subodh and Moreira et al.8,9 in Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) solid solution, which exhibits a drastic decrease in dielectric constant.
Subodh et al.8 calculated the tolerance factor for the Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) ceramic system, and concluded that the substitution by Ce(x) at the A-site (Sr2+) linearly affected the tolerance factor, resulting in the decrease in the value of εr and τf. However, Moreira et al.9 collected infrared and Raman spectra for Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) ceramics, and concluded that their observed decrease in εr was probably due to the presence of polar soft modes phonon, and the influence of extrinsic cerium ions and their associated vacancies.9 Furthermore, the amount of A-site vacancy was proportional to the x value. Increase in the number of vacancies, and the difference in ionic radii [Ce3+ (rCe,XII3+ = 1.34 Å), Sr2+ (rSr,XII2+ = 1.44 Å), Ce4+ (rCe,XII4+ = 1.14 Å), and Ti4+ (rTi,VI4+ = 0.605 Å)] resulted in the shrinkage of the B-site due to the decrease in the lattice parameters (Table 1).21,23 The decrease in εr with increasing x was probably caused by the shrinkage of the B-site; the octahedron normally occupied by the Ti ion.21 Conversely, τf is a composite parameter related to temperature coefficient of permittivity (τε), and the linear expansion coefficient, αL, is determined by the following relationship:
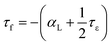 | (8) |
Fig. 5a indicates that the value of τf decreased almost linearly with increasing CeO2 content, due to the compensation that was entirely analogous to that of the εr values. Considering the effect of the monotonic increase in Ce(x) in SrTiO3, the net result diluted the ionic polarizability of SrTiO3, reduced εr and hence τf, which correspond to the previously reported data.7,19–21 In reality, the temperature coefficient of permittivity (τε) controls the value of the τf. Adjusting the value of τε to obtain a τf with a value of zero (no frequency drift) is probably the most difficult aspect in the development of a MW dielectric ceramic. When τf was plotted against εr, the relationship was almost linear (Fig. 5b), which is in accordance with the work of Cairns and Reaney et al.20 However, slight deviations occurred in τf, which were possibly caused by the gradual evolution in structure (Fig. 5b). First, the value of τf changed from a more positive (x = 0.3, τf = +420 ppm per °C) to a less positive value (x = 0.4, τf = +212 ppm per °C) at the onset of the cubic-to-tetragonal (x = 0.4) phase transition. Second, the τf value changed from a less positive (x = 0.4, τf = +212 ppm per °C) to near zero (x = 0.6, τf = +3 ppm per °C) at the onset of the tetragonal-to-orthorhombic (x = 0.6) phase transition, which is characterized by anti-phase and in-phase superstructure lattice (Fig. 5b). Therefore, τf in perovskite-like structure materials is fundamentally associated with the onset of structural phase transitions involving the tilting of the octahedra.19–21
Fig. 5c shows the variation in the Q × f value of Sr(1−3x/2)CexTiO3 (0.3 ≤ x ≤ 0.6) ceramics sintered in nitrogen. The Q × f value is affected by a number of factors, such as grain growth, oxygen vacancies, size of cation site, ordering of cation, shift in cation position, and divalent cation distribution.23–25 For all compositions with x ≤ 0.6, we observed that the Q × f value increased non-monotonically, which correlated with the formation of solid solution and existence of ordering. The onset of ordering expanded the original unit cell (x ≥ 0.5, Table 1), and split the major perovskite reflections. The presence of order is commensurate with the increase in Q × f to a maximum value of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 GHz at 4 GHz.26 For x ≥ 0.3, the Q × f values were obviously improved, however, the observed improvement weakened with increasing x (Fig. 5c). The corresponding improvement in Q × f is easy to understand, however, the increase was limited because of the excess amount of vacancy defects in the ST lattice (Fig. 4 and Table 2). The specific improvement in the Q × f value can be ascribed to the reduction in Ti4+ ions, and presence of vacancy defects (reaction (4)), because vacancy defects can generate anharmonic vibration, and thus, cause extrinsic dielectric loss.27 Therefore, the formation of oxygen vacancies (Fig. 4 and Table 2) is a plausible explanation for the increase in the anharmonicity of vibrations.26 For most dielectrics, a material with a larger εr has a smaller Q × f value due to the increasing anharmonic terms.
311 GHz at 4 GHz.26 For x ≥ 0.3, the Q × f values were obviously improved, however, the observed improvement weakened with increasing x (Fig. 5c). The corresponding improvement in Q × f is easy to understand, however, the increase was limited because of the excess amount of vacancy defects in the ST lattice (Fig. 4 and Table 2). The specific improvement in the Q × f value can be ascribed to the reduction in Ti4+ ions, and presence of vacancy defects (reaction (4)), because vacancy defects can generate anharmonic vibration, and thus, cause extrinsic dielectric loss.27 Therefore, the formation of oxygen vacancies (Fig. 4 and Table 2) is a plausible explanation for the increase in the anharmonicity of vibrations.26 For most dielectrics, a material with a larger εr has a smaller Q × f value due to the increasing anharmonic terms.
3.3 Relaxor behavior of SCT ceramics
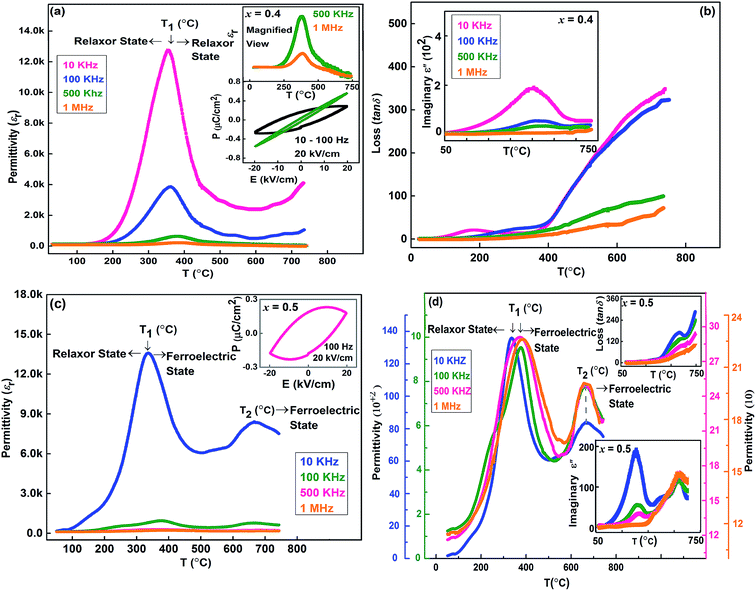
The temperature-dependent permittivity, imaginary part of permittivity, dielectric loss, and hysterics loop of Sr(1−3x/2)CexTiO3 ceramics (x = 0.4, 0.5) is shown in Fig. 6. In a pure and unstressed form, SrTiO3 is an incipient ferroelectric material, although chemical28,29 or isotopic substitution30 and stress application can easily disturb this sensitive state and induce ferroelectricity.2 Haeni et al. revealed the ferroelectricity in strained SrTiO3 thin film at room temperature.2 On the basis of infrared (IR) and Raman spectroscopy, Moreira et al. revealed the incipient ferroelectric nature of Sr(1−3x/2)CexTiO3 (x ≤ 0.4, sintered in air) ceramics.9,10 Experimental and theoretical results have also revealed that the physical properties of RE ion-doped ST are dominated by oxygen vacancies and lattice defects. Ang et al. observed the coexistence of several dielectric peaks with different physical characteristics in Bi-doped ST perovskite, and some of them disappeared with the addition of Bi.30,31 However, Durán et al. observed a permittivity anomalous peak in Pr-doped ST ceramics around 238 °C, which suggested that the ferroelectric state can exist at room temperature in a Pr-doped ST ceramic system.32 As illustrated in Fig. 6, the SCT ceramics displays a relaxor and normal ferroelectric behavior under high impurity doping. With compositions of x = 0.4 and 0.5, both samples displayed high permittivity (εr) anomaly (T1 ≤ 500 °C, Fig. 6a–c), which is the usual sign of a relaxor behavior. Nevertheless, the temperature Tm of εr maximum not only shifted towards higher temperature but also the εr anomaly shifted toward a lower value and nearly stabilized at 670 °C for x = 0.5 (Fig. 6b and c), which is a possible sign of normal ferroelectric state.33 On other hand, the higher values of permittivity (εr) at lower frequencies are due to the existence of different types of polarizations in the SCT ceramic. However, at high frequencies some of the polarizations may have less contribution to εr. This nature of variation is very much consistent with that of normal ferroelectrics. Furthermore, the same composition exhibited a hysteresis loop (P–E loop); therefore, the observed relaxation is a manifestation of relaxor ferroelectric behavior. Considering this phenomenon, we propose that the presence of Ce3+ and Ce4+ at the A-site (Sr sites) likely induce the formation of Ce3+/Ce4+ − VSr centers; this finding is consistent with that observed in Pr-doped SrTiO3 ceramics.34 The formation of Ce3+/Ce4+ − VSr centers is responsible for the appearance of a random strain field and local electric, which can induce a ferroelectric domain state and promote a relaxor ferroelectric behavior.14,15,34 In addition, the polarization originating from the ionic and/or dipole displacement contribution is known to be the off-center displacement for tetravalent Ti4+ ions from the anionic charge center of the oxygen octahedron in the ABO3 perovskite system.34,35The presence of oxygen vacancies in the ST ceramics distorts the actual ionic dipoles due to the presence of Ti4+ ions. The corresponding decay of polarization caused by the distorted ionic dipoles is a possible explanation for the observed relaxation phenomena. Based on these facts, it is reasonable to assume that the dipoles formed by off centered Ce ions behave as non-interaction dipoles, and hence the reorientation of the dipoles leads to the observed relaxor behavior. Therefore, it is reasonable to assume that there are two types of polar regions and/or dipoles existing: one is the nano-domain, which contributes to the ferroelectric state, and the other is micro-polar regions, which are the source leading to the slightly broading relaxor behavior.30 In fact, analog to the Sr(1−1.5x)BixTiO3 ceramics system, the compositional format of the novel solid solution “a relaxor ferroelectric + a normal ferroelectric” suggests plausible presence of different polarization mechanisms.29–31
3.4 Ferroelectric behavior of SCT ceramics
In contrast to the above phenomena, the orthorhombic solid solution Sr0.25Ce0.5TiO3 (x = 0.5, Fig. 6c and d) displayed a normal ferroelectric behavior (T2 = 670 °C, Fig. 6b and c), and this finding is consistent with that reported by Kamba et al.35 The ferroelectric behavior can be attributed to the decrease in the cation size; as a result, instabilities begin to set in. For Ti-based structural materials, the instability can lead to ferroelectricity.2,28,36 Furthermore, the slight broadening of the εr peaks at x = 0.5 (T2 = 670 °C, 10 kHz) is related to the compositional fluctuations and point defects, such as vacancies and/or grain boundaries, attributed to Ce(x) insertion effect in the solid solution.35 In analogy with the previous studies on Sr(1−x)PrxTiO3 (SPT) and Sr(1−x)CaxTiO3 (SCT) ceramics,34,37 inducing a ferroelectric state in doped incipient ferroelectric ceramics systems is closely correlated to the development of polar nanoregions (PNRs) around the defect sites,34 the size of which grows on approaching Tm from the high-temperature side because of the coupling with the soft ferroelectric mode.34,37 The consequent development of such a ferroelectric state suggests the presence of dipolar species with giant dipole moments at defect sites. These giant dipoles are able to create PNRs of sufficiently large size even at high temperatures; such that they can overlap and eventually lead to the development of a ferroelectric state.28,35 In contrast to the these phenomena, the smaller Ce3+ (rCe,XII3+ = 1.34 Å) and Ce4+ (rCe,XII4+ = 1.14 Å) than Sr2+ (rSr,XII2+ = 1.44 Å) can cause Ce3+/Ce4+ to take up off-centered positions and create electric dipoles around which PNRs can develop.34–37 Alternatively, Ti4+(rTi,VI4+ = 0.605 Å) near a Ce site may also occupy an off-centered position; as a result, local ferroelectric distortions may occur because of the favorable hybridization between Ti-d and O-2p orbitals36–38 assisted by a local strain attributed to the size mismatch between host and guest ions.In Fig. 6b and (d), the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) increased continuously and reached to the maximum value at approximately tan
δ) increased continuously and reached to the maximum value at approximately tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≤ 400 (10 kHz). Afterward, loss (tan
δ ≤ 400 (10 kHz). Afterward, loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) sharply decreased as the applied frequency increased. This is phenomenon could be attributed to the presence of oxygen vacancy in the ST lattice (Fig. 4a–d). The vacancies in the SCT ceramic system can be polarized in an alternating electric field; as a result, the dielectric loss increases. The loss (tan
δ) sharply decreased as the applied frequency increased. This is phenomenon could be attributed to the presence of oxygen vacancy in the ST lattice (Fig. 4a–d). The vacancies in the SCT ceramic system can be polarized in an alternating electric field; as a result, the dielectric loss increases. The loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) peak is slightly lower than the observed permittivity (εr) peak for a particular frequency, which further supports the suggestion of relaxor behavior of Sr(1−3x/2)CexTiO3. Further, the shoulder in the imaginary part of permittivity could be due to the decrease in the capacitance of the PNRs. The origin of this decrease in capacitance can be caused by two reasons: the permittivity and/or the geometry of the PNRs. However, in this situation it is also interesting to note that the relaxation above room temperature (RT) in the imaginary part of permittivity, attributed to Maxwell–Wagner relaxation, has been reported even in pure SrTiO3 ceramics.40 The asymmetric relaxation peaks in the imaginary part of the permittivity observed in Ce-doped ST can therefore have contributions from the Maxwell–Wagner process as well.
δ) peak is slightly lower than the observed permittivity (εr) peak for a particular frequency, which further supports the suggestion of relaxor behavior of Sr(1−3x/2)CexTiO3. Further, the shoulder in the imaginary part of permittivity could be due to the decrease in the capacitance of the PNRs. The origin of this decrease in capacitance can be caused by two reasons: the permittivity and/or the geometry of the PNRs. However, in this situation it is also interesting to note that the relaxation above room temperature (RT) in the imaginary part of permittivity, attributed to Maxwell–Wagner relaxation, has been reported even in pure SrTiO3 ceramics.40 The asymmetric relaxation peaks in the imaginary part of the permittivity observed in Ce-doped ST can therefore have contributions from the Maxwell–Wagner process as well.
The hysteresis loop (P–E loop) observed at room temperature (RT) in Sr(1−3x/2)CexTiO3 (x = 0.4 and 0.5) yields about an average remnant polarization of 0.35 μC cm−2 at different frequency. The lossy and the rounding of hysteresis loop often result from variable oxidation states of Ce and Ti ions, from oxygen vacancies, structure distortion or from both.31,39 For composition x = 0.5, the reduction in oxygen vacancies, and hence account for better ferroelectric properties. In order to further analyze the ferroelectric nature of Sr(1−3x/2)CexTiO3 ceramics, remnant polarization testing (Positive-Up–Negative-Down (PUND) procedure was proposed to identify intrinsic ferroelectricity.41,42 The existence of remnant polarization of 0.0072 μC cm−2 for x = 0.4 and 0.026 μC cm−2 for x = 0.5 is further strong evidence for the ferroelectric nature of Sr(1−3x/2)CexTiO3 ceramics as illustrating in Fig. 7.
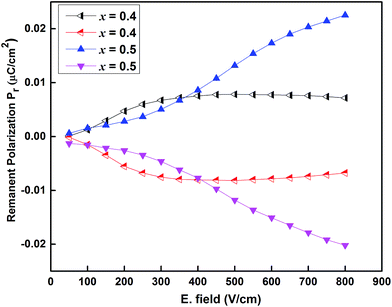 | ||
| Fig. 7 Intrinsic remnant polarization of the polish sintered samples of Sr(1−3x/2)CexTiO3 ceramics for composition with x = 0.4 and x = 0.5. | ||
4. Conclusions
Sr(1−3x/2)CexTiO3 (x = 0.1–0.6) ceramics were synthesized through a conventional solid-state method. In this method, non-stoichiometric variation was facilitated by incorporating Ce ions into the Sr-site of the ST lattice. XRD analysis revealed that the structure of the samples with x ≤ 0.3 appeared cubic but exhibited splitting and superstructure reflections consistent with tetragonal (x = 0.4) and orthorhombic (0.5 ≤ x ≤ 0.6) structures. Chemical analysis results demonstrated that the addition of small amounts of ceria (0.1 ≤ x ≤ 0.3) significantly promoted oxygen vacancy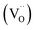 . By contrast, the addition of large amounts of ceria (0.4 ≤ x ≤ 0.6) inhibited this process. The orthorhombic solid solution (Sr0.25Ce0.5TiO3) sintered in nitrogen showed an intermediate εr (50), the highest Q × f (11
. By contrast, the addition of large amounts of ceria (0.4 ≤ x ≤ 0.6) inhibited this process. The orthorhombic solid solution (Sr0.25Ce0.5TiO3) sintered in nitrogen showed an intermediate εr (50), the highest Q × f (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 GHz), and the most stable τf (+3 ppm per °C) among RE-doped SrTiO3 ceramics. Finally, apart from novel dielectric behavior there are other evidences of the ferroelectric nature for the orthorhombic Sr0.25Ce0.5TiO3 solid solution. These results led us to conclude that A-site donor doping of SrTiO3 with Ce was not a feasible sintering condition for samples sintered in air. Instead, we proposed the favored sintering atmosphere to be the creation of more vacancy defects (Sr and oxygen vacancies) and the source of the novel dielectric, relaxor and ferroelectricity response, should be the expanding solubility limit of Sr(1−1.5x)CexTiO3 (x ≤ 0.6, sintered in nitrogen) ceramics. It is clear, therefore, that thermodynamics and/or sintering atmosphere can both play an important role in shaping the physical properties of these materials. The present enhancement in this work may open new possibilities for other properties and applications of this broadly functional perovskite material.
311 GHz), and the most stable τf (+3 ppm per °C) among RE-doped SrTiO3 ceramics. Finally, apart from novel dielectric behavior there are other evidences of the ferroelectric nature for the orthorhombic Sr0.25Ce0.5TiO3 solid solution. These results led us to conclude that A-site donor doping of SrTiO3 with Ce was not a feasible sintering condition for samples sintered in air. Instead, we proposed the favored sintering atmosphere to be the creation of more vacancy defects (Sr and oxygen vacancies) and the source of the novel dielectric, relaxor and ferroelectricity response, should be the expanding solubility limit of Sr(1−1.5x)CexTiO3 (x ≤ 0.6, sintered in nitrogen) ceramics. It is clear, therefore, that thermodynamics and/or sintering atmosphere can both play an important role in shaping the physical properties of these materials. The present enhancement in this work may open new possibilities for other properties and applications of this broadly functional perovskite material.
Acknowledgements
This work was supported by national natural science foundation of China (NSFC-61172004, 51572093) and Chinese Scholarship Council (CSC). The authors are grateful to the analytical testing centre and national lab for optoelectronics, Huazhong University of Science and Technology for XPS and SEM analysis.References
- Z. Wang, M. Cao, Q. Zhang, H. Hao, Z. Yao, Z. Wang, Z. Song, Y. Zhang, W. Hu and H. Liu, J. Am. Ceram. Soc., 2015, 98(2), 476–482 CrossRef CAS.
- J. H. Haeni, P. Irvin, W. Chang, R. Uecker, P. Reiche, Y. L. Li, S. Choudhury, W. Tian, M. E. Hawley, B. Craigo, A. E. Tagantsev, X. Q. Pan, S. K. Streiffer, L. Q. Chen, S. W. Kirchoefer, J. Levy and D. G. Scholm, Nature, 2004, 430, 758 CrossRef CAS PubMed.
- K. Uchida, S. Tsuneyuki and T. Schimizu, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(17), 107–174 CrossRef.
- Z. Lu, H. Zhang, W. Lei, D. C. Sinclair and I. M. Reaney, Chem. Mater., 2016, 28(3), 925–935 CrossRef CAS.
- D. J. Cumming, V. V. Kharton, A. A. Yaremchenko, A. V. Kovalevsky and J. A. Kilner, J. Am. Ceram. Soc., 2011, 94(9), 2993–3000 CrossRef CAS.
- D. J. Cumming, J. A. Kilner and S. Skinner, J. Mater. Chem., 2011, 21(13), 5021–5026 RSC.
- R. Ubic, K. Khamoushi, D. Iddles and T. Price, J. Ceram. Trans., 2005, 167, 21–30 CAS.
- G. Subodh, J. James, M. T. Sebastian, R. Paniago, A. Dias and R. L. Moreira, Chem. Mater., 2007, 19(16), 4077–4082 CrossRef CAS.
- R. L. Moreira, R. P. Lobo, G. Subodh, M. T. Sebastian, F. M. Matinaga and A. Dias, Chem. Mater., 2007, 19(26), 6548–6554 CrossRef CAS.
- R. L. Moreira, R. P. Lobo, G. Subodh, M. T. Sebastian, M. V. Jacob and A. Dias, J. Phys. D: Appl. Phys., 2009, 42, 075411 CrossRef.
- R. Ubic, G. Subodh, D. Gout, M. T. Sebastian and T. Proffen, Chem. Mater., 2009, 21(19), 4706–4710 CrossRef CAS.
- B. W. Hakki and P. D. Coleman, IRE Trans. Microwave Theory Tech., 1960, 8(4), 402–410 CrossRef.
- P. D. Battle, J. E. Bennett, J. Sloan, R. J. D. Tilley and J. F. Vente, J. Solid State Chem., 2000, 149, 360–369 CrossRef CAS.
- M. C. Stennett, I. M. Reaney, G. C. Miles, D. I. Woodward, A. R. West, C. A. Kirk and I. J. C. Levin, Appl. Phys. A: Mater. Sci. Process., 2007, 101(10), 104114 Search PubMed.
- X. Zhu, M. Fu, M. C. Stennett, P. M. Vilarinho, I. Levin, C. A. Randall, J. Gardner, F. D. Morrison and I. M. Reane, Chem. Mater., 2015, 27, 3250–3261 CrossRef CAS.
- A. V. Kovalevsky, S. Populoh, S. G. Patrício, P. Thiel, M. C. Ferro, D. P. Fagg, J. R. Frade and A. Weidenkaff, J. Phys. Chem. C, 2015, 119, 4466–4478 CAS.
- K. Kim, S. Y. Park, K. H. Lim, C. Shin, J. M. Myoung and Y. S. Kim, J. Mater. Chem., 2012, 22(43), 23120–23128 RSC.
- Y. Jung, W. Yang, C. Y. Koo, K. Song and J. Moon, J. Mater. Chem., 2012, 22(12), 5390–5397 RSC.
- P. L. Wise, I. M. Reaney, W. E. Lee, T. J. Price, D. M. Iddles and D. S. Cannell, J. Eur. Ceram. Soc., 2001, 21(10–11), 1723–1726 CrossRef CAS.
- D. L. Cairns, I. M. Reaney, N. Otten, D. Iddles and T. Price, J. Eur. Ceram. Soc., 2006, 26, 875–882 CrossRef CAS.
- H. Ohsato, T. Ohhashi, H. Kato, S. Nishigaki and T. Okuda, Jpn. J. Appl. Phys., Part 1, 1995, 34, 187–191 CrossRef CAS.
- R. D. Shannon, J. Appl. Phys., 1993, 73, 348–366 CrossRef CAS.
- H. Ohsato, J. Eur. Ceram. Soc., 2001, 21, 2703–2711 CrossRef CAS.
- R. Lowndes, F. Azough, R. Cernik and R. Freer, J. Eur. Ceram. Soc., 2012, 32, 3791–3799 CrossRef CAS.
- I. S. Kim, W. H. Jung, Y. Inaguma, T. Nakamura and M. Itoh, Mater. Res. Bull., 1995, 30, 307–316 CrossRef CAS.
- I. M. Reaney and D. Iddles, J. Am. Ceram. Soc., 2006, 89(7), 2063–2072 CAS.
- B. Ullah, W. Lei, Q. S. Cao, Z. Y. Zou, X. K. Lan, X. H. Wang and W. Z. Lu, J. Am. Ceram. Soc., 2016 DOI:10.1111/jace.14341.
- J. G. Bednorz and K. A Muller, Phys. Rev. Lett., 1984, 52, 2289–2292 CrossRef CAS.
- C. Ang, Y. Zhi, J. Scott, A. Loidl, R. Guo, A. S. Bhalla and L. E. Cross, J. Phys. Chem. Solids, 2000, 61, 191–196 CrossRef.
- C. Ang and Z. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(2), 957–961 CrossRef CAS.
- C. Ang and Z. Yu, J. Appl. Phys., 2002, 91(2), 1448–1494 Search PubMed.
- A. Durán, E. Martínez, J. A. Díaz and J. M. Siqueirosb, J. Appl. Phys., 2005, 97, 104109 CrossRef.
- H. Y. Ye, Q. Zhou, X. Niu, W. Q. Liao, D. W. Fu, Y. Zhang, Y. M. You, J. Wang, Z. N. Chen and R. G. Xiong, J. Am. Chem. Soc., 2015, 137(40), 13148–13154 CrossRef CAS PubMed.
- R. Ranjan, R. Hackl, A. Chandra, E. Schmidbauer, D. Trots and H. Boysen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 224109 CrossRef.
- S. Kamba, M. Savinov, F. E. Laufek, O. T. Ka, C. Kadlec, S. Veljko, E. J. John, G. Subodh, M. T. Sebastian, M. Klementova, V. Bovtun, J. Pokorny, V. Goian and J. Petzelt, Chem. Mater., 2009, 21, 811–819 CrossRef CAS.
- K. A. Miiller and H. Burkard, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19(7), 3593–3602 CrossRef.
- W. Kleemann, Int. J. Mod. Phys. B, 1993, 07(13), 2469–2507 CrossRef CAS.
- R. E. Cohen, Nature, 1992, 358, 136–138 CrossRef CAS.
- J. F. Scott, J. Phys.: Condens. Matter, 2008, 20(2), 021001 CrossRef.
- H. Neumann and G. Arlt, Ferroelectrics, 1986, 69(1), 179–186 CrossRef CAS.
- F. Liu, J. Li, Q. Li, Y. Wang, X. Zhao, Y. Hua, C. Wang and X. Liu, Dalton Trans., 2014, 43(4), 1691–1698 RSC.
- F. N. Sayed, B. P. Mandal, O. D. Jayakumar, A. Arya, R. M. Kadam, A. Dixit, R. Naik and A. K. Tyagi, Inorg. Chem., 2011, 50(22), 11765–11772 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18717j |
| This journal is © The Royal Society of Chemistry 2016 |