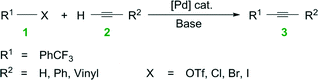Influence of water on the deprotonation and the ionic mechanisms of a Heck alkynylation and its resultant E-factors

Abstract

The influence of water on deprotonation and ionic mechanisms of a Heck alkynylation and its resultant E-factors were investigated. Estimation of the Hatta modulus, M_H < 0.02, in cationic deprotonation, anionic deprotonation, and the ionic mechanism each separately confirmed an infinitely slow rate of reaction with respect to the diffusive flux within the thin film of the immiscible aqueous–organic interface. As a consequence, intrinsic kinetic expressions for far-equilibrium conditions were derived from first principles for each mechanism. Analyses of Gibbs free energies revealed that water potentially switched the rate-determining steps of cationic and anionic deprotonation to any of oxidative addition of organohalide to form Pd-complex (ΔG⁺⁺ = 97.6 kJ mol⁻¹), coordination of the alkyne with the oxidative addition adduct (ΔG⁺⁺ = 97.6 kJ mol⁻¹), or ligand substitution to form the cationic Pd-complex (ΔG⁺⁺ = 94.9 kJ mol⁻¹). Hydrogen-bonding in the transfer mechanism might account for the switch. Water, in general, was found to influence which step governs each catalytic cycle and the magnitude of its Gibbs free energy. Transformation of the synthesis from batch to continuous-flow was also studied by analyses of E-factors within the thin film. The amount of waste generated, as indicted by estimations of E-factors, was less in continuous-flow operation than in batch when the fastest step of deprotonation (ligand substitution) was infinitely fast with respect to the diffusive flux. The concentration of hydrophilic phosphine ligand was observed to influence mass transport limitations and the E-factor. Increasing ligand concentrations beyond (10.5), (13.3), and (23.2) × 10⁻³ mol L⁻¹ for reaction temperatures of 353, 343, and 323 K increased the E-factor above its minimum value of 4.7, and it also induced mass-transfer-limitations. The switch from intrinsic to mass-transport-limited kinetics by finite changes in the ligand concentration explains ambiguity when performing aqueous-phase catalyzed Heck alkynylations and possibly multiphase Pd-catalyzed C–C cross-couplings in general. The potential exists to inadvertently mask the reactivity of useful ligands during discovery and to force mass transport limitations during manufacture. Understanding why the E-factor can be minimized is vital to the sustainable discovery and manufacture of fine chemicals, materials, natural products, and pharmaceuticals.

---

Introduction

Water is a potential solvent in organic synthesis because it is cheap, nontoxic, and nonflammable, yet it was seldom regarded as a useful reaction medium for many decades.¹ This unconventional solvent has gained attention in recent years because of its potential to accelerate organic transformations, dissolve inorganic salt by-products, and to separate products and catalyst.^1,2 Much remains to be understood, however, on the use of water in organic synthesis, especially its role in organometallic chemistry and the resultant impacts on chemical engineering.

The field of homogeneous, organometallic catalysis has been widely investigated with much emphasis on the development of new chemical methods using transition metals (e.g., Pt, Pd, Rh, Ru) and for good reason. Albeit Pd, as an example, is scarce, its versatility in C–C and C–N bond formations (e.g., Buchwald–Hartwig amination^3,4 and Heck,^5–11 Hiyama,^12,13 Negishi,^14–19 Sonogashira,^20–25 Stille,^26–28 and Suzuki couplings^10,29–33) continues to broadly impact society. For instance, the Pd-catalyzed Cu-free Sonogashira reaction (a.k.a., the Heck alkynylation) is the C–C coupling of an alkyne's terminal sp hybridized C with a sp² C of an aryl or vinyl halide, or triflate (see Scheme 1). Heck alkynylation is widely used in the preparation of pharmaceuticals,³⁴ natural products,³⁵ and materials with unique optical properties³⁶ (see Fig. 1).

Scheme 1 Copper-free Sonogashira coupling (a.k.a., Heck alkynylation).

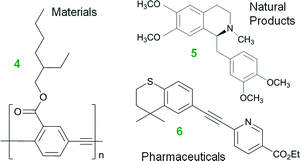Fig. 1 Materials (e.g., carbonyl (2-ethyl-hexyloxy)-PPE 4),³⁶ natural products (e.g., (+)-(S)-laudanosine 5, a kind of benzylisoquinoline alkaloids),³⁵ and pharmaceuticals (e.g., Tazarotene (AGN-190168) 6, for treatment of acne and psoriasis)³⁴ prepared by Heck alkynylations.

Continuous production of such compounds introduces engineering challenges. Solids handling of inorganic halide salt by-products, and the separation and recycling of homogeneous catalysts from organic product streams are roadblocks.³⁷ Catalyst recovery is of significant importance mainly because these transition metals (e.g., Pt, Pd, Rh, Ru) are rare in the planet. The design of water-soluble hydrophilic phosphines in biphasic systems introduces the opportunity for catalyst recovery, and it provides a reaction medium that solubilizes salt by-products. Water, however, has the potential to influence the reaction chemistry.

Two primary mechanisms that have been proposed for the Heck alkynylation are the carbopalladation³⁸ and the deprotonation²⁴ mechanisms. According to Ujaque, et al.'s density functional theory (DFT) calculations on a model system, the carbopalladation route for Heck alkynylations (in the absence of water) can be discarded.²⁰ Mårtensson, et al. also demonstrated experimentally that the carbopalladation cycle is not operative in organic systems.²³ However, the presence of water potentially switches the cross-coupling's mechanism from deprotonation to carbopalladation by reducing the Gibbs free energy barrier of the reductive elimination step in the carbopalladation catalytic cycle.³⁹ In the present work, the influence of water on cationic and anionic derivatives of the deprotonation mechanism of a Heck alkynylation are investigated to further examine whether or not water actually switches the governing mechanism to carbopalladation.

For the deprotonation pathway, two alternative routes have been proposed: the cationic and anionic mechanisms²³ shown in Fig. 2. The difference between the two variants of the deprotonation mechanism is the sequential order of the deprotonation steps. Both catalytic cycles, shown in Fig. 2a and b, undergo the reversible oxidative addition of the organohalide R¹X to the Pd⁰L_n complex 7 (or 7′). The resulting oxidative addition adduct, species 8 (or 8′), then undergoes reversible complexation to the alkyne, forming an alkyne-Pd complex 9 (or 9′). At this point, the two mechanisms proceed differently to form complex 11 (or 11′). In the cationic mechanism (Fig. 2a), the ligand L is generally thought to substitute X in species 9 leading to the formation of cationic Pd complex 10, which undergoes the deprotonation of alkyne by the addition of base. By a comparison, with the anionic mechanism (Fig. 2b), the deprotonation of alkyne occurs first giving rise to the anionic complex 10′. The L–X ligand substitution then takes place to form complex 11′.

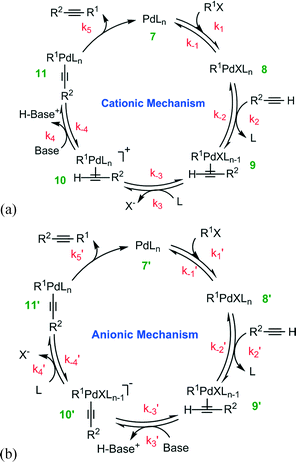Fig. 2 Proposed (a) cationic and (b) anionic mechanisms for the Pd-catalyzed Cu-free cross-coupling between a terminal alkyne and an aryl halide.

Both the cationic and the anionic mechanisms finish by reductive elimination of the alkyne product to regenerate the Pd(0) catalyst 7 (or 7′). General understanding that water influences each step is ascertained in the present study through a comparison of DFT calculations²⁰ with intrinsic reaction kinetics and the influence of mass transport limitations.

Solvent waste is a sustainability problem of synthetic chemistry that the engineering of continuous-flow syntheses could help address. The mass of the wastes generated relative to the mass of the desired products formed, the “E-factor”, typically ranges from 5 to 100 for fine chemicals and pharmaceuticals syntheses.⁴⁰ Values of the E-factor are not independent of the reactor design where the potential for transport limitations exists. Calculations must be performed up front to avoid misinterpretations of mechanistic theory, overlooking novel chemical methods, and the development of falsified kinetics that increase E-factor values. This is especially important for multiphase reactions where interfacial contact area and film thickness of biphasic systems can differ in batch from flow. Much opportunity remains to minimize the mass of chemical waste generated during synthesis and production.

The present study reports the influence of water on deprotonation (both cationic and anionic) and ionic mechanisms of a Heck alkynylation. The potential to transform synthetic chemistry from batch processing to continuous-flow is also examined by estimations of E-factors. The optimum hydrophilic ligand concentration for different temperatures is presented. Analyses of Hatta moduli undergird that higher ligand concentrations could force mass transport limited conditions, which mask the discovery and the development of novel chemical methods. The discoveries reported in the present work could significantly reduce the mass of chemical wastes generated during fine chemicals and pharmaceuticals syntheses, both in the laboratory and production.

Experimental and computational

Wet chemistry experimentation

Wet chemistry experiments were performed and the procedural details reported in a previous study. All reagents, research grade, were prepared in a glove box under nitrogen. Batch (in 4.0 mL vials, 13 mm I.D.) and capillary (0.1 mL PFA, 1/16′′ O.D., 1.0 mm I.D.) flow reactor experiments were completed each separately under isothermal conditions. Data were collected for reaction temperatures of 323, 343, and 353 K. Measurement of aliquots by gas chromatography (Varian 3800) enabled the monitoring of the reaction progress. No evidence of selectivity was observed.⁴¹

Numerical evaluation of kinetic parameters

Concentrations of substrates measured as a function of the reaction time were fit using nonlinear regression for each rate-determining step. The coupled ordinary differential equations were then solved using Polymath 6.1 by the Runge–Kutta–Fehlberg⁴² and the Rosenbrock numerical methods.⁴³ The kinetic parameters for each rate-determining step were next evaluated by the nonlinear least squares method for previously reported fractions of inactive Pd.³⁹ The calculations were repeated for each mechanism in order to develop the far-equilibrium kinetic expressions for cationic deprotonation (eqn (S1)†), anionic deprotonation (eqn (S3)†), and the ionic mechanism (eqn (S5)†). As a consequence, values of intrinsic rate constants were determined for each forward reaction step of each catalytic cycle.

Results and discussion

Model chemistry, the Heck alkynylation of 1-bromo-4-trifluoromethyl benzene with phenyl acetylene using water-soluble 3-(di-tert-butylphosphonium)-propane sulfonate (DTBPPS) (refer to Scheme 1),⁴¹ was evaluated in the present study in order to better understand the role of water on its postulated reaction mechanisms. Calculations of the Hatta moduli (M_H) in a previous investigation confirmed that infinitely slow reaction conditions existed during the wet chemistry experiments.³⁹ Our pursuit of understanding why water influences the catalysis next prompted us to derive and evaluate intrinsic kinetic expressions for cationic (eqn (S1)†) and anionic (eqn (S2)†) deprotonation (see ESI†).

Heck alkynylations via the deprotonation mechanism

Estimations of Gibbs free energies (ΔG⁺⁺) were made using the Eyring–Polanyi equation for the deprotonation catalytic cycles of Fig. 2. The free energies of reaction steps involving Pd intermediates each with n and (n – 1) coordinated ligand(s) were calculated, from first principles, by eqn (S12) and (S13).† Recently reported density functional theory (DFT) calculations of the Heck alkynylation of phenylacetylene and iodobenzene in purely organic solvents (pyrrolidine and dichloromethane)²⁰ predict an obvious distinction between the couplings performed with and without any water, as revealed in Fig. 3.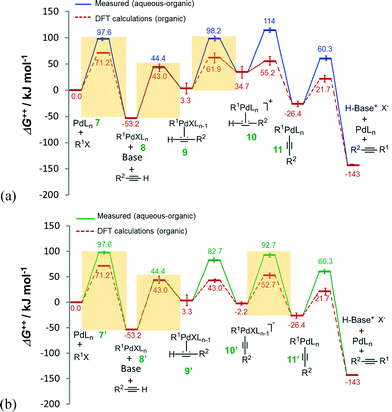

Fig. 3 Gibbs free energy (ΔG⁺⁺) profiles of the Heck alkynylation of an aryl iodide predicted by DFT calculations²⁰ (dashed-line) and calculated using eqn (S1)–(S4) and (S7)–(S13)† applied to wet chemistry experiments (solid-line) for (a) cationic and (b) anionic deprotonation.

The alkyne's substituent (R² from Scheme 1) is expected to influence DFT calculated ΔG⁺⁺ values by as much as 11.2 kJ mol⁻¹ (for R² = H, CF₃, OMe, NMe₂),²⁰ which is reported by the error bars of Fig. 3. The nature of the phosphine also introduces conformational diversity from 1.3 to 47.7 kJ mol⁻¹.⁴⁴ Albeit the phosphine and the substitution of the aryl iodide may influence Gibbs free energy to some extent, our comparison of the DFT calculations²⁰ with our data calculated (using eqn (S1)–(S13)†) from wet chemistry experiments using an aryl bromide provides fundamental insight on the participation of water, from step-to-step in the catalysis.

Water influences the reaction steps of cationic deprotonation. The Gibbs free energies of each step of cationic deprotonation are illustrated in Fig. 3a. As can be seen, the DFT calculations²⁰ support that coordination of the alkyne 2 with adduct 8 exhibits the largest ΔG⁺⁺ (at 96.2 kJ mol⁻¹) of any reaction step, and thus the formation of adduct 9 in organic solvent is considered rate-determining. In the presence of water, however, any step of, oxidative addition of organohalide 1 to complex 7 (ΔG⁺⁺ = 97.6 kJ mol⁻¹), coordination of the alkyne 2 with adduct 8 (ΔG⁺⁺ = 97.6 kJ mol⁻¹), or ligand substitution to form the cationic Pd complex 10 (ΔG⁺⁺ = 94.9 kJ mol⁻¹) could be the rate-determining step. Water clearly influences which step governs the catalytic cycle.

An evaluation of anionic deprotonation yields similar observations. It is generally understood that coordination of the alkyne 2 with adduct 8′ is the rate-determining step with ΔG⁺⁺ = 96.2 kJ mol⁻¹, as shown in Fig. 3b. Hydrogen-bonding in the transfer mechanism might account for the switch to any step of, oxidative addition of organohalide 1 to complex 7′ (ΔG⁺⁺ = 97.6 kJ mol⁻¹), coordination of the alkyne 2 with adduct 8′ (ΔG⁺⁺ = 97.6 kJ mol⁻¹), or ligand substitution to form the Pd complex 11′ (ΔG⁺⁺ = 94.9 kJ mol⁻¹), as the rate-determining step. It is possible that H-bonding impedes either the substitution of the hydrophilic ligand or the oxidative addition of the alkyne 2, resulting in higher free energy barriers. The finite difference in free energy is an important consideration as water, an unconventional solvent, also solubilizes halide salt by-products that would otherwise impede performing the reaction in flow. The ionic strength of the aqueous phase, a thermodynamic consequence of introducing halide salt-product, could further influence the steps of either cationic or anionic deprotonation.

Heck alkynylations via the ionic mechanism

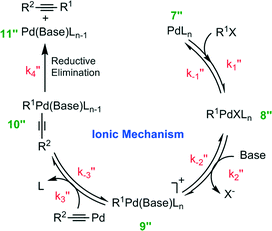
It has been reported that an external coordinating ligand (e.g., THF or PMePh₂) could replace the halide from the complex trans-[PdMeCl(PMePh₂)₂] in a Negishi cross coupling reaction,¹⁴ and this mechanism was named the ionic mechanism. The same observation was recently also made for the Heck alkynylation.¹⁴ The ionic mechanism for Heck alkynylation, as it was proposed by Garcia-Melchor, et al., is shown in Fig. 4.

Fig. 4 Proposed ionic mechanism for Heck alkynylation of a terminal alkyne and an aryl halide.

The first step, similar to the cationic and anionic mechanisms (Fig. 2), is the oxidative addition of the organohalide 1 to the complex 7′′. The cycle proceeds by the addition of base with the oxidative addition adduct 8′′. Here, it is possible that the corresponding phenylacetylide (i.e., R²–≡–Pd) exists in solution as a result of excess base.²⁰ Addition of this phenylacetylide to complex 9′′ forms Pd complex 10′′, which then undergoes reductive elimination to generate complex 11′′ and the alkyne product 3 (see Fig. 4). The ionic mechanism has also been studied by DFT²⁰ in order to ascertain its theoretical likelihood as the dominant catalytic pathway of Heck alkynylation.

The Gibbs free energy profiles for the ionic mechanism are reported in Fig. 5 with and without any water. In either scenario, the first step, oxidative addition of the organohalide 1 to the complex 7′′, is rate-determining where in the presence of water ΔG⁺⁺ = 97.6 kJ mol⁻¹ and without aqueous solvent ΔG⁺⁺ = 71.2 kJ mol⁻¹ (as predicted by DFT calculations²⁰). The obvious distinction between the two scenarios is shown by the ΔG⁺⁺ values of the phenylacetylide addition to complex 9′′. In the purely organic system, no free energy barrier is reported. However, water appears to influence the free energy by 11.8 kJ mol⁻¹. The observation undergirds that water molecules stabilize the ionic complex 9′′, potentially by H-bonding of the ligand. As we will next learn, the ligand plays a key role, not only in the cross-coupling's kinetics, but also in the generation of chemical waste.

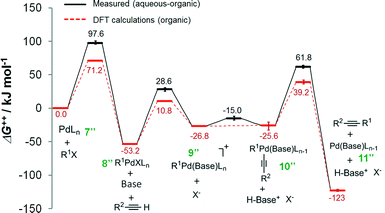Fig. 5 Gibbs free energy (ΔG⁺⁺) profiles of the Heck alkynylation of an aryl iodide predicted by DFT calculations²⁰ (dashed-line) and calculated using eqn (S5)–(S13)† applied to wet chemistry experiments (solid-line) for the ionic mechanism.

Analysis of the E-factor

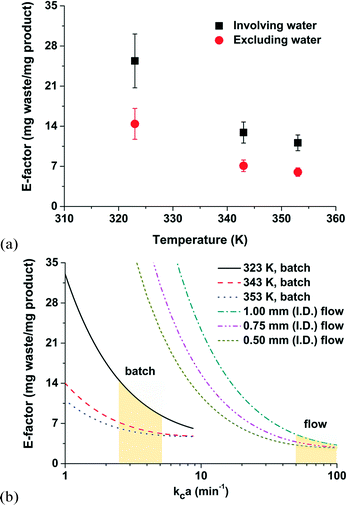
The concept of the E-factor is vital to the sustainable discovery and manufacture of fine chemicals, materials, natural products, and pharmaceuticals. Higher E-factor values, relatively speaking, are indication of more waste generated, and, as a consequence, more severe environmental impacts. Although the theoretical limits of most chemical reactions are well above the ideal E-factor (i.e., E-factor = 0), fundamental understandings that minimize E-factor values could reduce operating costs and capital expenditures with the positive outcome of an overall greener planet. Our analysis of E-factors of an aqueous-phase Heck alkynylation makes progress towards that goal.

As expected in Fig. 6a, the E-factor of the Heck alkynylation decreases with increasing reaction temperature because the reaction accelerates (i.e., Arrhenius temperature dependence) and thermodynamic solubility tends to increase.

Fig. 6 (a) E-factor values as a function of temperature estimated with and without water. (b) Calculated E-factor values in batch and flow as a function of the mass transfer coefficient k_ca. The shaded areas represent the experimental conditions of the present study while the extrapolations represent additional conditions encountered in batch and flow.

By its definition, water is excluded from the parameter. However, for the sake of a comparison, E-factor values calculated on the basis of water and organic solvent are also included in Fig. 6a. The larger E-factor values (where water is included) should not be interpreted as a system that will generate more waste. The opposite is true, case-by-case, depending on the chemistry, the number of total synthesis steps, and when the entire process is considered. Water, in this case of using hydrophilic ligand for Heck alkynylation, potentially minimizes the solvent mass required in downstream separation steps by two orders of magnitude.³⁹ Merit exists to redefine the definition of the E-factor where water is an unconventional solvent in organic synthesis.

A general consideration in any chemical manufacturing strategy is the implementation of batch or continuous-flow operation. The E-factor can be applied to simplify the decision making process. Let us consider the thin film of thickness x₀ at the aqueous–organic interface. The E-factor can be calculated based on the maximum attainable conversion within the thin film. As shown in Fig. 6b, E-factors were estimated to decrease with increasing k_ca values in the range of 1 to 100 min⁻¹. Here, k_c is the mass transfer coefficient and a is the liquid–liquid interfacial area. Values of k_ca are typically < 10 min⁻¹ in batch (in the range of 2.5–5.2 min⁻¹ in the present work) and from 50–100 min⁻¹ for 0.5–1.0 mm I.D. capillary microchannels where segmented flow is achieved.⁴⁵ In this example, the amount of waste generated is less in continuous-flow operation than in batch when the reaction rate is assumed to be infinitely fast with respect to the mass transfer rate.⁴¹

Let us now consider the case where the reaction rate within the thin film of thickness x₀ (at the aqueous–organic interface) may or may not be infinitely fast with respect to the mass transfer rate.^46,47 The Hatta modulus (M_H) is a useful parameter that distinguishes reaction rates from diffusive fluxes of substrates, catalytic intermediates or products (see eqn (S14)†). As shown in Table 1, estimation of the specific reaction rates of the formation of complex 10 and 11′ (k₃ and k₄′ from Fig. 2) and of the molecular diffusivities^41,48 enable estimation of the maximum M_H values (see eqn (S14)†) where α = 1, β = 0, γ = 0, and δ = 0.

Table 1 Hatta moduli (M_H) for each reaction temperature

Entry	T (K)	x 0 (μm)	k i (M^−1 s^−1)	[scr D, script letter D] (×10^9 m^2 s^−1)	Diaryl alkyne yield (%)	M H (×10^3)
1	353	0.1	1373	7.2	37 ± 7	4.10
2	343	0.1	998	5.8	70 ± 10	3.86
3	323	0.1	497	3.8	81 ± 10	3.37

---

From Table 1, the maximum M_H values of (4.10), (3.86), and (3.37) × 10⁻³ were calculated at 353, 343, and 323 K each separately for a film thickness on the order of 0.10 μm, which is the upper limit of the typical film thickness range for immiscible emulsions (in the range of 0.001 to 0.10 μm).⁴⁹ Values of M_H < 0.02 indicate an infinitely slow reaction,⁴⁷ and consequently diffusion did not control the kinetics for all temperatures reported herein.

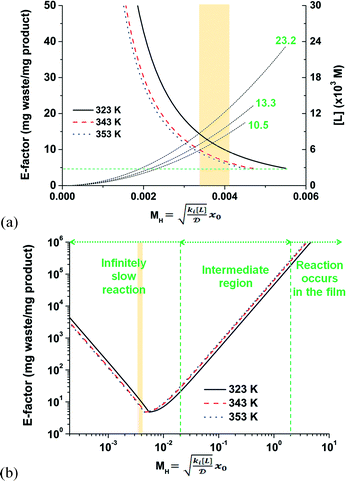
A trade-off exists between the chemical waste generated and the amount of ligand and precious metal consumed. On one hand, a greater mass of desired product is possible for a given residence time and with less waste generated by stoichiometrically increasing the ligand concentration with respect to the Pd loading (see eqn (S1–S6)†). On the other hand, accelerating the kinetics of this biphasic system any further by increasing the ligand loading has the potential to switch from intrinsic to mass-transport limited conditions. Fig. 7a illustrates the important point when considering either the cationic or the anionic deprotonation mechanism. Either deprotonation mechanism exhibits an overall lower free energy of product compared to the ionic mechanism (see Fig. 3 and 5). The fastest reaction step, whether the mechanism is cationic deprotonation or anionic deprotonation, is the ligand substitution. As a result, the E-factor is reported in Fig. 7a as a function of the maximum M_H values for each temperature studied. One observes that the E-factor decreases with increasing M_H values until the theoretical minimum is achieved (at 4.7) while varying the ligand concentration. Any excess ligand in the reaction mixture would, in principle, be considered waste because it would only increase the E-factor without any additional product generated. In this example, the maximum ligand concentrations are shown in Fig. 7a to be (10.5), (13.3), and (23.2) × 10⁻³ mol L⁻¹ for 353, 343, and 323 K, respectively. It is also important to note in Fig. 7a that the theoretical minimum E-factor is attainable where the reaction is infinitely slow with respect to mass transfer (i.e., M_H < 0.02).

Fig. 7 (a) The E-factor of the thin film (at 323, 343, and 353 K) and the free ligand concentration as functions of the Hatta modulus, M_H. (b) The E-factor as a function of M_H for an infinitely slow reaction in the film (i.e., reaction-rate-limited), the intermediate region, and where the reaction only occurs within the thin film (i.e., mass-transfer-limited). The shaded areas in both figures represent the conditions of the wet chemistry experiments.

Increasing the ligand concentration beyond the critical point where the E-factor is minimized has the potential to force mixed mass-transfer-reaction-rate and mass-transfer limitations. The existence of transport limitations can mask the discovery of useful ligands and actually contribute to the amount of waste generated at both the laboratory and production scales. Fig. 7b demonstrates that E-factor values climb (after its minimum has been reached) into the intermediate region (i.e., 0.02 < M_H < 2 and mixed mass-transfer-reaction-rate limited)⁴⁷ and beyond into the region where the reaction only occurs within the thin film (i.e., M_H > 2 and mass-transfer limited).⁴⁷ Note that the maximum conversion within the film (i.e., 100%) is achieved for values of M_H < 0.02. The transition point depends mainly on the film thickness x₀. In micro-scale segmented flow (e.g., Re < 1), for instance of two immiscible phases, the flow rate controls x₀.⁵⁰ Typical x₀ values in micro-scale segmented flows range from 1 to 10 μm.⁴⁵Fig. 8 illustrates the resultant E-factors at 353 K for M_H values from 0.01 to 10.

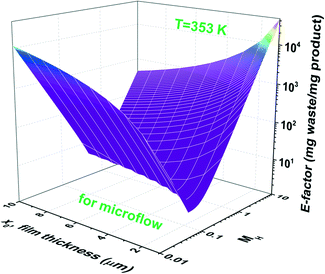Fig. 8 E-factors at 353 K for M_H values from 0.01 to 10 and aqueous–organic film thicknesses (x₀) from 1 to 10 μm.

One observes that values of x₀ influence both the amount of waste generated and the range of mass transport limitations. Where the reaction is infinitely slow, the E-factor decreases with decreasing values of x₀ whereas the opposite trend is observed for values of M_H > 2. The same trend is shown in Fig. S2 and S3† for 343 and 323 K, respectively.

The existence of the ionic mechanism, in theory, could result in the diffusive flux being less than the reaction rate for one step of the mechanism. The fastest reaction step, the addition of the phenylacetylide to form Pd complex 10′′ of Fig. 4, exhibits a much lower ΔG⁺⁺ value compared to any other step (see Fig. 5). The corresponding M_H values, in the range of 24.6–39.6, are due to k_i values on the order of 10¹² min⁻¹. However, the ionic mechanism depends on the existence of phenylacetylide in solution, which has yet to be experimentally validated. Furthermore, oxidative addition of the organohalide 1 to the complex 7′′, the rate-determining step of the ionic mechanism, predicts values of M_H < 0.02. It is therefore reasonable to conclude that intrinsic kinetics govern the Heck alkynylation, water influences each of the three catalytic cycles, and that the ligand concentration plays a key role in the existence of mass transport limitations and in the generation of unnecessary chemical waste.

Conclusions

A model Heck alkynylation was investigated in order to better understand the role of water on three postulated reaction mechanisms: cationic deprotonation, anionic deprotonation, and the ionic mechanism. Estimation of the Hatta modulus in each case confirmed an infinitely slow rate of reaction with respect to the diffusive flux within the thin film of aqueous–organic interfaces. As a consequence, intrinsic kinetic expressions for far-equilibrium conditions were derived from first principles for each mechanism.

Analyses of Gibbs free energies revealed that water potentially switched the rate-determining steps of cationic and anionic deprotonation. According to DFT calculations, the coordination of alkyne substrate to form alkyne-Pd complex governs the overall reaction in organic solvent. In the presence of water, however, any step of, oxidative addition of organohalide to form Pd-complex, coordination of the alkyne with the oxidative addition adduct, or ligand substitution to form the cationic Pd-complex could be the rate-determining step. Hydrogen-bonding in the transfer mechanism might account for the switch. It is possible that H-bonding impedes either the substitution of the hydrophilic ligand or the oxidative addition of the alkyne in either mechanism, resulting in higher free energy barriers. Water also introduced a Gibbs free energy barrier for the addition of the phenylacetylide to form Pd-complex in the ionic mechanism. Water, in general, was found to influence which step governs each catalytic cycle and the magnitude of its Gibbs free energy.

Estimations of the E-factor of the thin film at aqueous–organic interfaces made progress toward understanding why the chemical waste generated during Heck alkynylations could be minimized. The amount of waste generated, in the present work, was less in continuous-flow operation than in batch when the fastest step of deprotonation in the Heck alkynylation (ligand substitution) was infinitely fast with respect to the diffusive flux. Fundamental understandings that minimize E-factor values could reduce operating costs and capital expenditures with the positive outcome of an overall greener planet.

The concentration of hydrophilic phosphine ligand was observed to play a key role in the existence of mass transport limitations and in the generation of unnecessary chemical waste (i.e., by approximation of the E-factor). Increasing ligand concentrations beyond minimum E-factor values induced mass-transfer-limitations, which could impact both laboratory- and production-scale syntheses. The switch from intrinsic to mass-transport-limited kinetics by finite changes in the ligand concentration explains ambiguity when performing Heck alkynylations and possibly multiphase Pd-catalyzed C–C cross-couplings in general. The potential exists to mask the reactivity of useful ligands during discovery.

Acknowledgements

The present work was supported by the NSF under grant CBET-1550483.

References

1. R. N. Butler and A. G. Coyne, Chem. Rev., 2010, 110, 6302–6337.
2. A. Chanda and V. V. Fokin, Chem. Rev., 2009, 109, 725–748.
3. J. F. Hartwig, Angew. Chem., Int. Ed., 1998, 37, 2046–2067.
4. D. S. Surry and S. L. Buchwald, Chem. Sci., 2011, 2, 27–50.
5. A. F. Littke and G. C. Fu, J. Org. Chem., 1999, 64, 10–11.
6. J. Le Bars, U. Specht, J. S. Bradley and D. G. Blackmond, Langmuir, 1999, 15, 7621–7625.
7. Z. Bao, Y. Chen, R. Cai and L. Yu, Macromolecules, 1993, 26, 5281–5286.
8. C. Amatore and A. Jutand, Acc. Chem. Res., 2000, 33, 314–321.
9. B. Ruhland, A. Bombrun and M. A. Gallop, J. Org. Chem., 1997, 62, 7820–7826.
10. R. Narayanan, Molecules, 2010, 15, 2124–2138.
11. V. Farina, Adv. Synth. Catal., 2004, 346, 1553–1582.
12. M. L. Clarke, Adv. Synth. Catal., 2005, 347, 303–307.
13. J.-Y. Lee and G. C. Fu, J. Am. Chem. Soc., 2003, 125, 5616–5617.
14. M. García-Melchor, B. Fuentes, A. Lledós, J. A. Casares, G. Ujaque and P. Espinet, J. Am. Chem. Soc., 2011, 133, 13519–13526.
15. E.-I. Negishi, Q. Hu, Z.-H. Huang, M. Qian, G. Wang and H. Brown, Aldrichimica Acta, 2005, 38, 71–87.
16. J. E. Milne and S. L. Buchwald, J. Am. Chem. Soc., 2004, 126, 13028–13032.
17. C. Dai and G. C. Fu, J. Am. Chem. Soc., 2001, 123, 2719–2724.
18. C. Fischer and G. C. Fu, J. Am. Chem. Soc., 2005, 127, 4594–4595.
19. J. Zhou and G. C. Fu, J. Am. Chem. Soc., 2003, 125, 12527–12530.
20. M. García-Melchor, M. C. Pacheco, C. Nájera, A. Lledós and G. Ujaque, ACS Catal., 2011, 2, 135–144.
21. S. Thorand and N. Krause, J. Org. Chem., 1998, 63, 8551–8553.
22. R. Chinchilla and C. Nájera, Chem. Rev., 2007, 107, 874–922.
23. T. Ljungdahl, T. Bennur, A. Dallas, H. Emtenäs and J. Mårtensson, Organometallics, 2008, 27, 2490–2498.
24. A. Soheili, J. Albaneze-Walker, J. A. Murry, P. G. Dormer and D. L. Hughes, Org. Lett., 2003, 5, 4191–4194.
25. K. Sonogashira, J. Organomet. Chem., 2002, 653, 46–49.
26. V. Farina, S. Kapadia, B. Krishnan, C. Wang and L. S. Liebeskind, J. Org. Chem., 1994, 59, 5905–5911.
27. S. P. Mee, V. Lee and J. E. Baldwin, Angew. Chem., Int. Ed., 2004, 43, 1132–1136.
28. M. J. Plunkett and J. A. Ellman, J. Am. Chem. Soc., 1995, 117, 3306–3307.
29. S.-W. Kim, M. Kim, W. Y. Lee and T. Hyeon, J. Am. Chem. Soc., 2002, 124, 7642–7643.
30. D. W. Old, J. P. Wolfe and S. L. Buchwald, J. Am. Chem. Soc., 1998, 120, 9722–9723.
31. J. P. Wolfe and S. L. Buchwald, Angew. Chem., Int. Ed., 1999, 38, 2413–2416.
32. J. Zhou and G. C. Fu, J. Am. Chem. Soc., 2004, 126, 1340–1341.
33. A. F. Littke and G. C. Fu, Angew. Chem., Int. Ed., 1998, 37, 3387–3388.
34. A. O. King and N. Yasuda, in Organometallics in Process Chemistry, Springer, 2004, pp. 205–245.
35. D. Mujahidin and S. Doye, Eur. J. Org. Chem., 2005, 2005, 2689–2693.
36. U. H. Bunz, Chem. Rev., 2000, 100, 1605–1644.
37. C. E. Garrett and K. Prasad, Adv. Synth. Catal., 2004, 346, 889–900.
38. H. Dieck and F. Heck, J. Organomet. Chem., 1975, 93, 259–263.
39. J. C. Sabio, R. C. Domier, J. N. Moore, K. H. Shaughnessy and R. L. Hartman, Chem. Eng. Technol., 2015, 38, 1717–1725.
40. R. A. Sheldon, Chem. Commun., 2008, 3352–3365.
41. R. C. Domier, J. N. Moore, K. H. Shaughnessy and R. L. Hartman, Org. Process Res. Dev., 2013, 17, 1262–1271.
42. W. H. Press, Numerical recipes 3rd edition, The art of scientific computing, Cambridge university press, 2007.
43. G. Forsythe, M. Malcolm and C. Moler, Computer Methods for Mathematical Computation Prentice-Hall, Englewood Cliffs, New Jersey, 1st edn, 1977.
44. M. Besora, A. A. Braga, G. Ujaque, F. Maseras and A. Lledós, Theor. Chem. Acc., 2011, 128, 639–646.
45. M. N. Kashid, A. Renken and L. Kiwi-Minsker, Chem. Eng. Sci., 2011, 66, 3876–3897.
46. H. S. Fogler, Elements of Chemical Reaction Enginering, 4th edn, 2006.
47. O. Levenspiel, Chemical reaction engineering, 3rd edn, 1999.
48. D. P. Valencia and F. J. González, Electrochem. Commun., 2011, 13, 129–132.
49. H. Yang, S. R. Schmid, T. J. Kasun and R. A. Reich, Tribol. Trans., 2004, 47, 123–129.
50. C. Hu, C. Herz and R. L. Hartman, Green Process. Synth., 2013, 2, 611–623.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5re00034c

---