A review of research on the teaching and learning of chemical kinetics
Kinsey
Bain
and
Marcy H.
Towns
*
Department of Chemistry, Purdue University, West Lafayette, IN, USA. E-mail: mtowns@purdue.edu
First published on 11th January 2016
Abstract
We review literature on the teaching and learning of chemical kinetics at both the secondary and tertiary levels. Our aim in doing so is to summarize research literature, synthesize recommendations for future research, and suggest implications for practitioners. Two main bodies of literature emerged from the chemical kinetics education research: student understanding and instructional approaches to teaching. The student understanding findings are discussed in light of the anchoring concepts content map for general chemistry. We also review relevant literature about research on undergraduate mathematics education, as mathematics is often used as the primary language of communicating chemical kinetics. Finally, we discuss directions for future research and implications for practice.
Introduction
Chemical kinetics is an anchoring concept or “big idea” of the undergraduate chemistry curriculum based upon extensive research carried out by the American Chemical Society (ACS) Exams Institute (Holme and Murphy, 2012; Murphy et al., 2012; Holme et al., 2015). It relates to other concepts such chemical change, equilibrium, and thermodynamics and is taught regularly at both secondary and tertiary levels (Justi, 2002). It has the power to provide insight into the nature of chemical reactions and processes, because it ties observable phenomenon with theoretical aspects of chemistry that are modeled mathematically (Çakmakci et al., 2006). It is an area of chemistry that can be represented in three ways, macroscopically, submicroscopically, and symbolically (Johnstone, 1991; Talanquer, 2011; Taber, 2013). Following Talanquer's (2011) multi-dimensional framework further, it can also be described using other aspects of chemistry knowledge such as experiences, models, and visualizations. For example, chemical kinetics brings together various observations related to time and models related to composition, structure, and energy. Additionally, it can bring together various visualizations through mathematical, conceptual, or contextual approaches. Due to the complexity, importance, and prominence of chemical kinetics within the field of chemistry, research into student understanding and effective methods of teaching is crucial.Purpose
The purpose of this review is to summarize chemical kinetics educational research literature, synthesize recommendations for future research, and suggest implications for chemistry practitioners. This work builds on a prior review of teaching and learning chemical kinetics (Justi, 2002). While much of this literature comes from the chemistry education research (CER) community, we include a section on related rates research from the research on undergraduate mathematics education (RUME) community, in an attempt to integrate ideas across discipline-based education research (DBER) fields. In doing so we emphasize recommendations for future research and implications for practice in line with the National Research Council's DBER report (National Research Council, 2012).Sampling
Our initial criteria for inclusion of research in this review was that each peer-reviewed article be published in English and conducted at the tertiary level. However, the review was expanded to both the secondary and tertiary levels, due to the scarcity of literature in a tertiary context as shown in Table 1. A second criteria for inclusion was that each study must include research questions, present data and analysis, and describe implications for research and practice. Research using measurement instruments (such as concept or diagnostic tests) or implementing novel instructional practices (or material) must provide results of effectiveness in order to be included in this review.| Total number of articles reviewed | Secondary level | Tertiary level | Experts or in-service teachers | |
|---|---|---|---|---|
| Kinetics | 26 | 18 | 10 | 1 |
| Related Rates | 8 | 0 | 8 | 0 |
Herein, we review 34 studies from various science education research journals, including The Journal of Chemical Education, Chemistry Education Research and Practice, International Journal of Science Education, Journal of Research in Science Teaching, Mathematics Education Research Journal, Educational Studies in Mathematics, and others. Peer-reviewed conference proceedings were also included, as this is a common form of publication in the RUME community. Searches were conducted in the Education Resource Information Center (ERIC) database, using keyword searches, such as “chemical kinetics” and “reaction rates”, often coupled with phrases such as “student understanding” or “instruction.” The literature search was expanded to include citations within articles found initially. Another key source of literature was Justi's (2002) book chapter titled “Teaching and Learning Chemical Kinetics.” While completing this review, we continued to search recent issues of science education research journals in order to include the most recent work possible.
Student understanding of chemical kinetics
This section reviews literature investigating student understanding of chemical kinetics concepts through qualitative and quantitative methods. Such studies commonly produce findings regarding students' conceptions and alternative conceptions about chemical kinetics. The reviewed studies largely examine basic or foundational aspects, such as defining reaction rate, explaining effects of variables (e.g., temperature, concentration, and catalyst), and understanding activation energy. Some studies go further to investigate more complex concepts involving multi-step reaction mechanisms and reaction order. However, even these more complex ideas are still studied at a relatively simple level. This is likely due to the research context of the studies, largely being at the secondary or introductory undergraduate levels, as shown in Table 1. A similar trend was presented in Justi's (2002) book chapter over a decade ago.Most of the findings from the reviewed literature fit into an organizational structure from the anchoring concepts content map for general chemistry (Holme et al., 2015). Nearly all could be classified into six of the ten anchoring concepts identified by the ACS Exams Institute: (1) kinetics, (2) equilibrium, (3) energy and thermodynamics, (4) experiments, measurement, and data, (5) chemical reactions, and (6) intermolecular interactions. The findings are further organized according to the foundational understandings (and their particular articulations) associated with each anchoring concept. It is our hope that situating literature findings in such a way will be meaningful and useful for practitioners and researchers alike.
Kinetics
A large proportion of the alternative conceptions and student difficulties reported in the reviewed literature are classified under the anchoring concept of kinetics. Within this anchoring concept, there are six enduring understandings, five of which were used here to classify the literature findings (Holme et al., 2015). The enduring understandings each are further articulated in the content map by two more levels: subdisciplinary articulation and fine-grained detail. These levels of detail were crucial in assigning specific classifications to individual literature findings.The first kinetics enduring understanding is that “chemical change can be measured as a function of time and occurs over a wide range of time scales” (Holme et al., 2015). This is articulated in three ways, which are used to organize the alternative conceptions in Table 2. Analysis of the findings from the literature reviewed revealed that students have many difficulties in this area. Çakmakci's research with secondary and tertiary Turkish students (Çakmakci et al., 2006; Çakmakci, 2010; Bektaşli and Çakmakci, 2011) identified specific student difficulties in defining rate as shown in Table 2. These ranged from students' inability to state any sort of definition for the term rate to defining it incorrectly (e.g. reaction rate is time required for reactants to form products). Çakmakci's findings are consistent with other studies, such as those conducted by Boz and colleagues (Taştan-Kırık and Boz, 2010, 2012; Yalçınkaya et al., 2012) in which students defined reaction rate as simply reaction time or that rate depends on both the concentrations of the reactants and products.
| The rate of the reaction must be defined in a manner that is not dependent on which reactant or product is used to measure it. | |
| The reaction rate should incorporate reaction stoichiometry when it is defined. | |
| Inability to define rate of reaction (e.g. defining reaction rate as reaction time) | Çakmakci et al. (2006) and Bektaşli and Çakmakci (2011) |
| Rate is generally defined as the change in concentration of a reactant or product as a function of time. | |
| Chemical reactions may occur at a wide range of rates, and a key aspect of rate is related to the concentration of species involved in the reaction. | |
| Inability to define rate of reaction (e.g. defining reaction rate as reaction time) | Çakmakci et al. (2006) and Bektaşli and Çakmakci (2011) |
| Reaction rate is the time required for reactants to form products (or simply reaction rate is reaction time) | Akkuş et al. (2003), Çakmakci (2010), Çalik et al. (2010), Taştan-Kırık and Boz (2010), Kolomuç and Tekin (2011) and Yalçınkaya et al. (2012) |
| Reaction rate is the amount of substance turning into products per unit time at a constant temperature and concentration | Bektaşli and Çakmakci (2011), Taştan-Kırık and Boz (2012) and Yalçınkaya et al. (2012) |
| The reaction rate is the collision of A and B in a given time | Kolomuç and Tekin (2011) |
| Increasing the concentration of reactants increases the reaction time | Kurt and Ayas (2012) |
| The rate of reaction is/isn't affected by the concentration of reactant that take part in the reaction | Kolomuç and Tekin (2011) |
| Reaction rate depends on both the concentrations of reactants and the products | Yalçınkaya et al. (2012) |
| There is a linear relationship between the concentration of reactants and the reaction rate (students expected a higher rate from increasing concentrations of reactants) | Çakmakci et al. (2006) and Turányi and Tóth (2013) |
| When solids are included in reactions, surface area is an important factor in the rate of reaction. | |
| A reactive solid with a large surface area will react more rapidly than the same solid with a smaller surface area. | |
| Increasing the surface area (of reactants) increases the possibility of collision and the kinetic energy of the particles | Yalçınkaya et al. (2012) |
The next enduring understanding is that “empirically derived rate laws summarize the dependence of reaction rates on concentrations of reactants and temperature” (Holme et al., 2015). Our analysis of studies in this review revealed that this is the anchoring concept with the greatest array of alternative conceptions as shown in Table 3. Although the studies had a variety of aims, the most commonly reported alternative conceptions involved understanding the relationship between concentration of reactants and the reaction rate or the relationship between temperature and the reaction rate.
| The “order” of a reaction is derived from the exponent on the concentration term of a given reactant in the rate law. | |
| Increasing the concentration of reactants always increases the rate of reaction | Van Driel (2002), Taştan et al. (2010) and Kıngır and Geban (2012) |
| An increase in the initial concentration of reactants would increase/decrease the rate of a zero-order reaction | Çakmakci (2010) |
| The rate of reaction is/isn't affected by the concentration of reactant that take part in the reaction | Kolomuç and Tekin (2011) |
| Reaction rate depends on both the concentrations of reactants and the products | Yalçınkaya et al. (2012) |
| There is a linear relationship between the concentration of reactants and the reaction rate (students expected a higher rate from increasing concentrations of reactants) | Çakmakci et al. (2006) and Turányi and Tóth (2013) |
| Difficulty understanding the meaning behind the different orders of reactions | Yalçınkaya et al. (2012) |
| Rate laws are always determined experimentally, and the methods of initial rates or graphical depiction of rates provide the key method for determining rate laws. | |
| Concentrations of reactants in a rate equation have exponents equal to the stoichiometric coefficients of the reactants in the balanced equation for the reaction (no awareness of experimental determination of relation between rate, concentration, and order of reaction) | Çakmakci et al. (2006), Çakmakci and Aydogdu (2011), Kıngır and Geban (2012) and Turányi and Tóth (2013) |
| Reaction rate is equal to the product of concentrations and reactants | Kolomuç and Tekin (2011) |
| Once known, a rate law can be used to quantitatively predict concentrations of species involved in a reaction as a function of time. | |
| Increasing the concentration of reactants increases the reaction time | Kurt and Ayas (2012) |
| The temperature dependence of the reaction rate is contained in the rate constant. This temperature dependence is often well modeled by the Arrhenius model. | |
| Under most circumstances, an increase in temperature leads to an increase in reaction rate. | |
| When the temperature is increased, the rate of the endothermic reaction increases, but the rate of the exothermic reaction decreases | Hackling and Garnett (1985), Akkuş et al. (2003), Çakmakci and Leach (2005), Aydin et al. (2009), Çakmakci (2010), Sözbilir et al. (2010), Çakmakci and Aydogdu (2011), Kurt and Ayas (2012) and Taştan-Kırık and Boz (2012) |
| Increasing temperature increases the time necessary for a reaction to occur (decreases reaction rate) | Van Driel (2002) and Taştan-Kırık and Boz (2012) |
| A rise in temperature does not affect the rate of exothermic reactions | Çakmakci (2010) and Yalçınkaya et al. (2012) |
| Exothermic reactions occur faster than endothermic reactions | Çakmakci (2010), Sözbilir et al. (2010), Çakmakci and Aydogdu (2011), Kolomuç and Tekin (2011), Taştan-Kırık and Boz (2012) and Yalçınkaya et al. (2012) |
| Endothermic reactions occur faster than exothermic reactions | Çakmakci (2010), Sözbilir et al. (2010), Kolomuç and Tekin (2011) and Yalçınkaya et al. (2012) |
| Increasing the temperature of exothermic reactions increases the rate of the forward reaction | Yalçınkaya et al. (2012) |
| The rates of exothermic and endothermic reactions are equal if the temperatures are the same | Kolomuç and Tekin (2011) |
| Empirical fits of temperature data in kinetics can be used to estimate the activation energy. | |
| Temperature affects activation energy | Kaya and Geban (2012) |
| Increasing the temperature increases the activation energy | Yalçınkaya et al. (2012) |
| Increase in temperature decreases the activation energy | Taştan-Kırık and Boz (2012) |
| As temperature decreases the activation energy, it enables the reaction to increase its rate | Kolomuç and Tekin (2011) |
Boz and colleagues (Aydin et al., 2009; Taştan et al., 2010; Taştan-Kırık and Boz, 2012; Yalçınkaya et al., 2012) reported many of these alternative conceptions in their work. Interestingly, Taştan et al. (2010) studied tertiary students' ideas about reaction mechanism through open-ended questionnaires and semi-structured interviews and found that students believed that increasing the concentration of reactants would always increase the rate of reaction. The findings of Boz and others are corroborated by Çakmakci and colleagues (Çakmakci and Leach, 2005; Çakmakci et al., 2006; Çakmakci, 2010; Çakmakci and Aydogdu, 2011). Çakmakci and Leach (2005) studied secondary and tertiary Turkish students’ understanding of the effect of temperature on reaction rates, as a part of their many related studies. They reported that students believed when temperature is increased, the rate of endothermic reactions increased, but the rate of exothermic reaction decreases.
These findings are not isolated to studies aimed at investigating students' understanding of kinetics. In the Netherlands, Van Driel (2002) studied secondary students' particulate nature of matter conceptions in the context of chemical equilibrium and kinetics. There were two frequent student-reasoning patterns in the context of chemical kinetics as listed in Table 3. One was that as concentration decreases, the rate of reaction decreases which is in accord with Taştan's et al. (2010) findings. The second was that as temperature increases, the reaction time also increased (decrease in reaction rate).
The third kinetics enduring understanding is that “most chemical reactions take place by a series of more elementary reactions, called the reaction mechanism” (Holme et al., 2015). Comparatively fewer alternative conceptions relate to this articulation as shown in Table 4. As discussed above, Taştan et al. (2010) specifically studied tertiary students' understanding of reaction mechanism, establishing that students did not recognize the slow step of the mechanism to be the rate-determining step. Rather, students typically used the net reaction equation when generating their rate expression. This finding was not unique to their study; Çalik et al. (2010) also reported the same conclusion.
| It is possible to devise a series of reactions that, when summed, yield the overall reaction and provide a mechanism for how the reaction occurs. | |
| Chemical reactions often occur via multiple steps, called the reaction mechanism. | |
| Assumption that all reactions are elementary reactions (state rate law based on law of mass action) | Kıngır and Geban (2012) and Turányi and Tóth (2013) |
| One step in a mechanism, the rate determining step, is often much slower than others and this slow step tends to determine the overall reaction rate. | |
| No recognition of the slow step as the rate-determining step (typically use the net reaction equation) | Çalik et al. (2010) and Taştan et al. (2010) |
| Species that appear in a reaction mechanism but not in the overall reactions are called intermediates and their identification can provide important evidence about how well the mechanism describes the reaction. | |
| Conflation of “intermediate” and “activated complex” conceptions | Taştan et al. (2010) and Kolomuç and Tekin (2011) |
Kolomuç and colleagues (Çalik et al., 2010; Kolomuç and Tekin, 2011) also report other alternative conceptions from their studies. For example Kolomuç and Tekin (2011) studied Turkish in-service chemistry teachers' alternative conceptions of reaction rates and found that students conflated intermediate and activated complex concepts, which was also reported by Taştan et al. (2010).
“An elementary reaction requires that the reactants collide (interact) and have both enough energy and appropriate orientation of colliding particles for the reaction to occur” is another kinetics enduring understanding from the content map (Holme et al., 2015). Kolomuç and Tekin's (2011) study of in-service chemistry teachers revealed alternative conceptions that were categorized under two of the articulations for this enduring understanding. For example, students' reported that in reactions with high activation energy, the probability that molecules may collide is less, which is listed in Table 5. Such results are compatible with those of Boz and colleagues (Taştan-Kırık and Boz, 2012; Yalçınkaya et al., 2012). Among other findings, they report that students believe changing the temperature has a direct effect on changing the activation energy.
| The collision theory of reactions indicates that collisions result in products only if there is enough energy and if the orientation of the reactants is appropriate. | |
| The number of particles involved in a collision defines the reaction as unimolecular, bimolecular, or termolecular. | |
| Even if it is the given value of the activation energy, the rate of reaction depends on whether the particles are single-atom or multi-atom | Kolomuç and Tekin (2011) |
| At the molecular scale, reactions are required to overcome an energy barrier, called the activation energy, in order to take place. | |
| In reactions with high activation energy, the probability that molecules may collide is less | Kolomuç and Tekin (2011) |
| The energy required to initiate a reaction is called the activation energy. | |
| In many cases, overcoming the activation energy is achieved by high-speed collisions between rapidly moving molecules in a sample. | |
| Temperature affects activation energy | Kaya and Geban (2012) |
| Increasing the temperature increases the activation energy | Yalçınkaya et al. (2012) |
| Increase in temperature decreases the activation energy | Taştan-Kırık and Boz (2012) |
| As temperature decreases the activation energy, it enables the reaction to increase its rate | Kolomuç and Tekin (2011) |
| Exothermic reactions have lower activation energy than endothermic reactions | Taştan-Kırık and Boz (2012) and Yalçınkaya et al. (2012) |
| Activation energy is the kinetic energy of reactants molecules | Çakmakci (2010) |
| Activation energy is the (total) amount of energy released in a reaction | Çakmakci (2010) |
| In reactions with high activation energy, the probability that molecules may collide gets less | Kolomuç and Tekin (2011) |
| The higher the activation energy, the lower the reaction rate | Yalçınkaya et al. (2012) |
The final kinetics enduring understanding used in classifying the literature is that “catalysis increases the rate of reaction and has important applications in a number of subdisciplines of chemistry” (Holme et al., 2015). A large number of reviewed articles reported alternative conceptions about catalysts as presented in Table 6. In their instructional studies, Boz and colleagues (Taştan-Kırık and Boz, 2010, 2012; Yalçınkaya et al., 2012) reported numerous alternative conceptions, such as those that discussed how catalysts affect reaction rate by altering the kinetic energy of the molecules. Çakmakci and colleagues (Çakmakci, 2010; Çakmakci and Aydogdu, 2011) also reported findings related to this enduring understanding. For example, students' believed that catalysts do not affect or do not change the mechanisms of reaction.
| A catalyst increases the rate of the reaction by providing a new reaction pathway with a lower activation energy. | |
| The catalyst increases the average speed of the molecules (or increases the number of collisions) | Taştan-Kırık and Boz (2010, 2012) and Kurt and Ayas (2012) |
| A catalyst increases the yield of products | Çakmakci (2010), Yalçınkaya et al. (2012) and Turányi and Tóth (2013) |
| Catalyst increases reaction rate by decreasing the kinetic energy of the molecules | Yalçınkaya et al. (2012) |
| Catalysts provide an alternative reaction pathway that lowers this activation energy. | |
| A catalyst is needed to initiate reaction | Kıngır and Geban (2012) |
| A catalyst does not affect or does not change the mechanisms of a reaction (confusion of catalyst and intermediate in some cases) | Çakmakci (2010), Çakmakci and Aydogdu (2011), Kurt and Ayas (2012), Taştan-Kırık and Boz (2012) and Yalçınkaya et al. (2012) |
| A catalyst does not react with any of the reactants or products | Yalçınkaya et al. (2012) |
| Because a catalyst lowers the activation energy, it affects both forward and reverse reactions. | |
| A catalyst only speeds up the forward reaction (catalyst affects the rates of forward and reverse reactions differently) | Hackling and Garnett (1985), Voska and Heikkinen (2000), Akkuş et al. (2003), Bilgin and Geban (2006), Kıngır and Geban (2012) and Yalçınkaya et al. (2012) |
| A catalyst increases activation energy of the reaction | Taştan-Kırık and Boz (2010) and Kaya and Geban (2012) |
These findings also appeared in Voska and Heikkinen's (2000) study that used a ten-item two-tier diagnostic instrument, the Test to Identify Student Conceptualizations (TISC), in order to identify student ideas when solving chemical equilibrium problems. Among these second-semester general chemistry students at an American university, eleven alternative conceptions were identified, one of which related to chemical kinetics. Students commonly believed that a catalyst would speed up only the forward reaction (and not the reverse), an idea reported in at six of the reviewed papers.
Equilibrium
Many studies have investigated students' understanding of equilibrium concepts in CER (Garnett et al., 1995; Özmen, 2008). Due to the integrated nature of the concepts of equilibrium and chemical kinetics, researchers find that students often conflate these ideas (Voska and Heikkinen, 2000; Kousathana and Tsaparlis, 2002; Van Driel, 2002; Çakmakci and Leach, 2005; Çakmakci, 2010; Sözbilir et al., 2010; Çakmakci and Aydogdu, 2011; Turányi and Tóth, 2013). We review some examples below in the context of the ACS Exams Institute general chemistry content map to describe this confusion (Holme et al., 2015). These alternative conceptions may appear to be less prominent than those relating only the anchoring concept of kinetics; however, that appearance is only artificial in that we only sampled a few commonly cited papers that primarily studied students understanding of equilibrium ideas (Hackling and Garnett, 1985; Voska and Heikkinen, 2000; Kousathana and Tsaparlis, 2002; Van Driel, 2002; Akkuş et al., 2003; Bilgin and Geban, 2006).The first equilibrium enduring understanding is that “when opposing processes both occur at the same rate, the net change is zero” (Holme et al., 2015). Three alternative conceptions were classified in relation to this category and are listed in Table 7.
| Dynamic processes that achieve equilibrium may be phase changes or chemical reactions. | |
| Equilibrium is dynamic because rates of opposing process are the same, but the rate is not commonly zero. | |
| Forward reaction rate always equals the reverse reaction rate | Hackling and Garnett (1985) and Akkuş et al. (2003) |
| At the equilibrium the rates of forward and reverse reactions are zero | Bilgin and Geban (2006) and Taştan-Kırık and Boz (2010) |
| When equilibrium is re-established the rates of the forward and reverse reactions will be equal to those at the initial equilibrium | Hackling and Garnett (1985), Akkuş et al. (2003) and Bilgin and Geban (2006) |
| The equilibrium constant can be used in calculations that determine the amount of reactants or products present at equilibrium for a given initial state. | |
| The equilibrium state is characterized by a constant, designated K, which provides quantitative information of the extent of a reaction and is related to the ratio of the concentrations of reactants and products. | |
| At equilibrium the rate of the forward reaction will be faster or slower than the rate of the reverse reaction depending on the equilibrium constant value | Bilgin and Geban (2006) |
Geban and colleagues (Akkuş et al., 2003; Bilgin and Geban, 2006) conducted studies on Turkish students' chemical equilibrium conceptions. Akkuş et al. (2003) studied the effectiveness of a constructivist instructional approach in comparison with a traditional approach on students' understanding of chemical equilibrium concepts. Numerous alternative conceptions were identified and demonstrated that these students conflated chemical equilibrium and kinetics ideas including the relationship between the forward and reverse reaction rates.
Bilgin and Geban (2006) also conducted an instructional intervention study, comparing the effect of a cooperative learning approach on students' chemical equilibrium conceptions to a traditional approach. They utilized three measurement instruments in this study: the Chemical Equilibrium Concept Test (CECT), the Chemical Equilibrium Achievement Test (CEAT), and the Science Process Skills Test (SPST). Forty-five alternative conceptions were targeted by the CECT, many of which are conflated with chemical kinetics ideas. An example of one of these alternative conceptions is that at equilibrium the rates of forward and reverse reactions are zero.
The next equilibrium enduring understanding is that “for chemical and physical processes, the equilibrium state can be characterized via the equilibrium constant” (Holme et al., 2015). Only one alternative conception from Bilgin and Geban (2006) study aligns with this understanding. They found that students believe that when a system is at equilibrium, the rate of the forward reaction will be either faster or slower than the rate of the reverse reaction, depending upon the equilibrium constant value.
The next equilibrium enduring understanding used in classification is, “When the equilibrium constant is very large or small, products or reactants, respectively, are primarily present at equilibrium. Systems with K near 1 have significant amounts of both reactants and products present” (Holme et al., 2015). Studies with the primary aim to investigate student understanding of kinetics and thermodynamics (Sözbilir et al., 2010; Turányi and Tóth, 2013) or student understanding of equilibrium (Bilgin and Geban, 2006) reported misconceptions relating to this enduring understanding shown in Table 9, further reinforcing literature precedent that students conflate ideas from these domains.
| Very large or very small values of the equilibrium constant, K, indicate reactions strongly favoring products (in the former case) or reactants (in the latter). | |
| Reactions with very small values of K will have little formation of products, while reactions with very large values of K will proceed nearly completely to products. | |
| At equilibrium the rate of the forward reaction will be faster or slower than the rate of the reverse reaction depending on the equilibrium constant value | Bilgin and Geban (2006) |
| The larger the equilibrium constant, the faster a reaction occurs | Sözbilir et al. (2010) and Turányi and Tóth (2013) |
| The smaller the equilibrium constant, the faster a reaction occurs | Sözbilir et al. (2010) |
Sözbilir et al. (2010) investigated university students in Turkey to reveal their difficulties in determining the differences between chemical kinetics and thermodynamics concepts. A five-question open-ended diagnostic test was used to test students' ability to differentiate the concepts in each area. A subset of these participants was also interviewed to provide more in-depth explanations, clarifying written responses and probing conceptual understandings. The results showed that students struggled with conflating equilibrium and kinetics ideas, reporting that the equilibrium constant related (either directly or inversely) to the rate of reaction. Turányi and Tóth (2013) reported similar findings from their recent study in Hungary where students related the equilibrium constant to reaction rate.
The final equilibrium enduring understanding used is that “if perturbed, a system at equilibrium will respond in the direction that tends to offset the perturbation” (Holme et al., 2015). Three studies decades apart exposed the same alternative conception, that increasing the amount of reactant would decrease the rate of the reverse reaction as shown in Table 10 (Hackling and Garnett, 1985; Akkuş et al., 2003; Bilgin and Geban, 2006).
| The direction of change in a system that is perturbed from equilibrium is predictable—it will change so as to minimize the perturbation. | |
| The ability to predict the direction a reaction will progress for a given perturbation is a key concept. | |
| Reasoning based on perturbations of equilibrium can be used to determine conditions that maximize product formation in a reaction. | |
| When the amount of reactant is increased, the rate of the reverse reaction is decreased | Hackling and Garnett (1985), Akkuş et al. (2003) and Bilgin and Geban (2006) |
Energy and thermodynamics
As established in a recent review by Bain et al. (2014), there have been many investigations in the teaching and learning of thermodynamics, some of which demonstrated that students confound concepts in thermodynamics and kinetics. For example, the first energy and thermodynamics enduring understanding is that “breaking chemical bonds requires energy; formation of chemical bonds releases energy” (Holme et al., 2015). Çakmakci (2010) reported an alternative conception about the definition of activation energy listed in Table 11, where students believed that activation energy was the (total) amount of energy released in a reaction.| While breaking a chemical bond is always endothermic, chemical energy can be released via reactions because bonds are both broken and formed in the course of the reaction. | |
| The extent of energy release or absorption is dictated by the bonds broken in the reactants and the bonds formed in the products. | |
| Activation energy is the (total) amount of energy released in a reaction | Çakmakci (2010) |
The second energy and thermodynamics enduring understanding conflated with kinetics is that “the tendency of nature to disperse, particularly in terms of energy distribution, is embodied in the state function called entropy” (Holme et al., 2015). Sözbilir et al. (2010) reported that students related the magnitude of Gibb's free energy for a reaction to the reaction rate as listed in Table 12. For example, the larger the negative free energy change a reaction has, the faster it occurs.
| Gibb's free energy is a state function that simultaneously calculates entropy for the system and surroundings, and is useful for determining whether or not a process occurs spontaneously. | |
| Gibbs free energy is defined in such a way that the calculation of it provides insight into whether a process is spontaneous with a single calculation. | |
| The larger negative free energy change a reaction has, the faster it occurs | Sözbilir et al. (2010) |
Experiments, measurement, and data
Two of the alternative conceptions relate to the anchoring concept of experiments, measurement, and data. The first experiments, measurement, and data enduring understanding used in classifying the literature alternative misconceptions is that “quantitative observation of matter can be made at a wide range of distance, energy, frequency, and/or time scales” (Holme et al., 2015). Kolomuç and colleagues (Çalik et al., 2010; Kolomuç and Tekin, 2011), reported that students believe that reaction rate is the simply the time required for the reaction to go to completion as shown in Table 13. This alternative conception, while it relates to the kinetics anchoring concept as well, also has grounding in the experimentation anchoring concept.| Laboratory observation of reaction rates helps to establish the concept of reaction time scales empirically. | |
| Rate laws and reaction order are determined using empirical rate data. | |
| Reaction rate is the time required for reactants to form products(or simply reaction rate is reaction time) | Akkuş et al. (2003), Çakmakci (2010), Çalik et al. (2010), Taştan-Kırık and Boz (2010), Kolomuç and Tekin (2011) and Yalçınkaya et al. (2012) |
The other experiments, measurement, and data enduring understanding used in classifying the literature alternative conceptions is that “chemical measurements are based on mass, charge, temperature, pressure, volume, or interaction with electrons or photons” (Holme et al., 2015). Kousathana and Tsaparlis (2002) investigated secondary Greek students' errors in solving numerical chemical equilibrium problems. Student errors were categorized into five groups: equilibrium constant, stoichiometry, heterogeneous equilibria, disturbance of chemical equilibrium, and gas equilibria/ideal gas law. One of the main incorrect understandings observed was that students confused reaction yield and reaction rate ideas (Table 14). This same confusion was reported by Yalçınkaya et al. (2012).
| Stoichiometry provides an example of mass measurements being used in the laboratory, particularly for percentage yield | |
| Reaction yield and reaction rate concepts are the same concepts, directly relating to each other | Kousathana and Tsaparlis (2002) and Yalçınkaya et al. (2012) |
Chemical reactions
The alternative conception discussed in Table 14 was also classified under another anchoring concept, chemical reactions. The enduring understanding it related to was “chemical change can be controlled by choices of reactants, reaction conditions, or use of catalysts” (Holme et al., 2015). This confusion of reaction rate and reaction yield (Kousathana and Tsaparlis, 2002; Yalçınkaya et al., 2012) not only relates to mass measurements in laboratory (Table 14), but also theoretical yield calculations (Table 15).| Control of chemical reactions is often not fully accomplished, so details such as limiting reactants and percentage yields are important in characterizing what occurs. | |
| Stoichiometric calculations provide the theoretical yield, which can be used to determine percentage yield. | |
| Reaction yield and reaction rate concepts are the same concepts, directly relating to each other | Kousathana and Tsaparlis (2002) and Yalçınkaya et al. (2012) |
Intermolecular interactions
The final anchoring concept used to classify the alternative conceptions found in the review literature is intermolecular interactions. The intermolecular interaction enduring understanding used in classification was that “intermolecular forces are generally weaker, on an individual basis, than chemical bonds, but the presence of many such interactions may lead to overall strong interactions” (Holme et al., 2015). The results in Table 16 relate to the thermodynamic alternative conceptions found both in the energy and thermodynamics anchoring concept and the kinetics anchoring concepts. Boz and colleagues (Taştan-Kırık and Boz, 2012; Yalçınkaya et al., 2012) noted students’ belief that the kinetic energy of the molecules increased by decreasing volume, an alternative idea about the physical properties of gases.| Substances exist as a gas at room temperature when intermolecular forces are weak. Models for gas behavior can be quite general because these forces are small—the most common is the ideal gas model. | |
| Gases have physical properties that are often independent of the identity of the gas; the conceptual understanding of the relationships between these properties is important. | |
| Kinetic energy of molecules increases by decreasing volume | Taştan-Kırık and Boz (2012) and Yalçınkaya et al. (2012) |
Other
Some of the student difficulties from the literature did not fall under a specific classification in the general chemistry content map. For example, students encountered great difficulty characterizing how rate changes during a reaction (Table 17). These difficulties were noted by numerous studies. Some students believed that the reaction rate stayed constant throughout the duration of a reaction (Çakmakci et al., 2006; Bektaşli and Çakmakci, 2011; Kolomuç and Tekin, 2011). Others believed it either increased or decreased as the reaction progressed (Hackling and Garnett, 1985; Çakmakci et al., 2006; Çakmakci, 2010; Bektaşli and Çakmakci, 2011; Kolomuç and Tekin, 2011; Yalçınkaya et al., 2012). Still others had different ideas about reaction rate (Table 17).| Characterizing how rate changes during a reaction | |
| Reaction rate increases as the reaction progresses | Hackling and Garnett (1985), Çakmakci et al. (2006), Çakmakci (2010), Bektaşli and Çakmakci (2011) and Kolomuç and Tekin (2011) |
| Reaction rate decreases as the reaction progresses | Kolomuç and Tekin (2011) and Yalçınkaya et al. (2012) |
| Reaction rate is constant (as long as no reaction parameters are altered) | Çakmakci et al. (2006), Bektaşli and Çakmakci (2011) and Kolomuç and Tekin (2011) |
| Reaction rate increases up to a maximum value and remains constant at that value | Akkuş et al. (2003), Çakmakci et al. (2006), Bektaşli and Çakmakci (2011) and Kolomuç and Tekin (2011) |
| Reaction rate decreases down to a minimum value and remains constant at the value | Kolomuç and Tekin (2011) |
| Reaction rate increases up to a maximum value, remains constant, and eventual decreases gradually back to zero when the limiting reactant is consumed | Çakmakci et al. (2006), Aydin et al. (2009) and Taştan-Kırık and Boz (2010, 2012) |
Another group of alternative conceptions that did not fall under the general chemistry content map is about experimental factors that affect reaction rate (Table 18). Çakmakci et al. (2006) and Yalçınkaya et al. (2012) noted that students did not recognize volume or pressure as factors that may affect gaseous reaction rates. Another finding from these studies was that students believed that reactions in smaller containers were faster than those in larger containers, even if they were the same reaction conducted under the same conditions.
| Experimental conditions and reaction rates | |
| Reactions in smaller containers are faster than those in larger containers (same reaction and conditions, different container) | Çakmakci et al. (2006) and Yalçınkaya et al. (2012) |
| Volume and pressure not recognized as factors affecting gaseous reaction rates | Çakmakci et al. (2006) and Yalçınkaya et al. (2012) |
| When volume of reaction vessel is decreased, the rate of the reverse reaction is decreased | Hackling and Garnett (1985) and Bilgin and Geban (2006) |
Trends
In addition to the many alternative conceptions, review of this research yields three over-arching findings. Çakmakci and colleagues noted in numerous studies with both secondary and tertiary Turkish students that they tend to employ macroscopic modeling, rather than theoretical or particulate modeling when engaging with chemical kinetics material (Çakmakci and Leach, 2005; Çakmakci et al., 2006; Çakmakci and Aydogdu, 2011). In Çakmakci's work, the term modeling is used to characterize how students describe or explain phenomena. When comparing student data across levels, they found the nature of student explanations shifted from being more descriptive at the secondary level to being more explanatory or theoretical at the tertiary level. In these same studies, they noted that students use and draw upon everyday knowledge when trying to understand and explain chemical kinetics concepts, a finding noted elsewhere in the literature (e.g., Turányi and Tóth, 2013). Secondary students had a greater tendency to justify claims with everyday knowledge or restatements of available information. Tertiary students were more likely to use a theoretical model or causal mechanism when explaining chemical phenomena.Another common theme relates to graphical and visual representations. Students demonstrated difficulty interpreting graphical representations in the context of chemical kinetics problem solving situations (Çakmakci et al., 2006; Taştan et al., 2010; Çakmakci and Aydogdu, 2011; Kolomuç and Tekin, 2011). They also failed to grasp underlying scientific knowledge expressed through visual representation in similar settings (Çakmakci et al., 2006; Çakmakci and Aydogdu, 2011). Bektaşli and Çakmakci's (2011) data demonstrated that students' conceptions about rates are not consistent across contexts and domains; rather, their ideas' are dependent on the format and contextual features of the questions. For example, student achievement was higher when data were presented in a table instead of a graph. In a more recent study, Seçken and Seyhan (2015) investigated secondary Turkish students' academic achievement and anxiety in the context of graphical chemical reaction rate problems. Three measurement instruments were used: the Achievement Test of Reaction Rate (RRAT), the Graphical Test of Reaction Rate (RRGT), and the Anxiety Scale on the Use of Graphics (ASUG). Students obtained significantly higher mean scores on the RRAT compared to the RRGT. The students’ anxiety about problems with graphics was also found to be higher than those without, according to percentage and frequency data obtained through the ASUG. Student data also shows a statistically significant negative (but weak) Pearson correlation between RRGT achievement scores and their level of anxiety as shown by the ASUG.
A final theme that is pervasive throughout this body of literature is that students often conflate thermodynamics and kinetics concepts, such as the role of observed temperature changes or the effect of manipulating temperature conditions in chemical reactions (Çakmakci, 2010; Sözbilir et al., 2010; Çakmakci and Aydogdu, 2011; Turányi and Tóth, 2013). Additionally, students confuse chemical kinetics and equilibrium concepts, such as equating the size of the equilibrium constant to the speed of the reaction (Voska and Heikkinen, 2000; Kousathana and Tsaparlis, 2002; Van Driel, 2002; Çakmakci and Leach, 2005). As Çakmakci and Leach (2005) wrote, “Students' lack of understanding in thermodynamics and chemical equilibrium significantly influences their ideas about chemical kinetics.” Tables 2, 3 and 5–12 provide ample support from the chemical education research for this observation.
Effectiveness of instructional approaches for teaching chemical kinetics
In addition to the student-understanding-oriented research described above, researchers have investigated the effectiveness of different instructional approaches and materials on student learning, resulting in 11 publications. Most of these studies use a quasi-experimental design, gathering data through pre- and post-tests in non-equivalent comparison groups. A compiled list of the instruments used in these studies is cataloged in Table 19.| Instrument | Acronym | Format | Quality measure | Ref. |
|---|---|---|---|---|
| Reaction rate concept test | RRCT | Open-ended and multiple-choice questions | Cronbach α = 0.81; Kuder–Richardson Formula 20 (K–R 20) = 0.78; K–R 20 = 0.78; reliability coefficient = 0.78 | Çalik et al. (2010), Taştan-Kırık and Boz (2010, 2012) and Yalçınkaya et al. (2012) |
| Reaction rate concept test | RRCT | Multiple-choice questions | None; Cronbach α = 0.71; Cronbach α = 0.75 (pre), Cronbach α = 0.81 (post) | Kaya and Geban (2012), Kıngır and Geban (2012) and Cetin (2014) |
| Chemical reactions rate comprehension test | CRRCT | Open-ended questions | — |
Kolomuç and Tekin (2011)
*Modified version of the RRCT |
| Chemical kinetics concepts achievement test | CKCAT | Open-ended questions | — |
Çakmakci and Leach (2005), Çakmakci et al. (2006), Bektaşli and Çakmakci (2011) and Çakmakci and Aydogdu (2011)
*Modified version of the RRCT |
| Achievement test of reaction rate | RRAT | Multiple-choice questions | Cronbach α = 0.78 | Seçken and Seyhan (2015) |
| Kinetics versus thermodynamics diagnostic test | — | Open-ended questions | — | Sözbilir et al. (2010) |
| Chemical reaction rate questionnaire | — | Two-tier multiple-choice questions | K–R 20 = 0.85 | Supasorn and Promarak (2015) |
| Kinetics and thermodynamics instrument | — | Open-ended questions | — | Turányi and Tóth (2013) |
| Modified concept test | — | Open-ended and multiple-choice questions | — | Aydin et al. (2009) |
| Kinetics diagnostic instrument | — | Open-ended questions | — | Çakmakci (2010) |
| Test to identify student conceptualizations | TSIC | Two-tier multiple-choice questions | K–R 20 = 0.79 | Voska and Heikkinen (2000) |
| Chemical equilibrium concept test | CECT | Multiple-choice questions | Cronbach α = 0.78; Cronbach α = 0.87 | Akkuş et al. (2003) and Bilgin and Geban (2006) |
| Chemical equilibrium achievement test | CEAT | Multiple-choice questions | Cronbach α = 0.81 | Bilgin and Geban (2006) |
| Chemistry concept test | CCT | Open-ended and multiple-choice questions | Cronbach α = 0.75 | Kıngır and Geban (2012) |
| Graphical test on reaction rate | RRGT | Multiple-choice questions | Cronbach α = 0.697 | Seçken and Seyhan (2015) |
| Anxiety scale on the use of graphics | ASUG | Five-point Likert scale | Cronbach α = 0.935 | Seçken and Seyhan (2015) |
| Real-life relating test | RRT | Open-ended questions | — | Kurt and Ayas (2012) |
| Science process skills test | SPST | Multiple-choice questions | Cronbach α = 0.82; Cronbach α = 0.85; Cronbach α = 0.85; Cronbach α = 0.85 | Akkuş et al. (2003), Bilgin and Geban (2006) and Taştan-Kırık and Boz (2010, 2012) |
| Motivated strategies for learning questionnaire | MSLQ | Seven-point Likert scale | Cronbach α values calculated for each of 6 sections, ranging from 0.65 to 0.90 | Taştan-Kırık and Boz (2012) |
Three studies conducted with secondary students in Turkey used a conceptual change approach for teaching kinetics to determine if student understanding could be improved. In each case attention was placed on instruction in the experimental group, addressing students' alternative conceptions thus fostering the conditions for conceptual change (dissatisfaction, intelligibility, plausibility, and fruitfulness) through animations and guide sheets (Çalik et al., 2010), demonstrations (Kaya and Geban, 2012), or conceptual-change texts (Kıngır and Geban, 2012). In every case the conceptual change approach group significantly outperformed the traditional or control group, suggesting that these methods that can help students learn scientifically correct ways of conceptualizing kinetics. However, in all cases alternative conceptions were identified as listed in Tables 3–6.
Constructivist approaches to instruction using concept maps, videos/animations, hands-on activities, and small and large group discussions also produced improved learning in secondary and tertiary classrooms in Turkey, although alternative conceptions were still identified (see Tables 2, 3, 6, and 17) (Aydin et al., 2009; Kurt and Ayas, 2012).
Taştan-Kırık and Boz (2010, 2012) report the results of using a cooperative learning approach in two different secondary schools in Turkey on student understanding of reaction rates. Although the statistical handling of the data was different due to differences in scores on the Reaction Rate Concept Test (RRCT) and the Science Process Skill Test (SPST) at the two schools, the outcome was similar – the cooperative learning group performed at a statistically higher level than the traditional group. Interviews with the students were also part of this research design which allowed Taştan-Kırık and Boz to identify alternative conceptions listed in Tables 2–6, 16, and 17.
Three other approaches have also met with success in improving student understanding of kinetics. Çakmakci and Aydogdu (2011) designed and evaluated an evidence-informed instruction intervention, compared to a traditional instruction implementation, regarding chemical kinetics in a second semester general chemistry classroom at a university in Turkey. They developed a set of 10 tasks referred to as the Chemical Kinetics Concepts Achievement Test (CKCAT) based upon their prior work (Çakmakci et al., 2006; Çakmakci, 2010) in which the experimental group performed significantly better than the traditional group. Yalçınkaya et al. (2012) investigated case-based learning's effectiveness as a teaching strategy to challenge Turkish secondary students' alternative conceptions about chemical kinetics concepts. The case based group outperformed the traditional group on the RRCT. Although student interviews revealed many alternative conceptions as documented in Tables 1–3, 6, 7, and 13–18, the case-based group exhibited fewer of these conceptions than the traditional group. Cetin (2014) investigated argumentation instruction in a treatment versus control design in two-second semester general chemistry classrooms at a university in Turkey. Students in the argumentation classroom performed significantly better on the RRCT. Analysis of arguments constructed in both classrooms suggests that argumentation-based instruction can promoted greater conceptual understanding of reaction rate concepts while promoting scientific argumentation skills.
Finally, in the only study carried out in a country other than Turkey, Supasorn and Promarak (2015) studied the implementation of 5E inquiry and analogy instruction with the goal to enhance conceptual understanding of reaction rate for 44 secondary students in Thailand. The interventions utilized the 5E inquiry method, where students engage, explore, explain, elaborate, and evaluate concepts and understanding. Using a pre, post, and delayed-post test design to measure learning, the results demonstrated that instruction improved learning, and that for some areas of kinetics, that the enhanced conceptual understanding may be durable and lasting.
Indeed, for every intervention described in the literature, student understanding of concepts related to kinetics was improved. Turkish researchers have led the way in this area of research conducting 10 of 11 studies, and many of these in secondary classrooms. Further research in classrooms outside of Turkey is warranted to broaden the evidence for efficacy of these approaches. The evidence suggests that every type of intervention was effective in improving student understanding.
Measurement instruments
Many diagnostic/concept instruments were used in the 11 instructional approach studies in order to measure differences in student learning between the treatment and control groups. The instruments are listed in Table 19, although there was some confusion about the differences between the RRCT, CRRCT, and CKCAT instruments, as they are very similar and are cited as being developed from the same literature sources.It should be noted that to use these instruments in other settings the reliability and validity of the data collected would need to be ascertained. Researchers from Turkey have led the way in the development of these instruments, but they have not been used with other populations. Use of these instruments in other contexts and reporting the accompanying reliability and validity data would improve the utility of these instruments in CER.
Summary
These eleven studies demonstrate a variety of approaches for alternative instructional methods, largely designed for the secondary level. These alternative approaches included conceptual change, constructivist, cooperative learning, evidence-informed, case-based, explicit argumentation, and 5E inquiry and analogy instruction. The primary aim of each article was to present evidence of the effectiveness of instruction, typically in comparison to traditional teaching methods. The findings discussed in this section are promising in that they largely promote students' understanding of chemical kinetics concepts in ways that traditional instruction does not. These results should pique the interest of researchers and practitioners alike.Related rates mathematics research
Chemical kinetics is one of the areas of chemistry that utilizes mathematics as its primary representation to communicate observations, analyses, and interpretations (Becker and Towns, 2012). More specifically, kinetics is a practical application of related rates, such as studying the related rates of the disappearance of reactants and appearance of products in a chemical reaction. Better understanding students' conceptions of related rates (among other mathematics concepts) is crucial for both practitioners and researchers, as they are used in chemistry contexts such as kinetics. When researching or teaching crosscutting concepts and core ideas like rate, researchers and practitioners should be aware of the literature across subject areas so that students are best supported in developing and using deep, transferable knowledge (Cooper et al., 2015).Research on related rates problems indicates that students must possess and use fundamental mathematical knowledge pertaining to function, variable, differentiation, and rate. Literature suggests that students do not fully understand these concepts. For example, students at both the secondary and tertiary levels demonstrate underdeveloped conceptions of function and variable (Orton, 1983; Vinner and Dreyfus, 1989; Breidenbach et al., 1992; White and Mitchelmore, 1996; Clark et al., 1997; Carlson, 1998; Carlson et al., 2002; Aydin, 2014). One such example of this is White and Mitchelmore's (1996) finding that students have a “manipulation focus” wherein they manipulate variables without considering the concepts or ideas that they represent, treating them “as symbols to be manipulated rather than quantities to be related” (White and Mitchelmore, 1996). The literature also shows that even strong undergraduate mathematics students and beginning graduate students (those that earned A's) demonstrate alternative ideas about the function concept (Carlson, 1998). Students also struggle with the concept of the derivative (Orton, 1983; Ferrini-Mundy and Graham, 1991; Clark et al., 1997; Firouzian, 2013; Piccolo and Code, 2013; Hashemi et al., 2014; Rasmussen et al., 2014). Many students are able to follow derivative rules procedurally, without understanding the conceptual ideas behind it (Clark et al., 1997; Piccolo and Code, 2013). Engelke (2006) is also one of many studies to show that students demonstrate difficulty defining rate, let alone understanding how it changes over time.
RUME studies have also shown that students frequently fail to consider variable relationships and engage in fruitful reasoning patterns, unlike experts (Martin, 2000; Engelke, 2004; 2006; 2007; 2008; Engelke and CadwalladerOlsker, 2011). Similarly, these studies also reveal alignment with DBER in that students struggle more with conceptual steps when compared to procedural steps (Bodner and Herron, 2003; Carlson and Bloom, 2005; Gardner and Bodner, 2007; Hull et al., 2013; Kuo et al., 2013). These findings draw attention to research questions in chemical kinetics where students must consider mathematical relationships as they reason through problems. Accordingly, we call on faculty to promote the idea that equations hold meaning to understand relationships and concepts, rather than the idea that they are computational tools to obtain an answer. Focusing student attention of variables and relationships would serve to enhance conceptual understanding in kinetics, as well as other areas of chemistry. Although some of the findings from mathematics research may not have relevance in general chemistry, such as student difficulty with differentiation, these findings do have direct relevance for upper-level chemistry students and courses, as these courses frequently require and use calculus.
Discussion
Over half of the reviewed kinetics articles investigated students' understanding of kinetics focusing on foundational concepts of reaction rate or mechanism while others focused on how kinetics concepts relate to other areas, such as equilibrium and thermodynamics. Tables 2–18 display a compilation of alternative conceptions reported in this body of literature, organized according to the ACS Exams Institute general chemistry anchoring concepts content map (Holme et al., 2015). The other portion of the literature investigated instructional approaches to teaching chemical kinetics, primarily in secondary classrooms in Turkey. Across the literature reviewed there is a heavy emphasis on documenting misconceptions. Sadly there has been less research outside of Turkey on developing effective methods of helping students learn scientifically correct notions of chemical kinetics in light of our current understanding of how students learn (Smith et al., 1993; Bransford et al., 2000; Maskiewicz and Lineback, 2013).Students' modeling tendencies emerged as a theme in Çakmakci's research (Çakmakci and Leach, 2005; Çakmakci et al., 2006; Çakmakci and Aydogdu, 2011). Macroscopic modeling was typically used by students when solving chemical kinetics problems, rather than theoretical or particulate modeling.
The literature also suggests that students have difficulty interpreting and understanding graphical representations (Çakmakci et al., 2006; Taştan et al., 2010; Çakmakci and Aydogdu, 2011; Kolomuç and Tekin, 2011). These findings are not surprising in light of multiple external representations (MERs) research, which highlights difficulties that students' have understanding individual graphical representations as well as making connections between different representations (e.g., Ainsworth, 1999, 2006; Ainsworth and VanLabeke, 2004).
Students also conflate ideas, such as thermodynamics with kinetics or equilibrium with kinetics (Voska and Heikkinen, 2000; Kousathana and Tsaparlis, 2002; Van Driel, 2002; Çakmakci and Leach, 2005; Çakmakci, 2010; Sözbilir et al., 2010; Çakmakci and Aydogdu, 2011; Turányi and Tóth, 2013). This is not a surprising finding, as these confusions have emerged repeatedly in the CER literature (Hackling and Garnett, 1985; Cachapuz and Maskill, 1987; Banerjee, 1991; Quílez-Pardo and Solaz-Portolés, 1995; Johnstone et al., 1997; Thomas and Schwenz, 1998; Sözbilir and Bennett, 2006). Research specifically targeting students' understanding at these conceptual domain interfaces is a rarity; rather, research in individual conceptual domains (like those cited here) re-discovers student conflation/confusion. Explicit instruction targeting the interfaces of these conceptual bodies should be developed and implemented in order to study how students understand these conceptual domains. This is not unprecedented because what experts tacitly understand often needs to be made more explicit for novices (National Research Council, 2012).
Research in undergraduate mathematics education has demonstrated that solving related rates problems is not a trivial task for students (Martin, 2000; Engelke, 2004, 2006, 2007, 2008; Engelke and CadwalladerOlsker, 2011; Piccolo and Code, 2013). It's been shown that sometimes students struggle with more basic mathematical concepts that lay the foundation for understanding and solving related rates problems (Orton, 1983; Vinner and Dreyfus, 1989; Ferrini-Mundy and Graham, 1991; Breidenbach et al., 1992; White and Mitchelmore, 1996; Clark et al., 1997; Carlson, 1998; Carlson et al., 2002; Firouzian, 2013; Aydin, 2014; Hashemi et al., 2014; Rasmussen et al., 2014). Since it is clear that some of these fundamental conceptual ideas can be obstacles for students when solving related rates problems, we suggest that assessing student mathematical abilities and understandings may be advantageous for instructors. The Precalculus Concept Assessment (PCA) is a multiple-choice instrument that targets foundational ideas needed for calculus, such as rate of change and function. (Carlson et al., 2010). Using a tool such as this to assess students' prior mathematical knowledge could be helpful for chemistry instructors in that it could specifically reveal gaps in students' mathematical knowledge that chemistry professors assume students not only understand, but can apply.
Directions for future research and implications for practice
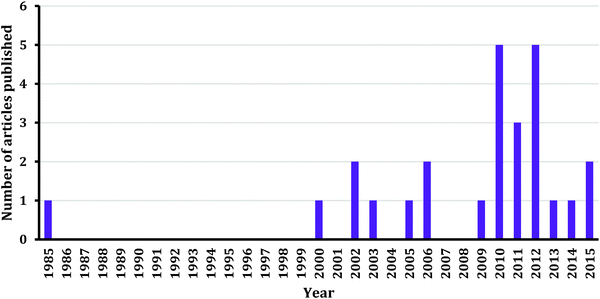
Based on the number of reviewed articles, more research is warranted in the area of teaching and learning chemical kinetics at the undergraduate level. We are confident that this call will be answered due to the increasing trend of conducting kinetics studies as shown in Fig. 1. In this section we outline directions for research based on the existing literature and the desire to translate findings into effective classroom practices.Research settings
As shown in Table 1, the majority of the reviewed kinetics research took place at the secondary level. There is a strong need for tertiary-level investigation, as it is largely under investigated. In addition, upper-level university research is scarce (both generally and specific to the teaching and learning of chemical kinetics) and is a prime area for future study (National Research Council, 2012). Chemical kinetics is taught throughout the chemistry curriculum in general chemistry, physical chemistry, biochemistry, and inorganic chemistry (Boyer, 2000; American Chemical Society Committee on Professional Training, 2008; Fox and Roehrig, 2015). Similarly, chemical kinetics is not exclusive material taught only to chemistry majors; rather, other science, technology, engineering, and mathematics (STEM) majors (e.g., biology, biochemistry, pharmacy, other life sciences) explore these concepts as well.Table 20 shows that an overwhelming amount of the reviewed work took place in Turkey. Moreover, studies conducted outside Turkey typically did not have a primary focus on kinetics, focusing more on equilibrium or thermodynamics. More research is needed in other countries to discover if similar findings emerge with students in other educational contexts.
| Turkey | The Netherlands | Greece | Hungary | Thailand | Australia | United States | |||
|---|---|---|---|---|---|---|---|---|---|
| Number of studies | Student understanding studies | Rate | 7 | — | — | — | — | — | — |
| Equilibrium | 2 | 1 | 1 | — | — | 1 | 1 | ||
| Thermodynamics | 1 | — | — | 1 | — | — | — | ||
| Instructional approaches studies | Conceptual change | 3 | — | — | — | — | — | — | |
| Constructivist | 2 | — | — | — | — | — | — | ||
| Cooperative learning | 2 | — | — | — | — | — | — | ||
| Other | 3 | — | — | — | 1 | — | — | ||
Research content
Expanding research to the university level opens inquiry into new kinetics content as well. Research on the teaching and learning of more advanced kinetics concepts, such as reaction order, mechanism, steady-state approximations, and enzyme kinetics is desperately needed. Some of these ideas are explored in general chemistry (e.g. reaction order), but, others are primarily taught in upper-level university students courses. Research should expand to investigate all kinetics content across the curriculum.Chemical kinetics is an area of chemistry where mathematics is frequently used as the language of chemistry, requiring students to translate between mathematical representations and the physical meaning that they represent (Becker and Towns, 2012). The paucity of research in this area is especially troubling, as it has been noted that students have difficulty with the mathematics in physical chemistry, of which chemical kinetics is a subset (Thompson et al., 2006; Bucy et al., 2007; Pollock et al., 2007; Christensen and Thompson, 2010, 2012; Hadfield and Wieman, 2010; Wemyss et al., 2011; Becker and Towns, 2012). It has also been documented that mathematical understanding and proficiency are connected to student success in physical chemistry (Nicoll and Francisco, 2001; Derrick and Derrick, 2002; Hahn and Polik, 2004). Yet, few studies in CER examine students' understanding of mathematics in the context of chemistry (Bain et al., 2014).
Furthermore, findings from the reviewed literature indicates that interpreting and understanding graphical representations is difficult for students (Engelke, 2004; Çakmakci et al., 2006; Taştan et al., 2010; Çakmakci and Aydogdu, 2011; Kolomuç and Tekin, 2011). More research is needed investigating students' understanding of MERs, using chemical kinetics as the context. Kinetics is an area of chemistry that uses many various representations, such as graphs and tables. Better understanding students' difficulties with individual representations, as well as their perceptual fluency translating across representations, would provide insight. Using other perspectives, such as Ainsworth's (2006) DeFT framework or Rau's (2015) findings would be a fruitful starting point.
Chemical kinetics is a unique area of chemistry in that it provides an explicit context for students to interact with models and modeling. This aspect has yet to be studied in any capacity, as all the reviewed studies focused on students' conceptual reasoning. How students reason through kinetics concepts and problems has not been examined whatsoever. For example, studying students' use of chemistry reasoning and mathematical reasoning when solving kinetics problems would be a novel way to drive forward research in this area. Similarly, another innovative exploration could examine students' understanding of models and modeling in a laboratory context, collecting and using kinetics data. The design, development, and evaluation of mathematical modeling assessments could also be highly useful for both research and practice.
Cross-disciplinary collaborations
This area of research would be ideal for forging collaborations across disciplines, filling a gap in the literature and responding to call for cross-disciplinary collaborations among DBER fields (National Research Council, 2012). An obvious area for collaboration is the intersection of chemistry and mathematics. Investigating related rates and graphical representations could be initial areas of collaborative investigation. Other disciplines, such as biology, would be ideal for forging collaborations to investigate kinetics at the university level.Instruction
Based on our current understanding of how students learn, students build their knowledge on their current conceptions, whether scientifically correct or not (Maskiewicz and Lineback, 2013). We believe that studying effective ways of teaching and supporting student learning based on their prior knowledge, whether it is correct or incorrect, is of critical importance.The reviewed kinetics articles provide a strong starting point (Tables 2–18) for both researchers and practitioners in developing instructional opportunities, such as clicker questions, peer-led team learning (PLTL) sessions, process oriented guided inquiry learning (POGIL) lessons, computer simulations, or laboratory activities. While many of the findings have origins in secondary contexts, they inform instruction at the tertiary level, where kinetics is taught both at introductory and upper levels. The message from the instructional literature is clear – every approach implemented was superior to a traditional classroom approach. Dissemination of effective approaches across educational contexts particularly moving from Turkey to other countries is important.
Studying the faculty that teach kinetics could also be a fruitful avenue for instructional research as well. This area of study is virtually untouched in CER (Fox and Roehrig, 2015; Mack and Towns, 2016). Doing so could provide insight into teacher thinking about the purposes for teaching kinetics ideas or their roles as an instructor for scaffolding students' reasoning about chemical kinetics at various levels and contexts. Investigating instructor teaching practices and facilitation would also be highly fruitful in light of recent research (Becker et al., 2015). For example, this could generate models for scaffolding student reasoning about chemical kinetics and mathematical concepts.
Research practice
As shown in Table 19, there are many different instruments being developed and used in research and practice. This is promising for the future of the field. However, because there is so much overlap, there should be collaboration and streamlining, to maximize efforts for the design, development, evaluation, and dissemination. More importantly, evaluation of the validity and reliability of these instruments in line with Arjoon et al. (2013) is key to the utility of these tools for meaningful instructional practice and research.Following the state of the art for measurement in quantitative research methodology is of utmost importance (Arjoon et al., 2013). In the same way, following rigorous methodology in qualitative or mixed methods research is also imperative (Tracy, 2010). This includes the use of a theoretical framework, strong experimental design, methods appropriate to answer the research question(s), some measure of credibility, and appropriate and thorough analysis. Such studies will fill the gaps in the literature, influencing both research and practice for years to come.
Finally, it is clear that we have a nearly exhaustive description of alternative conceptions related to chemical kinetics. What is sorely needed is research that establishes which educational approaches are effective across contexts and how differences in student learning can be measured and monitored leveraging the instruments that have been developed (see Table 19).
Acknowledgements
The National Science Foundation under grant DUE-1504371 supported this work. Any opinions, conclusions, or recommendations expressed in this review are those of the authors and do not necessarily reflect the views of the National Science Foundation. We wish to thank Ryan Bain and the Towns research group for their support and helpful comments on the manuscript.References
- Ainsworth S., (1999), The functions of multiple representations, Comput. Educ., 33, 131–152.
- Ainsworth S., (2006), DeFT: a conceptual framework for considering learning with multiple representations, Learn. Instr., 16, 183–198.
- Ainsworth S. and VanLabeke N., (2004), Multiple forms of dynamic representation, Learn. Instr., 14, 241–255.
- Akkuş H., Kadayifçi H., Atasoy B. and Geban Ö., (2003), Effectiveness of instruction based on the constructivist approach on understanding chemical equilibrium concepts, Res. Sci. Technol. Educ., 21, 210–227.
- American Chemical Society Committee on Professional Training, (2008), Undergraduate professional education in chemistry: ACS guidelines and evaluation procedures for bachelor's degree programs, Washington, DC: American Chemical Society.
- Arjoon J. A., Xu X. and Lewis J. E., (2013), Understanding the state of the art for measurement in chemistry education research: examining the psychometric evidence, J. Chem. Educ., 90, 536–545.
- Aydin Y., (2014), The effects of problem based approach on student's conceptual understanding in a university mathematics classroom, Procedia, Soc. Behav. Sci., 152, 704–707.
- Aydin S., Aydemir N, Boz Y., Cetin-Dindar A. and Bektas O., (2009), The contribution of constructivist instruction accompanied by concept mapping in enhancing pre-service chemistry teachers' conceptual understanding of chemistry in the laboratory course, J. Sci. Educ. Technol., 18, 518–534.
- Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15, 320–335.
- Banerjee A. C., (1991), Misconceptions of students and teachers in chemical equilibrium, Int. J. Sci. Educ., 13, 487–494.
- Becker N. and Towns M. H., (2012), Students' understanding of mathematical expressions in physical chemistry contexts: an analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13, 209–220.
- Becker N., Stanford C., Towns M. and Cole R., (2015), Translating across macroscopic, submicroscopic, and symbolic levels: the role of instruction facilitation in an inquiry-oriented physical chemistry class, Chem. Educ. Res. Pract., 16, 769–785.
- Bektaşli B. and Çakmakci G., (2011), Consistency of students' ideas about the concept of rate across different contexts, Educ. Sci., 36, 273–287.
- Bilgin İ. and Geban Ö., (2006), The effect of cooperative learning approach based on conceptual change condition on students' understanding of chemical equilibrium concepts, J. Sci. Educ. Technol., 15, 31–46.
- Bodner G. M. and Herron J. D., (2003), Problem solving in chemistry, in Gilbert J. K., De Jong O., Justi R., Treagust D. F. and Van Driel J. H. (ed.), Chemical education: towards research-based practice, Dordecht: Kluwer Academic Publishers, pp. 235–266.
- Boyer R., (2000), The new biochemistry: blending the traditional with the other, Biochem. Mol. Biol. Educ., 28, 292–296.
- Bransford J. D., Brown A. L. and Cocking R. R., (ed.), (2000), How people learn: brain, mind, experience, and school, expanded edition, Washington, DC: National Academy Press.
- Breidenbach D., Dubinsky E., Hawks J. and Nichols D., (1992), Development of the process function, Educ. Stud. Math., 23, 247–285.
- Bucy B. R., Thompson J. R. and Mountcastle D. B., (2007), Student (mis)application of partial differentiation to material properties, Proceedings of the 2006 Physics Education Research Conference of the American Institute of Physics.
- Cachapuz A. F. C. and Maskill R., (1987), Detecting changes with learning in the organization of knowledge: use of word association tests to follow the learning of collision theory, Int. J. Sci. Educ., 9, 491–504.
- Çakmakci G., (2010), Identifying alternative conceptions of chemical kinetics among secondary school and undergraduate students in Turkey, J. Chem. Educ., 87, 449–455.
- Çakmakci G. and Aydogdu C., (2011), Designing and evaluating an evidence-informed instruction in chemical kinetics, Chem. Educ. Res. Pract., 12, 15–28.
- Çakmakci G. and Leach J., (2005), Turkish secondary and undergraduate students' understanding of the effect of temperature on reaction rates, paper presented at the European Science Education Research Association Conference, Barcelona, Spain.
- Çakmakci G., Leach J. and Donnelly J., (2006), Students' ideas about reaction rate and its relationship with concentration or pressure, Int. J. Sci. Educ., 28, 1795–1815.
- Çalik M., Kolomuç A. and Karagölge Z., (2010), The effect of conceptual change pedagogy on students' conceptions of rate of reaction, J. Sci. Educ. Technol., 19, 422–433.
- Carlson M., (1998), A cross-sectional investigation of the development of the function concept, CMBS Issues Math. Educ., 7, 114–163.
- Carlson M. and Bloom I., (2005), The cyclic nature of problem solving: an emergent multidimensional problem-solving framework, Educ. Stud. Math., 58, 45–75.
- Carlson M., Jacobs S., Coe E., Larsen S. and Hsu E., (2002), Applying covariational reasoning while modeling dynamic events: a framework and a study, J. Res. Math. Educ., 33, 352–378.
- Carlson M., Oehrtman M. and Engelke N., (2010), The precalculus concept assessment: a tool for assessing students' reasoning abilities and understanding, Cognition Instruct., 28, 113–145.
- Cetin P. S., (2014), Explicit argumentation instruction to facilitate conceptual understanding and argumentation skills, Res. Sci. Technol. Educ., 32, 1–20.
- Christensen W. M. and Thompson J. R., (2010), Investigating student understanding of physics concepts and the underlying calculus concepts in thermodynamics, Proceedings of the 13th Annual Conference on Research in Undergraduate Mathematics Education.
- Christensen W. M. and Thompson J. R., (2012), Investigating graphical representations of slope and derivative without a physics context, Phys. Rev. Lett. Spec. Top. – Phys. Educ. Res., 8, 023101.
- Clark J. M., Cordero F., Cottrill J., Czarnocha B., DeVries D. J., St. John D., Tolias, G. and Vidakovic D., (1997), Constructing a schema: the case of the chain rule? J. Math. Behav., 16, 345–364.
- Cooper M. M., Caballero M. D., Ebert-May D., Fata-Hartley C. L., Jardeleza S. E., Krajcik J. S., Laverty J. T., Matz R. L., Posey L. A. and Underwood S. M., (2015), Challenge faculty to transform STEM learning: focus on core ideas, crosscutting concepts, and scientific practices, Science, 350(350), 281–282.
- Derrick M. E. and Derrick F. W., (2002), Predictors of success in physical chemistry, J. Chem. Educ., 79, 1013–1016.
- Engelke N., (2004), Related rates problems: identifying conceptual barriers, Paper presented at the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Toronto, Ontario.
- Engelke N., (2006), Teaching innovations for problems involving rates in calculus, paper presented at the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Mérida, México.
- Engelke N., (2007), A framework to describe the solution process for related rates problems in calculus, Paper presented at the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tahoe, NV.
- Engelke N., (2008), Developing the solution process for related rates problems using computer simulations, paper presented at the Conference on Research in Undergraduate Mathematics Education, San Diego, CA.
- Engelke N. and CadwalladerOlsker T., (2011), Supplemental instruction and related rates problems, paper presented at the Conference on Research in Undergraduate Mathematics Education, Portland, OR.
- Ferrini-Mundy J. and Graham K. G., (1991), An overview of the calculus curriculum reform effort: issues for learning, teaching, and curriculum development, Am. Math. Mon., 98, 627–635.
- Firouzian S. S., (2013), Correlations of students' ways of thinking about derivative to their success in solving applied problems, paper presented at the Conference on Research in Undergraduate Mathematics Education, Denver, CO.
- Fox L. J. and Roehrig G. H., (2015), Nationwide survey of the undergraduate physical chemistry course, J. Chem. Educ., 92(9), 1456–1465.
- Gardner D. E. and Bodner G. M., (2007), The existence of a problem-solving mindset among students taking quantum mechanics and its implications, in Ellison M. D. and Schoolcraft T. A. (ed.), Advances in teaching physical chemistry, US: American Chemical Society, pp. 155–173.
- Garnett P. J., Garnett P. J. and Hackling M. W., (1995), Students’ alternative conceptions in chemistry: a review of research and implications for teaching and learning, Stud. Sci. Educ., 25, 69–95.
- Hackling M. W. and Garnett P. J., (1985), Misconceptions of chemical equilibrium, Int. J. Sci. Educ., 7, 205–214.
- Hadfield L. C. and Wieman C. E., (2010), Student interpretations of equations related to the first law of thermodynamics, J. Chem. Educ., 87, 750–755.
- Hahn K. E. and Polik W. F., (2004), Factors influencing success in physical chemistry, J. Chem. Educ., 81, 567–572.
- Hashemi N., Abu M. S., Kashefi H. and Rahimi K., (2014), Undergraduate students’ difficulties in conceptual understanding of derivation, Procedia, Soc. Behav. Sci., 143, 358–366.
- Holme T. and Murphy K., (2012), The ACS Exams Institute undergraduate chemistry anchoring concepts content map I: general chemistry, J. Chem. Educ., 89, 721–723.
- Holme T., Luxford C. and Murphy K., (2015), Updating the general chemistry anchoring concepts content map, J. Chem. Educ., 92, 1115–1116.
- Hull M. M., Kuo E., Gupta A. and Elby A., (2013), Problem-solving rubrics revisited: attending to the blending of informal conceptual and formal mathematical reasoning, Phys. Rev. Lett. Spec. Top. – Phys. Educ. Res., 9, 010105.
- Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Lear., 7, 75–83.
- Johnstone A. H., MacDonald J. J. and Webb G., (1997), Misconceptions in school thermodynamics, Phys. Educ., 4, 248–250.
- Justi R., (2002), Teaching and learning chemical kinetics, in Gilbert J. K., De Jong O., Justi R. Treagust D. and Van Driel J. H. (ed.), Chemical Education: Towards Research-based Practice, Dordrecht, Kluwer, pp. 293–315.
- Kaya E. and Geban Ö., (2012), Facilitating conceptual change in rate of reaction concepts using conceptual change oriented instruction, Educ. Sci., 37, 216–225.
- Kıngır S. and Geban Ö., (2012), The effect of conceptual change approach on students' understanding of reaction rate concepts, H. Ü. J. Educ., 43, 306–317.
- Kolomuç A. and Tekin S., (2011), Chemistry teachers' misconceptions concerning concept of chemical reaction rate, Eurasian J. Phys. Chem. Educ., 3, 84–101.
- Kousathana M. and Tsaparlis G., (2002), Students' errors in solving numerical chemical-equilibrium problems, Chem. Educ. Res. Pract. Eur., 3, 5–17.
- Kuo E., Hull M. M., Gupta A. and Elby A., (2013), How students blend conceptual and formal mathematical reasoning in solving physics problems, Sci. Educ., 97(1), 32–57.
- Kurt S. and Ayas A., (2012), Improving students' understanding and explaining real life problems on concepts of reaction rate by using a four step constructivist approach, Energ. Educ. Sci. Technol. Part B: Soc. Educ. Stud., 4, 979–992.
- Mack M. R. and Towns M. H., (2016), Faculty beliefs about the purposes for teaching undergraduate physical chemistry courses, Chem. Educ. Res. Pract., 17, 80–99.
- Martin T., (2000), Calculus students' ability to solve geometric related-rates problems, Math. Educ. Res. J., 12, 74–91.
- Maskiewicz A. C. and Lineback J. E., (2013), Misconceptions are “so yesterday!”, CBE – Life Sci. Educ., 12, 352–356.
- Murphy K., Holme T., Zenisky A., Caruthers H. and Knaus K., (2012), Building the ACS exams anchoring concept content map for undergraduate chemistry, J. Chem. Educ., 89, 715–720.
- National Research Council, (2012), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, Washington, DC: The National Academies Press.
- Nicoll G. and Francisco J. S., (2001), An investigation of the factors influencing student performance in physical chemistry, J. Chem. Educ., 78, 99–102.
- Orton A., (1983), Students' understanding of differentiation, Educ. Stud. Math., 14, 235–250.
- Özmen H., (2008), Determination of students' alternative conceptions about chemical equilibrium: a review of research and the case of Turkey, Chem. Educ. Res. Pract., 9, 225–233.
- Piccolo C. and Code W. J., (2013), Assessment of students' understanding of related rates problems, paper presented at the Conference on Research in Undergraduate Mathematics, Denver, CO.
- Pollock E. B., Thompson J. R. and Mountcastle D. B., (2007), Student understanding of the physics and mathematics of process variables in P-V diagrams, Proceedings of the 2007 Physics Education Research Conference of the American Institute of Physics.
- Quílez-Pardo J. and Solaz-Portolés J. J., (1995), Students' and teachers' misapplication of Le Châtelier's principles: implications for the teaching of chemical equilibrium, J. Res. Sci. Teach., 32, 939–957.
- Rasmussen C., Marrongelle K. and Borba M. C., (2014), Research on calculus: What do we know and where do we need to go? ZDM Math. Educ., 46, 507–515.
- Rau M. A., (2015), Enhancing undergraduate chemistry learning by helping students make connections among multiple graphical representations, Chem. Educ. Res. Pract., 16, 654–669.
- Seçken N. and Seyhan H. G., (2015), An analysis of high school students' academic achievement and anxiety over graphical chemistry problems about the rate of reaction: the case of Sivas province, Procedia, Soc. Behav. Sci., 174, 347–354.
- Smith J. P., diSessa A. A. and Roschelle J., (1993), Misconceptions reconceived: a constructivist analysis of knowledge in transition, J. Learn. Sci., 3, 115–163.
- Sözbilir M. and Bennett J., (2006), Turkish prospective chemistry teachers' misunderstands of enthalpy and spontaneity, Chem. Educ., 11, 355–363.
- Sözbilir M., Pınarbaşı T. and Canpolat N., (2010), Prospective chemistry teachers' conceptions of chemical thermodynamics and kinetics, Eurasia J. Math. Sci. Technol. Educ., 6, 111–120.
- Supasorn S. and Promarak V., (2015), Implementation of 5E inquiry incorporated with analogy learning approach to enhance conceptual understanding of chemical reaction rate for grade 11 students, Chem. Educ. Res. Pract., 16, 121–132.
- Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14, 156–168.
- Talanquer V., (2011), Macro, submicro, and symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33, 179–195.
- Taştan-Kırık Ö. and Boz Y., (2010), Effect of cooperative learning on students' understanding of reaction rate, paper presented at the International Organization for Science and Technology Education Conference, Bled, Slovenia.
- Taştan-Kırık Ö. T. and Boz Y., (2012), Cooperative learning instruction for conceptual change in the concepts of chemical kinetics, Chem. Educ. Res. Pract., 13, 221–236.
- Taştan Ö., Yalçinkaya E. and Boz Y., (2010), Pre-service chemistry teachers’ ideas about reaction mechanism, J. Turk. Sci. Educ., 7, 47–60.
- Thomas P. L. and Schwenz R. W., (1998), College physical chemistry students' conceptions of equilibrium and fundamental thermodynamics, J. Res. Sci. Teach., 35, 1151–1160.
- Thompson J. R., Bucy B. R. and Mountcastle D. B., (2006), Assessing student understanding of partial derivatives in thermodynamics, Proceedings of the 2005 Physics Education Research Conference of the American Institute of Physics.
- Tracy S. J., (2010), Qualitative quality: eight “big-tent” criteria for excellent qualitative research, Qual. Inq., 16, 837–851.
- Turányi T. and Tóth Z., (2013), Hungarian university students' misunderstandings in thermodynamics and chemical kinetics, Chem. Educ. Res. Pract., 14, 105–116.
- Van Driel J. H., (2002), Students' corpuscular conceptions in the context of chemical equilibrium and chemical kinetics, Chem. Educ. Res. Pract. Eur., 3, 201–213.
- Vinner S. and Dreyfus T., (1989), Images and definitions for the concept of function, J. R. Math. Educ., 20, 356–366.
- Voska K. W. and Heikkinen H. W., (2000), Identification and analysis of student conceptions used to solve chemical equilibrium problems, J. Res. Sci. Teach., 37, 160–176.
- Wemyss T., Bajracharya R., Thompson J. R. and Wagner J. F., (2011), Student understanding of integration in the context and notation of thermodynamics: concepts, representations, and transfer, Proceedings of the 14th Annual Conference on Research in Undergraduate Mathematics Education.
- White P. and Mitchelmore M., (1996), Conceptual knowledge in introductory calculus, J. Res. Math. Educ., 27, 79–95.
- Yalçınkaya E., Taştan-Kırık Ö., Boz Y. and Yıldıran D., (2012), Is case-based learning an effective teaching strategy to challenge students' alternative conceptions regarding chemical kinetics? Res. Sci. Technol. Educ., 30, 151–172.
| This journal is © The Royal Society of Chemistry 2016 |