A flexible iron(II) complex in which zero-field splitting is resistant to structural variation

Abstract

The relationship between electronic structure and zero-field splitting dictates key design parameters for magnetic molecules. In particular, to enable the directed synthesis of new electronic spin based qubits, developing complexes where zero-field splitting energies are invariant to structural changes is a critical challenge. Toward those ends, we report three salts of a new compound, a four-coordinate iron(II) complex [Fe(C₃S₅)₂]²⁻ ([(18-crown-6)K]⁺ (1), Ph₄P⁺ (2), Bu₄N⁺ (3)) with a continuous structural variation in a single parameter, the dihedral angle (θ_d) between the two C₃S₅²⁻ ligands, as a function of counterion (θ_d = 89.98(4)° for 1 to 72.41(2)° for 3). Electron paramagnetic resonance data for 1–3 reveal zero-field splitting parameters that are unusually robust to the structural variation. Mössbauer spectroscopic measurements indicate that the structural variation in θ_d primarily affects the highest-energy 3d-orbitals (d_xz and d_yz) of the iron(II) ion. These orbitals have the smallest impact on the zero-field splitting parameters, thus the distortion has a minor effect on D and E. These results represent the first part of a directed effort to understand how spin state energies may be fortified against structural distortions for future applications of qubits in non-crystalline environments.

---

Introduction

The facile tunability of the magnetic properties of coordination complexes enables their future use for a number of applications, most prominently, quantum information processing (QIP).¹ In QIP, the quantum properties of a species are harnessed for vital scientific challenges, including accurate simulation of quantum phenomena² and the prediction of the folded conformations of proteins.³ Electronic spins show tremendous promise as qubits, the smallest units of a QIP system.⁴ Owing to their structural and electronic tunability, molecular electronic spins, particularly those of mononuclear transition metal complexes⁵ offer great potential.^6,7

Within the class of magnetic molecules, high-spin complexes provide an additional advantage, whereby the manifold of low-energy magnetic levels (M_S levels), may allow for multiple transitions within a single molecule to serve as qubits.⁸ Electron paramagnetic resonance (EPR) techniques can be harnessed to create qubits from pairs of M_S levels in transition metal complexes. In this context, high-spin species with S(2S + 1) potential M_S pairs available as candidate qubits offer the greatest promise. Here, the uniqueness of transition energies between pairs of M_S levels is vital to individual qubit manipulation. The zero-field splitting parameters D and E split the energies of the M_S levels at zero applied magnetic field according to the magnitude of |M_S| for each level. Thus, D and E ensure the singularity of each energy gap between M_S levels under a nonzero magnetic field.

The magnitudes and signs of D and E are dependent on the ligand field, and therefore are easily tunable by coordination geometry. For example, distortions of homoleptic S = 3/2 four-coordinate cobalt(II) complexes from idealized T_d to D_2d, S₄, or lower point-group symmetries generate a range of D values spanning nearly 100 cm⁻¹ and rhombicity indices (E/D) over the entire allowed range of 0 to 0.33.⁹ Note, this sensitivity is not restricted to Kramers, or half integer systems; it also applies to non-Kramers or integer spin states. One clear illustration of this structure-function relationship is evident in the trigonal pyramidal S = 2 iron(II) complexes [(TPA^R)Fe]⁻ where small changes in the ligand field create a 40 cm⁻¹ range in D and 6 cm⁻¹ range in E.¹⁰

The tunability of zero-field splitting offers promise for the design of molecules with transitions of the desired energy and identity. Yet, considering the potential application of magnetic molecules for qubits, designing systems where subtle structural variations will maintain chemical uniformity is critical. Application of high-spin complexes to QIP will likely employ them in starkly different environments than well-characterized crystal structures. It is therefore of prime importance to locate spin and structure combinations with M_S levels that do not appreciably change even with rather dramatic structural variation, as these will be most amenable to magnetic resonance-based QIP. Indeed, some implementations of QIP require surface isolation, where structural fluxionality is significant.¹¹ Several notable species, including polynuclear Mn and Fe coordination clusters¹² and mononuclear Tb complexes,¹³ display structural variation upon surfaces that significantly impact their M_S and M_J levels. Unintended changes in values of M_S (or M_J) and zero-field splitting shift the field and frequency required for manipulation. Further, the changes may impact the lifetimes of qubits formed from the M_S (or M_J) pairs in addition to the time required for individual computational operations. In this context, the utility of structurally robust species, such as [Fe₄(L)₂(dpm)₆],¹⁴ is noted. Here, variation in the molecular geometries at the surface are minimal and of little consequence to the magnetic properties.

Herein, we offer an alternative approach to overcoming this limitation: the development of design strategies for high-spin qubits that are electronically robust. In such a system, the allowed structural variations have little impact on the zero-field splitting parameters due to electronic rather than steric fortification. First and foremost, the formulation of such design principles requires building a comprehensive understanding of the impact of particular distortions on a given M_S level manifold.

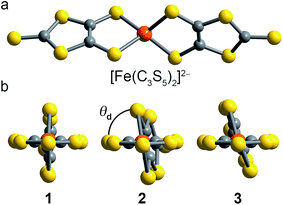
Toward that end, we focused our efforts on homoleptic pseudotetrahedral complexes featuring two planar, bidentate ligands. The dihedral angle between the two ligands can be singularly varied as a function of counterion, thereby allowing the study of the influence of structural variation on both D and E. In particular iron(II), with its anticipated S = 2 spin state, was selected to serve as an ideal spectroscopic handle to track the impact of the geometric changes on both the zero-field splitting and electronic environment. Iron offers the additional key advantage of Mössbauer activity, which enables complimentary electronic insight. We prepared and investigated three salts of the new complex [Fe(C₃S₅)₂]²⁻: [(18c6)K]₂[Fe(C₃S₅)₂] (1), (Ph₄P)₂[Fe(C₃S₅)₂] (2), and (Bu₄N)₂[Fe(C₃S₅)₂] (3) (see Fig. 1). Magnetic and spectroscopic investigations of this series reveal unexpectedly resilient zero-field splitting values despite a substantial change to the coordination geometry of the iron(II) ion. These results represent a first step forward in the development of high spin species with zero-field splitting values stable to structural distortions.

Fig. 1 (a) Molecular structure of [Fe(C₃S₅)₂]²⁻ as it appears in the crystal structure of 1. Orange, yellow, and gray spheres represent iron, sulphur, and carbon atoms, respectively. (b) Depictions of [Fe(C₃S₅)₂]²⁻ and dihedral angle (θ_d) in the structures of 1 (left), 2 (middle), and 3 (right), viewed down the longest molecular axis.

Results and discussion

The syntheses of the new complexes 1–3 proceeded via salt metatheses of the sodium or potassium salts of 4,5-dimercapto-1,3-dithiole-2-thionate¹⁵ (C₃S₅²⁻) with iron dichloride in organic solvents, as depicted in Scheme 1. Subsequent addition of 18-crown-6 (18c6), (Ph₄P)Br, or (Bu₄N)Br to the product enabled the isolation of 1–3 as dark red powders or microcrystalline solids which were readily purified by recrystallization. Single crystal X-ray diffraction studies revealed the structures depicted in Fig. 1, S1, and S2.† All [Fe(C₃S₅)₂]²⁻ complexes are four-coordinate with tetragonal elongations away from idealized tetrahedral geometry; specific structural metrics are provided in Table 1 and the ESI.† The Fe–S bond distances in 1–3 are extremely similar across the series and consistent with the mean Fe–S distance (2.31(7) Å) for reported mononuclear [Fe^IIS₄] complexes of iron(II) in the Crystal Structure Database (CSD).^16,17 The bite angles of the C₃S₅²⁻ ligands, as well as the Fe–S–Cα angles, are similarly invariant. In contrast, the variation in crystal packing forces from 1–3 induces a twist-like distortion of the C₃S₅²⁻ ligands (see Fig. 1). The dihedral angle (θ_d) between the C₃S₅²⁻ ligands ranges from 89.98(4)° in 1 to 81.38(2)° in 2 to 72.41(2)° in 3. Such singular modulation of a structural feature in the coordination environment of a series of transition metal complexes is uncommon. We attribute the demonstrated structural flexibility of the [Fe(C₃S₅)₂]²⁻ molecules to the low-coordinate nature of the iron(II) center and the planar bidentate ligands, which direct the system toward an idealized D_2d symmetry. Note, while the structural variation alters the ligand field geometry, the ligand set remains constant. Thus, this series of structures enables a clean, controlled investigation of electronic and magnetic properties as a function of the dihedral angle.

Scheme 1 Synthetic pathways to 1–3.

Table 1 Summary of structural parameters for the [Fe(C₃S₅)₂]²⁻ moieties in the crystal structures of 1–3

	1	2	3
a Between sulphur atoms of differing C3S5^2− ligands. b Bite angle for C3S5^2− ligand. c Dihedral angle graphically depicted in Fig. 1. The planes constructed for the calculation contained the central iron atom and coordinated sulphur atoms. d Closest intermolecular distance; occurs as end-on interactions between terminal thione groups of the C3S5^2− ligands for 1–3. e Closest intermolecular distance.
Fe–Save (Å)	2.350(1)	2.340(8)	2.347(8)
S–Fe–S (°)	121.60(5)^a	122.924(19)^a	134.00(2)^a
	119.61(6)^a	122.838(19)^a	124.75(2)^a
	116.53(6)^a	112.284(19)^a	109.45(2)^a
	114.95(5)^a	112.588(19)^a	106.50(2)^a
	93.19(6)^b	94.547(18)^b	93.18(2)^b
	92.96(6)^b	94.105(18)^b	92.93(2)^b
Fe–S–Cα (°)	97.38(3)	96.2(6)	97.5(3)
θ d (°)	89.98(4)	81.38(2)	72.41(2)
S⋯S^d (Å)	4.148(3)	4.127(2)	4.152(4)
Fe⋯Fe^e (Å)	9.666(5)	8.740(6)	8.573(5)

---

We probed the magnetostructural correlation in 1–3 by concerted magnetometric and spectroscopic studies. Variable-field, variable-temperature magnetic susceptibility data collected on ground polycrystalline samples at H_dc = 1000 Oe of 1–3 yield room temperature χ_MT values of 3.12, 3.22, and 3.34 cm³ K mol⁻¹ for 1, 2, and 3, respectively. These values are in accordance with S = 2 iron(II) ions with isotropic g_iso factors of 2.04, 2.07, and 2.11 for 1, 2, and 3 respectively (see Fig. S3†). The value of χ_MT remains constant with decreasing temperature, eventually dropping significantly below 40 K. The temperature dependence of χ_MT for a spin with nonzero D and E reflects the temperature-variant populations of the zero-field split M_S levels. Accordingly, we employed the program DAVE 2.0 (ref. 18) to model the low-temperature downturn as a consequence of zero-field splitting (see Fig. S3†). We applied the following spin Hamiltonian to model the zero-field energies of the M_S levels for 1–3, assuming a ground state spin of 2: Ĥ = DŜ_z² + E(Ŝ_x² − Ŝ_y²) + μ₀μ_BgH⃑·Ŝ. Here, the zero-field splitting is parameterized in terms of axial (D) and transverse (E) zero-field splitting terms with Ŝ and Ŝ_i² (i = x, y, and z) the spin operators, where μ₀ is the vacuum permittivity, μ_B is the Bohr magnetron, H⃑ the applied dc magnetic field, and g the isotropic g-factor. The best fits, averaged over data sets collected at 0.1, 0.5, and 1 T applied dc fields, provided g, D, and |E| values (Table 2). The parameters we obtained through this fit were extremely uniform across 1–3, with g values close to 2.05, D of ca. +5.8 cm⁻¹ and nonzero |E| values of ca. 0.6 cm⁻¹. The alternate explanation of the downturn, intermolecular coupling, is unlikely due to the combination of the long S⋯S and Fe⋯Fe distances observed in the single crystal structures, as well as the lack of significant intermolecular contacts between [Fe(C₃S₅)₂]²⁻ moieties (see Table 1).

Table 2 Summary of magnetic and spectral parameters for 1–3^a

	1	2	3
a Reported errors in EPR parameters were estimated by variance in quality of the simulation of the 406.4 GHz spectrum and the resonant field vs. frequency plot as a function of parameter variance. b Determined by EPR. c Obtained from value of χMT at 300 K. d Determined by fits of variable-temperature, variable-field χMT data. Errors determined by averaging over the fits to data sets collected at 0.1, 0.5, and 1 T dc applied fields.
g x	2.00(1)	2.00(3)	2.00(1)
g y	2.02(1)	2.07(1)	2.04(1)
g z	2.10(4)	2.10(3)	2.08(3)
D (cm^−1)	5.21(3)	5.35(5)	5.61(9)
E (cm^−1)	0.59(2)	0.60(2)	0.59(2)
E/D^b	0.11	0.11	0.10
g iso	2.04	2.07	2.11
g iso	2.04(1)	2.08(2)	2.07(1)
D (cm^−1)	5.6(1)	6.5(3)	5.5(2)
|E|^d (cm^−1)	0.5(3)	0.7(2)	0.7(1)
δ (mm s^−1)	0.680(1)	0.663(1)	0.677(1)
ΔEQ (mm s^−1)	4.326(2)	4.283(1)	4.330(1)

---

To better quantify the zero-field splitting across the structural range, we probed the molecules by high-field variable-frequency EPR spectroscopy.¹⁹ Spectra were acquired at 5 K on 1–3 at frequencies ranging from 50 to 419.2 GHz (see Fig. 2 and S4†). The spectra display a multitude of resonances that change position and intensity as a function of irradiating microwave frequency. The M_S levels involved, and their separation at zero-field, govern the frequency and field at which a given resonance is observed. Note that EPR transitions are split by nonzero D and E terms into three separate transitions (x- y- and z-components), which are further impacted by anisotropy of the g factor. For an S = 2 system, these factors lead to complex spectra, as seen for 1–3. Thus, variable frequency analyses were crucial for accurate quantification of g, D, and E.

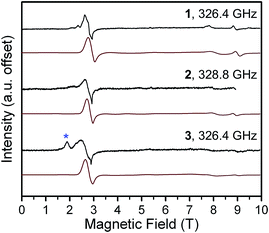Fig. 2 Select high-frequency, high-field EPR spectra for 1–3 at 5 K. Black lines correspond to experimental data collected at the frequencies listed on the graph. Red lines are simulations with parameters given in the main text and Table 2. The blue asterisk in the spectrum of 3 indicates a peak attributed to an impurity.

To collect and analyze all of the different spectra, we created plots of resonance field vs. excitation frequency and incorporated the transitions from sixteen, thirteen, and ten different frequencies for 1, 2, and 3, respectively (see Fig. 3 and S5†). Each black diamond in these figures represents a field/frequency combination where a transition occurred, as determined through inspection of the raw data. 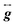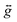The frequency dependences of the observed resonances were modeled for an S = 2 system with the same Hamiltonian used for the interpretation of the magnetic susceptibility data, except here we account for anisotropy in g with the g-tensor, : Ĥ = DŜ_z² + E(Ŝ_x² − Ŝ_y²) + μ₀μ_BH⃑··Ŝ. The best models of the frequency dependences for 1–3 yielded positive D, nonzero E, and g_x ≠ g_y ≠ g_z values (see Fig. 2, 3, S4, S5† and Table 2) similar to those obtained from magnetic susceptibility measurements. Further, these values are within the range of reported magnitudes by other high-frequency EPR studies of [Fe^IIS₄] complexes.²⁰

Fig. 3 Resonance field vs. microwave frequency for 1 constructed from data (♦) obtained at 5 K. Solid lines represent fits to the data, with parameters as given in Table 2. Red, green, and blue lines represent x-, y-, and z-transitions, respectively. Bold lines represent ground-state M_S = 0 → M_S = ±1 transitions.²¹ Faded lines depict excited state transitions; those stemming from ca. 3.6 cm⁻¹ correspond to excitations within the M_S = ±1 doublet. Excited state transitions are shown if they correspond to observed signals. See ESI† for discussion of z-transitions (blue).

The D and E parameters obtained from the foregoing analyses designate 1–3 as S = 2 species with ground M_S = 0 levels, with the M_S = ±1 levels ca. 5 cm⁻¹ higher in energy and M_S = ±2 levels at ca. 21 cm⁻¹ (see Fig. S6†).²¹ The nonzero E terms in 1–3 mix the M_S = ±1 levels, which causes them to split by 6E (ca. 3.6 cm⁻¹) at zero field. The M_S = ±2 levels are relatively less sensitive to E and split by ca. 3E²/D at zero field, which is ca. 0.2 cm⁻¹ for 1–3. The applied frequencies of our investigations span excitations up to 14 cm⁻¹ in energy. At the low temperatures of our measurements, the spectra are therefore predominantly indicative of the frequency dependences of the x-, y-, and z-components of the M_S = 0 → M_S = ±1 and intra-doublet M_S = ±1 transitions. As we incorporated the resonances most sensitive to E in our fits, we expect very little uncertainty in our fit of E. We note that the simulated frequency dependences of the x-, y-, and z-transitions match the observed transitions closely, as do simulated spectra (Fig. 2, S4 and S5†). Further, variable-temperature spectra corroborate the positive D in our fitted model, as signals attributed to the lowest-energy M_S = 0 level fade with increasing temperature while the M_S = ±1 intra-doublet excited-state resonances intensify (see Fig. 4, S6†). We note that low temperature magnetization data collected on 1–3 are well-modeled by the g, D, and E values of the foregoing spectroscopic analyses (see Fig. S7†). Together, these observations lend confidence in the values obtained for 1–3. It is important to note that the level of analysis here is permitted solely by the use of high frequency EPR, as the evaluation of D and E from powder samples is difficult by magnetic susceptibility analysis. Indeed, this difficulty is evident in the large uncertainties of the parameters determined by the χ_MT fits. Further, our own attempts to obtain E from low-temperature magnetization data fits yielded no appreciable difference in fit quality for |E| values ranging from ≈1.4 to less than 0.01 cm⁻¹. Thus, the foregoing analyses contrast the relative utility of high-frequency EPR vs. magnetization data in the fine-tuning of the M_S levels of high-spin qubits.

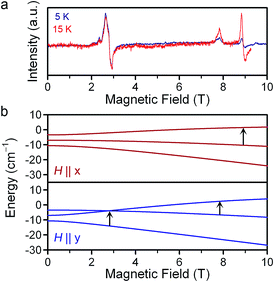Fig. 4 (a) Variable-temperature EPR spectra of 1 at 326.4 GHz applied microwave frequency. The intensities are normalized to that of the 3 T resonance. (b) Zeeman energy diagrams for the M_S = 0, ±1 (ref. 21) levels with the applied dc field aligned with the x- and y-axes. Solid black arrows indicate the parentage of the observed resonances in (a). Full Zeeman diagrams are in Fig. S6.†

To correlate the magnetic properties with electronic structure changes, we employed Mössbauer spectroscopy, which displays a marked sensitivity to electron density around a ⁵⁷Fe nucleus.^19b,22 In particular, we sought a deeper understanding of the robust zero-field splitting parameters as a function of the structural changes depicted in Fig. 1. All complexes feature well-resolved doublets at 80 K, with isomer shifts (δ) for 1–3 of 0.680(1), 0.663(1), and 0.677(1) mm s⁻¹ (see Fig. 5 and Table 2). These values are similar to other four-coordinate iron(II) complexes of thiolate ligands,^17b–d,23 and reflect a relatively covalent, electron-rich environment for the ⁵⁷Fe nucleus. The quadrupole splittings, |ΔE_Q|, for 1–3 are 4.326(1), 4.283(1), and 4.330(1) mm s⁻¹ respectively, magnitudes which are appropriate for high-spin iron(II) complexes.^23,24 This parameter is especially sensitive to asymmetry in the electron density around the ⁵⁷Fe nucleus in high-spin iron(II) compounds, where the sixth d-electron is essentially superimposed on a spherical, half-filled d⁵ shell. Thus, ΔE_Q readily detects distortions that shift the sixth electron between different orbitals, as can be the case in tetrahedral complexes.²⁵ Importantly, however, we find only a minor change in both δ and ΔE_Q from 1–3 and neither parameter trends with the variance in θ_d.

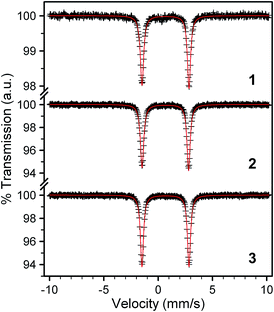Fig. 5 Mössbauer spectra for powder samples of 1–3 collected at 80 K. Black crosses represent experimental data while red lines represent the best fits to the spectra. The parameters for these fits are given in Table 2.

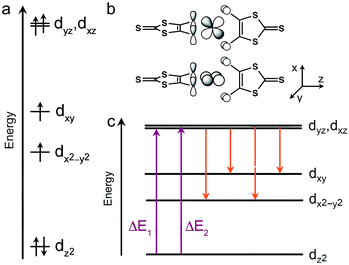
The similarity across 1–3 of both the Mössbauer and the zero-field splitting parameters can be understood through a simple molecular orbital (MO) picture. Derivation of such a model on the basis of experimental electronic absorption spectroscopy is complicated by the broad and intense absorptions of the C₃S₅²⁻ ligands.²⁶ Fortuitously, we note the similarity of the coordination geometries of 1–3 to molecular models of the [Fe^II(S-Cys)₄]²⁻ sites in certain rubredoxin proteins.^9,17b,c,f,23 Thus, we can construct a qualitative model for the purposes of discussion by connecting previously computed MOs for C₃S₅²⁻ (see Fig. 6)²⁷ and experimental results for model complexes.^23c,27 We pay particular attention to the sign of D, which here indicates that d_z² is the lowest energy d-orbital.^20a The simplest starting point occurs for θ_d = 90°, as in 1. Here, the lowest energy d_z² orbital is followed by the d_x²−y² and d_xy orbitals then the (d_xz, d_yz) pair. The d_xz and d_yz orbitals show appreciable overlap with the π-systems of the ligands (see Fig. 6b), in contrast to the d_z², d_xy, and d_x²−y² orbitals, which interact indirectly with lone-pairs of the thiolate donor atoms.^20a,23c Thus, we hypothesize that the change in θ_d from 1 to 3 most directly impacts the energies of the d_xz and d_yz orbitals.

Fig. 6 (a) Qualitative d-orbital splitting diagram and electron configuration for [Fe(C₃S₅)₂]²⁻ with θ_d = 90°. (b) Tilted coordinate axes and graphical depiction of the d_xz and d_yz orbitals of the iron(II) ion with reference to the S 3p orbitals of the C₃S₅²⁻ lowest unoccupied molecular orbitals. The x and y coordinate axes are selected for part (b) to best illustrate anisotropy in the π-interactions with the C₃S₅²⁻ ligands; otherwise we employ the more conventional setting, where the planes of C₃S₅²⁻ ligands bisect the x and y axes. (c) Spin-allowed (red) and spin-forbidden (orange) d–d transitions that contribute to D and E in 1–3. Note that ΔE₁ ≠ ΔE₂ when θ_d ≠ 90°.

The magnitude of ΔE_Q increases in concert with rising anisotropy of the ⁵⁷Fe 3d-electron density. High-spin iron(II), with 6 valence 3d-electrons, displays the spherical electron density of a half-filled d-shell overlaid with the contribution of one extra electron. Since each of the d-orbitals has its own inherent directionality, ΔE_Q is sensitive to factors that affect the ground state orbital occupied by the 6th electron. The lack of an appreciable change in ΔE_Q with θ_d therefore suggests that the distortion does not drastically affect the lower energy d orbitals in 1–3. Indeed, this hypothesis is consistent with the MO diagram in Fig. 6, where the variation in θ_d from 1 to 3 appears most influential to the highest-energy d_xz and d_yz orbitals due to appreciable overlap with the ligand π-system. A series of high spin iron(II) complexes bound to two planar, tridentate terpyridine-like ligands forms a nice counterexample.²⁸ Here, a 30° change in θ_d induces a shift in ΔE_Q from 0.75 to 3.58 mm s⁻¹, nearly a factor of 60 greater range than in 1–3. The large change in ΔE_Q for the former species versus1–3 likely stems from virtually degenerate d_xz, d_yz, and d_xy orbitals imparted by a nearly octahedral geometry. In turn, small geometric changes adjust the orbital occupied by the 6th 3d electron and induce an electron density sensitive to small structural distortions. In contrast, ΔE_Q is constant in 1–3 due to a structural change that exerts its maximal impact on higher energy orbitals.

The magnitudes and signs of D and E are crucially dependent on the energies of d–d excited states. Typically, three interactions dictate D and E (see Fig. 6c): the spin–orbit coupling between the ground electronic state and spin-allowed d–d excited states, then the spin–orbit coupling between the ground state and spin-forbidden d–d excited states, and finally spin–spin coupling between the unpaired 3d electrons. A contribution from a given excited state is stronger at lower energy, therefore contributions from spin-allowed transitions are generally taken to be more significant than the spin-forbidden transitions. Consideration of the spin-allowed transitions reveals contributions to D and E from only the excited states of d_z² → d_xz and d_z² → d_yz parentage (see ESI† for more details). Each contribution to D is equal and positive in magnitude. In the process of the twist distortion, the ground d_z² orbital is relatively unaffected while one of the d_xz/d_yz orbitals drops in energy and the other rises. Consequently, there is minimal change to the total spin-allowed contributions to D, in general agreement with our EPR data.

In contrast, the contribution to E from the d_z² → d_xz state opposes that from the d_z² → d_yz state. Therefore, where the d_xz and d_yz orbitals are degenerate, as expected for θ_d = 90°, E should be zero, as opposed to the results of our EPR analysis. An increase in θ_d would cause inequality in the π-interactions, leading to a splitting of the energies of the d_xz and d_yz orbitals. Thus, a steady increase in E would be expected due to incomplete cancelation of the two spin-allowed contributions, again in contrast with experimental data. These discrepancies highlight a more complex origin for E in 1–3 than spin-allowed contributions. The lack of dependence of E on the θ_d twist may suggest that spin-forbidden excited states and spin–spin coupling are the primary sources of rhombicity in 1–3. Interestingly, the Tanabe–Sugano diagram for tetrahedral d⁶ ions reveals low-lying triplet transition energies that are insensitive to modest changes in ligand field strength.²⁹ This invariance may explain some of the insensitivity of D and E to the changes in the ligand field for 1–3 if spin-forbidden excitations are important therein. Indeed, targeting species where excited states are stable to changes in the ligand field strength may offer a path to the rational design of qubits where zero-field splitting is resistant to distortion. Ultimately, however, the origins of the nonzero E and the resilience of D and E to changes in θ_d remain perplexing questions that theory can hopefully address. The foregoing observations underline the importance of spin-forbidden and spin–spin contributions to D and E not only in [Fe^IIS₄] moieties, but also systems for which there is no primary low-lying transition that dominates D and E.^20a,23b,30

Together, the Mössbauer and EPR data suggest that the twist affects primarily higher-lying 3d orbitals. This scenario is fortuitous for the design of stable zero field splitting parameters, as the associated d–d transition states are of suppressed relevance in determining D and E. The 20° range in θ_d exhibited in 1–3 does not completely track the twist progression from the D_2d geometry of 1 to the square planar D_2h geometry corresponding to θ_d = 180°. Thus, upon initial inspection, the degree to which 1–3 survey the sensitivity of D and E to the twist distortion may appear truncated. However, considerable analysis of the stability of the S = 2 state as a function of structural variation in pseudotetrahedral iron(II) species revealed the stability of the S = 1 state in the D_2h geometry.³¹ Indeed, magnetic analysis of the lone example in the CSD of a square planar iron(II) complex of bidentate dithiolate ligands revealed a S = 1 spin state.³² Here, the square planar geometry yields S = 1 state through strong d_xy-thiolate interactions, which render the d_xy orbital energetically inaccessible. A close inspection of the CSD entries for mononuclear, pseudotetrahedral high-spin [Fe^IIS₄] complexes with bidentate ligands reveals θ_d angles between 84 and 90°. Thus, the range of θ_d which we are afforded in [Fe(C₃S₅)₂]²⁻ is likely limited by the stability of the S = 2 state, suggesting this series constitutes the representative range of accessible dihedral angles.

Outlook

Employing high spin molecules for quantum information processing may require isolation of the species in environments that differ from well-studied crystalline structures, for example, on surfaces,¹¹ or in solution,³³ where fluxionality is almost certain. For many complexes, such distortions unpredictably impact D and E, therefore hindering the viability of the system for QIP. Thus, the development of high spin molecules with robust zero-field splitting parameters would be of significant utility. The foregoing investigation represents the first such effort to find structural distortions that only weakly impact the zero-field splitting of a complex. Beyond the tremendous impact of this research on the rational design of molecules for QIP, developing an improved understanding of these structure/function relationships informs any structural EPR study. For example, the field of bioinorganic chemistry has achieved substantial insight via comparative analyses of EPR spectra of paramagnetic active sites and synthetic molecular mimics.³⁴ Future research efforts will focus on distortions in other metal ions and oxidation states that affect predominantly the highest-energy d-orbitals. Of immediate interest are four-coordinate complexes of cobalt(II).³⁵

Acknowledgements

We thank Dr Johan Van Tol, Dr Andrew Ozarowski, Prof. T. David Harris, Prof. John Anderson, Ms Lakshmi Bhaskaran, and Ms Audrey Gallagher for insightful discussions and experimental assistance. We also thank Profs. Martin Kirk and James McCusker for invaluable and thoughtful ligand field discussion. We acknowledge support from Northwestern University, the International Institute for Nanotechnology, the State of Illinois (DCEO Award no. 10-203031), the United States Air Force (AOARD award no. 134031), and the National Science Foundation through award DMR-1309463 and a graduate research fellowship (S. M. G.; DGE-1449440). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by an NSF Cooperative Agreement (DMR-1157490) and the state of Florida.

Notes and references

1. (a) M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 10th anniversary edn, 2010; (b) J. Stolze and D. Suter, Quantum Computing: A Short Course from Theory to Experiment, Wiley-VCH, Weinheim, 2nd edn, 2008.
2. (a) R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467–488; (b) S. Lloyd, Science, 1993, 273, 1073–1078; (c) A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707.
3. A. Perdomo-Ortiz, N. Dickson, M. Drew-Brook, G. Rose and A. Aspuru-Guzik, Sci. Rep, 2012, 2, 571.
4. (a) T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45–53; (b) J. J. L. Morton, D. R. McCamey, M. A. Eriksson and S. A. Lyon, Nature, 2011, 479, 345–353; (c) D. D. Awschalom, L. C. Bassett, A. S. Dzurak, E. L. Hu and J. R. Petta, Science, 2013, 339, 1174–1179; (d) R. J. Warburton, Nat. Mater., 2013, 12, 483–493; (e) G. W. Morley, Electron Paramagn. Reson., 2015, 24, 62–76.
5. (a) M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508; (b) M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626; (c) K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304; (d) J. M. Zadrozny, J. Niklas, O. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844.
6. (a) M. Affronte, F. Troiani, A. Ghirri, A. Condini, M. Evangelisti, V. Corradini, S. Carretta, P. Santini, G. Amoretti, F. Tuna, G. Timco and R. E. P. Winpenny, J. Phys. D: Appl. Phys., 2007, 40, 2999–3004; (b) G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546; (c) F. Troiani and M. Affronte, Chem. Soc. Rev., 2010, 40, 3119–3129.
7. (a) S. C. Benjamin, A. Ardavan, G. A. D. Briggs, D. A. Britz, D. Gunlycke, J. Jefferson, M. A. G. Jones, D. F. Leigh, B. W. Lovett, A. N. Khlobystov, S. A. Lyon, J. J. L. Morton, K. Porfyrakis, M. R. Sambrook and A. M. Tyryshkin, J. Phys.: Condens. Matter, 2006, 18, S867–S883; (b) K. Sato, S. Nakazawa, S. Nishida, R. D. Rahimi, T. Yoshino, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa and T. Takui, EPR of Free Radicals in Solids II, ed. A. Lund and M. Shiotani, Springer, 2nd edn, 2012, ch. 4, pp. 177–204.
8. M. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
9. (a) K. Fukui, H. Ohya-Nishiguchi and N. Hirota, Bull. Chem. Soc. Jpn., 1991, 64, 1205–1212; (b) K. Fukui, N. Kojima, H. Ohya-Nishiguchi and N. Hirota, Inorg. Chem., 1992, 31, 1338–1344; (c) K. Fukui, H. Masuda, H. Ohya-Nishiguchi and H. Kamada, Inorg. Chim. Acta, 1995, 238, 73–81; (d) D. Maganas, S. Milikisyants, J. M. A. Rijnbeek, S. Sottini, N. Levesanos, P. Kyritsis and E. J. J. Groenen, Inorg. Chem., 2010, 49, 595–605; (e) D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741–8754; (f) J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217.
10. (a) W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126; (b) E. Cremades and E. Ruiz, Inorg. Chem., 2011, 50, 4016–4020; (c) M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Inorg. Chem., 2011, 50, 7460–7477.
11. A. Cornia, M. Mannini, P. Sainctavit and R. Sessoli, Chem. Soc. Rev., 2011, 40, 3076–3091.
12. (a) F. Moro, V. Corradini, M. Evangeslisti, R. Biagi, V. de Renzi, U. del Pennino, J. C. Cezar, R. Inglis, C. J. Milios and E. K. Brechin, Nanoscale, 2010, 2, 2698–2703; (b) J. A. J. Burgess, L. Malavolti, V. Lanzilotto, M. Mannini, S. Yan, S. Ninova, F. Totti, S. Rolf-Pissarczyk, A. Cornia, R. Sessoli and S. Loth, Nat. Commun., 2015, 6, 8216,  DOI:10.1038/ncomms9216.
13. (a) M. Mannini, P. Sainctavit, R. Sessoli, C. Cartier dit Moulin, F. Pineider, M.-A. Arrio, A. Cornia and D. Gatteschi, Chem.–Eur. J., 2008, 14, 7530–7535; (b) L. Margheriti, D. Chiappe, M. Mannini, P.-E. Car, P. Sainctavit, M.-A. Arrio, F. B. de Mongeot, J. C. Cezar, F. M. Piras, A. Magnani, E. Otero, A. Caneschi and R. Sessoli, Adv. Mater., 2010, 22(48), 5488–5493.
14. H₃L = 11-(acetylthio)-2,2-bis(hydroxymethyl)undecan-1-ol; Hdpm = dipivaloylmethane; (a) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197; (b) M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M.-A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421.
15. K. S. Varma, A. Bury, N. J. Harris and A. E. Underhill, Synthesis, 1987, 837.
16. F. H. Allen, Acta Crystallogr., 2002, B58, 380–388.
17. (a) M. Churchill and J. Wormald, Inorg. Chem., 1971, 10, 1778–1782; (b) R. Lane, J. A. Ibers, R. B. Frankel, G. C. Papefthymiou and R. H. Holm, J. Am. Chem. Soc., 1977, 99, 84–98; (c) D. Coucouvanis, D. Swenson, N. C. Baenziger, C. Murphy, D. G. Holah, N. Sfarnas, A. Simopoulos and A. Kostikas, J. Am. Chem. Soc., 1981, 103, 3350–3362; (d) D. Coucouvanis, P. Stremple, E. D. Simhon, D. Swenson, N. C. Baenziger, M. Draganjac, L. T. Chan, A. Simopoulos, V. Papaefthymiou, A. Kostikas and V. Petrouleas, Inorg. Chem., 1983, 22, 293–308; (e) J. A. Kovacs, J. K. Bashkin and R. H. Holm, Polyhedron, 1987, 6, 1445–1456; (f) A. Silver, S. A. Koch and M. Millar, Inorg. Chim. Acta, 1993, 205, 9–14; (g) X.-Y. Yu, G.-X. Jin and L.-H. Weng, Chem. Commun., 2004, 1542–1543.
18. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggot, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358.
19. (a) A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Dover Publications, Inc., New York, 1986; (b) R. Drago, Physical Methods for Chemists, Saunders College Publishing, Philadelphia, 2nd edn, 1992; (c) J. Krzystek, A. Ozarowski and J. Telser, Coord. Chem. Rev., 2006, 250, 2308–2324.
20. (a) M. J. Knapp, J. Krzystek, L. C. Brunel and D. N. Hendrickson, Inorg. Chem., 2000, 39, 281–288; (b) A. L. Barra, A. K. Hassan, A. Janoschka, C. L. Schmidt and V. Schünemann, Appl. Magn. Reson., 2006, 30, 385–397; (c) G. Mathies, S. D. Chatziefthimiou, D. Maganas, Y. Sanakis, S. Sottini, K. Kyritsis and E. J. J. Groenen, J. Magn. Reson., 2012, 224, 94–100.
21. At the fields/frequencies of this study the M_S levels are highly mixed, especially the M_S = ±1 levels. For simplicity, we employ labels corresponding to the high-field limit, where the M_S levels are pure.
22. Mössbauer Spectroscopy Applied to Inorganic Chemistry, ed. G. J. Long and F. Grandjean, Plenum Press, New York, 1984.
23. (a) A. Kostikas, V. Petrouleas, A. Simopolous, D. Coucouvanis and D. G. Holah, Chem. Phys. Lett., 1976, 38, 582–584; (b) M. T. Werth, D. M. Kurtz, B. D. Howes and H. H. Boi, Inorg. Chem., 1989, 28, 1357–1361; (c) V. V. Vrajmasu, E. L. Bominaar, J. Meyer and E. Münck, Inorg. Chem., 2002, 41, 6358–6371; (d) A. Jacques, M. Clémancey, G. Blondin, V. Fourmond, J.-M. Latour and O. Sénèque, Chem. Commun., 2013, 49, 2915–2917.
24. Our measurements do not afford definitive evidence for the sign of ΔE_Q, though there is considerable literature evidence that it is negative for iron(II) in the coordination environments of 1–3; see ref. 23c.
25. P. R. Edwards, C. E. Johnson and R. J. P. Williams, J. Chem. Phys., 1967, 47, 2074–2082.
26. G. B. Ferreira, E. Hollauer, N. M. Comerlato and J. L. Wardell, Inorg. Chim. Acta, 2006, 359, 1239–1247.
27. M. S. Gebhard, S. A. Koch, M. Millar, F. J. Devlin, P. J. Stephens and E. I. Solomon, J. Am. Chem. Soc., 1991, 113, 1640–1649.
28. J. Elhaïk, D. J. Evans, C. A. Kilner and M. A. Halcrow, Dalton Trans., 2003, 1693–1700.
29. B. N. Figgis and M. A. Hitchman, Ligand Field Theory and its Applications, Wiley-VCH, New York, 1999.
30. F. Neese, J. Am. Chem. Soc., 2008, 128, 10213–10222.
31. (a) J. Cirera, E. Ruiz and S. Alvarez, Chem.–Eur. J., 2006, 12, 3162–3167; (b) J. Cirera, E. Ruiz and S. Alvarez, Inorg. Chem., 2008, 47, 2871–2889.
32. K. Ray, A. Begum, T. Weyhermüller, S. Piligkos, J. van Slageren, F. Neese and K. Wieghardt, J. Am. Chem. Soc., 2005, 127, 4403–4415.
33. N. A. Gershenfeld and I. L. Chuang, Science, 1997, 275, 350–356.
34. J. Telser, J. Krzystek and A. Ozarowski, JBIC, J. Biol. Inorg. Chem., 2014, 19, 297–318.
35. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721.

---

Footnote

† Electronic supplementary information (ESI) available: Methods and additional characterization and discussion. CCDC 1064089–1064091. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc02477c

---