High symmetry or low symmetry, that is the question – high performance Dy(III) single-ion magnets by electrostatic potential design

Abstract

A series of mononuclear lanthanide Zn–Dy–Zn type single-molecule magnets (SMMs) were synthesized and magnetically characterized. The four molecules ([Zn₂(L¹)₂DyCl₃]·2H₂O (1), [Zn₂(L¹)₂Dy(MeOH)Br₃]·3H₂O (2), [Zn₂(L¹)₂Dy(H₂O)Br₂]·[ZnBr₄]_0.5 (3) and [Zn₂(L²)₂DyCl₃]·2H₂O (4)) all display remarkable magnetic relaxation behavior with a relatively high energy barrier and hysteresis temperature, despite possessing a low local geometry symmetry of the center Dy(III) ions. Ab initio studies revealed that the symmetry of the charge distribution around the Dy(III) ion is the key factor to determine the relaxation of the SMMs. The four complexes orient their magnetic easy axes along the negative charge-dense direction of the first coordination sphere. The entire molecular magnetic anisotropy was therefore controlled by a single substituent atom in the hard plane which consists of five coordination atoms (perpendicular to the easy axis), and the lower charge distribution on this hard plane in combination with the nearly coplanarity of the five coordination atoms ultimately lead to the prominent magnetic slow relaxation. This offers an efficient and rational method to improve the dynamic magnetic relaxation of the mononuclear lanthanide SMMs that usually possess a low local geometry symmetry around the lanthanide(III) center.

---

Introduction

Since the first single-molecule magnet (SMM), Mn₁₂Ac, was discovered in the 1990s, many magnetic molecules exhibiting a slow relaxation of magnetization have been synthesized and magnetically characterized. Large negative zero-field splitting and ground state spin are regarded as two essential factors to obtain an SMM with a high relaxation barrier (U_eff) and blocking temperature (T_B), which play a crucial role in the technological applications of SMMs, involving the field of quantum computers, spintronics devices and high-density information storage.^1–6 The intrinsic strong spin–orbit coupling and large magnetic anisotropy render the lanthanide ions as the ideal candidates for constructing SMMs with a high relaxation barrier compared to transition metal-based SMMs. Even in the single 4f-center system, i.e. mononuclear lanthanide SMMs or single-ion magnets (SIMs), significantly slow relaxations of the magnetization with high energy barriers for magnetization reversal have been observed.⁷ The relatively simple structure of the lanthanide SIMs is convenient for chemists to improve the understanding of the magneto-structural correlation.^8–14 Compared to the transition metal system, however, the magnetic structure of the lanthanides is more complex due to their strong spin–orbit coupling. Recent research reveals that the single-ion magnetic anisotropy of lanthanide ions is extremely sensitive to subtle changes of the ligand field (LF) and the local geometrical symmetry. The electrostatic potential distribution around the spin center plays an important role.^15,16

With the fast development of the lanthanide based SMMs, the record reversal barrier of the mononuclear SMMs is continuously broken, whereas improving the blocking temperature seems much more difficult. Magnetic hysteresis, as an important criterion of SMMs, was only observed at low temperatures. It is mostly ascribed to the faster quantum tunnelling of magnetization (QTM) through the barriers, which reduces the thermally activated relaxation across the barrier, commonly referred as the Orbach process, and/or the thermally assisted QTM (TA-QTM). Usually a high axial symmetry around the spin center favors the suppression of QTM, rendering the thermally active Orbach relaxation prominent. Some lanthanide-based molecules possessing a high order axial symmetry, such as D_4d, D_3h, D_2d, D_5h, C₅ and C_∞v, have been designed and synthesized to reduce the QTM and to develop novel SMMs with improved energy barriers and blocking temperature.^11,17–19 However, high local symmetry is not easy to achieve due to the intrinsic high coordination numbers and variable coordination modes of the lanthanide ions, as a low symmetry system is usually observed for lanthanide-containing complexes.

The electron density distribution of the lanthanide(III) ions is strongly angular dependent. It has a preferred orientation under the electrostatic potential generated by the ligand donor atoms. In other words, the charge distribution of the ligand provides an efficient way to control the magnetic anisotropy. This principle has been illustrated in terms of “oblate” and “prolate” electron density distributions in a recent review.^20a It was shown that for the terbium(III) and dysprosium(III)-based SMMs, a strong anisotropy can be achieved by using axial ligand fields, whereas equatorial ligand fields favour erbium(III)-based SMMs. This inference has been verified by the archetypal family of phthalocyanine (Pc) complexes [Bu₄N][LnPc₂] (Ln = Tb and Dy) and their analogues, and the latter model has been obtained by a few Er-based SIMs with an equatorial ligand field.^19b,21a

Although there are many exciting works on the lanthanide-based mononuclear and multinuclear SMMs, the relaxation barriers have reached 938 K (ref. 7) and the blocking temperature increased to an impressive 14 K (T_B),²² there are still some open questions like the source of the slow magnetic relaxation of 4f-based SMMs, the relaxation mechanism, and the key factors influencing the magnetic anisotropy. Therefore, it presents a challenge to design and synthesize an ideal system to study and understand well the relaxation behavior of lanthanide SIMs, for example, does the geometrical or electronic symmetry of molecule determine the relaxation behavior? It is a very complicated task to construct certain charge configurations induced by the coordination donor atoms in the ligands because of the high coordination number and flexible coordination model of the lanthanide complexes.

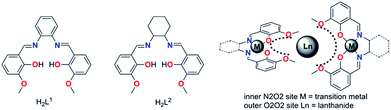
Recently, several SMM studies on Zn–Dy and Zn–Dy–Zn^19a,23,24 type complexes constructed by the Schiff based ligands have revealed that the phenoxo-oxygen donor atoms possess relatively larger negative charges than the aldehyde-oxygen donor atoms or methoxyl oxygen atoms within the ligand. An axial high charge distribution along the magnetic easy axis will enhance the energy barriers of Dy(III)-based SMMs but no impressive hysteresis temperature was achieved. Even in a series of linear Zn(II)–Ln(III)–Zn(II) type molecules,^23c in which all the higher electron density induced by four phenoxo-oxygen atoms was distributed in the opposite position of the Dy(III) ion, no significant SMM behavior was observed. Given the very recent report of the first trigonal pyramidal erbium SMM^21b that revealed a strictly prolate f-electron density is not required to stabilize a crystal field that favors SMM behavior, the geometric design principles to minimize electronic repulsions between the electron densities of the lanthanide ions and the ligands should be used carefully. Especially for low symmetry systems, the tiny deviation of the coordination atoms from the easy axis and/or the hard plane (perpendicular to the easy axis) could introduce a transversal anisotropy component and reduce the U_eff significantly. Fortunately, we verified these key factors in a series of air-stable mononuclear lanthanide based Zn–Dy–Zn type SMMs formed by salen-type ligands H₂L¹ and H₂L² (Schemes 1 and 2), which possess plentiful phenoxyl and methoxyl oxygen donor atoms with higher and lower negative charge distribution, and they were elaborately placed in nearly parallel and perpendicular arrangement to the easy axis, respectively.

Scheme 1 The schematized construction of these SMMs.

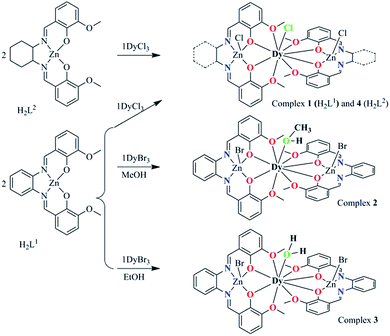Scheme 2 The synthesis procedure for 1–4 and their core structures. The green coordination atoms represent the substitutable positions.

In comparison to the highly symmetrical geometric structure usually found in high performance lanthanide SIMs, only a C₂ axis exists through the Cl and Dy(III) center in two of these molecules. There are nine coordinated oxygen atoms in the first coordination sphere of the Dy(III) ion, in which five oxygen atoms with a lower electron density constitute a hard plane with a pseudo C₅ axis surrounding the Dy(III) center, and the phenoxyl atoms with a high electron density located on the two sides of this hard plane. This special electron density distribution results in a significant SMM behaviour with magnetic hysteresis at a temperature as high as 12 K and a large relaxation barrier over 430 K. It is more important that one of the coordination atoms in this hard plane could be replaced by other substituents while maintaining the other coordination atoms, which allows us to fine-tune the hard plane in the first coordination sphere, and consequently control the magnetic anisotropy of the molecule. Furthermore, another similar ligand with the same inner tetradentate coordination O2O2 site was used to probe the influence beyond the first coordination sphere on the slow magnetic relaxation.

Herein we provide an experimental case involving four novel Zn–Dy–Zn SMMs for exploring the impact of the subtle change of the electron density in the first and second coordination sphere on dynamic magnetic relaxation behavior.

Experimental

All chemicals and solvents were obtained from commercial sources and were used as received, without further purification. The starting Zn(II) complex [Zn(L)] was synthesized according to the procedure reported by Wong et al.²⁵

Synthesis of complexes 1–4

A similar procedure was employed in preparing all complexes; hence, only the preparation of complex 1 was described in detail. A solution of DyCl₃·6H₂O (12 mg, 0.03 mmol) in methanol (10 mL) was added to a suspension solution of ZnL¹ (27 mg, 0.06 mmol) in acetonitrile. The mixture was stirred and heated under reflux (6 hours). After cooling to room temperature, the solution was filtered. The crystals of product were obtained by diffusing diethyl ether slowly into the solution in a sealed container. Elemental analysis calcd (%) for 1, C₄₄H₄₀Cl₃DyN₄O₁₀Zn₂: C, 44.62; H, 3.40; N, 4.73; found: C, 44.70; H, 3.12; N, 4.73. ZnL² was used instead of ZnL¹ for synthesizing 4, DyBr₃ was used instead of DyCl₃·6H₂O for synthesizing 2, and ethanol and DyBr₃ were used instead of methanol and DyCl₃·6H₂O when synthesizing 3. Elemental analysis calcd (%) for 2, C₄₅H₄₆Br₃DyN₄O₁₂Zn₂: C, 39.51; H, 3.39; N, 4.10; found: C, 39.88; H, 3.43; N, 4.20; elemental analysis calcd (%) for 3, C₄₄H₃₈Br₄DyN₄O₉Zn_2.5: C, 37.42; H, 2.71; N, 3.97; found: C, 37.60; H, 2.80; N, 4.02. Elemental analysis calcd (%) for 4, C₄₄H₅₀Cl₃DyN₄O₉Zn₂: C, 44.84; H, 4.28; N, 4.75; found: C, 44.79; H, 4.11; N, 4.65.

Physical measurements

Elemental (C, H and N) analyses (EA) were performed on a Perkin-Elmer 2400 analyzer. Samples were fixed by eicosane to avoid movement during magnetic measurements. Static magnetic measurements and alternating-current (ac) susceptibility measurements under an oscillating field of 3 Oe in the frequency range from 1 to 1000 Hz were performed on the polycrystalline samples using a Quantum-Design MPMS magnetometer, respectively. The magnetization hysteresis loops were measured on a Quantum Design MPMS XL-5 SQUID magnetometer at low sweep rate (100–300 Oe min⁻¹). For a sweep rate of more than 50 Oe s⁻¹, the measurement was performed on the Quantum Design PPMS magnetometer. Magnetic data were corrected for the diamagnetism of the samples using Pascal's constants and the sample holder.

Crystallographic data collection and refinement

Data were collected on a Nonius Kappa CCD diffractometer with Mo Kα radiation (λ = 0.71073 Å). Empirical absorption corrections were applied using the Sortav program. All structures were solved using the direct method and refined by full-matrix least squares on F² using the SHELX program.²⁶ H atoms were located using a difference Fourier synthesis.

Results and discussion

Synthesis and characterization

We utilize the classic compartment salen-type Schiff base as the ligand, which has been widely used to build d–f heteronuclear complexes with magnetic or luminescent properties. We also developed a series of salen-type dinuclear and tetranuclear SMMs with a relatively rigid and aromatic cyclic backbone ligand.²⁷ In order to construct a more simple system, i.e. mononuclear lanthanide SMMs, hexadentated (N2O2O2) salen-type Schiff base N,N′-bis(3-methoxysalicylidene)phenylene-1,2-diamine (H₂L¹) and N,N′-bis(3-methoxysalicylidene)-1,2-diaminocyclohexane (H₂L²) were used (Scheme 1), in which the inner N2O2 site was occupied initially by diamagnetic Zn(II) ions leaving the outer O2O2 cavity for the larger lanthanide ions, and consequently two Zn–L fragments encapsulating Zn–Dy–Zn type compounds were obtained.

All the complexes 1–4 were obtained using similar synthesis procedures. The starting Zn-based precursors [ZnL] (L = L¹ and L²) were synthesized according to the procedure reported by Wong et al.²⁵ The reaction of the ZnL complex with DyCl₃ or DyBr₃ in 2 : 1 mole ratio gave four complexes with the general formula [Zn₂(L¹)₂DyCl₃]·2H₂O (1), [Zn₂(L¹)₂Dy(MeOH)Br₃]·3H₂O (2), [Zn₂(L¹)₂Dy(H₂O)Br₂]·[ZnBr₄]_0.5 (3) and [Zn₂(L²)₂DyCl₃]·2H₂O (4) (Scheme 2). When complex 1 was obtained, we noticed that the Cl⁻ anion in the nine-coordinated environment surrounding the Dy(III) center is prone to be substituted to fine-tune the local coordination geometry and further possibly control the mononuclear magnetic anisotropy of the Dy(III) ion.

As the first strategy, the Br⁻ anion was used to replace Cl⁻, however, as the bromine is too large to be located at the chlorine position, a methanol molecule unexpectedly occupies the position resulting in complex 2. Then, we attempted to replace the MeOH molecule with EtOH, and interestingly another unexpected structure, complex 3, was obtained, in which the MeOH molecule in 2 was replaced by a H₂O molecule. The synthesis of 1–3 indicates that the spatial position of the replaceable Cl⁻ in 1 is suitable to accommodate a molecule with a size between Cl⁻ and MeOH. These complexes provide the opportunity to fine tune the first coordination sphere surrounding the Dy(III) center. In order to explore the influence of the far coordination region, another salen-type Schiff based N,N′-bis(3-methoxysalicylidene)-1,2-diaminocyclohexane (H₂L², Schemes 1 and 2) was used to build [Zn₂(L²)₂DyCl₃] (4) and maintain the first coordination sphere configuration.

The geometric structures of complexes 1–4 are depicted in Fig. 1, S1† and the crystal data are listed in Table S1.† Complexes 1 and 4 are constructed from the ligands H₂L¹ and H₂L² and they nearly possess the same coordination atoms in the first coordination sphere. They crystallize in the same monoclinic space group C2/c. 2 and 3 are constructed using H₂L¹ but crystallize in the triclinic, P1̄ and monoclinic, P21/c space groups respectively due to the different recrystallization conditions. In the four complexes, the Zn(II) ions invariably occupy the internal N2O2 site and further complete the five-coordinated square-pyramidal geometry using one Cl⁻ (for 1 and 4) or Br⁻ (for 2 and 3) at the apical position. The Dy(III) ion is encapsulated by the two ZnL fragments with the outer O2O2 coordination site lying nearly perpendicularly to each other, consequently located in a pocket consisting of eight oxygen atoms and one substitutable atom. The Dy(III) ions of complexes 1–4 have a similar first coordination sphere, only differing in the outer diamine moiety. As for 1, 2 and 3, the first coordination sphere surrounding the Dy(III) center differs in the ninth substituent group Cl⁻, MeOH and H₂O besides the same eight oxygen atoms from two ligands (Fig. 1). The shortest distances between the neighboring Dy(III) ions in 1–4 are longer than 10 Å due to the large ZnL spacer.

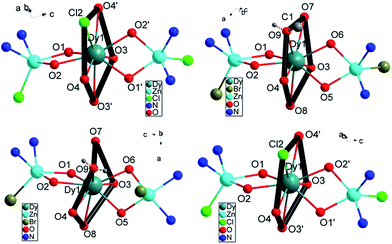Fig. 1 The core structure for 1 (top left), 2 (top right), 3 (bottom left), 4 (bottom right). The outer backbone of the ligands and counter anions are omitted for clarity.

The local symmetry of the Dy(III) ions in complexes 1–4 was analysed using the parameter S of the continuous-shape-measures (CShMs) method,^28,29 which allowed us to quantify the degree of distortion of the coordination sphere (S value equals 0, corresponding to a perfect polyhedron and a larger value indicates a greater deviation from the ideal geometry). The relatively large S values of 2.1–3.6 (Table S2†) reveal that the coordination environment of the Dy(III) center in 1–4 has a low geometrical symmetry. The structures are almost in the same degree of deviation compared to the ideal spherical capped square antiprism (C_4v), spherical tricapped trigonal prism (D_3h) and Muffin-shape (C_s), in which C₄ and C₃ axial symmetries are often observed for SIMs. In fact, as for the monoclinic C2/c crystal system for 1 and 4, there is a C₂ symmetric axis in the molecules through Cl and Dy atoms (Fig. S2,† black dashed line).

Interestingly, further inspection of the coordination environment of the Dy(III) center in 1–4 reveals that there is a five-membered ring consisting of four methoxyl oxygen atoms from two ligands and one chlorine atom (for 1 and 4) or oxygen atom in MeOH (for 2) or in H₂O (for 3) (Fig. 1, thick black ring). It is almost perpendicular to the Zn–Dy–Zn direction. Given a least-square plane defined by the five coordination atoms, the deviations of the individual atoms from this least-square plane are not large, except for complex 3 (Table S3†). The charge density from the ab initio calculations (Table S4†) reveals the lower charge density distribution of the pentagonal ring consisting of four methoxyl oxygen atoms and one substitutable atom (Fig. 1, thick black ring). In contrast, a larger negative charge is distributed on phenoxyl oxygen atoms, which results in the shorter bonding distance of Dy–O and an axially enhanced LF. The axial electron density distribution has been found to induce a high energy barrier but the significant magnetic hysteresis was not detected.²³

Magnetic behavior

The static magnetic measurements were performed on the polycrystalline samples using a Quantum-Design MPMS magnetometer. The temperature dependence of the magnetic susceptibility χ_MT for 1–4 is shown in Fig. S3.† The values of χ_MT are 14.09, 14.27, 14.04 and 14.29 cm³ K mol⁻¹ at 300 K for 1–4 respectively, which are in good agreement with the theoretical value for one free Dy(III) ion (S = 5/2, L = 5, ⁶H_15/2, g = 4/3). On lowering the temperature, the χ_MT product decreases gradually, which is likely due to the thermal depopulation of the Ln(III) Stark sublevels. The magnetization of 1–4 from zero to 50 kOe dc field at 2, 3, 5 and 8 K are shown in Fig. S4.† The maximum values of magnetization reaching 4.9, 4.8, 4.9 and 5.1 Nβ and the lack of saturation at 50 kOe are likely attributed to the crystal-field effect and the existence of low lying excited states.

In order to probe the magnetic dynamic behavior of these complexes, the ac susceptibilities at various frequencies and temperatures in the absence of a dc field are measured and depicted in Fig. 2 and S9 and S10.†

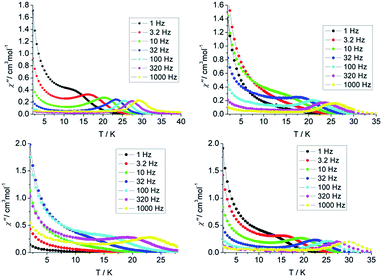Fig. 2 Temperature dependence of the out-of-phase susceptibility (χ′′) plots of 1 (top left), 2 (top right), 3 (bottom left), 4 (bottom right), between 1 and 1000 Hz under zero dc field.

Both in-phase (χ′) and out-of-phase (χ′′) susceptibilities show significant frequency dependence peaks at a relatively high temperature range, which clearly indicates that the slow relaxation of magnetization arises from SMM properties. The maximum peaks of the out-of-phase signals were found from 10 K to 30 K for an oscillating field range of 1 Hz to 1000 Hz. The first clear peaks are observed at 3.2, 32, 320 and 3.2 Hz for 1–4 respectively. The increasing of χ′ and χ′′ below 10 K is indicative of the quantum tunnelling of the magnetization (QTM) at a zero dc field. The frequency magnitude of the first maximum peaks for 1–4 reflects the impact of QTM on the SMMs, where the lower one mostly indicates the existence of a slower QTM process where the thermally activated Orbach relaxation process occurs prominently. In order to suppress or minimise the QTM it is necessary to lift the degeneracy of the states to prevent the spins relaxing through tunnelling. This can be achieved by applying a dc field. As shown in Fig. S11 and S12,† the χ′ and χ′′ tails nearly vanished under a 1000 Oe dc field and the peaks can be observed even at the lower frequency of 1 Hz, which indicates the QTM is suppressed efficiently.

To confirm whether the relaxation in 1–4 is a thermally activated mechanism, the natural log of the relaxations, τ extracted from the peak maxima of χ′′, were plotted versus 1/T to check for Arrhenius-type linearity which is normally referred to the Orbach relaxation of the magnetization (τ = τ₀ exp(U_eff/k_BT), Fig. 3). It is interesting to note that the curvature in the ln(τ) versus 1/T plot under zero field was observed for 1, and the QTM process was usually responsible for this deviation from Arrhenius-type linearity. Owing to the Kramers nature of the Dy(III) ion at zero field, dipole–dipole and hyperfine interactions should be responsible for the mixing of the two Kramers ground states that allows the zero-field quantum tunnelling dynamics of the magnetization. To remove the QTM effect, the ac magnetic susceptibility measurements under application of a 1000 field and on a diluted sample with a Y(III) analogue with 1/20 molar ratio were performed. This does efficiently suppress the QTM process with the diminishing χ′′ signals at the low temperature range (Fig. S14 and S15†). It is also noteworthy that the plots of ln(τ) versus 1/T either under 1000 field or for the diluted sample still exhibit an obvious curvature which indicates that perhaps another relaxation pathway is also operative (Fig. 3 left). The presence of multiple relaxation processes is possible, as reported in a few SIMs.^30–32 In view of this, we fitted the magnetic data with the eqn (1) considering the spin–lattice relaxation of both the Raman and Orbach processes.³³

1/τ = CTⁿ + τ₀⁻¹ exp(−U_eff/k_BT) (1)

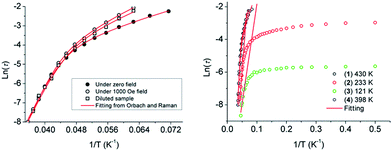Fig. 3 Plots of ln(τ) versus 1/T at zero field, 1000 Oe dc field and of the samples with 20 times magnetic site dilution for 1 (left), and for 1–4 under zero field (right). The red solid lines represent the fitting of the frequency-dependent data by eqn (1) for 1 and 4 and the pure Arrhenius fitting at the high-temperature linear region for 2 and 3.

The first and second terms correspond to the Raman and Orbach processes, respectively. In general, n = 9 for Kramers ions, but when both the acoustic and optical phonons are considered depending on the structure of energy levels, n values between 1 and 6 are reasonable.³⁴Eqn (1) affords U_eff/k_B = 430 K, τ₀ = 7.4 × 10⁻¹¹ s in the absence of the dc field, U_eff/k_B = 481 K, τ₀ = 1.3 × 10⁻¹¹ s under 1000 Oe dc field, and U_eff/k_B = 434 K, τ₀ = 7.0 × 10⁻¹¹ s for the samples with 20 times magnetic site dilution, respectively (see Fig. 3 left, Table S6†). Complex 4 displays a similar relaxation behavior to 1, and the same eqn (1) was used to fit the plot of ln τ versus 1/T and give the energy barrier of U_eff/k_B = 398 K with τ₀ = 3.5 × 10⁻¹⁰ s.

However for 2 and 3, there is an apparent cross procedure from the temperature-dependent regime associated with thermally active Orbach relaxation to a temperature-independent regime related to the QTM upon lowering the temperature. The high-temperature region (19–24 K for 2, 17–22 K for 3) was fitted using the pure Arrhenius law, which resulted in the estimated effective energy barrier to the magnetization reversal of U_eff/k_B = 233 K with τ₀ = 2.5 × 10⁻⁸ s for 2 and U_eff/k_B = 121 K with τ₀ = 8.5 × 10⁻⁷ s for 3 in the absence of the dc field. The relaxation time of QTM for 2 and 3 are extracted from the ac susceptibility as 51.3 ms and 3.5 ms, respectively, whereas the slower QTM process occurred in 1 and 4. In our case, the relaxation barriers increase in the order of 3 < 2 < 1, 4 corresponding to their QTM time trends.

Generally, the effective relaxation barrier of the Orbach process is comparable with the energy difference between the ground and first excited states. The CASSCF/CASPT2/RASSI method was used to calculate the fine energy spectrum of complexes 1–4 (see computation details in ESI†). The obtained energy gap of 497 K and 398 K between the ground and the first excited states in 1 and 4 are close to the fitting values extracted from the modified Arrhenius analysis, whereas an apparent deviation was observed in 2 and 3. The origin of this discrepancy may be related to the presence of additional relaxation processes (for example, tunnelling in the ground state induced by dipolar–dipolar interactions or vibronic coupling) that are important for the extracted experimental U_eff values but were not considered in the U_calcd values.^15,35 Moreover, the value of U_eff in 2 and 3 should be treated with caution owing to the fact that the high temperature peak maximum data are limited in the fitting of U_eff from the pure Arrhenius fitting. On the other hand, the tunnelling effect was usually quantified by the transverse anisotropy component. The calculated values of g_x 0.0012, g_y 0.0018 for 2 and g_x 0.0023, g_y 0.0036 for 3 are larger than g_x 0.0000, g_y 0.0002 for 1 and g_x 0.0002, g_y 0.0005 for 4 (Table S5†), which confirms that the QTM in 2 and 3 with relative larger transverse anisotropy components is pronouncedly higher than 1 and 4.

To confirm the SMM behavior of these complexes, magnetic hysteresis, another important characteristic of magnetic bistability of a magnet, was also measured at different temperatures on polycrystalline samples (see Fig. 4) with the sweep rate used in a traditional SQUID magnetometer (100–300 Oe min⁻¹). A significant hysteresis was still detected under 8 K, 6 K, 4 K and 8 K for 1–4, respectively. As for 1, if the sweep rate of the field was increased to 50 Oe s⁻¹ and 200 Oe s⁻¹, the hysteretic behavior could be even detected at 10 K and 12 K, respectively (Fig. S7 and S8†). To the best of our knowledge, these hysteresis temperatures are among the highest ones reported to date for the Dy(III)-based SIMs.^19a,16b,36

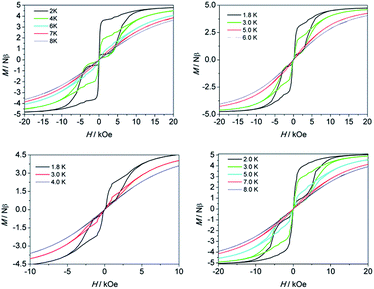Fig. 4 Magnetization (M) vs. applied dc field (H) on a Quantum Design MPMS XL-5 SQUID magnetometer for 1 (top left), 2 (top right), 3 (bottom left) and 4 (bottom right).

For the lanthanide-based SIMs, the butterfly type loops were often observed. The close up of the hysteresis at a zero field is attributed to the QTM process. To deduce the QTM effect, the 20 times magnetic site dilution samples with yttrium for 1 are also measured at low temperatures. The loop was still recorded well, which indicates that it is a single-ion feature rather than the long-range ordering. A remanence of 1.2 Nβ and a coercive field of 300 Oe was found at 1.8 K and the opening of the loop at zero field could still be observed until 4 K (Fig. S13†).

The calculated g values for 1–4 are listed in Table S5.† The g_z values close to 20 indicate that the four systems display significantly strong uniaxial magnetic anisotropy for Dy(III) ions. However, we noticed that they differ in the energy barriers (U_eff, under zero field) and hysteresis temperatures (under the same sweep rate used in a traditional SQUID magnetometer). For 1–4, the energy barriers and hysteresis temperatures are 430 K, 233 K, 121 K, 398 K and 8 K, 6 K, 4 K and 8 K, respectively. Both of the two parameters increase in the order of 3 < 2 < 1 ≈ 4 which is consistent with the increasing trend of the g_z values 19.7884 (3) < 19.8462 (2) < 19.9615 (1) ≈ 19.9658 (4). The significant magnetic relaxation behavior mainly arises from the correspondingly large magnetic anisotropy. Moreover, the reduced g_z value, usually accompanying relatively high g_x and g_y values, can be considered as a characteristic of the transverse anisotropy component. The system with a slower QTM process favours the occurrence of thermally active magnetic relaxations. It is very crucial to make clear what introduces the transverse anisotropy component, however, the influencing factors are more complicated than assumed. The symmetry of the local coordination environment is one of the indispensable factors. Usually a relatively high axial symmetry results in a high magnetic anisotropy. The coordination sphere especially within the closest region, and even the second peripheral ligand surrounding the magnetic easy axis, will influence the magnetic anisotropy significantly. The direction of the calculated anisotropy axis was shown in Fig. S1† and Table S5,† which nearly parallels with the Zn–Dy–Zn direction and being perpendicular (with angle of 90°) to the C₂ axis of the molecule 1 and 4. The same phenoxyl oxygen atoms surround the principal axis (or J_z vector) with a high charge density distribution in 1–4, which generates a strong easy-axis ligand field (vide infra for ab initio calculations Table S4†). On the other hand, the hard plane composed of one substitutable group and four methoxyl oxygen atoms possesses a lower charge density distribution (see Fig. S1†). The results demonstrate that a joint contribution, combining the enhanced high negative charge distribution along the magnetic easy axis with a decreased electrostatic distribution within the hard plane, may ultimately lead to high performance SMMs capable of retaining their magnetization at more practical temperatures irrespective of the low symmetry of the coordination environment.

In our case, the significant axially high and equatorially low negative charge distributions around the oblate Dy(III) ion induced by ligands are observed which leads to significant SMM behaviors. As for the SIMs system, the magnetic anisotropy is related to the fine electronic structures, as described previously, depending on which J_z sublevel of the lanthanide ions has a characteristic electronic distribution. For Dy(III) ions, the pure ground state sublevel with a maximum |J_z| value of 15/2 has a larger electronic distribution on the equatorial plane (hard plane) than along the principal axis, whereas a sublevel with a minimum |J_z| value of 1/2 has a larger distribution along the principal axis. If coordination atoms with larger negative charges are located along the axis and/or lower electronic distribution around the equatorial plane, it will strongly stabilize the former (m_15/2 state) due to the decreased electron repulsion and lead to significantly easy axial anisotropic ground states, whereas the latter (m_1/2 state) becomes relatively unstable. Inspecting the closest electrostatic potential distribution surrounding the Dy(III) center in 1–4, there is nearly the same charge distribution along the magnetic easy axis, therefore the electron distribution in the hard plane was considered as the key factor in introducing the transverse anisotropy and QTM, and finally influencing the whole molecular magnetic anisotropy.³⁷

However, despite much lower electronic density distributed on the hard plane of 3, which displayed a relative weak magnetic anisotropy reflected in their slightly smaller calculated g_z values and SMM properties with lower energy and hysteresis temperature. There might be other important factors to determine the single-ion magnetic anisotropy besides the special electrostatic potential distribution pandering to the electron density distributions of the lowest ground states m_J in 4f ions. A more detailed inspection of the hard plane reveals that the deviations of the five coordination atoms from their least-square planes are different due to the key substituent coordination atom (Table S3†). Complexes 2 and 3 display relatively more apparent deviation from the hard plane than 1 and 4.

For each 4f-ion, the charge distribution of the sublevels with the maximum J_z quantum number, characterized by the angle θ_max (the angle from the equatorial plane), will diffuse the maximum electric density.^20b For the Tb(III) ion, the maximum distribution angle θ_max found in the equatorial plane is 0°, whereas θ_max increases to 34° for the Dy(III) ion.^23c Thus the positions of the coordination donor atoms with different deviation from the equatorial plane generate different electronic repulsion strengths between the 4f electrons and donor atoms. The relatively large repulsion might lead to a reduction of anisotropy.^20a,23c For our case, the substitutable coordination atom in the equatorial plane of 3 displays the largest deviation (Table S3†), followed by 2, 4, and 1. If the substitutable coordination atom deviates from the equatorial plane seriously, the electrons of Dy(III) and donor atoms are most likely to meet each other in the direction of distributing highest electron density, and the electronic repulsion between them may ultimately lead to a relatively weak magnetic anisotropy system, which might be mostly responsible for the different SMM behaviors in 1–4. On the other hand, the four complexes possess two coordination phenoxyl atoms which are axially the same along the easy axis, and the five substitutable atoms in the hard plane act as the key adjusting knob, of which the deviation from the hard plane will lead to the distortion of the assumed pentagonal-bipyramid geometry and consequently influence the molecular magnetic anisotropy.

Conclusions

In summary, a series of air-stable Zn–Dy–Zn lanthanide SIMs displaying a remarkably slow magnetic relaxation behavior were facilely synthesized. They afford the relatively high relaxation energy barrier for the reversal of the magnetization and hysteresis temperature among the Dy(III)-based mononuclear SMMs. More importantly, although they display a significantly low geometrical symmetry, the relatively strong magnetic anisotropy and significant SMM behaviors were observed. The magnetic data analysis and theoretical calculations showed that the symmetry of charge distribution around the Dy(III) ion is the key factor to determine the slow relaxation of these molecules. It provides a practical idea to design new lanthanide SMMs despite the lanthanide-containing complexes usually having a high coordination number and flexible coordination geometry.

Acknowledgements

This work was supported by the NSFC (21290171, 21321001, 21102039, 21571008 and 21572048), the National Basic Research Program of China (2013CB933401, 2010CB934601), the BNLMS (20140108), and the Educational Commission of Heilongjiang Province (1254G045, 12541639).

Notes and references

1. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141.
2. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006.
3. J. van Slageren, Top. Curr. Chem., 2012, 321, 199.
4. D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268.
5. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179.
6. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357.
7. C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem.–Eur. J., 2013, 19, 1457.
8. N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694.
9. M. A. AlDamen, J. Clemente Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874.
10. (a) S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448; (b) S. D. Jiang, B. W. Wang, H. L. Sun, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730.
11. S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, A. Camón, M. Evangelisti, F. Luis, M. J. Martínez-Pérez and J. Sesé, J. Am. Chem. Soc., 2012, 134, 14982.
12. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224.
13. J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558.
14. J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003.
15. D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770.
16. (a) N. F. Chilton, D. E. Collison, J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551; (b) L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413.
17. (a) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110; (b) P. Zhang, L. Zhang and J. K. Tang, Dalton Trans., 2015, 44, 3923; (c) L. Ungur, S. Y. Lin, J. K. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894; (d) J. K. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer Berlin Heidelberg press, 2015; (e) S. Gao, Molecular Nanomagnets and Related Phenomena, Structure and Bonding, Springer Berlin Heidelberg press, 2015, p. 164.
18. R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673.
19. (a) J. L. Liu, Y. C. Chen, Y. Z. Zheng, W. Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. L. Tong, Chem. Sci., 2013, 4, 3310; (b) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952.
20. (a) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078; (b) J. Sievers, Z. Phys. B: Condens. Matter Quanta, 1982, 45, 289.
21. (a) P. Zhang, L. Zhang, C. Wang, S. Xue, S. Y. Lin and J. K. Tang, J. Am. Chem. Soc., 2014, 136, 4484; (b) A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 5864.
22. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236.
23. (a) T. Kajiwara, M. Nakano, K. Takahashi, S. Takaishi and M. Yamashita, Chem.–Eur. J., 2011, 17, 196; (b) A. Watanabe, A. Yamashita, M. Nakano, T. Yamamura and T. Kajiwara, Chem.–Eur. J., 2011, 17, 7428; (c) M. Maeda, S. Hino, K. Yamashita, Y. Kataoka, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2012, 41, 13640; (d) S. Hino, M. Maeda, K. Yamashita, Y. Kataoka, M. Nakano, T. Yamamura, H. Nojiri, M. Kofu, O. Yamamurod and T. Kajiwara, Dalton Trans., 2013, 42, 2683; (e) M. A. Palacios, S. Titos-Padilla, J. Ruiz, J. M. Herrera, S. J. Pope, E. K. Brechin and E. Colacio, Inorg. Chem., 2014, 53, 1465; (f) A. Upadhyay, S. K. Singh, C. Das, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. Commun., 2014, 50, 8838; (g) I. Oyarzabal, J. Ruiz, J. M. Seco, M. Evangelisti, A. Camón, E. Ruiz, D. Aravena and E. Colacio, Chem.–Eur. J., 2014, 20, 14262; (h) I. Oyarzabal, J. Ruiz, E. Ruiz, D. Aravena, J. M. Seco and E. Colacio, Chem. Commun., 2015, 51, 12353; (i) J. P. Costes, S. T. Padilla, I. Oyarzabal, T. Gupta, C. Duhayon, G. Rajaraman and E. Colacio, Chem. Eur. J., 2015 DOI:10.1002/chem.201501500.
24. H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1.
25. W. K. Lo, W. K. Wong, W. Y. Wong, J. P. Guo, K. T. Yeung, Y. K. Cheng, X. P. Yang and R. A. Jones, Inorg. Chem., 2006, 45, 9315.
26. (a) G. M. Sheldrick, SHELXS-97, Program for X-ray Crystal Structure Solution, University of Göttingen, Germany, 1997; (b) G. M. Sheldrick, SHELXL-97, Program for X-ray Crystal Structure Refinement, University of Göttingen, Germany, 1997.
27. (a) P. H. Lin, W. B. Sun, M. F. Yu, G. M. Li, P. F. Yan and M. Murugesu, Chem. Commun., 2011, 47, 10993; (b) P. F. Yan, P. H. Lin, F. Habib, T. Aharen, M. Murugesu, Z. P. Deng, G. M. Li and W. B. Sun, Inorg. Chem., 2011, 50, 7059; (c) W. B. Sun, B. L. Han, P. H. Lin, H. F. Li, P. Chen, Y. M. Tian, M. Murugesu and P. F. Yan, Dalton Trans., 2013, 42, 13397.
28. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693.
29. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, Shape v. 2.0, Universitat de Barcelona, Barcelona, 2010.
30. S. Titos-Padilla, J. Ruiz, J. M. Herrera, E. K. Brechin, W. Wersndorfer, F. Lloret and E. Colacio, Inorg. Chem., 2013, 52, 9620.
31. J. L. Liu, K. Yuan, J. D. Leng, L. Ungur, W. Wernsdorfer, F. S. Guo, L. F. Chibotaru and M. L. Tong, Inorg. Chem., 2012, 51, 8538.
32. E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130.
33. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, U.K, 1970.
34. K. N. Shirivastava, Phys. Status Solidi B, 1983, 117, 437.
35. (a) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125; (b) M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139.
36. R. A. Layfield, Organometallics, 2014, 33, 1084.
37. (a) F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242; (b) S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513.

---

Footnote

† Electronic supplementary information (ESI) available: Additional magnetic data, additional figures and computational details. CCDC 929546, 974436–974438 for 1–4. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc02986d

---