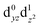Open Access Article
Open Access ArticleA five-coordinate Mn(IV) intermediate in biological water oxidation: spectroscopic signature and a pivot mechanism for water binding†
Marius
Retegan
a,
Vera
Krewald
a,
Fikret
Mamedov
b,
Frank
Neese
a,
Wolfgang
Lubitz
a,
Nicholas
Cox
*a and
Dimitrios A.
Pantazis
*a
aMax Planck Institute for Chemical Energy Conversion, Stiftstrasse 34-36, 45470 Mülheim an der Ruhr, Germany. E-mail: nicholas.cox@cec.mpg.de; dimitrios.pantazis@cec.mpg.de
bMolecular Biomimetics, Department of Chemistry – Ångstrom Laboratory, Uppsala University, Box 523, 75120 Uppsala, Sweden
First published on 17th November 2015
Abstract
Among the four photo-driven transitions of the water-oxidizing tetramanganese–calcium cofactor of biological photosynthesis, the second-last step of the catalytic cycle, that is the S2 to S3 state transition, is the crucial step that poises the catalyst for the final O–O bond formation. This transition, whose intermediates are not yet fully understood, is a multi-step process that involves the redox-active tyrosine residue and includes oxidation and deprotonation of the catalytic cluster, as well as the binding of a water molecule. Spectroscopic data has the potential to shed light on the sequence of events that comprise this catalytic step, which still lacks a structural interpretation. In this work the S2–S3 state transition is studied and a key intermediate species is characterized: it contains a Mn3O4Ca cubane subunit linked to a five-coordinate Mn(IV) ion that adopts an approximately trigonal bipyramidal ligand field. It is shown using high-level density functional and multireference wave function calculations that this species accounts for the near-infrared absorption and electron paramagnetic resonance observations on metastable S2–S3 intermediates. The results confirm that deprotonation and Mn oxidation of the cofactor must precede the coordination of a water molecule, and lead to identification of a novel low-energy water binding mode that has important implications for the identity of the substrates in the mechanism of biological water oxidation.
Introduction
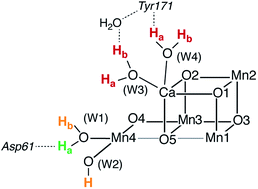
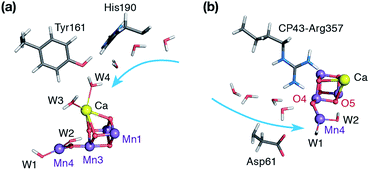
Nature's water splitting catalyst, the oxygen-bridged tetramanganese–calcium cofactor known as the oxygen-evolving complex (OEC), is found in the unique protein–pigment complex photosystem II (PSII) of oxygenic photosynthesis.1–7 The catalytic cycle of the cofactor is comprised of five distinct redox intermediates, the Sn states, where the subscript indicates the number of stored oxidizing equivalents (n = 0–4) required to split two water molecules and release dioxygen.8 Light absorption and subsequent charge separation leads to the generation of the primary oxidant of PSII (P680˙+), an oxidized multi-chlorophyll pigment assembly. P680˙+ is coupled to the chemical catalysis occurring at the Mn4O5Ca cofactor via a redox-active tyrosine residue YZ which acts as a single-electron gate. After four charge separation events, the transiently formed S3YZ˙ state decays to the S0 state via an unknown mechanistic sequence, with concomitant release of triplet dioxygen and rebinding of one water molecule. The catalytic cycle is summarized in Fig. 1, which also shows the geometric conformations, protonation states and oxidation state distributions of the inorganic core of the OEC in each of the S0–S3 states.9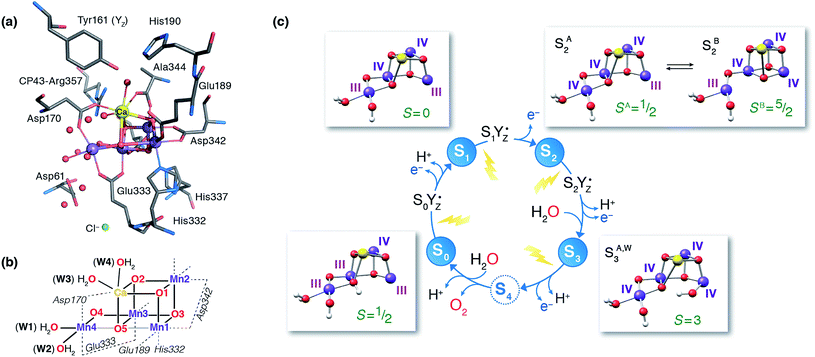 | ||
| Fig. 1 (a) A view of the Mn4Ca cluster and its environment, according to one of the S1-state XFEL crystallographic models of Suga et al.10 (monomer A of dataset 4UB6). (b) Schematic depiction and labeling scheme for the inorganic core of the OEC. (c) The catalytic cycle with spectroscopically consistent models of the inorganic core and their spin states, adapted from ref. 9. In the present work we focus on the multi-step S2–S3 transition. | ||
Recent crystallographic studies that utilized femtosecond X-ray free-electron laser (XFEL) pulses provided a reliable atomistic structure of the OEC in its dark-stable S1 state,10 correcting, supplementing and extending the structural information that was available from previous X-ray diffraction (XRD)11–13 and extended X-ray absorption fine structure (EXAFS) studies.14–17 One intriguing feature of certain S-states is their heterogeneity. Specifically, in the S2 state, with Mn oxidation states of Mn(IV)3Mn(III), the cluster exists in two interconvertible structural forms18,19 that correspond to two distinct EPR signals.18,20 They differ in the distribution of Mn oxidation states and the internal connectivity of the cluster with respect to the O5 bridge (see Fig. 1) and are referred to as the “open-cubane” SA2 (spin S = 1/2, g ≈ 2.0 multiline signal) and the “closed-cubane” SB2 (spin S ≥ 5/2, g ≥ 4.1 signals).
The S3 state of the OEC is similarly characterized by heterogeneity, but in contrast to S2 the relevant phenomenology has not been fully rationalized in terms of well-defined structural forms.21,22 It remains also unclear whether these forms are interconvertible. The majority S3 state species is an EPR detectable spin S = 3 form.21,23 The OEC cluster in this state is composed of four octahedrally coordinated Mn(IV) ions,9,14,21 and is insensitive to near-infrared (NIR) light; Fig. 1 depicts a computational model of the inorganic core that is consistent with these observables. The minority S3 state species, for which no EPR signal has yet been detected, has yet to be directly accessed experimentally. This population responds to NIR illumination at cryogenic temperatures by forming a split S′2YZ˙ EPR signal, where the inorganic cluster is reduced by the nearby YZ residue to an “S2-like” electronic configuration.24–32 As such, this species is expected to represent a precursor of the all-octahedral S3 state form. The structural identity of this species is unknown and its properties are puzzling because Mn NIR photochemistry, observed also in lower S-states, is typically associated with the oxidation state 3+, whereas an all-Mn(IV) cluster is expected for the S3 state.9,21
The primary difficulty in combining all these observations is the complexity of the S2–S3 transition, which involves two structurally and electronically distinct but interconvertible starting points and encompasses oxidation of the Mn cofactor, proton removal, binding of a water molecule, and possibly further rearrangements. Beyond a better understanding of the catalyst itself, developing spectroscopically consistent atomistic models for species involved in the S2–S3 transition has implications for the mechanism of O–O bond formation. Two mechanisms are commonly discussed in current literature: (i) a nucleophilic attack type mechanism involving a terminal oxo ligand at the outer Mn4 and a Ca2+-bound water or hydroxide,33–37 and (ii) radical-type coupling between two Mn bound oxygen ligands.38–41 In principle both mechanisms would involve a structural change in the S2 to S3 transition. For the nucleophilic attack type mechanism, a coordination change at the outer Mn site has been proposed to stabilize a high-spin Mn(V) species in the S4 state,42,43 whereas in the radical coupling scenario this step instead involves the binding/relocation of the final substrate site, and as such it more readily rationalizes the increase in coordination number of the catalyst upon forming the S3 state and recent substrate exchange experiments.14,21,44,45
The identity of the two water substrates is inextricably linked with S-state progression. Experimental data shows that the two water molecules bind at different steps of the cycle. The first one binds after O2 release and is incorporated into the oxo-bridge framework of the cofactor upon formation of the S0 state. This water has been assigned to the O5 bridge of the cluster, which is thought to be a bridging OH in the S0 state9,46 and a fluxional oxo bridge in the S2 state.18,19 The second water binds, or at least is reorganized, during the S2–S3 transition21,41,44,45,47 that prepares the catalyst for the O–O bond formation step. The origin of this water is uncertain, and discussions regarding its incorporation cannot be easily disentangled from those regarding the identity of substrate oxygens.37,48 Existing information on the structure of the catalyst has allowed formulation of two reasonable suggestions for water binding to a Mn ion during the S2–S3 transition: it may represent a loosely bound second-sphere water that coordinates a metal site progression to the S3 state,40,41,49 or instead it may be a Ca-bound water, specifically W3,19 that simply shifts to a Mn ion.
To better appreciate the differences between these suggestions, it is important to keep in mind that in the S2 state the cluster exists in the two interconvertible structures depicted in Fig. 1 and it is not a priori clear if only one of them is catalytically relevant, and if so, which one. The first water binding scenario,50 an element of Siegbahn's detailed computational water oxidation model,40,41,51 involves binding of a (non-crystallographic) spectator water molecule to the open coordination site of the Mn1 ion of an SA2-type structure (Fig. 2a). According to this scenario, after YZ oxidation by P680˙+ the W1 ligand loses a proton. Subsequently Mn1, a Mn(III) in the SA2 state, is oxidized to Mn(IV) and thus can bind an additional water molecule. Binding and deprotonation of the incoming water molecule are coupled, with deprotonation assisted by the hydrogen bonding network on the side of the chloride ion, as shown in Fig. 2a.50 An alternative mechanism was proposed by Guidoni and coworkers.19 In this scenario, after deprotonation of W1 the cluster assumes an SB2-type structure upon Mn oxidation and a water that is already bound to calcium (W3), moves to occupy the empty coordination site of Mn4, the Mn(III) ion of the SB2 structure.19,52 This W3 shift would be accompanied by reorganization of water molecules along a channel associated with Ca, resulting in replenishment of the Ca-bound waters (Fig. 2b).19
 | ||
| Fig. 2 Schematic depiction of two major suggestions for water binding during the S2–S3 transition. Top: A model involving water binding to the Mn1 ion of an SA2-type conformer.50 Bottom: A model involving the shift of a Ca-bound water to the Mn4 ion of an SB2-type conformer.19 | ||
Both suggestions involve water binding at Mn ions present as pentacoordinate Mn(III) in the S2 state, at a site that lies along the Jahn–Teller axis of the former Mn(III) ion, located opposite the O5 bridge, i.e. they can both be described as “internal” water insertion within the Mn4O5Ca framework. On the other hand, they involve ions on opposite sides of the cluster and may differ fundamentally in substrate identity, a critical mechanistic determinant. Moreover, they have distinct implications for the role of the S2 valence/structural isomerism in the mechanism, the role of calcium, and the regulation of the enzyme's substrate access and delivery mechanisms.
It is not obvious which mode of progression from the S2 state can best accommodate the available spectroscopic information on the S3 state and the experimentally detected S2–S3 intermediates. Here we attempt to address this question by identifying plausible intermediates in the S2 to S3 transition by matching predicted properties of computational models with available experimental data, principally from near-infrared (NIR) absorption studies and EPR spectroscopy. The outcomes of this work are: (a) an understanding of the central mechanistic role of the S2-state structural polymorphism, (b) the characterization of an S3-state intermediate that contains a five-coordinate Mn(IV) site, which rationalizes NIR absorption activity and is consistent with EPR spectroscopic observations, and (c) the identification of a new low-energy water binding pathway that has important implications for understanding PSII regulation and the biological water oxidizing mechanism.
Methodology
Structural models
Quantum chemical models for the structure of the OEC have been developed that combine information and constraints from X-ray crystallography, EXAFS, XAS profiles, and magnetic resonance spectroscopy.9 As in previous work,9,18,21,53–56 the models comprise 238–241 atoms (depending on protonation state and inclusion of an additional water ligand) and include the amino acid residues coordinating the Mn4O5Ca cofactor (from protein chain D1 unless otherwise indicated): Asp170, Glu189, His332, Glu333, Asp342, Ala344, and CP43-Glu354, as well as two H2O molecules on Ca2+ ion and an H2O plus a hydroxide on the terminal Mn4 ion. They also include the structurally and electronically critical residues Asp61, Tyr161 (YZ), His190, His337, and CP43-Arg357, the backbones of Leu343, Ser169, and Gly171, plus eight hydrogen-bonded crystallographic water molecules. The protonation states of all ligands were set consistently with previous studies that focused on state-specific evaluation of spectroscopic parameters,57 and by self-consistent and experimentally corroborated modeling of the S0, S1, S2, and S3 states.9 Density functional theory calculations employed initial geometries originating from the S2 state isomers reported in Pantazis et al.18 (SA2YZ and SB2YZ) and Retegan et al.56 (SA2YZ˙ and SB2YZ˙), using permutations of protonation states (for water-derived ligands), hydrogen-bond orientations (for second-sphere waters) and side-chain rotations of non-coordinating amino acid residues.Computational details
All calculations were performed with ORCA.58 Geometry optimizations used the BP86 functional59,60 with self-consistently applied atom-pairwise dispersion corrections61 and the zero-order regular approximation (ZORA) to account for scalar relativistic effects.62–64 Backbone constraints from the 1.9 Å crystallographic model of PSII were applied to α-carbon atoms and to one α-carbon hydrogen in order to maintain the overall protein chain conformation. The ZORA-TZVP basis sets65 were used for all elements except carbon and hydrogen, for which the basis set was reduced to ZORA-SVP. The calculations used the resolution of the identity (density fitting) approximation; to eliminate any potential errors arising from this approximation, a large decontracted def2-TZVP/J auxiliary basis set was used.66 Optimizations were performed with the conductor-like screening model (COSMO)67 with a dielectric constant of 8.0. Tight SCF convergence and increased integration grids (Grid6 and IntAcc 6.0 in ORCA convention) were applied.The transition state searches for water binding were initiated from multiple starting arrangements of the incoming water molecule and used the “hybrid Hessian” feature of ORCA: this involves a frequent exact recomputation of the part of the Hessian that corresponds to the terminal Mn4 ion, its direct ligands and the incoming water molecule, in order to best identify and follow the water binding mode. To facilitate the search for water-binding transition states, Asp61, CP43-Arg357 and some crystallographic water molecules in the vicinity of Asp61 were omitted from the transition state optimizations. Exploratory calculations with the presence of Asp61 and vicinal crystallographic waters led to technical complications because of formation of various hydrogen-bonding rearrangements that led all transition state searches towards directions not relevant to the water binding event, thus the residue had to be omitted. Although this is an approximation, we can estimate that the effect is not major, in view of the flexibility of the Asp61 seen in molecular dynamics simulations,52,68 and specifically because the side chain was shown to rotate upon W1 deprotonation,52 which makes its involvement in water binding ambiguous. A unique transition state was optimized through these searches and conclusively identified as a first-order saddle point by calculation of its analytic second derivatives that led to a single imaginary frequency corresponding to the water binding mode.
Magnetic and spectroscopic parameters were computed by the broken-symmetry DFT (BS-DFT) approach using the TPSSh functional69 with the RIJCOSX approximation70 to Coulomb and exact exchange (with GridX6), using the same scalar relativistic Hamiltonian and basis sets. Details regarding the application of BS-DFT for magnetic and EPR parameters of manganese-oxo systems can be found in recent work.9,18,57,71–74 All possible BS determinants (MS eigenfunctions) were computed and from their energy differences the values of all six pairwise exchange coupling constants were determined using singular value decomposition. These values were subsequently used to construct the Heisenberg–Dirac–van Vleck (HDvV) Hamiltonian which was diagonalized using the orca_eca utility program to obtain the full spectrum of spin eigenvalues. Time-dependent (TD-DFT) calculations of excitation energies followed the same setup as for the single-point calculations described above, but employed the long-range corrected CAM-B3LYP functional.75 Complete active space self-consistent field (CASSCF) and N-electron valence perturbation theory (NEVPT2) calculations76,77 employed an active space of 12 electrons in 20 orbitals. Local zero-field splitting (ZFS) parameters were obtained with the recently introduced local complete active space configuration interaction (L-CASCI) approach,78 using the same active space as for the CASSCF calculations.
Results and discussion
Initial formation of tyrosyl radical species
The presence of two structural forms in the S2 state raises the question whether both forms are mechanistically relevant, or if instead only one form proceeds to the S3 state. In the mechanistic progression suggested by Siegbahn, it is only the open-cubane SA2 form that progresses to the S3 state. In stark contrast, computational studies by Guidoni favor the progression of the closed-cubane SB2 form. Given the correspondence of these two structural forms to the two EPR signals of the S2 state, the experimental EPR literature also contains apparently contradictory suggestions regarding the progression of the multiline g ≈ 2 or of the g ≈ 4.1 S2 state signals to the S3 state.22,79By modeling the initial S2 oxidation event we observe that upon one-electron oxidation of the S2 state models the resultant electronic state contains the YZ radical, as expected, i.e. SA2YZ˙ and SB2YZ˙.56 The phenolic proton of YZ in both these forms is transferred from the tyrosyl to its hydrogen-bonding partner, His190. Both structural forms remain close in energy in our calculations, with the closed-cubane form higher in energy as in the S2-state models: SB2YZ˙ is 2.7 kcal mol−1 higher than SA2YZ˙, compared to 2.4 kcal mol−1 for the SB2/SA2 pair. This electronic S2YZ˙ state represents the first intermediate in the S2 to S3 transition, formed during electron shuttling between the Mn4O5Ca cofactor and P680˙+. Importantly, neither of these structural models can progress to S3, that is, they do not convert to a valence isomer where the electron hole shifts to the Mn cluster,56 presumably because the intrinsic redox potential of the Mn4CaO5 cluster at this state is not low enough to reduce the YZ˙ radical. Therefore, oxidation of the cofactor must be coupled to one of the additional chemical processes described above in connection with the S2–S3 transition: cofactor deprotonation and/or water binding. Of these, only deprotonation rationalizes the required redox tuning of the complex. Experimental results also favor deprotonation on the donor side preceding the oxidation event.5,80
Deprotonation of the cluster in the S2–S3 transition
Asp61, a second-sphere amino acid that forms a hydrogen bond with the terminal water W1 of Mn4, has been implicated in deprotonation of the OEC.5,13,41,49,50,52,68,81,82 This would suggest that the two titratable Mn4-bound ligands (W1, W2) situated most closely to Asp61, are probable sites for deprotonation in the S2–S3 transition. To address this point we compared relative energies of deprotonated structures to estimate relative acidities of the titratable groups W1, W2, W3, and W4 in both the open and the closed-cubane configurations of the S2 and S2YZ˙ states. Similar calculations have been reported by Robertazzi et al. for the S1 state.83 In these calculations, prohibiting structural relaxation and repulsive electrostatic interactions from second-sphere residues (including omission of Asp61) allows us to include in our comparison deprotonation of Ca-bound waters, for which the extensive reorganization of the hydrogen-bonding network upon relaxation would be hard to capture adequately.The energetically most favorable proton removal site in both S2 and S2YZ˙ states for both structural forms (open and closed-cubane) is on W1, specifically the proton H-bonding to Asp61 (see Table 1 and Fig. 3). Removal of any other proton from W1 or W2 costs at least 10 kcal mol−1 more in energy and deprotonation of Ca-bound waters in either the open or the closed-cubane structures is strongly disfavored. Upon deprotonation of W2 in the open-cubane form, Mulliken spin populations of 0.4 on O(W2) and 2.7 on Mn4 are found, indicating development of Mn(III)-oxyl radical character at this site prior to structural relaxation.84 In models with a deprotonated W3 or W4 significant spin population develops on the resulting OH ligands, up to −0.5 for W3 deprotonation in the open-cubane form. Formation of the tyrosyl radical does not alter the observed trends, but it increases the relative acidities of Ca-bound waters. Table 1 reports relative energies referenced to the most acidic group within each given model. If we instead compare relative energies between different structural types (SA2/SB2), we observe that W1 and W2 deprotonation in the closed-cubane form is consistently disfavored by more than 10 kcal mol−1 relative to W1 or W2 deprotonation in the open-cubane form (see Table S1†), implying that the SA2 forms are more susceptible to deprotonation than their SB2 isomers. This is a reasonable conclusion that relates to the oxidation states of the Mn4 ion in these forms: the Mn4(IV) in the open-cubane form is better stabilized by a negatively charged ligand than the Mn4(III) ion in the closed-cubane form.
| Site | SA2YZ | SB2YZ | SA2YZ˙ | SB2YZ˙ |
|---|---|---|---|---|
| W1a | 0.0 | 0.0 | 0.0 | 0.0 |
| W1b | 16.3 | 13.8 | 16.6 | 13.1 |
| W2 | 17.9 | 13.5 | 17.1 | 10.8 |
| W3a | 56.4 | 44.0 | 39.4 | 26.0 |
| W3b | 50.6 | 38.1 | 35.6 | 21.2 |
| W4a | 50.6 | 34.5 | 34.6 | 19.8 |
| W4b | 51.5 | 34.9 | 36.3 | 21.0 |
Oxidation of the cluster in the S2–S3 transition
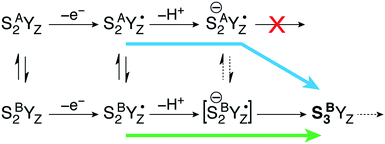
Moving on to the next event that occurs in the S2–S3 transition, the present calculations provide a definitive answer to the question which structural form of S2 can be oxidized by the YZ˙ radical after deprotonation of W1: oxidation of the Mn(III) ion of the inorganic core occurs exclusively in the closed-cubane form. Specifically, a deprotonated SA(−)2YZ˙ species retains its electronic configuration even after complete structural relaxation; the Mn1(III) ion of the inorganic cluster is stable. It cannot be oxidized by the tyrosyl radical and does not appear to be affected by the deprotonation of the Mn4(IV) ligand W1 at the opposite side of the cluster. By contrast, the deprotonated closed-cubane SB(−)2YZ˙ form proved to be unstable and spontaneously relaxed to a form where the Mn4(III) ion of the cluster is oxidized to Mn(IV) and the tyrosyl radical is reduced to its closed-shell form with concomitant proton transfer from His190. Spin populations confirm the presence of four high-spin Mn(IV) ions (2.80–2.89 unpaired electrons on all Mn centers) and the absence of any other spin accumulation site. This type of electronic configuration corresponds to the S3 state of the OEC and the closed-cubane species thus obtained will be referred to as SB3. This state nominally corresponds to an intermediate proposed in a recent ab initio molecular dynamics study of the S2–S3 transition by Narzi et al.52 Note that according to the present results, an SA3 species does not exist as a distinct minimum because it is electronically unstable and reverts via internal electron transfer to SA(−)2YZ˙. Since the SB3 structure is the first S3-type species formed in the catalytic progression, it can be considered as the “entry point” to the S3 state. Importantly, compared to its isomeric SA(−)2YZ˙ form, SB3 is found to be stabilized by 15.4 kcal mol−1.The above theoretical results are consistent with chemical intuition. Within the interconvertible S2 state model the Mn(III) is located at the outer Mn (Mn4 for SB2) or within the cubane (Mn1 for SA2).18,19 Of these two structures, only SB2 contains a Mn(III) ion with titratable ligands, and thus only the SB2 structure can be “redox tuned” with deprotonation, allowing advancement to S3.
This is a clear conclusion, but it can be realized via at least two conceivable pathways. According to the first scenario (green pathway in Fig. 4), the closed cubane form becomes stabilized upon tyrosine oxidation, in contrast to the parent SA2YZ/SB2YZ species for which the open-cubane form is instead more stable.52 This implies that the SB2YZ˙ species may directly proceed via coupled proton and electron transfer to SB3. This sequence of events emerges from the computational study of Narzi et al.,52 which suggests that YZ oxidation stabilizes the closed-cubane form by 2.6 kcal mol−1 compared to the open-cubane form, and facilitates proton shuttling from the W1 ligand of Mn4 to Asp61, coupled to electron transfer from Mn4 to the tyrosyl radical.
With the methods used in the present paper, however, we do not observe such stabilization of the closed-cubane SB2YZ˙ form compared with SA2YZ˙ (see above).85 Additionally, if we consider deprotonation as a distinct step, the SA2YZ˙ form must be easier to deprotonate for the reasons raised in the preceding section, i.e. a Mn4(IV)-bound water is intrinsically more acidic than a Mn4(III)-bound water. This leads us to propose an alternative scenario (blue pathway in Fig. 4), which requires separate proton transfer and electron transfer steps. The barrier for structural interconversion through transposition of the O5, which was computed at ca. 6 kcal mol−1 for the preceding SA2/SB2 states18 must be even lower after deprotonation because of the trans-effect of the newly formed OH(W1) ligand. Specifically, deprotonation of W1 results in reduction of the Mn4–O5 Mayer bond order86,87 by 26%, from 0.88 to 0.66. Therefore, the more easily formed SA(−)2YZ˙ species can readily shift towards a closed-cubane structural rearrangement that is, however, coupled to intramolecular electron transfer. Since [SB(−)2YZ˙] cannot be identified as a distinct stationary point, it is not possible to confirm whether it is a requisite transient intermediate in the transformation of SA(−)2YZ˙ to SB3, or whether it is avoided altogether in the case O5 transposition and electron transfer from the Mn cluster to the YZ radical occur simultaneously. However, even if [SB(−)2YZ˙] would form transiently, it would spontaneously evolve into SB3, which lies 15.4 kcal mol−1 lower than SA(−)2YZ˙, an energy difference suggestive of a strong thermodynamic driving force. Regardless of the details of the progression, the identical conclusion is reached: only the closed-cubane form, a structural form that appears for the first time in the S2 state of the catalytic cycle, progresses to the S3 state. It is noted that EPR data suggest that Ca2+ is necessary to proceed past the low-spin S2YZ˙ state.88–90 Based on the above, Ca2+ may play a role in allowing efficient open/closed cubane interconversion, in stabilizing the closed-cubane state, or in enabling reduction of the tyrosyl radical by the Mn(III) ion of the inorganic cluster.56
Structure of the SB3 intermediate
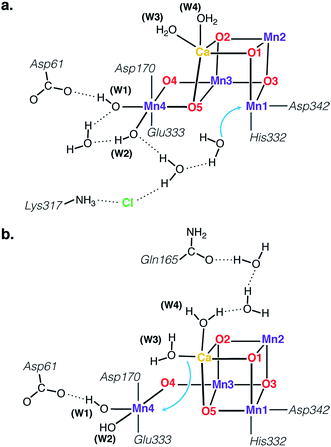
The species obtained immediately upon the spontaneous electronic reorganization described above contains a Mn4 site that is approximately square pyramidal as in the SB2 structure from which it is derived, with a wide O4–Mn4–O(W2) angle of 154.7°. This angle defines a free coordination site in the internal side of the cluster, opposite the O5 bridge of the closed cubane subunit and in the orientation that the Mn(III) Jahn–Teller axis had in the S2 state. This site can serve as coordination site for an incoming water, possibly W3 (Fig. 2b).19 However, we find that structural relaxation of this structure occurs by rotation of the hydroxy ligands W1 and W2 within the plane perpendicular to the Asp170/Glu333 Mn–O bonds, affording an energy stabilization of ca. 5 kcal mol−1 and leading to the SB3 minimum where Mn4 adopts a coordination geometry intermediate between trigonal bipyramidal and square pyramidal (Fig. 5). The widest angle is now O4–Mn4–O(W1) at 146.2° (compared to 97.3° at the initial point). The OH(W2) group is rotated towards the O5 bridge of the Mn3O4Ca cubane subunit, forming an intramolecular hydrogen bond.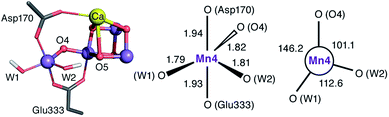 | ||
| Fig. 5 Depiction of the inorganic core of the SB3 species and geometric parameters (Å and degrees) of its Mn4 center. | ||
Five-coordinate Mn(IV) centers are uncommon, but not unprecedented. We are not aware of crystallographically characterized examples of synthetic complexes that display a similar coordination environment, but trigonal bipyramidal complexes supported by N4-donor ligands have been reported by Borovik.42,91,92 As will be shown in the following, this unusual coordination geometry at the Mn4(IV) site of SB3 is responsible for a range of properties that rationalize a large part of the available experimental observations.
Electronic structure and absorption profile of the SB3 intermediate
To study the S3 state by EPR, dark-adapted (S1-state) samples are illuminated by two flashes at room temperature and rapidly frozen to cryogenic temperatures.24,25,93 As described in the introduction, this procedure captures an EPR signal consistent with a structure that contains four octahedrally coordinated Mn(IV) ions, which is considered the end point of the S2–S3 transition.21 Compared to the structural forms present in the S2 state, this “final” S3 species is characterized by an open-cubane topology, but with the crucial difference that the coordination number of all Mn ions is six, due to insertion of a water-derived ligand (see the S3 state model of Fig. 1). To facilitate the following discussion we refer to this all-octahedral model as SA,W3, that is an S3 state structure with metal-oxo connectivity of the open-cubane type, where “W” in the superscript indicates the ligation of an additional terminal ligand (H2O or OH).But as described in the introduction, a second, minority S3-state population has been inferred from the development of additional features in the EPR spectrum following NIR illumination at cryogenic temperatures, without modification of the original EPR signal.24,25 NIR sensitivity is not limited to the S3 state. It is a common feature of the lower S states, where the inability of the reaction center (P680) to absorb in the 740–900 nm spectral range has pointed towards the OEC cluster acting as the chromophore.94 The absorption which promotes the conversion of the multiline signal to the g = 4.1 signal, has been assigned to a ligand field transition localized on the unique Mn(III) ion,94,95 in line with the presence of a near-infrared band in the MCD spectrum of a mixed valent Mn(III, IV) complex.96,97 Similarity of the action spectrum induced in the 720–860 nm region in both S2 and S3 states, indicated the presence of an analogous mechanism for the NIR sensitivity of the cluster in the S3 state, therefore extending the requirement of a Mn(III) ion to this state.30 It was nevertheless argued by Havelius et al. that the assignment is circumstantial, and that other mechanisms can give rise to the observed NIR sensitivity without the constraint related to the presence of a Mn(III) ion.32 In the following we demonstrate that the SB3 structure described above is indeed NIR active and explains all relevant experimental observations owing to the unique five-coordinate Mn(IV) center.
The structural models that we have discussed as different S3-state species, SB3 and SA,W3, have to account for the different photochemistry of the S3-state populations based on the different coordination environment of the Mn4(IV) ion. To test this, we calculated the absorption spectra of the two structures using time-depended density functional theory. The reliability of TD-DFT to predict the position of d–d transitions for mononuclear Mn(IV) complexes has been previously established, with reported deviations of less than 500 cm−1 compared to experiment for the low energy transitions that are of interest in the present context.98,99 The present results confirm that the change in the local geometry of the outer Mn4 ion from five-coordinate (SB3) to six-coordinate (SA,W3) has a significant effect on the position of the d–d excitations. Using the CAM-B3LYP functional, no near-infrared absorptions were computed for the SA,W3 structure, with the lowest transition around 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1 (549 nm), whereas in SB3 the first transition is significantly lower in energy and occurs at ca. 11
230 cm−1 (549 nm), whereas in SB3 the first transition is significantly lower in energy and occurs at ca. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 cm−1 (838 nm). A similar picture is obtained with the PBE0 functional, which predicts the same transitions as CAM-B3LYP, only red-shifted for both models by 30–40 nm.
930 cm−1 (838 nm). A similar picture is obtained with the PBE0 functional, which predicts the same transitions as CAM-B3LYP, only red-shifted for both models by 30–40 nm.
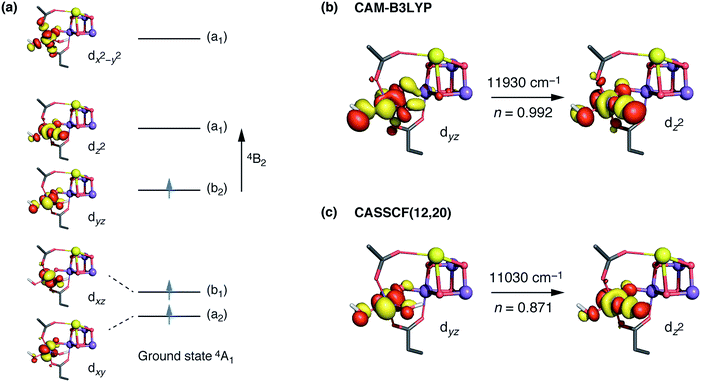
The interpretation of the absorption spectra is facilitated by the use of natural transition orbitals (Fig. 6b). These reduce the inherent complexity of dealing with several molecular orbitals that contribute to a given excited state to a simple picture of one electron being promoted from a donor to an acceptor orbital. Fig. 6 shows the orbital diagram for the Mn4 ion of species SB3, along with the CAM-B3LYP natural transition orbitals that describe the lowest excitation, a near-IR d–d transition from the dyz to the dz2 orbital of Mn4(IV). The change of ligand field to the approximately octahedral geometry of SA,W3 increases the separation between the t2g-derived dyz and the eg-derived dz2 orbitals of Mn4, shifting the excitation energy to much higher values.
CASSCF calculations using an active space comprising all d electrons and orbitals of all four Mn ions, CAS(12,20), agree with the TD-DFT results. Specifically, the lowest-energy d–d transition for SB3 is predicted by CASSCF at ca. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 cm−1 (907 nm), whereas that of SA,W3 at 18
030 cm−1 (907 nm), whereas that of SA,W3 at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 cm−1 (551 nm). The CASSCF orbitals that dominate the lowest-energy transition are depicted in Fig. 6 and show very close agreement with the TD-DFT natural transition orbitals. The corresponding TD-DFT natural transition orbital pair and CASSCF orbitals for SA,W3 are shown in Fig. S2.† To refine the CASSCF energies we included the effects of dynamical electron correlation by performing N-electron valence state perturbation theory (NEVPT2) calculations on top of the CASSCF(12,20) reference wave functions. These calculations represent the highest level of theory employed in the present work. The NEVPT2 excitation energies are blue-shifted compared to the CASSCF energies: the lowest SA,W3 transition is shifted to 22
160 cm−1 (551 nm). The CASSCF orbitals that dominate the lowest-energy transition are depicted in Fig. 6 and show very close agreement with the TD-DFT natural transition orbitals. The corresponding TD-DFT natural transition orbital pair and CASSCF orbitals for SA,W3 are shown in Fig. S2.† To refine the CASSCF energies we included the effects of dynamical electron correlation by performing N-electron valence state perturbation theory (NEVPT2) calculations on top of the CASSCF(12,20) reference wave functions. These calculations represent the highest level of theory employed in the present work. The NEVPT2 excitation energies are blue-shifted compared to the CASSCF energies: the lowest SA,W3 transition is shifted to 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (454 nm), while the lowest-energy transition for the five-coordinate SB3 species is predicted to be at 13
000 cm−1 (454 nm), while the lowest-energy transition for the five-coordinate SB3 species is predicted to be at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 cm−1 (735 nm), in even better agreement with the experimental absorption maximum of ca. 740–760 nm.30,31 Overall, both TD-DFT and multiconfigurational ab initio methods confirm that the unusual geometry of the five-coordinate Mn4(IV) ion in SB3 leads to absorption in the NIR region, consistent with the experimental observations for the population of the S3 state that remains unobserved by EPR.
610 cm−1 (735 nm), in even better agreement with the experimental absorption maximum of ca. 740–760 nm.30,31 Overall, both TD-DFT and multiconfigurational ab initio methods confirm that the unusual geometry of the five-coordinate Mn4(IV) ion in SB3 leads to absorption in the NIR region, consistent with the experimental observations for the population of the S3 state that remains unobserved by EPR.
This result also implies that the response of the OEC to near-IR has a different electronic structure origin in different S-states, since NIR absorption in the S3 state clearly does not arise from—and does not require—the presence of a Mn(III) ion.
Spin state and EPR properties of the SB3 intermediate
In the previous section it was shown that SB3 and SA,W3 are consistent with their assignment as NIR-active and NIR-inactive species, respectively. The close agreement of the SA,W3 properties (spin state of S = 3, 55Mn hyperfine coupling constants and small fine structure splitting) with EPR data has been theoretically confirmed in our recent work.21 Here, we address the more complicated question whether the predicted properties of the NIR-active SB3 can be consistent with the fact that the NIR-active component of the S3 state has not been identified so far in EPR studies. Two factors play a role in this respect: the ground state spin multiplicity of the cluster and the magnitude of the zero-field splitting.Broken-symmetry DFT calculations on the SB3 model suggest that it is characterized by a high-spin ground state. As expected from previous work on synthetic Mn3CaO4 cubanes,100,101 ferromagnetic coupling is dominant within the cubane subunit, with J12 and J23 exceeding 30 cm−1, while J13 is somewhat weaker at 10 cm−1 (see Fig. S3† for depiction of all computed exchange coupling constants). Thus, the Mn3(IV)CaO4 cube is an intrinsically high-spin unit (S = 9/2).101 The coupling between Mn3 and Mn4, J34, further regulates the total spin state. In the present model of SB3 the weakly ferromagnetic (1.3 cm−1) J34 leads to a ground state total spin of S = 6, the maximum spin possible for the given system. J34 is quite sensitive to small structural perturbations, therefore the ground state multiplicity can be lowered if we allow for only small changes in the Mn3–Mn4 interaction, but our simulations indicate a lower bound of S = 3 for the present magnetic topology.
EPR-detected states originating from the S3 species identified here with the SB3 model are known to correspond to high-spin states of the inorganic cluster. Specifically, the state formed after NIR excitation at 77 K of the NIR-active form of S3 contains a tyrosyl radical (with an EPR signal at g ≈ 2) interacting with a high-spin form of the inorganic cluster (attributed to S = 7/2, with an EPR signal observed around g ≈ 5).24–29,32 Since this state results from the one-electron oxidation of tyrosine YZ by the inorganic cofactor, it is designated as S′2YZ˙, where S′2 denotes an electronic configuration of the Mn cluster that is singly reduced compared to S3, but at a geometry similar to its parent S3 state. A comparable EPR signal measured in samples advanced to S3 and stored for extended periods at liquid nitrogen temperature, points towards a similar configuration of the OEC formed in the absence of the YZ˙ radical, where the reduced state of the cluster is generated via charge recombination with the plastoquinone QA−.102 This S′′2YZ state is also associated with a similar high-spin configuration of the inorganic cluster.26 Both of these states are stricto sensu “off-cycle” states with respect to physiological catalytic progression and not directly accessible with our computational methods (see the ESI† for a more detailed discussion). Nevertheless, the high-spin nature of SB3 is clearly consistent with the high-spin states attributed to EPR signals of the S′2YZ˙ and S′′2YZ states.
Next, we focus on the zero-field splitting of SB3. High field EPR measurements of a mononuclear Mn(IV) complex found that in an octahedral ligand field the D parameter is small and axial, ca. 0.25 cm−1,103 a result in line with ligand-field theory considerations. Experimental results are also available for five-coordinate Mn(IV) complexes. In a trigonal bipyramidal ligand field much larger D values, from 0.88 up to 3.0 cm−1, are obtained compared to the six-coordinate metal ion, depending on the protonation of the axial oxygen atom.42,91,104 To investigate the corresponding properties of SB3 we employed a recently developed ab initio method for the calculation of the on-site ZFS splitting in polynuclear complexes of arbitrary nuclearity. The method, termed L-CASCI,78 essentially represents a multireference calculation in an active space constructed from the orbitals localized on the metal center of interest. Using this approach we calculated sequentially the ZFS parameters of all four Mn ions of SB3. In line with experimental results from synthetic mononuclear complexes, the largest value was calculated for the five-coordinate Mn4 ion, D = 2.14 cm−1, with significant rhombicity E/D = 0.10.
It is interesting to analyze the dependence of the ZFS parameters on the principal structural modifications that define the coordination geometry at the Mn4 ion, since this also allows one to understand the connection with the EPR-detectable form of the S3 state (SA,W3). In this respect the O4–Mn4–W1 angle represents a critical parameter, and to establish a connection with the local D of Mn4, the spectroscopic parameters were re-evaluated for geometries where modifications were limited to this particular angle (Fig. 7). The calculated values show that increasing the O4–Mn4–W1 angle from its optimized equilibrium value of 146°, in essence opening up a sixth coordination site at the Mn4 ion, results in diminished local zero-field splitting, whereas even larger values for D are obtained if this angle is made less obtuse.
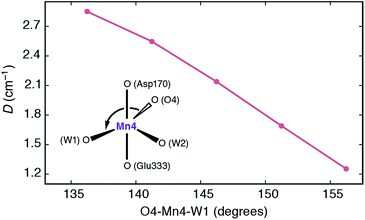 | ||
| Fig. 7 Dependence of the local zero-field splitting parameter D for the Mn4 ion of SB3 on the O4–Mn4–W1 angle. | ||
The trend can be rationalized by decomposing the D value in terms of state contributions. This reveals that the first excited state, which is also responsible for the NIR sensitivity of the OEC cluster (see Fig. 6), has the largest contribution to the total D value among the spin conserving excited states. This state results from a transition between the dyz and dz2 orbitals (Fig. 6a). An increase in the O4–Mn4–W1 angle would affect the two orbitals in opposite ways, with dyz being stabilized and dz2 being destabilized. The net effect would be an increase in the energy separation between the ground state and the first excited state, which, due to the fact the energy difference enters at the denominator of the equations used to calculated the ZFS parameters, leads to a smaller D value—and vice versa. The correlation between the O4–Mn4–W1 angle and the dyz–dz2 orbital energy difference is shown in Fig. S4.†
Given the above properties of SB3, it is expected that the interplay between the large zero field splitting and the high-spin state would either lead to a very broad EPR signal that would be difficult to detect at low microwave frequencies (X and Q-band), or to complex signals that underlie the signal of the final majority S3 state species (attributed to SA,W3), explaining why it has yet to be characterized.
Water binding in the S2–S3 transition
As discussed above, the SB3 structure can be identified with the NIR-active component of the S3 state, while simultaneously its spin state and unusually high local ZFS of the five-coordinate Mn4 ion support its assignment as the EPR “silent” species of the S3 state. It is evident that the SB3 structure does not represent the end point of the S2 to S3 transition, but the entry point to the S3 state. To complete the transition an additional water molecule needs to bind to the Mn4O5Ca cluster, rendering all Mn ions octahedral, as required by the SA,W3 structure identified and described in Cox et al.21 Having established a structurally defined sequence of events, we can address the question highlighted in the introduction (Fig. 2), namely how water binds to the OEC at this catalytic step.First of all, the requirement to progress through the closed-cubane SB3 intermediate cannot be reconciled in any obvious way with the water binding hypothesis depicted in Fig. 2a. The only way for this binding event to be realized would be for the SB3 state to isomerize to an “SA3” state, thus creating an available coordination site at Mn1. However, as explained above such a state is not stable and would exist only in the form of SA(−)2YZ˙, with a Mn(III) ion at the Mn1 position. Its associated Jahn–Teller axis along the internally available coordination site eliminates any driving force for binding of an additional ligand.
Instead, the requisite SB3 intermediate imposes the five-coordinate Mn4(IV) ion as the water binding site. Two possibilities exist in this respect. The first one involves the “internal” water binding depicted in Fig. 2b, with the incoming ligand probably originating from the W3 Ca-bound water, as suggested by Bovi et al.19 The second possibility is indicated by the wide O4–Mn4–W1 angle of SB3 (Fig. 5) and would involve “external” water binding to the OEC, at the Mn4 site previously occupied by W1 in the S2 state. Both possibilities would be consistent with the SB3 geometry and with the presence of distinct water channels that terminate at Mn4 and Ca (see Fig. 8).11,81,105–111
We have tried to locate a transition state for a W3-binding event or for coordination of the water that bridges W2 and W3, but our attempts have been unsuccessful. Possible reasons may be that the concerted rearrangements for this type of water binding cannot be adequately incorporated in our quantum cluster models, or that the immediate coordination product is disfavored energetically owing to structural congestion in the internal side of the cluster. To test the second possibility we tried to optimized directly the “internal” and “external” water coordination products for a variety of hydrogen-bonding interactions of the new water with its environment (see Table S2†). The results indicate that in the absence of any secondary rearrangements, “external” water binding is favored over “internal” water binding at Mn4 by ca. 10 kcal mol−1.112 Therefore, although the “internal” water binding pathway cannot be excluded in principle, the “external” pathway seems more easily realizable. Indeed, locating a transition state for this type of water binding proved straightforward.
The water molecule that binds to Mn4 according to this pathway was already positioned at close proximity to Mn4 by hydrogen bonding interaction with O4. The transition state displays an imaginary frequency which corresponds to formation of a bond between Mn4 and this new ligand (“Wnew”) with a simultaneous widening of the O4–Mn4–W1 angle and pivoting of OH(W1) towards OH(W2) (Fig. 9). The metal ion eventually adopts an octahedral geometry upon completion of the Wnew binding; the adduct is labeled SB,W3 according to the nomenclature conventions adopted in the present work. The energy barrier for this water addition was computed to be only 4.5 kcal mol−1. Interestingly, the addition product SB,W3 is predicted to be essentially isoenergetic with the reactants (stabilized by 0.2 kcal mol−1), indicating a fine balance between ligand field stabilization of the two distinct coordination geometries (distorted trigonal bipyramidal for SB3, distorted octahedral for SB,W3), the Mn4–Wnew bond energy, and the reorganization of the hydrogen-bonding network. We note that these energy values should be considered approximate because the present computational models do not fully include the response of the protein and of the surrounding hydrogen-bonding network to the structural rearrangements described above, and they also do not incorporate entropic contributions. Interestingly, despite not modeling exactly the same molecular process, the computed barrier is in good agreement with the activation energy of 5 kcal mol−1 reported by Vassiliev et al. for the end-point of this channel in their multiple steered molecular dynamics simulations of water permeation in PSII,109 showing that two vastly different theoretical approaches converge to a similar conclusion regarding the energetics of water access to the Mn4 site.
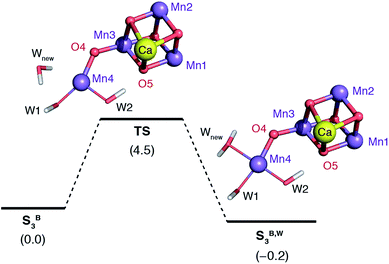 | ||
| Fig. 9 Schematic diagram for the binding of a water molecule (Wnew) to the Mn4 of a reduced-size model of SB3 (coordinating amino acids are omitted for clarity). Relative energies in kcal mol−1. | ||
Importantly, this type of water binding is not only favorable based on computed energetics, but is also aligned with recent experimental and theoretical studies of ammonia interaction with the OEC.53,55,113,114 These studies suggest that NH3 interacts with the inorganic cluster in the S2 state through coordination at Mn4, from precisely the same side of the cluster and at the same coordination site, that is, by displacement of W1. This supports the notion that NH3 accesses the cluster through the same water channel (referred to in the literature as “narrow channel”106 or “channel 2”111) suggested here to be involved in the delivery of Wnew during the S2–S3 transition. It can also explain the partial inhibition of NH3-treated PSII samples under steady-state conditions, in the sense that ammonia competes for a water binding site.115
We note that for any water binding mechanism (“internal” or “external”) that involves Mn4 as the water binding site of a closed-cubane species, a subsequent reorganization would be required to reach the end-point of the transition, the SA,W3 state (Fig. 1). This can be achieved, for example, with a transposition of the Mn3-oxo bonds as described in ref. 116 and 117. The associated barrier for this process is estimated at more than 10 kcal mol−1.116,117 This final step stabilizes the coordination of the new Mn-bound water by ca. 10 kcal mol−1,9,21 (or even more according to ref. 117) providing a driving force for second substrate binding/inclusion.
Identities of substrates
Even though the SB3 intermediate and the mode of water binding resulting from this work implicate a completely different sequence of events in the S2–S3 transition than that proposed by Siegbahn, the “end-point” SA,W3 species represents the same structural type and connectivity. Therefore, the subsequent steps for O–O bond formation may well be similar to what has been previously suggested by computational studies based on this type of S3-state model. However, even if the catalytic evolution of the OEC past the S3 state actually follows an oxo–oxyl coupling38,40,41,51 at the interior of the cluster, the water binding mechanism proposed in the present study has fundamentally different consequences for enzymatic regulation and the identity of substrates. This is because within the oxo–oxyl coupling scenario the sequence described above implies that the second substrate of the reaction (besides the O5 bridge49,53,118) is not the water molecule that binds during the S2 to S3 transition (Wnew) but may instead be W2, as suggested by the observation that W2 pivots in close proximity to O5 upon formation of the SB3 intermediate (Fig. 5).Experimental support for this assignment, as opposed to the binding of a non-crystallographic water as substrate at Mn1 (Fig. 2a), comes from membrane-inlet mass spectrometry (MIMS) measurements, which monitor the uptake of H218O into the product O2 molecule.119 MIMS data has shown that the exchange kinetics for both substrates are very similar for the S2 and S3 states,7,48,120 hence they are probably both associated with the Mn4O5Ca cofactor in the S2 and S3 states in the same way.48,120 Within the S2–S3 transition mechanism proposed here, the incoming water Wnew is unlikely to be a substrate. This can be in principle consistent with the experimental observations under two mechanistic scenarios for O–O bond formation: if the substrates are O5 and W2, as suggested by Cox and Messinger,48 then they represent an oxo bridge and a hydroxyl in both the S2 and the S3 states and thus are consistent with the above, while the same can be true if one substrate is instead a Ca-bound water that becomes involved in O–O bond formation as a nucleophile at a subsequent step of the catalytic cycle.34,35,37 In either case, the water that binds to form the final S3 state is not required to be a substrate.
Conclusions
We have investigated the S2–S3 transition in the catalytic cycle of the oxygen evolving complex with the aim to discover structural models that can explain the available spectroscopic observations on intermediates. Our results suggest that after formation of the tyrosyl radical in the S2 state, deprotonation of S2YZ˙ is a necessary condition for catalytic progression. Regardless of whether deprotonation has to precede Mn oxidation by the tyrosyl radical or whether the two processes are coupled, the outcome is the same, that is the formation of an S3-state intermediate with all-Mn(IV) ions, which contains a closed-cubane subunit and a terminal “dangler” five-coordinate Mn(IV) ion with a coordination geometry intermediate between square pyramidal and trigonal bipyramidal. We note that a trigonal bipyramidal dangler Mn has recently been suggested as the active form of the catalyst in the S4 state from model chemistry studies.42,43 However, the S2 to S3 intermediate proposed here is not the final S3 state and the putative activated oxygen (substrate) site is an equatorial ligand.The spectroscopic properties of this species explain fully the observations regarding the presence of a near-IR-active population in the S3 state of the OEC, without the need to invoke the presence of a Mn(III) ion. The formation of this species is also consistent with the OEC rearrangements proposed by molecular dynamics studies of Guidoni and coworkers.52 At this point of the catalytic cycle the OEC switches completely to a high-spin topology, which may be important for allowing subsequent low-barrier single product formation to proceed.
The presence of this species as a requisite intermediate in the S2–S3 transition implies that water binding takes place only after deprotonation and oxidation of the inorganic cluster. Thus, the new water molecule binds not to a Mn(III) site, but to a five-coordinate Mn(IV) ion. The transition state for a low-energy water binding mode from the external side of the cluster has been identified. This mode implicates the water channel of PSII which terminates close to the O4 bridge and the Mn4 ion of the cluster. The new water ligand binds to the five-coordinate Mn4(IV) at the “external” side of the inorganic cluster in a similar way that ammonia was shown to interact with the OEC in the S2 state,53,55,113,114 indicating a common delivery pathway. The most significant mechanistic implication is that the water molecule that binds in the S2–S3 transition does not serve as an immediate substrate, in agreement with the recent suggestion by Cox and Messinger.48 In addition, its binding is coupled to the proton shuttle terminating at the dangler Mn4, suggesting that Asp61 gates both proton release and water coordination in a concerted fashion.68,111,121,122
The S2–S3 progression model and water binding pathway proposed here form a good basis for structural rationalization of several complex experimental observations. These include experiments that require reinterpretation to account for the structural heterogeneity in the S3 state, and experiments on PSII mutants or PSII samples subjected to special chemical or physical treatments such as Ca2+/Sr2+ exchange. Structure-based explanations of such data will follow soon. Most importantly, the enhanced atomistic understanding of the S2–S3 transition provides strong support to the idea that structural flexibility and polymorphism is not an incidental feature of the OEC, but a means by which access to active forms of the catalyst is controlled and regulated.
Acknowledgements
We thank the Max Planck Society for financial support and the COST Action CM1305 ECOSTBio (Explicit Control Over Spin States in Technology and Biochemistry). FM was supported by the Swedish Research Council, the Knut and Alice Wallenberg Foundation and the Swedish Energy Agency.Notes and references
-
R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Blackwell, Oxford, 2001 Search PubMed
.
- J. P. McEvoy and G. W. Brudvig, Chem. Rev., 2006, 106, 4455–4483 CrossRef CAS PubMed
.
- V. Krewald, M. Retegan and D. A. Pantazis, Top. Curr. Chem., 2016, 371, 23–48 CrossRef PubMed
.
- N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596 CrossRef CAS PubMed
.
- H. Dau and M. Haumann, Coord. Chem. Rev., 2008, 252, 273–295 CrossRef CAS
.
- D. J. Vinyard, G. M. Ananyev and G. C. Dismukes, Annu. Rev. Biochem., 2013, 82, 577–606 CrossRef CAS PubMed
.
-
W. Hillier and J. Messinger, in Photosystem II. The Light-Driven Water:Plastoquinone Oxidoreductase, ed. T. Wydrzynski and K. Satoh, Springer, Dordrecht, 2005, pp. 567–608 Search PubMed
.
- B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457–475 CrossRef CAS PubMed
.
- V. Krewald, M. Retegan, N. Cox, J. Messinger, W. Lubitz, S. DeBeer, F. Neese and D. A. Pantazis, Chem. Sci., 2015, 6, 1676–1695 RSC
.
- M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2014, 517, 99–103 CrossRef PubMed
.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed
.
- B. Loll, J. Kern, W. Saenger, A. Zouni and J. Biesiadka, Nature, 2005, 438, 1040–1044 CrossRef CAS PubMed
.
- K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Science, 2004, 303, 1831–1838 CrossRef CAS PubMed
.
- M. Haumann, C. Müller, P. Liebisch, L. Iuzzolino, J. Dittmer, M. Grabolle, T. Neisius, W. Meyer-Klaucke and H. Dau, Biochemistry, 2005, 44, 1894–1908 CrossRef CAS PubMed
.
- A. Grundmeier and H. Dau, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 88–105 CrossRef CAS PubMed
.
- C. Glöckner, J. Kern, M. Broser, A. Zouni, V. Yachandra and J. Yano, J. Biol. Chem., 2013, 288, 22607–22620 CrossRef PubMed
.
- J. Yano and V. Yachandra, Chem. Rev., 2014, 114, 4175–4205 CrossRef CAS PubMed
.
- D. A. Pantazis, W. Ames, N. Cox, W. Lubitz and F. Neese, Angew. Chem., Int. Ed., 2012, 51, 9935–9940 CrossRef CAS PubMed
.
- D. Bovi, D. Narzi and L. Guidoni, Angew. Chem., Int. Ed., 2013, 52, 11744–11749 CrossRef CAS PubMed
.
- A. Haddy, Photosynth. Res., 2007, 92, 357–368 CrossRef CAS PubMed
.
- N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808 CrossRef CAS PubMed
.
- A. Boussac, A. W. Rutherford and M. Sugiura, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 576–586 CrossRef CAS PubMed
.
- A. Boussac, M. Sugiura, A. W. Rutherford and P. Dorlet, J. Am. Chem. Soc., 2009, 131, 5050–5051 CrossRef CAS PubMed
.
- N. Ioannidis and V. Petrouleas, Biochemistry, 2000, 39, 5246–5254 CrossRef CAS PubMed
.
- A. Boussac, M. Sugiura, Y. Inoue and A. W. Rutherford, Biochemistry, 2000, 39, 13788–13799 CrossRef CAS PubMed
.
- Y. Sanakis, N. Ioannidis, G. Sioros and V. Petrouleas, J. Am. Chem. Soc., 2001, 123, 10766–10767 CrossRef CAS PubMed
.
- N. Ioannidis and V. Petrouleas, Biochemistry, 2002, 41, 9580–9588 CrossRef CAS PubMed
.
- A. Boussac, M. Sugiura, T.-L. Lai and A. W. Rutherford, Philos. Trans. R. Soc., B, 2008, 363, 1203–1210 CrossRef CAS PubMed
.
- N. Ioannidis, G. Zahariou and V. Petrouleas, Biochemistry, 2006, 45, 6252–6259 CrossRef CAS PubMed
.
- A. Boussac, M. Sugiura, D. Kirilovsky and A. W. Rutherford, Plant Cell Physiol., 2005, 46, 837–842 CrossRef CAS PubMed
.
- J.-H. Su, K. G. V. Havelius, F. M. Ho, G. Han, F. Mamedov and S. Styring, Biochemistry, 2007, 46, 10703–10712 CrossRef CAS PubMed
.
- K. G. V. Havelius, J.-H. Su, G. Han, F. Mamedov, F. M. Ho and S. Styring, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 11–21 CrossRef CAS PubMed
.
- V. L. Pecoraro, M. J. Baldwin, M. T. Caudle, W.-Y. Hsieh and N. A. Law, Pure Appl. Chem., 1998, 70, 925–929 CrossRef CAS
.
- J. S. Vrettos, J. Limburg and G. W. Brudvig, Biochim. Biophys. Acta, Bioenerg., 2001, 1503, 229–245 CrossRef CAS
.
- J. P. McEvoy and G. W. Brudvig, Phys. Chem. Chem. Phys., 2004, 6, 4754–4763 RSC
.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, J. Am. Chem. Soc., 2008, 130, 3428–3442 CrossRef CAS PubMed
.
- D. Vinyard, S. Khan and G. Brudvig, Faraday Discuss., 2015 10.1039/c1035fd00087d
.
- P. E. M. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1999, 121, 117–127 CrossRef CAS
.
- P. E. M. Siegbahn, Chem.–Eur. J., 2008, 14, 8290–8302 CrossRef CAS PubMed
.
- P. E. M. Siegbahn, Acc. Chem. Res., 2009, 42, 1871–1880 CrossRef CAS PubMed
.
- P. E. M. Siegbahn, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1003–1019 CrossRef CAS PubMed
.
- R. Gupta, T. Taguchi, B. Lassalle-Kaiser, E. L. Bominaar, J. Yano, M. P. Hendrich and A. S. Borovik, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5319–5324 CrossRef CAS PubMed
.
- R. D. Britt, D. L. M. Suess and T. A. Stich, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5265–5266 CrossRef CAS PubMed
.
- T. Noguchi, Philos. Trans. R. Soc., B, 2008, 363, 1189–1195 CrossRef CAS PubMed
.
- H. Suzuki, M. Sugiura and T. Noguchi, Biochemistry, 2008, 47, 11024–11030 CrossRef CAS PubMed
.
- R. Pal, C. F. A. Negre, L. Vogt, R. Pokhrel, M. Z. Ertem, G. W. Brudvig and V. S. Batista, Biochemistry, 2013, 52, 7703–7706 CrossRef CAS PubMed
.
- H. Dau, P. Liebisch and M. Haumann, Phys. Scr., 2005, 2005, 844 CrossRef
.
- N. Cox and J. Messinger, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1020–1030 CrossRef CAS PubMed
.
- P. E. M. Siegbahn, J. Am. Chem. Soc., 2013, 135, 9442–9449 CrossRef CAS PubMed
.
- P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2012, 14, 4849–4856 RSC
.
- P. E. M. Siegbahn, Phys. Chem. Chem. Phys., 2014, 16, 11893–11900 RSC
.
- D. Narzi, D. Bovi and L. Guidoni, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8723–8728 CrossRef CAS PubMed
.
- M. Pérez Navarro, W. M. Ames, H. Nilsson, T. Lohmiller, D. A. Pantazis, L. Rapatskiy, M. M. Nowaczyk, F. Neese, A. Boussac, J. Messinger, W. Lubitz and N. Cox, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15561–15566 CrossRef PubMed
.
- M. Retegan, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2013, 9, 3832–3842 CrossRef CAS PubMed
.
- T. Lohmiller, V. Krewald, M. Pérez Navarro, M. Retegan, L. Rapatskiy, M. M. Nowaczyk, A. Boussac, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, Phys. Chem. Chem. Phys., 2014, 16, 11877–11892 RSC
.
- M. Retegan, N. Cox, W. Lubitz, F. Neese and D. A. Pantazis, Phys. Chem. Chem. Phys., 2014, 16, 11901–11910 RSC
.
- W. Ames, D. A. Pantazis, V. Krewald, N. Cox, J. Messinger, W. Lubitz and F. Neese, J. Am. Chem. Soc., 2011, 133, 19743–19757 CrossRef CAS PubMed
.
- F. Neese, WIREs Computational Molecular Science, 2012, 2, 73–78 CrossRef CAS
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS
.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS
.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef
.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- A. Klamt and D. Schüürman, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC
.
- I. Rivalta, M. Amin, S. Luber, S. Vassiliev, R. Pokhrel, Y. Umena, K. Kawakami, J. R. Shen, N. Kamiya, D. Bruce, G. W. Brudvig, M. R. Gunner and V. S. Batista, Biochemistry, 2011, 50, 6312–6315 CrossRef CAS PubMed
.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS
.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, E. Bill, W. Lubitz, J. Messinger and F. Neese, Chem.–Eur. J., 2009, 15, 5108–5123 CrossRef CAS PubMed
.
- M. Orio, D. A. Pantazis, T. Petrenko and F. Neese, Inorg. Chem., 2009, 48, 7251–7260 CrossRef CAS PubMed
.
- F. Neese, W. Ames, G. Christian, M. Kampa, D. G. Liakos, D. A. Pantazis, M. Roemelt, P. Surawatanawong and S. F. Ye, Adv. Inorg. Chem., 2010, 62, 301–349 CrossRef CAS
.
- N. Cox, W. Ames, B. Epel, L. V. Kulik, L. Rapatskiy, F. Neese, J. Messinger, K. Wieghardt and W. Lubitz, Inorg. Chem., 2011, 50, 8238–8251 CrossRef CAS PubMed
.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS
.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS
.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS
.
- M. Retegan, N. Cox, D. A. Pantazis and F. Neese, Inorg. Chem., 2014, 53, 11785–11793 CrossRef CAS PubMed
.
- M. Chrysina, G. Zahariou, N. Ioannidis and V. Petrouleas, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 487–493 CrossRef CAS PubMed
.
- A. Klauss, M. Haumann and H. Dau, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16035–16040 CrossRef CAS PubMed
.
-
F. M. Ho, in Molecular Solar Fuels, ed. T. J. Wydrzynski and W. Hillier, The Royal Society of Chemistry, Cambridge, 2012, pp. 208–248 Search PubMed
.
- H. Ishikita, W. Saenger, B. Loll, J. Biesiadka and E.-W. Knapp, Biochemistry, 2006, 45, 2063–2071 CrossRef CAS PubMed
.
- A. Robertazzi, A. Galstyan and E. W. Knapp, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1316–1321 CrossRef CAS PubMed
.
- B. Lassalle-Kaiser, C. Hureau, D. A. Pantazis, Y. Pushkar, R. Guillot, V. K. Yachandra, J. Yano, F. Neese and E. Anxolabehere-Mallart, Energy Environ. Sci., 2010, 3, 924–938 CAS
.
- The structural models used in the present work assume that the proton has left the system, as indicated by the minus charge used on the state designations, and is no longer residing on Asp61.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS
.
- I. Mayer, Int. J. Quantum Chem., 1984, 26, 151–154 CrossRef CAS
.
- A. Boussac and A. W. Rutherford, Biochemistry, 1988, 27, 3476–3483 CrossRef CAS
.
- A. Boussac, J. L. Zimmermann and A. W. Rutherford, Biochemistry, 1989, 28, 8984–8989 CrossRef CAS PubMed
.
- M. Sivaraja, J. Tso and G. C. Dismukes, Biochemistry, 1989, 28, 9459–9464 CrossRef CAS PubMed
.
- T. H. Parsell, R. K. Behan, M. T. Green, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2006, 128, 8728–8729 CrossRef CAS PubMed
.
- S. A. Cook and A. S. Borovik, Acc. Chem. Res., 2015, 48, 2407–2414 CrossRef CAS PubMed
.
- T. Matsukawa, H. Mino, D. Yoneda and A. Kawamori, Biochemistry, 1999, 38, 4072–4077 CrossRef CAS PubMed
.
- A. Boussac, J.-J. Girerd and A. W. Rutherford, Biochemistry, 1996, 35, 6984–6989 CrossRef CAS PubMed
.
- A. Boussac, S. Un, O. Horner and A. W. Rutherford, Biochemistry, 1998, 37, 4001–4007 CrossRef CAS PubMed
.
- R. Baxter, E. Krausz, T. Wydrzynski and R. J. Pace, J. Am. Chem. Soc., 1999, 121, 9451–9452 CrossRef CAS
.
- P. J. Smith, S. Peterson, V. M. Masters, T. Wydrzynski, S. Styring, E. Krausz and R. J. Pace, Biochemistry, 2002, 41, 1981–1989 CrossRef CAS PubMed
.
- S. Chattopadhyay, R. A. Geiger, G. Yin, D. H. Busch and T. A. Jackson, Inorg. Chem., 2010, 49, 7530–7535 CrossRef CAS PubMed
.
- K. Bane, R. A. Geiger, S. A. Chabolla and T. A. Jackson, Inorg. Chim. Acta, 2012, 380, 135–140 CrossRef CAS
.
- S. Mukherjee, J. A. Stull, J. Yano, T. C. Stamatatos, K. Pringouri, T. A. Stich, K. A. Abboud, R. D. Britt, V. K. Yachandra and G. Christou, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2257–2262 CrossRef CAS PubMed
.
- V. Krewald, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2013, 135, 5726–5739 CrossRef CAS PubMed
.
- J. H. A. Nugent, S. Turconi and M. C. W. Evans, Biochemistry, 1997, 36, 7086–7096 CrossRef CAS PubMed
.
- C. Duboc and M.-N. Collomb, Chem. Commun., 2009, 2715–2717 RSC
.
- R. Gupta, T. Taguchi, A. S. Borovik and M. P. Hendrich, Inorg. Chem., 2013, 52, 12568–12575 CrossRef CAS PubMed
.
- J. W. Murray and J. Barber, J. Struct. Biol., 2007, 159, 228–237 CrossRef CAS PubMed
.
- F. M. Ho and S. Styring, Biochim. Biophys. Acta, Bioenerg., 2008, 1777, 140–153 CrossRef CAS PubMed
.
- F. M. Ho, Photosynth. Res., 2008, 98, 503–522 CrossRef CAS PubMed
.
- A. Gabdulkhakov, A. Guskov, M. Broser, J. Kern, F. Müh, W. Saenger and A. Zouni, Structure, 2009, 17, 1223–1234 CrossRef CAS PubMed
.
- S. Vassiliev, T. Zaraiskaya and D. Bruce, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 1671–1678 CrossRef CAS PubMed
.
- S. Vassiliev, P. Comte, A. Mahboob and D. Bruce, Biochemistry, 2010, 49, 1873–1881 CrossRef CAS PubMed
.
- S. Vassiliev, T. Zaraiskaya and D. Bruce, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 1148–1155 CrossRef CAS PubMed
.
- For completeness, we compared the possible product for insertion of water at the Mn1 site of an open-cubane topology. This was found to be the least favorable binding mode, more than 12 kcal mol−1 higher than the water binding at Mn4 from the external side of the cluster, and requires a proton transfer to the O5 bridge in order to be stabilized.
- J. Schraut and M. Kaupp, Chem.–Eur. J., 2014, 20, 7300–7308 CrossRef CAS PubMed
.
- P. H. Oyala, T. A. Stich, R. J. Debus and R. D. Britt, J. Am. Chem. Soc., 2015, 137, 8829–8837 CrossRef CAS PubMed
.
- A. Boussac, A. W. Rutherford and S. Styring, Biochemistry, 1990, 29, 24–32 CrossRef CAS PubMed
.
- M. Shoji, H. Isobe and K. Yamaguchi, Chem. Phys. Lett., 2015, 636, 172–179 CrossRef CAS
.
- M. Capone, D. Bovi, D. Narzi and L. Guidoni, Biochemistry, 2015, 54, 6439–6442 CrossRef CAS PubMed
.
- L. Rapatskiy, N. Cox, A. Savitsky, W. M. Ames, J. Sander, M. M. Nowaczyk, M. Rögner, A. Boussac, F. Neese, J. Messinger and W. Lubitz, J. Am. Chem. Soc., 2012, 134, 16619–16634 CrossRef CAS PubMed
.
- J. Messinger, M. Badger and T. Wydrzynski, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 3209–3213 CrossRef CAS
.
- H. Nilsson, T. Krupnik, J. Kargul and J. Messinger, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1257–1262 CrossRef CAS PubMed
.
- R. J. Debus, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 19–34 CrossRef CAS PubMed
.
- L. Vogt, D. J. Vinyard, S. Khan and G. W. Brudvig, Curr. Opin. Chem. Biol., 2015, 25, 152–158 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc03124a |
| This journal is © The Royal Society of Chemistry 2016 |