Rapid oxidative hydrogen evolution from a family of square-planar nickel hydride complexes

Abstract

A series of square-planar nickel hydride complexes supported by bis(phosphinite) pincer ligands with varying substituents (–OMe, –Me, and –Bu^t) on the pincer backbone have been synthesized and completely characterized by NMR spectroscopy, IR spectroscopy, elemental analysis, and X-ray crystallography. Their cyclic voltammograms show irreversible oxidation peaks (peak potentials from 101 to 316 mV vs. Fc⁺/Fc) with peak currents consistent with overall one-electron oxidations. Chemical oxidation by the one-electron oxidant Ce(NBu₄)₂(NO₃)₆ was studied by NMR spectroscopy, which provided quantitative evidence for post-oxidative H₂ evolution leading to a solvent-coordinated nickel(II) species with the pincer backbone intact. Bulk electrolysis of the unsubstituted nickel hydride (3a) showed an overall one-electron stoichiometry and gas chromatographic analysis of the headspace gas after electrolysis further confirmed stoichiometric production of dihydrogen. Due to the extremely high rate of the post-oxidative chemical process, electrochemical simulations have been used to establish a lower limit of the bimolecular rate constant (k_f > 10⁷ M⁻¹ s⁻¹) for the H₂ evolution step. To the best of our knowledge, this is the fastest known oxidative H₂ evolution process observed in transition metal hydrides. Quantum chemical calculations based on DFT indicate that the one-electron oxidation of the nickel hydride complex provides a strong chemical driving force (−90.3 kcal mol⁻¹) for the production of H₂ at highly oxidizing potentials.

---

Introduction

Virtual H₂ carriers such as alcohols and saturated N-heterocycles that are liquids at room temperature constitute important alternatives to the use of H₂ in commercial fuel cells.^1–3 They are easy to store compared to gaseous dihydrogen and in principle, could be part of a reversible fuel cell with the dehydrogenated products also being liquids at room temperature. Developing catalysts containing earth-abundant elements to dehydrogenate these fuels to produce protons and electrons ergoneutrally, is therefore relevant for fuel cell applications.^4–6

Scheme 1 shows a conceptual pathway for the dehydrogenation of organic fuels involving homogenous molecular catalysts.⁴ Dehydrogenation of the fuel in the presence of a base typically leads to transition metal hydride intermediates, ubiquitous in transfer hydrogenation processes,^7–9 which shuttle H₂ equivalents from a sacrificial donor (for example, an alcohol) to an acceptor molecule such as a ketone. Subsequent electro-oxidation and deprotonation of the metal hydride, a two-electron one-proton process, results in a solvent-coordinated species, as shown in Scheme 1. To design an energy-efficient electrocatalytic cycle for this transformation, it is important that both of the steps shown in Scheme 1 are close to ergoneutrality. In this work, we focused on the latter step, i.e. the electrochemical oxidation of a series of metal hydride complexes.

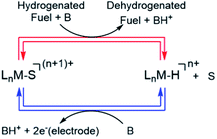Scheme 1 Electrocatalytic cycle for electro-dehydrogenation of H-containing liquid fuels (L_n = ligand, S = coordinating solvent, M = transition metal, n = integer, B = base).

The electro-oxidation of metal hydrides has been a subject of interest due to its predominantly irreversible nature which often suggests a subsequent fast chemical step leading to undesired products.^10–13 Tilset and coworkers have reported that electron removal from the metal center in group VI hydrides enhances the acidity of the hydride by approximately 20 pK_a units leading to deprotonation, forming a reduced metal species that would spontaneously lose another electron at the operating potential, thereby constituting an overall two electron process.^10,14 Depending on the pK_a of the oxidized hydride, a suitable base can act as the proton acceptor and a solvent molecule such as acetonitrile as a ligand that stabilizes the coordinatively unsaturated metal species resulting from proton loss, as shown in eqn (1) for a generic neutral hydride complex.^10,14,15

In the absence of a suitable base the stoichiometry of the electrochemical oxidation of the metal hydride has been found to be an overall one-electron process in a few systems rather than the two-electron process discussed above.^10,13 One of the observed outcomes of this one-electron process has been H₂ evolution^13,16,17 with a net oxidation of one electron per metal hydride, as shown in eqn 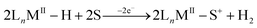(2).

One mechanism of H₂ evolution has been suggested by Collman et al.¹³ in the case of a porphyrin-based Ru-hydride system. They hypothesize that two molecules of the oxidized Ru-hydride converge in an associative fashion to form a bridging [Ru(III)–H⋯H–Ru(III)] complex which subsequently loses H₂ by solvent coordination to yield two equivalents of the Ru(II)-solvento species, the overall transformation shown in eqn (2). The other mechanism that has been evoked¹⁰ is deprotonation–oxidation, wherein a neutral metal hydride accepts a proton from the cation radical to make an H₂ complex. A solvent molecule then displaces H₂ from the latter, and the Ru(I) species loses an electron to the electrode and coordinates a solvent, leading to the same overall stoichiometry shown in eqn (2).

In this work, we have studied the oxidation of a new family of d⁸ square-planar nickel hydride complexes supported by bis(phosphinite) pincer ligands (POCOP ligands).^18–21 This work expands the understanding of metal hydride oxidation. These nickel pincer complexes were synthesized and completely characterized by ¹H, ³¹P, ¹³C NMR spectroscopy, solid-state IR spectroscopy, elemental analysis, and X-ray crystallography. One-electron oxidation of all these complexes was found to be irreversible, and the nature of the post-oxidative chemical transformations leading to facile H₂ evolution were explored by a combination of chemical and electrochemical studies, density functional theory (DFT) based calculations and electrochemical simulations. The bimolecular rate constant for H₂ evolution was found to be at least 10⁷ M⁻¹ s⁻¹ which is, to the best of our knowledge, the fastest known oxidative H₂ evolution reaction observed in transition metal hydride complexes.^13,22 This reactivity highlights the challenges of developing earth-abundant metal hydride complexes as catalytic intermediates in the ergoneutral oxidation of liquid fuels.

Results and discussion

Synthesis and characterization of nickel pincer complexes

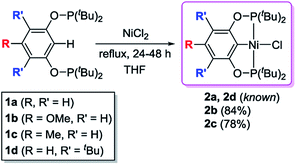
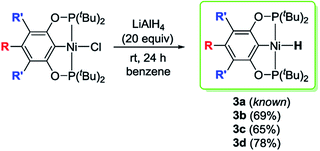
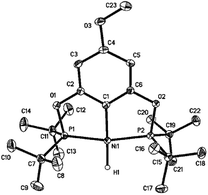
The desired nickel pincer hydrides 3a–d were successfully synthesized in three consecutive steps following a procedure similar to the one reported by Guan et al.²³ Related bis(phosphinite) pincer ligands (1a–d, POCOP ligands) were prepared by Brookhart's method involving the treatment of substituted resorcinol derivatives with two equivalents of P(^tBu)₂Cl in the presence of NaH.^24,25 These ligands require handling under inert atmosphere to avoid hydrolysis, which takes place in ambient atmosphere.²⁶ Nickel pincer chlorides 2a and 2d were prepared through cyclometalation of 1a and 1d with anhydrous NiCl₂.^23,25 Nickel chlorides 2b and 2c were synthesized similarly (78–84% isolated yields) and characterized by ¹H, ³¹P{¹H}, ¹³C{¹H} NMR spectroscopy, and elemental analysis (Scheme 2). Solid-state structures of 2b and 2c were also determined by X-ray crystallography (see ESI†). Both of the complexes adopt a square planar geometry around the Ni(II) center, a typical structure for this type of pincer complexes reported by Zargarian²⁶ and Guan.²³ Alternatively, 2a–d could also be formed by refluxing a mixture of a resorcinol derivative, P(^tBu)₂Cl, dimethylaminopyridine (DMAP), NiCl₂, and 1,4-dioxane (solvent) in a single reaction vessel for several days (Scheme 3). Although this method avoids the separation of the air-sensitive POCOP ligands, the corresponding isolated yields of 2a–d were much lower (19–37%).

Scheme 2 Synthesis of the ^tBu[POCOP]NiCl complexes.

Scheme 3 Single-pot synthesis of the ^tBu[POCOP]NiCl complexes.

Reactions of 2a–d with excess LiAlH₄ (20 equivalents) at room temperature generated the desired nickel pincer hydride complexes 3a–d as light yellow solids in good isolated yields (65–78%, Scheme 4). Complexes 3b–d are not reported in the literature and therefore were completely characterized by ¹H, ³¹P{¹H}, ¹³C{¹H} NMR spectroscopy, IR spectroscopy, and elemental analysis. The ¹H NMR spectra of 3b–d recorded in C₆D₆ revealed the characteristic Ni–H resonances as triplets at δ −8.06 (²J_H–P = 52 Hz), −7.98 ppm (²J_H–P = 52 Hz), and −7.90 (²J_H–P = 52 Hz), respectively. The singlet resonance observed in the ³¹P{¹H} NMR spectra of all of the nickel hydride species is consistent with a C₂-symmetric structure. Solid-state IR spectroscopy showed distinct, moderately strong Ni–H stretching bands near 1791 cm⁻¹ (for 3b), 1768 cm⁻¹ (for 3c), and 1810 cm⁻¹ (for 3d). Compounds 3b–d have been further characterized by X-ray crystallography (Fig. 1, see ESI†). The hydride ligands in all of these nickel hydride complexes were located and refined. Crystal data and refinement parameters for the nickel hydride complexes are given in Table 1.

Scheme 4 Synthesis of the ^tBu[POCOP]NiH complexes.

Fig. 1 X-ray crystal structure of 3b (50% probability level). Selected bond lengths (Å) and angles (deg): Ni(1)–H(1) 1.47(2), Ni(1)–C(1) 1.8876(14), Ni(1)–P(1) 2.1155(6), Ni(1)–P(2) 2.1161(6), P(1)–Ni(1)–P(2) 165.288(17), C(1)–Ni(1)–H(1) 177.9(8), P(1)–Ni(1)–H(1) 95.7(8), P(2)–Ni(1)–H(1) 99.0(8).

Table 1 Crystal data and refinement parameters for 3b–d

	3b	3c	3d
Empirical formula	C23H42O3P2Ni	C23H42O2P2Ni	C30H56O2P2Ni
Crystal system	Monoclinic	Monoclinic	Monoclinic
Space group	P21/n	P21/n	P21/n
a, E	9.756(3)	9.528(3)	15.131(3)
b, E	19.408(6)	20.201(7)	12.589(2)
c, E	14.026(4)	13.4341(5)	17.529(3)
α, deg	90	90	90
β, deg	104.528(6)	100.908(7)	106.717(4)
γ, deg	90	90	90
Volume, E^3	2570.9(14)	2539.1(16)	3197.8(11)
Z	4	4	4
No. of data collected	64 153	80 520	66 747
No. of unique data, Rint	14 241, 0.0784	13 995, 0.0707	14 087, 0.0980
R 1, wR2 (I > 2σ(I))	0.0493, 0.0990	0.0571, 0.1174	0.0527, 0.1088
R 1, wR2 (all data)	0.0949, 0.1152	0.0868, 0.1264	0.0988, 0.1271

---

Synthesis of the nickel pincer acetonitrile complex

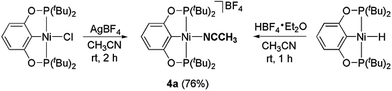
The related nickel pincer acetonitrile complex (4a) was independently synthesized from two different routes (Scheme 5). In one of the methods, the chloride ligand in 2a was abstracted by an Ag(I) salt in acetonitrile to form the desired complex 4a. Tetrafluoroborate (BF₄⁻), remains as a counter-anion. In the second method, the corresponding nickel hydride complex 3a was protonated by HBF₄·Et₂O to afford complex 4a. In this reaction, H₂ is released as the only other byproduct. Complex 4a has been characterized by ¹H, ³¹P{¹H}, ¹³C{¹H} NMR spectroscopy, IR spectroscopy, and elemental analysis. In the ¹H NMR spectrum, the resonance corresponding to the Ni–NCCH₃ appeared at δ 2.63 as a broad triplet. A strong C≡N stretch for the acetonitrile moiety present in complex 4a was observed at 2290 cm⁻¹ in the IR spectrum. A similar nickel acetonitrile complex was reported by Crabtree and Hazari during their investigation related to the electrocatalytic production of hydrogen.²⁷

Scheme 5 Synthesis of the nickel pincer acetonitrile complexes.

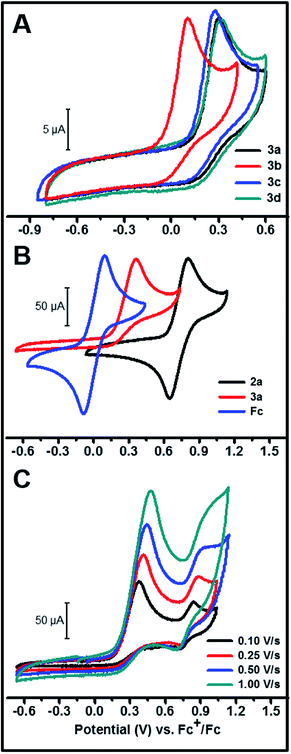
Electrochemistry of the nickel hydride complexes

The cyclic voltammograms of the hydride complexes 3a–d are shown in Fig. 2A. A mixture of THF–MeCN 1 : 4 by volume respectively, was employed as the solvent mixture for all electrochemistry experiments as 3a–d are only partially soluble in MeCN. All of these complexes show an irreversible oxidation peak, assigned to a metal-centered oxidation, at slightly different peak potentials depending on the substituent on the aromatic ring (peak potentials ranging from 101 to 316 mV vs. Fc⁺/Fc). The complete irreversibility in the CV of these hydride complexes suggests a fast chemical step involving a hydride, proton or H-atom transfer following initial electron transfer from the molecule to the electrode.²⁸ The peak areas in these CVs are comparable to the peak area observed in an equimolar solution of ferrocene or the corresponding chloride complex 2a (Fig. 2B and S4†) under similar conditions. This provides evidence that the peak is due to a one-electron oxidation and argues against the deprotonation pathway in eqn (1), which would result in a two-electron oxidation.

Fig. 2 (A) CV of 1 mM solutions of 3a–d in 1 : 4 by volume THF–MeCN (0.1 M TBABF₄, TBA = tetra-N-butyl ammonium) at 250 mV s⁻¹. (B) Comparison of CVs of 4 mM solutions of 2a, 3a and ferrocene in 1 : 4 by volume THF–MeCN (0.1 M TBABF₄) measured at a scan rate of 250 mV s⁻¹. (C) CV of 3a beyond the first one-electron oxidation in THF (0.1 M TBABF₄) for different scan rates.

On scanning further positive from the peak potential of the initial Ni(III)H/Ni(II)H oxidation in the CV, another wave was observed ca. 0.5 V positive of the initial wave (Fig. 2C). This second partially reversible wave probably corresponds to the Ni(III/II) couple of a new species generated during the first oxidation, with a ligand being less donating compared to the hydride ligand in 3a, as evidenced by the more positive E_1/2 of this couple. The magnitude of this second oxidation peak relative to the first decreases with decreasing scan rate suggesting that this second Ni(II) species is partially converting to another species on the seconds time scale.

To probe the nature of the products formed upon oxidation, a one-electron chemical oxidant, Ce(NBu₄)₂(NO₃)₆,²⁹ was added in 1/3 equivalent increments to 3a dissolved in a 50 : 50 mixture of CD₃CN and C₆D₆ in a J. Young NMR tube and the resultant changes monitored by ¹H and ³¹P{¹H} NMR spectroscopy (Fig. 3). The triplet centered at δ −8.39 (J = 52 Hz) corresponds to the hydride resonance in 3a. With incremental addition of the Ce(IV) oxidant to 3a, we observed a gradual disappearance of the hydride resonance of 3a from the ¹H NMR spectrum. In the ³¹P{¹H} NMR spectrum, the intensity of the peak at δ 221.42 ppm corresponding to 3a also decreased with the addition of the chemical oxidant. After the addition of 1 equivalent of the Ce(IV) salt, the resonance for 3a was completely replaced with the new resonance at δ 199.57 ppm corresponding to the nickel-solvento species 4a (Fig. 3). After the initial addition of the Ce(IV) salt, bubbles appeared in the NMR tube as well as a singlet peak in the ¹H NMR spectrum (δ 4.42 ppm, Fig. 3 inset) corresponding to H₂ production.³⁰ To quantify the amount of H₂ produced, 3a was taken in two NMR tubes (5 mg each, 0.011 mmol) each sealed with a septum and dissolved in 0.2 mL d⁸-THF. Sub-stoichiometric amounts of 2,6-dimethylbenzoic acid and Ce(NBu₄)₂(NO₃)₆, each in 0.8 mL of CD₃CN were added to the first and second NMR tubes respectively. The integration of the H₂ peak in the ¹H NMR spectrum (δ 4.55 ppm in this solvent mixture) was quantified using acid addition to the second test tube as a calibrant (Fig. S1†). To be noted is the fact that the calibration sample contains twice the amount of H₂ per Ni–H as we are using an acid as the proton source. By this method, H₂ production on one electron oxidation by Ce(IV) amounted to 95%, which corresponds to the stoichiometry in eqn (2). These observations provide strong evidence for the oxidative H₂ evolution pathway (eqn (2)).

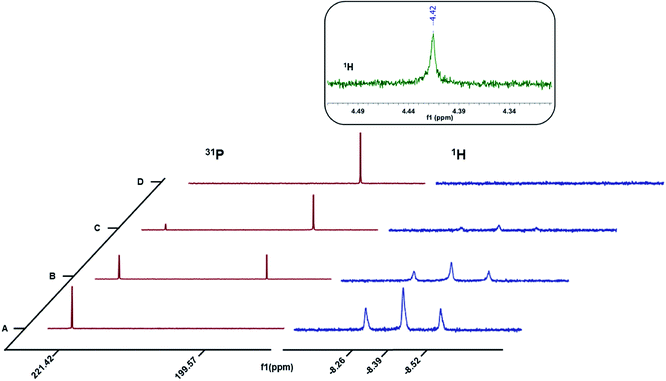Fig. 3 ¹H and ³¹P{¹H} NMR spectra for the oxidation of 3a with ca. (A) 0 equiv. (B) 0.33 equiv. (C) 0.66 equiv. and (D) 1 equiv. Ce(NBu₄)₂(NO₃)₆.

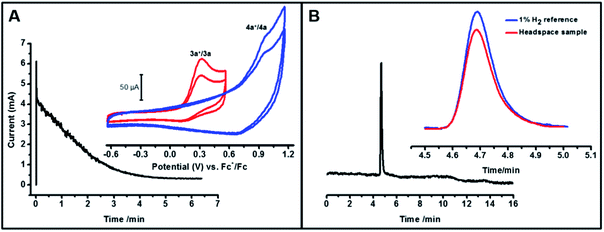
To further quantify the electron stoichiometry and the amount of dihydrogen produced, we performed a constant potential electrolysis of 3 mL of a 1.23 mM solution of 3a in THF : MeCN (1 : 4 by volume), maintaining a potential ca. 200 mV positive of the Ni(III)H/Ni(II)H peak potential. For this amount of 3a and a net one-electron oxidation, the total charge to be passed for 100% faradaic efficiency would be 356 mC. Integrating the current versus time plot for the electrolysis (Fig. 4A) gave 354 mC, confirming a net one-electron stoichiometry with respect to 3a for the oxidation. After the electrolysis was complete, a 3 mL aliquot of the headspace above the solution was analyzed by gas chromatography. The results shown in Fig. 4B clearly indicate hydrogen production based on the retention time of a standard 1% H₂ gas sample. Comparison of the areas of the sample versus the reference gave an H₂ partial pressure of at least 0.007 atm in the 4.5 mL of headspace which corresponds to 1.3 × 10⁻³ mmol H₂ and a yield of at least 70% based on eqn (2). The yield is a lower bound given the solubility of H₂ in the solvent mixture as well as possible crossover between the two chambers of the H-cell through diffusion. The new peak in the post-electrolysis cyclic voltammogram shown in Fig. 4A inset (blue) is tentatively assigned to the Ni-solvento species (4a) formed during the electrolysis (Fig. S7†).

Fig. 4 (A) Current vs. time plot for the bulk electrolysis of 3a in a 1 : 4 THF–MeCN solvent mixture in presence of 0.1 M TBABF₄. Constant potential electrolysis was performed at 500 mV vs. Fc⁺/Fc which is ca. 200 mV positive of the peak oxidation potential of 3a. Inset shows the CVs of the sample taken before (red) and after (blue) the electrolysis experiment at 1 V s⁻¹, which shows the formation of 4a. (B) Gas chromatogram for the headspace of the solution after bulk electrolysis. Inset shows the magnified image of the H₂ peak superimposed on the 1% H₂ standard.

Mechanistic insights from DFT-based calculations

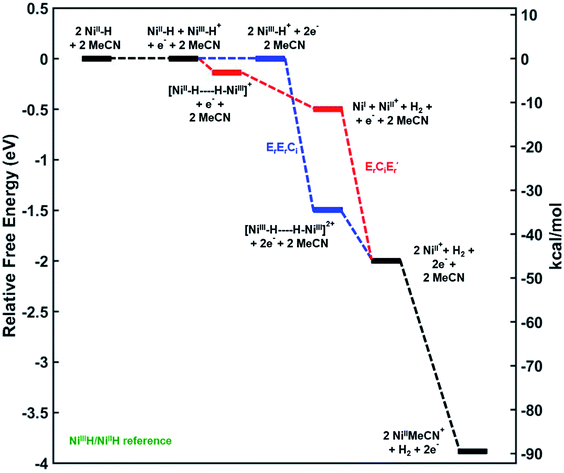
In order to better understand the mechanism of the oxidative H₂ evolution process, we calculated the relative free energies of plausible intermediates along two different reaction coordinates corresponding to the disproportionation and deprotonation–oxidation mechanisms (Fig. 5). The relative free energies of all intermediates are referenced to the 3a⁺/3a couple. As a result, note that the free energies of 3a⁺ and 3a are the same in Fig. 5.³¹

Fig. 5 Reaction coordinate diagram with mechanisms E_rE_rC_i (in blue) and E_rC_iE_r′ (in red) leading to H₂ evolution. Relative free energies given in eV and kcal mol⁻¹. Level of theory: Gaussian09™/M06/LANL2DZ(Ni)/6-311G(d) (C,H,O,N,P)/SMD(MeCN). ‘E’ and ‘C’ denote electrochemical and chemical steps respectively, and ‘r’ and ‘i’ denote reversible and irreversible steps respectively.

Mechanism 1: bimolecular disproportionation (E_rE_rC_i). Two Ni(III)–H cations are generated from the oxidation of two molecules of 3a at the 3a⁺/3a potential which is taken as the reference for comparing the relative free energies of all other intermediates. From two molecules of Ni(III)–H, the formation of an H₂-bridged structure (see ESI†) is energetically downhill by −34.8 kcal mol⁻¹ which is the highest driving force in the overall transformation. H₂ loss from this structure to generate two cationic coordinatively unsaturated Ni(II) species is again downhill by about −11.5 kcal mol⁻¹. The final step involving ligation of these species by MeCN is a very energetically favorable process leading to the products.

Mechanism 2: deprotonation–oxidation (E_rC_iE_r′). As seen in Fig. 5 the deprotonation of the protic H from the newly generated Ni(III)–H cation by the hydridic H of a Ni(II)–H in the depletion layer of the electrode could also result in H₂ evolution. However, formation of the bridging structure (see ESI†) in this case is downhill only by ca. −3 kcal mol⁻¹. H₂ dissociation from this bimolecular intermediate leads to a coordinatively unsaturated neutral Ni(I) species and the cationic Ni(II) species. A second electron-transfer step oxidizing the Ni(I) to Ni(II), which is energetically favorable at the (Ni(III)H/Ni(II)H) electrode potential, followed by MeCN coordination yields the products. The last step is the same as in mechanism 1.

From the electrode potential of the Ni(III)H/Ni(II)H couple, all intermediates in either pathway are energetically downhill. However, the association step to form the Ni(III)–Ni(III) H₂ bridging structure has a much higher driving force (−34.8 kcal mol⁻¹) compared to the analogous step in mechanism 2 (−3.2 kcal mol⁻¹).

Changes in the pK_a and BDFE of 3a on one-electron oxidation were computed at the same level of theory as above using isodesmic reaction schemes with reference compounds (see Computational details). The results shown in Tables S1 and S2† indicate substantial thermodynamic activation towards deprotonation as well as H-atom abstraction (see ESI†) which is in line with the high exergonicity of the whole process at the (Ni(III)H/Ni(II)H) potential leading to H₂ evolution. Our calculations predict a decrease in pK_a of about 46 units on going from Ni(II)H to the Ni(III)H cation (Table S2†). This result was cross-verified with five other density functionals ranging from local GGA to hybrid-GGA^32,33 and was found to be consistent (Fig. S8†). This difference in pK_a is much higher than the values reported in the literature for octahedral Ru hydrides.¹⁰ This result is consistent with the high oxidation potential of the parent hydride 3a as compared to those reported for the Ru hydrides.

Given the calculated pK_a values of the Ni(III)H cation we expect deprotonation of the metal hydride by the solvent. However, our observation of quantitative H₂ production (vide supra) from the Ni complexes provides evidence against any net contribution from deprotonation of the Ni(III)H cation by the solvent. The likely pathway involves half the nickel hydrides deprotonating after oxidation at the electrode surface, with the released protons reacting with Ni(II) hydride diffusing towards the electrode surface in the depletion layer to make H₂, followed by the oxidation of the deprotonated Ni at the electrode to a Ni(II) species (E_rC_iE_r′).

Electrochemical simulation to obtain rate constant for the following chemical reaction

Fast scan-rate CV experiments using ultramicroelectrodes were performed in an attempt to observe a return wave after oxidation of 3a (Fig. S2†), which would then enable a reliable estimate of the rate of the following chemical reaction. However, the CV's were irreversible up to a scan-rate of 2000 V s⁻¹. Concentration dependent CVs down to 0.125 mM 3a also did not show a return reduction wave (Fig. S3†). Even higher scan rates or lower concentrations did not yield anything substantive due to the ratio of faradaic to capacitive current becoming too low for meaningful interpretations. We therefore simulated our electrochemical data in DigiElch 7™ to estimate the lower limit of the rate of the following chemical reaction. CVs were simulated from two different regimes, viz. scan rate of 4 V s⁻¹ using a 3 mm diameter disk electrode, and scan rate of 400 V s⁻¹ using an 11 μm diameter disk electrode were chosen (see ESI† for complete details of the simulations). 400 V s⁻¹ was the highest scan rate at which the faradaic and capacitive components of the current could be reasonably separated.

To estimate the standard electron-transfer rate constant k_s, experimentally measured CVs of the corresponding chloride complex 2a were simulated with a planar 1D semi-infinite diffusion model as implemented in DigiElch 7™, shown in Fig. S4.† Estimates of the lower limit of the uncompensated resistance of the cells, R_u, were made based on the cell geometry and published electrolyte conductivities.³⁴ A sensitivity analysis was then performed to estimate the range of R_u and k_s that fit this data (see ESI† for details).

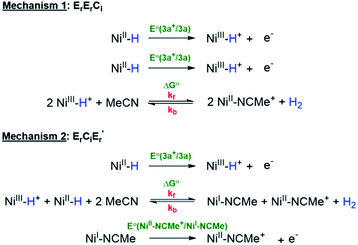
Using this information, CVs of 3a were simulated according to both of the mechanisms (Scheme 6) viz. bimolecular disproportionation (E_rE_rC_i) and deprotonation-oxidation (E_rC_iE_r′) and the results are summarized in Fig. 6 and Table 2. The reported k_f and E° correspond to approximately the lowest values above which there is no return wave in the CVs, which was verified by sensitivity analysis of the simulation (Fig. S5b†).

Scheme 6 Mechanisms for hydrogen production.

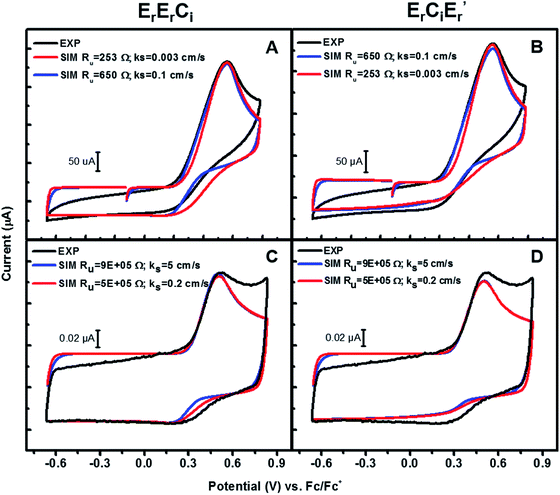Fig. 6 Experiments and simulations of CVs of 3a at (A) and (B) 4 V s⁻¹ with a 3 mm diameter working electrode; (C) and (D) 400 V s⁻¹ with a 11 μm diameter working electrode. See ESI† for details.

Table 2 Simulated lower limits of E° and k_f for E_rE_rC_i and E_rC_iE_r′ mechanisms in the two limits: At 4 V s⁻¹, limit I: k_s = 0.1 cm s⁻¹ & R_u = 650 Ω. Limit II: k_s = 0.003 cm s⁻¹ & R_u = 253 Ω. At 400 V s⁻¹, limit I: k_s = 5 cm s⁻¹ & R_u = 9 × 10⁵ Ω. Limit II: k_s = 0.2 cm s⁻¹ & R_u = 5 × 10⁵ Ω

Mechanism	Scan rate (V s^−1)	E°(min) (V) vs. Fc^+/Fc		k f(min) (M^−1 s^−1)
		I	II	I	II
ErErCi	400	0.33	0.33	1.0 × 10^7	1.0 × 10^7
	4	0.30	0.30	1.0 × 10^6	1.0 × 10^6
ErCiEr′	400	0.35	0.35	5.0 × 10^6	5.0 × 10^6
	4	0.32	0.32	7.0 × 10^4	2.5 × 10^4

---

At 400 V s⁻¹, the predicted lower limit for k_f is on the order of 10⁷ M⁻¹ s⁻¹ for E_rE_rC_i and 5 × 10⁶ M⁻¹ s⁻¹ for E_rC_iE_r′, both mechanisms therefore being extremely facile. Higher scan-rate simulations with smaller electrodes provide a higher and therefore better estimate for k_f and E° than their lower scan-rate counterparts. Consistent with these expectations, the simulations at 4 V s⁻¹ gave slightly lower values for k_f(min) and E°_(min), shown in Table 2. It is interesting to note the difference in the bimolecular rates of these two mechanisms predicted by the simulations, with k_f (E_rE_rC_i) being slightly larger than k_f (E_rC_iE_r′) in either frequency regime by a factor of two, although both mechanisms fit the experimental data equally well.

Conclusions

If earth-abundant metal hydrides are to be employed as electrocatalysts in fuel cells (Scheme 1), it is important to fully understand their reactivity on electron transfer out of the metal–hydrogen bond. The nickel(II) hydrides synthesized in this work have proven to be highly stable targets for such electrochemical studies. We have shown in this work that the one-electron oxidation in these d⁸ square-planar nickel hydride complexes leads to highly exergonic and extremely rapid post-oxidative H₂ evolution instead of the production of protons and electrons as was originally desired. This work therefore highlights an important challenge in using transition metal hydrides to electro-oxidize hydrogen containing liquid fuels in a fuel cell. It is possible that site isolation of these hydrides on a solid support would suppress this bimolecular H₂ evolution pathway on oxidation, and lead to protons and electrons instead. However the high positive potentials required for the first oxidation of these hydrides render them unlikely targets for ergoneutral electrocatalysts.

Experimental details

Cyclic voltammetry

Cyclic voltammetry experiments were performed with a SP-200 potentiostat from Bio-Logic Co. with a glassy carbon 3 mm diameter disk electrode (MF-2012) or a carbon fibre tip 11 μm diameter ultramicroelectrode (MF-2007) from BASi Inc. as the working electrode, a Ag/AgNO₃(10 mM), MeCN electrode as the non-aqueous reference electrode, and a Pt wire as the counter electrode in a typical three-electrode cell. TBABF₄ (0.1 M) was used as the supporting electrolyte. All experiments were done under N₂ in a glove-box.

Bulk electrolysis was performed in an ‘H-cell’ with two cylindrical glass chambers of 2 cm diameter connected by a glass joint fitted with a sintered glass frit. A 2 cm × 3 cm rectangular piece of carbon cloth suspended into the analyte solution with a copper wire was used as the working electrode. A finely polished and air-dried silver wire (0.032′′ diameter) was used as the pseudo reference in the same chamber. A polished Pt wire (0.032′′ diameter) was used as the counter electrode in the other compartment of the cell. Both compartments were sealed with rubber septa to prevent the escape of any gas generated. After bulk electrolysis, percent H₂ was determined by headspace analysis using a Shimadzu Gas Chromatograph equipped with a 100 μL sample loop, a TCD, and a CarbonPLOT column with N₂ carrier gas. Percent H₂ was quantified by a one point calibration with a 1% H₂ standard.

General experimental information

Unless otherwise noted, all organometallic compounds were prepared and handled under a nitrogen atmosphere using standard Schlenk and glovebox techniques. Dry and oxygen-free solvents (benzene, THF, pentane, and ether) were collected from an Innovative Technology PS-MD-6 solvent purification system and used throughout the experiments. Toluene and C₆D₆ were distilled from a deep purple solution of Na and benzophenone under a nitrogen atmosphere. CH₃CN was dried using CaH₂ and stored over 4 Å molecular sieves. Other solvents such as CD₂Cl₂ and CDCl₃ were used as received from commercial sources. ¹H, ¹³C, and ³¹P NMR spectra were recorded on a Bruker Avance-400 MHz spectrometer. Chemical shift values in ¹H and ¹³C NMR spectra were referenced internally to the residual solvent resonances, whereas ³¹P NMR spectra were referenced externally to 85% H₃PO₄ (0 ppm). Infrared spectra were recorded in the solid state on a Thermo Scientific Nicolet 4700 FT-IR spectrometer equipped with smart orbit diamond attenuated total reflectance (ATR) accessory. Elemental analysis was performed by the CENTC Elemental Analysis Facility at the University of Rochester Using a Perkin Elmer 2400 Series II elemental analyzer in CHN mode. Preparation of 1,3-(^tBu₂PO)₂C₆H₄ (1a),²⁴ 5-OCH₃-1,3-(^tBu₂PO)₂C₆H₃ (1b),²⁴ 5-CH₃-1,3-(^tBu₂PO)₂C₆H₃ (1c),²⁴ 4,6-(^tBu)₂-1,3-(^tBu₂PO)₂C₆H₂ (1d),²⁵2a,²³2d,²⁵ and 3a²³ have been previously reported in the literature.

Synthesis of [5-OCH₃-1,3-(^tBu₂PO)₂C₆H₂]NiCl (2b)

Under a nitrogen atmosphere, 50 mL of toluene was added to a mixture of 1b (0.86 g, 2.0 mmol) and anhydrous NiCl₂ (285 mg, 2.2 mmol), giving an orange suspension. While the solution was being refluxed for 24 h, an orange solution resulted with some undissolved residues. After the mixture was cooled to room temperature, the residues were removed by gravity filtration and a clear orange filtrate was obtained. The volume of the orange filtrate was reduced to ca. 5 mL, and then Et₂O was added to cause precipitation of a yellow solid. The product was collected by filtration, washed with Et₂O, and dried under vacuum to afford a yellow powder of 2b (875 mg, 84% yield). X-ray-quality crystals were grown by allowing a layer of pentane to slowly diffuse into a saturated CH₂Cl₂ solution of the complex at 0 °C. ¹H NMR (400 MHz, CDCl₃, δ): 1.42 (virtual triplet, PC(CH₃)₃, J_P–H = 8 Hz, 36H), 3.65 (s, OCH₃, 3H), 5.98 (s, ArH, 2H). ¹³C{¹H} NMR (101 MHz, CDCl₃, δ): 28.13 (s, PC(CH₃)₃), 39.32 (t, J_P–C = 7.1 Hz, PC(CH₃)₃), 55.47 (s, OCH₃), 91.98 (t, J_P–C = 6.1 Hz, ArC), 114.24 (t, J_P–C = 22.2 Hz, ArC), 161.38 (s, ArC), 169.68 (t, J_P–C = 10.1 Hz, ArC). ³¹P{¹H} NMR (162 MHz, CDCl₃, δ): 185.66 (s). Anal. calcd for C₂₃H₄₁ClO₃P₂Ni: C, 52.96; H, 7.92. Found: C, 52.93; H, 7.89.

Synthesis of [5-CH₃-1,3-(^tBu₂PO)₂C₆H₂]NiCl (2c)

This compound was prepared from 1c (1.66 g, 4.02 mmol) and anhydrous NiCl₂ (573 mg, 4.42 mmol) in 78% yield (1.59 g) by a procedure similar to that used for 2b. X-ray-quality crystals were grown by allowing a layer of pentane to slowly diffuse into a saturated CH₂Cl₂ solution of the complex at 0 °C. ¹H NMR (400 MHz, CDCl₃, δ): 1.41 (virtual triplet, PC(CH₃)₃, J_P–H = 8 Hz, 36H), 2.13 (s, CH₃, 3H), 5.18 (s, ArH, 2H). ¹³C{¹H} NMR (101 MHz, CDCl₃, δ): 21.55 (s, CH₃), 28.13 (s, PC(CH₃)₃), 39.27 (t, J_P–C = 7.1 Hz, PC(CH₃)₃), 105.92 (t, J_P–C = 6.1 Hz, ArC), 120.56 (t, J_P–C = 21.2 Hz, ArC), 139.02 (s, ArC), 169.44 (t, J_P–C = 10.1 Hz, ArC). ³¹P{¹H} NMR (162 MHz, CDCl₃, δ): 184.04 (s). Anal. calcd for C₂₃H₄₁ClO₂P₂Ni: C, 54.63; H, 8.17. Found: C, 54.75; H, 8.07.

Synthesis of [5-OCH₃-1,3-(^tBu₂PO)₂C₆H₂]NiH (3b)

Under a nitrogen atmosphere a suspension of LiAlH₄ (729 mg, 19.2 mmol) and 2b (500 mg, 0.96 mmol) in 40 mL of benzene was stirred at room temperature for 24 h. The resulting mixture was filtered through a short plug of Celite to afford a yellow solution. After the solvent was evaporated under vacuum, the desired nickel hydride 3b was isolated as a light yellow powder (322 mg, 69% yield). X-ray-quality crystals were grown by layering CH₃OH on a saturated THF solution of the hydride at 0 °C and allowing it to slowly diffuse. ¹H NMR (400 MHz, C₆D₆, δ): −8.06 (t, J_P–H = 52 Hz, NiH, 1H), 1.32 (virtual triplet, PC(CH₃)₃, J_P–H = 8 Hz, 36H), 3.36 (s, OCH₃, 3H), 6.56 (s, ArH, 2H). ¹³C{¹H} NMR (101 MHz, C₆D₆, δ): 28.56 (t, J_P–C = 3.0 Hz, PC(CH₃)₃), 37.88 (t, J_P–C = 9.1 Hz, PC(CH₃)₃), 55.06 (s, OCH₃), 92.12 (t, J_P–C = 6.1 Hz, ArC), 133.36 (t, J_P–C = 15.2 Hz, ArC), 162.50 (s, ArC), 169.09 (t, J_P–C = 10.1 Hz, ArC). ³¹P{¹H} NMR (162 MHz, C₆D₆, δ): 218.20 (s). IR (ATR, cm⁻¹): ν_Ni–H = 1790. Anal. calcd for C₂₃H₄₂O₃P₂Ni: C, 56.70; H, 8.69. Found: C, 56.28; H, 8.63.

Synthesis of [5-CH₃-1,3-(^tBu₂PO)₂C₆H₂]NiH (3c)

This compound was prepared from 2c (500 mg, 0.99 mmol) and LiAlH₄ (751 mg, 19.8 mmol) in 65% yield (294 mg) by a procedure similar to that used for 3b. X-ray-quality crystals were grown by layering CH₃OH on a saturated hexane solution of the nickel hydride at 0 °C and allowing it to slowly diffuse. ¹H NMR (400 MHz, C₆D₆, δ): −7.98 (t, J_P–H = 52 Hz, NiH, 1H), 1.33 (virtual triplet, PC(CH₃)₃, J_P–H = 8 Hz, 36H), 2.19 (s, CH₃, 3H), 6.67 (s, ArH, 2H). ¹³C{¹H} NMR (101 MHz, C₆D₆, δ): 21.94 (s, CH₃), 28.57 (s, PC(CH₃)₃), 37.85 (t, J_P–C = 8.1 Hz, PC(CH₃)₃), 105.78 (s, ArC), 138.72 (s, ArC), 139.10 (t, J_P–C = 16.2 Hz, ArC), 168.94 (t, J_P–C = 9.1 Hz, ArC). ³¹P{¹H} NMR (162 MHz, C₆D₆, δ): 216.22 (s). IR (ATR, cm⁻¹): ν_Ni–H = 1768. Anal. calcd for C₂₃H₄₂O₂P₂Ni: C, 58.62; H, 8.98. Found: C, 58.78; H, 8.92.

Synthesis of [4,6-(^tBu)₂-1,3-(^tBu₂PO)₂C₆H₂]NiH (3d)

This compound was prepared from 2d (500 mg, 0.83 mmol) and LiAlH₄ (630 mg, 16.6 mmol) in 78% yield (379 mg) by a procedure similar to that used for 3b. X-ray-quality crystals were grown by layering CH₃OH on a saturated hexane solution of the nickel hydride at 0 °C and allowing it to slowly diffuse. ¹H NMR (400 MHz, C₆D₆, δ): −7.90 (t, J_P–H = 56 Hz, NiH, 1H), 1.36 (virtual triplet, PC(CH₃)₃, J_P–H = 8 Hz, 36H), 1.60 (s, C(CH₃)₃, 18H), 7.32 (s, ArH, 1H). ¹³C{¹H} NMR (101 MHz, C₆D₆, δ): 28.53 (s, PC(CH₃)₃), 30.48 (s, C(CH₃)₃), 34.38 (s, C(CH₃)₃), 37.64 (t, J_P–C = 9.1 Hz, PC(CH₃)₃), 123.09 (s, ArC), 125.83 (t, J_P–C = 5.1 Hz, ArC), 146.07 (t, J_P–C = 16.2 Hz, ArC), 163.92 (t, J_P–C = 9.1 Hz, ArC). ³¹P{¹H} NMR (162 MHz, C₆D₆, δ): 215.04 (s). IR (ATR, cm⁻¹): ν_Ni–H = 1810. Anal. calcd for C₃₀H₅₆O₂P₂Ni: C, 63.28; H, 9.91. Found: C, 62.95; H, 9.75.

Synthesis of [(1,3-(^tBu₂PO)₂C₆H₃)Ni(NCCH₃)]BF₄ (4a)

Method A (through halide substitution):. Under a nitrogen atmosphere, a flame-dried 50 mL Schlenk flask was charged with 2a (300 mg, 0.61 mmol), AgBF₄ (142 mg, 0.73 mmol), and 15 mL CH₃CN. The resulting mixture was stirred at room temperature for four hours to obtain a light yellow solution with some insoluble white precipitate. The solution was filtered through a short plug of Celite, washed with THF (2 × 10 mL), and the resulting filtrate was evaporated under vacuum to afford the desired nickel–acetonitrile complex 4a as a light yellow powder (271 mg, 76% yield).

Method B (through protonation):. Under a nitrogen atmosphere, a flame-dried 50 mL Schlenk flask was loaded with 3a (100 mg, 0.22 mmol), HBF₄·Et₂O (33 μL, 0.24 mmol), and 10 mL CH₃CN. The resulting mixture was stirred at room temperature for one hour and the resulting solution was evaporated under vacuum to afford the desired product (89 mg, 69% yield). ¹H NMR (400 MHz, CDCl₃, δ): 1.46 (virtual triplet, PC(CH₃)₃, J_P–H = 7.2 Hz, 36H), 2.28 (s, free CH₃CN, 3H), 2.63 (s, Ni–NCCH₃, 3H), 6.49 (d, J_H–H = 8.0 Hz, ArH, 2H), 7.04 (t, J_H–H = 7.6 Hz, ArH, 1H). ¹³C{¹H} NMR (101 MHz, CDCl₃, δ): 4.17 (s, Ni–NCCH₃), 27.89 (s, PC(CH₃)₃), 40.04 (t, J_P–C = 7.9 Hz, PC(CH₃)₃), 106.17 (t, J_P–C = 5.8 Hz, ArC), 122.66 (t, J_P–C = 18.4 Hz, Ni–NCCH₃), 131.01 (s, ArC), 136.06 (s, ArC), 169.78 (t, J_P–C = 8.1 Hz, ArC), resonances arising from free CH₃CN are also present in the spectrum. ³¹P{¹H} NMR (162 MHz, CDCl₃, δ): 197.60 (s). ³¹P{¹H} NMR (162 MHz, CD₃CN, δ): 199.55 (s). IR (ATR, cm⁻¹): ν_C≡N = 2290.

Computational details

All quantum chemical calculations based on density functional theory (DFT)^35–37 were performed using the Gaussian09 software package.³⁸ Intermediates were optimized in the gas phase using the M06 functional³⁹ to obtain the lowest energy structures along with their electronic energies. A 6-311g* basis set^40–43 was employed for all the s- and p-block elements and the LANL2DZ basis set^44,45 with effective core potentials for Ni. Subsequent harmonic analyses were performed on all the optimized structures to obtain bond frequencies and thermal corrections to the free energy,^46,47 which were added to the previously calculated electronic energies to obtain the absolute free energies in the gas phase. Solvation energies for the optimized structures were obtained at the same level of theory using the SMD (Solvation Model Density) model⁴⁸ for acetonitrile, which is a polarizable continuum solvent model.

The standard reaction free energy for each set of reactants and products was then calculated according to eqn (3). Standard state corrections were made to the free energies to account for the change in going from 1 mol per 24.46 L (gas phase) to 1 M (solution phase), which amounts to RT ln(24.46) or 1.89 kcal mol⁻¹.

ΔG°^SMD(MeCN)_reaction = ΔG°^SMD(MeCN)_products − ΔG°^SMD(MeCN)_reactants (3)

To compute the bond dissociation free energy (BDFE) and pK_a for 3a in MeCN, an isodesmic scheme, involving the nickel hydride complexes 3a and 3a⁺ and a set of reference molecules, was employed as shown in eqn (4)–(10).

BDFE(M–H) = ΔG°₁ + BDFE(R–H) (6)

pK_a(M–H) = −log₁₀[exp(−ΔG°₂/RT)] + pK_a(B–H) (9)

ΔpK_a = pK_a(M^III–H) − pK_a(M^II–H) = (ΔG°₂(3a⁺) − ΔG°₂(3a))/(2.303RT) (10)

Reported values of BDFE(R–H) and pK_a(B–H) in MeCN solvent for a set of reference molecules were taken from literature;^49,50 ΔG°₁ and ΔG°₂ were computed by our DFT method discussed above, employing the SMD model for MeCN.⁴⁸ For pK_a calculations, additional benchmarking was performed using other density functionals viz. M06L,⁵¹ B3LYP,^52–54 B3P86,^53,55 BP86 ^52,55,56 and ωB97xD.⁵⁷ All electrochemical simulations were performed using DigiElch 7™.⁵⁸

Acknowledgements

This work was funded by the Center for Electrocatalysis, Transport Phenomena, and Materials (CETM) for Innovative Energy Storage, an Energy Frontier Research Center funded by the U.S. Department of Energy, and the ESD NYSTAR program. S. R would like to thank Andrew Ingram and Kate Waldie for the GC experiment.

Notes and references

1. R. H. Crabtree, Energy Environ. Sci., 2008, 1, 134–138.
2. C. M. Araujo, D. L. Simone, S. J. Konezny, A. Shim, R. H. Crabtree, G. L. Soloveichik and V. S. Batista, Energy Environ. Sci., 2012, 5, 9534–9542.
3. S. P. Annen, V. Bambagioni, M. Bevilacqua, J. Filippi, A. Marchionni, W. Oberhauser, H. Schönberg, F. Vizza, C. Bianchini and H. Grützmacher, Angew. Chem., Int. Ed. Engl., 2010, 49, 7229–7233.
4. P. Driscoll, E. Deunf, L. Rubin, O. Luca, R. Crabtree, C. Chidsey, J. Arnold and J. Kerr, in ECS Transactions, The Electrochemical Society, 2011, vol. 35, pp. 3–17.
5. P. F. Driscoll, E. Deunf, L. Rubin, J. Arnold and J. B. Kerr, J. Electrochem. Soc., 2013, 160, G3152–G3158.
6. M. Bevilacqua, C. Bianchini, A. Marchionni, J. Filippi, A. Lavacchi, H. Miller, W. Oberhauser, F. Vizza, G. Granozzi, L. Artiglia, S. P. Annen, F. Krumeich and H. Grützmacher, Energy Environ. Sci., 2012, 5, 8608–8620.
7. W. Baratta, G. Chelucci, S. Gladiali, K. Siega, M. Toniutti, M. Zanette, E. Zangrando and P. Rigo, Angew. Chem., Int. Ed. Engl., 2005, 44, 6214–6219.
8. A. Fujii, S. Hashiguchi, N. Uematsu, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1996, 118, 2521–2522.
9. M. Yamakawa, H. Ito and R. Noyori, J. Am. Chem. Soc., 2000, 122, 1466–1478.
10. K. T. Smith, C. Roemming and M. Tilset, J. Am. Chem. Soc., 1993, 115, 8681–8689.
11. O. B. Ryan, M. Tilset and V. D. Parker, J. Am. Chem. Soc., 1990, 112, 2618–2626.
12. O. B. Ryan, K. Smith and M. Tilset, J. Organomet. Chem., 1991, 421, 315–322.
13. J. P. Collman, P. S. Wagenknecht and N. S. Lewis, J. Am. Chem. Soc., 1992, 114, 5665–5673.
14. V. Skagestad and M. Tilset, J. Am. Chem. Soc., 1993, 115, 5077–5083.
15. C. Bianchini, M. Peuzzini, A. Ceccanti, F. Laschi and P. Zanello, Inorg. Chim. Acta, 1997, 259, 61–70.
16. T.-Y. Cheng, D. J. Szalda, J. Zhang and R. M. Bullock, Inorg. Chem., 2006, 45, 4712–4720.
17. M. J. Krafft, M. Bubrin, A. Paretzki, F. Lissner, J. Fiedler, S. Záliš and W. Kaim, Angew. Chem., Int. Ed. Engl., 2013, 52, 6781–6784.
18. O. V. Ozerov, C. Guo, L. Fan and B. M. Foxman, Organometallics, 2004, 23, 5573–5580.
19. L.-C. Liang, P.-S. Chien and P.-Y. Lee, Organometallics, 2008, 27, 3082–3093.
20. R. B. Lansing, K. I. Goldberg and R. A. Kemp, Dalton Trans., 2011, 40, 8950–8958.
21. N. Grüger, L.-I. Rodríguez, H. Wadepohl and L. H. Gade, Inorg. Chem., 2013, 52, 2050–2059.
22. C. Rettenmeier, H. Wadepohl and L. H. Gade, Chem.–Eur. J., 2014, 20, 9657–9665.
23. S. Chakraborty, J. A. Krause and H. Guan, Organometallics, 2009, 28, 582–586.
24. I. Göttker-Schnetmann, P. White and M. Brookhart, J. Am. Chem. Soc., 2004, 126, 1804–1811.
25. T. Chen, L. Yang, L. Li and K.-W. Huang, Tetrahedron, 2012, 68, 6152–6157.
26. V. Pandarus and D. Zargarian, Organometallics, 2007, 26, 4321–4334.
27. O. R. Luca, J. D. Blakemore, S. J. Konezny, J. M. Praetorius, T. J. Schmeier, G. B. Hunsinger, V. S. Batista, G. W. Brudvig, N. Hazari and R. H. Crabtree, Inorg. Chem., 2012, 51, 8704–8709.
28. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001.
29. H. A. Muathen, Indian J. Chem., 1991, 30, 522–524.
30. G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, Organometallics, 2010, 29, 2176–2179.
31. B. H. Solis and S. Hammes-Schiffer, Inorg. Chem., 2011, 50, 11252–11262.
32. S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439–10452.
33. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
34. K. M. Kadish, J. Q. Ding and T. Malinski, Anal. Chem., 1984, 56, 1741–1744.
35. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
36. P. Hohenberg, Phys. Rev., 1964, 136, B864–B871.
37. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
38. Gaussian 09, Revision D.01, M. J. Frisch, et al., Gaussian, Inc., Wallingford CT, 2009.
39. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
40. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
41. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
42. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
43. A. V. Mitin, J. Baker and P. Pulay, J. Chem. Phys., 2003, 118, 7775–7782.
44. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
45. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
46. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
47. J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442–13444.
48. A. V Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
49. J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001.
50. R. H. Morris, J. Am. Chem. Soc., 2014, 136, 1948–1959.
51. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118.
52. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
53. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
54. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
55. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
56. J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802.
57. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2009, 131, 174105–174113.
58. M. Rudolph, J. Electroanal. Chem., 2003, 543, 23–39.

---

Footnotes

† Electronic supplementary information (ESI) available: Supplementary electrochemical data, electrochemical simulation data, Cartesian coordinates and energies of DFT optimized structures, sample input files and X-ray analyses. CCDC 1418625–1418630. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc03189c

‡ These authors contributed equally.

---