Open Access Article
Open Access ArticlePolymorphism influences singlet fission rates in tetracene thin films†
Dylan H.
Arias‡
 ab,
Joseph L.
Ryerson‡
ab,
Jasper D.
Cook
b,
Niels H.
Damrauer
ab,
Joseph L.
Ryerson‡
ab,
Jasper D.
Cook
b,
Niels H.
Damrauer
 *b and
Justin C.
Johnson
*a
*b and
Justin C.
Johnson
*a
aNational Renewable Energy Laboratory, Golden, Colorado 80401, USA. E-mail: Justin.Johnson@nrel.gov
bDepartment of Chemistry and Biochemistry, University of Colorado, Boulder, Colorado 80309, USA. E-mail: Niels.Damrauer@colorado.edu
First published on 6th November 2015
Abstract
We report the effect of crystal structure and crystallite grain size on singlet fission (SF) in polycrystalline tetracene, one of the most widely studied SF and organic semiconductor materials. SF has been comprehensively studied in one polymoprh (Tc I), but not in the other, less stable polymorph (Tc II). Using carefully controlled thermal evaporation deposition conditions and high sensitivity ultrafast transient absorption spectroscopy, we found that for large crystallite size samples, SF in nearly pure Tc II films is significantly faster than SF in Tc I films. We also discovered that crystallite size has a minimal impact on the SF rate in Tc II films, but a significant influence in Tc I films. Large crystallites exhibit SF times of 125 ps and 22 ps in Tc I and Tc II, respectively, whereas small crystallites have SF times of 31 ps and 33 ps. Our results demonstrate first, that attention must be paid to polymorphism in obtaining a self-consistent rate picture for SF in tetracene and second, that control of polymorphism can play a significant role towards achieving a mechanistic understanding of SF in polycrystalline systems. In this latter context we show that conventional theory based on non-covalent tetracene couplings is insufficient, thus highlighting the need for models that capture the delocalized and highly mobile nature of excited states in elucidating the full photophysical picture.
Introduction
Overcoming fundamental limits to photovoltaic (PV) efficiency, first laid out by Shockley and Quiesser,1 could lower barriers to utilization of solar power in a variety of practical scenarios. Singlet fission (SF) is a process with the potential to enhance PV efficiencies to beyond the Shockley–Quiesser limit, increasing the theoretical maximum power conversion efficiency from ∼33% to ∼45%.2–4 During SF an excited singlet exciton splits into two triplet excitons each with approximately half the energy, a process which could accentuate the performance of a lower bandgap semiconductor such as silicon by generating photocurrent via triplet injection or energy transfer rather than losing excess photon energy to heat. SF is analogous to multiple exciton generation in, e.g. semiconductor nanocrystals,5 with the added potential of molecular and crystallographic control through chemical synthesis. While much theoretical6–14 and experimental15–21 work has focused on the mechanism of SF, it has only been utilized in a few PV device moieties.22–25 From the limited number of applications, it is clear that taking full advantage of SF requires a more complete understanding of the mechanism and a wider array of systems supporting efficient SF.Only a few classes of molecules have demonstrated efficient SF, including carotenoids,26,27 perylene diimides,28,29 semiconducting polymers30 and polyacenes.16–21,23–25 Electronic coupling, energetics, and mixing between singlet, charge transfer, and doubly excited states determine whether the SF mechanism is a mediated or direct process.31 These can be affected by molecular structure, such as changing the energetics by adding electron donating or withdrawing groups to the chromophore;32 and can also be affected by the crystal structure, which can be influenced by substitution of side chains16,33–35 or altering the film preparation conditions to access unique polymorphs.8,36,37 In addition to these controlling properties, which may be thought of as intrinsic to the molecular and crystallographic structure, there may be extrinsic effects due to defects, impurities, interfaces, and differing dielectric environments. Whereas it has long been observed that crystallite size, and therefore grain boundaries, affects charge carrier mobilities and other semiconductor properties,38,39 only recently has it been shown that crystallite size affects the rate of SF in polyacenes, specifically in polycrystalline films of tetracene.40 The variation of SF times reported for polycrystalline tetracene15,41–44 may thus reflect measurements made on films of unknown or uncontrolled crystallite size as well as the underappreciated role of polymorphism within thin films, even in relatively small proportion.
In this article, we present results directly determining the effects of crystal polymorph and crystallite size on the rate of SF in polycrystalline tetracene thin films. We deposited films of two polymorphs of tetracene45–47 and varied the crystallite size for each one. Using ultrafast transient absorption spectroscopy, we show that for larger grain size, Tc II films exhibit faster SF than the more commonly deposited and studied Tc I films. In addition, consistent with the results of Piland et al.,40 we found that for Tc I, smaller crystallites lead to significantly faster SF. However, Tc II films exhibit a drastically reduced dependence on crystallite size. Examination of the crystal structures of the two polymorphs leads to some rationale for the distinct behaviour, but calculation of electronic couplings between pairs of molecules suggests the highest SF rate should occur between two specific partners in the Tc I polymorph, in apparent disagreement with experiment. We argue that gaining intuition about the rate of SF in systems like tetracene requires more comprehensive models that simultaneously account for the influence of effects not dominated by an individual pairwise interaction.
Results
Film structural characterization
Polycrystalline tetracene thin films were prepared by thermal evaporation onto glass microscope coverslips. The substrate holder and evaporator geometry enabled up to 10 nearly identical films to be deposited simultaneously. The evaporation system was housed within a nitrogen glovebox, allowing samples to be sealed for optical measurements without ever being exposed to air. Substrates at room temperature or heated to 65 °C produced predominantly Tc I films while substrates cooled to liquid nitrogen temperature (−180 °C) yielded predominantly Tc II films.X-Ray diffraction allows for a simple differentiation between film types (Fig. 1a). Tetracene molecules deposited on dielectric substrates align with the long molecular axis nearly perpendicular to the substrate plane, causing the crystal ab-plane to be parallel to the surface while the c-axis is directed toward the surface normal. Polycrystalline domains are isotropically distributed about the substrate normal, leaving only the (00c) peaks observable in XRD. The peaks at 7.3° and 6.9° are assigned to diffraction from the (001) planes of Tc I and Tc II, respectively.47 Inspection of the crystal structure provides initial justification for this assignment, as tighter packing along the c-axis is evident for Tc II compared with Tc I, leading to the lower diffraction angles for Tc II. The calculated diffraction spectrum (Fig. S3†) from the full crystal structure reveals an excellent match between experiment and expected spectra. By fitting to two peak functions and extracting the peak areas, we generally measured ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 polymorph ratios under optimized conditions (Fig. 1a), although there is a thickness dependence for the ratio of Tc II
1 polymorph ratios under optimized conditions (Fig. 1a), although there is a thickness dependence for the ratio of Tc II![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc I during cold depositions (thicker films favour more enrichment of Tc I character). Heated substrates generally induced purer Tc I films compared with room temperature substrates. In addition, Tc II films transform into Tc I films over a few weeks to months, although this could be dramatically slowed by storage below room temperature. Only samples with verified polymorph purity ≥90% were used in the optical experiments. By varying the deposition rate, considerable control of crystallite grain size was achieved (Fig. 1b). Fast deposition rates near 5.0 Å s−1 yielded crystallites measured with atomic force microscopy (AFM) to be 150–350 nm, whereas slower deposition rates, 0.5–1.0 Å s−1, produced much larger 750 nm to 2 μm sized crystallites. We chose four film types to investigate the complementary effects of crystal structure and film crystallinity (see Fig. 1b) on optical properties and SF dynamics.
Tc I during cold depositions (thicker films favour more enrichment of Tc I character). Heated substrates generally induced purer Tc I films compared with room temperature substrates. In addition, Tc II films transform into Tc I films over a few weeks to months, although this could be dramatically slowed by storage below room temperature. Only samples with verified polymorph purity ≥90% were used in the optical experiments. By varying the deposition rate, considerable control of crystallite grain size was achieved (Fig. 1b). Fast deposition rates near 5.0 Å s−1 yielded crystallites measured with atomic force microscopy (AFM) to be 150–350 nm, whereas slower deposition rates, 0.5–1.0 Å s−1, produced much larger 750 nm to 2 μm sized crystallites. We chose four film types to investigate the complementary effects of crystal structure and film crystallinity (see Fig. 1b) on optical properties and SF dynamics.
 | ||
| Fig. 1 (a) XRD showing the (001) peak for the four film types. (b) AFM images of Tc I (top) and Tc II (bottom) films, with small (left) and large (right) crystallites. Scale bars = 2 μm. (c) Orientation of the dimers in the ab-plane corresponding to an [a b] translation vector of [1/2 1/2] in Tc I (top) and Tc II (bottom). (d) View of the herringbone structure in the ab-plane. Centroid molecule distances between the centre molecule and the nearest-neighbours are Tc I [1 0] = 6.056 Å, [−1/2 1/2] = 4.773 Å, and [1/2 1/2] = 5.125 Å; Tc II [1 0] = 5.909 Å, [−1/2 1/2] = 4.711 Å, and [1/2 1/2] = 4.787 Å. See ESI† for details of dimer distances and labelling. | ||
Absorption and fluorescence
The absorption and fluorescence spectra of the four films are shown in Fig. 2a. All four films exhibit the characteristic Davydov splitting and vibrational progression of polycrystalline tetracene in the absorption spectrum; with the two polymorphs having different peak ratios between the Davydov peaks (the higher energy split Davydov peak is much larger in Tc I). However, a simple correlation between absorption and film type, employed in other SF systems,37 is complicated by film birefringence, which leads to thickness dependent vibronic peak ratios.48 The fluorescence spectra are qualitatively similar, with both films exhibiting a vibronic progression of peaks and red-shifted feature previously assigned to defects or excimers.40 However, the amplitude of this feature is greater in Tc II films compared to Tc I films. Time correlated single photon counting (TCSPC) with 395 nm excitation revealed multiexponential singlet decay kinetics (Fig. 2b) that differed primarily in the initial fast decay component, commonly assigned to SF dynamics. Fitting using a series of three exponentials convolved with the instrument response gave fastest time constants of 85 ps (Tc I large), 65 ps (Tc I small), 40 ps (Tc II large), and 50 ps (Tc II small). | ||
| Fig. 2 (a) 80 nm thick film absorption (solid) and emission (dashed) spectra. (b) Time-resolved emission traces. The Tc II, large film was 20 nm thick. We observed no thickness dependence to SF dynamics (see Fig. S8†). | ||
Ultrafast transient absorption
We used ultrafast transient absorption spectroscopy with 400 nm excitation and ∼250 femtosecond time resolution to investigate directly both the singlet and triplet dynamics with a higher time resolution and a larger range of excitation densities than is available with TCSPC. Fig. 3a shows the TA spectra at ∼1 ps delay for the Tc I large crystallite film and Tc II large crystallite film at moderate excitation densities of ∼55 × 1017 cm−3. While there is very little spectral difference between films, a combination of spectral fitting and singular value decomposition (SVD)49,50 elucidated differences in SF dynamics. At low pump fluences, two main SVD principal components were found; one “singlet-like” and one “triplet-like” (see ESI†). Spectral fitting was also performed by treating each TA spectrum as a linear combination of singlet and triplet spectra. The singlet spectrum was chosen as the 1 ps spectrum, as an insignificant concentration of triplets would be formed at this time delay. As the SF time constant is around 100 ps in tetracene,40 we used the ∼5 ns spectrum as the triplet spectrum (Fig. 3b). At each time delay, we used a linear combination of these two spectra to fit the TA spectrum. This built up the singlet and triplet kinetics seen in Fig. 3c and d. We fitted the curves with a kinetic model including ground, singlet, correlated triplet pair 1(TT), and triplet states, with SF, exciton annihilation, and spontaneous relaxation channels for each state (Fig. 4, see Table S3† for all fit parameters). This model is similar to one previously used to describe polycrystalline tetracene thin film kinetics.44 Tc I films with large crystallites have a SF time, 1/ksf in Fig. 4, of ∼120 ps, which significantly decreases to ∼35 ps as the crystallite grain size is decreased. Tc II films, however, have significantly faster SF times that do not show a strong dependence on crystallite grain size, with a SF time of ∼20–35 ps for both large and small crystallites. Although the fitting procedure produced accurate time constants and spectra, the amplitudes of spectral features could not be assigned a meaningful quantitative value (i.e., extinction coefficient) due to strongly overlapping features and unknown optical parameters. As a result, the vertical axis in Fig. 3d reflects a normalized population fraction and not a true quantum yield.Fig. 5 shows exponential decay time constants extracted using a global fit as a function of fluence for the singlet- and triplet-like SVD components (see Fig. S7†). Increasing pump fluence leads to faster decay times, indicative of exciton–exciton annihilation.41 At low fluences, the trend in decay times from SVD is consistent with the trend in SF rates extracted from the kinetic modelling: Tc I films with large crystallites have the slowest SF rate, which speeds up considerably with small crystallites. The Tc II films have the same SF rate within experimental reproducibility regardless of crystallite grain size.
 | ||
| Fig. 5 Time constants associated with the singlet exciton decay from global fit of SVD data for all four film types from low to high fluence. Lines are guides to the eye. | ||
Dimer electronic coupling
Fig. 1d shows the relevant dimer pairs in the ab-plane associated with any given Tc chromophore for Tc I or II. We assumed the so-called mediated mechanism of SF and utilized one-electron orbital coupling matrix elements, tAB, of these dimer pairs (A refers to one of the chromophores and B to the other) to calculate the diabatic couplings, V, between a singlet exciton state (S1S0 or S0S1) and the SF product state written as a singlet-coupled pair of triplets, 1TT (eqn (1) and (2), see ESI† for details).7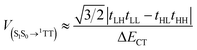 | (1) |
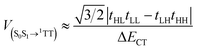 | (2) |
In eqn (1) and (2) H = HOMO, L = LUMO, and ΔECT is the energy difference between S1 and the virtual intermediate CT state. We estimate the variation in CT energies between Tc I (less stable CT state) and II (more stable CT state) to be at most ∼7% based on the assumption of localized charges and centroid-to-centroid distance changes in the dimers in one particular direction ([1/2 1/2]). This effect is small in comparison with variations in orbital couplings. To highlight the impact of these on diabatic coupling for SF, we use a common value of ΔECT = 600 meV for both Tc I and II, estimated from electroabsorption.51 The calculated diabatic couplings for SF are summarized in Table 1 (full calculation results in ESI†). The largest in both Tc I and Tc II are for the [1/2 1/2] dimer. As depicted in Fig. 1c, Tc I has a substantial slip along the major axis of the molecules whereas this slip is absent in Tc II. This geometric slip leads to a more significant asymmetry in the importance of the electron-transfer and hole-transfer mediated pathways that contribute – through destructive interference (see ESI†) – to the diabatic coupling. Because the cancellation of terms is incomplete, the overall coupling remains significant. In contrast, the reduced slip in the Tc II [1/2 1/2] dimer leads to more closely matched contributions from electron- and hole-transfer pathways, and following destructive interference, to a smaller overall value for the SF coupling. This result highlights the need to account for molecular orientation in addition to the molecular distances.
| Tc I [−1/2 1/2] | Tc II [−1/2 1/2] | Tc I [1/2 1/2] | Tc II [1/2 1/2] | Tc I [1 0] | Tc II [1 0] | |
|---|---|---|---|---|---|---|
| a Largest SF couplings are highlighted in bold. | ||||||
| V (S1S0→1TT) | 4.5 | 3.4 | 0.6 | 8.5 | 0.05 | 1.4 |
| V (S0S1→1TT) | 7.2 | 6.2 | 16 | 1.8 | 0.05 | 1.4 |
Discussion
We conclude from the results presented in Fig. 2b, 3, and 5 that Tc II films undergo SF faster than Tc I; and that Tc I films have a significant dependence on morphology while the dependence is reduced in Tc II films. Inspection of the molecular separation in the crystal ab-plane (Fig. 1d) reveals that the intermolecular distances for partners involved in all relevant and unique pairwise interactions in Tc II are slightly smaller than for Tc I. This difference in structure and nearest neighbour interactions could lead to faster SF via stronger coupling or mixing amongst singlet, charge transfer, and triplet states.8 In particular, mixing between singlets and charge transfer states, determined by the strength of the electronic coupling, can play a significant role mediating SF in pentacene crystals.52 However, the SF-relevant coupling depends both on geometry and distance. The noticeable slip between molecules along the major axis is also expected to influence the SF rate (Fig. 1c). Unexpectedly, calculations of key matrix elements7 for dimer pairs from the unit cell show a decrease in SF-relevant coupling in Tc II compared with Tc I in the [1/2 1/2] direction from 16 meV to 8.5 meV (as well as overall), in apparent disagreement with experimental data. However, with strong electronic delocalization in tetracene, it may be necessary to move beyond the dimer picture of coupling, and consider that due to its overall higher density, the Tc II structure may support stronger exciton delocalization, which may lower CT energies,53 enhance population in multiexciton states, and increase the SF rate.14The change in intermolecular coupling could also alter the transport properties, affecting the SF rate in an indirect manner.54 For example, if transport is fastest in Tc II films, the photogenerated singlets may diffuse to SF-enhanced geometries at crystallite surfaces more efficiently than in Tc I films, effectively negating the size dependence that occurs in Tc I crystallites. If this hypothesis is correct, growth of large Tc II single crystals, currently being explored, should lead to slowed SF as excitations should not reach surfaces within the SF time. An alternative explanation is that grain boundaries in Tc I films sustain intermolecular geometries similar to those found in Tc II. In this case, increased access to the boundaries in smaller crystallites would increase the SF rate in Tc I films, but not Tc II. In principle, our TA data set could inform about exciton transport through analysis of exciton annihilation rates, which have previously been used to calculate diffusion constants and lengths.55 However, conventional models assume fully localized excitations undergoing incoherent transfer and may not be fully applicable to tetracene. Spatially resolved transient absorption microscopy54,56 is a more direct measure of transport and could shed light on the nature of the exciton migration in Tc I vs. Tc II films and at crystallite interfaces. Such experiments will help to determine if transport is an important factor leading to the difference between Tc I and Tc II behaviour or if instead the intrinsic crystal structure results in variations in intermolecular electronic coupling that compel the altered dynamics.
Conclusions
In summary, we fabricated polycrystalline tetracene thin films of two polymorphs with varying crystallite sizes. Using ultrafast transient absorption spectroscopy, we discovered that for large crystallite sizes, singlet fission is significantly faster in polymorph Tc II than in Tc I, and that, unlike in Tc I films, in Tc II films the crystallite size has little or no effect on the SF rate. These results highlight the defining role that polymorphism can play in the SF rate in tetracene and that precise control over the structure of films of even the most well-studied compounds can lead to new understanding. These general principles are likely to be true for many organic semiconductors in which exciton delocalization, migration, and fission simultaneously influence excited state dynamics.Methods
Film deposition
Tetracene (benz[b]anthracene, 98%, CAS # 92-24-0) was purchased from Aldrich and used without further purification. Glass coverslips were washed with hexane and acetone, plasma cleaned, and kept in a glovebox before depositions. Depositions were performed with a resistively heated alumina crucible under high vacuum (10−6 to 10−7 Torr). The deposition rate and substrate temperature were varied during depositions from 0.5–5.0 Å s−1 and 85–340 K, depending on the desired film type and crystallite size.Time-resolved emission
Fluorescence decays were recorded exciting using the second harmonic of a Ti:sapphire oscillator (395 nm) and detecting 535 nm emission. The resulting data were fit to a multiexponential decay function convoluted with the instrument response function (see ESI† for details and all fitted parameters).Transient absorption
Ultrafast TA measurements were performed using a Coherent Libra amplifier, a TOPAS-C optical parametric amplifier, and an Ultrafast Systems LLC Helios Spectrometer. Using the absorption coefficients and measuring the energy of the pump focused through a series of pinholes, we calculated excitation densities from 1017 to 1019/cm−3. At higher fluences, SVD revealed an additional principal component with a small singular value that we ascribe to an acoustic mode caused by sample heating (see ESI†); we subtracted off this mode before the spectral fitting procedure and kinetic modelling, as those methods do not include an acoustic mode.Acknowledgements
The authors thank B. Schatschneider for the calculated .cif file for the Tc II polymorph. This material is based on work supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Biosciences, and Geosciences. D. H. A., J. L. R. and J. C. J. acknowledge Contract No. DE-AC36-08GO28308 with NREL and D. H. A., J. D. C., and N. H. D. acknowledge Contract No. DE-FG02-07ER15890.Notes and references
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- H. Shpaisman, O. Niitsoo, I. Lubomirsky and D. Cahen, Sol. Energy Mater. Sol. Cells, 2008, 92, 1541–1546 CrossRef CAS.
- M. J. Y. Tayebjee, A. A. Gray-weale and T. W. Schmidt, J. Phys. Chem. Lett., 2012, 3, 2749–2754 CrossRef CAS.
- M. C. Beard, J. C. Johnson, J. M. Luther and A. J. Nozik, Philos. Trans. R. Soc., A, 2015, 373, 20140412 CrossRef PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103 CrossRef PubMed.
- E. C. Alguire, J. E. Subotnik and N. H. Damrauer, J. Phys. Chem. A, 2015, 119, 299–311 CrossRef CAS PubMed.
- X. Feng, A. B. Kolomeisky and A. I. Krylov, J. Phys. Chem. C, 2014, 118, 19608–19617 CAS.
- J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- L. Wang, Y. Olivier, O. V. Prezhdo and D. Beljonne, J. Phys. Chem. Lett., 2014, 5, 3345–3353 CrossRef CAS PubMed.
- S. R. Yost, J. Lee, M. W. B. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao, K. Johnson, M. Y. Sfeir, M. G. Bawendi, T. M. Swager, R. H. Friend, M. A. Baldo and T. van Voorhis, Nat. Chem., 2014, 6, 492–497 CrossRef CAS PubMed.
- S. M. Parker, T. Seideman, M. A. Ratner and T. Shiozaki, J. Phys. Chem. C, 2014, 118, 12700–12705 CAS.
- P. E. Teichen and J. D. Eaves, J. Chem. Phys., 2015, 143, 044118 CrossRef PubMed.
- E. M. Grumstrup, J. C. Johnson and N. H. Damrauer, Phys. Rev. Lett., 2010, 105, 257403 CrossRef PubMed.
- R. D. Pensack, A. J. Tilley, S. R. Parkin, T. S. Lee, M. M. Payne, D. Gao, A. A. Jahnke, D. G. Oblinsky, P.-F. Li, J. E. Anthony, D. S. Seferos and G. D. Scholes, J. Am. Chem. Soc., 2015, 137, 6790–6803 CrossRef CAS PubMed.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS PubMed.
- J. J. Burdett and C. J. Bardeen, Acc. Chem. Res., 2013, 46, 1312–1320 CrossRef CAS PubMed.
- V. K. Thorsmølle, R. D. Averitt, J. Demsar, D. L. Smith, S. Tretiak, R. L. Martin, X. Chi, B. K. Crone, A. P. Ramirez and A. J. Taylor, Phys. Rev. Lett., 2009, 102, 017401 CrossRef PubMed.
- M. W. B. Wilson, A. Rao, J. Clark, R. S. S. Kumar, D. Brida, G. Cerullo and R. H. Friend, J. Am. Chem. Soc., 2011, 133, 11830–11833 CrossRef CAS PubMed.
- A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Nat. Phys., 2015, 11, 352–357 CrossRef CAS.
- J. N. Schrauben, Y. Zhao, C. Mercado, P. I. Dron, J. L. Ryerson, J. Michl, K. Zhu and J. C. Johnson, ACS Appl. Mater. Interfaces, 2015, 7, 2286–2293 CAS.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. van Voorhis and M. A. Baldo, Acc. Chem. Res., 2013, 46, 1300–1311 CrossRef CAS PubMed.
- L. Yang, M. Tabachnyk, S. L. Bayliss, M. L. Bo, K. Broch, N. C. Greenham, R. H. Friend and B. Ehrler, Nano Lett., 2015, 15, 354–358 CrossRef CAS PubMed.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS PubMed.
- C. Wang and M. J. Tauber, J. Am. Chem. Soc., 2010, 132, 13988–13991 CrossRef CAS PubMed.
- S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135, 14701–14712 CrossRef CAS PubMed.
- N. Renaud and F. C. Grozema, J. Phys. Chem. Lett., 2015, 6, 360–365 CrossRef CAS PubMed.
- A. J. Musser, M. Al-Hashimi, M. Maiuri, D. Brida, M. Heeney, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2013, 135, 12747–12754 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- E. Busby, J. Xia, Q. Wu, J. Z. Low, R. Song, J. R. Miller, X.-Y. Zhu, L. M. Campos and M. Y. Sfeir, Nat. Mater., 2015, 14, 426–433 CrossRef CAS PubMed.
- S. W. Eaton, S. A. Miller, E. A. Margulies, L. E. Shoer, R. D. Schaller and M. R. Wasielewski, J. Phys. Chem. A, 2015, 119, 4151–4161 CrossRef CAS PubMed.
- K. Kolata, T. Breuer, G. Witte and S. Chatterjee, ACS Nano, 2014, 8, 7377–7383 CrossRef CAS PubMed.
- J. Herz, T. Buckup, F. Paulus, J. U. Engelhart, U. H. F. Bunz and M. Motzkus, J. Phys. Chem. A, 2015, 119, 6602–6610 CrossRef CAS PubMed.
- R. J. Dillon, G. B. Piland and C. J. Bardeen, J. Am. Chem. Soc., 2013, 135, 17278–17281 CrossRef CAS PubMed.
- J. L. Ryerson, J. N. Schrauben, A. J. Ferguson, S. C. Sahoo, J. Michl, A. J. Nozik and J. C. Johnson, J. Phys. Chem. C, 2014, 118, 12121–12132 CAS.
- H. Moon, R. Zeis, E.-J. Borkent, C. Besnard, A. J. Lovinger, T. Siegrist, C. Kloc and Z. Bao, J. Am. Chem. Soc., 2004, 126, 15322–15323 CrossRef CAS PubMed.
- D. Knipp, R. A. Street, A. Volkel and J. Ho, J. Appl. Phys., 2003, 93, 347–355 CrossRef CAS.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS PubMed.
- J. J. Burdett, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2011, 135, 214508 CrossRef PubMed.
- S.-H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef PubMed.
- A. Wappelt, A. Bergmann, A. Napiwotzki, H. J. Eichler, H. J. Jüpner, A. Kummrow, A. Lau and S. Woggon, J. Appl. Phys., 1995, 78, 5192 CrossRef CAS.
- M. W. B. Wilson, A. Rao, K. Johnson, S. Gélinas, R. di Pietro, J. Clark and R. H. Friend, J. Am. Chem. Soc., 2013, 135, 16680–16688 CrossRef CAS PubMed.
- U. Sondermann, A. Kutoglu and H. Bässler, J. Phys. Chem., 1985, 33, 1735–1741 CrossRef.
- E. Venuti, R. G. Della Valle, L. Farina, A. Brillante, M. Masino and A. Girlando, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104106 CrossRef.
- B. Schatschneider, S. Monaco, A. Tkatchenko and J. J. Liang, J. Phys. Chem. A, 2013, 117, 8323–8331 CrossRef CAS PubMed.
- W. Hofberger, Phys. Status Solidi A, 1975, 30, 271–278 CrossRef CAS.
- C. Ruckebusch, M. Sliwa, P. Pernot, A. de Juan and R. Tauler, J. Photochem. Photobiol., C, 2012, 13, 1–27 CrossRef CAS.
- I. H. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, 2004, 1657, 82–104 CrossRef CAS PubMed.
- L. Sebastian, G. Weiser and H. Bassler, Chem. Phys., 1981, 61, 125–135 CrossRef CAS.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2014, 141, 074705 CrossRef PubMed.
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS PubMed.
- Y. Wan, Z. Guo, T. Zhu, S. Yan, J. C. Johnson and L. Huang, Nat. Chem., 2015, 7, 785–792 CrossRef CAS PubMed.
- Y. Tamai, H. Ohkita, H. Benten and S. Ito, J. Phys. Chem. Lett., 2015, 6, 3417–3428 CrossRef CAS PubMed.
- C. Y. Wong, B. L. Cotts, H. Wu and N. S. Ginsberg, Nat. Commun., 2015, 6, 5946 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional theoretical description, film preparation conditions, and optical characterization and kinetic modelling details. See DOI: 10.1039/c5sc03535j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |